Abstract
The voltage-controlled magnetic anisotropy (VCMA) effect, which manifests itself as variation of anisotropy of a thin layer of a conductive ferromagnet on a dielectric substrate under the influence of an external electric voltage, can be used for the development of novel information storage and signal processing devices with low power consumption. Here it is demonstrated by micromagnetic simulations that the application of a microwave voltage to a nanosized VCMA gate in an ultrathin ferromagnetic nanowire results in the parametric excitation of a propagating spin wave, which could serve as a carrier of information. The frequency of the excited spin wave is twice smaller than the frequency of the applied voltage while its amplitude is limited by 2 mechanisms: (i) the so-called “phase mechanism” described by the Zakharov-L’vov-Starobinets “S-theory” and (ii) the saturation mechanism associated with the nonlinear frequency shift of the excited spin wave. The developed extension of the “S-theory”, which takes into account the second limitation mechanism, allowed us to estimate theoretically the efficiency of the parametric excitation of spin waves by the VCMA effect.
Similar content being viewed by others
Introduction
Electric field control of magnetization in ferromagnets attracts a lot of attention of researchers in magnetism as it makes possible the development of novel magnetic recording and signal processing devices having low power consumption and compatible with standard CMOS technology. The electric field control could be realized using different magnetoelectric effects (see, e.g. review refs 1 and 2), among which of a particular interest is the recently discovered effect of the voltage-controlled magnetic anisotropy (VCMA)3,4,5. The VCMA effect manifests itself as a variation of the perpendicular magnetic anisotropy at the interface between a ferromagnetic metal and an insulator under the application of an interface voltage. This effect has many attractive features, including linearity (variation of the anisotropy energy is directly proportional to the applied voltage)4,6, absence of a hysteresis7,8, possibility of relatively large variations of the anisotropy field9,10 and practical absence of inertia (at least, in the gigahertz frequency range)11,12. These features make VCMA promising for various practical applications. In particular, the VCMA effect has been already proposed for use in magnetic recording13,14,15, control of motion of domain walls16,17,18 and skyrmions19 and for excitation of a ferromagnetic resonance11,12,20.
Recently, we have demonstrated analytically21 that by applying to a ferromagnetic metal - insulator interface a microwave voltage of a frequency ωp = 2πfp and a sufficient magnitude, it is possible to overcome the threshold of parametric excitation of half-frequency (ωSW = ωp/2) short spin waves (SWs) in ferromagnetic nanowires (at the same time, the linear excitation of SWs by VCMA, when ωSW = ωp, in a zero bias magnetic field is not possible12,21,22). This means that the VCMA effect could be promising for excitation of propagating SWs in unbiased nanosized magnetic waveguides, where these SWs can be used for microwave signal processing.
It should be noted, however, that overcoming the parametric excitation threshold does not guarantee a stable excitation of propagating SWs. In the externally driven parametric process the excitation of monochromatic half-frequency propagating SWs could be hindered by many connected parasitic nonlinear phenomena, such as modulational instability, auto-oscillations and even developed turbulence of parametrically excited SWs23. The exact manifestation of these nonlinear phenomena depends on the strength of the microwave driving signal, SW spectrum of a magnetic sample and peculiarities of the parametric interaction between the driving signal and parametric SWs in a given sample geometry.
The conditions necessary for a stable parametric excitation of SWs were studied in details for two- and three-dimensional geometry in the case of spatially uniform parametric pumping in the framework of the so-called L’vov-Zakharov-Starobinets “S-theory”23,24,25. The “S-theory” shows that the amplitudes of the excited SWs are limited by the “phase mechanism”23, which is the disappearance of the phase correlation between the pumping signal and the excited SWs due to the nonlinear interaction between the SWs. The “S-theory” allows one to calculate the SW amplitudes, thus providing a theoretical estimate for the parametric excitation efficiency. Unfortunately, the conclusions of the conventional “S-theory”23 cannot be directly translated to our case of VCMA-induced parametric excitation of SWs, where the ferromagnetic sample has to be quasi-one-dimensional (nanowire) in order to guarantee a definite direction of the SW propagation21 and the microwave parametric pumping is localized in the region of the VCMA gate electrode.
In our current work we study the peculiarities of the parametric excitation of SWs at a VCMA interface using the micromagnetic simulations. As it is shown below, in a real nanowire geometry the achievable magnitudes of the electric field of the microwave parametric pumping could reach the magnitudes that not only are above the threshold of parametric excitation, but are sufficient to sustain a stable generation of SWs propagating far away from the region of pumping localization and having narrow frequency linewidth. The comparison of our simulation results with the analytical results obtained using the modified “S-theory” demonstrates that in one-dimensional nanoscale ferromagnets the amplitudes of the parametrically excited SWs are limited not only by the classical “phase mechanism” (characteristic for the “S-theory” in bulk ferromagnets23), but, also, by an additional limiting mechanism caused by the dependence of the SW group velocity on the SW amplitude, which appears due to a non-zero nonlinear SW frequency shift.
Results
Micromagnetic simulations
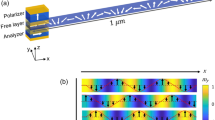
A sketch of a particular SW waveguide geometry used in our micromagnetic simulations is shown in Fig. 1. We consider a nanowire waveguide of the thickness h and width wy made from a conductive ferromagnetic material and grown on a thin MgO dielectric layer. Note, that since VCMA is a purely interface effect4,5,8, the nanowire should be ultrathin (h ~ l nm), and, owing to the perpendicular growth anisotropy, ultrathin magnetic nanowires and films in a zero bias magnetic field, typically, exist in the static magnetic state in which the film magnetization is directed out-of-plane26,27. This magnetic configuration will be considered below.
On top of the nanowire there is a conductive excitation (or input) gate, which creates a microwave electric field E at the VCMA dielectric-ferromagnetic interface. This electric field drives microwave oscillation of the perpendicular interface anisotropy  (where β is the magnetoelectric coefficient). The input gate covers only a part of the length Lg of the nanowire waveguide. In such a geometry the SWs excited at the input gate could propagate outside the input gate region, where they could be influenced by other gates performing signal processing functions and, eventually, received by an output gate.
(where β is the magnetoelectric coefficient). The input gate covers only a part of the length Lg of the nanowire waveguide. In such a geometry the SWs excited at the input gate could propagate outside the input gate region, where they could be influenced by other gates performing signal processing functions and, eventually, received by an output gate.
First, we performed the simulations for a CoFeB nanowire of the thickness h = 0.8 nm, width wy = 20 nm with a gate length of Lg = 40 nm (see Methods). It is known21, that in a narrow nanowire waveguide the excitation threshold is lower than in a wider waveguides, and, therefore, the SW parametric excitation efficiency should be higher. The magnitude of the microwave anisotropy field was fixed at ΔBa = 50 mT, which corresponds to the experimentally reachable magnitude of the electric field E = 0.78 V/nm ( )12, while the frequency fp of this field was varied.
)12, while the frequency fp of this field was varied.
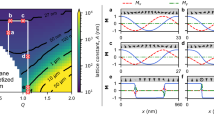
In our simulations the in-plane components of the variable nanowire magnetization (normalized by the static magnetization Ms) were calculated under the center of the excitation gate as functions of the pumping frequency fp. These curves are shown in Fig. 2(a). It is clear that in the range fp ∈ [4.73, 4.86] GHz the amplitude of the excited magnetization precession significantly exceeds the thermal fluctuation level. The difference between the x and y components of the variable magnetization, i.e. nonzero precession ellipticity, naturally appears due to the in-plane shape anisotropy of the nanowire and this ellipticity remains almost constant within frequency range of parametric excitation. Frequency spectrum of the excited magnetization precession contains one dominant peak (Fig. 2(b)), the maximum of which is located exactly at the half of the pumping frequency fp (Fig. 2(d)). This means that the microwave voltage applied to the excitation gate leads to the parametric excitation of SWs. Note, that the frequency distribution of excited SWs is very narrow–its width (half width at half maximum, HWHM) is equal to 9–13 MHz. This is several times smaller than in the case of SWs of the same frequency excited linearly (i.e. by the in-plane microwave field), when  . When the amplitude of the magnetization oscillations becomes larger, smaller additional peaks appear in the frequency spectrum (see curve for fp = 4.73 GHz in Fig. 2(b)). However, even in that case of higher amplitude of the excited SWs the parametric excitation process remains stable, which is confirmed by the existence of only one dominant peak in the frequency spectrum of the excited SWs.
. When the amplitude of the magnetization oscillations becomes larger, smaller additional peaks appear in the frequency spectrum (see curve for fp = 4.73 GHz in Fig. 2(b)). However, even in that case of higher amplitude of the excited SWs the parametric excitation process remains stable, which is confirmed by the existence of only one dominant peak in the frequency spectrum of the excited SWs.
Amplitude and frequency of the excited spin waves.
Normalized in-plane components  of the variable nanowire magnetization under the center of the excitation gate as functions of the pumping frequency for ΔΒa = 50 mT, wire width wy = 20 nm and gate length Lg = 40 nm (a) and mx as a function of the pumping amplitude ΔΒa at fp = 4.8 GHz (c): symbols - micromagnetic simulations, lines - analytical theory. The frequency spectra of the micromagnetically calculated magnetization precession under the gate region and the position of their maximums as a function of the pumping frequency fp are presented in the frames (b,d), respectively.
of the variable nanowire magnetization under the center of the excitation gate as functions of the pumping frequency for ΔΒa = 50 mT, wire width wy = 20 nm and gate length Lg = 40 nm (a) and mx as a function of the pumping amplitude ΔΒa at fp = 4.8 GHz (c): symbols - micromagnetic simulations, lines - analytical theory. The frequency spectra of the micromagnetically calculated magnetization precession under the gate region and the position of their maximums as a function of the pumping frequency fp are presented in the frames (b,d), respectively.
For a fixed pumping frequency the SW are excited, as expected, only above a certain threshold pumping magnitude ΔΒth and above this threshold the SW amplitude increases monotonically (Fig. 2(c)). The threshold depends on the excitation frequency, mainly due to the frequency dependence of the SW group velocity (see Eq. (2)). In particular, the parametric excitation is absent for fp > 4.86 GHz because at higher frequencies the threshold becomes larger then the applied pumping amplitude ΔΒa = 50 mT. At the pumping frequencies below 4.73 GHz the parametric excitation is also absent, but for a different reason. For fp < 4.73 GHz half of the pumping frequency lies below the bottom of the SW spectrum in the nanowire and, therefore no propagating SW can be excited parametrically in this frequency range at all.
However, when the pumping frequency is larger than fp > 4.73 GHz, the pumping excites propagating SWs moving along the nanowire in both directions from the excitation gate. This is clearly illustrated by Fig. 3 where three instantaneous magnetization distributions in the nanowire, corresponding to three moments separated by a quarter of a period of the magnetization precession, are presented. It is clear that the maximum of the precession amplitude moves away from the gate region and propagates for a distance that is significantly larger than the gate length. The wave number of the excited SWs depends on the excitation frequency–in the considered geometry of a nanowire with perpendicular static magnetization a higher pumping frequency fp corresponds to a higher SW wave number k. The shortest SW excited in the considered case at fp = 4.86 GHz has the wave number k ≈ 8 μm−1. The determination of the SW wave number for fp = 4.73 GHz is complicated, since the SW propagation length is comparable to the SW wavelength, so that the propagation maxima and minima of the dynamical magnetization are not clearly distinguishable. However, it should be noted, that, rather unexpectedly, even for this lowest excitation frequency, that should correspond to the excitation of a ferromagnetic resonance21, the propagation of SWs having a non-zero wave vector is seen (Fig. 3(a)). This unexpected feature will be explained below.
Spin wave profiles.
Micromagnetic snapshots of the distributions of variable magnetization in a nanowire near the pumping gate at the moments separated by a time intervals equal to the quarter of the magnetization precession period. A part of the nanowire waveguide of the length equal to 1 μm is shown around the pumping gate, which is indicated by a black rectangle. The pumping frequency is fp = 4.73 GHz (a) and fp = 4.8 GHz (b), while the pumping amplitude is ΔBa = 50 mT.
Note also, that, as always for the parametric excitation in a continuous media, SW wave number depends only on the pumping frequency and, due to the nonlinear frequency shift, on the pumping amplitude (see below), but not on the length of the excitation gate Lg. The propagation length lp = v/Γ of the excited SWs depends on their wave number–it increases with k, since the SW group velocity v increases with k faster than the SW damping rate Γ (until  , where ω0 is the ferromagnetic resonance frequency. Otherwise the opposite relation takes place).
, where ω0 is the ferromagnetic resonance frequency. Otherwise the opposite relation takes place).
From Fig. 3 one can also see that the excited SWs are uniform across the nanowire width. This is absolutely natural, since for such a narrow nanowire all the SW modes that are nonuniform across the nanowire width have much higher frequencies fSW, which simply don’t satisfy the parametric resonance condition fSW = fp/2. For much wider nanowires (hundreds of nanometers in width) the resonant condition could be satisfied for several SW modes having different profiles across the nanowire width. In this case the parametric pumping could excite a nonuniform mode–this depends on the interplay between the SW radiation losses and the coupling with pumping (e.g. see an example in ref. 28).
Theory
In order to find an explanation to the features of the SW excitation process seen in the numerical modeling and to derive an approximate analytical expression for the SW excitation efficiency we developed a theoretical model presented below. We start from the system of modified Bloembergen equations describing the process of parametric excitation of SWs29,30:

which describes the temporal and spatial evolution of the envelope amplitudes a1 and a2 of the excited SWs having the carrier wave vectors k and (−k) and frequency ωk = ωp/2, respectively (the second equation of the system could be obtained by the replacement a1,2 → a2,1 and v → (−v)). Here v and Γ are the SW group velocity and damping rate (which includes both natural damping and nonuniform resonance line broadening due to technological imperfections),  is the Fourier image of the microwave anisotropy field,
is the Fourier image of the microwave anisotropy field,  is the efficiency of the parametric interaction, where
is the efficiency of the parametric interaction, where  is the Fourier transform of the coordinate-dependent demagnetization tensor21. Characteristics of SWs having the carrier wave vectors k and (−k) are the same, since SW spectrum in the considered perpendicularly magnetized nanowire is reciprocal. Equation (1) contains the so-called nonadiabatic pumping term
is the Fourier transform of the coordinate-dependent demagnetization tensor21. Characteristics of SWs having the carrier wave vectors k and (−k) are the same, since SW spectrum in the considered perpendicularly magnetized nanowire is reciprocal. Equation (1) contains the so-called nonadiabatic pumping term  31 which should be taken into account since the SW wavelength is greater than the pumping localization length.
31 which should be taken into account since the SW wavelength is greater than the pumping localization length.
We also take into account the nonlinear frequency shift T caused by the SW “self-interaction” and the nonlinear 4-wave (4-magnon) interaction between the parametrically excited “pairs” of SWs having wave vectors k and (−k), which is described by the Hamiltonian  , where ck is the SW amplitude (see “S-theory” in ref. 23). Note, that in bulk samples this 4-magnon interaction between the SW “pairs” is the only important mechanism limiting (or determining) the amplitudes of the parametrically excited SWs. All the other nonlinear interaction processes between the SWs could be disregarded, as in the traditional “S-theory” for bulk magnetic samples (see ref. 23). The validity of this approximation will be confirmed from the comparison between the analytical results of the above presented model and the results of the micromagnetic simulations. The magnitudes of the nonlinear coefficients in the model could be evaluated using the formalism of ref. 32 (see Methods). In the range of relatively long SWs (
, where ck is the SW amplitude (see “S-theory” in ref. 23). Note, that in bulk samples this 4-magnon interaction between the SW “pairs” is the only important mechanism limiting (or determining) the amplitudes of the parametrically excited SWs. All the other nonlinear interaction processes between the SWs could be disregarded, as in the traditional “S-theory” for bulk magnetic samples (see ref. 23). The validity of this approximation will be confirmed from the comparison between the analytical results of the above presented model and the results of the micromagnetic simulations. The magnitudes of the nonlinear coefficients in the model could be evaluated using the formalism of ref. 32 (see Methods). In the range of relatively long SWs ( ) both nonlinear coefficients could be approximately evaluated as
) both nonlinear coefficients could be approximately evaluated as  , where Bint is the modulus of the static internal field in the nanowire.
, where Bint is the modulus of the static internal field in the nanowire.
The threshold of the parametric excitation of SWs could be calculated from Eq. (1) in the linear approximation, setting T = S = 0. Following the method from ref. 30 one can obtain an implicit equation determining the parametric excitation threshold:

In the limiting case of a small gate length Γ ≪ v/Lg one could obtain from Eq. (2) a well-known31 explicit expression  , where
, where  is the measure of the pumping “nonadiabaticity”; in our case of rectangular pumping profile
is the measure of the pumping “nonadiabaticity”; in our case of rectangular pumping profile  . From this expression it is clear that the threshold becomes higher with the increase of the radiation losses Γrad = v/Lg. Since the SW group velocity v is higher for shorter SWs having higher eigenfrequencies, it is clear that the frequency range of the parametric excitation is larger for a larger gate size Lg at a fixed pumping amplitude and, naturally, this range increases with the increase of the pumping amplitude bp. In principle, at a very high bp the nonlinear processes other than those considered here could take place and could change this tendency. However, this issue lies beyond the scope of our current work.
. From this expression it is clear that the threshold becomes higher with the increase of the radiation losses Γrad = v/Lg. Since the SW group velocity v is higher for shorter SWs having higher eigenfrequencies, it is clear that the frequency range of the parametric excitation is larger for a larger gate size Lg at a fixed pumping amplitude and, naturally, this range increases with the increase of the pumping amplitude bp. In principle, at a very high bp the nonlinear processes other than those considered here could take place and could change this tendency. However, this issue lies beyond the scope of our current work.
To calculate the amplitudes of the parametrically excited SWs one needs to find stationary solutions of the system Eq. (1). Note, that at this stage the nonlinear frequency shift T could be disregarded, since the SW spectrum is continuous and with the increase of the SW amplitude the SW wave vector changes in such a way, that the resonance condition ωp = 2ωk(|a|) is satisfied. This process, which in not described by the system Eq. (1), will be explicitly discussed below.
The analytical solution of the system Eq. (1) could be found only in the simplest case, when the parametric pumping is spatially uniform and covers all the magnetic film23,30, while in the general case this system allows only a numerical solution. The analysis of the numerical solutions of Eq. (1) has shown that the amplitude of the parametrically excited SW could be estimated with reasonable accuracy using the following approximate expression:

This approximate expression differs from the exact analytical one, obtained for the case of a spatially uniform pumping, only by the presence of the coefficient C. Here  is the maximum value of the SW envelope amplitude in the nanowire, which commonly occurs at the boundary of the pumping area (left and right boundaries for a1 and a2, respectively). Thus, it is the maximum amplitude of a SW propagating from the area of pumping localization. The coefficient C increases from 1 up to C ~ 2 when the radiation losses Γrad = v/Lg (existing due to the finite pumping localization and finite SW group velocity) increase in comparison with the intrinsic SW damping Γ. Our simulations showed also that the dependence of the coefficient C on the degree of nonadiabaticity α is sufficiently weak to be neglected.
is the maximum value of the SW envelope amplitude in the nanowire, which commonly occurs at the boundary of the pumping area (left and right boundaries for a1 and a2, respectively). Thus, it is the maximum amplitude of a SW propagating from the area of pumping localization. The coefficient C increases from 1 up to C ~ 2 when the radiation losses Γrad = v/Lg (existing due to the finite pumping localization and finite SW group velocity) increase in comparison with the intrinsic SW damping Γ. Our simulations showed also that the dependence of the coefficient C on the degree of nonadiabaticity α is sufficiently weak to be neglected.
The appearance of the coefficient C in Eq. (3) is related to the spatial localization of the parametric pumping under the gate of the length Lg. In the case of a spatially localized pumping the spatial profiles of the parametrically excited spin waves become nonuniform. Namely, for weakly localized pumping, when ΓLg/v ≫ 1, SW profiles ai(x) are almost uniform within the pumping region except small regions near the pumping area boundaries. When the pumping becomes more localized (the ratio ΓLg/v decreases), these boundary regions occupy larger relative area and finally, for a sufficiently localized pumping, there are no regions with constant SW profiles at all. Nonuniform SW profiles affect both the values of the excitation (V) terms and nonlinear (S) terms in the right-hand-side part of Eq. (1), an interplay of which determines the excited SW amplitude. For a more localized pumping, when the region where  becomes larger, both pumping and nonlinear terms decrease, but the nonlinear S-term decreases faster since it contains three spin wave mode amplitudes contrary to one SW amplitude in the V-term. Consequently, the resulting maximal spin wave mode amplitude amax increases when the pumping becomes more spatially localized (for a fixed value of the numerator in Eq. (3)). This effect is taken into account by the coefficient C which increases from 1 to roughly 2 with the decrease of the ratio ΓLg/v, as was found from numerical simulations of Eq. (1). Note, that this does not mean that a decrease of the gate length Lg leads to an increase of excited SW amplitudes at given pumping, because the threshold
becomes larger, both pumping and nonlinear terms decrease, but the nonlinear S-term decreases faster since it contains three spin wave mode amplitudes contrary to one SW amplitude in the V-term. Consequently, the resulting maximal spin wave mode amplitude amax increases when the pumping becomes more spatially localized (for a fixed value of the numerator in Eq. (3)). This effect is taken into account by the coefficient C which increases from 1 to roughly 2 with the decrease of the ratio ΓLg/v, as was found from numerical simulations of Eq. (1). Note, that this does not mean that a decrease of the gate length Lg leads to an increase of excited SW amplitudes at given pumping, because the threshold  , which also determines excited SW amplitudes (Eq. (3)), becomes larger for a more localized pumping, as described by Eq. (2) and the increase of the threshold is significantly greater than the variation of the coefficient C.
, which also determines excited SW amplitudes (Eq. (3)), becomes larger for a more localized pumping, as described by Eq. (2) and the increase of the threshold is significantly greater than the variation of the coefficient C.
Let us now discuss the effect of the nonlinear frequency shift (described by the coefficient T) on the process of parametric excitation of SWs. As it was pointed earlier, this frequency shift leads to the change of the SW wave vector with the increase of the SW amplitude. If all the parameters in Eq. (1) are only weakly dependent on the SW wave vector, one can simply neglect the nonlinear shift in Eq. (1) and use the approximate Eq. (3) for evaluation of amplitudes of the excited SWs. In our case, however, this assumption is not correct. Although the parameters V, Γ and S are weak functions of the SW wave vector, the SW group velocity v changes significantly with the wave vector k variation. Note also, that the nonlinear frequency shift coefficient in our case is negative, T < 0, that is related to the perpendicular anisotropy of magnetic nanowire. Thus, with the increase of the SW amplitude the SW spectrum shifts down and the half of the pumping frequency will now correspond to a higher SW wave vector and, therefore, to a higher value of the SW group velocity. Thus, with the increase of the SW amplitude the radiation losses increase, which leads to the additional limitation of the amplitude of the excited SWs.
To account for this effect rigorously, one needs to insert the dependence v = f(k(|a|)) into Eqs (2, 3) and to obtain a complex implicit equation for the excited SW amplitudes. On the other hand, to obtain an approximate analytical solution one can use an approximate dispersion relation for SWs in an ultrathin nanowire in the form:  and obtain a simple approximate expression for the SW group velocity in the form:
and obtain a simple approximate expression for the SW group velocity in the form:  . Here ω0 is the frequency of ferromagnetic resonance and
. Here ω0 is the frequency of ferromagnetic resonance and  for k ≪ 1/λex (see expression for Ak, Eq. (9), in the Methods section). The parametric excitation threshold Eq. (2) can be expressed as23
for k ≪ 1/λex (see expression for Ak, Eq. (9), in the Methods section). The parametric excitation threshold Eq. (2) can be expressed as23  , where
, where  . In our case of a highly nonadiabatic pumping and relatively high radiation losses the coefficient Cv is equal to Cv ≈ 1. Combining these expressions and taking into account the amplitude dependence of the SW frequency
. In our case of a highly nonadiabatic pumping and relatively high radiation losses the coefficient Cv is equal to Cv ≈ 1. Combining these expressions and taking into account the amplitude dependence of the SW frequency  we find that the increase of the SW amplitude leads to the following increase of the total SW losses in the system:
we find that the increase of the SW amplitude leads to the following increase of the total SW losses in the system:  . Solving now Eq. (3) taking into account the explicit power dependence of the SW losses, we finally get
. Solving now Eq. (3) taking into account the explicit power dependence of the SW losses, we finally get

where  . It should be noted, that for a relatively large nonlinear frequency shift
. It should be noted, that for a relatively large nonlinear frequency shift  , that is realized in our geometry, the resulting SW amplitude, given by Eq. (4), very weakly depends on the value of the coefficient C, which cannot be found analytically. Thus, in our case we can simply use C = 2, as for the case of a high radiation losses.
, that is realized in our geometry, the resulting SW amplitude, given by Eq. (4), very weakly depends on the value of the coefficient C, which cannot be found analytically. Thus, in our case we can simply use C = 2, as for the case of a high radiation losses.
Using Eq. (4) we can describe the frequency dependence of the excited SW amplitudes, obtained from the micromagnetic simulations. The quantity calculated from the micromagnetic simulations is the sum of the partial SWs amplitudes at the center of the excitation gate,  . This quantity can be expressed as
. This quantity can be expressed as  , where the coefficient
, where the coefficient  . The value C∑ = 2 corresponds to low radiation losses, when the amplitudes of the forward- and backward-propagating parametrically excited SWs are almost constant within the pumping region. With the increase of the SW group velocity (and, therefore, with the increase of the radiation losses) the value of the coefficient C∑ decreases. The relation between envelope amplitude A∑ and the real magnetization amplitude Mx,y are given by23,32
. The value C∑ = 2 corresponds to low radiation losses, when the amplitudes of the forward- and backward-propagating parametrically excited SWs are almost constant within the pumping region. With the increase of the SW group velocity (and, therefore, with the increase of the radiation losses) the value of the coefficient C∑ decreases. The relation between envelope amplitude A∑ and the real magnetization amplitude Mx,y are given by23,32

where

and Ak, Bk are the coefficients of the Holstein-Primakoff transformation (see Eqs (9 and 10) in the Methods section).
The resulting analytical expression for the frequency dependence of the amplitude (mx) of the parametrically excited SWs gives a good quantitative description of the results of our micromagnetic simulations for C∑ = 1.7 (see Fig. 2(a,c)). Note, that C∑ is the only fitting parameter used, as all the other quantities were calculated from the nanowire geometry and the material parameters. Note also, that if we neglect the effect of the nonlinear frequency shift and use Eq. (3) instead of Eq. (4) the analytically calculated SW amplitudes will be significantly overestimated. Thus, the change of the SW group velocity due to the nonlinear adjustment of the SW wave vector is critically important in the process of parametric excitation of SWs in magnetic nanowires. Also, it is due to this adjustment that we see the propagating SW profiles at the lowest excitation frequency (Fig. 3). The standing ferromagnetic resonance at this frequency could be excited only when the pumping amplitude (and, therefore, the amplitude of the excited variable magnetization) is sufficiently low to produce any evident nonlinear shift of the SW wave vector.
In order to verify the developed analytical theory we performed micromagnetic simulations for a different width of the nanowire (50 nm) and a different gate length (100 nm), setting also the anisotropy constant to  . This change did not lead to any qualitative difference in the micromagnetic results and we observed SW excitation in the frequency range fp ∈ [3.3, 3.57] GHz, which corresponds to the following wave number range of the excited SWs: k ≤ 11 μm−1. The developed analytical theory gave a good quantitative description of the micromagnetic results for C∑ = 1.9 (see Fig. 4). The higher value of the coefficient C∑ for this case then for the first studied geometry (C∑ = 1.7) is natural, since in this case the radiation loses Γrad = v/Lg are smaller due to larger length Lg of the pumping area.
. This change did not lead to any qualitative difference in the micromagnetic results and we observed SW excitation in the frequency range fp ∈ [3.3, 3.57] GHz, which corresponds to the following wave number range of the excited SWs: k ≤ 11 μm−1. The developed analytical theory gave a good quantitative description of the micromagnetic results for C∑ = 1.9 (see Fig. 4). The higher value of the coefficient C∑ for this case then for the first studied geometry (C∑ = 1.7) is natural, since in this case the radiation loses Γrad = v/Lg are smaller due to larger length Lg of the pumping area.
Amplitude of excited spin waves.
Normalized in-plane components mx,y = Mx,y/Ms of the variable nanowire magnetization under the center of the excitation gate as functions of the pumping frequency for ΔBa = 50 mT, wire width wy = 50 nm and gate length Lg = 100 nm. Symbols - micromagnetic simulations, lines - analytical theory.
Finally, let us discuss the issue of stability of the SW parametric excitation. As it follows from the results presented above, the only important nonlinear interactions between the excited SWs are the 4-wave processes responsible for “self-action” (described by the nonlinear coefficient T) and the processes of the interaction between the SW “pairs” (described by the nonlinear coefficient S). All the other 4-wave scattering processes, which could lead to the SW instability, are weak due to quasi-one-dimensional character of our system (nanowire) and the monotonic character of the of the SW spectrum of the nanowire. The 3-wave processes in our geometry have zero efficiency at all as long as the static magnetization is aligned with one of the symmetry axis of nanowire32. The 2-magnon scattering processes, which could take place due to the defects present in a nanowire, in the studied case of ultrathin magnetic nanowires should be weak, since the characteristic size of the possible defects in the nanowire material (nm) is substantially smaller than the characteristic SW wavelength (100 nm and more). Finally, the non-adiabatic character of the applied parametric pumping fixes not only the sum of phases of the excited SWs, but also the difference of these phases31, which makes the SW excitation process stable with respect to the appearance of magnetization auto-oscillations23.
Discussion
In this work it has been demonstrated that a local microwave variation of the magnetic anisotropy caused by the application of a microwave electric field could excite propagating SWs in an ultrathin ferromagnetic nanowire via the parametric excitation mechanism. The excited SWs could propagate for distances that are large compared to the size of the excitation gate, could have relatively large amplitudes and narrower spectral linewidth comparing to linearly excited SWs. These properties are very desirable for applications of the excites SWs in the nanoscale microwave signal processing devices. It is confirmed that, similar the case of a spatially uniform parametric pumping, the amplitudes of the excited SWs are limited by the “phase mechanism” resulting from 4-wave interaction between the excited SW “pairs”. However, in the case of a spatially localized parametric pumping in a magnetic nanowire due to a significant dependence of the SW group velocity on the wave vector a nonlinear shift of the SW frequency should be taken into account to obtain a correct estimation of the amplitude of the excites SW.
Methods
Micromagnetic simulations
Our micromagnetic simulations were performed using the parallel micromagnetic solver GPMagnet33,34. The length of the nanowire L = 2 μm was chosen to be sufficiently large to avoid the possible reflections from the far edges of the waveguide. The gate region of the length Lg was placed at the nanowire center. The material parameters of the ferromagnetic waveguide used in our simulations were: saturation magnetization Ms = 1.6 × 106 A/m, exchange constant Aex = 2.0 × 10−11 J/m, out-of-plane anisotropy constant K⊥ = 1.55 × 106 J/m3 and Gilbert damping constant αG = 0.01, that corresponds to the typical parameters of CoFeB. Within the excitation gate region the anisotropy field was considered to be time varying:  , where
, where  is the static part, whereas fp and ΔΒa are the frequency and the amplitude of the microwave-frequency anisotropy field, respectively. Thermal fluctuations corresponding to the temperature T = 1 K were taken into account.
is the static part, whereas fp and ΔΒa are the frequency and the amplitude of the microwave-frequency anisotropy field, respectively. Thermal fluctuations corresponding to the temperature T = 1 K were taken into account.
Calculation of nonlinear coefficients
A general way to calculate the coefficients of nonlinear SW interaction in ferromagnetic films is presented in ref. 32. In the notation of ref. 32 the coefficients T and S are the 4-magnon scattering coefficients T ≡ Wkk,kk and  . Since the tensor
. Since the tensor  is diagonal (in coordinate system shown in Fig. 1) all 3-magnon processes have zero efficiency until static magnetization is aligned with one of the symmetry axis of nanowire, so one doesn’t need take into account the renormalization of 4-magnon coefficients due to nonresonant 3-magnon processes. Noting this one can obtain following expressions for the nonlinear coefficients in the case of zero external magnetic field
is diagonal (in coordinate system shown in Fig. 1) all 3-magnon processes have zero efficiency until static magnetization is aligned with one of the symmetry axis of nanowire, so one doesn’t need take into account the renormalization of 4-magnon coefficients due to nonresonant 3-magnon processes. Noting this one can obtain following expressions for the nonlinear coefficients in the case of zero external magnetic field


where


 is the SW eigenfrequency, λex is the material exchange length and
is the SW eigenfrequency, λex is the material exchange length and  is the static internal field in nanowire. In the range of relatively long SWs (
is the static internal field in nanowire. In the range of relatively long SWs ( ) the above expressions reduce to
) the above expressions reduce to  .
.
Additional Information
How to cite this article: Verba, R. et al. Excitation of propagating spin waves in ferromagnetic nanowires by microwave voltage-controlled magnetic anisotropy. Sci. Rep. 6, 25018; doi: 10.1038/srep25018 (2016).
References
Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D: Appl. Phys. 38, R123 (2005).
Tong, W.-Y., Fang, Y.-W., Cai, J., Gong, Y.-W. & Duan, C.-G. Theoretical studies of all-electric spintronics utilizing multiferroic and magnetoelectric materials. Comput. Mater. Sci. 112, part B, 467 (2015).
Weisheit, M. et al. Electric field-induced modification of magnetism in thin-film ferromagnets. Science 315, 349 (2007).
Duan, C.-G. et al. Surface magnetoelectric effect in ferromagnetic metal films. Phys. Rev. Lett. 101, 137201 (2008).
Endo, M., Kanai, S., Ikeda, S., Matsukura, F. & Ohno, H. Electric-field effects on thickness dependent magnetic anisotropy of sputtered MgO/Co40Fe40B20/Ta structures. Appl. Phys. Lett. 96, 212503 (2010).
Tsujikawa, M. & Oda, T. Finite electric field effects in the large perpendicular magnetic anisotropy surface Pt/Fe/Pt(001): A first-principles study. Phys. Rev. Lett. 102, 247203 (2009).
Ha, S.-S. et al. Voltage induced magnetic anisotropy change in ultrathin Fe80Co20/MgO junctions with Brillouin light scattering. Appl. Phys. Lett. 96, 142512 (2010).
Shiota, Y. et al. Quantitative evaluation of voltage-induced magnetic anisotropy change by magnetoresistance measurement. Appl. Phys. Express 4, 043005 (2011).
Maruyama, T. et al. Large voltage-induced magnetic anisotropy change in a few atomic layers of iron. Nat. Nanotech. 4, 158 (2009).
Nakamura, K. et al. Giant modification of the magnetocrystalline anisotropy in transition-metal monolayers by an external electric field. Phys. Rev. Lett. 102, 187201 (2009).
Nozaki, T. et al. Electric-field-induced ferromagnetic resonance excitation in an ultrathin ferromagnetic metal layer. Nat. Phys. 8, 491 (2012).
Zhu, J. et al. Voltage-induced ferromagnetic resonance in magnetic tunnel junctions. Phys. Rev. Lett. 108, 197203 (2012).
Shiota, Y. et al. Induction of coherent magnetization switching in a few atomic layers of FeCo using voltage pulses. Nat. Mater. 11, 39 (2012).
Wang, W.-G., Li, M., Hageman, S. & Chien, C. L. Electric-field-assisted switching in magnetic tunnel junctions. Nat. Mater. 11, 64 (2012).
Nozaki, T. et al. Magnetization switching assisted by high-frequency-voltage-induced ferromagnetic resonance. Appl. Phys. Express 7, 073002 (2014).
Schellekens, A., Van den Brink, A., Franken, J. & Swagten, H. J. M. amd Koopmans, B. Electric-field control of domain wall motion in perpendicularly magnetized materials. Nat. Commun. 3, 847 (2012).
Bauer, U., Emori, S. & Beach, G. S. D. Voltage-gated modulation of domain wall creep dynamics in an ultrathin metallic ferromagnet. Appl. Phys. Lett. 101, 172403 (2012).
Bernand-Mantel, A. et al. Electric-field control of domain wall nucleation and pinning in a metallic ferromagnet. Appl. Phys. Lett. 102, 122406 (2013).
Zhang, X., Zhou, Y., Ezawa, M., Zhao, G. P. & Zhao, W. Magnetic skyrmion transistor: skyrmion motion in a voltage-gated nanotrack. Sci. Rep. 5, 11369 (2015).
Shiota, Y. et al. High-output microwave detector using voltage-induced ferromagnetic resonance. Appl. Phys. Lett. 105, 192408 (2014).
Verba, R., Tiberkevich, V., Krivorotov, I. & Slavin, A. Parametric excitation of spin waves by voltage-controlled magnetic anisotropy. Phys. Rev. Applied 1, 044006 (2014).
Verba, R., Tyberkevych, V. & Slavin, A. Excitation of propagating spin waves in an in-plane magnetized ferromagnetic strip by voltage-controlled magnetic anisotropy. in Magnetics Conference (INTERMAG) 2015, IEEE, doi:10.1109/INTMAG.2015.7157010.
L’vov, V. S. Wave Turbulence Under Parametric Excitation (Springer-Verlag, New York, 1994).
Zautkin, V. V., Zakharov, V. E., L’vov, V. S., Musher, S. L. & Starobinets, S. S. Parallel spin-wave pumping in yttrium garnet single crystals. Sov. Phys. JETP 62, 1782 (1972).
Zakharov, V., L’vov, V. & Starobinets, S. Spin-wave turbulence beyond the parametric excitation threshold. Sov. Phys. Usp. 18, 896 (1975).
Heinrich, B. & Cochran, J. F. Ultrathin metallic magnetic films: magnetic anisotropies and exchange interactions. Adv. in Phys. 42, 523 (1993).
Yang, H. X. et al. First-principles investigation of the very large perpendicular magnetic anisotropy at Fe|MgO and Co|MgO interfaces. Phys. Rev. B 84, 054401 (2011).
Brächer, T. et al. Mode selective parametric excitation of spin waves in a Ni81Fe19 microstripe. Appl. Phys. Lett. 99, 162501 (2011).
Bloembergen, N. Nonlinear optics (Addison-Wesley Pub. Co., 1965).
Kalinikos, B. A. & Kostylev, M. P. Parametric amplification of spin wave envelope solitons in ferromagnetic films by parallel pumping. IEEE Trans. Mag. 33, 3445 (1997).
Melkov, G. A., Serga, A. A., Tiberkevich, V. S., Kobljanskij, Y. V. & Slavin, A. N. Nonadiabatic interaction of a propagating wave packet with localized parametric pumping. Phys. Rev. E 63, 066607 (2001).
Krivosik, P. & Patton, C. E. Hamiltonian formulation of nonlinear spin-wave dynamics: Theory and applications. Phys. Rev. B 82, 184428 (2010).
Lopez-Diaz, L. et al. Micromagnetic simulations using graphics processing units. J. Phys. D: Appl. Phys. 45, 323001 (2012).
Giordano, A., Finocchio, G., Torres, L., Carpentieri, M. & Azzerboni, B. Semi-implicit integration scheme for Landau–Lifshitz–Gilbert-Slonczewski equation. J. Appl. Phys. 111, 07D112 (2012).
Acknowledgements
We acknowledge the Center for NanoFerroic Devices (CNFD) and the Nanoelectronics Research Initiative(NRI) for the partial support of this work. The work was also supported in part by the National Science Foundation of the USA (grants Nos. ECCS-1305586, DMR-1015175), by the MTO/MESO grant N66001-11-1-4114 from DARPA and by contracts from the U.S. Army TARDEC, RDECOM. The work of M.C. and G.F. was supported by the project PRIN2010ECA8P3 from Italian MIUR.
Author information
Authors and Affiliations
Contributions
M.C. and G.F. planned and performed micromagnetic simulations. R.V., V.T. and A.S. developed theoretical model. All authors analyzed the data and co-wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Verba, R., Carpentieri, M., Finocchio, G. et al. Excitation of propagating spin waves in ferromagnetic nanowires by microwave voltage-controlled magnetic anisotropy. Sci Rep 6, 25018 (2016). https://doi.org/10.1038/srep25018
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep25018
This article is cited by
-
Bifurcation to complex dynamics in largely modulated voltage-controlled parametric oscillator
Scientific Reports (2024)
-
A spinwave Ising machine
Communications Physics (2023)
-
A magnonic directional coupler for integrated magnonic half-adders
Nature Electronics (2020)
-
Towards magnonic devices based on voltage-controlled magnetic anisotropy
Communications Physics (2019)
-
Magnetoelectric Spin Wave Modulator Based On Synthetic Multiferroic Structure
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.