Abstract
We here identify by ab initio calculations a new type of three-dimensional (3D) carbon allotropes that consist of phenyl rings connected by linear acetylenic chains in sp+sp2 bonding networks. These structures are constructed by inserting acetylenic or diacetylenic bonds into an all sp2-hybridized rhombohedral polybenzene lattice, and the resulting 3D phenylacetylene and phenyldiacetylene nets comprise a 12-atom and 18-atom rhombohedral primitive unit cells in the  symmetry, which are characterized as the 3D chiral crystalline modification of 2D graphyne and graphdiyne, respectively. Simulated phonon spectra reveal that these structures are dynamically stable. Electronic band calculations indicate that phenylacetylene is metallic, while phenyldiacetylene is a semiconductor with an indirect band gap of 0.58 eV. The present results establish a new type of carbon phases and offer insights into their outstanding structural and electronic properties.
symmetry, which are characterized as the 3D chiral crystalline modification of 2D graphyne and graphdiyne, respectively. Simulated phonon spectra reveal that these structures are dynamically stable. Electronic band calculations indicate that phenylacetylene is metallic, while phenyldiacetylene is a semiconductor with an indirect band gap of 0.58 eV. The present results establish a new type of carbon phases and offer insights into their outstanding structural and electronic properties.
Similar content being viewed by others
Introduction
The valence electrons of carbon atom are capable of forming sp3-, sp2- and sp-hybridized states that support four basic types of single, double, triple, and aromatic carbon-carbon bonds1,2,3,4. These different bonding states in various compounds have a profound impact on a wide range of properties of carbon-based materials. At ambient conditions, graphite, which is structurally related to polycyclic benzenoid aromatic hydrocarbon, is the thermodynamically most stable carbon configuration. The polycyclic carbon atoms form a two-dimensional (2D) benzenoid sp2 bonding network with a bond angle of 120° and a bond length of 0.142 nm. Diamond, which is related to polycyclic saturated hydrocarbon, is the second most stable allotrope of carbon with all the carbon atoms in a methane-like tetrahedral sp3 bonding state with a bond angle of 109.5° and a bond length of 0.154 nm as in alkanes, forming a very rigid three-dimensional (3D) carbon network. Linear carbyne, which is related to polyyne-like unsaturated hydrocarbon with alternating single and triple carbon-carbon bonds rather than a cumulene structure, forming the simplest one-dimensional (1D) carbon chain, and it has been recently synthesized4, despite its rather high energy of about 1 eV per atom above that of graphite.
Since the discovery of fullerenes5, nanotubes6, and graphene7, considerable theoretical and experimental efforts have been made to search and assess new potential carbon allotropes8,9,10,11,12,13,14,15,16,17,18,19,20. Intriguing among them are the so-called graphyne and graphdiyne21,22,23,24, which are constructed by replacing one-third of the C–C bonds in graphene sheet with acetylenic (–C≡C–) or diacetylenic (–C≡C–C≡C–) linkages. Analogously, graphyne nanotubes25 and fullereneynes26 are also proposed theoretically. Thus far, large-scale graphyne and graphdiyne films composed of sp+sp2 hybrid network27,28,29 have been successfully synthesized under laboratory conditions. Motivated by sp+sp2-hybridized 2D carbon allotropes, an sp+sp3-hybridized 3D diamondyne was suggested by inserting triple yne-bonds into all the C–C bonds in cubic diamond30,31,32. In addition, a new material termed porous aromatic frameworks (PAFs) via inserting rigid phenyl rings into all the C–C bonds of diamond was reported33,34,35. These studies open a new approach to constructing 3D covalent carbon network structures.
In this work we report ab initio total-energy and phonon calculations36,37,38,39,40,41 that predict a new type of 3D carbon phases in  (
( ) symmetry constructed by inserting linear acetylenic chains into an sp2-hybridized rh6 polybenzene lattice3. The resulting 3D network structures of phenylacetylene and phenyldiacetylene consist of benzene rings bonding together with acetylene or diacetylene, which topologically correspond to 2D graphyne and graphdiyne, respectively. They are energetically more favorable than the sp-hybridized 1D carbyne chains and the recently reported sp+sp3-hybridized 3D diamondyne, and they are all dynamically stable. Moreover, 3D-phenylacetylene is metallic and 3D-phenyldiacetylene is semiconductor with an indirect band gap of 0.58 eV, in contrast to the semimetallic nature of graphite. These results provide new insights for the development of novel carbon allotropes.
) symmetry constructed by inserting linear acetylenic chains into an sp2-hybridized rh6 polybenzene lattice3. The resulting 3D network structures of phenylacetylene and phenyldiacetylene consist of benzene rings bonding together with acetylene or diacetylene, which topologically correspond to 2D graphyne and graphdiyne, respectively. They are energetically more favorable than the sp-hybridized 1D carbyne chains and the recently reported sp+sp3-hybridized 3D diamondyne, and they are all dynamically stable. Moreover, 3D-phenylacetylene is metallic and 3D-phenyldiacetylene is semiconductor with an indirect band gap of 0.58 eV, in contrast to the semimetallic nature of graphite. These results provide new insights for the development of novel carbon allotropes.
Results and Discussion
We first present the structural characterization of the simplest 3D phenylacetylene network constructed by inserting triple (–C≡C–) yne-bonds into the rh6 polybenzene lattice (see Fig. 1a), as well as the so-called 2D graphyne by inserting triple yne-bonds into an expanded graphene sheet21. This new carbon phase has a  (
( ) symmetry as that of rh6 polybenzene3 and topologically corresponds to 2D γ-graphyne24. In the hexagonal representation, it has a 36-atom hexagonal unit cell (see Fig. 1b) with lattice parameters a = 11.6050 Å, c = 3.6443 Å, occupying the 18h1 (0.8579, 0.9289, 0.4849) and 18h2 (0.8617, 0.7233, 0.6021) Wyckoff positions. The carbon atoms on the 18h1 sites form three benzene rings, as in rh6 carbon, with aromatic sp2 hybridization, while the carbon atoms on the 18h2 sites form nine triple yne-bonds located between the benzene rings with an ethyne-type sp-hybridization. As in rh6 carbon3, this structure also can be regarded as a three-dimensional chiral crystalline modification of carbyne connected via zigzag benzene rings with alternating single, triple and aromatic carbon-carbon bonds. It contains three distinct carbon-carbon bond lengths, a longer bond of 1.433 Å (C1–C1) in the benzene rings and two shorter bonds of 1.389 Å (C1–C2) and 1.232 Å (C2–C2) associated with the single and triple bond in carbyne chains, respectively. Meanwhile, there are three different bond angles, 171.13° for
) symmetry as that of rh6 polybenzene3 and topologically corresponds to 2D γ-graphyne24. In the hexagonal representation, it has a 36-atom hexagonal unit cell (see Fig. 1b) with lattice parameters a = 11.6050 Å, c = 3.6443 Å, occupying the 18h1 (0.8579, 0.9289, 0.4849) and 18h2 (0.8617, 0.7233, 0.6021) Wyckoff positions. The carbon atoms on the 18h1 sites form three benzene rings, as in rh6 carbon, with aromatic sp2 hybridization, while the carbon atoms on the 18h2 sites form nine triple yne-bonds located between the benzene rings with an ethyne-type sp-hybridization. As in rh6 carbon3, this structure also can be regarded as a three-dimensional chiral crystalline modification of carbyne connected via zigzag benzene rings with alternating single, triple and aromatic carbon-carbon bonds. It contains three distinct carbon-carbon bond lengths, a longer bond of 1.433 Å (C1–C1) in the benzene rings and two shorter bonds of 1.389 Å (C1–C2) and 1.232 Å (C2–C2) associated with the single and triple bond in carbyne chains, respectively. Meanwhile, there are three different bond angles, 171.13° for  C1–C2–C2 along the carbyne chains, 119.39° for
C1–C2–C2 along the carbyne chains, 119.39° for  C1–C1–C1 inside and 120.21° for
C1–C1–C1 inside and 120.21° for  C1–C1–C2 out of the zigzag benzene rings, respectively. On the other hand, in the rhombohedral representation, it has a 12-atom primitive unit cell with equilibrium lattice parameters a = 6.8094 Å, α = 116.889°, occupying the 6 h (0.3428, 0.5560, 0.5560) and 6 h (0.4638, 0.4638, 0.8788) position, thus this 3D-phenylacetylene is also termed as rh12 carbon.
C1–C1–C2 out of the zigzag benzene rings, respectively. On the other hand, in the rhombohedral representation, it has a 12-atom primitive unit cell with equilibrium lattice parameters a = 6.8094 Å, α = 116.889°, occupying the 6 h (0.3428, 0.5560, 0.5560) and 6 h (0.4638, 0.4638, 0.8788) position, thus this 3D-phenylacetylene is also termed as rh12 carbon.
 symmetry.
symmetry.(a) Rh6 polybenzene in an all sp2 3D bonding network with lattice parameters a = 6.9022 Å, c = 3.470 Å, occupying the 18 h (0.8805, 0.1195, 0.5576) position, which comprises three zigzag benzene rings as its building blocks. (b) Rh12 phenylacetylene with lattice parameters a = 11.6050 Å and c = 3.6443 Å. The 18h1 (0.8579, 0.9289, 0.4849) atoms form three benzene rings and 18h2 (0.8617, 0.7233, 0.6021) atoms form nine acetylenic yne-bonds located between the benzene rings. (c) Rh18 phenyldiacetylene with lattice parameters a = 16.0963 Å and c = 4.1987 Å. The atoms on 18h1 (0.1023, 0.0511, 0.5065) site form three benzene rings; The atoms on 18h2 (0.1008, 0.8992, 0.4507) and 18h3 (0.1435, 0.8565, 0.3755) sites form nine butadiyne located between the benzene rings. The primitive cell is marked by yellow lines.
The construction of 3D-phenylacetylene can also be applied to design a 3D-phenyldiacetylene network (see Fig. 1c) by inserting butadiyne (–C≡C–C≡C–) segments between the benzene rings in the rh6 polybenzene lattice. The resulting structure has a 54-atom hexagonal unit cell with an equilibrium lattice parameters a = 16.0963 Å, c = 4.1987 Å, occupying the 18h1 (0.1023, 0.0511, 0.5065), 18h2 (0.1008, 0.8992, 0.4507), and 18h3 (0.1435, 0.8565, 0.3755) Wyckoff positions. The carbon atoms on the 18h1 sites form three benzene rings, while the carbon atoms on the 18h2 and 18h3 sites form nine diyne-bonds. This 3D network structure has a  symmetry as in rh6 carbon, and topologically corresponds to 2D graphdiyne24, thus there are four distinct carbon-carbon bond lengths, a longer bond of 1.427 Å (C1–C1) is associated with the carbon atoms in the benzene rings and three shorter bonds of 1.395 Å (C1–C2), 1.233 Å (C2–C3), and 1.338 Å (C3–C3) are along the chains between the benzene rings. Note that the carbon chains are not perfectly linear with the bond angles of 172.54° for
symmetry as in rh6 carbon, and topologically corresponds to 2D graphdiyne24, thus there are four distinct carbon-carbon bond lengths, a longer bond of 1.427 Å (C1–C1) is associated with the carbon atoms in the benzene rings and three shorter bonds of 1.395 Å (C1–C2), 1.233 Å (C2–C3), and 1.338 Å (C3–C3) are along the chains between the benzene rings. Note that the carbon chains are not perfectly linear with the bond angles of 172.54° for  C1–C2–C3 and 180° for
C1–C2–C3 and 180° for  C2–C3–C3. In the rhombohedral representation, it has an 18-atom primitive unit cell, thus it also termed as rh18 carbon. The two new structures introduced here represent a new type of carbon allotropes that consist of phenyl rings connected by linear acetylenic chains in sp+sp2 bonding networks.
C2–C3–C3. In the rhombohedral representation, it has an 18-atom primitive unit cell, thus it also termed as rh18 carbon. The two new structures introduced here represent a new type of carbon allotropes that consist of phenyl rings connected by linear acetylenic chains in sp+sp2 bonding networks.
The total energies of rh12 phenylacetylene and rh18 phenyldiacetylene as a function of volume are shown in Fig. 2 in comparison with the results for diamond, graphite, rh6 carbon, carbyne, and diamondyne. Our calculated energetic data establish the stability sequence: diamondyne < carbyne < rh18 < rh12 < rh6. It is clearly seen that the rh12 and rh18 polybenzene-ynes are located between the energy range for rh6 carbon and carbyne, with an energy gain of about 0.07 eV per atom, while the diamondyne is out of the energy range, and even less favorable than carbyne.
By fitting the calculated total energy as a function of volume to Murnaghan’s equation of state42, we obtain the bulk modulus (B0) of rh12 and rh18 carbon as 195 and 129 GPa, respectively. The atomic densities are estimated to be 2.50, 1.69, and 1.14 g/cm3 for rh6, rh12, and rh18 carbon, respectively, which are considerably different from 3.51 g/cm3 for diamond and 2.27 g/cm3 for graphite. We can see that with increasing of the acetylenic chain length, the atomic density and bulk modulus are decreasing to a level even lower than those of graphite. The calculated equilibrium structural parameters, total energy, and bulk modulus for diamond, rh6 polybenzene, rh12-phenylacetylene, rh18-phenyldiacetylene, and graphite are listed in Table 1 and compared to available experimental data43.
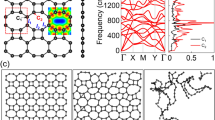
We next examine the dynamic stability of the 3D sp+sp2 bonding networks by phonon mode analysis. Figure 3a shows the phonon band structures and density of state (DOS) for the 3D phenylacetylene. The obtained phonon eigenvalues can be explained well by considering the bonding nature of the phenyl and triple carbon-carbon bonds. The vibrational modes due to the triple yne-bond can be observed clearly around 2150 cm−1 with the carbon-carbon bond length of 1.232 Å (C2–C2) and the vibrational modes due to the phenyl bonds are distributed around 1500 cm−1 with the carbon-carbon bond length of 1.433 Å (C1–C1). The combination modes of phenyl and triple bonds of carbon atoms can be seen clearly below 730 cm−1. No imaginary frequencies were observed throughout the entire phonon band structures, thus confirming the dynamic stability of the 3D-phenylacetylene. Meanwhile, there is a large phonon band gap in the frequency range of 1500 and 2100 cm−1. Similar dynamic stability and vibrational modes are also confirmed for 3D phenyldiacetylene as shown in Fig. 3b. However, in the latter case there are two yne-modes around 2148 and 2193 cm−1 due to the diyne bonds related to the C2 and C3 carbon atoms.
Results for rh12 phenylacetylene (a) and rh18 phenyldiacetylene (b). The spectra due to the triple bonds and phenyl bonds occur around 2150 cm−1 and 1500 cm−1, respectively. A clearer picture for the low vibrational modes is given in Fig. S1 in Supplementary Information.
To further examine the thermal stability, we have also performed ab initio molecular dynamics simulations using a 1 × 1 × 2 hexagonal supercell, which contains 6 primitive cells. After being heated at room temperature (300 K) and 1000 K for 3 ps with a time step of 1 fs, no structural changes occurred for both rh12 and rh18 carbon. These results show that rh12 and rh18 carbon are viable carbon allotrope for experimental synthesis.
Figure 4 shows the calculated electronic band structures and projected density of states (PDOS) by using the hybrid functionals (HSE06)39. The calculated band gap for diamond is about 5.36 eV, which is closed to the experimental data of 5.47 eV43, indicating the validity of the HSE06 method in predicting the band gaps for diamond and related sp3 bonded carbon structures. For 3D-phenylacetylene, as shown in Fig. 4a, there are three bands around the A, K and M points across the Fermi level, resulting in the metallic nature of the system. Meanwhile, for 3D-phenyldiacetylene, as shown in Fig. 4b, the conduction band minimum and valence band maximum are located at the L and Γ point, respectively, showing a semiconductor character with an indirect band gap of 0.58 eV. Moreover, from the PDOS, we can see that the states around the Fermi level are mainly coming from the 2p orbitals, which define the metallic nature for phenylacetylene and the band gap for phenyldiacetylene.
To understand the bonding nature of electrons in both rh12 and rh18 carbon, the electron density difference (EDD) and electron localization function (ELF) maps are illustrated in Fig. 5. The EDD maps represent the variation of electron density in terms of chemical bonding. One can make an EDD plot by subtracting the overlapping atomic electron density from the self-consistent electron density of a crystal. The ELF maps can give a clear and quantitative description on the basic chemical bond (high ELF values 1 > ELF > 0.5 indicate the formation of covalent bonds)44,45,46, which was initially proposed by Becke and Edgecombe45 based on Hartree-Fock theory, and generalized by Savin et al.46 based on density functional theory. From the EDD maps shown in Fig. 5a,b, we can be seen that there is a larger gain of electron density between triple bonded carbons. Meanwhile, from the ELF maps shown in Fig. 5c,d, we can see that the electrons are well localized along the carbon chain, and the enhanced localization between triple bonded carbons can be seen clearly, which is more than the localization between the single and aromatic bonded carbons. These results show the strong triple bonding nature in the sp+sp2 hybrid networks. Furthermore, to understand the aromaticity in the phenyl rings, the nuclear-independent chemical shift NICS(0) at the center of the phenyl rings are calculated using the gauge-including atomic orbital (GIAO) method at the B3LYP/6-311 + G(d,p) level47. The NICS(0) values are estimated to be −8.16 ppm for benzene, −5.23 ppm for rh12 carbon, and −6.57 ppm for rh18 carbon. These results show that the aromaticity in phenyl rings of rh12 and rh18 carbon are smaller than the aromaticity in benzene.
(a,b) The electron density difference (EDD) for rh12 carbon (a) and rh18 carbon (b) with an isodensity of 0.1 e/Å3. The blue colour denotes a gain and the yellow colour a loss of electron density. (c,d) The electron localization function (ELF) for rh12 carbon (c) and rh18 carbon (d) with an isosurface level of 0.75.
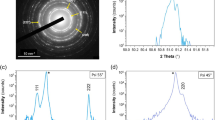
Finally, we plot in Fig. 6a simulated x-ray diffraction (XRD) patterns for graphite, diamond, rh6 polybenzene, rh12 phenylacetylene, rh18 phenyldiacetylene and and fcc C60, compared to the experimental data for chimney soot and detonation soot48. It is shown that the main (101) peak at 30° for rh6 should shift to 26° for rh12 and 22.4° for rh18 carbon. The main (101) peak at 26° for rh12 is very close to the main (002) peak at 26.5° for graphite, thus rh12 carbon may coexist with graphite in the detonation soot (see Fig. 6b and the Fig. 2 in ref. 48). On the other hand, for chimney soot, as shown in Fig. 6b, there is a sharp peak at 29.8°, which is fit well by the rh6 (101) diffraction peak, while a broad diffraction around 23°, which matches the rh18 (101) diffraction peak. These results suggest that rh12 and rh18 carbon as well as rh6 carbon may be present in chimney soot, carbon black or detonation soot48.
(a) Simulated XRD patterns for graphite, diamond, rh6 polybenzene, rh12 phenylacetylene, rh18 phenyldiacetylene, and fcc C60. (b) Experimental XRD patterns for chimney soot and detonation soot48. The black, green, and red arrows indicate the XRD peaks corresponding to the main peak for rh6, rh12, and rh18 carbon, respectively. X-ray wavelength is 1.5406 Å with a copper source.
Conclusions
In conclusion, we have identified by ab initio calculations a new type of three-dimensional carbon allotropes that consist of phenyl rings connected by linear acetylenic chains in sp+sp2 bonding networks. The resulting 3D phenylacetylene and phenyldiacetylene network structures in  (
( ) symmetry are topologically corresponding to 2D graphyne and graphdiyne, respectively, and they are energetically more favorable than the sp-hybridized 1D carbyne chains and the recently reported sp+sp3-hybridized 3D diamondyne. Phonon calculations show that these newly predicted structures are all dynamically stable. Electronic band and density of states calculations indicate that 3D-phenylacetylene with acetylenic yne-bonds is metallic, while 3D-phenyldiacetylene with diacetylenic yne-bonds is a semiconductor with an indirect band gap of 0.58 eV. Moreover, a detailed XRD analysis shows that phenylacetylene and phenyldiacetylene 3D network structures as well as rh6 polybenzene match the experimental diffraction peaks seen in the carbon black, diesel soot or chimney soot48. Our findings suggest a novel strategy in constructing carbon framework structures that may help solve the structures of the newly discovered but unidentified carbon phases seen in recent detonation experiments.
) symmetry are topologically corresponding to 2D graphyne and graphdiyne, respectively, and they are energetically more favorable than the sp-hybridized 1D carbyne chains and the recently reported sp+sp3-hybridized 3D diamondyne. Phonon calculations show that these newly predicted structures are all dynamically stable. Electronic band and density of states calculations indicate that 3D-phenylacetylene with acetylenic yne-bonds is metallic, while 3D-phenyldiacetylene with diacetylenic yne-bonds is a semiconductor with an indirect band gap of 0.58 eV. Moreover, a detailed XRD analysis shows that phenylacetylene and phenyldiacetylene 3D network structures as well as rh6 polybenzene match the experimental diffraction peaks seen in the carbon black, diesel soot or chimney soot48. Our findings suggest a novel strategy in constructing carbon framework structures that may help solve the structures of the newly discovered but unidentified carbon phases seen in recent detonation experiments.
Methods
Our calculations are carried out using the density functional theory as implemented in the Vienna ab initio simulation package (VASP)36. The generalized gradient approximation (GGA) developed by Armiento-Mattsson (AM05)37 were adopted for the exchange-correlation potential. The all-electron projector augmented wave (PAW) method38 was adopted with 2s22p2 treated as valence electrons. A plane-wave basis set with a large energy cutoff of 800 eV was used. Forces on the ions are calculated through the Hellmann-Feynman theorem allowing a full geometry optimization. The energy minimization is done over the atomic and electronic degrees of freedom using the conjugate gradient iterative technique. Convergence criteria employed for both the electronic self-consistent relaxation and the ionic relaxation were set to 10−8 eV and 0.01 eV/Å for energy and force, respectively. A hybrid density functional method based on the Heyd-Scuseria-Ernzerhof scheme (HSE06)39 has been used to calculate electronic properties. Phonon calculations are performed using the phonopy code40 based on the supercell approach41 with a (1 × 1 × 2) 72-atom hexagonal supercell for rh12 and a (1 × 1 × 2) 108-atom hexagonal supercell for rh18 carbon. Ab initio molecular dynamics simulations under constant temperature (300 K and 1000 K) and volume (NVT) were performed to check thermal stability with a time step of 1 fs up to 3 ps. The nuclear-independent chemical shift NICS(0) at the center of the phenyl rings are calculated using the gauge-including atomic orbital (GIAO) method at the B3LYP/6-311 + G(d,p) level47 as as implemented in Gaussian03.
Additional Information
How to cite this article: Wang, J.-T. et al. Three-Dimensional Carbon Allotropes Comprising Phenyl Rings and Acetylenic Chains in sp+sp2 Hybrid Networks. Sci. Rep. 6, 24665; doi: 10.1038/srep24665 (2016).
References
Belenkov, E. A. & Greshnyakov, V. A. Classification of structural modifications of carbon. Phys. Solid State 55, 1754–1764 (2013).
Wang, J. T., Chen, C. F. & Kawazoe, Y. New carbon allotropes with helical chains of complementary chirality connected by ethene-type π-conjugation. Sci. Rep. 3, 3077, doi: 10.1038/srep03077 (2013).
Wang, J. T., Chen, C. F., Wang, E. G. & Kawazoe, Y. A new carbon allotrope with six-fold helical chains in all-sp2 bonding networks. Sci. Rep. 4, 4339, doi: 10.1038/srep04339 (2014).
Chalifoux, W. A. & Tykwinski, R. R. Synthesis of polyynes to model the sp-carbon allotrope carbyne. Nature Chem. 2, 967–971 (2010).
Kroto, H. W., Heath, J. R., Obrien, S. C., Curl, R. F. & Smaliey, R. E. C60: Buckminsterfullerene. Nature 318, 162–163 (1985).
Iijima, S. Helical microtubules of graphitic carbon. Nature 354, 56–58 (1991).
Novoselov, K. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Diederich, F. Carbon scaffolding: building acetylenic all-carbon and carbon-rich compounds. Science 369, 199–207 (1994).
Karfunkel, H. R. & Dresslert, T. New hypothetical carbon allotropes of remarkable stability estimated by modified neglect of diatomic overlap solid-state self-consistent field computations. J. Am. Chem. Soc. 114, 2285–2288 (1992).
Mao, W. L. et al. Bonding changes in compressed superhard graphite. Science 302, 425–427 (2003).
Sheng, X. L., Yan, Q. B., Ye, F., Zheng, Q. R. & Su, G. T-Carbon: A novel carbon allotrope. Phys. Rev. Lett. 106, 155703, doi: 10.1103/PhysRevLett.106.155703 (2011).
Niu, H. Y. et al. Families of superhard crystalline carbon allotropes constructed via cold compression of graphite and nanotubes. Phys. Rev. Lett. 108, 135501, doi: 10.1103/PhysRevLett.108.135501 (2012).
Li, Q. et al. Superhard monoclinic polymorph of carbon. Phys. Rev. Lett. 102, 175506, doi: 10.1103/PhysRevLett.102.175506 (2009).
Wang, J. T., Chen, C. F. & Kawazoe, Y. Low-temperature phase transformation from graphite to sp3 orthorhombic carbon. Phys. Rev. Lett. 106, 075501, doi: 10.1103/PhysRevLett.106.075501 (2011).
Wang, J. T., Chen, C. F. & Kawazoe, Y. Mechanism for direct conversion of graphite to diamond. Phys. Rev. B 84, 012102, doi: 10.1103/PhysRevB.84.012102 (2011).
Wang, J. T., Chen, C. F. & Kawazoe, Y. Orthorhombic carbon allotrope of compressed graphite: Ab initio calculations. Phys. Rev. B 85, 033410, doi: 10.1103/PhysRevB.85.033410 (2012).
Wang, J. T., Chen, C. F. & Kawazoe, Y. Phase conversion from graphite toward a simple monoclinic sp3-carbon allotrope. J. Chem. Phys. 137, 024502, doi: 10.1063/1.4732538 (2012).
Amsler, M. et al. Crystal structure of cold compressed graphite. Phys. Rev. Lett. 108, 065501, doi: 10.1103/PhysRevLett.102.065501 (2012).
Zhao, Z. S. et al. Tetragonal allotrope of group 14 elements. J. Am. Chem. Soc. 134, 12362–12365 (2012).
Niu, C. Y., Wang, X. Q. & Wang, J. T. K 6 carbon: A metallic carbon allotrope in sp3 bonding networks. J. Chem. Phys. 140, 054514, doi: 10.1063/1.4864109 (2014).
Baughman, R. H., Eckhardt, H. & Kertesz, M. Structure-property predictions for new planar forms of carbon: Layered phases containing sp2 and sp atoms. J. Chem. Phys. 87, 6687–6699 (1987).
Haley, M. M., Brand, S. C. & Pak, J. J. Carbon networks based on dehydrobenzoannulenes: Synthesis of graphdiyne substructures. Angew. Chem. Int. Ed. Engl. 36, 836–838 (1997).
Kim, Bog G. & Choi, H. J. Graphyne: Hexagonal network of carbon with versatile Dirac cones. Phys.Rev. B 86, 115435, doi: 10.1103/PhysRevB.86.115435 (2012).
Narita, N., Nagai, S., Suzuki, S. & Nakao, K. Optimized geometries and electronic structures of graphyne and its family. Phys. Rev. B 58, 11009–11014 (1998).
Coluci, V. R., Braga, S. F., Legoas, S. B., Galv, D. S. & Baughman, R. H. Families of carbon nanotubes: Graphyne-based nanotubes. Phys. Rev. B 68, 035430, doi: 10.1103/PhysRevB.68.035430 (2003).
Baughman, R. H., Galvào, D. S., Cui, C., Wang, Y. & Tománek, D. Fullereneynes: a new family of porous fullerenes. Chem. Phys. Lett. 204, 8–14 (1993).
Li, G. X. et al. Architecture of graphdiyne nanoscale films. Chem. Commun. 46, 3256–3258 (2010).
Ivanovskii, A. L. Graphynes and graphdiynes. Prog. Sol. State Chem. 41, 1–19 (2013).
Kehoe, J. M. et al. Carbon networks based on dehydrobenzoannulenes. 3. Synthesis of graphyne substructures. Org. Lett. 2, 969–972 (2000).
Hirsch, A. The era of carbon allotropes. Nat. Mater. 9, 868–871 (2010).
Jo, J. Y. & Kim, B. G. Carbon allotropes with triple bond predicted by first-principle calculation: Triple bond modified diamond and T-carbon. Phys. Rev. B 86, 075151, doi: 10.1103/PhysRevB.86.075151 (2012).
Huang, L., Xiang, Z. & Cao, D. A porous diamond carbon framework: a new carbon allotrope with extremely high gas adsorption and mechanical properties. J. Mater. Chem. A 1, 3851–3855 (2013).
Ben, T. et al. Gas storage in porous aromatic frameworks (PAFs). Energy Environ. Sci. 4, 3991–3999 (2011).
Ren, H. et al. Targeted synthesis of a 3D porous aromatic framework for selective sorption of benzene. Chem. Comm. 46, 291–293 (2010).
Ben, T. et al. Targeted synthesis of a porous aromatic framework with high stability and exceptionally high surface area. Angew. Chem., Int. Ed. 48, 9457–9460 (2009).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Armiento, R. & Mattsson, A. E. Functional designed to include surface effects in self-consistent density functional theory. Phys. Rev. B 72, 085108, doi: 10.1103/PhysRevB.72.085108 (2005).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Krukau, A. V., Vydrov, O. A., Izmaylov, A. F. & Scuseria, G. E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 125, 224106, doi: 10.1063/1.2404663 (2006).
Togo, A., Oba, F. & Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106, doi: 10.1103/PhysRevB.78.134106 (2008).
Parlinski, K., Li, Z. Q. & Kawazoe, Y. First-principles determination of the soft mode in cubic ZrO2 . Phys. Rev. Lett. 78, 4063–4066 (1997).
Murnaghan, F. D. The compressibility of media under extreme pressures. Proc. Nat. Acad. Sci. USA 30, 244–247 (1944).
Occelli, F., Loubeyre, P. & Letoullec, R. Properties of diamond under hydrostatic pressures up to 140 GPa. Nature Mater. 2, 151–154 (2003).
Silvi, B. & Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 371, 683–686 (1994).
Becke, A. D. & Edgecombe, K. E. A simple measure of electron localization in atomic and molecular systems. J. chem. Phys. 92, 5397–5403 (1990).
Savin, A. et al. Electron localization in solid-state structures of the elements: the diamond structure. Angew. Chem. Int. Ed. 31, 187–188 (1992).
Lee, C., Yang, W. T. & Parr, R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789 (1988).
Pantea, D., Brochu, S., Thiboutot, S., Ampleman, G. & Schol, G. A morphological investigation of soot produced by the detonation of munitions. Chemosphere 65, 821–831 (2006).
Acknowledgements
This study was supported by the National Natural Science Foundation of China (Grant No. 11274356) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB07000000). C.F.C. acknowledges support by DOE under Cooperative Agreement No. DE-NA0001982. Y.K. acknowledges support by the Russian Megagrant Project No. 14.B25.31.0030. We are thankful to the crew of the Computational Center of the Institute of Physics, Chinese Academy of Sciences, for their support at the Supercomputing facilities.
Author information
Authors and Affiliations
Contributions
J.-T.W., C.F.C., H.-D.L., H.M. and Y.K. designed the study and wrote the paper; J.-T.W. carried out ab initio simulations; all authors discussed the results and contributed to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wang, JT., Chen, C., Li, HD. et al. Three-Dimensional Carbon Allotropes Comprising Phenyl Rings and Acetylenic Chains in sp+sp2 Hybrid Networks. Sci Rep 6, 24665 (2016). https://doi.org/10.1038/srep24665
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep24665
This article is cited by
-
Machine learning the metastable phase diagram of covalently bonded carbon
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.