Abstract
We report an ab initio study of the effect of hydrostatic pressure and uniaxial strain on electronic properties of KNa2Bi, a cubic bialkali bismuthide. It is found that this zero-gap semimetal with an inverted band structure at the Brillouin zone center can be driven into various topological phases under proper external pressure. We show that upon hydrostatic compression KNa2Bi turns into a trivial semiconductor with a conical Dirac-type dispersion of electronic bands at the point of the topological transition while the breaking of cubic symmetry by applying a uniaxial strain converts the compound into a topological insulator or into a three-dimensional Dirac semimetal with nontrivial surface Fermi arcs depending on the sign of strain. The calculated phonon dispersions show that KNa2Bi is dynamically stable both in the cubic structure (at any considered pressures) and in the tetragonal phase (under uniaxial strain).
Similar content being viewed by others
Introduction
Alkali metal bismuthides form a group of compounds which attract much attention as materials with a variety of interesting physical properties. The Bi-based binary compounds, A3Bi (A = Na, K, Rb), belong to a special class of topological electronic states, three-dimensional (3D) Dirac semimetals1,2,3, where the valence and conduction bands touch at discrete points at the Fermi level. Such materials with a conical 3D dispersion of electronic bands at one or more crossing points and with nontrivial surface states (so-called Fermi arcs) are being given much attention1,2,3,4,5,6,7,8.
The 3D conical dispersion relations can also be achieved at the point of semimetal (metal) - to - semiconductor topological transition by tuning a system parameter such as alloying composition or chemical doping9,10,11. For example, in zinc-blende crystals of HgCdTe the conical dispersion with some peculiar properties similar to those in Dirac and Weyl semimetals is achieved by changing cadmium concentration11. By varying a chemical composition and thereby tuning both the strength of spin-orbit coupling and the lattice parameters, one can also convert a system into a topological insulator9. Another possibility of tuning the topological order is to apply an external strain what was theoretically demonstrated for a number of narrow gap cubic semiconductors like α-Sn (grey tin), HgTe and InSb12,13,14,15,16,17 or to combine the strain with adjusting the alloy composition18.
Up to now there is a lack of data concerning the electronic properties of ternary alkali bismuthides, such as KNa2Bi. Unlike the well known K3Bi and Na3Bi which have a hexagonal low temperature phase19,20 the crystal structure of KNa2Bi is cubic,  21. In this paper we theoretically demonstrate that KNa2Bi, a zero-gap semimetal with an inverted band structure at the Brillouin zone center, can be driven into different topological phases by applying pressure. We show that under hydrostatic compression the compound undergoes a transition to a conventional semiconductor with a conical Dirac-like dispersion of electronic bands at the point of the topological transition whereas upon uniaxial strain the compound can be converted into a topological insulator or into a three-dimensional Dirac semimetal with nontrivial Fermi arcs on the surfaces.
21. In this paper we theoretically demonstrate that KNa2Bi, a zero-gap semimetal with an inverted band structure at the Brillouin zone center, can be driven into different topological phases by applying pressure. We show that under hydrostatic compression the compound undergoes a transition to a conventional semiconductor with a conical Dirac-like dispersion of electronic bands at the point of the topological transition whereas upon uniaxial strain the compound can be converted into a topological insulator or into a three-dimensional Dirac semimetal with nontrivial Fermi arcs on the surfaces.
Results and Discussion
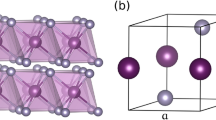
KNa2Bi crystallizes in the cubic  structure21 composed of four face-centered sublattices mutually shifted by
structure21 composed of four face-centered sublattices mutually shifted by  along the body diagonal. The sublattices occupied by Na atoms are symmetry equivalent. The lattice parameter, a = 7.97 Å, which is used in the calculation, was obtained by the total energy minimization and is slightly larger than the experimental value, aexp = 7.896 Å. Positions of atoms are shown in Table 1.
along the body diagonal. The sublattices occupied by Na atoms are symmetry equivalent. The lattice parameter, a = 7.97 Å, which is used in the calculation, was obtained by the total energy minimization and is slightly larger than the experimental value, aexp = 7.896 Å. Positions of atoms are shown in Table 1.
 structure.
structure.Equilibrium electronic structure
Figure 1(a,b) displays the effect of spin-orbit coupling on electronic bands of KNa2Bi. We also calculated the phonon spectrum to show the dynamical stability of KNa2Bi in the cubic structure (Fig. 1(e)). It is obvious that low-energy electronic properties of KNa2Bi are determined by the bands located around the Γ point since away from the Brillouin zone center the valence and conduction bands are well separated. The arrangement of bands around the Fermi level near the BZ center is shown in Fig. 1(c,d).
Electronic structure of KNa2Bi calculated (a) without spin-orbit coupling and (b) with spin-orbit interaction. (c,d) Bulk band dispersion in the vicinity of Γ shown to illustrate the effect of SOC and the band inversion. The bands consisted of s-like and p-like states in the Γ point are shown by red and blue lines, respectively. (e) Phonon spectrum of KNa2Bi calculated with (red solid lines) and without (black dashed lines) SOC.
In the absence of spin-orbit coupling (SOC), three bands which are linear combinations of p-like states are degenerate in the Γ point at the Fermi level and the s-type band is lower in energy (Fig. 1(c)). The SOC changes the structure of the valence bands (Fig. 1(d)): three degenerate bands split into two Γ8 bands degenerate at Γ and a split-off state, Γ7. The s-type band, Γ6, is now between the Γ8 and Γ7 bands. Thus, with and without taking into account the spin-orbit interaction KNa2Bi is a zero-gap semimetal in which the conduction and valence bands are degenerate at the Γ point. The account of SOC cannot lift the degeneracy of the Γ8 bands, which is a consequence of the cubic symmetry.
Another feature is the inversion of band structure around the Γ point. According to the normal band-filling order, the valence band edge should be formed of Bi p orbitals while the conduction band edge should be composed of s-type states. However in KNa2Bi the Γ6 band appears below the Γ8 bands composed of Bi p states. The energy gap (εS(Γ6) − εP(Γ8)) is negative: about −0.09 eV in the calculation without spin-orbit coupling and increases up to −0.65 eV with the account of SOC.
Electronic structure under hydrostatic lattice compression
First we analyzed the electronic structure of KNa2Bi under hydrostatic lattice compression. Figure 2 shows the evolution of electronic bands under pressure in the vicinity of the Γ point. Upon the compression, the cubic phase remains dynamically stable. At low pressures, the compound is still a zero-gap semimetal with an inverted band order. The compression leads to a decrease of the gap between bands Γ6 and Γ8 at the Γ point. The variation of the energy gap with pressure is shown in Fig. 2(d). At V/V0 ≈ 0.81, the gap vanishes and all three bands become degenerate at the Fermi level (Fig. 2(b)). At the crossing point, two of the bands have a conical dispersion, which is crossed in the middle by the third band. A subsequent increase of pressure opens up an energy gap between the valence and conduction bands. Simultaneously the inverted band character around the Γ point disappears, i.e. the sequence of bands restores to normal: the s-type band, Γ6, is now above the Γ8 bands composed of Bi p-type states (Fig. 2(c)).
Evolution of the KNa2Bi electronic spectrum under hydrostatic lattice compression: (a) at V0 (P = 0, a topologically nontrivial semimetal), (b) V/V0 = 0.81 (P ≈ 5 GPa, the point of topological transition) and (c) V/V0 = 0.73 (P ≈ 9.4 GPa, a trivial gapped semiconductor). Open (blue) circles indicate the bands formed by Bi p orbitals while the bands mainly composed of s-type states are shown by solid (red) circles. (d) Energy gap εS(Γ6) − εP(Γ8) at the Γ point as a function of volume. The positive gaps correspond to a topologically trivial phase when the band inversion disappears. Open triangles show pressure values as a function of V/V0.
A similar semiconductor-to-semimetal topological transition in the crystals of HgCdTe was reported11. Upon tuning of the alloying composition the semiconductor band structure becomes gapless at the critical value of cadmium concentration and the conical band dispersion with peculiar properties appears at the BZ center.
Electronic structure under uniaxial strain
Topological properties of KNa2Bi can be also changed by applying an external strain and thereby breaking the cubic symmetry. A strain was applied in the [001] direction (c axis). Such a strain lowers the crystal symmetry to a tetragonal one (Fig. 3(a)). The tetragonal structure of KNa2Bi is dynamically stable at all considered uniaxial strains. It turned out that the system responds differently to the compression and expansion: upon expansion the material becomes a 3D topological Dirac semimetal while the uniaxial compression converts the compound into a topological insulator. In both cases, the inverted band order in the vicinity of the Γ point remains that is an important sign of nontrivial topology. Figure 3(c,d) show the electronic band structure of KNa2Bi calculated with c = a0 ± 10% a0 at constant volume. The lattice optimization does not introduce any qualitative changes. To facilitate comparison we also used the primitive tetragonal unit cell to calculate the electronic structure of the unstrained compound (Fig. 3(b)).
(a) (Top) Atomic positions in a tetragonal lattice and (bottom) high-symmetry points in the corresponding bulk Brillouin zone and in the projected surface BZ along the [001] and [100] directions. (b–d) Electronic band structure of KNa2Bi calculated (b) without strain and (c,d) under uniaxial lattice expansion/compression at constant volume.
A topological insulator
When a uniaxial compression breaks the cubic symmetry the degeneracy of the Γ8 bands is lifted. The splitting creates a direct energy gap at the Γ point between the valence px,y-type Bi states and the conduction band composed mainly of pz Bi orbitals (Fig. 3(d)). And an indirect energy gap appears near the Γ point because of the band inversion between Bi px,y and pz states in the (kx, ky) plane. Since the inverted band order at the Γ point is preserved, the phase remains topologically nontrivial.
The topologically nontrivial character of the phase should be manifested in the existence of topological surface states. The calculated density of electronic states for the semi-infinite Bi&K- and Na-terminated (001) surfaces and for the (100) surface of KNa2Bi is shown in Fig. 4 together with the corresponding Fermi surfaces (in the inserts). All the data are presented as a color intensity plot. In the unstrained case (Fig. 4(b)), the surface states with a Dirac-type crossing are inside the projected valence bands due to the mixing with bulk electronic states. These topological surface states are clearly seen on the (001) surface (Fig. 4(b, left, middle)). The crossing (Dirac) point is located about 0.03 eV (0.45 eV) below the Fermi level depending on the surface termination.
Projected densities of electronic states, obtained from ab initio based tight-binding model calculations for the semi-infinite systems: the Bi&K and Na terminated (001) surfaces and the (100) surface (a) under uniaxial lattice compression, (b) at the equilibrium lattice parameter and (c) under uniaxial lattice expansion. The densities are shown by a color scale reflecting the localization in the outermost surface layer (in units of states/eV). Inserts show the corresponding Fermi surfaces with spin in-plane components for the topological surface states.
Upon a uniaxial lattice compression, the surface Dirac point on the Bi&K-terminated (001) surface moves up towards the energy gap. With increasing strain, the surface states are split off from the gap edges and form a Dirac cone inside the gap (Fig. 4(a, left)). Such gapless topological states are also observed on surface (100) (Fig. 4(a, right)). On the (001) surface the spin texture in the upper part of the Dirac cone has a clockwise helical structure whereas in the case of the (100) surface it is strongly warped because of the lack of C4 symmetry in the (kz, ky) plane. Additionally, each layer along the [100] direction is composed of four crystallographically non equivalent atoms. In the case of Na termination, the topological states with a Dirac-type crossing remain inside the bulk valence bands (Fig. 4(a, middle)). However there is another surface state, it split off from the edges of the conduction bands, but when merging with bulk valence bands the state loses its surface character.
A Dirac semimetal
When a uniaxial expansion removes the band degeneracy at the Γ point a fundamental band gap does not appear (Fig. 3(c)). The valence and conduction bands cross at two points exactly at the Fermi level. As a result, a pair of 3D Dirac nodes shows up on the rotational kz axis (the ΓZ direction) at ±kz ≈ 0.2π/c (the position depends on applied strain). One of the crossing bands is composed of Bi 6px,y states and the other mostly of Bi 6pz states. Since both bands are doubly degenerate each crossing point has a four-fold degeneracy.
The 3D Dirac cones and the inverted band order at the Γ point suggest the existence of nontrivial surface states (Fermi arcs). In the case of (001) surface, the projection of bulk electronic bands is superimposed on the nontrivial surface states arising owing to the band inversion at the Γ point and the Fermi surface represents just a point. The surface states show up along the edges of projected valence and conduction bands with the crossing at the Γ point (Fig. 4(c, left)).
On the (100) surface, however, the projected bulk Dirac nodes and the nontrivial surface states are separated in the momentum space and can be visible (Fig. 4(c, right)). The Fermi surface composed of two half-circle Fermi arcs is closed with two singular points corresponding to the projection of bulk Dirac nodes. The spin texture of Fermi arcs has a helical structure, but the value of spin is not defined at the singular points.
Discussion
To describe the change in the band dispersion at the point of extremum (the Γ point) under pressure, we have constructed a low-energy effective k · p-model Hamiltonian22 by considering the rotational (C4, along the kz axis), time-reversal and inversion symmetries. Since the inverted band order in the vicinity of Γ is a characteristic feature of the compound and is conserved under any uniaxial strain we do no consider s-type states. Only low-energy electronic states around the Γ point which are mostly consist of Bi 6px,y,z orbitals are used as basis states:  ,
,  ,
,  and
and  . The superscript indicates the parity and the arrow — the direction of spin moment. Due to the in-plane isotropy, components
. The superscript indicates the parity and the arrow — the direction of spin moment. Due to the in-plane isotropy, components  can be easily replaced by
can be easily replaced by 
 . The coupling of the basis states with the same parity (p-orbital hybridization) is also accounted for. So the parity operator is τ0, a zero Pauly matrix. In such a basis set, the Hamiltonian can be written as
. The coupling of the basis states with the same parity (p-orbital hybridization) is also accounted for. So the parity operator is τ0, a zero Pauly matrix. In such a basis set, the Hamiltonian can be written as

Here  ,
,  , k± = kx ± iky. So the parameters of the effective model are M0,1,2, A and β. In the Hamiltonian the topology of band structure is solely determined by parameter M0 which corresponds to the energy difference between basis orbitals. Other parameters are fixed in our calculation so as to reproduce both topological transitions: M1 = 1.0 eVÅ2, M2 = −1.0 eVÅ2, A = 1.0 eVÅ2 and β = 1.0 eVÅ). If M0M1 < 0 the system is a topological insulator, otherwise (M0M1 > 0) it is a Dirac semimetal. The spectra of Hamiltonian,
, k± = kx ± iky. So the parameters of the effective model are M0,1,2, A and β. In the Hamiltonian the topology of band structure is solely determined by parameter M0 which corresponds to the energy difference between basis orbitals. Other parameters are fixed in our calculation so as to reproduce both topological transitions: M1 = 1.0 eVÅ2, M2 = −1.0 eVÅ2, A = 1.0 eVÅ2 and β = 1.0 eVÅ). If M0M1 < 0 the system is a topological insulator, otherwise (M0M1 > 0) it is a Dirac semimetal. The spectra of Hamiltonian,  , are presented in Fig. 5.
, are presented in Fig. 5.
Band dispersions obtained from H(k) (eq. 1) with (a) M = 0, (b) M > 0 and (c) M < 0. The size of green (blue) circles reflects the contribution of 
 and
and  electronic states to the bands.
electronic states to the bands.
Let us consider three possible situation: M0 = 0, M0 > 0 and M0 < 0. If M0 = 0 (Fig. 5(a)) the compound is a zero-gap semimetal. Two double degenerate bands with square dispersion along all the directions of the BZ are touching at the Γ point and the crossing point has a four-fold degeneracy. Under hydrostatic compression, the stability of the system in the topological semimetal phase (M = 0) is provided by the cubic symmetry when all the basis orbitals are equivalent and have the same energy. To make M0 non-zero the band degeneracy at the Γ point should be lifted. Upon positive (negative) uniaxial strain, E(|Pz, ↑(↓)〉) is greater (less) than E(|Px(y), ↑(↓)〉) and, so, M0 < 0 (M0 > 0). In the case of M0 > 0 (Fig. 5(b)), the band gap is not global. The system posses a semimetal band structure with two Dirac points at  . Along the kx direction the gapped bands have a square dispersion. The case of M0 < 0 (Fig. 5(c)) corresponds to a topological insulator with hybridized gap. All three presented situations are similar to the tight-binding results.
. Along the kx direction the gapped bands have a square dispersion. The case of M0 < 0 (Fig. 5(c)) corresponds to a topological insulator with hybridized gap. All three presented situations are similar to the tight-binding results.
An analysis of the parity of occupied electronic states also reveals two phases in KNa2Bi from the viewpoint of  index classification. The
index classification. The  index was obtained from the parity of occupied electronic states at the time-reversal invariant points of the bulk Brillouin zone12 and also using Z2Pack software package. In the case of topological insulator (M0 < 0), the invariants are
index was obtained from the parity of occupied electronic states at the time-reversal invariant points of the bulk Brillouin zone12 and also using Z2Pack software package. In the case of topological insulator (M0 < 0), the invariants are  . It coincides with the results of surface band structure calculations: topological surface states exist on all possible surfaces. In the case of a Dirac semimetal (M0 > 0), the situation is different:
. It coincides with the results of surface band structure calculations: topological surface states exist on all possible surfaces. In the case of a Dirac semimetal (M0 > 0), the situation is different:  that corresponds to a weak topological insulating phase. This fact is also supported by the existence of surface states only on the (100) and (010) surfaces.
that corresponds to a weak topological insulating phase. This fact is also supported by the existence of surface states only on the (100) and (010) surfaces.
To describe possible spin textures of surface states let us consider the Hamiltonian consisting of the spin-orbit contribution, which includes both Bychkov-Rashba (BR) and Dresselhaus terms and an additional “kinetic”-like term23:

Here kx, ky are in-plane components of momentum,  . α and β determine the strength of the RB and Dresselhaus spin-orbit interactions and γ defines the “kinetic”-like term. σ1, σ2 and σ3 are Pauly matrices. The BR and “kinetic”-like terms are isotropic, the Dresselhaus term has C2 symmetry and so can be considered as a warping.
. α and β determine the strength of the RB and Dresselhaus spin-orbit interactions and γ defines the “kinetic”-like term. σ1, σ2 and σ3 are Pauly matrices. The BR and “kinetic”-like terms are isotropic, the Dresselhaus term has C2 symmetry and so can be considered as a warping.
In Fig. 6 three spin configurations corresponding to those shown in Fig. 4 are presented. Upon uniaxial compression, on the (001) surface of KNa2Bi (Fig. 4(a, left)) the spin texture in the upper part of the Dirac cone has a strong clockwise helicity without any warping. To obtain a similar spin texture we set α = 1, β = 0, γ = 10 (Fig. 6(a)). In this case, only the BR interaction contributes to the in-plane components of spin while the out-of-plane component is determined by the “kinetic”-like term. The existence of the non-zero out-of-plane spin component is proved by our TB calculations. The “kinetic” term also reduces the radius of isoenergetic contour and leads to a square dispersion of surface states with increasing k-vector.
Spin texture of isoenergetic contours in the upper part of a Dirac cone on the basis of the proposed Hamiltonian (eq. 2).
(a) α = 1, β = 0, γ = 10 (b) α = 0, β = 1, γ = 10 (c) α = 0.65, β = 0.35, γ = 10. The energy level is shown by a red dashed line.
The in-plane spin texture in the Dirac cone on the (100) surface (Fig. 4(a, left)) is fully described by the Dresselhaus term which has a C2 symmetry (we set α = 0, β = 1, γ = 10, Fig. 6(b)). In this case the spin texture is strongly warped because of the lack of C4 rotational symmetry on the (100) and (010) surfaces due to the strain along the [001] direction. Such a warping was also observed in the spin texture of bulk states in the tensile-strained HgTe24. In both considered cases there is no warping in the energy spectrum: the dispersions along kx and ky directions are the same.
The most interesting is the case of surface states on the (100) surface of KNa2Bi under uniaxial expansion (Fig. 4(c, right)). If in the previous cases the spin texture can be described using either the BR or Dresselhaus contributions, in this case, you need to consider all three terms in the Hamiltonian. The difference between α and β leads to spin helicity, so if α = β, the spin will be directed strictly along the positive (negative) ky axis, depending on whether kx < 0 (kx > 0). Finally, the “kinetic”-like term results in a more isotropic dispersion. Without this term (γ = 0) in the α = β limit the isoenergetic contour would consist of two parallel lines with the opposite spin direction. If α ≠ β the dispersion along the kx and ky directions is different (Fig. 6(c)). And when kx = 0 the in-plane components of spin disappear, which corresponds to the bulk Dirac points. Thus, using a simple k · p-model, we can describe all possible spin texture configurations on the surfaces of KNa2Bi. This model can also be used for related compounds with cubic symmetry.
Similar strain-induced transitions were predicted theoretically for gray tin (α-Sn) and HgTe12,13,16,17,25. The existence of topological surface states in the strained HgTe was also demonstrated experimentally by ARPES measurements14. At zero pressure, like KNa2Bi, α-Sn and HgTe are gapless semimetals with the inverted bulk band structure in the vicinity of Γ and surface states located on the edge of the conduction bands and inside the valence bands, indicating a nontrivial topology25. These semimetals are turned into 3D topological insulators by applying a uniaxial compression12. The strain induces a band gap in the bulk whereas the topological surface states acquire a gapless Dirac-cone dispersion, thereby giving a metallic character to the 3D topological insulators12,13,25. Like in the case of KNa2Bi the gapless surface states in HgTe is found to be sensitive to the surface termination14. Under uniaxial expansion of HgTe the degeneracy at Γ is also lifted but a fundamental band gap does not appear. Like in KNa2Bi the valence and conduction bands form a pair of Dirac points in the Z–Γ–Z line18.
Conclusion
We have analyzed theoretically the effect of external strain on the electronic properties of KNa2Bi, a cubic bialkali bismuthide. Under hydrostatic compression KNa2Bi, a zero-gap semimetal with the inverted band order around the BZ center, undergoes a transition to a conventional gapped semiconductor with a conical Dirac-like dispersion of electronic bands at the point of the topological transition. Simultaneously the sequence of different symmetry bands restores to normal. We find that topological Dirac-like surface states exist even in the unstrained compound as long as the band structure is inverted. It is also shown that KNa2Bi can be driven into distinct topologically nontrivial phases by breaking the cubic symmetry. Under uniaxial lattice expansion the compound is converted into a three-dimensional Dirac semimetal with nontrivial Fermi arcs on the surface while a nontrivial topological insulating phase can be realized by applying a uniaxial lattice compression.
Methods
The electronic structure calculations were performed in the mixed-basis pseudopotential approach26,27,28 with the exchange and correlation energy functional evaluated within the generalized gradient approximation29. Spin-orbit coupling (SOC) was incorporated into the pseudopotential scheme via Kleinman’s formulation30 and was treated fully self-consistently31. Phonon dispersions were calculated using the linear response technique32 in combination with the mixed-basis pseudopotential method28. Integrations over the Brillouin zone (BZ) were performed by sampling a 8 × 8 × 8 mesh corresponding to 29 and 75 k points in the irreducible part of the cubic and tetragonal BZ, respectively, combined with a Gaussian broadening with a smearing parameter of 0.01 eV. The projected density of surface states was calculated using ab initio based tight-binding formalism33,34.
Additional Information
How to cite this article: Sklyadneva, I. Y. et al. Pressure-induced topological phases of KNa2Bi. Sci. Rep. 6, 24137; doi: 10.1038/srep24137 (2016).
References
Wang, Z. et al. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 85, 195320 (2012).
Liu, Z. K. et al. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science 343, 864–867 (2014).
Xu, S.-Y. et al. Observation of Fermi arc surface states in a topological metal. Science 347, 294–298 (2015).
Young, S. M. et al. Dirac semimetal in three dimensions. Phys. Rev. Lett. 108, 140405 (2012).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Wang, Z., Weng, H., Wu, Q., Dai, X. & Fang, Z. Three-dimensional Dirac semimetal and quantum transport in Cd3As2 . Phys. Rev. B 88, 125427 (2013).
Neupane, M. et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2 . Nat Commun 5 (2014).
Borisenko, S. et al. Experimental realization of a three-dimensional Dirac semimetal. Phys. Rev. Lett. 113, 027603 (2014).
Xu, S.-Y. et al. Topological phase transition and texture inversion in a tunable topological insulator. Science 332, 560–564 (2011).
Brahlek, M. et al. Topological-metal to band-insulator transition in (Bi1−xInx)2Se3 thin films. Phys. Rev. Lett. 109, 186403 (2012).
Orlita, M. et al. Observation of three-dimensional massless Kane fermions in a zinc-blende crystal. Nat Phys 10, 233–238 (2014). Article.
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Dai, X., Hughes, T. L., Qi, X.-L., Fang, Z. & Zhang, S.-C. Helical edge and surface states in HgTe quantum wells and bulk insulators. Phys. Rev. B 77, 125319 (2008).
Brüne, C. et al. Quantum hall effect from the topological surface states of strained bulk HgTe. Phys. Rev. Lett. 106, 126803 (2011).
Feng, W. et al. Strain tuning of topological band order in cubic semiconductors. Phys. Rev. B 85, 195114 (2012).
Küfner, S. & Bechstedt, F. Topological transition and edge states in HgTe quantum wells from first principles. Phys. Rev. B 89, 195312 (2014).
Küfner, S. & Bechstedt, F. Topological states in α−Sn and HgTe quantum wells: A comparison of ab initio results. Phys. Rev. B 91, 035311 (2015).
Rauch, T., Achilles, S., Henk, J. & Mertig, I. Spin Chirality Tuning and Topological Semimetals in Strained HgTexS1−x . Phys. Rev. Lett. 114, 236805 (2015).
Kerber, H., Deiseroth, H.-J. & Walther, R. Crystal structure of α-tripotassium bismuthide, α-K3Bi. Z. Kristallogr. NCS 213, 473 (1998).
Tegze, M. & Hafner, J. Electronic structure of alkali-pnictide compounds. J. Phys. Condens. Matter 4, 2449 (1992).
Kerber, H. Beiträge zur Festkörpeichemie von Trialkalimetallpniktiden und Clusterverbindungen mit Indium. Ph.D. thesis, Universität Gesamthochschule Siegen, Germany (1997).
Yang, B.-J. & Nagaosa, N. Classification of stable three-dimensional Dirac semimetals with nontrivial topology. Nature Communications 5, 4898 (2014).
Nechaev, I. A., Echenique, P. M. & Chulkov, E. V. Inelastic decay rate of quasiparticles in a two-dimensional spin-orbit coupled electron system. Phys. Rev. B 81, 195112 (2010).
Zaheer, S. et al. Spin texture on the Fermi surface of tensile-strained HgTe. Phys. Rev. B 87, 045202 (2013).
Wu, S.-C., Yan, B. & Felser, C. Ab initio study of topological surface states of strained HgTe. Europhys. Lett. 107, 57006 (2014).
Louie, S. G., Ho, K.-M. & Cohen, M. L. Self-consistent mixed-basis approach to the electronic structure of solids. Phys. Rev. B 19, 1774–1782 (1979).
Meyer, B., Elsässer, C., Lechermann, F. & Fähnle, M. FORTRAN90, Program for Mixed-Basis-Pseudopotential Calculations for Crystals (Max-Planck-Institut für Metallforschung, Stuttgart).
Heid, R. & Bohnen, K.-P. Linear response in a density-functional mixed-basis approach. Phys. Rev. B 60, R3709–R3712 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Kleinman, L. Relativistic norm-conserving pseudopotential. Phys. Rev. B 21, 2630–2631 (1980).
Heid, R., Bohnen, K.-P., Sklyadneva, I. Y. & Chulkov, E. V. Effect of spin-orbit coupling on the electron-phonon interaction of the superconductors Pb and Tl. Phys. Rev. B 81, 174527 (2010).
Baroni, S., de Gironcoli, S., Dal Corso, A. & Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515–562 (2001).
Marzari, N. & Vanderbilt, D. Maximally localized generalized wannier functions for composite energy bands. Phys. Rev. B 56, 12847–12865 (1997).
Zhang, W., Yu, R., Zhang, H.-J., Dai, X. & Fang, Z. First-principles studies of the three-dimensional strong topological insulators Bi2Te3, Bi2Se3 and Sb2Te3 . New Journal of Physics 12, 065013 (2010).
Acknowledgements
We acknowledge financial support of the University of the Basque Country UPV/EHU (grant No. GIC13-IT-756-13), the Departamento de Educación del Gobierno Vasco, the Spanish Ministerio de Ciencia e Innovación (Grant No. FIS2010-19609-C02-01), the Spanish Ministry of Economy and Competitiveness MINECO Project FIS2013-48286-C2-1-P and the Saint Petersburg State University (project No. 15.61.202.2015).
Author information
Authors and Affiliations
Contributions
The calculations were performed mainly by I.Y.S. and I.P.R. with contributions by R.H. and K.-P.B. The idea of the study was proposed by E.V.C. and P.M.E.; I.Y.S. and I.P.R. wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sklyadneva, I., Rusinov, I., Heid, R. et al. Pressure-induced topological phases of KNa2Bi. Sci Rep 6, 24137 (2016). https://doi.org/10.1038/srep24137
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep24137
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.