Abstract
Disordered structures such as liquids and glasses, grains and foams, galaxies, etc. are often represented as polyhedral tilings. Characterizing the associated polyhedral tiling is a promising strategy to understand the disordered structure. However, since a variety of polyhedra are arranged in complex ways, it is challenging to describe what polyhedra are tiled in what way. Here, to solve this problem, we create the theory of how the polyhedra are tiled. We first formulate an algorithm to convert a polyhedron into a codeword that instructs how to construct the polyhedron from its building-block polygons. By generalizing the method to polyhedral tilings, we describe the arrangements of polyhedra. Our theory allows us to characterize polyhedral tilings and thereby paves the way to study from short- to long-range order of disordered structures in a systematic way.
Similar content being viewed by others
Introduction
Disordered structures are often represented as polyhedral tilings1,2,3,4,5,6,7,8,9,10,11. For example, in studying the atomic structures of amorphous materials, the space can be divided into the so-called Voronoi polyhedra, where each polyhedron encloses its associated atom1,2,3,4,5,6,7,8. The shape of the polyhedron relates to how the associated atom is surrounded by its neighbouring atoms. The short-range order of a disordered structure can be thus characterized by what polyhedra constitute its associated polyhedral tiling, while the long-range order by how the polyhedra are arranged. So far, some attempts have been made to classify individual polyhedra1,11,12,13,14,15,16 and periodic tilings for crystals17,18. However, there have been no methods to describe what polyhedra are tiled in what way. If we could describe the arrangements of polyhedra, our understanding of the disordered structures would be deepened.
In this work, we create the theory of how the polyhedra are tiled. For this purpose, we use the hierarchy of structures of polytopes19,20: a polyhedron (3-polytope) is a tiling by polygons (2-polytopes), a polychoron (4-polytope) is a tiling by polyhedra and so on. We first formulate a code for polyhedra (p3-code) and then generalize it to polychora. The code for polychora (p4-code) allows us to describe what polyhedra are tiled in what way.
Results
Polygon-sequence codeword
A polyhedron can be regarded as a tiling by polygons of the surface of a three-dimensional object that is topologically the same as a three-dimensional sphere. According to the idea developed by L. Euler, A. M. Legendre, F. Möbius and P. R. Cromwell19, we assume that polygons are glued such that (1) any pair of polygons meet only at their sides or corners and that (2) each side of each polygon meets exactly one other polygon along an edge. In this picture, the vertex is a point on the polyhedron at which the corners of polygons meet (Supplementary Fig. S1a) and we say that the corners contribute to the vertex. We also say that a polygon (side) contributes to a vertex if one of its corners (endpoints) contributes to the vertex. Similarly, the edge is a line segment on the polyhedron along which the sides of polygons meet (Supplementary Fig. S1b). The interior area of a polygon is the face of the polyhedron.
We first deal with simple polyhedra, where every vertex is degree three. Here, the degree of a vertex is the number of edges connected to that vertex21. Afterwards, the method will be generalized to non-simple ones. We formulate the p3-code in such a way that the codeword of a polyhedron (simply, p3) instructs how to construct it from its building-block polygons. For this purpose, we combine a polygon-sequence codeword (ps2) and a side-pairing codeword (sp) as p3 = ps2;sp, where “;” is a separator.
The ps2-codeword is denoted as

Here, p2(i) is the number of sides on the polygon i, where i is the identification number (ID). F is the number of faces on the polyhedron. Generating ps2 thus reduces to assigning polygon IDs. To visually distinguish already-encoded polygons from to-be-encoded ones, we assume that all polygons are coloured at first and make each polygon transparent when encoded. We call a side of a transparent polygon glued to a coloured one a dangling side. To identify each side, we introduce the side-ID ij. Here, the side ij means the jth side of the polygon i and the side-ID ij represents an integer: ij = j +  . We also assign corner IDs so that the endpoints of the side ij are the corners ij + 1 and ij for 1 ≤ j < p2(i) (Fig. 1a). The smallest-ID dangling side (s-side) plays a key role in encoding. The ps2-codeword is generated as follows (Fig. 1b,c):
. We also assign corner IDs so that the endpoints of the side ij are the corners ij + 1 and ij for 1 ≤ j < p2(i) (Fig. 1a). The smallest-ID dangling side (s-side) plays a key role in encoding. The ps2-codeword is generated as follows (Fig. 1b,c):
-
1
-
(a) Choose a side as the initial side and the polygon 1 is the one having that side.
-
(b) Assign IDs (11, 12, 13, ···,
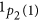 ) to the sides of the polygon 1 from the initial side in a clockwise (CW) direction.
) to the sides of the polygon 1 from the initial side in a clockwise (CW) direction. -
(c) Make the polygon 1 transparent except for the corners and sides.
-
-
2
-
(a) The next polygon i (2 ≤ i ≤ F) is the coloured one glued to the s-side.
-
(b) Assign IDs (i1, i 2, i 3, ···,
 ) to the sides of the polygon i from the side glued to the s-side in a CW direction.
) to the sides of the polygon i from the side glued to the s-side in a CW direction. -
(c) Make the polygon i transparent except for the corners and sides.
-
-
3
-
(a) Repeat the procedure 2 until all polygons get transparent.
-
Encoding and decoding a polyhedron.
Schlegel diagrams are used to illustrate polyhedra20,22. POV-Ray software23 is used to generate pictures. (a) Corner IDs (red) and side IDs (blue). (b) A Schlegel diagram is a projection of a polyhedron onto a plane. Note that the interior of the face abc on the polyhedron is mapped to the exterior of the outside face abc on the diagram. A counter CW direction around an inside polygon on the diagram, for example z→x→a→c, corresponds to a CW direction around its corresponding polygon on the polyhedron. (c) Encoding procedures. The red lines indicate the s-sides. (d) How to assign edge IDs. (e) Decoding procedures. Open circles indicate i-vertices, while filled circles indicate degree-one vertices.
For latter convenience in formulating the p4-code, we assign edge IDs as follows. First we tentatively assign the smaller side ID to the edge and then relabel the IDs so that the edge i is the one with the ith smallest tentative ID as illustrated in Fig. 1d. We also assign vertex IDs in a similar manner. First we tentatively assign the smallest corner ID to the vertex and then relabel the IDs. Since the properties of simple polyhedra are not assumed, the algorithm for generating ps2 can be used to assign face, edge and vertex IDs not only to simple polyhedra, but also to non-simple ones.
We note that p2(F − 1) and p2(F) can be deduced from p2(1) p2(2) p2(3) ··· p2(F −2) (see Supplementary Note and Supplementary Fig. S2). However, we purposely admit the small redundancy in ps2 to explicitly express all information about the polygons of the polyhedron.
Tentative side-pairing codeword
To formulate sp and the decoding algorithm, we first introduce the zeroth tentative side-pairing codeword (tsp(0)). We then formulate an algorithm to recover the original polyhedron from ps2;tsp(0). Finally, we remove redundancy in tsp(0) step-by-step to obtain sp.
We first introduce a plot as follows. A plot consists of a single dangling side or a chain of dangling sides. Here, two dangling sides are considered to be chained when they contribute to the same vertex contributed by two transparent polygons. Let x be the smallest side ID of a plot. We define the ID of that plot as x (Fig. 2a). We call the smallest-ID plot the s-plot. Note that all the sides of each plot are glued to the same coloured polygon.
If we encode a polyhedron twice, we know all the IDs of the polygons and sides from the beginning in the second time of encoding. When the polygon (i − 1) gets transparent, the coloured polygon i is glued to the s-side, so that the s-plot is glued to the polygon i. For example, in encoding the polyhedron shown in Fig. 2b, the polygon 2 in P1 is glued to the s-plot 11 (Fig. 2c). Here, Pi is the object obtained when the polygon i gets transparent. In P7 (Fig. 2d), the polygon 8 is glued to the plot 56 in addition to the s-plot 34. We call such an additional plot an a-plot. The smallest-ID side of the a-plot 56, which is the side 56, is glued to the side 85. We call such a pair an a-pair 8556. The sides 104 and 54 also form the a-pair 10454 (Fig. 2e).
By collecting the a-pairs, we define tsp(0) as

Here, the sides ya(i) and xa(i) form the a-pair ya(i)xa(i), where ya(i) > xa(i) and ya(i) < ya(i + 1). Na is the number of a-pairs. For example, tsp(0) of the polyhedron shown in Fig. 2b is 855610454.
Decoding algorithm
To formulate a decoding algorithm, we consider the sequence D1 D2 D3 ··· DF, where Di is the partial polyhedron obtained when the polygon i is decoded. For the encoding process, we also consider the sequence E1 E2 E3 ··· EF. Here, Ei is the partial polyhedron obtained by removing the coloured polygons from Pi (Fig. 3a,b). For Di and Ei, if a side is not glued to the other polygon, we call it a dangling side. To define the plot, we consider a pair of two dangling sides to be chained if they contribute to the same vertex contributed by two polygons.
Procedures to recover a polyhedron.
D8 (=E8) of the polyhedron shown in Fig. 2b can be constructed from D7 (=E7) and ps2;tsp(0) = 458585574755433;855610454. (a) How to construct E7 from P7. If we ignore colour, the coloured E7 is considered to be identical with E7. (b) E8 consists of the polygon 8 and E7. (c) How to rectify i-vertices (open circles). (d) Since p2(8) = 7, the polygon 8 is a 7-gon. (e) The side 81 of the 7-gon is glued to the s-side 34 of D7. An i-vertex is generated (blue circle). (f) We glue together the sides 85 and 56 as tsp(0) instructs. Another i-vertex is generated (red circle). (g) We glue the sides 82 and 74 together to rectify the blue i-vertex. (h) We also glue the sides 84 and 63 together to rectify the red i-vertex. D8 thus obtained is identical with E8.
We formulate an algorithm to recover the original polyhedron from ps2;tsp(0) so as to satisfy Di = Ei at any i. If we assign side IDs (11, 12, 13, ···,  ) to a p2(1)-gon, then the resultant object D1 is identical with E1. Assume Di − 1 = Ei − 1 for 2 ≤ i ≤ F. To construct Di (=Ei) from Di − 1 and ps2;tsp(0), we introduce a rectification mechanism as follows. Since Di is the partial polyhedron of a simple polyhedron, Di must not have any degree-four vertex contributed by three polygons. We call such a vertex an illegal vertex (i-vertex). However, we allow intermediate products to transiently have i-vertices. When an i-vertex is generated, we rectify it by gluing together the two dangling sides contributing to it (Fig. 3c). Using the rectification mechanism, Di can be constructed as follows. We first glue the side i1 of the polygon i to the s-side of Di − 1 (Fig. 3d,e). This is because Ei consists of the polygon i and Ei − 1 in such a way that the side i1 of the polygon i is glued to the s-side of Ei − 1. In addition, if ya(n) (1 ≤ n ≤ Na) is the side ID of the polygon i, then we glue the side ya(n) to the side xa(n) of Di − 1 (Fig. 3f) –for the polygon i in Ei is glued to not only the s-plot, but also the a-plot xa(n) of Ei − 1 (Fig. 3b). If the product has i-vertices, we rectify them so that all the sides of the s-plot and a-plots get glued to the polygon i properly to satisfy Di = Ei (Fig. 3g,h).
) to a p2(1)-gon, then the resultant object D1 is identical with E1. Assume Di − 1 = Ei − 1 for 2 ≤ i ≤ F. To construct Di (=Ei) from Di − 1 and ps2;tsp(0), we introduce a rectification mechanism as follows. Since Di is the partial polyhedron of a simple polyhedron, Di must not have any degree-four vertex contributed by three polygons. We call such a vertex an illegal vertex (i-vertex). However, we allow intermediate products to transiently have i-vertices. When an i-vertex is generated, we rectify it by gluing together the two dangling sides contributing to it (Fig. 3c). Using the rectification mechanism, Di can be constructed as follows. We first glue the side i1 of the polygon i to the s-side of Di − 1 (Fig. 3d,e). This is because Ei consists of the polygon i and Ei − 1 in such a way that the side i1 of the polygon i is glued to the s-side of Ei − 1. In addition, if ya(n) (1 ≤ n ≤ Na) is the side ID of the polygon i, then we glue the side ya(n) to the side xa(n) of Di − 1 (Fig. 3f) –for the polygon i in Ei is glued to not only the s-plot, but also the a-plot xa(n) of Ei − 1 (Fig. 3b). If the product has i-vertices, we rectify them so that all the sides of the s-plot and a-plots get glued to the polygon i properly to satisfy Di = Ei (Fig. 3g,h).
To summarize, the original polyhedron can be recovered from ps2;tsp(0) as follows (Fig. 1e):
-
1
-
(a) The polygon 1 is a p2(1)-gon.
-
(b) Assign IDs (11, 12, 13, ···,
 ) to its sides in a CW direction. The resultant object is D1.
) to its sides in a CW direction. The resultant object is D1.
-
-
2
-
(a) The next polygon i (2 ≤ i ≤ F) is a p2(i)-gon.
-
(b) Assign IDs (i1, i 2, i 3, ···,
 ) to its sides in a CW direction.
) to its sides in a CW direction. -
(c) Glue the side i1 of the polygon i to the s-side of Di − 1.
-
(d) If ya(n) (1 ≤ n ≤ Na) is the side ID of the polygon i, then glue the side ya(n) to the side xa(n) of Di − 1.
-
(e) If i-vertices are generated, then rectify them and repeat this procedure until no i-vertices remain. The resultant object is Di.
-
-
3
-
(a) Repeat the procedure 2 until all polygons are placed.
-
Side-pairing codeword
In decoding ps2;tsp(0), Di = Ei at any i. However, what we need is just DF = EF. By allowing Di ≠ Ei for 1 ≤ i ≤ F − 1, we can make the more compact sp as described below.
We remove redundancy in tsp(0) step-by-step. To examine ya(Na)xa(Na) for necessity, we consider the first test codeword denoted as

which is obtained by stripping ya(Na)xa(Na) off from tsp(0). Then we attempt to decode ps2;test(1). When the polygon having the side ya(Na) is decoded, we will fail to glue the sides ya(Na) and xa(Na) together, because the a-pair ya(Na)xa(Na) is missing in test(1). However, we can proceed decoding. If the missing a-pair is cured and the original polyhedron is successfully reproduced in the subsequent decoding process, then we call the a-pair the curable a-pair. Otherwise, we call it the non-curable a-pair. If the a-pair is curable, then we can remove ya(Na)xa(Na) from tsp(0). We therefore set the first tentative side-pairing codeword as tsp(1) = test(1). On the other hand, if the a-pair is non-curable, then tsp(1) = tsp(0).
To examine ya(Na+1 − i)xa(Na + 1 − i) (2 ≤ i ≤ Na) for curability, we consider the ith test codeword test(i), which is obtained by stripping ya(Na + 1 − i)xa(Na + 1 − i) off from tsp(i − 1). Then we attempt to decode ps2;test(i). If the a-pair is curable, then tsp(i) = test(i), otherwise, tsp(i) = tsp(i − 1).
We repeat the above-mentioned procedure and  is what we call sp. For example, tsp(0) of the polyhedron shown in Fig. 2b is 855610454. The a-pair 10454 is non-curable (Supplementary Fig. S3a), while the a-pair 8556 is curable (Supplementary Fig. S3b). As a result, sp = 10454. Since the polyhedron is encoded as 458585574755433: 10454, we call it a 458585574755433;10454-polyhedron, or a 4(58)25274752432;10454-polyhedron for short.
is what we call sp. For example, tsp(0) of the polyhedron shown in Fig. 2b is 855610454. The a-pair 10454 is non-curable (Supplementary Fig. S3a), while the a-pair 8556 is curable (Supplementary Fig. S3b). As a result, sp = 10454. Since the polyhedron is encoded as 458585574755433: 10454, we call it a 458585574755433;10454-polyhedron, or a 4(58)25274752432;10454-polyhedron for short.
Representative codeword
Our encoding starts with choosing an initial side. A different initial side for the same polyhedron may give a different p3-codeword. There are 2E possible initial sides for a polyhedron. Here, E is the number of edges on the polyhedron. We also examine the mirror-image polyhedron, which gives additional 2E possibilities. A maximum of 4E different codewords can be obtained from a polyhedron and its mirror image. To determine the representative one, we introduce the lexicographical number Lex(p3). Given that ps2 and sp can be read as positive F- and 2Nna-digit integers, we define Lex(p3) as the concatenation of the two numbers. Here, Nna is the number of non-curable a-pairs. We use the codeword with the smallest Lex(p3) as the representative one.
Non-simple polyhedron
On the analogy of the n-regular graph21, we call the polyhedron whose vertices are all degree n the n-regular polyhedron. 3-regular polyhedra are simple, while, for n > 3, n-regular polyhedra are non-simple. In encoding [decoding], if we regard that two dangling sides are chained when they contribute to the same vertex contributed by (n − 1) transparent polygons [polygons] and modify an i-vertex to be a vertex contributed by a pair of two dangling sides and n transparent polygons [polygons], our p3-code is straightforwardly applicable to n-regular polyhedra. For example, the octahedron is encoded as “4-regular 38”. The icosahedron is “5-regular 320”. However, if a non-simple polyhedron is non-regular, this method cannot be used. To deal with all non-simple polyhedra, we formulate a method that uses a one-to-one correspondence between a non-simple polyhedron and its associated simple one as described below.
Any non-simple polyhedron can be transformed into its associated simple polyhedron by cutting every vertex of degree d (>3) and replacing it with a d-gonal cross section22. For example, a non-simple pentagonal pyramid can be transformed into a pentagonal prism by cutting the apex (Fig. 4a,b). By marking the cross sections, a one-to-one correspondence can be established between any non-simple polyhedron and its associated simple one. Using the one-to-one correspondence, we encode a non-simple polyhedron. Here, we modify the s-side to be the smallest-ID dangling side in real polygons (not cross sections) so that the face, edge and vertex IDs of a non-simple polyhedron determined from its associated simple polyhedron using an algorithm described below conform to those determined directly from itself using the algorithm described above. The p3-codeword of a non-simple polyhedron is generated as follows:
-
1
Choose a side of a non-simple polyhedron as an initial side.
-
2
Construct its associated simple polyhedron by cutting every vertex of degree d (>3) and replacing it with a d-gonal cross section.
-
3
Encode the associated simple polyhedron from the initial side corresponding to the one determined in the procedure 1.
-
4
Put a dot on p2(i) if the polygon i is the cross section; for example, a codeword for the pentagonal pyramid is
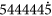 , or
, or  for short, indicating that the polygon 7 is a cross section.
for short, indicating that the polygon 7 is a cross section. -
5
The edge and face IDs can be assigned as illustrated in Fig. 4c.
Non-simple polyhedron.
(a) A pentagonal pyramid. (b) The simple polyhedron obtained by cutting the degree-five vertex of the pentagonal pyramid shown in (a). The cross section is coloured blue. (c) How to assign edge and face IDs, being expressed with Schlegel diagrams. We first assign edge and face IDs to the associated simple polyhedron. If we shrink the cross sections to the vertices, some edges and faces disappear. We therefore relabel the edge and face IDs. The red and blue numbers are edge and face IDs, respectively.
Since ps2 contains dots, it is not a number. We therefore define Lex(ps2) as the concatenation of two numbers ps2(1) and ps2(2). Here, ps2(1) is a number obtained from ps2 by replacing every number without a dot to 0 and then by removing all dots, while ps2(2) is obtained by removing all dots from ps2. For example, Lex is the concatenation of 0000005 and 5444445, namely, 00000055444445.
is the concatenation of 0000005 and 5444445, namely, 00000055444445.
Note that, if a vertex is concave, cutting the vertex may not be well defined. However, by assuming that a polyhedron is flexible, we can inflate it so that a concave vertex becomes a convex one. Then we can cut the vertex.
Decoding is achieved easily. We first construct the associated simple polyhedron and then shrink the cutting sections to the vertices.
The duality of polyhedra can be used to make a codeword more compact. Every polyhedron has its associated dual, which is constructed as follows21:
-
1
Draw a vertex vi* of the dual polyhedron on each face fi of the original polyhedron.
-
2
Draw an edge eij* of the dual, if the faces fi and fj share an edge e, to connect the vertices vi* and vj* such that eij* crosses e, but does not cross the other edges.
There is a one-to-one correspondence between the original polyhedron and its dual. For example, the dual of an octahedron is a hexahedron (Fig. 5a,b). Reversely, the dual of a hexahedron is an octahedron (Fig. 5b). A p3-codeword for the octahedron is 66( )6, while a p3-codeword for the hexahedron is 46. Using the duality, we encode the octahedron as ★46. Here, “★” indicates that the octahedron is the dual of the 46-polyhedron. We define Lex (★46) as the concatenation of Lex (★), which we define as 1 and Lex(46). Therefore, Lex (★46) is 1444444. On the other hand, Lex(66(
)6, while a p3-codeword for the hexahedron is 46. Using the duality, we encode the octahedron as ★46. Here, “★” indicates that the octahedron is the dual of the 46-polyhedron. We define Lex (★46) as the concatenation of Lex (★), which we define as 1 and Lex(46). Therefore, Lex (★46) is 1444444. On the other hand, Lex(66( )6) is 0040404040404066464646464646. Since Lex (★46) is the smallest, the representative p3 for the octahedron is ★46, which is more compact than 66(
)6) is 0040404040404066464646464646. Since Lex (★46) is the smallest, the representative p3 for the octahedron is ★46, which is more compact than 66( )6. We also note that the hexahedron can be encoded as ★66(
)6. We also note that the hexahedron can be encoded as ★66( )6, but it is not the representative codeword. For reference, the representative p3-codewords for the tetrahedron, hexahedron, octahedron, dodecahedron and icosahedron are 34, 46, ★46, 512 and ★512, respectively.
)6, but it is not the representative codeword. For reference, the representative p3-codewords for the tetrahedron, hexahedron, octahedron, dodecahedron and icosahedron are 34, 46, ★46, 512 and ★512, respectively.
Consider that we calculate p3 for a polyhedron by encoding its dual for a given initial side of the original polyhedron. To determine the initial side for encoding the dual, we use the one-to-one correspondence between the original polyhedron and its dual. For example, in encoding an octahedron shown in Fig. 5, when we choose the side cb of the polygon cbf as the initial side, the edge cb is the edge 1 and the vertex c is the vertex 1. The edge and vertex are mapped to the edge hl and face hlmi of the dual. Using this relation, we choose the initial side for encoding the dual so that 1s are assigned to the edge hl and face hlmi. Thus, the initial side is determined to be the side hl of the polygon hlmi.
Our p3-code is more robust and efficient than the previous methods for polyhedra1,11,12,13,14,15,16 (see Supplementary Note). However, what is really stupendous is that only our theory can be generalized to polyhedral tilings as described below.
Code for polychora
We regard a polychoron as a tiling by polyhedra of the surface of a four-dimensional object that is topologically the same as a four-dimensional sphere. We assume that polyhedra are glued together such that (1) any pair of polyhedra meet only at their faces, edges, or vertices and that (2) each face of each polyhedron meets exactly one other polyhedron along a ridge. The 0-face, peak and ridge are a point, line segment and area on the polychoron, where the vertices, edges and faces of polyhedra meet, respectively (Supplementary Fig. S1c–e). The interior space of a polyhedron is the cell of the polychoron.
We first deal with polychora whose peaks are all contributed by three polyhedra. Afterwards, the method will be generalized to polychora in general. The p4-codeword consists of a polyhedron-sequence codeword (ps3) and a face-pairing codeword (fp) and is denoted as p4 = ps3;fp.
The ps3-codeword is denoted as

where C is the number of cells on the polychoron and p3(i) is the p3-codeword for the polyhedron i. To assign IDs to the polyhedra, we use edge (face) IDs ij. Here, the edge (face) ij is the jth edge (face) of the polyhedron i. In encoding, each polyhedron is coloured at first, but gets transparent when encoded. We call a face of a transparent polyhedron glued to a coloured one a dangling face. The smallest-ID dangling face (s-face) plays a key role in encoding. The ps3-codeword is generated as follows (Fig. 6 and Supplementary Fig. S4):
-
1
-
(a) Choose a face of a polyhedron and an edge of that face as the initial face and edge, respectively; the polyhedron 1 is the one having the initial face.
-
(b) Determine p3(1) by encoding the polyhedron 1 in such a way that the face 11 (edge 11) becomes the initial face (edge).
-
(c) Make the polyhedron 1 transparent except for the vertices and edges.
-
-
2
-
(a) The next polyhedron i (2 ≤ i ≤ C) is the coloured one glued to the s-face.
-
(b) Determine p3(i) by encoding the polyhedron i in such a way that the face i1 (edge i1) is glued to the s-face (the smallest-ID edge of the s-face).
-
(c) Make the polyhedron i transparent except for the vertices and edges.
-
-
3
-
(a) Repeat the procedure 2 until all polyhedra get transparent.
-
Encoding a polychoron.
Procedures are illustrated with three-dimensional Schlegel diagrams (a projection from four- to three-dimensional space). The polychoron abcdefgh consists of two 3333-polyhedra and four 34443-polyhedra. The face abc and edge ab of the outside polyhedron abcd are chosen as the initial face and edge, respectively. The red lines indicate the s-face and the dashed one indicates the smallest-ID edge of the s-face. See Supplementary Fig. S4 for details in the edge and face IDs. Note that a counter CW direction around a face of inside polyhedra on the Schlegel diagram, for example f→e→g around the face feg of the polyhedron fegh, corresponds to a CW direction around its corresponding face on the polychoron in four-dimensional space.
As with the case of polyhedra, this method can be used to assign cell, ridge, peak and 0-face IDs to polychora in general.
To define zeroth tentative face-pairing codeword tfp(0), we explain plots for polychora. If a pair of two dangling faces contribute to a peak contributed by two transparent polyhedra, the dangling faces are considered to be chained. A single dangling face or chained dangling faces form a plot; the plot here is a two-dimensional object. We assign plot IDs so that the smallest-ID face of the plot x is the face x. If the polyhedron i in Pi − 1 is glued to plots other than the s-plot, we call them a-plots. By the a-pair wzv, we mean that the face w (of the polyhedron i) is glued to the face v of the a-plot v in such a way that the edge z (of the face w) is glued to the smallest-ID edge of the face v. By collecting the a-pairs, tfp(0) is denoted as

Here, wa(i) > va(i) and wa(i) < wa(i + 1).
In decoding, by a dangling face, we mean a face that is not glued to the other polyhedron. If a pair of dangling faces contribute to a peak that is also contributed by three polyhedra, we call that peak an illegal peak (i-peak). The i-peak can be rectified by gluing together the two dangling faces contributing to it. The original polychoron can be recovered from its ps3;tfp(0) as follows (Supplementary Figs S5 to S7):
1.
-
(a) Decode p3(1) to obtain the polyhedron 1, assigning face and edge IDs.
2.
-
(a) Decode p3(i) to obtain the next polyhedron i (2 ≤ i ≤ C), assigning face and edge IDs.
-
(b) Glue the face i1 of the polyhedron i to the s-face of Di−1 in such a way that the edge i1 is glued to the smallest-ID edge of the s-face.
-
(c) If wa(n) (1 ≤ n ≤ Na) is the face ID of the polyhedron i, then glue the face wa(n) to the face va(n) of Di−1 in such a way that the edge za(n) is glued to the smallest-ID edge of the face va(n).
-
(d) If i-peaks are generated, then rectify them and repeat this procedure until no i-peaks remain.
3.
-
(a) Repeat the procedure 2 until all polyhedra are placed.
By an similar argument for sp, the redundancy in tfp(0) can be removed step-by-step with generating tfp(1), tfp(2), tfp(3), ··· and tfp(Na) is what we call fp.
A maximum of 12P different p4-codewords can be obtained from a polyhedron and its mirror image, where P is the number of peaks on the polychoron. Given that ps3 and fp can be read as C- and 3Nna -digit numbers, respectively, we define Lex(p4) as the concatenation of the two numbers. We use the lexicographically smallest p4 as the representative one.
Affected polychora
We first define the degree of a peak as the number of polyhedra contributing to that peak. We call a peak of degree more than three an affected peak. We say a polychoron without an affected peak to be non-affected. Reversely, an affected polychoron has one or more affected peaks. The p4-code for non-affected polychora formulated above can be generalized to affected ones by using a one-to-one correspondence between an affected polychoron and its associated non-affected one as described below.
Any affected polychora can be transformed into a non-affected one by cutting its affected peaks. However, when different affected peaks are incident to the same 0-face, different non-affected polychora are obtained depending on the order of cutting. Therefore, we first assign peak IDs and then cut the affected peaks in the ascending order of peak ID.
Suppose that we create a cross-section cell (cs-cell) by cutting an affected peak XY, connecting the 0-faces X and Y. We say its 0-face to be type-X (type-Y), if it is the cross section of a peak incident to X (Y). The ridges of the cs-cell are classified into three types: type-X ridges consisting of only type-X 0-faces, type-XY ridges consisting of both type-X and type-Y 0-faces and type-Y ridges consisting of only type-Y 0-faces. In other words, by cutting a peak XY, it is mapped to a cs-cell in such a way that its endpoints are mapped to either type-X or type-Y ridges. Note that the type-X and -Y ridges do not adjoin each other because the type-XY ridges separate them and that the number of the type-XY ridges is the same as the degree of the peak XY. In the example shown in Fig. 7, by cutting the affected peak XY of degree four, the 0-faces X and Y are mapped to the cross-section ridges a′b′c′d′ and e′f′g′h′, respectively. Four cross-section ridges a′d′h′e′, b′a′e′f′, c′b′f′g′ and d′c′g′h′ are type-XY.
How to deal with affected peaks.
(a) Three-dimensional Schlegel diagram of a polychoron abcdefghXY. The hexahedron abcdefgh is the outside polyhedron. The red peak XY is an affected peak contributed by four polyhedra abfeXY, bcgfXY, dcghXY and adheXY. (b) Three-dimensional Schlegel diagram of a polychoron obtained by cutting the affected peak XY.
Based on the above discussion, an affected polychoron can be encoded as follows:
-
1
Choose a face and an edge of an affected polychoron as an initial face and edge and then assign peak IDs.
-
2
Cut the affected peaks in the ascending order of peak ID.
-
3
Encode the associated non-affected polychoron from the initial face and edge corresponding to the ones used in procedure (1).
-
4
To identify the cs-cell that is created when we cut an affected peak, we denote, for example, the p3-codeword for a cs-hexahedron as
 . Here, four double lines on 4 designate that the cs-hexahedron is mapped from the affected peak of degree four and that the four 4-gonal faces contribute to the type-XY ridges.
. Here, four double lines on 4 designate that the cs-hexahedron is mapped from the affected peak of degree four and that the four 4-gonal faces contribute to the type-XY ridges.
For example, a p4-codeword for a polychoron shown in Fig. 7a is  , where H = 46 and
, where H = 46 and  .
.
Decoding is achieved easily. We first reproduce the associated non-affected polychoron and then shrink the cs-cells to the corresponding affected peaks.
To define Lex(p4), we define Lex(ps3) for a non-simple polychoron as the concatenation of Lex(ps3(1)) and Lex(ps3(2)). Here, ps3(1) is the codeword obtained from ps3 as follows. We first replace every p3 with 0 except p3s for the cs-cells corresponding to the affected peaks. We then deal with the p3s for the affected peaks and replace the digits without double lines with 0 and remove the double lines. The ps3(2)-codeword is the one obtained by removing double lines from ps3. For example, Lex( ) is the concatenation of 0000000X and HHHHHHHH, namely, 0000000XHHHHHHHH. Here, X = 044440.
) is the concatenation of 0000000X and HHHHHHHH, namely, 0000000XHHHHHHHH. Here, X = 044440.
As in the case of polyhedra, the duality of polychora20 can be used to make a codeword more compact. For example, by using the duality, the representative p4-codewords for 5-, 8-, 16-, 24-, 120- and 600-cells12 are encoded as T4, H8, ★H8, O24, D12 and ★D12, respectively. Here, T, O and D are the representative p3-codewords for the tetrahedron 34, octahedron ★H and dodecahedron 512, respectively. Note that “★” in “★H8” indicates the dual of H8 and Lex (★p4) is defined as the concatenation of Lex (★) and Lex(p4).
Describing a polyhedral tiling
Since a complex of polyhedra can be regarded as a partial polychoron, the p4-code can be used to describe the arrangement of polyhedra in polyhedral tilings. The complex of polyhedra shown in Fig. 8, for example, is encoded as a partial p4-codeword OtHG3rd4(HG3rd)4H. Here, by a partial p4, we mean that decoding it results in a partial polychoron. Ot (=464(46)44) and H (=46) are the representative p3s of the truncated octahedron and hexahedron, respectively. G3rd (=6(48)3(64)6(84)36) is the third smallest p3 of the great rhombicuboctahedron.
Codeword for a complex of polyhedra.
A central truncated octahedron (green) is surrounded by six hexahedra (blue) and eight great rhombicuboctahedra (yellow). By choosing the 4-gon having the initial edge indicated by the arrow as the initial face, the arrangement is encoded as OtHG3rd4(HG3rd)4H. The numbers near the polyhedra are their polyhedron IDs.
Discussion
In this work, we have created the theory of polyhedral tilings, which allows us to convert a local arrangement of polyhedra into a partial p4-codeword that represents what polyhedra are tiled in what way. Traditionally, the index c3c4c5∙∙∙ has been used to classify polyhedra in polyhedral tilings of liquids, glasses, grains and foams, where ci is the number of i-gons on the polyhedron1,2,3,4,5,6,9,11. However, the index sometimes fails to distinguish polyhedra with different structures, which prevents a close investigation of disordered structures. For example, the 35664453-polyhedron and 34566543-polyhedrdon have the same index, 2222000···. Although the Weinberg code may be a possible remedy and has been used recently11, its codeword is lengthy and therefore redundant, still hampering our understanding of disordered structures. For example, the Weinberg codeword of the most frequently found polyhedron in the Poisson-Voronoi tessellation is “ABCACDEFAFGHIBIJKDKLELMGMNHNJNMLKJIHGFEDCB”. In contrast, using our p3 code, the same polyhedron is encoded as “356645445”. We also note that when the Voronoi polyhedron associated with an atom is encoded as 356645445, the atom is surrounded by neighbouring atoms forming a ★356645445-polyhedron. Our method thus allows us to describe polyhedral tilings succinctly, which is essential to understand disordered structures. In addition, although the short-range order can be studied by the previous methods, the long-range order cannot. Only our theory allows us to characterize what polyhedra are tiled in what way and thereby paves the way to study from short- to long-range order of disordered structures in a systematic way. Moreover, our theory can be generalized to higher-dimensional polytopes to study disordered structures of any dimension.
Additional Information
How to cite this article: Nishio, K. and Miyazaki, T. How to describe disordered structures. Sci. Rep. 6, 23455; doi: 10.1038/srep23455 (2016).
References
Bernal, J. D. The Bakerian Lecture, 1962. The Structure of Liquids. Proc. R. Soc. Lond. A 280, 299–322 (1964).
Finney, J. Random Packings and Structure of Simple Liquids. 1. Geometry of Random Close Packing. Proc. R. Soc. Lond. A 319, 479–493 (1970).
Finney, J. Random Packings and Structure of Simple Liquids. 2. Molecular Geometry. Proc. R. Soc. Lond. A 319, 495–507 (1970).
Yonezawa, F. Glass Transition and Relaxation of Disordered Structures. Solid State Phys. 45, 179–254 (1991).
Sheng, H. W., Luo, W. K., Alamgir, F. M., Bai, J. M. & Ma, E. Atomic packing and short-to-medium-range order in metallic glasses. Nature 439, 419–425 (2006).
Hirata, A. et al. Geometric Frustration of Icosahedron in Metallic Glasses. Science 341, 376–379 (2013).
Nishio, K., Kōga, J., Yamaguchi, T. & Yonezawa, F. Confinement-Induced Stable Amorphous Solid of Lennard–Jones Argon. J. Phys. Soc. Jpn. 73, 627–633 (2004).
Nishio, K., Miyazaki, T. & Nakamura, H. Universal Medium-Range Order of Amorphous Metal Oxides. Phys. Rev. Lett. 111, 155502 (2013).
Kraynik, A. M., Reinelt, D. A. & van Swol, F. Structure of random monodisperse foam. Phys. Rev. E 67, 031403 (2003).
Ramella, M., Boschin, W., Fadda, D. & Nonino, M. Finding galaxy clusters using Voronoi tessellations. Astron. Astrophys. 368, 11 (2001).
Lazar, E. A., Mason, J. K., MacPherson, R. D. & Srolovitz, D. J. Complete Topology of Cells, Grains and Bubbles in Three-Dimensional Microstructures. Phys. Rev. Lett. 109, 095505 (2012).
Coxeter, H. S. M. Introduction to Geometry, Ch. 10, 148–159; Ch. 22, 396–414 (Wiley, 1989).
Weinberg, L. A Simple and Efficient Algorithm for Determining Isomorphism of Planar Triply Connected Graphs. IEEE Trans. Circuit Theory 13, 142–148 (1966).
Manolopoulos, D. E., May, J. C. & Down, S. E. Theoretical studies of the fullerenes: C34 to C70. Chem. Phys. Lett. 181, 105–111 (1991).
Brinkmann, G. Problems and scope of spiral algorithms and spiral codes for polyhedral cages. Chem. Phys. Lett. 272, 193–198 (1997).
Fowler, P. W. & Manolopoulos, D. E. An Atlas of Fullerenes, Ch. 2, 15–42 (Dover Publications, 2007).
Friedrichs, O. D., Dress, A. W. M., Huson, D. H., Klinowski, J. & Mackay, A. L. Systematic enumeration of crystalline networks. Nature 400, 644–647 (1999).
Lord, E. A., Mackay, A. L. & Ranganathan, S. New Geometries for New Materials, Ch. 8.8, 145–149 (Cambridge University Press, 2006).
Cromwell, P. R. Polyhedra, Ch. 5, 181–218 (Cambridge University Press, 1999).
Ziegler, G. M. Lectures on Polytopes, Ch. 5, 127–148 (Springer, 2012).
Wilson, R. J. Introduction to Graph Theory, Ch. 1, 8–31 (Pearson, 2012).
Wilson, R. & Stewart, I. Four Colors Suffice: How the Map Problem Was Solved, Ch. 3 and 4, 28–54, (Princeton University Press, 2013).
Persistence of Vision Pty. Ltd., Williamstown, Victoria, Australia. http://www.povray.org/
Author information
Authors and Affiliations
Contributions
K.N. conceived the original idea of code for polytopes. K.N. and T.M. polished up the idea.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Nishio, K., Miyazaki, T. How to describe disordered structures. Sci Rep 6, 23455 (2016). https://doi.org/10.1038/srep23455
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep23455
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


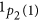 ) to the sides of the polygon 1 from the initial side in a clockwise (CW) direction.
) to the sides of the polygon 1 from the initial side in a clockwise (CW) direction. ) to the sides of the polygon i from the side glued to the s-side in a CW direction.
) to the sides of the polygon i from the side glued to the s-side in a CW direction.


 ) to its sides in a CW direction. The resultant object is D1.
) to its sides in a CW direction. The resultant object is D1. ) to its sides in a CW direction.
) to its sides in a CW direction.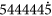 , or
, or  for short, indicating that the polygon 7 is a cross section.
for short, indicating that the polygon 7 is a cross section.



 . Here, four double lines on 4 designate that the cs-hexahedron is mapped from the affected peak of degree four and that the four 4-gonal faces contribute to the type-XY ridges.
. Here, four double lines on 4 designate that the cs-hexahedron is mapped from the affected peak of degree four and that the four 4-gonal faces contribute to the type-XY ridges.