Abstract
Design and synthesis of three-dimensional metallic carbons are currently one of the hot issues in contemporary condensed matter physics because of their fascinating properties. Here, based on first-principles calculations, we discover a novel stable metallic carbon allotrope (termed H18 carbon) in  (
( ) symmetry with a mixed sp2-sp3 hybridized bonding network. The dynamical stability of H18 carbon is verified by phonon mode analysis and molecular dynamics simulations and its mechanical stability is analyzed by elastic constants, bulk modulus and shear modulus. By simulating the x-ray diffraction patterns, we propose that H18 carbon would be one of the unidentified carbon phases observed in recent detonation experiments. The analysis of the band structure and density of states reveal that this new carbon phase has a metallic feature mainly due to the C atoms with sp2 hybridization. This novel 3D metallic carbon phase is anticipated to be useful for practical applications such as electronic and mechanical devices.
) symmetry with a mixed sp2-sp3 hybridized bonding network. The dynamical stability of H18 carbon is verified by phonon mode analysis and molecular dynamics simulations and its mechanical stability is analyzed by elastic constants, bulk modulus and shear modulus. By simulating the x-ray diffraction patterns, we propose that H18 carbon would be one of the unidentified carbon phases observed in recent detonation experiments. The analysis of the band structure and density of states reveal that this new carbon phase has a metallic feature mainly due to the C atoms with sp2 hybridization. This novel 3D metallic carbon phase is anticipated to be useful for practical applications such as electronic and mechanical devices.
Similar content being viewed by others
Introduction
Carbon has a variety of structural allotropes due to its ability of different hybridizations1. It is well known that there exist three carbon allotropes in natural materials, that is, graphite, diamond and amorphous carbon, containing the sp2, sp3 and mixed sp2/sp3 hybridized carbon atoms2, respectively. In the past three decades, intensive theoretical and experimental efforts have been focused on synthesizing new allotropes of carbon, among which, the zero-dimensional (0D) fullerenes3, one-dimensional (1D) carbon nanotubes4 and two-dimensional (2D) graphene5 are the three most prototypical examples. So far, many new carbon allotropes such as 1D sp-carbyne, 2D sp-sp2-graphyne and three-dimensional (3D) sp-sp3-yne-diamond have been experimentally fabricated or theoretically predicted6,7, most of them exhibit their intriguing mechanical and electronic properties. Recently, a new carbon allotrope with hardness even higher than diamond has also been observed by compressing graphite with pressure over 17 GPa8. Motivated by this experimental finding, several carbon crystalline phases such as monoclinic M-carbon9, bct-C4 carbon10, W-carbon11, O-carbon12 and Z-carbon13 were proposed to simulate this high-pressure carbon phase. These prototypical examples have given rise to significant impacts in material and information sciences, stimulating experimental and theoretical attentions on carbon allotropes14,15,16,17,18,19,20,21,22,23.
Among various types of carbon materials, metallic carbon allotropes exhibit more fascinating properties, e.g., a highly efficient catalytic property due to its high electronic density of states (DOS) at the Fermi level24. It was also identified that metallic carbon becomes magnetic when the Stoner-like criterion25,26 is satisfied. Furthermore, metallic carbon showed a number of intriguing properties such as phonon-plasmon coupling27, superconductivity28,29 and negative differential resistance30. Consequently, the exploration of metallic carbon candidates have attracted considerable attention in the synthesis and design of new carbon allotropes. However, all of the 3D carbon allotropes mentioned above are semiconductors or insulators.
There have so far been few progresses in search of 3D metallic carbon. Some hypothetical 3D carbon allotropes such as ThSi2-type tetragonal carbon31, hexagonal H-6 carbon32 and K4 carbon33 have been proposed to be metallic. However, all of such structures were found to be dynamically unstable19,34,35. In 2012, a simple cubic phase of carbon was reported to be metallic under 3 TPa, but it becomes unstable when pressure is removed36. Recently, a 3,4-connected T6 carbon allotrope was proposed to be metallic, but it was also unstable at temperature about 500 K37. More recently, a 3D metallic K6 carbon with pure sp3 hybridization was reported to have a high DOS at the Fermi level38, however, its stability is too low to be synthesized. To our knowledge, all of these theoretical predictions of 3D metallic carbon allotropes have not been experimentally realized so far.
Here, based on first-principles total-energy and phonon calculations39,40,41,42,43,44,45,46, we discover a new stable 3D metallic carbon allotrope in  (
( ) symmetry with a mixed sp2-sp3 hybridized bonding network. This new phase is composed of eighteen atoms per hexagonal primitive cell (hereafter termed H18 carbon), having a larger atom density of 3.135 g/cm3 compared to 2.28 g/cm3 for graphite. The calculated elastic constants show that the H18 carbon is a brittle material. From the analysis of the phonon spectra, we find that H18 carbon does not have any unstable vibration modes. Interestingly, the simulated x-ray diffraction (XRD) pattern of H18 carbon matches one of the unidentified carbon phases observed in recent detonation experiments47. The calculated band structure and DOS of H18 carbon manifest a metallic feature mainly due to the C atoms with sp2 hybridization. The H18 carbon has great potential application in electronics, mechanics and some other related fields due to its novel properties.
) symmetry with a mixed sp2-sp3 hybridized bonding network. This new phase is composed of eighteen atoms per hexagonal primitive cell (hereafter termed H18 carbon), having a larger atom density of 3.135 g/cm3 compared to 2.28 g/cm3 for graphite. The calculated elastic constants show that the H18 carbon is a brittle material. From the analysis of the phonon spectra, we find that H18 carbon does not have any unstable vibration modes. Interestingly, the simulated x-ray diffraction (XRD) pattern of H18 carbon matches one of the unidentified carbon phases observed in recent detonation experiments47. The calculated band structure and DOS of H18 carbon manifest a metallic feature mainly due to the C atoms with sp2 hybridization. The H18 carbon has great potential application in electronics, mechanics and some other related fields due to its novel properties.
Results
Figure. 1 shows the structure of H18 carbon with a 3D  -
- hybridized bonding network in
hybridized bonding network in  (
( ) symmetry. Here, the hexagonal primitive cell contains eighteen C atoms with equilibrium lattice parameters a = b = 7.125 Å, c = 2.605 Å. The C1, C2 and C3 atoms in Fig. 1 are bonded to four, four and three neighboring carbon atoms, thus forming
) symmetry. Here, the hexagonal primitive cell contains eighteen C atoms with equilibrium lattice parameters a = b = 7.125 Å, c = 2.605 Å. The C1, C2 and C3 atoms in Fig. 1 are bonded to four, four and three neighboring carbon atoms, thus forming  ,
,  and
and  bonds, respectively. The calculated bond lengths
bonds, respectively. The calculated bond lengths  ,
,  ,
,  and
and  are 1.591, 1.631, 1.475 and 1.317 Å, respectively. Note that
are 1.591, 1.631, 1.475 and 1.317 Å, respectively. Note that  is between the bond lengths (1.420 and 1.544 Å) of graphite and diamond which have
is between the bond lengths (1.420 and 1.544 Å) of graphite and diamond which have  and
and  bonds, respectively. Because of a mixed bonding of
bonds, respectively. Because of a mixed bonding of  and
and  ,
,  carbon has five different bond angles of 107.5°, 110.1°, 110.4°, 115.2° and 129.6°, contrasting with 109.5° for
carbon has five different bond angles of 107.5°, 110.1°, 110.4°, 115.2° and 129.6°, contrasting with 109.5° for  hybridized diamond and 120° for
hybridized diamond and 120° for  hybridized graphite. Such several bond distortions in
hybridized graphite. Such several bond distortions in  carbon implies the presence of strain, leading to a decrease of the relative stability compared to diamond and graphite as discussed below. In Table 1, we list the calculated lattice parameters, equilibrium densities, bond lengths and cohesive energies of diamond, graphite, Rh6, T6, BC8 and H18 carbons. We find that our results agree well with previous DFT calculations and experiments21,22,37. We note that the equilibrium bulk atom density of H18 carbon is 3.135 g/cm3, larger than that (2.28 g/cm3) of graphite21.
carbon implies the presence of strain, leading to a decrease of the relative stability compared to diamond and graphite as discussed below. In Table 1, we list the calculated lattice parameters, equilibrium densities, bond lengths and cohesive energies of diamond, graphite, Rh6, T6, BC8 and H18 carbons. We find that our results agree well with previous DFT calculations and experiments21,22,37. We note that the equilibrium bulk atom density of H18 carbon is 3.135 g/cm3, larger than that (2.28 g/cm3) of graphite21.
In order to check the stability of H18 carbon, we perform the analyses of total energy, phonon mode and elastic constants as well as molecular dynamic (MD) simulations.
(i) Total energy: Figure 2 shows the calculated total energies of H18 carbon, diamond, graphite, BC8, T6 and Rh6 carbon as a function of volume per atom. It is seen that graphite and diamond are more thermodynamically stable than H18 carbon as well as other carbon phases. We note, however, that H18 carbon is not only much more stable than BC8 carbon (which has been suggested to be the derivative of cubic diamond under pressure of ∼1100 GPa48,49,50), but also more stable than T6 carbon and Rh620,37. In particular,  carbon has a relatively smaller 18-atom hexagonal unit cell compared to Rh6 (see Fig. 2). From the energy-volume curves of carbon allotropes (Fig. 2), one expects that Rh6 carbon can be transformed into H18 carbon by applying a certain pressure.
carbon has a relatively smaller 18-atom hexagonal unit cell compared to Rh6 (see Fig. 2). From the energy-volume curves of carbon allotropes (Fig. 2), one expects that Rh6 carbon can be transformed into H18 carbon by applying a certain pressure.
(ii) Phonon mode: The calculated phonon band structure and DOS are displayed in Fig. 3. It is found that there is no negative frequencies throughout the entire Brillioun zone, indicating the dynamical stability of  carbon. In Fig. 3, the highest vibrational frequency of H18 carbon amounts to ∼1837 cm−1 at A point, which is higher than ∼1400 cm−1 of the perfectly
carbon. In Fig. 3, the highest vibrational frequency of H18 carbon amounts to ∼1837 cm−1 at A point, which is higher than ∼1400 cm−1 of the perfectly  bonded diamond51 as well as ∼1600 cm−1 of the π-conjugated graphite52. We note that there exists a wide band gap of ∼230 cm−1 between 1449 and 1679 cm−1 near the K point. These features of phonon spectra of H18 carbon are anticipated to be measured by future experiments. In Fig. 3, we also plot the atom-resolved phonon DOS contributed by C1, C2 and C3 atoms, respectively. Obviously, the highest frequency modes around 1750 cm−1 originate from the vibrations of the strong
bonded diamond51 as well as ∼1600 cm−1 of the π-conjugated graphite52. We note that there exists a wide band gap of ∼230 cm−1 between 1449 and 1679 cm−1 near the K point. These features of phonon spectra of H18 carbon are anticipated to be measured by future experiments. In Fig. 3, we also plot the atom-resolved phonon DOS contributed by C1, C2 and C3 atoms, respectively. Obviously, the highest frequency modes around 1750 cm−1 originate from the vibrations of the strong  C3 − C3 bonds with a bond length of 1.317 Å, while the second highest frequency modes around 1450 cm−1 arise from the mixed
C3 − C3 bonds with a bond length of 1.317 Å, while the second highest frequency modes around 1450 cm−1 arise from the mixed  -
- C2 − C3 bonds with a bond length of 1.475 Å. These characters of H18 carbon are different from both graphite with bond length of 1.420 Å and diamond with bond length of 1.544 Å.
C2 − C3 bonds with a bond length of 1.475 Å. These characters of H18 carbon are different from both graphite with bond length of 1.420 Å and diamond with bond length of 1.544 Å.
(iii) Elastic constants: In the linear elastic regime, the elastic constant tensor is constituted a symmetric 6 × 6 matrix with 21 independent components, where only C11, C12, C13, C33 and C44 are independent in the hexagonal lattice53. According to the Born stability conditions53, the elastic constants of the hexagonal lattice should satisfy  >
> 

 ,
,  > 0,
> 0,  > 0 and
> 0 and  < C33 (C11 + C12). The calculated elastic constants of H18 carbon as well as diamond, T6, BC8 and Rh6 carbons are listed in Table 2. Specifically, the calculated elastic constants Cij of H18 carbon satisfy well all of the conditions, indicating that the structure of H18 carbon is mechanically stable. The bulk modulus and shear modulus obtained by Voigt-Reuss-Hill approximation54 are also listed in Table 2. The magnitude of the bulk modulus of H18 carbon is fairly large as 360 GPa, which amounts to about four fifths of that (435 GPa) of diamond and even larger than that (337 GPa) of T6 carbon37. This result indicates that H18 carbon is more resistant to hydrostatic compression compared to T6 carbon. The B/G ratio of H18 carbon is about 1.0, close to that (0.83) of diamond, implying that H18 carbon can be characterized as a brittle material according to the Paugh criterion55.
< C33 (C11 + C12). The calculated elastic constants of H18 carbon as well as diamond, T6, BC8 and Rh6 carbons are listed in Table 2. Specifically, the calculated elastic constants Cij of H18 carbon satisfy well all of the conditions, indicating that the structure of H18 carbon is mechanically stable. The bulk modulus and shear modulus obtained by Voigt-Reuss-Hill approximation54 are also listed in Table 2. The magnitude of the bulk modulus of H18 carbon is fairly large as 360 GPa, which amounts to about four fifths of that (435 GPa) of diamond and even larger than that (337 GPa) of T6 carbon37. This result indicates that H18 carbon is more resistant to hydrostatic compression compared to T6 carbon. The B/G ratio of H18 carbon is about 1.0, close to that (0.83) of diamond, implying that H18 carbon can be characterized as a brittle material according to the Paugh criterion55.
(iv) MD simulations: To examine the thermal stability of H18 carbon, we carried out the ab initio MD simulations with the canonical (NVT) ensemble at temperature of 300, 1000 and 1500 K, respectively. The system is modeling with a 2 × 2 × 3 supercell containing 216 carbon atoms and the time step of 1 fs is used. The potential energy fluctuation of H18 carbon in MD simulation at 1000 and 1500 K are presented in Fig. (4a,b), respectively. We can see that the potential energy fluctuation are very small and geometry of H18 carbon remains intact after heating up to 1000 K for 6 picoseconds. With the temperature increasing up to 1500 K, we find that the H18 carbon becomes graphitization gradually (see in Fig. (4b)). These results have indicated that H18 carbon, once synthesized, can sustain the structure even at temperature of 1000 K. For comparison, Ab initio MD simulations for T6 carbon with the same setting and a 2 × 4 × 4 supercell containing 192 carbon atoms show that it is unstable even at 500 K37. Based on our MD simulations, we can say that H18 carbon is much more stable than T6 carbon at high temperature.
In addition, to evidence the experimental observation of H18 carbon, we plot the simulated XRD spectra of graphite, diamond, BC8, T6, Rh6 and H18 carbons in Fig. 5(a,b), together with the experimental XRD data of TNT/RDX detonation soot in Fig. 5(c). In the experimental XRD data47, the diffraction lines arising from graphite ( ), diamond (
), diamond ( ) and other unknown (
) and other unknown ( ) carbon phases were reported. As shown in Fig. 5(b,c,i) the (001), (101) and (201) peaks of H18 carbon match well with the experimental XRD spectra located at 34.4°, 37.4° and 45.5°, respectively and (ii) the (111) peak of H18 carbon that overlaps with the (111) peak of diamond can be associated with the second-strongest experimental XRD peak at 43.9°. Meanwhile, the (110) and other peaks of
) carbon phases were reported. As shown in Fig. 5(b,c,i) the (001), (101) and (201) peaks of H18 carbon match well with the experimental XRD spectra located at 34.4°, 37.4° and 45.5°, respectively and (ii) the (111) peak of H18 carbon that overlaps with the (111) peak of diamond can be associated with the second-strongest experimental XRD peak at 43.9°. Meanwhile, the (110) and other peaks of  carbon can not be clearly identified in the experimental XRD patterns, but may be overlapped with neighboring peaks of other carbon phases. Note that the position of (100) and (101) peaks of T6 are very close to the position of (001) and (101) peaks of
carbon can not be clearly identified in the experimental XRD patterns, but may be overlapped with neighboring peaks of other carbon phases. Note that the position of (100) and (101) peaks of T6 are very close to the position of (001) and (101) peaks of  carbon, respectively. Since H18 carbon is thermodynamically more stable than T6 carbon as mentioned above, it is most likely that the experimental XRD peaks near 34° and 37° would be predominantly associated with H18 carbon rather than T6 carbon. Therefore, we propose that
carbon, respectively. Since H18 carbon is thermodynamically more stable than T6 carbon as mentioned above, it is most likely that the experimental XRD peaks near 34° and 37° would be predominantly associated with H18 carbon rather than T6 carbon. Therefore, we propose that  carbon is one of the unidentified carbon phases which were explicitly present in recent detonation experiments47.
carbon is one of the unidentified carbon phases which were explicitly present in recent detonation experiments47.
Comparison of simulated and experimental X-ray diffraction (XRD) patterns.
(a) Simulated XRD patterns for graphite, diamond, BC8, T6 and Rh6 carbon. (b) Simulated XRD patterns for H18 carbon. (c) Experimental XRD patterns for detonation soot (sample Alaska C)47.  ,
,  ,
,  indicate graphite, diamond, unknown-carbon, respectively. The X-ray wavelength we adopted is 1.54059 Å.
indicate graphite, diamond, unknown-carbon, respectively. The X-ray wavelength we adopted is 1.54059 Å.
To provide more physical quantities that are accessible from experiments, we also simulated the Raman spectra of  carbon and compared the results with graphite, diamond and T6 carbon structures. The simulation results are presented in Fig. 6. From Fig. 6, we can see that the E2g mode in graphite is estimated to be 1586 cm−1, which is well agreement with the experimental data of 1581 cm−1 56. The T2g mode in diamond is estimated to be 1326 cm−1, which is close to the experimental data of 1333 cm−1 57. Although the main XRD peaks of T6 and
carbon and compared the results with graphite, diamond and T6 carbon structures. The simulation results are presented in Fig. 6. From Fig. 6, we can see that the E2g mode in graphite is estimated to be 1586 cm−1, which is well agreement with the experimental data of 1581 cm−1 56. The T2g mode in diamond is estimated to be 1326 cm−1, which is close to the experimental data of 1333 cm−1 57. Although the main XRD peaks of T6 and  carbon are close to each other, their Raman spectra show rather different characters. For T6 carbon, there is only one main peak A1g presents at 1762 cm−1. However, we find that, for
carbon are close to each other, their Raman spectra show rather different characters. For T6 carbon, there is only one main peak A1g presents at 1762 cm−1. However, we find that, for  , there are two main peaks A1g at 1035 and 1849 cm−1, respectively. In addition, both T6 and
, there are two main peaks A1g at 1035 and 1849 cm−1, respectively. In addition, both T6 and  carbon also show some weaker peaks (Eg and B2g for T6, E1g and E2g for
carbon also show some weaker peaks (Eg and B2g for T6, E1g and E2g for  ). All the features above may be helpful for identifying this new carbon phase in further experiments.
). All the features above may be helpful for identifying this new carbon phase in further experiments.
Finally, we discuss the electronic properties of H18 carbon. The band structures and partial density of states (PDOS) are displayed in Fig. 7(a,b), respectively. It is seen that the Fermi level crosses the bands near the A and  points, giving rise to the presence of the electron (hole) pocket around A (
points, giving rise to the presence of the electron (hole) pocket around A ( ). Thus, H18 carbon is metallic. It is noted that the metallic feature obtained using the semilocal DFT calculation with the Perdew-Burke-Ernzerhof (PBE) functional is preserved in the hybrid DFT calculation with the Heyd, Scuseria and Ernzerhof (HSE06) functional58,59 [see Fig. 7(a)]. From the PDOS projected onto C1, C2 and C3 atoms [Fig. 7(b)], we find that the electronic states near
). Thus, H18 carbon is metallic. It is noted that the metallic feature obtained using the semilocal DFT calculation with the Perdew-Burke-Ernzerhof (PBE) functional is preserved in the hybrid DFT calculation with the Heyd, Scuseria and Ernzerhof (HSE06) functional58,59 [see Fig. 7(a)]. From the PDOS projected onto C1, C2 and C3 atoms [Fig. 7(b)], we find that the electronic states near  dominantly involve the
dominantly involve the  character of C3. In order to elucidate the origin of the metallic feature in H18 carbon, we calculate the charge density of the partially occupied bands in the energy windows of
character of C3. In order to elucidate the origin of the metallic feature in H18 carbon, we calculate the charge density of the partially occupied bands in the energy windows of  −0.5 to
−0.5 to  + 0.5 eV [see Fig. 7(c)]. It is seen that the
+ 0.5 eV [see Fig. 7(c)]. It is seen that the  orbital of C3 atoms largely contribute to the charge density, forming a delocalized network. On the basis of the PDOS [Fig. 7(b)] and the charge character near
orbital of C3 atoms largely contribute to the charge density, forming a delocalized network. On the basis of the PDOS [Fig. 7(b)] and the charge character near  [Fig. 7(c)], we can say that the metallicity of H18 carbon is attributed to a large delocalization of the
[Fig. 7(c)], we can say that the metallicity of H18 carbon is attributed to a large delocalization of the  orbital of C3 atoms with
orbital of C3 atoms with  hybridization.
hybridization.
Electronic band structures, density of states and decomposed charge density of H18 carbon.
(a) Electronic band structures calculated using GGA-PBE (red lines) and HSE06 hybrid functional (blue lines). (b) The projected density of states (PDOS) for C1, C2 and C3 atom at GGA-PBE level. The Fermi level is set at 0 eV. (c) The charge density isosurfaces (0.01 e/Å3) of the partially occupied band of H18 carbon.
Conclusion
Our first-principles DFT total energy and phonon calculations discover a novel stable carbon allotrope (termed H18 carbon) which is metallic. The analyses of the total energy, phonon mode and elastic constants as well as molecular dynamic simulations obviously show that this new carbon allotrope exists as a stable structure. More importantly, we demonstrate that the H18 carbon may be one of the candidates of the unidentified carbon phases which appeared in the XRD spectrum analysis of a recent detonation experiment. In particular,  carbon has a metallic feature mainly due to the
carbon has a metallic feature mainly due to the  orbitals of
orbitals of  hybridized carbon atoms. Unlike previously reported 3D metallic carbon allotropes,
hybridized carbon atoms. Unlike previously reported 3D metallic carbon allotropes,  carbon can not only keep its metallicity at ambient pressure but also can likely maintain its structure at high temperatures. This novel 3D metallic carbon phase is anticipated to be useful for practical applications such as electronics and mechanics devices. Our findings will attract immediate broad interest and stimulate further experimental and theoretical studies for this new carbon allotrope.
carbon can not only keep its metallicity at ambient pressure but also can likely maintain its structure at high temperatures. This novel 3D metallic carbon phase is anticipated to be useful for practical applications such as electronics and mechanics devices. Our findings will attract immediate broad interest and stimulate further experimental and theoretical studies for this new carbon allotrope.
Methods
The present total-energy and phonon calculations were carried out by using the density functional theory. Both local density approximation (LDA) in the form of Ceperley-Alder39 and the generalized gradient approximation (GGA) developed by Perdew, Burke and Ernzerhof (PBE)40 are adopted for the exchange-correlation potential as implemented in the Vienna 
 simulation package (VASP)41,42,43. All the discussions in this paper are based on the results got by GGA-PBE method, except for special notations. The all-electron projector augmented wave (PAW)44 method is adopted with C 2
simulation package (VASP)41,42,43. All the discussions in this paper are based on the results got by GGA-PBE method, except for special notations. The all-electron projector augmented wave (PAW)44 method is adopted with C 2 2
2 treated as valence electrons. A plane-wave basis set with an energy cutoff of 800 eV is used. The Gaussian smearing with a smearing factor of 0.05 eV is used in the calculations. The Brillouin zone (BZ) is sampled by a 9 × 9 × 21 Monkhorst-Pack (MP) special
treated as valence electrons. A plane-wave basis set with an energy cutoff of 800 eV is used. The Gaussian smearing with a smearing factor of 0.05 eV is used in the calculations. The Brillouin zone (BZ) is sampled by a 9 × 9 × 21 Monkhorst-Pack (MP) special  -point grid including
-point grid including  -point. The geometries are optimized with no symmetry constraints, the convergence criteria employed for both the electronic self-consistent relaxation and the ionic relaxation are set to 10−7 eV and 10−3 eV/Å for electronic energy and Hellmann-Feynman force, respectively. Phonon dispersion curves are calculated by using the package phonopy45,46 with the forces calculated with VASP code. The first-principles molecular dynamics simulations are performed in the canonical (NVT) ensemble with the Nosé thermostat60. Each simulation lasted for 6 ps, with a time step of 1 fs. All the calculations in this work are performed at zero pressure.
-point. The geometries are optimized with no symmetry constraints, the convergence criteria employed for both the electronic self-consistent relaxation and the ionic relaxation are set to 10−7 eV and 10−3 eV/Å for electronic energy and Hellmann-Feynman force, respectively. Phonon dispersion curves are calculated by using the package phonopy45,46 with the forces calculated with VASP code. The first-principles molecular dynamics simulations are performed in the canonical (NVT) ensemble with the Nosé thermostat60. Each simulation lasted for 6 ps, with a time step of 1 fs. All the calculations in this work are performed at zero pressure.
Additional Information
How to cite this article: Zhao, C.-X. et al. H18 Carbon: A New Metallic Phase with sp2-sp3 Hybridized Bonding Network. Sci. Rep. 6, 21879; doi: 10.1038/srep21879 (2016).
References
Miller, E. D., Nesting, D. C. & Badding, J. V. Quenchable Transparent Phase of Carbon. Chem. Mater. 9, 18–22 (1997).
Balaban, A. T. Carbon and its nets. Computers Math. Applic. 17, 397–416 (1989).
Kroto, H. W., Heath, J. R., Obrien, S. C., Curl, R. F. & Smaliey, R. E. C60: Buckminsterfullerene. Nature (London) 318, 162–163 (1985).
Iijima, S. Helical microtubules of graphitic carbon. Nature (London) 354, 56–58 (1991).
Novoselov, K. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Diederich, F. & Kivala, M. All-carbon scaffolds by rational design. Adv. Mater. 22, 803–812 (2010).
Hirsch, A. The era of carbon allotropes. Nature Mater. 9, 868–871 (2010).
Mao, W. L. et al. Bonding changes in compressed superhard graphite. Science 302, 425–427 (2003).
Li, Q. et al. Superhard monoclinic polymorph of carbon. Phys. Rev. Lett. 102, 175506 (2009).
Umemoto, K., Wentzcovitch, R. M., Saito, S. & Miyake, T. Body-centered tetragonal C4: A viable sp3 carbon allotrope. Phys. Rev. Lett. 104, 125504 (2010).
Wang, J. T., Chen, C. F. & Kawazoe, Y. Low-temperature phase transformation from graphite to sp3 orthorhombic carbon. Phys. Rev. Lett. 106, 075501 (2011).
Wang, J. T., Chen, C. F. & Kawazoe, Y. Orthorhombic carbon allotrope of compressed graphite: Ab initio calculations. Phys. Rev. B 85, 033410 (2012).
Zhao, Z. S. et al. Novel superhard carbon: C-centered orthorhombic C8 . Phys. Rev. Lett. 107, 215502 (2011).
Wang, J. T., Chen, C. F., Wang, D. S., Mizuseki, H. & Kawazoe, Y. Phase stability of carbon clathrates at high pressure. J. Appl. Phys. 107, 063507 (2010).
Wang, J. T., Chen, C. F. & Kawazoe, Y. New cubic carbon phase via graphitic sheet rumpling. Phys. Rev. B 85, 214104 (2012).
Sheng, X. L., Yan, Q. B., Ye, F., Zheng, Q. R. & Su, G. T-carbon: A novel carbon allotrope. Phys. Rev. Lett. 106, 155703 (2011).
Wang, X. Q., Li, H. D. & Wang, J. T. Prediction of a new two-dimensional metallic carbon allotrope. Phys. Chem. Chem. Phys. 15, 2024–2030 (2013).
Wang, J. T., Chen, C. F. & Kawazoe, Y. Phase conversion from graphite toward a simple monoclinic sp3-carbon allotrope. J. Chem. Phys. 137, 024502 (2012).
Wang, J. T., Chen, C. F. & Kawazoe, Y. New carbon allotropes with helical chains of complementary chirality connected by ethene-type π-conjugation. Sci. Rep. 3, 03077 (2013).
Wang, J. T., Chen, C. F., Wang E. G. & Kawazoe, Y. A new carbon allotrope with six-fold helical chains in all-sp2 bonding networks. Sci. Rep. 4, 04339 (2014).
Furthmüller, J., Hafner, J. & Kresse, G. Ab initio calculation of the structural and electronic properties of carbon and boron nitride using ultrasoft pseudopotentials. Phys. Rev. B 50, 15606 (1994).
Occelli, F., Loubeyre, P. & Letoullec, R. Properties of diamond under hydrostatic pressures up to 140 GPa. Nature Mater. 2, 151–154 (2003).
Grimsditch, M. & Ramdas, A. K. Brillouin scattering in diamond. Phys. Rev. B 11, 3139 (1975).
Bergeret, C., Cousseau, J., Fernandez, V., Mevellec, J. Y. & Lefrant, S. Spectroscopic evidence of carbon nanotubes metallic character loss induced by covalent functionalization via nitric acid purification. J. Phys. Chem. C 112, 16411–16416 (2008).
Ohldag, H. et al. π-electron ferromagnetism in metal-free carbon probed by soft x-ray dichroism Phys. Rev. Lett. 98, 187204 (2007).
Peng, H. W. et al. Origin and enhancement of hole-induced ferromagnetism in first-row d0 semiconductors Phys. Rev. Lett. 102, 017201 (2009).
Piscanec, S., Lazzeri, M., Robertson, J., Ferrari, A. C. & Mauri, F. Optical phonons in carbon nanotubes: Kohn anomalies, peierls distortions and dynamic effects. Phys. Rev. B 75, 035427 (2007).
Terrones, H. et al. New metallic allotropes of planar and tubular carbon. Phys. Rev. Lett. 84, 1716 (2000).
Kociak, M. et al. Superconductivity in ropes of single-walled carbon nanotubes. Phys. Rev. Lett. 86, 2416 (2001).
Ni, Y. et al. The transport properties and new device design: the case of 6,6,12-graphyne nanoribbons. Nanoscale. 5, 4468 (2013).
Hoffmann, R., Hughbanks, T., Kertesz, M. & Bird, PH. A hypothetical metallic allotrope of carbon. J. Am. Chem. Soc. 105, 4831–4832 (1983).
Tamor, M. A. & Hass, K. C. Hypothetical superhard carbon metal. J. Mater. Res. 5, 2273C2276 (1990).
Itoh, M. et al. New Metallic Carbon Crystal. Phys. Rev. Lett. 102, 055703 (2009).
Yao, Y. et al. Comment on New metallic carbon crystal. Phys. Rev. Lett. 102, 229601 (2009).
Liang, Y., Zhang, W. & Chen, L. Phase stabilities and mechanical properties of two new carbon crystals. Europhys. Lett. 87, 56003 (2009).
Martinez-Canales, M., Pickard, C. J. & Needs, R. J. Thermodynamically stable phases of carbon at multiterapascal pressures. Phys. Rev. Lett. 108, 045704 (2012).
Zhang, S. H., Wang, Q., Chen, X. S. & Jena, P. Stable three-dimensional metallic carbon with interlocking hexagons. PNAS. 110, 18809–18813 (2013).
Niu, C. Y., Wang, X. Q. & Wang, J. T. K6 carbon: A metallic carbon allotrope in sp3 bonding networks J. Chem. Phys. 140, 054514 (2014).
Perdew, J. P. & Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 23, 5048 (1981).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Kresse, G. & Hafner, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Togo, A., Oba, F. & Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106 (2008).
Togo, A. Phonopy, http://phonopy.sourceforge.net/.
Pantea, D., Brochu, S., Thiboutot, S., Ampleman, G. & Schol, G. A morphological investigation of soot produced by the detonation of munitions. Chemosphere 65, 821–831 (2006).
Yin, M. T. Si-1 (BC-8) crystal phase of Si and C: Structural properties, phase stabilities and phase transitions. Phys. Rev. B 30, 1773–1776 (1984).
Johnston, R. L. & Hoffmann, R. Superdense carbon, C8: supercubane or analog of γ-silicon ? J. Am. Chem. Soc. 111, 810–819 (1989).
Knudson, M. D., Desjarlais, M. P. & Dolan, D. H. Shock-wave exploration of the high-pressure phase of carbon. Science 322, 1822–1825 (2004).
Ward, A., Broido, D. A., Stewart, D. A. & Deinzer, G. Ab initio theory of the lattice thermal conductivity in diamond Phys. Rev. B 80, 125203 (2009).
Maultzsch, J., Reich, S., Thomsen, C., Requardt, H. & Ordejón, P. Phonon dispersion in graphite. Phys. Rev. Lett. 92, 075501 (2004).
Mouhat, F. & Coudert, F. X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 90, 224104 (2014).
Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. (London) 65, 350 (1952).
Pugh, S. F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos.Mag. 45, 823–843 (1954).
Ferrari, A. C. et al. Raman spectrum of graphene and graphene layers. Phys. Rev. Lett. 97, 187401 (2006).
Kobashi, K., Nishimura, K., Kawate, Y. & Horiuchi, T. Synthesis of diamonds by use of microwave plasma chemical-vapor deposition: morphology and growth of diamond films. Phys. Rev. B 38, 4067 (1988).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened coulomb potential. J. Chem. Phys. 118, 8207 (2003).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Erratum: Hybrid functionals based on a screened coulomb potential. J. Chem. Phys. 124, 219906 (2006).
Nose, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511C519 (1984).
Acknowledgements
This work is supported by the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant No.20114101110001), the NSFC of China (Grant No. 11504332 and 11274280), the China Postdoctoral Science Foundation (2015M580633) and the National Basic Research Program of China (No. 2012CB921300); Jian-Tao Wang acknowledges support from the NSFC of China (Grant No. 11274356) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB07000000). Jun-Hyung Cho acknowledges support from National Research Foundation of Korea (Grant No. 2015R1A2A2A01003248).
Author information
Authors and Affiliations
Contributions
C.Y.N., C.X.Z., J.H.C., Y.J. and J.T.W. designed the study and wrote the paper; C.Y.N. and C.X.Z. carried out first-principles simulations; Z.J.Q. and X.Y.R. participated in writing of the manuscript; all authors discussed the results and contributed to the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhao, CX., Niu, CY., Qin, ZJ. et al. H18 Carbon: A New Metallic Phase with sp2-sp3 Hybridized Bonding Network. Sci Rep 6, 21879 (2016). https://doi.org/10.1038/srep21879
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep21879
This article is cited by
-
Carbon clusters formed from shocked benzene
Nature Communications (2021)
-
Orthorhombic C36: a sp2–sp3 carbon with pressure-induced metallization and superconductivity
Journal of Materials Science (2021)
-
Novel carbon nano-onions from paraffinum liquidum for rapid and efficient removal of industrial dye from wastewater
Environmental Science and Pollution Research (2020)
-
The art of designing carbon allotropes
Frontiers of Physics (2019)
-
A novel hybrid sp-sp2 metallic carbon allotrope
Frontiers of Physics (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

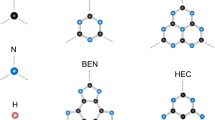

 (
( ) symmetry with single and double bonds. The carbon atoms on 6
) symmetry with single and double bonds. The carbon atoms on 6  (0.2579, 0.1289, 0), 6 m (0.583, 0.7915, 0.5) and 6 m (0.8933, 0.4467, 0.5) Wyckoff positions are denoted by C1 (gray), C2 (orange) and C3 (green), respectively.
(0.2579, 0.1289, 0), 6 m (0.583, 0.7915, 0.5) and 6 m (0.8933, 0.4467, 0.5) Wyckoff positions are denoted by C1 (gray), C2 (orange) and C3 (green), respectively.




