Abstract
We use a newly developed technique that is based on the information flow concept to investigate the causal structure between the global radiative forcing and the annual global mean surface temperature anomalies (GMTA) since 1850. Our study unambiguously shows one-way causality between the total Greenhouse Gases and GMTA. Specifically, it is confirmed that the former, especially CO2, are the main causal drivers of the recent warming. A significant but smaller information flow comes from aerosol direct and indirect forcing and on short time periods, volcanic forcings. In contrast the causality contribution from natural forcings (solar irradiance and volcanic forcing) to the long term trend is not significant. The spatial explicit analysis reveals that the anthropogenic forcing fingerprint is significantly regionally varying in both hemispheres. On paleoclimate time scales, however, the cause-effect direction is reversed: temperature changes cause subsequent CO2/CH4 changes.
Similar content being viewed by others
Introduction
During the past five decades, the earth has been warming at a rather high rate ((1951–2012; 0.12 [0.08 to 0.14] °C per decade), International Panel of Climate Change, IPCC-2013)1, resulting in a scientific and social concern. This warming trend is observed in both field2,3 and model data4 and affects the atmosphere both over the land and over the ocean. Based on the published evidence IPCC attributes this temperature increase to the total increase in radiative forcing and asserts that this is primarily caused by the increase in the atmospheric concentration of CO2 during the last 200 years. However, the warming rate changes with time, raising questions regarding the causes underlying the observed trends5. Another problem is the relatively large uncertainty in the different external forcing components6,7,8,9 that consequently leads to a rather large scatter in the global climate simulations and may have overestimated recent global warming10,11. The following phrase from the executive summary of Ch 10. of the recent IPPC-2013 assessment (after stating that humans activities extremely likely caused more than half of the observed GMTA increase) might serve for summarising the actual situation: “Uncertainties in forcings and in climate models’ temperature responses to individual forcings and difficulty in distinguishing the patterns of temperature response due to greenhouse gases and other anthropogenic forcings prevent a more precise quantification of the temperature changes attributable to greenhouse gases”.
Therefore ‘detection’ and ‘attribution’ are still regarded as key priorities in climate change research. IPCC defines ‘detection’ as the process of demonstrating that climate has changed in some statistical sense, which means that the likelihood of occurrence by chance due to internal variability alone is small. Besides statistical analysis of observed data, typically climate models are used to predict the expected responses to external forcing and then the consistency of this response pattern is evaluated with respect to different components of the climate system1.
The more challenging problem is to ‘attribute’ this detected climate change to the most likely external causes within some defined level of confidence. As already noted in the Third Assessment Report11, unequivocal attribution would require controlled experimentation with the climate system. Since that is not possible, in practice attribution of anthropogenic climate change is understood to mean demonstration that a detected change is ‘consistent with the estimated responses to the given combination of anthropogenic and natural forcing’ and ‘not consistent with alternative, physically plausible explanations of recent climate change that exclude important elements of the given combination of forcings12. Therefore attribution analysis is mainly performed through the application of Global Circulation Models that allow testing for causal relationships between anthropogenic forcing, natural variability and temperature evolutions.
Pattern-based fingerprint studies pioneered by13 have provided strong scientific evidence of a significant human influence on global atmospheric temperature changes. Recent updates based on multimodel analysis14,15,16 confirm that the primary components of external forcing over the past century are human-caused increases in greenhouse gases, stratospheric ozone depletion and change in atmospheric aerosol content, all reflecting human influence on climate16,17.
A recent modelling study18 confirms CO2 as the principal knob governing earth’s temperature. Despite principal plausibility being achieved in this way there are still several open research questions, one being the “missing heat”10,11,19. Also, as the state-of-the-art climate models mostly overestimated the global warming during the last 20 years10, additional data driven and model independent corroboration is desirable to support the attribution assessment1.
As a common practice in data-based attribution studies, the above-mentioned consistency assessment is usually through correlation and/or regression analysis. A fundamental problem here, however, is that correlation between different variables does not necessarily imply causation20. As stated by Barnard21: “That correlation is not causation is perhaps the first thing that must be said.” Therefore the actual high correlation between rising CO2 levels and increasing surface temperatures alone is insufficient to prove that the increased radiative forcing resulting from the increasing GHG atmospheric concentrations is indeed causing the warming of the earth. Another problem contributing to the remaining uncertainty is the unclear feedback mechanism between global temperature variability and GHG dynamics22,23 that could contribute to amplify the global warming rate. A first study based on statistical methods for testing causality of human influence on climate24 applied Granger causality25. They found bi-directional causality between Northern and Southern Hemisphere temperatures, a result that is however not conclusive as these temperatures are not independent from each other and are both driven by the global forcing. Further work26,27,28 based on an improved methodology however confirmed that anthropogenic forcings seem to “Granger cause” temperature changes. In this study, we use a recently developed mathematical method29,30,31,32, which is capable of quantitatively evaluating the drive and feedback causal relation between time series, to address the importance of the different forcing components on climate in a quantitative but model independent way. This new method is based on the information flow (IF) concept31. The whole new formalism is derived from first principles, rather than as an empirically defined ansatz, with the property of causality guaranteed in proven theorems. This is in contrast to other causality analyses, say that based on Granger causality25,33,34 or convergent cross mapping (CCM)35. The resulting formula is concise in form, involving only the common statistics, namely sample covariances. It also allows an explicit discrimination between correlation and causality: causation implies correlation, but not vice versa. For more details, refer to the method section.
Results and Discussion
We use this technique to analyse the recently measured global mean surface air temperature anomalies (GMTA)36 and various reconstructed external forcings covering the period from 1850 to 2005 (156 years)37. To introduce the method we calculate the information flow (IF) in nat (natural unit of information) per unit time [nat/ut] from the 156 years annual time series of global CO2 concentration to GMTA as 0.348 ± 0.112 nat/ut and −0.006 ± 0.003 nat/ut in the reverse direction. Obviously, the former is significantly different from zero, while the latter, in comparison to the former, is negligible. This result unambiguously shows a one-way causality in the sense that the recent CO2 increase is causing the temperature increase, but not the other way around. The results prove to be robust against detrending the data (SI, Table SI2), selecting shorter time periods as e.g. using only the last 100 years, or against using decadal means only (results not shown). It is difficult to achieve a similarly clear result when using Granger causality, as in this case the reverse causality between GMTA and CO2 forcing is also significant whereas with CCM only the direction from GMTA to CO2 is found to be significant (SI, Tables SI-1 and SI-2).
The atmospheric CO2 content serves only as proxy for its radiative forcing and therefore we now examine in more detail the causal relations between the major climate forcings and GMTA. The correlation and the IF between the major reconstructed radiative forcings37 (for the used identifiers in37 see SI, Table SI-3) and the GMTA time series are given in Table 1, correlations and causations significant at the 95% level and that are larger than 0.1 nat/ut are in bold. The calculated significant IF from the total radiative forcing to GMTA (Table 1) is basically in agreement with results presented by28 (their Table 2, Model I), finding a significant one-directional Granger causality between these two variables. The calculated Granger causalities between the different forcing components and GMTA are also largely in agreement with the IF results (SI, Table SI-2). However the non-quantitative nature of Granger causality makes it difficult to disregard the significant reverse causalities from GMTA to anthropogenic and greenhouse gas forcing, as could be done in case of the very small reverse information flows.
The values in Table 1 clearly confirm that the total greenhouse gases (GHG), especially the CO2, are the main drivers of the changing global surface air temperature. The radiative forcing caused by aerosols and aerosol-cloud interactions is also important, but significantly smaller (0.2 vs. 0.3 nat/ut). Neither solar irradiance nor volcanic forcing contributes in a significant manner to the long-term GMTA evolution. This is true in spite of short episodes of volcanic forcing that are clearly visible in the time series as they are of insufficient strength to make significant long-term contributions to the GMTA dynamics. Selecting only short data records around a volcanic eruption will however result in a significant causality relation (SI, Table SI-4) for that specific period. For the known major natural modes, the information flows between the Pacific Decadal Oscillation (PDO) and Atlantic Multidecadal Oscillation (AMO) from and to the global surface temperatures are close to 0.0, so essentially no causality relations could be identified here, in contrast to the significant correlation between AMO and GMTA time series (Table 1). This is a good real world example that illustrates the basic fact: correlation does not mean causation. It further questions the assumed fundamental role of the AMO for the global climate as speculated in38.
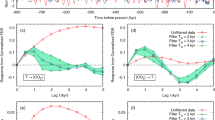
We also try to determine when human activities started to significantly influence the GMTA. Time dependent change in IF from CO2 radiative forcing to GMTA since 1880 is presented in Fig. 1. Significant values larger than 0.1 nat/ut are observed only beginning from about 1960. That this is not an effect of the increasing time series length has been tested see SI, Figs SI-1 and SI-2. In this case a qualitative similar result could have been obtained by using Granger causality (SI Fig. SI-3).
Global information flow from radiative CO2 forcing to GMTA.
Shown is the time dependence of the information flow between CO2 forcing and GMTA when calculating segments with increasing lengths beginning from 1850 to the actual displayed year. Statistically significant values are indicated by the dark squares in the lower part of the figure and the dashed horizontal line at 0.1 [nat/ut] indicates the threshold for relevant flows.
The same approach can be applied to investigate the IF between the different forcing components and model derived global surface temperature. As the models are governed by well-known physical equations we might expect even higher causality measures in this case. Indeed the correlation coefficients between the different forcings and the historical CMIP5 overall ensemble temperatures are all higher compared to the one between forcings and observed GMTA (Table 2). The IF from the total forcing to the simulated GMTA is indeed slightly increased, confirming the important influence of the external forcing on the GMTA. As expected, ensemble averaging has the effect of enhancing the relative importance of the external forcing component compared to internal model variability. However the IF from single forcing components to the simulated GMTA is always significantly smaller and in the case of aerosol forcing and aerosol-cloud interactions even becomes insignificant (Table 2) compared to the IF to the observed GMTA. As this result is in disagreement to the analysis based on observed temperatures it might point to differences with relation to the model specific implementations of aerosol and aerosol-cloud interactions in the CMIP5 models9,39.
Further we apply this technique to analyse paleoclimatological air temperature (PAT)40 and CO2/CH4 data from the EPICA Dome C ice cores41,42 from the last 800,000 years. Both time series are interpolated on the same time steps of 1000 years using the AICC201243,44 chronology. As already known the two data set are highly correlated with a correlation coefficient of 0.842 ± 0. By calculating the IF in nat per unit time from the 1000 year interpolated PAT time series to CO2 concentration we get 0.123 ± 0.060 nat/ut and −0.054 ± 0.040 nat/ut in the reverse direction. Therefore we have on these long time scales a significant IF only from the temperature data to the CO2, but not in the other direction, exactly opposite to that seen in the data from the last 156 years. This result proves robust against using different ice age/gas age chronologies (SI, Tables SI-5 and SI-6 comparing EDC3 and AICC2012 chronology) and against using the recent corrected CO2 data from Bereiter45 (SI, Table SI-7). The time step chosen for interpolation influences neither the strong correlation (always around 0.88 for the EDC3 chronology) nor the significant causation (SI, Table SI-8). This supports the hypothesis that on geological time scales air temperature changes are causing the subsequent changes in CO2 concentration. This was already hypothesized by46, who claimed that CO2 lagged Antarctic deglacial warming by 800 ± 200 years, during a specific deglaciation event (Termination III ~ 240,000 years ago). Recently Parrenin et al.47, did not find any significant asynchrony in the timing between atmospheric CO2 and Antarctic temperature changes during the last deglaciation event (Termination TI). If we apply causality analysis only to data from event TI (22000–10000 years), we do get a bidirectional significant flow of 0.120 ± 0.074 nat/ut from PAT to CO2 and 0.484 ± 0.168 nat/ut from CO2 to PAT pointing to a synchronous behaviour or even a leading CO2 signal (see Table SI-9). Using the old EDC3 chronology would have given a very different result, with CO2 changes clearly causing PAT changes (Table SI-10). Because of the inherent nonlinear dynamics of the climate system, changes in correlation during single events could even be expected35. The causality analysis indicates that for the full 800,000 years time series PAT is indeed leading CO2 because of the significant IF from PAT to CO2. This is in principal agreement with the conclusion from Nes et al.48 that has been derived using convergent cross mapping. However, when interpolating to time steps longer than 3000 years the IF decreases (Table SI-8). Because of this it is not possible to specify a time lag of maximal IF in contrast to the 6000 year time lag found by Nes et al.48. Data from another strong greenhouse gas, namely methane CH4, are also available from EPICA Dome C covering the same time period as the CO2 data49. Again, as for CO2, we find a strong significant correlation between PAT and CH4 of 0.777. The IF from PAT to CH4 for the interpolated time series (1000 years time step) equals 0.393 ± 0.051 nat/ut and 0.007 ± 0.025 nat/ut in the reverse direction. Therefore the causal drive of temperature on the CH4 dynamics is even stronger than for CO2. This supports the expectation that on paleoclimatological time scales changing temperature could be held responsible for following changes in greenhouse gas (CO2/CH4) concentrations.
Another crucial research question that we can address with this new method is “where is the recently increasing anthropogenic forcing likely to cause the most pronounced consequences?”. In order to assess which regions of the earth are more ‘sensitive’ to anthropogenic forcings and where natural modes of variability contribute more to the temperature series, we applied the same type of causality analysis as used in29 to the globally-gridded GMTA product. Due to the historically sparse data availability we could use only data from 1950 onwards and excluded regions South and North of 70 degrees. Looking first at the natural climate modes we see that PDO mainly shows significant IF over the North Pacific (Fig. 2A) and AMO mainly over the North Atlantic (Fig. 2B). This kind of expected result provides an additional first order validation of the method when applied to climate data. When analysing the IF from the global anthropogenic forcing to the GMTA (Fig. 3), in the Northern Hemisphere, we identified several regions of significant high causality. For example, IF takes largest values in Europe, North America and China, densely populated and industrialized areas having shown strong recent warming2. On the other hand there are also regions with high causality like Siberia, the Sahel zone and Alaska that are not that much influenced by human activities. In the Southern Hemisphere, however, this IF distribution displays a most unexpected pattern, with high values in a large swath of the southern Atlantic, South Africa, parts of the Indian Ocean and Australia. This is true for both the total anthropogenic forcing (Fig. 3A) and the radiative forcing caused by CO2 alone (Fig. 3B). Therefore, despite CO2 being a globally well-mixed gas, the IF to surface temperature is regionally very different, showing sensitive areas. Indeed, most of these depicted sensitive regions have shown especially strong warming during the last 60 years see Fig. 4 of2. Analysis of the spatial distributions of the IFs between solar forcing and GMTA (Fig. 4A) and volcanic forcing and GMTA (Fig. 4B) shows that over the considered period these flows are basically insignificant, in agreement with the previous analysis with the global mean values.
Global information flow from internal climate variability to GMTA.
Shown is the spatial distribution of the information flow between the Atlantic Multidecadal Oscillation (AMO) and the gridded global mean temperature anomalies (GMTA) (A) and the distribution of the information flow between the Pacific Decadal Oscillation (PDO) and the gridded global mean temperature anomalies (GMTA) (B). The maps were created by the authors using the m-map toolbox included in Matlab®.
Global information flow from anthropogenic forcing to GMTA.
Shown is the spatial distribution of the information flow between the total anthropogenic forcing and the gridded global mean temperature anomalies (GMTA) (A) and the spatial distribution of the information flow between the radiative forcing caused by CO2 and the gridded global mean temperature anomalies (GMTA) (B). The maps were created by the authors using the m-map toolbox included in Matlab®.
Global information flow from natural forcing to GMTA.
Shown is the spatial distribution of the information flow between solar forcing and the gridded global mean temperature anomalies (GMTA) (A) and the spatial distribution of the information flow between the radiative forcing caused by volcanic activity and the gridded global mean temperature anomalies (GMTA) (B). The maps were created by the authors using the m-map toolbox included in Matlab®.
Conclusions
Using the IF concept we were able to confirm the inherent one-way causality between human activities and global warming, as during the last 150 years the increasing anthropogenic radiative forcing is driving the increasing global temperature, a result that cannot be inferred from traditional time delayed correlation or ordinary least square regression analysis. Natural forcing (solar forcing and volcanic activities) contributes only marginally to the global temperature dynamics during the last 150 years. Human influence, especially via CO2 radiative forcing, has been detected to be significant since about the 1960s. This provides an independent statistical confirmation of the results from process based modelling studies. Investigation of the temperature simulations from the CMIP5 ensemble is largely in agreement with the conclusion drawn from the observational data. However on very long time scales (800,000 years) the IF is only significant in the direction from air temperature to CO2. This supports the idea that the feedback of GHGs to temperature changes seems to be much slower than the fast response of temperature to changes in GHGs48.
The spatial explicit analysis strongly indicates that the increasing anthropogenic forcing is causing very differing effects regionally with some regions in the southern hemisphere showing large IF values. Regions of significant IF do coincide with regions having stronger than average recent warming trends. Our observational data-based study, therefore, not only provides complementary support for the results from global circulation modelling, but also calls for attention for further research in regions of increased sensitivity to the forcing resulting from anthropogenic activities.
Material and Methods
The global mean surface air temperature anomalies were obtained from the HadCRUT4 dataset36,50. Datasets spanning the period 1850–2013 were obtained for the global mean temperature, temperatures of the Southern and Northern Hemispheres; the gridded data have a 5° × 5° resolution. The Meinshausen historical forcing data37,51 cover the period from 1765 to 2005. The overlap period of the two datasets, 1850–2005 (156 years), is hence chosen for our analysis. Air temperature, CO2 and CH4 data for the last 800,000 years from the Antarctic EPICA Dome C ice cores40,41,42,49 were obtained from51. These non-equidistant temperature, CO2 and CH4 data were interpolated on different equidistant time steps using Akima52 spline interpolation. The ice core data were downloaded from the NOAA ice core data base (ftp://ftp.ncdc.noaa.gov/pub/data/paleo/icecore/antarctica/ assessed last time October 2015). All CMIP5 model data were downloaded using the KNMI Climate Explorer53.
We follow Liang29,54 to evaluate the cause-effect relation between time series. Causality is measured as the time rate of information flowing from one time series to another. It has long been recognized that a nonzero IF, or information transfer as it may appear in the literature, from an event to another logically tells the strength of the causality from the former to the latter and a vanishing causality must entail a zero flow. This recognition is further supported by the recent discovery34 that transfer entropy33 and Granger causality25, the two most extensively studied formalisms of IF and causality analysis respectively, turn out to be equivalent up to a factor of 2.
In causality analysis, a principle (actually the only quantitatively stated fact) that must be verified is that, when the evolution of a dynamical event (say A) is independent of another (say B), then the causality from B to A is nil. It has long been found that Granger causality and transfer entropy fail to verify this principle in many applications, giving rise to spurious causalities; for a systematic investigation, see34. A remarkable example is examined in55, where for a carefully designed chaotic system, transfer entropy (and hence Granger causality test) not only fails to reproduce the preset one-way causality, but, as the parameter varies, the thus-obtained causality can be completely reversed! These problems have been extensively studied in the past decade, and, for a dynamical system, the dependence of transfer entropy and/or Granger causality on the autodependency coefficient has been blamed for the failure (see references in29,54).
One may argue that IF or causality is a real physical notion and a real physical notion should be rigorously formulated, rather than empirically proposed as what have been done before. Indeed, recently it has been shown that IF actually can be derived from first principles. Given a two-dimensional system

where  (i = 1, 2) indicate white noises;
(i = 1, 2) indicate white noises;  and
and  are arbitrary functions of X and t, Liang35 proved that the rate of information (in terms of Shannon entropy) flowing from
are arbitrary functions of X and t, Liang35 proved that the rate of information (in terms of Shannon entropy) flowing from  to
to  is:
is:

where  is the marginal density of
is the marginal density of  and E stands for mathematical expectation (units: nats per unit time). Remarkably, Eq. (2) has the above stringent principle of causality naturally embedded. This is stated in two theorems in Liang32, which read, loosely speaking, if the evolution of
and E stands for mathematical expectation (units: nats per unit time). Remarkably, Eq. (2) has the above stringent principle of causality naturally embedded. This is stated in two theorems in Liang32, which read, loosely speaking, if the evolution of  is independent of
is independent of  , then
, then  .
.
When only two time series, say  and
and  , are given, we first need a model to fulfill the IF evaluation. For linear systems, the maximum likelihood estimator of (2) turns out to be very concise in form29:
, are given, we first need a model to fulfill the IF evaluation. For linear systems, the maximum likelihood estimator of (2) turns out to be very concise in form29:

where  (i, j = 1, 2) is the sample covariance between
(i, j = 1, 2) is the sample covariance between  and
and  and
and  the sample covariance between
the sample covariance between  and
and  , with Δt being the time stepsize (units nats per unit time). If
, with Δt being the time stepsize (units nats per unit time). If  is nonzero,
is nonzero,  is causal to
is causal to  ; if not, it is noncausal.
; if not, it is noncausal.
The above tight formula is explicitly expressed in terms of the sample covariances of the involved time series and their derivatives. In a strict sense, it is precise only for linear systems (the original Eq. (2) applies to any systems, though), but the validations have shown that it is a good approximation for nonlinear time series and has seen remarkable success with highly nonlinear touchstone systems, such as the aforementioned system in55 which fails transfer entropy and hence Granger causality tests. The formula also confirms in a quantitative way that causation implies correlation, whereas correlation does not imply causation. The quantitative nature of this formulation allows disregarding small absolute information flows (<0.1 nat/ut) as insignificant as is done in this article.
The confidence interval estimation also follows Liang29,54; it is based on the observation that, for a large ensemble, the maximum likelihood estimate of a parameter approximately obeys a normal distribution around its true value. All given confidence intervals are significant at the 95% level. Analysis software was coded in R and MATLAB (for generating the maps). Using the respective implementations of Granger causality and CCM in the R software packages “MSBVAR”, “lmtest” and “multispatialCCM” we could perform comparisons with Liang causality56.
Additional Information
How to cite this article: Stips, A. et al. On the causal structure between CO2 and global temperature. Sci. Rep. 6, 21691; doi: 10.1038/srep21691 (2016).
References
IPCC 2013: Summary for Policymakers. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Stocker, T. F. et al. (eds.), Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA (2013).
Jones, P. D. et al. Hemispheric and large-scale land surface air temperature variations: an extensive revision and an update to 2010. J. Geophys. Res. 7, D05127, 10.1029/2011JD017139 (2012).
Levitus, S. et al. World ocean heat content and thermosteric sea level change (0–2000m), 1955–2010. Geophys. Res. Let. 39, L10603, 10.1029/2012GL051106 (2012).
Miller, R. L. et al. CMIP5 historical simulations (1850–2012) with GISS ModelE2. J. Adv. Model. Earth Syst. 6, 441–477, 10.1002/ 2013MS000266 (2014).
Macías, D., Stips, A. & Garcia-Gorriz, E. Application of the singular spectrum analysis technique to study the recent hiatus on the global surface temperature record. PloS ONE 9, e107222, 10.1371/journal.pone.0107222 (2014).
Stephens, G. L. et al. An update on earth’s energy balance in light of the latest global observations. Nature Geoscience 5, 10.1038/NGEO1580 (2012).
Schmidt, G. A., Shindell, D. T. & Tsigaridis, K. Reconciling warming trends. Nature Geoscience 7, 158–160, 10.1038/ngeo2105 (2014).
Huber, M. B. & Knutti, R. Natural variability, radiative forcing and climate response in the recent hiatus reconciled. Nature Geoscience. 10.1038/NGEO2228 (2014).
Regayre, L. A. et al. Uncertainty in the magnitude of aerosol-cloud radiative forcing over recent decades. Geophys. Res. Lett. 41, 9040–9049, 10.1002/2014GL062029 (2014).
Fyfe, J. C., Gillet, N. P. & Zwiers, F. W. Overestimated global warming over the past 20 years. Nature Climate Change 3, 767–769 (2013).
Tollefson, J. The case of the missing heat. Nature 505, 276–278 (2014).
IPCC, Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change. Houghton, J. T. et al. (eds.) Cambridge University Press, Cambridge, United Kingdom, 881pp (2001).
Santer, B. D. et al. A search for human influences on the thermal structure of the atmosphere. Nature 382, 39–46 (1996).
Santer, B. D. et al. Incorporating model quality information in climate change detection and attribution studies. Proc. Natl. Acad. Sci. USA 106, 14778–14783, 10.1073/pnas.0901736106 (2009).
Santer, B. D. et al. Identifying human influences on atmospheric temperature. Proc. Natl. Acad. Sci. USA, 10.1073/pnas.1210514109 (2012).
Jones, G. S., Stott, P. A. & Christidis, N. Attribution of observed historical near-surface temperature variations to anthropogenic and natural causes using CMIP5 simulations, J. Geophys. Res. Atmos. 118, 4001–4024, 10.1002/jgrd.50239 (2013).
Hegerl, G. C. et al. Understanding and attributing climate change. Climate Change 2007: The Physical Science Basis, Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Solomon, S. et al. (eds.) Cambridge University Press, Cambridge, United Kingdom (2007).
Lacis, A. A., Schmidt, G. A., Rind, R. & Ruedy, R. A. Atmospheric CO2: Principal Knob Governing Earth’s Temperature. Science 330, 356–359 (2010).
Trenberth, K. E. & Fasullo, J. T. Tracking Earth’s Energy. Science 328, 316–317, 10.1126/science.1187272 (2010).
Sies, H. A new parameter for sex education. Nature 332, 495, 10.1038/332495a0 (1988).
Barnard, G. A. Causation. Encyclopedia of Statistical Sciences 1, Kotz, S. Jansen, N. & Read, C. (eds.) (John Wiley, New York), 387–389 (1982).
Cox, P. M., Betts, R. A., Jones, C. D., Spall, S. A. & Totterdell, I. J. Acceleration of global warming due to carbon-cycle feedbacks in a coupled climate model. Nature 408, 184–187 (2000).
Friedlingstein, P. et al. Positive feedback between future climate change and the carbon cycle. Geophys. Res. Lett. 28, 1543–1546 (2001).
Kaufmann, R. K. & Stern, D. I. Evidence for human influence on climate from hemispheric temperature relations. Nature 388, 39–44 (1997).
Granger, C. W. J. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica 37, 424–438 (1969).
Attanasio, A. Testing for linear Granger causality from natural/anthropogenic forcings to global temperature anomalies. Theor. Appl. Climatol. 110, 281–289 (2012).
Triacca, U., Attanasio, A. & Pasini, A. Anthropogenic global warming hypothesis: testing its robustness by Granger causality analysis. Environmetrics 24, 260–268 (2013).
Stern, D. I. & Kaufmann, R. K. Anthropogenic and natural causes of climate change. Climatic Change 122, 257–269 (2014).
Liang, X. S. Unraveling the cause-effect relation between time series. Phys. Rev. E 90, 10.1103/PhysRevE.90.052150 (2014).
Ay, N. & Polani, D. Information flows in causal networks. Advs. Complex Syst. 11, 10.1142/S0219525908001465 (2008).
Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 85, 461 (2000).
Liang, X. S. Information flow within stochastic systems. Phys. Rev. E 78, 031113 (2008).
Barnett, L., Barrett, A. B. & Seth, A. K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 103, 238701 (2009).
Smirnov, D. A. Spurious causalities with transfer entropy. Phys. Rev. E 87, 042917 (2013).
Sugihara, G. et al. Detecting causality in complex ecosystems. Science 338, 496–500 (2012).
Morice, C. P., Kennedy, J. J., Rayner, N. A. & Jones, P. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 dataset. J. Geophys. Res. 117, D08101, 10.1029/2011JD017187 (2012).
Meinshausen, M. et al. The RCP GHG concentrations and their extension from 1765 to 2300. Climatic Change 10.1007/s10584-011-0156-z (2011).
Kerr, R. A. A North Atlantic climate pacemaker for the centuries. Science 288, 1984–1986 (2000).
Lee, L. A. et al. The magnitude and causes of uncertainty in global model simulations of cloud condensation nuclei. Atmos. Chem. Phys. 13, 8879–8914, 10.5194/acp-13-8879-2013 (2013).
Jouzel, J. et al. Orbital and Millennial Antarctic Climate Variability over the Past 800,000 Years. Science 317, 793–797 (2007).
Luthi, D. et al. High-resolution carbon dioxide concentration record 650,000–800,000 years before present. Nature 453, 379–382, 10.1038/nature06949 (2008).
Luthi, D. et al. EPICA Dome C Ice Core 800KYr Carbon Dioxide Data. IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series # 2008-055. NOAA/NCDC Paleoclimatology Program, Boulder CO, USA (2008).
Veres, D. et al. The Antarctic ice core chronology (AICC2012): an optimized multi-parameter and multi-site dating approach for the last 120 thousand years. Clim. Past 9, 1733–1748, 10.5194/cp-9-1733-2013 (2013).
Bazin, L. et al. An optimized multi-proxy, multi-site Antarctic ice and gas orbital chronology (AICC2012): 120–800 ka. Clim. Past 9, 1715–1731, 10.5194/cp-9-1715-2013 (2013).
Bereiter et al. Revision of the EPICA Dome C CO2 record from 800 to 600kyr before present. Geophys. Res. Lett. 42, 542–549, 10.1002/2014GL061957 (2015).
Caillon, N. et al. Timing of atmospheric CO2 and Antarctic temperature changes across Termination III. Science 299, 1728–1731, 10.1126/science.1078758 (2003).
Parrenin, F. et al. Synchronous change of atmospheric CO2 and Antarctic temperature during the last deglacial warming. Science 339, 1060–1063, 10.1126/science.1226368 (2013).
Nes, E. H. et al. Causal feedbacks in Climate Change. Nature Climate Change 10.1038/nclimate2568 (2015).
Loulergue, L. et al. Orbital and millennial-scale features of atmospheric CH4 over the past 800,000 years. Nature 453, 383–386, 10.1038/nature06950 (2008).
Jones, P., Harpham, C., Osborn, T. & Salmon, M. Temperature, http://www.cru.uea.ac.uk/cru/data/temperature/ (2014). Date of access: 11/11/2014.
National Oceanic and Atmospheric Administration, World Data Center for Paleoclimatology. Ice Core, http://www.ncdc.noaa.gov/paleo/icecore/ (2014). Date of access: 30/10/2015.
Akima, H. A method of univariate interpolation that has the accuracy of a third-degree polynomial. ACM Transactions on Mathematical Software 17, 341–366 (1991).
Koninklijk Nederlands Meteorologisch Instituut, KNMI Climate Explorer http://climexp.knmi.nl/ (2014). Date of access 13/11/2014.
Liang, X. S. Information flow and causality as rigorous notions ab initio. (to be published; a reprint is available at http://arxiv.org/abs/1503.08389).
Hahs, D. W. & Pethel, S. D. Distinguishing anticipation from causality: Anticipatory bias in the estimation of information flow. Phys. Rev. Lett. 107, 128701 (2011).
Meinshausen, M. RCP concentration calculations and data, http://www.pik-potsdam.de/~mmalte/rcps (2012). Date of access: 11/11/2014.
Acknowledgements
The authors thank the Climatic Research Unit of the University of East Anglia for providing the surface temperature data used in the present work (HadCRUT4) and the Potsdam Institute for Climate Impact Research for the forcing data, as well as the EPICA Dome C team and NOAA for EPICA Dome C data provision. We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP5 and we thank the climate modelling groups for producing and making available their model outputs. S. L. was supported by Jiangsu Provincial Government through the “2015 Jiangsu Program for Innovation Research and Entrepreneurship Groups” and Jiang Chair Professorship, by the National Science Foundation of China under Grant No. 41276032 and by the State Oceanic Administration through the Special Program on Global Change and Air-Sea Interaction (GASI-IPOVAI-06).
Author information
Authors and Affiliations
Contributions
A.S. idea, writing and data processing, D.M. writing, data processing and figures, C.C. writing, E.G. writing, S.L. writing and methodology of data processing. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Stips, A., Macias, D., Coughlan, C. et al. On the causal structure between CO2 and global temperature. Sci Rep 6, 21691 (2016). https://doi.org/10.1038/srep21691
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep21691
This article is cited by
-
Association of risk perception and transport mode choice during the temporary closure of a major inner-city road bridge: results of a cross-sectional study
European Transport Research Review (2023)
-
On the Evolution of Symbols and Prediction Models
Biosemiotics (2023)
-
Analysis of regional climate variables by using neural Granger causality
Neural Computing and Applications (2023)
-
What is the link between temperature, carbon dioxide and methane? A multivariate Granger causality analysis based on ice core data from Dome C in Antarctica
Theoretical and Applied Climatology (2023)
-
Contribution of Solar Irradiance Variations to Surface Air Temperature Trends at Different Latitudes Estimated from Long-term Data
Pure and Applied Geophysics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.