Abstract
Greigite (Fe3S4) is a ferrimagnetic mineral with vital functions in both the bio-geochemical cycle and novel technological applications. However, the ground state electronic structure of this material has not been fully characterized by either experiment or theory. In the present study, ab initio calculations using the hybrid functional method have been performed to investigate the electronic structure and magnetic properties. It is found that the cubic structure observed under ambient temperature is a half metal and is metastable. A more stable monoclinic structure slightly distorted from the cubic form is found. The structural distortion is induced by charge ordering and associated with a metal-to-insulator transition, resulting in a semiconductive ground state with a bandgap of ~0.8 eV and a magnetic moment of 4 μB per formula unit. The results predict, similar to the magnetite (Fe3O4), a Verwey transition may exist in greigite, although it has not yet been observed experimentally.
Similar content being viewed by others
Introduction
Greigite (Fe3S4) is a ferrimagnetic mineral that was first discovered in lake sediments from California, USA1. It is probably formed by bacteriological reduction of iron2 and is widespread in nature including lacustrine sediments, magnetotactic bacterium3 and hydrothermal vein deposits4. Greigite has attracted great interests in geophysics and biology because it records the ancient geomagnetic field and environmental processes that are important for paleomagnetic and environmental magnetic studies5,6,7,8. Also, the half metallic electronic structure of greigite at ambient condition with a high curie temperature makes it a candidate for spintronic application9. Moreover, greigite has been suggested to be useful as an anode material in lithium-ion batteries10.
Similar to its iron oxide counterpart magnetite (Fe3O4)11, greigite has an inverse spinel structure (Fe3+A(Fe2+BFe3+B)S2−4). Here the subscripts A and B represent the tetrahedral and octahedral iron site, respectively. Magnetite is the oldest magnetic material known to humans and has received intense investigations12,13,14,15,16,17,18,19. One of the most interesting observations is the Verwey transition, in which the resistivity abruptly increases when the temperature decreases to ~120 K13. This transition in the resistivity of magnetite was later found to be related to a metal-to-insulator transition induced by the charge ordering. The charge ordering at low temperature also introduces structural distortion that transforms the cubic structure at ambient condition to a monoclinic structure20. In view of the similarity in the crystal structure of both greigite and magnetite, Verwey transition is likely to occur in greigite21. However, so far no direct confirmation has been reported. A local coercivity minimum was observed in greigite at 130 K, which is close to the Verwey transition temperature of magnetite21. However, the local coercivity minimum was suggested to be associated with domain walls present in the samples. In another study10, electrical measurement showed the microcrystalline Fe3S4 was metallic at temperature as low as 5 K, indicating no Verwey transition.
In comparison with magnetite greigite is less studied. This is not only due to a much later discovery of this mineral but also due to the challenges in obtaining high-quality samples for experimental measurements. In particular, greigite is thermodynamically unstable relative to pyrite (FeS2)22. Therefore, in natural environments, greigite commonly occurs in fine-grained mixtures with pyrite. A number of methods have also been reported to synthesize greigite23,24,25,26,27,28,29. But, it is still very difficult to synthesize greigite samples with high purity and high crystallinity. The purity and crystallinity of greigite samples can severely affect the results of the magnetic properties and other measurements. For instance, the initial magnetic moment per formula unit of greigite was reported to be ~2.2 μB2,29 but was increased dramatically to ~3.7 μB with an improved sample10. The latter value, however, is still lower than that of magnetite of ~4.0 μB per formula unit30. It is believed that the quality of greigite samples is responsible for the discrepancy and the apparent absence of Verwey transition.
Despite previous theoretical studies, the ground state electronic structure and magnetic property of greigite remain unclear and need to be further investigated. An ab initio calculation using the generalized gradient approximation (GGA) augmented with an on-site Hubbard Ueff parameter (GGA + U) on the iron atom had been performed29. From matching the calculated magnetic moment to the available experimental values, it was suggested that a Ueff value of 1 eV would give an accurate description of the properties of greigite with a half metallic ground state. However, the calculations showed the results are highly sensitive to the choice of the Ueff value. As well, the dependence of the Ueff value on the environment and oxide state of the iron atom was not considered. Different Ueff values have been proposed for Fe 3d orbitals in different materials (e.g. a much larger Ueff value of 3.2 eV was used for magnetite31). The Ueff value is also dependent on the exchange correlation functional used32. Moreover, the initial spin state was not set to be the inverse spinel structure in the GGA + U calculation29 (i.e. mixed valence Fe2+Fe3+ was not considered at the octahedral sites). Therefore no charge ordering induced distortion was observed and the monoclinic structure similar to Fe3O4 was predicted to be energetically unfavorable. To overcome the empiricism of the Hubbard+U model, hybrid functionals that mix a portion of the exact nonlocal exchange of Hartree–Fock theory with the exchange density functional are often used to provide a “parameter free” and more reliable description of the electronic structure. In the present study, ab initio calculations using the Heyd-Scuseria-Ernzerhof screened hybrid functional (HSE06)33 were performed to investigate the ground state electronic structure and magnetic properties of greigite. The results are found to be sensitive to the initial choice of the spin configuration. For example, the greigite structure remains cubic when the spin configuration was initialized with all the octahedral Fe sites having the same spin. In this case, the ground state is half-metallic and is consistent with the previous study29. However, when the calculation was initialized with the inverse spinel spin state (Fe3+A(Fe2+BFe3+B)S2−4), charge ordering induced distortion is found and leads to an energetically more stable monoclinic structure. The monoclinic structure is a semiconductor with a net magnetic moment value of 4.0 μB per Fe3S4 formula unit. The presented results suggest that, similar to magnetite, a Verwey transition can occur in greigite at low temperature. The theoretical results encourage further measurements of greigite with a high purity and high crystallinity sample in order to verify this prediction. In magnetite, the Fe:O stoichiometry is known to have profound effects on the observed Verwey transition13 and the measured magnetic moment per formula unit also vary with the particle sizes and surface structures34,35.
Results and Discussion
In the present study, a  model constructed from the conventional cubic unit cell of greigite with a = 9.876 Å1 and consisted of 28 atoms (4 formula units) was used for the HSE calculations (Fig. 1). The Anderson condition that requires two Fe3+ and two Fe2+ ions in each corner-sharing FeB tetrahedron was used in the charge ordering calculation36. HSE calculation on a more complicated charge ordering scheme will require a much larger model and is beyond our available computational resource. Two different initial spin states were studied. The first model assumed a magnetic moment of 4.0 μB on each Fe at the tetrahedral sites and −4.0 μB on each of the octahedral sites (HSE(I)). In the second model (HSE(II)), the inverse spinel configuration with charge ordering is considered. In the HSE(II) model, the initial spin was set to 4.0 μB at the tetrahedral Fe sites, −4.0 μB at half of the octahedral sites and −3.0 μB on the remaining half of the octahedral sites. To verify the validity of the HSE method on iron containing compounds, test calculations on magnetite were performed. An insulating ground state with the inverse spinel monoclinic magnetite structure with a net magnetic moment of 4.0 μB per Fe3O4 formula unit was obtained (See supplementary information, Fig. S1). The result is consistent with a previous study18 indicating that the HSE method is appropriate for greigite.
model constructed from the conventional cubic unit cell of greigite with a = 9.876 Å1 and consisted of 28 atoms (4 formula units) was used for the HSE calculations (Fig. 1). The Anderson condition that requires two Fe3+ and two Fe2+ ions in each corner-sharing FeB tetrahedron was used in the charge ordering calculation36. HSE calculation on a more complicated charge ordering scheme will require a much larger model and is beyond our available computational resource. Two different initial spin states were studied. The first model assumed a magnetic moment of 4.0 μB on each Fe at the tetrahedral sites and −4.0 μB on each of the octahedral sites (HSE(I)). In the second model (HSE(II)), the inverse spinel configuration with charge ordering is considered. In the HSE(II) model, the initial spin was set to 4.0 μB at the tetrahedral Fe sites, −4.0 μB at half of the octahedral sites and −3.0 μB on the remaining half of the octahedral sites. To verify the validity of the HSE method on iron containing compounds, test calculations on magnetite were performed. An insulating ground state with the inverse spinel monoclinic magnetite structure with a net magnetic moment of 4.0 μB per Fe3O4 formula unit was obtained (See supplementary information, Fig. S1). The result is consistent with a previous study18 indicating that the HSE method is appropriate for greigite.
PBE calculations
The structural information and magnetic moment of Fe3S4 computed with different methods are summarized and compared in Table 1. Calculations using the PBE functional predicted a low spin (1.9 μB per Fe3S4 formula unit) cubic structure with a lattice parameter of 9.467 Å. The lattice parameter is 4.1% shorter than the experimental value of 9.876 Å1. The magnetic moment is also much smaller than the experimental value of 3.7 μB10. These results show the localized nature of Fe 3d orbitals is not correctly described by the PBE functional, leading to an itinerant ground state. The itinerant Fe 3d electrons participate in the bonding and overestimate the interatomic interactions leading to a smaller volume and a low spin state. The density of state (DOS) and projected DOS (pDOS) analyses show that the electronic structure from the PBE functional is metallic with Fe 3d orbitals dominating the Fermi level (Fig. S2).
Cubic structure from the HSE(I) calculation
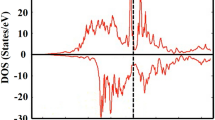
As mentioned above, hybrid functional methods such as the HSE may be more appropriate for highly correlated systems. The optimized structure from the spin model I (HSE(I)) assuming a ferrimagnetic arrangement of the spins at the tetrahedral and octahedral sites remains to be cubic due to the absence of charge ordering. The calculated cubic lattice parameter a of 10.029 Å is only 1.5% larger than the experimental value. The result shows the hybrid functional HSE method indeed performs much better than the PBE functional discussed above. Improvements are also evident in the interatomic distances: The FeA-S and FeB-S distances are 2.257 and 2.459 Å, which are substantially longer than the PBE values of 2.133 and 2.320 Å. The net magnetic moment per Fe3S4 formula has increased to a more reasonable value of 4.0 μB. The optimized cubic structure is a half metal that is conductive in one spin channel but insulating in the other. The result agrees with the experimental observation at ambient temperature. It is noteworthy that calculations employing the PBE functional produced a metallic state in contradiction to the experiment. As shown in Fig. 2, the spin-up FeA 3d orbitals and the spin-down FeB 3d orbitals are completely filled and locating about 1.0 eV below the Fermi level. The spin polarized electrons at the Fermi level are dominated by FeB 3d orbitals with minor contributions from the spin-polarized S 3p orbitals. It is interesting to note that a bandgap is opened in both spin channels of the tetrahedral FeA atoms, indicating that the spin current can only travel through the channel connected by the octahedral FeB atoms and the sulfur atoms. The pDOS of all octahedral FeB atoms are identical, showing that there is no charge ordering. The absence of any charge ordering can be understood as follows: the valence electrons are hopping between the octahedral Fe atoms, resulting in an identical valence state of the octahedral FeB atoms rather than the expected inverse spinel state of (Fe3+)A(Fe2+BFe3+B)S2−4.
Monoclinic structure from the HSE(II) calculation
In the HSE(I) calculation above, no charge ordering is considered in the initial spin state. Although the calculated electronic structure is consistent with the experimental result at ambient temperature, it may be a metastable state. In contrast, the HSE(II) geometry optimization calculation that initialized with a charge ordered state, resulted in a monoclinic structure slightly distorted from the cubic precursor with lattice parameters a = 7.120 Å, b = 7.090 Å, c = 10.080 Å and β = 90.010° (Table 1). Most significantly, the monoclinic structure is energetically more favorable with a total energy difference of 0.377 eV per Fe3S4 formula unit lower than the cubic structure from the HSE(I) calculation. The cubic-monoclinic structural distortion in greigite is very subtle. The calculated X-ray diffraction (XRD) pattern of the monoclinic structure is almost identical to the cubic structure (Fig. S3) indicating it is very difficult to distinguish the two structures by XRD measurements. To verify that the small distortion is not due to numerical errors, we repeated the geometry optimization in two steps. First only the internal coordinates were optimized with a fixed cell, then followed by a full optimization of both the cell and the atomic coordinates. This two-step procedure produced the same monoclinic structure.
In the monoclinic structure, the net magnetic moment is 4.0 μB per Fe3S4 formula unit. As a result of the distortion, there are now several different Fe-S bonds. (Fig. 3) Unlike the HSE(I) calculation in which all the octahedral FeB atoms are identical, Bader atomic charge analysis shows that the octahedral FeB atoms in the HSE(II) calculation separate in two distinctive groups, confirming that a charge ordering state is obtained. From Bader charge analysis37, the FeB1 and FeB2 atoms illustrated in Fig. 3 have an average charge of 6.70e and 6.89e, respectively. Each FeB1 atom donated 1.30e to their nearest neighbor sulfur atoms, slightly more than the 1.11e from the FeB2 atoms. Thus, the FeB1 atoms should be formally in the Fe3+ state, a higher oxidation state than the Fe2+ of the FeB2. The charge difference between the FeB1 and FeB2 atoms is much less than the formal charge difference of one electron between Fe3+ and Fe2+ ions. This is consistent with the result of the previous study on magnetite18. The contrasting Fe-S bond lengths can be explained by the different oxidation states of the Fe atoms. For this purpose, it is easier to focus on the local structure of the sulfur atoms since they are all 4 coordinated. Due to the charge ordering (i.e. different oxidation state on the octahedral Fe atoms), the sulfur atoms can also be separated into two groups ((2FeB1-FeB2-FeA)S1 and (FeB1-2FeB2-FeA)S2). The tetrahedral FeA atoms have a smaller coordination number than the octahedral FeB atoms, so the charge donation of the FeA atom should be larger than the FeB atoms. Thus, the order of the charge transfer of the Fe-S bonds should be FeA-S > FeB1-S > FeB2-S. On the other hand, charge transfer in FeB2-S2 should be larger than FeB2-S1, because the S1 atom already obtained more electrons from the nearest neighbor (2FeB1-FeA) than the S2 atom that has a nearest neighbor of FeB1-FeB2-FeA. From the charge transfer analysis, the trend in the bond strength is expected to be FeA-S2 > FeA-S1 > FeB1-S2 > FeB1-S1 > FeB2-S2 > FeB2-S1. This analysis is consistent with the order of the bond length predicted from the HSE(II) calculation.
The electronic band structure and density of states (DOS) are shown in Fig. S4 and Fig. 4, respectively. The charge ordering induced structural distortion is accompanied by a metal-to-insulator transition resulting in a ferrimagnetic semiconductor with a bandgap of ~0.8 eV. Consistent with the atomic charge analysis, the pDOS also shows two groups of octahedral FeB atoms. Compare with the FeB2 atom, the FeB1 atom has a larger number of charges transferred to the sulfur atoms and the orbital energies become lower as the valence electrons are less screened. Above the Fermi level, both of the FeB1 and FeB2 atoms have a peak in the conduction band separated by ~2 eV. The peak of the higher oxidation FeB1 is located at ~2 eV above the Fermi level, the same as that of the tetrahedral FeA atom. It is significant to point out that, the charge ordering is accompanied by a concomitant spin ordering. The FeB22+ ion has an integrated magnetic moment of 3.46 μB/atom, which is smaller than the FeB13+ ion (3.87 μB/atom) due to the extra spin-up electrons. The pDOS results support the conclusion that the ground state of the monoclinic Fe3S4 structure is an inverse spinel state of Fe3+A(Fe2+BFe3+B)S2−4. The net magnetic moment of 4.0 μB per Fe3S4 formula unit derived mainly from the Fe atoms with minor contributions from the sulfur atoms.
To further examine the validity of the HSE results, GGA+U calculations using different U values were performed. Similar results with the HSE calculations were obtained. GGA+U calculations starting with the initial spin as HSE(I) and HSE(II) also resulted in cubic structures and monoclinic structures, respectively. Moreover, from the comparison of the total energies shown in Fig. S5, the monoclinic structure is found to be more stable than the cubic structure when the U value is larger than 1 eV. Therefore, results obtained from the ad hoc correction of GGA with an empirical Hubbard U on the Fe atoms are consistent with the HSE calculations presented above, thus validating our conclusions.
Conclusions
The electronic structure of greigite (Fe3S4) has been studied by the ab initio hybrid functional HSE method. A metastable half-metallic cubic structure is obtained when the calculation was initiated without the consideration of charge ordering. This result is consistent with experiments at ambient temperature suggesting that greigite is a potential spintronic material. In contrast, when charge ordering is considered, the inverse spinel state Fe3+A(Fe2+BFe3+B)S2−4 becomes most stable. The converged charge ordering state has a distorted monoclinic structure and is more stable than the cubic structure by 0.377 eV per Fe3S4 formula unit. The net magnetic moment of the monoclinic structure is 4.0 μB per Fe3S4 formula unit, which is similar to that of magnetite. The spin polarization was derived mainly from the Fe atoms with minor contributions from the sulfur atoms. The structural distortion is associated with a metal-to-insulator transition and the monoclinic structure becomes a ferrimagnetic semiconductor with a bandgap of ~0.8 eV. Due to the high computational demand of HSE calculations, the trimer on order proposed for magnetite19 will require a much larger structural model and is beyond our computational ability. The present results predict the Verwey transition, which has not yet been observed experimentally, may exist in greigite. Further experiment with high purity and high crystallinity samples is needed to confirm this prediction.
Method
Total energy and electronic structure calculations presented in this study were performed using the Vienna Ab initio Simulation Package (VASP)38. The projector augmented wave (PAW) method39 was used to describe the valence configuration, 3d64s2 for Fe and 3s23p4 for sulfur. The generalized gradient Perdew, Burke and Ernzerhof (PBE)40 exchange-correlation density function was employed. Plane-wave expansion with an energy cutoff of 400 eV was used. The Brillouin zone is sampled with a 6 × 6 × 4 Monkhorst–Pack k-point grid. All calculations were performed in the spin-unrestricted method without spin-orbit coupling. Convergence in geometry optimization was reached when the Hellmann-Feynman forces on the internal coordinates and the cell parameters are better than 0.006 eV/Å. The energy convergence criterion for the electronic self-consistent calculation was 10−4 eV.
Additional Information
How to cite this article: Wu, M. et al. Electronic structures of greigite (Fe3S4): A hybrid functional study and prediction for a Verwey transition. Sci. Rep. 6, 21637; doi: 10.1038/srep21637 (2016).
References
Skinner, B. J., Erd, R. C. & Grimaldi, F. S. Greigite, the thiospinel of iron; a new mineral, Am. Mineral. 49, 543–555 (1964).
Spender, M. R., Coey, J. M. D. & Morris, A. H. The Magnetic Properties and Mossbauer Spectra of Synthetic Samples of Fe3S4, Can. J. Phys. 50, 2313–2326 (1972).
Bazylinski, D. A. et al. Controlled biomineralization of magnetite (Fe3O4) and greigite (Fe3S4) in a magnetotactic bacterium. Appl. Environ. Microb. 61, 3232–3239 (1995).
Radusinovic, D. R. Greigite from the lojane chromium deposit, Macedonia. Am. Mineral. 51, 209–215 (1956).
Snowball, I. F. & Thompson, R. The occurrence of greigite in sediments from Loch Lomond, J. Quat. Sci. 3, 121–125 (1988).
Snowball, I. F. & Thompson, R. A stable chemical remanence in Holocene sediments, J. Geophys. Res. 95, 4471–4479 (1990).
Ron, H. et al. Greigite detected as dominating remanence carrier in late Pleistocene sediments, Lisan Formation, from Lake Kinneret (Sea of Galilee), Israel. Geophys. J. Int. 170, 117–131 (2007).
Roberts, A. P. et al. Characterization of hematite (a-Fe2O3), goethite (a-FeOOH), greigite (Fe3S4) and pyrrhotite (Fe7S8) using first-order reversal curve diagrams. J. Geophys. Res. 111, B12S35 (2006).
Wang, J., Cao, S. H., Wu, W. & Zhao, G. M. The Curie temperature and magnetic exchange energy in half-metallic greigite Fe3S4 . Phys. Scr. 83, 045702 (2011).
Li, G. W. et al. High-Purity Fe3S4 greigite microcrystals for magnetic and electrochemical performance. Chem. Mater. 26, 5821–5829 (2014).
Verwey, E. J. W., Haayman, P. W. & Romeijn, F. C., Physical Properties and Cation Arrangement of Oxides with Spinel Structures II. Electronic Conductivity. J. Chem. Phys. 15, 181–187 (1947).
Nadoll, P., Angerer, T., Mauk, J. L., French, D. & Walshe, J. The chemistry of hydrothermal magnetite: A review. Ore Geo. Rev. 61, 1–32 (2014).
Verwey, E. J. W. Electronic conduction of magnetite (Fe3O4) and its transition point at low temperatures. Nature 144: 327–328 (1939).
Calhoun, B. A. Magnetic and Electric Properties of Magnetite at Low Temperatures. Phys. Rev. 94, 1577–1585 (1954).
Callen, E. Magnetic Properties of Magnetite. Phys. Rev. 150, 367–376 (1966).
Tossell, J. A., Vaughan, D. J. & Johnson, K. H. Electronic structure of Ferric iron octahedrally coordinated to oxygen. Nature physical science 244, 42–45 (1973).
Iizumi, M. et al. Structure of Magnetite (Fe3O4) below the Verwey Transition Temperature. Acta Cryst. B38, 2121–2133 (1982).
Jeng, H. T., Guo, G. Y. & Huang, D. J. Charge-Orbital Ordering and Verwey Transition in Magnetite. Phys. Rev. Lett. 93, 156403 (2004).
Senn, M. S., Wright, J. P. & Attfield, J. P. Charge order and three-site distortions in the Verwey structure of magnetite. Nature 481, 173–176 (2012).
Wright, J. P., Attfield, J. P. & Radaelli, P. G. Charge ordered structure of magnetite Fe3O4 below the Verwey transition. Phys. Rev. B 66, 214422 (2002).
Chang, L. et al. Fundamental magnetic parameters from pure synthetic greigite (Fe3S4). J. Geophys. Res. 113, B06104 (2008).
Berner, R. A. Thermodynamic stability of sedimentary iron sulfides. Am. J. Sci. 265, 773–785 (1967).
Nakazawa, H. & Sakaguchi, K. Anhydrous synthesis of greigite, Mineral. J. 6, 458–463 (1972).
Qian, X. F. et al. The preparation and phase transition of nanocrystalline iron sulfides via toluene-thermal process. Mater. Sci. Eng. B 64, 170–173 (1999).
Chen, X. Y., Zhang, X. F., Wan, J. X., Wang, Z. H. & Qian, Y. T. Selective fabrication of metastable greigite (Fe3S4) nanocrystallites and its magnetic properties through a simple solution-based route, Chem. Phys. Lett. 403, 396–399 (2005).
Lyubutin, I. S. et al. Magnetic, structural and electronic properties of iron sulfide Fe3S4 nanoparticles synthesized by the polyol mediated process. J. Nanopart. Res. 15, 1397 (2013).
Lin, C. R. et al. Fe3S4 and Fe3O4 magnetic nanocrystals: magneto-optical and Mössbauer spectroscopy study. Materials Research Express 1, 025033 (2014).
Bauer, E. et al. Fe3S4 (greigite) formation by vapor–solid reaction. J. Mater. Chem. A 2, 1903–1913 (2014).
Devey, A. J., Grau-Crespo, R. & de Leeuw, N. H. Electronic and magnetic structure of Fe3S4: GGA+U investigation. Phys. Rev. B 79, 195126 (2009).
Aragon, R. Magnetization and exchange in nonstoichiometric magnetite. Phys. Rev. B 46, 5328–5333 (1992).
Piekarz, P., Parlinski, K. & Oles, A. M. Origin of the Verwey transition in magnetite: Group theory, electronic structure and lattice dynamics study. Phys. Rev. B 76, 165124 (2007).
Rohrbach, A., Hafner, J. & Kresse, G. Electronic correlation effects in transition-metal sulfides. J. Phys.: Condens. Matter 15, 979–996 (2003).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Poddar, P., Fried, T. & Markovich, G. First-order metal-insulator transition and spin-polarized tunneling in Fe3O4 nanocrystals. Phys. Rev. B 65, 172405 (2002).
Jordan, K. et al. Scanning tunneling spectroscopy study of the electronic structure of Fe3O4 surface. Phys. Rev. B 74, 085416 (2006).
Anderson, P. W., Ordering and antiferromagnetism in ferrites. Phys. Rev. 102, 1008–1013 (1956).
Henkelman, G., Arnaldsson, A. & Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 36, 354–360 (2006).
Kresse, G. & Hafner, J. Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements. J. Phys. Condens. Matter 6, 8245–8257 (1994).
Bloechl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Acknowledgements
JST and YMP wish to thank the Natural Science and Engineering Research Council of Canada (NSERC) for the Discovery Grants. WM wish to thank the Zhejiang Provincial Natural Science Foundation of China (LQ16E010003) for the research grants. All calculations were performed at the Westgrid Computer Cluster on generous allocations of computing resources to JST and YMP.
Author information
Authors and Affiliations
Contributions
M.W., J.S.T. and Y.M.P. planned the research. M.W. performed all the calculations and the analysis. M.W., J.S.T. and Y.M.P. wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wu, M., Tse, J. & Pan, Y. Electronic structures of greigite (Fe3S4): A hybrid functional study and prediction for a Verwey transition. Sci Rep 6, 21637 (2016). https://doi.org/10.1038/srep21637
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep21637
This article is cited by
-
Polycrystalline texture causes magnetic instability in greigite
Scientific Reports (2021)
-
A first-principles study of the effect of vacancy defects on the electronic structures of greigite (Fe3S4)
Scientific Reports (2018)
-
Pressure-induced structural and spin transitions of Fe3S4
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


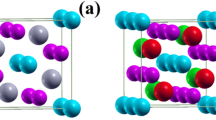

 model of Fe3S4 containing 28 atoms.
model of Fe3S4 containing 28 atoms.

