Abstract
Discovery of two-dimensional (2D) topological insulator such as group-V films initiates challenges in exploring exotic quantum states in low dimensions. Here, we perform first-principles calculations to study the geometric and electronic properties in 2D arsenene monolayer with hydrogenation (HAsH). We predict a new σ-type Dirac cone related to the px,y orbitals of As atoms in HAsH, dependent on in-plane tensile strain. Noticeably, the spin-orbit coupling (SOC) opens a quantum spin Hall (QSH) gap of 193 meV at the Dirac cone. A single pair of topologically protected helical edge states is established for the edges and its QSH phase is confirmed with topological invariant Z2 = 1. We also propose a 2D quantum well (QW) encapsulating HAsH with the h-BN sheet on each side, which harbors a nontrivial QSH state with the Dirac cone lying within the band gap of cladding BN substrate. These findings provide a promising innovative platform for QSH device design and fabrication operating at room temperature.
Similar content being viewed by others
Introduction
Two-dimensional (2D) topological insulators (TIs), known as quantum spin Hall (QSH) insulators, have attracted significant researches interest in condensed matter physics and materials science. The unique characteristic of 2D TI is generating a gapless edge state inside the band insulating gap, in which the edge state is topologically protected by time-reversal symmetry (TRS)1,2 and more robust against backscattering than the 3D TI, making 2D TIs better suited for coherent spin transport related applications. The prototypical concept of QSH insulator is first proposed by Kane and Mele in graphene3,4, in which the spin-orbit coupling (SOC) opens a band gap at the Dirac point. However, the associated gap due to rather weak second-order effective SOC is too small (~10–3 meV), which makes the QSH state in graphene only appear at an unrealistically low temperature. Quantized conductance through QSH edge states have been experimentally demonstrated in HgTe/CdTe5,6 and InAs/GaSb7,8 quantum-wells (QWs), showing an interesting in further experimental studies and possible applications.
Currently, there is a great interest in searching for new QSH insulators in 2D materials with controllable quantum phase transitions and tunable electronic and spin properties. Remarkably, the orbital filtering effects (OFE) in engineering the band feature has been received intense attentions in designing QSH insulators. For instance, stanene9 has a small band gap of 0.1 eV where the pz orbital dominates the effective low-energy band structure. Through hydrogenation, the SOC can be confined both on the px and py orbitals of stanene, enhancing its band gap to 0.3 eV. In fact, the band gap enhancement in QSH phase can also be realized by decorating organic molecule ethynyl on stanene film10. The strong SOC can be sufficed by bismuth element, which drives QSH and QAH states11. More recently, an approach to design a large-gap QSH state on a semiconductor surface by a substrate orbital selection process is also proposed12. These demonstrate that OFE is an effective way to enhance QSH effect in 2D materials with s and p orbitals dominating the conduction and valence bands.
Group-V honeycomb structures have recently attracted interests as novel 2D materials with intriguing electronic properties. Interestingly, the monolayer form of black phosphorous, phosphorene (α-P), has been reported experimentally to have a direct band gap and high carrier mobility, which can be exploited in the electronics13,14. The Bi or Sb ultrathin films15,16,17,18, another 2D group-V films with the strongest SOC, have been proposed to harbor large-gap QSH phases, ample to applications at room temperature. More recently, arsenene in α and β phases has been proposed to be energetically stable19,20,21,22. These materials with high mechanical stretchability, which can reversibly withstand extreme mechanical deformation, are useful to stretchable display devices, broadband photonic tuning and aberration-free optical imaging19,20,21. More importantly, we find the pristine arsenene can be a QSH insulator, but its band gap is relative small, unfavorable to possible room temperature applications22. However, the band topology of hydrogenated arsenene (HAsH) have not been reported up to date. It is thus reasonable to ask whether or not HAsH becomes a nontrivial QSH insulator, which maybe largely widens its application in spintronics.
In this work, based on first-principles calculations, we predict a σ-type Dirac cone at the K point in HAsH. The key is the OFE from decorated hydrogen atoms, in which the out-of-plane pz is filtered from p orbitals, forming sp2 hybridization, in analogy to planar graphene. A QSH phase with a band-gap as large as 193 meV at the Fermi level is obtained, available to practical application at room temperature. A single pair of topologically protected helical edges is established and its QSH phase is confirmed with Z2 = 1. We also propose a QW encapsulating HAsH between the BN sheet on each side, maintaining a nontrivial QSH state with the Dirac cone lying within the band gap of cladding BN substrate. These results provide an ideal platform for development of high-performance electronic devices in spintronics.
Methods
First-principles calculations based on density-functional theory (DFT)23 are performed by the Vienna ab initio simulation package24, using the projector- augmented-wave potential. The exchange-correlation functional is treated using the Perdew-Burke-Ernzerhof (PBE)25 generalized-gradient approximation. The energy cutoff of the plane waves is set to 500 eV with the energy precision of 10–5 eV. The Brillouin zone (BZ) is sampled by using a 9 × 9 × 1 Gamma-centered Monkhorst–Pack grid and the vacuum space is set to 30 Å to minimize artificial interactions between neighboring slabs. All structures are fully optimized, including cell parameters and atomic coordinates, until the residual forces are less than 0.01 eV/Å. The SOC is included in the self-consistent calculations of electronic structure.
Results and Discussion
Bulk As has four allotropes and the most stable one is gray As20, which is rhombohedral with two atoms per primitive cell. Thus, it can be viewed as a stacking of the bilayers along the [111] direction, as shown in Fig. 1(a). Unlike the planar graphene, the arsenene has a buckled configuration with a buckling distance h = 1.39 Å and bond length d = 2.51 Å (Fig. 1(b)), in consistent with that of Ref. 19 and 20. Figure 1(c) displays the calculated band structures of arsenene, which is indirect-gap semiconductor with a gap of 1.64 eV at the Fermi level. In this respect, its valence band maximum (VBM) locates the Γ point, while conduction band minimum (CBM) on M-Γ path, in agreement with the previous results20.
(a) Side view of the rhombohedrally (ABC) stacked layered structure of gray arsenic; (b) The side and top views of buckled honeycomb structure from gray arsenic; (c)The band structure of arsenene; (d) d1–d4 are the various bond lengths of corresponding position, the buckling heights was also marked as h; (e) Total energy with respect to lattice constant. The insert is Brillouin zone. The violet and silver balls denote arsenic and hydrogen atoms, respectively.
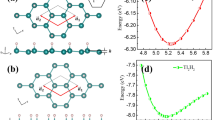
Hydrogenation has been proven to be an efficient way in engineering the electronic properties in 2D materials10,26,27,28,29,30,31,32. Thus, we saturate the uncoordinated As atoms with hydrogen atoms alternating on both sides of As sheet, in which d1−d4 represents the various bond lengths between As atoms (Fig. 1(d)). In sharp contrast to the graphane and silicane33,34, the structural relaxation make the σ-bond direction of As-H atoms tiled and finally perpendicular to As-As bonds, indicating hydrogen-induced arsenic dimerization with respect to tensile strain, as listed in Table 1. Figure 1(e) gives the total energy per unit cell as a function of lattice constant a. Interestingly, it displays two local minima in energy, where refer to the corresponding stable phases as buckled and planar states in order to highlight the size of buckling or interlayer distance in these two distinct states (Table 1).
External strains can drastically change the geometric structures and thus influence the electronic properties of HAsH correspondingly. As shown in the insert of Fig. 2, when applying the tensile strain, the As–As dimerization occurs clearly, leading to an indirect-direct gap transition. Further increasing to 4.20 Å, the As-As dimerization is suppressed, along with the arsenene plane becoming flat. In this case, a clear band crossing appears at the K point (Fig. 2(c)), as compared with the original indirect-gap semiconductor feature. If the lattice constant reaches 4.64 Å, it becomes completely flat with As–As bonds being equivalent, due to the complete dimerization breaking (Fig. 2(d)). The two energy bands crosses linearly at the K (and K′ = −K) point, suggesting the existence of Dirac-cone feature without SOC. Thus it can be considered as a gapless semiconductor, or alternatively, as a semi-metal with zero density of states at the Fermi level. Further increasing the lattice constant, the Dirac-cone preserves with the crossing at the Γ point shifting toward higher energy, which can be attributed to the simultaneous release of out-of-plane buckling in arsenene. For instance, if the lattice parameter increases as much as 28%, i.e., from a = 3.62 Å to a = 4.64 Å, the As–As bonds simply elongate from 2.48 Å to 2.68 Å, only corresponding to a stretch of 8%. As expected, it is geometric transition from buckling to planar one that plays a key role in the presence of the Dirac cone.
To prove the dynamic stability of this structure (a = 4.64 Å), we present the calculated phonon spectrum in Fig. 3(a). All phonon branches are positive, which indicates that this structure is kinetically stable. Moreover, Fig. 3(b) shows 3D band structure around the Dirac point at a = 4.64 Å. we can see two Dirac cones located at the K and K′ = −K points, similar valley symmetry as in graphene3,4. However, the energy spectrum here is no longer electron-hole symmetric, thus neither the scattering mechanism nor transport properties will be identical for the electron and hole doping cases. The linear dispersion holds up to 2.0 eV for holes, while the massless electrons acquire mass rapidly away from the K point, demonstrating that it is more promising for making unipolar field effect devices than for making ambipolar ones with graphene.
Now, we highlight the importance of the OFE9,10,11,12 in determining the origin of Dirac cone at a = 4.64 Å. In the absence of hydrogen atoms (Fig. 4(a)), one can see two Dirac cones located at the K point. By projecting the component of bands, the upper Dirac cone (green circles) originates from the px,y orbitals, whereas the lower one (blue circles) originates from pz orbital. Through fully-hydrogenation, the As-pz orbital bond to H-s orbital is filtered, making the low Dirac cone disappear (Fig. 4(b)). Thus, the remaining Dirac cone mainly comes from As-px,y orbitals rather than from pz orbital, as illustrated by the size of the circles near the Fermi energy. In this case, the px,y orbitals form σ bonds between As-As atoms, demonstrating an in-plane Dirac cone feature. Figure 4(c) further illustrates the schematic plot of energy level dispersion. As expected, the chemical bonding of As-As atoms makes the s and px,y orbitals forming the bonding and anti-bonding states, in the energy consequence of σ < π < π* < σ*, The planar honeycomb geometry separates in-plane (px,y) and out-plane (pz) orbitals, forming their own Dirac cones with σ and π characters, respectively (Fig. 4(a)). The hybridization between the π orbitals and induced H-1s orbital suppresses the π-type Dirac cone, leaving the σ-type Dirac cone intact. In addition, the Fermi level is raised by introduced hydrogen atoms and thus forming the semi-metallic states.
(a) Band structure of monolayer arsenene with a = 4.64 Å. (b)the aforementioned system but with H saturated and the contributions from s, px,y and pz orbitals, while red, green and blue dots represent the contribution of s, px,y and pz orbitals. (c) Schematic diagram of the electronic transition. The line thickness represents orbital degeneracy, whereas the red dot represents an occupied electron. The Fermi levels are at energy zero.
The As atom has an intrinsically larger SOC than a carbon atom, which may lead to many intriguing quantum properties in arsenene, such as the QSH effect3,4,35, in addition to its massless Dirac fermion as in graphene. To confirm this, we focus on the effect of SOC on band structures at 4.64 Å, as displayed in Fig. 5(a). One can see that the degeneracy at the Dirac points is lifted. The valence bands are downshifted whereas the conduction bands are upshifted, forming a large band gap of 193 meV by SOC, as illustrated in Fig. 4(c). As observed in previously reported 2D TIs like phosphorene36, ZrTe5, HfTe537 and GaSe38, the SOC-induced band-gap opening at the Fermi level is a strong indication of the existence of topologically nontrivial phases. We have carried out test calculations based on the hybrid functional HSE06 to assess the robustness of our results. As shown in Fig. 5(b), the band gap around Dirac point is increased to 339 meV, but the band character is not changed, which is agreement with our PBE results.
(a,b) Band structures of hydrogenated arsenene with SOC using PBE and HSE06. Here, the insert is Brillouin zone. (c) Electronic structure of helical edge states of hydrogenated arsenene, the left subpanel shows the total density of states while the right subpanel shows the corresponding spin polarization in two channels.
To identify the nontrivial band topology in 2D HAsH, we calculate the topologically invariant Z2 number (γ) following the approach proposed by Fu and Kane39, due to the presence of inversion symmetry. Here, the invariants v can be derived from the parities of wave function at the four time-reversal-invariant momenta (TRIM) points Ki, namely one Γ point and three M points in the Brillouin zone, as illustrated in the insert of Fig. 5(a). The topological index ν are established by

where δ is the product of parity eigenvalues at the TRIM points, ξ = ±1 are the parity eigenvalues and N is the number of the occupied bands. According to the Z2 classification, ν = 1 characterizes a QSH insulator, whereas ν = 0 represents a trivial band topology. As expected, in the equilibrium state, the products of the parity eigenvalues at these three symmetry points: M(0.0, 0.5), M(0.5, 0.5) and M(0.5, 0.0) are both −1, while at Γ(0.0, 0.0) and displays +1, yielding a nontrivial topological invariant Z2 = 1.
The SOC induced band gap opening near the Fermi level indicates possible existence of 2D TI state that are helical with the spin-momentum locked by TRS. To check this, we calculated the topological edge states of HAsH by the Wannier90 package40. We construct the maximally localized Wannier functions (MLWFs) and fit a tight-binding Hamiltonian with these functions. Then, the edge Green’s function41 of a semi-infinite HAsH is constructed and the local density of state (LDOS) is calculated, as shown in Fig. 5(b). Clearly, all the edge bands are seen to link the conduction and valence bands and span the 2D band energy gap, yielding a 1D gapless edge states. Besides, the counter-propagating edge states exhibit opposite spin polarizations, in accordance with the spin-momentum locking of 1D helical electrons. All the above results consistently indicate that hydrogenated arsenene is an ideal 2D TI.
The substrate materials are inevitable in device application, thus the free-standing HAsH monolayer should eventually be deposited or grown on a substrate. As a 2D large-gap insulator with a high dielectric constant, the h-BN sheet has been successfully used as the substrate to grow graphene or assemble 2D stacked nanodevices42,43. Considering that the HAsH surface is chemically active, we adopt the encapsulation technology, which has been used in Flip-Chip44, to encapsulate HAsH monolayer forming a hybrid QW from the degradation effect by the environmental gases, which, if not prevented, would destroy the QSH states. Figure 6(a) show the QW structure of HAsH monolayer sandwiched on  BN sheet, where the lattice mismatch is only about 6.3%. After full relaxation with the van der Waals (vdW) forces45, HAsH almost retain the original structure with a distance between the adjacent h-BN layers of 2.38 Å. The calculated binding energy is about −0.77 eV per unit cell, showing that they are typical van der Waals interactions. The calculated band structure with SOC is shown in Fig. 6(b). In these weakly coupled QW structure, the HAsH monolayer remains semiconducting, there is essentially no charge transfer between the adjacent layers and the states around the Fermi level are dominantly contributed by HAsH. If we compare the bands of HAsH with and without the cladding BN sheet, little difference is observed. Evidently, the robustness of QSH effect can be preserved in this QW structure.
BN sheet, where the lattice mismatch is only about 6.3%. After full relaxation with the van der Waals (vdW) forces45, HAsH almost retain the original structure with a distance between the adjacent h-BN layers of 2.38 Å. The calculated binding energy is about −0.77 eV per unit cell, showing that they are typical van der Waals interactions. The calculated band structure with SOC is shown in Fig. 6(b). In these weakly coupled QW structure, the HAsH monolayer remains semiconducting, there is essentially no charge transfer between the adjacent layers and the states around the Fermi level are dominantly contributed by HAsH. If we compare the bands of HAsH with and without the cladding BN sheet, little difference is observed. Evidently, the robustness of QSH effect can be preserved in this QW structure.
Conclusions
In summary, based on first-principles calculations, we predict a new σ-type Dirac cone related to the px,y orbitals of As atoms in HAsH, dependent on in-plane tensile strain. The key is to separate the in-plane px,y and out-of-plane pz orbitals via hydrogenation and strain. Noticeably, spin-orbit coupling (SOC) can open a nontrivial QSH gap of 193 meV at the Dirac cone. A single pair of topologically protected helical edge states is established for the edge of HAsH and its QSH states are confirmed with topological invariant Z2 = 1. We propose a QW encapsulating HAsH between the h-BN sheet on each side, maintaining a nontrivial QSH state with the Dirac cone lying within the band gap of cladding BN sheet. These findings provide a promising innovative platform for QSH device design and fabrication operating at room temperature.
Additional Information
How to cite this article: Wang, Y.-P. et al. Controllable band structure and topological phase transition in two-dimensional hydrogenated arsenene. Sci. Rep. 6, 20342; doi: 10.1038/srep20342 (2016).
References
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X. L. & Zhang, S. C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Kane, C. L. & Mele, E. J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 95, 226801 (2005).
Kane, C. L. & Mele, E. J. Z2 Topological Order and the Quantum Spin Hall Effect. Phys. Rev. Lett. 95, 146802 (2005).
Bernevig, B. A., Hughes, T. L. & Zhang, S. C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science. 314, 1757–1761 (2006).
König, M. et al. Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science. 318, 766–770 (2007).
Liu, C., Hughes, T. L., Qi, X. L., Wang, K. & Zhang, S. C. Quantum Spin Hall Effect in Inverted Type-II Semiconductors. Phys. Rev. Lett. 100, 236601 (2008).
Du, L., Knez, I., Sullivan, G. & Du, R. R. Robust Helical Edge Transport in Gated InAs/GaSb Bilayers. Phys. Rev. Lett. 114, 096802 (2015).
Xu, Y. et al. Large-Gap Quantum Spin Hall Insulators in Tin Films. Phys. Rev. Lett. 111, 136804 (2013).
Zhang, R. W. et al. Ethynyl-functionalized stanene film: a promising candidate as largegap quantum spin Hall insulator. New J. Phys. 17, 083036 (2015).
Niu, C. et al. Functionalized Bismuth Films: Giant Gap Quantum Spin Hall and Valley-Polarized Quantum Anomalous Hall States. Phys. Rev. B. 91, 041303 (2015).
Zhou, M. et al. Formation of quantum spin Hall state on Si surface and energy gap scaling with strength of spin orbit coupling. Scientific Reports. 4, 7102 (2014).
Wu, M., Fu, H., Zhou, L., Yao, K. & Zeng, X. C. Nine new phosphorene polymorphs with non-honeycomb structures: a much extended family. Nano Lett. 15(5), 3557–62 (2015).
Yu, G., Jiang, L. & Zheng, Y. Two-dimensional Kagome phosphorus and its edge magnetism: a density functional theory study. J. Phys.: Condens. Matter. 27, 255006 (2015).
Bihlmayer, G., Koroteev, Y. M., Chulkov, E. V. & Blügel, S. Surface- and edge-states in ultrathin Bi–Sb films. New Journal of Physics. 12, 065006 (2010).
Hirahara, T. et al. Topological metal at the surface of an ultrathin Bi1−xSbx alloy film. Phys. Rev. B. 81, 165422 (2010).
Li, X. R. et al. Prediction of large-gap quantum spin hall insulator and rashba-dresselhaus effect in two-dimensional g-TlA (A = N, P, As and Sb) monolayer films. Nano Research. 8, 2954–2962 (2015).
Lee, J., Tian, W. C., Wang, W. L. & Yao, D. X. Two-Dimensional Honeycomb Monolayer of Nitrogen Group Elements and the Related Nano-Structure: A First-Principle Study. Scientific Reports. 5, 11512 (2015).
Kamal, C. & Ezawa, M. Arsenene: Two-dimensional Buckled and Puckered Honeycomb Arsenic Systems. Phys. Rev. B. 91, 085423 (2015).
Zhu, Z., Guan, J. & Tománek, D. Strain-induced metal-semiconductor transition in monolayers and bilayers of gray arsenic: A computational study. Phys. Rev. B. 91, 161404 (2015).
Wang, Y. P., Zhang, C. W., Ji, W. X. & Wang P. J. Unexpected band structure and half-metal in non-metal-doped arsenene sheet. Applied Physics Express. 8, 065202 (2015).
Wang Y. P. et al.Tunable quantum spin Hall effect via strain in two-dimensional arsenene monolayer. J. Phys. D: Appl. Phys. 49, 055305 (2016).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. B. 136(3B), B864–B871 (1964).
Kresse, G. & Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865 (1996).
Cao, G., Zhang, Y. & Cao, J. Strain and chemical function decoration induced quantum spin Hall effect in 2D silicene and Sn film. Physics Letters A. 379, 1475–1479 (2015).
Song, Z. et al. Quantum spin Hall insulators and quantum valley Hall insulators of BiX/SbX (X = H, F, Cl and Br) monolayers with a record band band gap. NPG Asia Materials. 6, e147 (2014).
Jin, K. H. & Jhi. S. H. Quantum anomalous Hall and quantum spin-Hall phases in flattened Bi and Sb bilayers. Scientific Reports. 5, 8426 (2015).
Liu, C. C. et al. Low-Energy Effective Hamiltonian for Giant-Gap Quantum Spin Hall Insulators in Honeycomb X-Hydride/Halide (X = N-Bi) Monolayers. Phys. Rev. B. 90, 085431 (2014).
Zhao, H., Zhang, C. W., Ji, W. X., Zhang, R. W., Li, S. S., Yan, S. S., Zhang, B., Li, P. & Wang, P. J. Unexpected Giant-Gap Quantum Spin Hall Insulator in Chemically Decorated Plumbene Monolayer. Sci. Rep 6, 20152 (2016).
Chou, B. H. et al. Hydrogenated ultra-thin tin films predicted as two dimensional topological insulators. New Journal of Physics 16(11), 115008 (2014).
Freitas, R. R. Q., Rivelino, R., de Brito Mota, F. & de Castilho, C. M. C. Topological Insulating Phases in Two-Dimensional Bismuth-Containing Single Layers Preserved by Hydrogenation. J. Phys. Chem. C 119(41), 23599 (2015).
Zhou, J., Wu, M. M., Zhou, X. & Sun. Q. Tuning electronic and magnetic properties of graphene by surface modification. Applied Physics Letters. 95, 103108 (2009).
Zhang, C. W. & Yan, S. S. First-Principles Study of Ferromagnetism in Two-Dimensional Silicene with Hydrogenation. J. Phys. Chem. C. 116(6), 4163–4166 (2012).
Fukui, T. & Hatsugai, Y. Topological aspects of the quantum spin-Hall effect in graphene: Z2 topological order and spin Chern number. Phys. Rev. B. 75, 121403(R) (2007).
Liu, Q., Zhang, X., Abdalla, L. B., Fazzio, A. & Zunger, A. Switching a Normal Insulator into a Topological Insulator via Electric Field with Application to Phosphorene. Nano Letters. 15, 1222–1228 (2015).
Weng, H., Dai, X. & Fang, Z. Transition-metal pentatelluride ZrTe5 and HfTe5: A paradigm for large-gap quantum spin Hall insulators. Phys. Rev. X. 4, 011002 (2014).
Zhu, Z., Cheng, Y. & Schwingenschlögl, U. Topological phase transition in layered GaS and GaSe. Phys. Rev. Lett. 108, 266805 (2012).
Fu, L. & Kane, C. L. Time reversal polarization and a Z2 adiabatic spin pump. Phys. Rev. B. 74, 195312 (2006).
Mostofi, A. A. et al. Wannier90: A tool for obtaining maximally-localised Wannier functions. Computer Physics Communications. 178, 685–699 (2008).
Sancho, M. P. L., Sancho, J. M. L. & Rubio, J. Highly convergent schemes for the calculation of band and surface Green functions. J. Phys. F. 15, 851–858 (1985).
Kim, K. K. et al. Synthesis of monolayer hexagonal boron nitride on Cu foil using chemical vapor deposition. Nano letters. 12, 161–166 (2011).
Yang, W. et al. Epitaxial growth of single-domain graphene on hexagonal boron nitride. Nature materials. 12, 792–797 (2013).
Suryanntayana, D., Hsiao, R., Gall, T. P. & Mccreary, J. M. Enhancement of Flip-Chip life by encapsulation. IEEE Trans, Compon. Hybrids, Manuf Technol. 14, 218 (1991).
Klimeš, J., Bowler, D. R. & Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B. 83, 195131 (2011).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No.11274143, 61571210 and 11304121) and Research Fund for the Doctoral Program of University of Jinan (Grant No. XBS1433).
Author information
Authors and Affiliations
Contributions
Y.P.W. and C.W.Z. conceived the study and wrote the manuscript. W.X.J. and P.L. performed the first-principles calculations. F.L. and M.J.R. prepared figures 1–2, 6. X.L.C., M.Y. and P.J. Wang prepared figures 3–5. All authors read and approved the final manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wang, Yp., Ji, Wx., Zhang, Cw. et al. Controllable band structure and topological phase transition in two-dimensional hydrogenated arsenene. Sci Rep 6, 20342 (2016). https://doi.org/10.1038/srep20342
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep20342
This article is cited by
-
Density-Generalized Theory Study of Electronic Structure, Magnetic, and Optical Properties of Mn-Doped and Mn-X (X = B, C, N, O, and F) Co-doped Arsenenes
Journal of Superconductivity and Novel Magnetism (2022)
-
Recent advances in photodynamic therapy based on emerging two-dimensional layered nanomaterials
Nano Research (2020)
-
Arsenene Nanotube as a Chemical Sensor to Detect the Presence of Explosive Vapors: A First-Principles Insight
Journal of Inorganic and Organometallic Polymers and Materials (2018)
-
Emerging novel electronic structure in hydrogen-Arsenene-halogen nanosheets: A computational study
Scientific Reports (2017)
-
Unconventional band inversion and intrinsic quantum spin Hall effect in functionalized group-V binary films
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.