Abstract
Cancer cells manoeuvre through extracellular matrices (ECMs) using different invasion modes, including single cell and collective cell invasion. These modes rely on MMP-driven ECM proteolysis to make space for cells to move. How cancer-associated alterations in ECM influence the mode of invasion remains unclear. Further, the sensitivity of the two invasion modes to MMP dynamics remains unexplored. In this paper, we address these open questions using a multiscale hybrid computational model combining ECM density-dependent MMP secretion, MMP diffusion, ECM degradation by MMP and active cell motility. Our results demonstrate that in randomly aligned matrices, collective cell invasion is more efficient than single cell invasion. Although increase in MMP secretion rate enhances invasiveness independent of cell–cell adhesion, sustenance of collective invasion in dense matrices requires high MMP secretion rates. However, matrix alignment can sustain both single cell and collective cell invasion even without ECM proteolysis. Similar to our in-silico observations, increase in ECM density and MMP inhibition reduced migration of MCF-7 cells embedded in sandwich gels. Together, our results indicate that apart from cell intrinsic factors (i.e., high cell–cell adhesion and MMP secretion rates), ECM density and organization represent two important extrinsic parameters that govern collective cell invasion and invasion plasticity.
Similar content being viewed by others
Introduction
In vivo, cells are known to utilize a gamut of different migration strategies for their movement. Single cell migration is the best-studied mechanism and is important in various processes including development, immune surveillance and cancer metastasis1,2,3. In epithelial cancers, invasion is often triggered by conversion from a cell–cell adhesion-rich ‘epithelial state’ to a cell–cell adhesion-weak ‘mesenchymal state’ in a process termed epithelial to mesenchymal transition (EMT)4. Collective cell migration5,6 and collective cell invasion7,8 represent a second mode of cell movement wherein cell–cell adhesions remain intact and cells move collectively9,10. During collective cell motility, a front-rear asymmetry is maintained whereby leader cells at the front row sense extracellular guidance cues through a combination of chemotaxis and haptotaxis and dictate the overall direction of movement for the cell cohort. A common feature of both single and collective cell invasion is the requirement for extracellular matrix (ECM) remodeling, achieved primarily through matrix degrading enzymes like matrix metalloproteinases (MMPs), which generate paths via ECM degradation11,12. Interestingly, inhibition of degrading machinery or blockage of cell–matrix adhesions leads to amoeboidal mode of migration wherein cells squeeze through pre-existing pores in the matrix using actomyosin contractility13. Thus, instead of arresting cell invasion, alterations in cell–cell adhesions, cell–matrix adhesions and proteolytic machinery lead to alterations in the strategies used by cancer cells to invade.
In addition to the molecular properties of tumour cells themselves, the ECM is itself a major determinant of the mode of cell invasion. In interstitial tissues, ECM organization can differ significantly from one location to another depending on the density and orientation of collagen I, the major constituent of the interstitial ECM14. During invasion, cancer cells manoeuvre through both sparse matrices comprised of randomly oriented fibres with large pore sizes and dense matrices comprised of aligned collagen bundles with pore sizes of few microns. The tumour microenvironment itself is known to undergo drastic alterations in composition and organization during cancer progression15. Similar to fibrosis, many malignancies are associated with increased deposition of fibrillar collagens16,17, with increased expression of collagen I associated with increased risk of cancer metastasis18,19. In many epithelial tissues, the organization of collagen fibrils also changes from curly to linear effected by cancer cell-secreted crosslinking enzymes like lysyl oxidase (LOX)20. Increase in ECM density and crosslinking progressively stiffen the ECM, which in turn influences cell motility through increased integrin signalling21. Interestingly, integrin signalling also influences ECM remodeling via activation of MMPs, which generate migration tracks by proteolytic cleavage of the ECM through membrane-localized as well as soluble MMPs11,22,23. Given the wide heterogeneity in ECM organization, invading tumour cells are confronted with different extracellular structures, which in turn are likely to influence the mode of motility in multiple ways. Some of the critical ECM features influencing the mode of cell motility include confinement (set by pore size)24,25, fibre alignment (along which cells may align and migrate)26,27 and bulk properties of the matrix20,21,28,29.
As detailed in the above paragraphs, ECM density and orientation, cell polarity, cell–cell contact strength and cell–ECM interactions interdependently control efficiency and the mode of cancer cell invasion13,30. However, due to the enormous biological and biophysical complexity of this cell–ECM ensemble, it is extremely difficult to experimentally gauge how these interactions contribute to cancer cell invasion. Hence, it seems appropriate to use mathematical and simulation tools, which have contributed significantly to our understanding of cancer31,32,33,34, to understand plasticity in cancer cell invasion. Several classes of computational models have been developed to address various aspects of cell invasion during cancer progression. Of the various types of models, discrete models, such as cellular automata, cellular Potts model (CPM) and agent based models, are particularly well suited for studying multiscale population dynamics35,36. Of special interest is the cell-based, CPM, a multi-particle lattice description, that is capable of modeling cell–cell and cell–ECM interactions37. In CPM, physical properties of biological entities (e.g., cell, ECM fibre, etc.) can be taken into account by modeling them as multi-pixel deformable objects and evolving their position/state as per experimentally motivated predefined rules38,39,40. Further, it is possible to combine these models with other mechanistic rules as well as partial differential equation (PDE)-based reaction–diffusion systems for capturing phenomena occurring at different length-scales and time-scales37,41,42,43.
Despite the existence of many models that have been developed for the purpose of understanding cancer invasion, several questions remain unanswered. For example, Bauer et al.41,42 used a hybrid CPM to understand the role of cell migration, growth and adhesion to understand tumour induced angiogenesis. However, the migration in their model was a result of directed chemotaxis, whereas cells can undergo migration due to self-polarization even in the absence of chemokine gradients44. The CPM developed by Kabla45 incorporates polarity and migration potential of single cells in order to understand migration patterns of cell collectives. However, the effects of cellular microenvironment, which are crucial for cancer cell invasion, were missing in this description. Most of these drawbacks were addressed by Szabo et al.46 in their concise description that takes into account all the crucial ingredients – cell–cell and cell–ECM interactions, cell polarization and ECM topography – and their role in cancer cell invasion. Modeling along similar lines was also done in refs 47, 48, 49. Despite these modeling efforts, various questions remain unanswered and warrant explanation. For example, what is the role of cell–cell adhesion with respect to ECM remodeling and maintaining invasiveness of cancer cells? What is a more efficient mode of invasion (single or collective) and when would the cells prefer to switch from one mode to the other? How does ECM confinement and proteolytic abilities collectively dictate the mode and efficiency of cell invasion? In short, although the existing models indeed address the effect of various aforementioned factors on avascular cancer cell invasion, they do not elucidate how these factors conspire together to dictate the mode and efficiency of invasion and what invasion strategies cells may flexibly follow upon tuning these factors13,30.
In this paper, we probe the contributions of cell–cell adhesion, MMP dynamics, ECM density and organization on the mode of cancer cell invasion and attempt to address the issue of cell invasion plasticity13,30. Our computational framework uses CPM-based formalism to model a cell aggregate positioned at the centre of an ECM lattice of given density and organization. Cells possess intrinsic motility and history-dependent polarity (preferred direction of motion). Rule-based mechanistic formulation was used to implement MMP-mediated ECM fibre degradation. Pre-existing gaps and spaces created by ECM degradation allow for movement of cells within the lattice. Using this formulation we found that the overall speed and pattern of cell invasion depended greatly on cell–cell adhesiveness and MMP secretion rates. While greater cell–cell adhesiveness was required for collective cell invasion, higher cell–cell adhesion was also associated with less amount of ECM degradation. The increase in MMP secretion rate at intermediate fibre densities was observed to make individual invasion more effective as compared to collective cell invasion. On the other hand, high MMP secretion rates foster collective cell invasion at high fibril densities. Aligned matrices, which provide contact guidance cues to cells, serve as an exception to the requirement of high MMPs where invasion is possible even at low MMP secretion rates. Finally, we have compared some of our in-silico predictions with experiments by tracking the invasion of MCF-7 human breast cancer cells using sandwich cultures. Taken together, our results suggest that the interplay between cell–cell adhesion, MMP secretion rate and ECM organization, which can be thought of as intrinsic tuning parameters of cancer cells, can lead to plasticity in cancer cell invasion.
Materials and Methods
Cellular invasion through dense ECM networks is influenced by several factors including steric hindrance from the environment, formation of migration tracks by ECM proteolysis (mediated by MMPs), self motility of cells and adhesion energies between different entities (e.g., cell–cell adhesion, cell–matrix adhesion, etc). One of the major bottlenecks in understanding cell invasion is attributed to the multiscale nature of processes involved. While cell invasion is a cell-scale phenomenon, changes in interface energies associated with local cell movement, MMP secretion, MMP diffusion and ECM degradation occur at the sub-cellular level. Thus, for simulating cell invasion, it is important to develop a framework which combines multiple processes occurring at different length-scales and time-scales. Cellular Potts models (CPMs), also called Graner-Glazier-Hogeweg (GGH) models, are cell-based models that provide a convenient way to integrate cellular mechanics with sub-cellular reaction diffusion dynamics38,39,40. To tackle the multiscale phenomena of cell invasion, we have developed a Monte Carlo simulation-based CPM integrated with reaction–diffusion dynamics of MMP molecules. In our model, diffusing MMP molecules degrade ECM fibres and change cell–ECM interactions thereby integrating reaction–diffusion dynamics of MMP with GGH algorithm. Models like these, which integrate processes occurring at different length and times scales and obey different dynamics (e.g. GGH algorithm and reaction–diffusion dynamics), are referred to as multiscale hybrid models43,50,51. In our model, cells are placed on top of a non-degradable substrate and surrounded by an interstitial ECM network comprised of ECM fibres and interstitial fluid (Fig. 1A). The software package CompuCell3D (CC3D)40 was combined with custom written C++/python routines for implementing our model.
Model schematic (A) ECM was modeled as a 2D space (Ω) of 1 × 1 mm2. Ω is discretized into pixels of dimensions 2 μm × 2 μm. ECM fibres were represented by straight lines 1 pixel (2 μm) thick and 30–40 μm long. Each cell was represented by a 2D area ≈400 μm2 (coloured 2D boxes). Pixels that neither belong to a cell nor to an ECM fibre were considered as fluid pixels. MMP molecules were modeled by a continuous field. (B) Cells were modelled as active particles with intrinsic motility. The direction of cell motility, also referred as cell polarity ( ), was calculated based on the average of the cell displacements in the last 10 Monte Carlo steps (MCS). (C) Distinct adhesion energies were defined for interfaces between adjacent entities, that is Jcf (cell–fluid), Jcc (cell–cell), Jce (cell–ECM), Jee (ECM-ECM), Jef (ECM–fluid) and Jff (fluid–fluid). (D) Soluble MMP molecules, secreted by cells, can undergo diffusion and also degrade the ECM fibre, when the number of MMP molecules at any pixel increases beyond a threshold value of 1. Subsequently, the fibre is deleted from that pixel by changing the pixel type to ‘fluid pixel’.
), was calculated based on the average of the cell displacements in the last 10 Monte Carlo steps (MCS). (C) Distinct adhesion energies were defined for interfaces between adjacent entities, that is Jcf (cell–fluid), Jcc (cell–cell), Jce (cell–ECM), Jee (ECM-ECM), Jef (ECM–fluid) and Jff (fluid–fluid). (D) Soluble MMP molecules, secreted by cells, can undergo diffusion and also degrade the ECM fibre, when the number of MMP molecules at any pixel increases beyond a threshold value of 1. Subsequently, the fibre is deleted from that pixel by changing the pixel type to ‘fluid pixel’.
Model components
Making use of the spherical symmetry of solid tumours/tumour spheroids, 2-dimensional (2D) computational models have been used for studying various aspects of 3-dimensional (3D) tumour invasion including 3D branching, angiogenesis and cell migration41,42,52. Using a similar approach in this study, we have developed a 2D model of cancer invasion, wherein ECM fibres and cells were placed inside a 2D lattice (1 mm × 1 mm size) (Fig. 1A). Making use of the symmetry property of 3D spheroids helped us in simplifying the complexity of cancer cell invasion in 3D and developing a computationally tractable model of cellular invasion, wherein we simulate invasion of a group of cells placed at the centre of our simulation grid. This setup only mimics metastatic dissemination of a group of cancer cells and does not model cancer progression. The lattice size was selected such that each cell had to migrate at least 400 μm (double the population length scale) before touching the lattice boundary. ECM was represented by a meshed network of fibres, with each fibre represented by a straight line 2 μm in thickness and 30–40 μm in length. In our model, all ECM fibres were aligned in a 2D plane instead of having 3D positioning. This approximation helped us to incorporate the effect of mechanical hindrance in our model with an increasing number of ECM fibres providing greater hindrance (as a cell cannot cross over a fibre without degrading it). While the fibre orientation was assumed to be random for most of the simulations (unless indicated otherwise), the effect of fibre density was incorporated in our model by changing the total number of fibres in the lattice. Cells were represented as 2D deformable surfaces of mean area ≈400 μm2, comparable to the size of biological cells53. Cells are capable of changing their position and morphology over time, subject to area and perimeter constraints. While the area constraint prevents the cell area from becoming too large or too small, the perimeter constraint ensures that cells do not undergo excessive deformations. Cells were assumed to possess intrinsic motility, modeled by associating a preferred direction of migration (i.e., polarity,  ) and motility strength (μ0). The polarity (
) and motility strength (μ0). The polarity ( ) was calculated based on the last 10 displacements (Fig. 1B) as done elsewhere45. After placing ECM fibres and cells in the lattice, the remaining free pixels were considered as ‘fluid’ pixels, which represent the interstitial fluid between the ECM pores42. Adhesion energies were used to model the extent of adhesion between adjacent entities, i.e., between two ECM fibres (Jee), cell–ECM (Jce), ECM–fluid (Jef), cell–cell (Jcc), cell–fluid (Jcf) and fluid–fluid (Jff) (Fig. 1C). While high values of adhesion energy represents weak adhesion, strong adhesion was modeled by low values of adhesion energy.
) was calculated based on the last 10 displacements (Fig. 1B) as done elsewhere45. After placing ECM fibres and cells in the lattice, the remaining free pixels were considered as ‘fluid’ pixels, which represent the interstitial fluid between the ECM pores42. Adhesion energies were used to model the extent of adhesion between adjacent entities, i.e., between two ECM fibres (Jee), cell–ECM (Jce), ECM–fluid (Jef), cell–cell (Jcc), cell–fluid (Jcf) and fluid–fluid (Jff) (Fig. 1C). While high values of adhesion energy represents weak adhesion, strong adhesion was modeled by low values of adhesion energy.
Interactions and evolution in CPM
Spatiotemporal evolution of the simulation lattice was governed by the random movement of individual pixels subject to transition probabilities based on the Monte Carlo method40. Algorithmically, during each move, two neighboring pixels were chosen randomly, with one designated as the source pixel and the other one as the target pixel. An attempt to update the lattice was made only when both the source and the target pixels represented either a cell pixel or a fluid pixel. In other words, ECM fibre pixels did not participate in the random Monte Carlo updates. Further, if both pixels belonged to the same cell (i.e., σ(source) = σ(target)), then also no changes were made to the lattice. Otherwise, the source pixel attempted to occupy the target pixel based on Monte Carlo acceptance probability. To do this, the total system energy associated with the configuration before the move (Ei) and the configuration after the move (Ef) were calculated as per the following equation:

where,
σ(i): ID of the cell to which pixel i belongs
τ(σ): type of the cell σ
Jτ1,τ2: boundary energy per unit length between cells of type τ1 and τ2
λp: perimeter constraint of a cell
λa: inverse compressibility or area constraint of a cell
a(c): current area of the cell c
p(c): current perimeter of the cell c
a0: target (preferential) area of a cell
p0: target (preferential) perimeter of a cell
w(c): energy due to active motility of the cell c
Between two different configurations, if ΔE = (Ef − Ei) < 0, the proposed move was always accepted. Else, the move was accepted with a probability p calculated using the expression  . Using this dynamics, the system tries to move towards a lower energy configuration with Tm representing the likelihood of accepting a thermodynamically unfavorable move (i.e., it increases the system energy instead of decreasing). This expression of probability of accepting a move is based on the widely used Boltzmann acceptance function54, with Tm referred to as Boltzmann temperature. In CPM, Tm does not reflect any conventional thermal temperature; instead, it represents the strength of noise in the dynamics45. Low values of Tm makes the system evolution highly deterministic raising the possibility of the system getting trapped at a local minima. In contrast, a very high value of Tm causes the system to accept any proposed move. Further, owing to the fact that agitation of cell membrane in biological systems plays a role similar to that performed by temperature in thermodynamics, Tm is also called the magnitude of effective membrane fluctuations40,41,42. High values of Tm may lead to increase in cell body re-arrangements and motility40. In contrast, low values of Tm correspond to cells with very low fluctuations in cell boundary. A successful move increased the volume of the cell containing the source pixel and decreased the volume of the cell containing the target pixel by one pixel. Each Monte Carlo step (MCS) corresponded to repeating this exercise N times (N being the total number of lattice pixels that can be evolved) irrespective of whether the moves were accepted or not.
. Using this dynamics, the system tries to move towards a lower energy configuration with Tm representing the likelihood of accepting a thermodynamically unfavorable move (i.e., it increases the system energy instead of decreasing). This expression of probability of accepting a move is based on the widely used Boltzmann acceptance function54, with Tm referred to as Boltzmann temperature. In CPM, Tm does not reflect any conventional thermal temperature; instead, it represents the strength of noise in the dynamics45. Low values of Tm makes the system evolution highly deterministic raising the possibility of the system getting trapped at a local minima. In contrast, a very high value of Tm causes the system to accept any proposed move. Further, owing to the fact that agitation of cell membrane in biological systems plays a role similar to that performed by temperature in thermodynamics, Tm is also called the magnitude of effective membrane fluctuations40,41,42. High values of Tm may lead to increase in cell body re-arrangements and motility40. In contrast, low values of Tm correspond to cells with very low fluctuations in cell boundary. A successful move increased the volume of the cell containing the source pixel and decreased the volume of the cell containing the target pixel by one pixel. Each Monte Carlo step (MCS) corresponded to repeating this exercise N times (N being the total number of lattice pixels that can be evolved) irrespective of whether the moves were accepted or not.
In the above expression, four different energy terms contribute to the total energy of the system (Etotal). These are due to adhesive interactions between different entities (e.g., cell–cell, cell–matrix, cell–fluid, etc.) and energy associated with changes in cell size, changes in cell perimeter and with the intrinsic motility of cells. Adhesive/repulsive dynamics between different entities as well as between two species of the same entity was accounted for by considering an interface energy (e.g., Jcc, Jce, etc.) (Fig. 1C). Lower values of interface energies represent greater adhesion and higher values model the lower adhesion. If the cell–cell adhesion energy (Jcc) is lower than the cell–matrix (Jce) or cell–fluid (Jcf) energies, any move (movement of a pixel of a cell) resulting in an increase of contact surface area between two neighboring cells will be accepted as it will decrease the system energy. Conversely, if Jcc is higher than Jce or Jcf, any proposed move resulting in increase of cell–cell adhesion will be rejected due to the high energy of the proposed state40. Physically, lower values of Jcc represent stronger cell–cell adhesion (e.g., higher membrane concentration of E-cadherin-β-catenin complexes55). Next, each cell was assigned a target area (a0) with changes in cell area from this value being energetically unfavourable. Area constraint has been used to model bulk cell stiffness (or inverse compressibility) and is related to the internal pressure40. Similarly, the perimeter constraint (λp) forces the cell to maintain its perimeter close to the preferred perimeter (p0) and ensures that cells do not develop extreme deformed configurations. Hence, this constraint can be used to model the ease with which a cell can change its shape and is therefore related to the line tension/cortical stiffness of the cell. While bulk stiffness can be estimated using Atomic Force Microscopy (AFM) experiments of cell indentation, cortical stiffness can be estimated using micropipette aspiration experiments. In our simulations, all cells have a0 = 400 μm2 and p0 = 35 μm. The last term w(σ) in Equation (1) accounts for the intrinsic motility of cells and is given by the expression  45. Here, μ0 represents the strength of cell motility,
45. Here, μ0 represents the strength of cell motility,  represents the unit vector in the direction of preferred polarity for cell c and vector rc represents centre of mass of the cell c. While μ0 was kept constant in all simulations, the value of
represents the unit vector in the direction of preferred polarity for cell c and vector rc represents centre of mass of the cell c. While μ0 was kept constant in all simulations, the value of  at any time t was modeled as an adaptive quantity set as the average of the displacements during the the previous τ MCS normalized to unity45 (Fig. 1B). Specifically, Equation (2) was used to find the preferred polarity of the cell c at time t and was updated after every MCS.
at any time t was modeled as an adaptive quantity set as the average of the displacements during the the previous τ MCS normalized to unity45 (Fig. 1B). Specifically, Equation (2) was used to find the preferred polarity of the cell c at time t and was updated after every MCS.

where,
τ: time scale of polarity evolution.
displacement(t): displacement of cell’s centre of mass c between tth and (t + 1)th MCS.
The parameter τ can be tuned to model persistence of cell migration. While we have used τ = 10 in all our simulations as done elsewhere45,56, one set of simulations were performed to study the effect of τ on cell invasion dynamics (Supp. Fig. S2).
MMP dynamics and ECM degradation
In addition to the Metropolis equation based copy index events governed by Equation (1), a GGH algorithm can be integrated with other objects such as chemical field(s)40. The dynamics of a chemical field can be described by reaction–diffusion systems. Such chemical field can then be integrated into the main GGH algorithm by modeling the effect of this field on other system components. This approach has been used to model processes such as growth factor-dependent cell growth and oxygen-dependent cell apoptosis43. In our model, a separate field was maintained for soluble MMPs which are secreted by cells when they come in contact with ECM fibres (Fig. 1D). Whenever a cell comes in contact with ECM fibre(s) it secretes MMPs at the rate of λ per second at the site of ECM fibre(s), where λ represents the intrinsic MMP production rate. This ECM-dependent MMP secretion rule was chosen in line with our observations that increase in ECM density enhances MMP secretion23. Similar ECM density-dependent MMP secretion profile was observed when MCF-7 cells were cultured on collagen with varying densities (Supp. Fig. S1). Further, since the actual values of the MMP secretion rates are not known for cancer cells, the effect of λ was studied by varying its value from 0.01 to 0.1 s−1 57. This secretion dynamics of MMP was modelled using CC3D ‘Secretion plugin’58. These secreted MMP molecules then diffuse in the medium with a diffusion coefficient (D) of 1.0 × 10−9 cm2.s−1. In addition to secretion and diffusion, soluble MMPs have a defined lifetime and degrade after some time. Therefore, MMP degradation (with a degradation rate δMMP of 0.002 s−1) was also considered in the MMP dynamics. Diffusion and degradation of MMP molecules were modelled using reaction–diffusion dynamics given by equation-(3).

where, [MMP](x, t): MMP count at pixel x and time t
D: Diffusion coefficient of MMP
δMMP: degradation rate of MMP
The diffusion coefficient and degradation rate were kept constant across all the simulations. Since the rate of all the MMP events (i.e. MMP secretion, MMP diffusion and MMP degradation) have units of sec−1 and one MCS corresponds to 36 seconds (see below), the PDE solver, used to solve the reaction–diffusion system, was called 36 times in a single MCS. Forward Euler method-based PDE solver, available as part of CC3D package, was used to solve reaction diffusion system of MMP dynamics40. Since one pixel in our model represents a higher order ECM structure instead of a single fibril molecule, instead of modeling the exact ECM degradation reaction, a threshold-based approach was used to model ECM degradation. Precisely, after every MCS, ECM degradation was effected at all pixel locations where MMP count was greater than or equal to 1 (Fig. 1D). A threshold of 1 was chosen as MMP secretion was also performed on a single pixel basis. A similar approach has been used to model cell quiescence and necrosis in multiscale model of cancer stem cell-driven phenotypical heterogeneity59. Growth factor-dependent cell growth, oxygen-dependent cell apoptosis can also be modelled using this approach43. At these locations, to mimic ECM degradation, ECM fibres were removed by changing the pixel type to fluid and the count of MMP at that pixel location was reduced by 1. Removal of ECM fibres from the lattice is expected to influence cell–ECM adhesion and GGH dynamics thereby integrating MMP reaction–diffusion dynamics with GGH-based cell mechanics model.
Parameter values and assumptions
All parameters used in the model were either chosen from the literature or determined by optimizing the model to recapitulate previously observed phenomena. Specifically, values of all adhesion energies (JXX), inverse compressibility (λa) and strength of noise in the dynamics or magnitude of effective membrane fluctuations (Tm) were taken directly from the literature42. The value of the perimeter constraint (λp) was assumed in the simulations. The strength of intrinsic motility μ0 was chosen such that the cells showed rotational motion when confined within a non-degradable circular geometry56 (Supp. Video-V1) and showed translational motion when placed in ECM with pre-existing paths. Subsequently, the value of MCS was estimated to be 36 seconds so as to obtain cell speeds (≈23 μm.h−1) comparable to experiments56,60 (Supp. Text). MMP diffusion timescales were estimated from the literature61. Since the exact life time of MMP molecules is not known, MMP degradation rate was taken from previous computational model57. Finally, cell–cell adhesion energy (i.e., Jcc) and MMP secretion rate (λ) were varied to explore the effect of cell–cell adhesion and MMP secretion rate on cell migration dynamics. To probe the role of cell–cell adhesion in cell invasion, three values of Jcc (i.e., 1, 16 and 40) were chosen. These values were choosen so that (i) at the lowest value (i.e., Jcc = 1), cells have a higher propensity to adhere to other cells as compared to ECM fibres or fluid, (ii) at the moderate value (i.e., Jcc = 16), cells have equal propensity to adhere to other cells or ECM fibre and (iii) at the highest value (i.e., Jcc = 40), cells have more propensity to adhere to fluid or fibre as compared to other cells. Finally, to dissect the role of MMP secretion rate in mediating cell invasion, MMP secretion rate was varied from 0.01 s−1 to 0.1 s−1 to cover one order of magnitude as done before57. Although we have defined our model in generic terms by focussing mainly on cellular phenotype rather than particular cell type, the model parameters can be tuned to mimic the behavior of specific cell types. For example, high MMP secretion (λ) and low cell–cell adhesion (Jcc >> 1) can be used to model the behavior of highly invasive cancer cells. Similarly, low MMP secretion rate and high cell–cell adhesion can be used to mimic the behavior of less invasive cells. Other parameters, which we have kept constant in all our simulations to avoid an excess number of parameters, can be used to model other biophysical properties of the cells. For example, the fact that MDA-MB-231 cells are softer than MCF-7 cells62 may be modeled by using lower values of λa and λp for MDA-MB-231 cells. In our simulations we kept λa and λp constant as our intention was to probe the collective influence of cell–cell and cell–ECM interactions on cell invasion. Lastly, since the present model was aimed at studying cancer invasion only, two factors relevant to cancer progression – cell division and/or continuous supply of cells from tumour mass – were not taken into consideration in our model. Though the CC3D steppable ‘MitosisSteppable’ can be used to implement cell division40, not taking cell division into account helped us in reducing the parameter space of our model. In one set of preliminary simulations performed by taking cell division into account, results did not deviate much from those obtained in the absence of cell division (Supp. Section-5). Also, to study the potential role of cell supply from primary tumour on cell invasion, a set of simulations were performed where cells were continuously added to the primary cell site. While the pattern of invasion could not be compared due to very large number of cells, MMP secretion and ECM degradation profile showed simlar behaviour in the presence of cell supply (Supp. Section-6).
Quantification of invasion
Four quantities including the total distance moved by a cell ( ), cell translocation (
), cell translocation ( ), radius of gyration (RoG) and percentage ECM degradation were used to quantify cancer cell invasion. While the first three quantities were used to determine the spreading or migration capabilities of a cell, the fourth metric was used to quantify MMP-mediated ECM degradation. While
), radius of gyration (RoG) and percentage ECM degradation were used to quantify cancer cell invasion. While the first three quantities were used to determine the spreading or migration capabilities of a cell, the fourth metric was used to quantify MMP-mediated ECM degradation. While  was used to track the mobility or dynamicity of a cell,
was used to track the mobility or dynamicity of a cell,  represents the displacement of a cell from its initial position and is a measure of migration persistence. In contrast to
represents the displacement of a cell from its initial position and is a measure of migration persistence. In contrast to  and
and  which are cell level measures, RoG was determined to calculate the population scattering. Further, since loss of basement membrane has been used as a metric of tumour invasiveness63, percentage ECM degradation was also quantified in our simulations to assess cancer cell invasion.
which are cell level measures, RoG was determined to calculate the population scattering. Further, since loss of basement membrane has been used as a metric of tumour invasiveness63, percentage ECM degradation was also quantified in our simulations to assess cancer cell invasion.
We tracked individual cell trajectories during the simulations. The population averaged total distance travelled by cells ( ) in 1800 MCS (≈18 hours) was calculated by adding the centroidal movements between successive MCS steps (i.e., 36 seconds) for each of 69 cells and then averaging, i.e.,
) in 1800 MCS (≈18 hours) was calculated by adding the centroidal movements between successive MCS steps (i.e., 36 seconds) for each of 69 cells and then averaging, i.e.,

where dj,t corresponds to the distance travelled by the jth cell at MCS time step t and N represents the total number of cells in the population (N = 69 in our case). In addition, the population averaged net translocation ( ) was determined by calculating the distance between the initial (t = 0) and final (i.e., after 1800 MCS or t ≈ 18 h) position of each cell and then averaged for the whole cell population, i.e.,
) was determined by calculating the distance between the initial (t = 0) and final (i.e., after 1800 MCS or t ≈ 18 h) position of each cell and then averaged for the whole cell population, i.e.,

where Position(j,t) corresponds to the position of jth cell at MCS time t. To quantify the extent of cell scattering at the end of simulations (after ≈18 hours), RoG with respect to the initial population centre was also quantified as per the following expression:

where, N corresponds to the total number of cells in the population and dj is the distance of the jth cell from the initial tumour centroid ((250, 250) in our case). Finally, ECM degradation was quantified by calculating the difference in the number of fibre pixels between the initial and final simulation steps. The percentage ECM degradation was then quantified with respect to the initial number of fibre pixels.
Sandwich Gel Invasion Assay
For the sandwich gel invasion assay, cells were plated on collagen-coated glass-bottom dishes (HiMedia) and layered with 3D collagen I (Corning) gel on top. Coverslips were functionalized by treating with 0.1 N NaOH and silane (Sigma) for 15 minutes each followed by 0.5% glutaraldehyde (50%, Sigma) for 20 min, at room temperature. Functionalized coverslips were coated with 1 μg/cm2 of rat tail 2D collagen I (C3867, Sigma). MCF-7 cells were plated on the coverslips in DMEM media (Gibco) supplemented with 10% FBS (HiMedia) and allowed to incubate for 3 hours in the CO2 incubator. Cells were plated at two specific densities (5 × 103 and 25 × 103 cells per cm2) so as to have a predominance of single cells at the lower density and groups of cells at the higher density. Post incubation, media was aspirated and cells were layered with 3D collagen type I on top at three different densities of 0.5, 1 and 2 mg/ml, respectively, as per previously established protocols64. 3D collagen was allowed to gel by keeping the entire set up at 37 °C in the CO2 incubator for 30 minutes. Post gel formation, fresh media was added on top and kept for incubation for 24 hours. For protease inhibition drug studies, fresh media was supplemented with 5 μM of GM6001 drug (Merck). Imaging was done with an inverted phase contrast microscope (Olympus) at 20× magnification over a period of 12 hours at 20 minutes interval. Total cell translocation (distance moved from initial position) was calculated after 12 hours using the manual tracking plugin of ImageJ (NIH). For single cell migration, trajectories of individual cells were tracked. For collective cell migration, trajectories of cells moving in groups were quantified to determine the net translocation. Atleast 20 cells per condition were analyzed and the experiments repeated twice.
Results
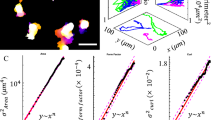
Collective cell invasion requires lesser ECM degradation than single cell invasion
Cell-cell adhesions represent one of the key factors governing cancer metastasis. While loss of cell–cell adhesion is known to trigger EMT65,66,67,68,69, overexpression of cell–cell adhesion checks EMT70,71,72. In contrast to the single cell mode of invasion where cell–cell adhesion does not play any role, many cancer cells are also known to exhibit collective invasion wherein cell–cell adhesions remain intact73. To see if our model can recapitulate the influence of cell–cell adhesion on the mode of invasion, we performed simulations for varying values of cell–cell adhesion energy (Jcc), that is Jcc = {1, 16 and 40}, with Jcc = 1 corresponding to high cell–cell adhesion, Jcc = 16 corresponding to medium cell–cell adhesion and Jcc = 40 corresponding to low cell–cell adhesion. In these simulations, MMP secretion rate (λ) was kept constant at λ = 0.05 s−1. All other parameters were kept fixed (as described in Table 1). For these simulations, a cell aggregate of 69 cells of initial diameter 20 μm each were placed at the centre of a randomly aligned ECM lattice (Fig. 2A left-most). The ECM lattice was generated using a custom written C++ utility (Supp. Text). For comparing the cell invasion patterns obtained for different values of Jcc, simulations were run for 1800 MCS (≈18 hours) and repeated 10 times per condition for statistical comparison between the different cases.
Influence of cell–cell adhesion energy (Jcc) on invasion efficiency.
(A) Temporal patterns of invasion of a group of cells enmeshed in a fibrillar ECM network for different levels of cell–cell adhesion. Upper Panel: High cell–cell adhesion (Jcc=1). Middle Panel: Medium cell–cell adhesion (Jcc = 16). Lower Panel: Low cell–cell adhesion (Jcc = 40). Model components: Blue pixels represent fluid, yellow pixels represent ECM fibres and coloured boxes represent cells. (B) Quantification of cell migration pattern with number of clusters and average size of cell cluster after 1800 MCS. (C) percentage ECM degradation for different values of Jcc. (D) Temporal profile of total number of MMP molecules present in the lattice for varying values of Jcc. (E) Total distance moved by cells ( ) and net cell translocation (
) and net cell translocation ( ) for different values of Jcc. Inset shows representative trajectory of a single cell. Error bars: ±standard error of mean (SEM).
) for different values of Jcc. Inset shows representative trajectory of a single cell. Error bars: ±standard error of mean (SEM).
The Jcc values chosen to mimic different extents of cell–cell adhesion successfully recapitulated the different modes of invasion (Fig. 2A, Supp. Videos V2,V3–V4). While cells were found to scatter in different directions when cell–cell adhesion was low (i.e., Jcc = 40) (Fig. 2A right-lower panel), cells moved collectively when cell–cell adhesion was high (i.e., Jcc = 1) (Fig. 2A right-upper panel). To get a quantitative estimate of the mode of cell invasion for varying cell–cell adhesion, clustering of cell population was quantified by counting the number of clusters and the size distribution of the clusters at the end of the simulation (i.e., after 1800 MCS). While the population having larger cluster size and lower number of clusters resembles the collective mode of migration, the population with smaller cluster size and higher number of small clusters is indicative of individual mode of migration. The quantification showed that the loss of cell–cell adhesion, i.e., increase in Jcc values, triggered the breaking of the population into large number of smaller clusters, thereby leading to the individual cell invasion (Fig. 2B). These results successfully recapitulate the observed EMT process where loss of cell–cell adhesion triggers mesenchymal model of migration65,66,67,68.
Since cell invasion requires ECM degradation, the simulation data was analyzed to determine the extent of ECM degradation for different extents of Jcc. This was done by quantifying the percentage reduction in the total number of fibre pixels at the end of 1800 MCS. Surprisingly, in spite of having identical MMP secretion rate (i.e., λ = 0.05 s−1) and no direct dependence of fibre degradation on cell–cell adhesion, the population of cells with differing cell–cell adhesion propensities showed significant difference in ECM degradation, with minimum degradation observed at highest cell–cell adhesion and maximum degradation observed at lowest cell–cell adhesion (Fig. 2C). Since fibre degradation is mediated by MMP molecules, to check the basis for lesser degradation at higher cell–cell adhesion, the temporal profile of total MMP count was tracked for different values of cell–cell adhesion. Interestingly, though all cells possessed the same MMP secretion capabilities, MMP secretion was highest at lowest cell–cell adhesion (Fig. 2D) indicating that the lower degradation at higher cell–cell adhesion was due to decrease in levels of MMP secretion. This decrease in MMP density for population of cells with high cell–cell adhesion may be due to lower cell–ECM interaction, i.e., the number of ECM fibres in contact with single cells is greater than when the cells are in clusters, leading to greater MMP secretion by single cells than cells in groups.
Given that cell scattering leads to greater ECM degradation, we next tested if this enhanced degradation led to enhanced invasion. Invasion was characterized by two different metrics: the total distance moved by the cells ( ) and the net cell translocation (
) and the net cell translocation ( ) (i.e., displacement of cells from their respective initial positions to their final positions) after 1800 MCS. While greater
) (i.e., displacement of cells from their respective initial positions to their final positions) after 1800 MCS. While greater  implies greater movement, it may not imply greater invasion, as it is possible for a cell to return to it’s starting point, particularly if it moves diffusively. Hence,
implies greater movement, it may not imply greater invasion, as it is possible for a cell to return to it’s starting point, particularly if it moves diffusively. Hence,  was tracked as a metric of effective invasion. The total distance travelled by cells (
was tracked as a metric of effective invasion. The total distance travelled by cells ( ) was maximum when cells moved collectively and dropped sharply with decrease in cell–cell adhesion (Fig. 2E). Greater distance moved by cells in groups was due to dynamic rearrangements within the group wherein cells constantly changed their positions within the cluster as they moved collectively (Supp. Video V2). However, single cells moved by a lesser distance compared to cells in groups suggestive of more persistent invasion by single cells, achieved through higher ECM degradation (Fig. 2E)74. Compared to
) was maximum when cells moved collectively and dropped sharply with decrease in cell–cell adhesion (Fig. 2E). Greater distance moved by cells in groups was due to dynamic rearrangements within the group wherein cells constantly changed their positions within the cluster as they moved collectively (Supp. Video V2). However, single cells moved by a lesser distance compared to cells in groups suggestive of more persistent invasion by single cells, achieved through higher ECM degradation (Fig. 2E)74. Compared to  , the net cell translocation (
, the net cell translocation ( ) was less sensitive to changes in cell–cell adhesion, with minimum value observed at highest cell–cell adhesion (Fig. 2E). The net cell translocation was also dependent on the time scale of polarity evolution (τ), with increase in τ values leading to increase in cell translocation for all values of cell–cell adhesion (Supp. Fig. S2, materials and methods). In addition to
) was less sensitive to changes in cell–cell adhesion, with minimum value observed at highest cell–cell adhesion (Fig. 2E). The net cell translocation was also dependent on the time scale of polarity evolution (τ), with increase in τ values leading to increase in cell translocation for all values of cell–cell adhesion (Supp. Fig. S2, materials and methods). In addition to  and
and  , RoG, another indicator of cell scattering, was also quantified and found to have cell–cell adhesion dependency similar to
, RoG, another indicator of cell scattering, was also quantified and found to have cell–cell adhesion dependency similar to  (Supp. Fig. S3A). Additionally, the big error bars in
(Supp. Fig. S3A). Additionally, the big error bars in  and RoG measures arise due to the heterogeneity in the distribution of cell translocation (Supp. Fig. S3B). Together, our results suggest that while loss of cell–cell adhesion leads to individual mode of migration, our model predicts that the collective invasion requires lesser ECM degradation than single cell invasion, with dynamic re-arrangements occurring in groups of collectively moving cells.
and RoG measures arise due to the heterogeneity in the distribution of cell translocation (Supp. Fig. S3B). Together, our results suggest that while loss of cell–cell adhesion leads to individual mode of migration, our model predicts that the collective invasion requires lesser ECM degradation than single cell invasion, with dynamic re-arrangements occurring in groups of collectively moving cells.
MMP secretion rate influences cell invasiveness and invasion pattern
Though no direct inter-dependence between cell–cell adhesion and MMP secretion rate was assumed, our simulation results demonstrate that lesser degradation is achieved when cells move collectively. While the above simulations were performed for a fixed MMP secretion rate (λ = 0.05 s−1), given that different cell types possess different proteolytic abilities, it is possible that MMP secretion rate may dictate the pattern of invasion. To test this, simulations were performed for varying cell–cell adhesion (Jcc = 1, 16 and 40) and varying MMP secretion rates (λ = 0.01–0.1 s−1). As before, quantification was done after 1800 MCS. As expected, increase in MMP secretion rate led to increase in both cell movement and cell translocation for all values of Jcc (Fig. 3A–C), with greatest amplification at lowest cell–cell adhesion (i.e., Jcc = 40). A similar influence was observed for cell scattering quantified using RoG of the cell population (Supp. Fig. S4). This enhancement in invasion at higher MMP secretion rates was associated with greater ECM degradation (Fig. 3D). Further, quantification of cluster size and number of clusters revealed differences only when cell–cell adhesion was weak (i.e., Jcc = 40), with increase in MMP secretion rate leading to further scattering indicative of single cell invasion (Fig. 3E,F). Together, these results suggest that increase in MMP secretion rate leads to increased invasion and ECM degradation23.
Collective influence of MMP secretion rate (λ) and cell–cell adhesion (Jcc) on cancer cell invasiveness and migration pattern.
(A) Represented images of cell migration pattern for varying cell–cell adhesion (Jcc) and for varying MMP secretion rates (λ) after 1800 MCS. (B) Total distance moved by cells for varying λ and Jcc. (C) Net translocation of cells from their respective initial positions. (D) percentage ECM degradation at different MMP secretion rates and cell–cell adhesion. (E,F) Mode of invasion quantified by tracking number of clusters (E) and cluster size (F) after 1800 MCS. Error bars: ±SEM.
Increase in MMP secretion rate increases efficiency of collective invasion in dense matrices
In the simulations thus far, fibre density was kept constant. However, density of the tumour-associated ECM has been shown to play a pivotal role on cancer progression13,23,24,25,65,75, with increased deposition of fibrillar ECM proteins like collagen and fibronectin reported in various epithelial cancers16,76,77. Such an increase in ECM density has been shown to cause increased ECM degradation via increase in MMP secretion rates23. Increased ECM density has also been shown to foster collective cell migration through cell jamming78. However, the combined influence of cell–cell adhesion and ECM density on cell invasiveness is incompletely understood. To address this question, simulations were performed at varying fibre densities for varying extents of cell–cell adhesion. MMP secretion rate was kept constant at λ = 0.05 sec−1. ECM fibre density was varied by varying the number of ECM fibres (ξ) in the lattice (ξ = 400, 600 and 1000, respectively) (Fig. 4A). Simulation results suggested that the invasion dynamics was significantly altered with change in fibre density, with increase in ECM density limiting the extent of invasion (Fig. 4B). Given that in our simulations, the total number of MMPs secreted is proportional to the number of ECM fibre pixels in contact with the cells (Materials and Methods), higher fibre densities should lead to greater MMP secretion and higher ECM degradation. While this was found to be true (Supp. Fig. S5A, S5B), the net translocation was still minimum at the highest fibril density (i.e., ξ = 1000), demonstrating the dominant influence of ECM density in limiting invasion (Fig. 4C). Similar to  , the RoG-based assessment of population scattering also suggested that the cell scattering was suppressed greatly at the highest fibre density (i.e., ξ = 1000) (Supp. Fig. S5C). Moreover, increase in cell–cell adhesion further amplified the effect of fibre density, with higher cell–cell adhesion leading to greater reduction in the extent of invasion.
, the RoG-based assessment of population scattering also suggested that the cell scattering was suppressed greatly at the highest fibre density (i.e., ξ = 1000) (Supp. Fig. S5C). Moreover, increase in cell–cell adhesion further amplified the effect of fibre density, with higher cell–cell adhesion leading to greater reduction in the extent of invasion.
Combined influence of MMP secretion rate and ECM density on invasion.
(A) Position of cell cluster at the beginning of simulation for three different fibre densities (ξ = 400, 600 and 1000, respectively). (B) Pattern of cell scattering at the end of 1800 MCS at varying fibre densities and varying Jcc. MMP secretion rate was kept constant at λ = 0.05 s−1. (C) Net translocation of cells at varying fibre densities and varying Jcc. (D) Net translocation of cells at varying fibre densities and varying Jcc for λ = 0.1 s−1. Error bar: ±SEM.
In our model, in addition to fibre density, MMP secretion also depends on the MMP secretion rate (λ). Since fibre density-mediated MMP secretion alone was not able to circumvent the effect of steric hindrance on cancer invasion, we next investigated if increase in MMP secretion rate can promote cancer invasiveness. To test this, simulations were performed with a two-fold higher value of MMP secretion rate (i.e., λ = 0.1 sec−1 (Supp. Fig. S5D). Increase in MMP secretion rate led to increase in the extent of ECM proteolysis (Supp. Fig. S5E) and translocation across all the conditions, with greatest increase observed when cell–cell adhesion was high (Fig. 4D). Together, these results suggest that while increase in ECM density hinders cell invasion, increase in MMP secretion rate fosters it. Interestingly, it was observed that while two fold increase in MMP secretion rate was sufficient to suppress the effect of increase in ECM density (from ξ = 400 to ξ = 1000) at moderate and high cell–cell adhesion (i.e., Jcc ≤ 16), only partial suppression was achieved at low cell–cell adhesion (i.e., Jcc = 40). Cell scattering, quantified using RoG, was also increased with increase in MMP secretion rate and showed similar dependence on cell–cell adhesion (Supp. Fig. S5F). Together, these results indicate that when cells invade collectively through dense matrices, increasing the MMP secretion rate may be one of the strategies to increase invasion efficiency. Conversely, if the MMP secretion of the cells is on the lower side, cells can invade more effectively if they migrate individually by undergoing EMT.
Alignment of ECM fibres can sustain invasion without proteolysis
In addition to alterations in ECM density, ECM organization also undergoes significant alterations during cancer progression15. This is brought about by enzymes like lysyl oxidase (LOX) which crosslink the matrix and make it more linearized20. Such alignment of matrix has been shown to trigger EMT and increase cancer invasiveness63. Simulations performed with aligned ECMs at the highest density (i.e., ξ = 1000, to mimic stiff matrices) in the presence of proteolysis showed that loss of cell–cell adhesion indeed increased cell translocation and ECM degradation (Supp. Fig. S6). These results are consistent with recent findings where induction of EMT (which causes loss of cell–cell adhesion)79 and ECM stiffness were shown to increase tumour invasiveness63. While secreted MMPs degrade tumour ECM, thereby making tracks for migration, crosslinking of fibres may enable cells to make use of aligned fibres as a contact guidance cue and migrate with minimum ECM proteolysis utilizing the space available between neighboring sets of crosslinked fibres. To test the hypothesis that matrix alignment can sustain cell migration by providing contact guidance, simulations were performed without proteolysis at different fibre densities and two fibre orientation(ψ): random and aligned (Fig. 5A). To generate aligned matrices, C++ routine was used to generate a mesh of fibres with all fibres aligned in the horizontal direction (Supp. Text). The generated *.PIFF files were then used as input in the CompuCell3D model. In these simulations, in addition to varying fibre density and orientation, cell–cell adhesion was also varied to test how single cell invasion and collective cell invasion fared under these conditions. In the absence of proteolysis, in matrices with randomly aligned fibres, cell translocation was limited to the same extent for all values of cell–cell adhesion, with highest translocation observed at the lowest fibre density (Fig. 5B,C-left, Supp. Videos V5,V6,V7,–V8). Translocation was significantly enhanced when fibres were aligned, with maximum translocation observed at lowest fibre density and highest cell–cell adhesion (Fig. 5C, Supp. Fig. S7A, Supp. Videos V9,V10,V11–V12). Consistent with greater translocation in aligned matrices, cell scattering also increased in aligned matrices (Supp. Fig. S7B). In addition to increase in invasiveness, contact guidance was quite observable in aligned matrices where cells moved in the direction of fibre alignment (Supp. Videos V9,V10,V11–V12). Our model results predict that ECM fibre alignment can sustain both singly invading cells and the cells invading in groups. To assess the role of cell–ECM adhesion in sustaining this invasion, simulations were performed where cell–ECM adhesion energy (i.e., Jce) was set equal to cell–fluid interface energy (i.e., Jcf) to model a case where cells had no preference to adhere to an ECM fibre. On quantification, except for a mild increase (specifically for ξ = 1000, Jcc = 1), no major changes in cell translocation were observed upon decreasing the cell–ECM adhesion (Supp. Fig. S8). Together, our results suggest that ECM alignment is capable of sustaining both single cell and collective cell invasion even in the absence of ECM proteolysis.
Aligned matrices can sustain cell invasion even without ECM proteolysis.
(A) Position of cell cluster at the beginning of simulations for two different fibre orientations (ψ) (random and aligned) (ξ = 1000). (B) Representative images for cell migration pattern for aligned matrices at varying ECM densities and cell–cell adhesion. MMP secretion was turned off. (C) Net translocation of cells at varying fibre densities and varying Jcc in random and aligned matrices. Error bar: ±SEM.
Comparing model results with experiments: invasion of MCF-7 cells using sandwich gels
Our in-silico results have demonstrated the contributions of cell–cell adhesion (Jcc), MMP secretion rate (λ), ECM density (ξ) and ECM alignment (ψ) in regulating tumour cell invasion. In these simulations, to maintain generality of cell invasion, we focused mainly on variation in cellular phenotype (Jcc and λ) and ECM properties (ξ and ψ) without focusing on specific cell line. To compare and contrast our simulation results with a particular cell line, we performed invasion studies with MCF-7 cells using sandwich gels. Similar to our computational framework wherein cells invade outward into the surrounding matrix, for the experimental studies, MCF-7 cells were plated on collagen coated glass coverslips and overlayed with 3D collagen (Fig. 6A) so as to create a sandwich. To study the influence of ECM fibre density on cell invasion, three densities of 3D collagen (0.5, 1.0 and 2.0 mg/ml) were used. Cell invasion was studied using MCF-7 cells plated at two densities (5 × 103 and 25 × 103 cells per cm2) to study invasion by both single cells and cells moving in groups (Fig. 6B, Supp. Videos V13 and V14) (Materials and methods). Cell invasion was tracked for 12 hours and cell translocation (displacement from initial position) was determined using the ‘Manual Tracking’ plug-in of ImageJ. For single cell migration, trajectories of individual cells were tracked. For collective cell migration, trajectories of cells moving in groups were quantified (Fig. 6C).
Invasion of MCF-7 cells in sandwich cultures.
(A) Cells were cultured on collagen-coated glass coverslips and overlaid with a layer of 3D collagen so as to create a sandwich. (B) Representative images of cell positioning at t = 0 at two different cell densities. (C) Tracks of cell migration for singly invading cells and cells invading in groups. (D) Translocation of MCF-7 cells moving singly and in groups. (E) Translocation of MCF-7 cells in sandwich gels fabricated with 1 mg/ml collagen in the presence of the broad spectrum MMP inhibitor GM6001. Errorbar: ±SEM. ‘**’ indicates statistical significance (p < 0.05).
Consistent with our simulation results (Fig. 4), increase in collagen density caused a drop in cell translocation for singly invading cells. However, almost no difference was observed for collectively invading cells (Fig. 6D). Specifically, for singly invading cells, increase in collagen density from 0.5 mg/ml to 1 mg/ml caused a significant drop (~50%) in cell translocation. A similar trend was observed in our simulations for λ = 0.05 and 0.1 s−1 and Jcc = 40 (low cell–cell adhesion) when ECM fibre density (ξ) was increased from 400 to ≥600 (Fig. 4C,D). When experiments were performed with the MMP inhibiting drug GM6001 on 1 mg/ml collagen gels, in line with our simulation results (Fig. 5C-Left), a drop in cell translocation was observed in both singly moving and collectively moving cells, highlighting the direct contribution of MMPs in sustaining invasion (Fig. 6E). Similar to our results, GM6001 treatment has also been shown to inhibit the invasion of MDA-MB-231 cells from 3D spheroids embedded in 3D native type 1 collagen gels81. In conclusion, in line with our simulation predictions, our experimental results demonstrate the influence of ECM density in providing steric hindrance to cell movement and the role of MMPs in reducing this hindrance by proteolysis.
Discussion
Cell invasion is central to cancer metastasis with ECM properties regulating the efficiency and pattern of invasion. In this paper, we present an in-silico model to understand the modes of cancer cell dissemination from a group of cells. Our study demonstrates the importance of ECM density and organization in fostering collective invasion through both proteolytic and non-proteolytic mechanisms. Our model makes two important predictions. First, our model predicts that collective cell invasion requires lesser ECM degradation compared to individual cells for achieving similar invasion, suggesting collective cell invasion may be more efficient than single cell invasion. While increase in ECM density inhibits collective cell invasion, higher MMP secretion rate is required for sustaining it, particularly in dense matrices. Additionally, although increase in MMP secretion enhances both single and collective cell invasion, inhibition of MMP secretion in individually migrating cells causes a transition to collective cell invasion as observed experimentally78. Secondly, our results suggest that both single and collective cell invasion can be sustained without any proteolysis in aligned matrices. In line with our in-silico predictions, our experiments demonstrate the influence of ECM density in restricting the invasion of MCF-7 cells by providing steric hindrance and the necessity of MMP activity for sustaining invasion. Collectively, our study highlights the importance of ECM density and organization in dictating cell invasiveness and illustrates the multiple mechanisms for collective invasion to be sustained (Fig. 7).
Regulation of cell invasiveness and mode of invasion.
Cancer cells can switch between different strategies to invade. Collective invasion is the more efficient form of invasion since it requires lesser overall secretion of MMP and ECM fibril degradation, when compared to individual cell invasion. Increased ECM density for randomly aligned fibres provide greater confinement for the migrating cells and reduce their invasion. However, the cells can increase their MMP secretion rate to counter this effect and still invade collectively. If the cells cannot secrete enough MMP, then they can undergo EMT by loss of cell–cell adhesions (i.e., increasing cell–cell adhesion energy, Jcc) and invade individually. If the cells have lower MMP secretion rate, then they can align the ECM fibrils for effective invasion, irrespective of cell–cell interaction energies.
Although both single and collective cell invasion have been observed during cancer progression, a direct comparison between the two modes of invasion has not been done due to experimental challenges. Further, since both modes of invasion require cells to move by degrading the surrounding ECM, how ECM degradation is altered between single and collective cell invasion remains unclear. Our results suggest that, at moderate to high ECM densities, collective invasion is more efficient compared to single cell invasion as cells moving in groups invade to the same extent with lesser ECM degradation (Fig. 2C,E). This was also observed experimentally at collagen densities of 1 mg/ml and higher. Spheroid invasion experiments in 3D gels often show groups of cells invading radially outward with few isolated individual cells invading outward faster. Given the higher degradation potential of single cells, it is possible that these single cells serve as ‘leader cells’ and increase the efficiency of collective invasion by reducing steric hindrance and creating small migration tracks that can be subsequently widened by collectively moving cells with lesser degradation11. Alternatively, it is also possible that collective cell invasion may be possible without any leader cells. This is clear from our simulations wherein collective invasion was unaltered even though cells continuously switched places within the group (Supp. Video V2). Though such motion of cells within the group during invasion is yet to be experimentally demonstrated, epithelial cells are known to exhibit rotational motion under confinement both in vitro and in vivo81. This rotational motion is attributed to our polarization evolution rule, which tends to align the polarization of any cell with its velocity and allows for cells to continue to move even in confined geometries56 (Supp. Video V1). The continuous movement of cells moving collectively within the group also implies that for achieving invasion to the same extent as that of single cells, collectively moving cells take a more circuitous route, therefore suggesting that collective cell invasion is less persistent than single cell invasion.
Higher MMP secretion is typically associated with enhanced ECM degradation11,23,57,82. Though basal value of MMP secretion rate is a cell type-specific property, the absolute number of MMPs secreted by a given cell is sensitive to several intrinsic and extrinsic factors. While integrin-mediated cell–ECM signalling can increase MMP activity83, MMP secretion can be inhibited or abolished pharmacologically using protease inhibitory drugs like GM6001 and SB3-CT11,23. Though increase in MMP secretion rate increased the efficiency of both single and collective cell invasion, our results suggest that single cell invasion at low to intermediate ECM density is more sensitive to MMP secretion rate (Fig. 3C,D). This may be due to greater contact of single cells with the surrounding ECM as opposed to collectively moving cells, where only the outer layer of cells are in contact with the matrix. Higher invasive potential of cells upon EMT may also be attributed to greater cell–ECM interactions leading to greater ECM degradation84,85. Together, these results highlight the sensitivity of single cell invasion to MMP secretion rate.
In vivo, the collagen-rich interstitial matrix is known to inhibit cell invasion. Paradoxically, cancer progression is associated with increased deposition of fibrillar collagen, with increase in ECM density correlated with increased malignancy. Increased invasiveness of cancer cells in dense matrices may be driven by enhanced integrin signalling, which in turn activates MMP-mediated ECM degradation86,87,88,89,90. Thus, cancer invasiveness depends both on ECM density and levels of MMP secretion. To study their collective influence on invasion, simulations were performed at different ECM fibre densities and moderate levels of MMP secretion. Our results demonstrate that increase in ECM density suppresses single cell invasion to a greater extent. In contrast, collective cell invasion is less sensitive to changes in ECM density (Fig. 4B,C). Similar to our simulation results, invasion of MCF-7 cells on sandwich collagen gels of varying densities also showed a significant decrease in cell translocation for individually moving cells and almost no change in cell translocation for collectively moving cells (Fig. 6D). Additionally, our simulation results also illustrate that increase in MMP secretion rate can mitigate the effect of increase in ECM density thereby fostering invasion. For example, the suppression in collective invasion effected by an increase in ECM density from ξ = 400 to ξ = 1000 is completely abolished by a 2-fold increase in MMP secretion rate (Fig. 4D). Such increase in MMP secretion can be induced by ECM density itself, as observed in experiments of MDA-MB-231 cells cultured on substrates of varying collagen density23. However, for single cells, the two-fold increase in MMP secretion rate only partially overrides the increase in steric hindrance effected by increase in ECM density. Thus, these results suggest that invasiveness is collectively regulated by ECM density and MMP secretion rate and cells can switch between single and collective mode of invasion depending on the levels of MMP secretion in order to invade effectively.
In the presence of MMPs, loss of cell–cell adhesion and alignment of ECM fibres have been shown to increase cell invasion63. Consistent with these observations, our simulations for aligned and dense matrices showed greater ECM invasion for cells with low cell–cell adhesion (Supp. Fig. S6). In contrast to MMP-mediated proteolytic invasion, inhibition of MMPs induces cells to opt for a non-proteolytic mechanism of cell migration, wherein cells use actomyosin contractility to squeeze through pre-existing pores in the matrix91. It is possible that the efficiency of such non-proteolytic modes of invasion can be further enhanced by alignment of ECM fibres, which serve as contact guidance cues. Such linearization of matrices has been documented in vivo via crosslinking of collagen fibres through enzymes like LOX20. However, the extent to which MMPs may be necessary for this mode of invasion is unclear. Our simulations of invasion in aligned matrices without any MMP activity suggest that aligned matrices can provide suitable contact guidance cues that can sustain invasion even without any proteolysis (Fig. 5). Interestingly, our results also suggest that collectively migrating cells can maximally use the contact guidance provided by aligned ECM fibres as ECM alignment induced faster invasion at high cell–cell adhesion.
Although our model was used for studying cell invasion in the context of carcinomas, this model can easily be extended to understand invasion in other types of cancers. First, many of the components of our model are also applicable for other types of cancers. For example, cell–ECM adhesion plays a critical role in invasion in other types of cancers as well including, gliomas and sarcomas92. Thus, invasion of glioma cells embedded as spheroids in collagen gels, can also be explored using multiscale CPM computational models93. Further, the case of Jcc = 40 which models single cell invasion is applicable for all cells invading individually and is hence applicable to nearly all types of cancers91,94. Further, this model can easily be extended to study the influence of other physiological structures that play a part in cancer invasion. For example, similar to tissue specific cells modeled in42, one can easily incorporate non-degradable tissue specific structures (e.g., cells or other interfaces) to model tracks such as subpial glial space and vessel walls which are used by invading cells to invade the brain94.
In summary, this paper demonstrates the multiple ways in which collective cell invasion can be sustained by tuning several cellular and sub-cellular processes and ECM features. However, no cellular heterogeneity within the tumour population was assumed in these simulations. Given the existence of cellular heterogeneity within the tumour population95, understanding the effect of ECM density and organization on cancer invasion of a heterogeneous population will be one of the future directions of this work.
Additional Information
How to cite this article: Kumar, S. et al. Proteolytic and non-proteolytic regulation of collective cell invasion: tuning by ECM density and organization. Sci. Rep. 6, 19905; doi: 10.1038/srep19905 (2016).
References
Ridley, A. J. et al. Cell migration: integrating signals from front to back. Science 302, 1704–1709 (2003).
Friedl, P. & Weigelin, B. Interstitial leukocyte trafficking and immune function. Nat. Immunol. 9, 839–848 (2008).
Valastyan, S. & Cristofanilli, M. Tumor metastasis: Molecular insights and evolving paradigms. Cell 147, 275–292 (2011).
Lamouille, S., Xu, J. & Derynck, R. Molecular mechanisms of epithelial-mesenchymal transitions. Nat. Rev. Mol. Cell Biol. 15, 178–196 (2014).
Friedl, P., Hegerfeldt, Y. & Tusch, M. Collective cell migration in morphogenesis and cancer. Int. J. Dev. Biol. 48, 441–449 (2004).
Weijer, C. J. Collective cell migration in development. J. Cell Sci. 122, 3215–3223 (2009).
Friedl, P. & Wolf, K. Tube travel: the role of proteases in individual and collective cancer cell invasion. Cancer Res. 68, 7247–7249 (2008).
Friedl, P., Locker, J., Sahai, E. & Segall, J. E. Classifying collective cancer cell invasion. Nat. Cell Biol. 14, 777–783 (2012).
Theveneau, E. & Mayor, R. Cadherins in collective cell migration of mesenchymal cells. Curr. Opin. Cell Biol. 24, 677–684 (2012).
Li, L., Hartley, R., Reiss, B. & Sun, Y. E-cadherin plays an essential role in collective directional migration of large epithelial sheets. Cell. Mol. Life Sci. 2779–2789 (2012).
Wolf, K. et al. Multi-step pericellular proteolysis controls the transition from individual to collective cancer cell invasion. Nat. Cell Biol. 9, 893–904 (2007).
Mason, S. D. & Joyce, J. A. Proteolytic networks in cancer. Trends Cell Biol. 21, 228–237 (2011).
Friedl, P. & Wolf, K. Plasticity of cell migration: a multiscale tuning model. J. Cell Biol. 188(1), 11–19 (2010).
Boot-Handford, R. P. & Tuckwell, D. S. Fibrillar collagen: the key to vertebrate evolution? A tale of molecular incest. Bioessays 25, 142–151 (2003).
Egeblad, M., Rasch, M. G. & Weaver, V. M. Dynamic interplay between the collagen scaffold and tumor evolution. Curr. Opin. Cell Biol. 22, 697–706 (2010).
Kauppila, S., Stenback, F., Risteli, J., Jukkola, A. & Risteli, L. Aberrant type I and type III collagen gene expression in human breast cancer in vivo. J. Pathol. 186, 262–268 (1998).
Provenzano, P. P. et al. Collagen reorganization at the tumor-stromal interface facilitates local invasion. BMC Med. 4 (2006).
Ramaswamy, S., Ross, K. N., Lander, E. S. & Golub, T. R. A molecular signature of metastasis in primary solid tumors. Nat. Gen. 33, 49–54 (2003).
Provenzano, P. P. et al. Collagen density promotes mammary tumor initiation and progression. BMC Med. 6, 11 (2008).
Levental, K. R. et al. Matrix cross linking forces tumor progression by enhancing integrin signaling. Cell 139(5), 891–906 (2009).
Paszek, M. J. et al. Tensional homeostasis and the malignant phenotype. Cancer Cell 8(3), 241–254 (2005).
Alexander, N. R. et al. Extracellular matrix rigidity promotes invadopodia activity. Curr. Biol. 18, 1295–9 (2008).
Das, A., Kapoor, A., Mehta, G. D., Ghosh, S. K. & Sen, S. Extracellular matrix density regulates extracellular proteolysis via modulation of cellular contractility. J. Carcinog. Mutagen. S13 (2013).
Wolf, K. et al. Physical limits of cell migration: control by ECM space and nuclear deformation and tuning by proteolysis and traction force. J. Cell Biol. 201(7), 1069–1084 (2013).
Liu, Y. J. et al. Confinement and low adhesion induce fast amoeboid migration of slow mesenchymal cells. Cell 160(4), 659–672 (2015).
Doyle, A. D., Wang, F. W., Matsumoto, K. & Yamada, K. M. One-dimensional topography underlies three-dimensional fibrillar cell migration. J. Cell Biol. 184(4), 481–490 (2009).
Kraning-Rush, C. & Reinhart-King, C. Controlling matrix stiffness and topography for the study of tumor cell migration. Cell Adh. Migr. 6, 274–279 (2012).
Ulrich, T. A., de Juan Pardo, E. M. & Kumar, S. The mechanical rigidity of the extracellular matrix regulates the structure, motility and proliferation of glioma cells. Cancer Res. 69(10), 4167–4174 (2009).
Pathak, A. & Kumar, S. Independent regulation of tumor cell migration by matrix stiffness and confinement. Proc. Natl. Acad. Sci. (USA) 109, 10334–10339 (2012).
Friedl, P. & Alexander, S. Cancer invasion and the microenvironment: plasticity and reciprocity. Cell 147, 992–1009 (2011).
Quaranta, V., Weaver, A. M., Cummings, P. T. & Anderson, A. R. A. Mathematical modeling of cancer: The future of prognosis and treatment. Clinica Chimica Acta 357, 173–179 (2005).
Byrne, H. M. Dissecting cancer through mathematics : from the cell to the animal model. Nat. Rev. Cancer 10, 221–230 (2010).
Gammon, K. Mathematical modelling: Forecasting cancer. Nature 491, S66–S67 (2012).
Savage, N. Modelling: Computing cancer. Nature 491, S62–S63 (2012).
Cristini, V. & Lowengrub, J. Multiscale modeling of cancer: an integrated experimental and mathematical modeling approach (Cambridge University Press, 2010).
Rejniak, K. A. & Anderson, A. R. Hybrid models of tumor growth. Wiley Interdisciplinary Reviews: Systems Biology and Medicine 3, 115–125 (2011).
Szabó, A. & Merks, R. Cellular potts modeling of tumor growth, tumor invasion and tumor evolution. Frontier Oncology 3, 87 (2013).
Graner, F. & Glazier, J. A. Simulation of biological cell sorting using a two-dimensional extended potts model. Phys. Rev. Lett. 69, 2013 (1992).
Glazier, J. A. & Graner, F. Simulation of the differential adhesion driven rearrangement of biological cells. Phys. Rev. E 47, 2128 (1993).
H. Swat, M. et al. Multi-scale modeling of tissues using CompuCell3D. Meth. Cell Biol. 110, 325–366 (2012).
Bauer, A. L., Jackson, T. L. & Jiang, Y. Topography of extracellular matrix mediates vascular morphogenesis and migration speeds in angiogenesis. PLoS Comp. Biol. 5, e1000445 (2009).
Bauer, A. L., Jackson, T. L. & Jiang, Y. A cell-based model exhibiting branching and anastomosis during tumor-induced angiogenesis. Biophys. J. 92, 3105–3121 (2007).
Jiang, Y., Pjesivac-Grbovic, J., Cantrell, C. & Freyer, J. P. A multiscale model for avascular tumor growth. Biophys. J. 89, 3884–3894 (2005).
Wang, X., He, L., Wu, Y. I., Hahn, K. M. & Montell, D. J. Light-mediated activation reveals a key role for Rac in collective guidance of cell movement in vivo. Nat. Cell Biol. 12, 591–7 (2010).
Kabla, A. J. Collective cell migration: leadership, invasion and segregation. J. R. Soc. Interface 9, 3268–78 (2012).
Szabó, A., Varga, K., Garay, T., Hegedus, B. & Czirók, A. Invasion from a cell aggregate-the roles of active cell motion and mechanical equilibrium. Phys. Biol. 9, 016010 (2012).
Scianna, M. & Preziosi, L. A hybrid model describing different morphologies of tumor invasion fronts. Math. Model. Nat. Phenom. 7, 78–104 (2012).
Li, J. F. & Lowengrub, J. The effects of cell compressibility, motility and contact inhibition on the growth of tumor cell clusters using the cellular potts model. J. Theo. Biol. 343, 79–91 (2014).
Scianna, M., Preziosi, L. & Wolf, K. A cellular Potts model simulating cell migration on and in matrix environments. Math. Biosci. and Engg. 10, 235–261 (2013).
Alarcon, T., Byrne, H. & Maini, P. Towards whole-organ modelling of tumour growth. Prog. Biophys. Mol. Biol. 85, 451–472 (2004).
Alarcón, T., Byrne, H. M. & Maini, P. K. A multiple scale model for tumor growth. Multiscale Model Simul. 3, 440–475 (2005).
Jiao, Y. & Torquato, S. Emergent behaviors from a cellular automaton model for invasive tumor growth in heterogeneous microenvironments. PLoS Comp. Biol. 7, e1002314 (2011).
Arya, S. K., Lee, K. C., Bin Dah’alan, D., Daniel & Rahman, A. R. A. Breast tumor cell detection at single cell resolution using an electrochemical impedance technique. Lab on a chip 12, 2362–8 (2012).
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 21 (1953).
Ramis-Conde, I., Drasdo, D., Anderson, A. R. & Chaplain, M. A. Modeling the influence of the E-cadherin-β-catenin pathway in cancer cell invasion: a multiscale approach. Biophys. J. 95, 155–165 (2008).
Doxzen, K. et al. Guidance of collective cell migration by substrate geometry. Integr. Biol. 5, 1026–1035 (2013).
Saitou, T. et al. Mathematical modeling of invadopodia formation. J. Theor. Biol. 298, 138–46 (2012).
Swat, M. H. et al. Compucell3d reference manual version-3.7.2.
Sottoriva, A. et al. Cancer stem cell tumor model reveals invasive morphology and increased phenotypical heterogeneity. Cancer Res. 70, 46–56 (2010).
Vedula, S. R. K. et al. Emerging modes of collective cell migration induced by geometrical constraints. Proc. Natl Acad. Sci. USA 109, 12974–9 (2012).
Collier, I. E. et al. Diffusion of mmps on the surface of collagen fibrils: The mobile cell surface – collagen substratum interface. PLoS One 6, e24029 (2011).
Lee, M. H. et al. Mismatch in mechanical and adhesive properties induces pulsating cancer cell migration in epithelial monolayer. Biophys. J. 102, 2731–2741 (2012).
Wei, S. C. et al. Matrix stiffness drives epithelial – mesenchymal transition and tumour metastasis through a TWIST1 – G3BP2 mechanotransduction pathway. Nat. Cell. Biol. 17 (2015).
Keely, P. J., Fong, A. M., Zutter, M. M. & Santoro, S. A. Alteration of collagen-dependent adhesion, motility and morphogenesis by the expression of antisense alpha 2 integrin mrna in mammary cells. J. Cell Sci. 108, 595–607 (1995).
Kumar, S., Das, A. & Sen, S. Extracellular matrix density promotes EMT by weakening cell-cell adhesion. Mol. BioSyst. 10, 838–850 (2014).
Polyak, K. & Weinberg, R. A. Transitions between epithelial and mesenchymal states: acquisition of malignant and stem cell traits. Nat. Rev. Cancer 9, 265–273 (2009).
Nieto, M. A. The ins and outs of epithelial to mesenchymal transition in health and disease. Ann. Rev. Cell. Dev. Biol. 27, 347–376 (2011).
Cano, A. et al. The transcription factor Snail controls epithelial-mesenchymal transitions by repressing E-cadherin expression. Nat. Cell Biol. 2, 76–83 (2000).
Batlle, E. et al. The transcription factor Snail is a repressor of E-cadherin gene expression in epithelial tumour cells. Nat. Cell Biol. 2, 84–89 (2000).
Vleminckx, K., Vakaet, L., Mareel, M., Fiers, W. & van Roy, F. Genetic manipulation of E-cadherin expression by epithelial tumor cells reveals an invasion suppressor role. Cell 66, 107–19 (1991).
Christofori, G. & Semb, H. The role of the cell-adhesion molecule E-cadherin as a tumour-suppressor gene. Trends Bioc. Sci 24, 73–6 (1999).
Tripathi, V., Popescu, N. C. & Zimonjic, D. B. DLC1 induces expression of E-cadherin in prostate cancer cells through Rho pathway and suppresses invasion. Oncogene 33, 724–33 (2013).
Baum, B. & Georgiou, M. Dynamics of adherens junctions in epithelial establishment, maintenance and remodeling. J. Cell Biol. 192, 907–917 (2011).
Zaman, M. H., Matsudaira, P. & Lauffenburger, D. A. Understanding effects of matrix protease and matrix organization on directional persistence and translational speed in three-dimensional cell migration. Ann. Biomed. Engg. 35, 91–100 (2007).
Provenzano, P. P., Eliceiri, K. W. & Keely, P. J. Matrix density-induced mechanoregulation of breast cell phenotype, signaling and gene expression through a FAK-ERK linkage. Oncogene 28, 4326–4343 (2009).
Zhu, G. G. et al. Immunohistochemical study of type I collagen and type I pN-collagen in benign and malignant ovarian neoplasms. Cancer 75, 1010–1017 (1995).
Huijbers, I. J. et al. A role for fibrillar collagen deposition and the collagen internalization receptor endo180 in glioma invasion. PLoS ONE 5, 1–12 (2010).
Haeger, A., Krause, M., Wolf, K. & Friedl, P. Cell jamming: Collective invasion of mesenchymal tumor cells imposed by tissue confinement. Biochim. Biophys. Acta. 1840, 2386–2395 (2014).
Tiwari, N., Gheldof, A., Tatari, M. & Christofori, G. EMT as the ultimate survival mechanism of cancer cells. Seminars in Cancer Biol. 22, 194–207 (2012).
Sabeh, F., Shimizu-Hirota, R. & Weiss, S. J. Protease-dependent versus independent cancer cell invasion programs: three-dimensional amoeboid movement revisited. J. Cell Biol. 185, 11–19 (2009).
Rø rth, P. Fellow travellers: emergent properties of collective cell migration. EMBO Reports 13, 984–991 (2012).
Sternlicht, M. D. The stromal proteinase MMP3/stromelysin-1 promotes mammary carcinogenesis. Cell 98, 137–146 (1999).
Branch, K. M., Hoshino, D. & Weaver, A. M. Adhesion rings surround invadopodia and promote maturation. Biol. Open 1, 711–722 (2012).
Ning, J., Liu, W., Zhang, J., Lang, Y. & Xu, S. Ran GTPase induces EMT and enhances invasion in non-small cell lung cancer cells through activation of PI3K-AKT pathway. Oncology Res. Featuring Preclini. and Clini. Cancer Thera. 21, 67–72 (2013).
Yilmaz, M. & Christofori, G. EMT, the cytoskeleton and cancer cell invasion. Cancer Met. Rev. 28, 15–33 (2009).
Lu, P., Weaver, V. M. & Werb, Z. The extracellular matrix : A dynamic niche in cancer progression. J Cell Biol. 196, 395–406 (2012).
Song, W., Jackson, K. & McGuire, P. G. Degradation of type IV collagen by matrix metalloproteinases is an important step in the epithelial-mesenchymal transformation of the endocardial cushions. Dev. Biol. 227, 606–617 (2000).
Karagiannis, E. D. & Popel, A. S. Distinct modes of collagen type I proteolysis by matrix metalloproteinase (MMP) 2 and membrane type I MMP during the migration of a tip endothelial cell: insights from a computational model. J. Theo. Biol. 238, 124–45 (2006).
Wolf, K. & Friedl, P. Mapping proteolytic cancer cell-extracellular matrix interfaces. Clin. Exp. Met. 26 (2009).
Linder, S., Wiesner, C. & Himmel, M. Degrading Devices: Invadosomes in Proteolytic Cell Invasion. Annu. Rev. Cell Dev. Biol. 74, 185–211 (2011).
Wolf, K. et al. Compensation mechanism in tumor cell migration: Mesenchymal-amoeboid transition after blocking of pericellular proteolysis. J. Cell Biol. 160, 267–277 (2003).
Hegedüs, B., Marga, F., Jakab, K., Sharpe-Timms, K. L. & Forgacs, G. The interplay of cell-cell and cell-matrix interactions in the invasive properties of brain tumors. Biophys. J 91, 2708–2716 (2006).
Kaufman, L. et al. Glioma expansion in collagen I matrices: analyzing collagen concentration-dependent growth and motility patterns. Biophys. J. 89, 635–650 (2005).
Bellail, A. C., Hunter, S. B., Brat, D. J., Tan, C. & Van Meir, E. G. Microregional extracellular matrix heterogeneity in brain modulates glioma cell invasion. Interna. J. Biochemi. & Cell Biol. 36, 1046–1069 (2004).
Meacham, C. E. & Morrison, S. J. Tumour heterogeneity and cancer cell plasticity. Nature 501, 328–337 (2013).
Acknowledgements
S.S. acknowledges funding from Department of Science and Technology, India (SR/SO/BB-0016/2011). M. M. I. acknowledges funding from DBT-IYBA (BT/06/IYBA/2012) and Department of Science and Technology, India (SR/FTP/ETA-45/2012).
Author information
Authors and Affiliations
Contributions
S.K. conducted the simulations and analysed the data. A.K. and S.D. performed experiments and analyzed the experimental data. S.K., M.M.I. and S.S. conceived the simulations, discussed the data and wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kumar, S., Kapoor, A., Desai, S. et al. Proteolytic and non-proteolytic regulation of collective cell invasion: tuning by ECM density and organization. Sci Rep 6, 19905 (2016). https://doi.org/10.1038/srep19905
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep19905
This article is cited by
-
Synthetic living materials in cancer biology
Nature Reviews Bioengineering (2023)
-
Multiscale computational modeling of aortic valve calcification
Biomechanics and Modeling in Mechanobiology (2023)
-
Development of a coupled modeling for tumor growth, angiogenesis, oxygen delivery, and phenotypic heterogeneity
Biomechanics and Modeling in Mechanobiology (2023)
-
Mechanical Pressure Driving Proteoglycan Expression in Mammographic Density: a Self-perpetuating Cycle?
Journal of Mammary Gland Biology and Neoplasia (2021)
-
From individual to collective 3D cancer dissemination: roles of collagen concentration and TGF-β
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.