Abstract
Quantum information and quantum computation have achieved a huge success during the last years. In this paper, we investigate the capability of quantum Hash function, which can be constructed by subtly modifying quantum walks, a famous quantum computation model. It is found that quantum Hash function can act as a hash function for the privacy amplification process of quantum key distribution systems with higher security. As a byproduct, quantum Hash function can also be used for pseudo-random number generation due to its inherent chaotic dynamics. Further we discuss the application of quantum Hash function to image encryption and propose a novel image encryption algorithm. Numerical simulations and performance comparisons show that quantum Hash function is eligible for privacy amplification in quantum key distribution, pseudo-random number generation and image encryption in terms of various hash tests and randomness tests. It extends the scope of application of quantum computation and quantum information.
Similar content being viewed by others
Introduction
With the rapid development of quantum communication, quantum key distribution (QKD) is the most mature branch of quantum communication. The goal of QKD is to create an absolutely secure key between two communicating parties. QKD generally contains three steps: (1) raw key sifting, (2) error reconciliation and (3) privacy amplification. As an important step of QKD, the privacy amplification process is implemented by adopting universal hash functions1. However, these hash functions are generally constructed based on mathematics complexity and thus they are computationally secure. Because the fundamental principles of quantum mechanics ensure lots of quantum cryptographic protocols2,3,4 with unconditional security, this stimulates us to consider the privacy amplification problem in the context of quantum information and intend to get a more secure solution to the privacy amplification process.
In this paper, we construct a quantum Hash function (QHF) by subtly modifying the quantum walks (QW) model5,6,7,8,9,10,11,12,13 and it can be used for the privacy amplification process of QKD systems with higher security by means of the physical principles of quantum mechanics. As a byproduct, QHF can also be used for pseudo-random number generation due to its inherent chaotic dynamics and further we propose a novel QHF-based image encryption algorithm. Numerical simulations and performance comparisons show that QHF is eligible as a hash function for privacy amplification in QKD, pseudo-random number generation and image encryption in terms of various hash tests and randomness tests.
Compared to the QW-based algorithm14, the novelty of the present QHF-based scheme lies in that the constructed QHF can be not only used for pseudo-random number generation and further image encryption, but also used for the privacy amplification process of QKD systems with higher security. It extends the scope of application of quantum computation and quantum information.
Results
The construction of QHF
QHF can be constructed by subtly modifying QW. QW has two models: discrete QW and continuous QW5. The basic discrete QW includes two quantum systems: walker and coin. The state of the walker-coin system is denoted by a vector in the Hilbert space  , where the subscripts p and c stand for the walker and the coin, respectively. The motion of the walk is conditioned by the coin state via a conditional shift operator
, where the subscripts p and c stand for the walker and the coin, respectively. The motion of the walk is conditioned by the coin state via a conditional shift operator

where the summation symbol denotes the sum over all possible positions. The evolution of the total quantum system can be implemented by repeating the global unitary operator

where  is the identity operator and
is the identity operator and  is the coin operator applied on the coin state. Hence the final state
is the coin operator applied on the coin state. Hence the final state  after t steps is expressed by
after t steps is expressed by

and the probability of locating the walker at position x after t steps is

where  is the initial state of the total quantum system.
is the initial state of the total quantum system.
In a discrete-time QW, the coin operator is fixed. The resulting probability distribution relies on only the initial coin state and the step number. Suppose the coin operator at each step depends on a binary string, i.e., message and accordingly a QHF is constructed, similar to that in Ref.15. The input of the constructed QHF is a binary string, i.e., message and the resulting probability distribution is used as the output hash value. The coin state is the control parameter so the constructed QHF is a keyed one. The nth bit of the message controls the nth step of the walk. Here we introduce two coin operators, i.e., the Grover operator  16 and the coin operator
16 and the coin operator  17 in equation (5) and equation (6) respectively. The message bit “0” denotes
17 in equation (5) and equation (6) respectively. The message bit “0” denotes  and “1” for
and “1” for  .
.


The construction process of the QHF is as follows:
-
1
Select the parameters (n, (α, β, χ, δ)) and the message with arbitrary length.
-
2
Run the one-dimensional two-particle discrete-time QW on a circle under the control of the message and generate the output hash value, i.e., the probability distribution. Here α, β, χ, δ are the amplitudes of the initial coin state
 . n is the node number of a circle.
. n is the node number of a circle. -
3
Multiply all values in the resulting probability distribution by 108 modulo 256 to form a binary string as a secret key K, i.e., the hash value.
The hash property of the proposed QHF
In this section, we performed several hash tests to evaluate the performance of the proposed QHF. The message can be randomly chosen as shown in Supplemental materials.
Statistical distribution of hash value
Based on the principles of quantum mechanics, the security of the QHF can be proved partly by the uniform distribution of the hash value. The plots of the ASCII codes of the message and its hash value are shown in Supplementary Fig. S1 online. Supplementary Fig. S1(a) demonstrates that the ASCII code of the message is located within a small range, but in Supplementary Fig. S1(b), the hash value of the message in hexadecimal format is scattered uniformly.
Sensitivity of hash value to message
C1, C2, C3 and C4 represent the message and the message with tiny modifications respectively. The results listed below show the high sensitivity to the message and the tiny changes.
Condition 1: The original message;
Condition 2: Change the 8th bit from 0 to 1;
Condition 3: Delete the last bit of the message;
Condition 4: Insert a bit in front of the 100th bit.
The corresponding 128-bit hash value in the hexadecimal format is given by:
Condition 1: 8AE72983687E9AD1B6FCA54546AE7799;
Condition 2: 3BD58DB7B86827AE6323E6E496A634A8;
Condition 3: E9678E1EA9180A8EE01AA008EB46E989;
Condition 4: E9277B78B3D62DEB77839DB9E90F210D.
The plots of the hash values are shown respectively in Supplementary Fig. S2 online and it is clearly indicated that any tiny modification to the message or the key will cause a substantial change in the final hash value.
Statistical analysis of diffusion and confusion
The diffusion and confusion tests are performed as follows:
-
1
Select a message and generate the corresponding hash value.
-
2
Change one bit of the message randomly and generate a new hash value.
-
3
Compare the two hash values and count the changed bits called Bi.
-
4
Repeat steps (1) to (3) N times.
The corresponding distribution and the histogram of Biare shown respectively in Supplementary Figs S3(a) and S3(b) online, where N = 10,000.
Minimum changed bit number  ;
;
Maximum changed bit number  ;
;
Mean changed bit number  ;
;
Mean changed probability  ;
;
Standard variance of the changed bit number  ;
;
Standard variance of the changed probability  .
.
Next the diffusion and confusion tests are performed with N = 1024, 2048, 10,000, respectively, as shown in Table 1. We concluded from the tests that the mean changed bit number B and the mean changed probability P are close to the ideal value 64 and 50% respectively. ΔB and ΔP are very little, so that it demonstrates the stability of diffusion and confusion. The excellent statistical effect ensures that it is impossible to forge plaintext-cipher pairs given known plaintext-cipher pairs.
Collision analysis
It is hard to provide a mathematical proof on the capability of collision resistance of chaotic hash functions. Thus, we performed the following test for collision resistance:
-
1
Select an original message randomly and generate the corresponding hash value in ASCII format.
-
2
Choose a bit in the message randomly and change its value.
-
3
Generate a new hash value.
-
4
Compare these two hash values and count the number of ASCII characters with the same value at the same location.
Moreover, the absolute difference of the two hash values, i.e., d and the theoretical number of ω with different values through N independent tests, i.e., WN(ω) can be computed according to the following formulas:



where ei and e’i are the ith entries of the original and new hash values, respectively. The function t(·) converts the entries to their equivalent decimal value. We run this test N = 10, 000 times and listed the maximum, minimum and mean of d in Supplementary Table 1 online respectively. In equation (8), ω = 0, 1, …, s. The experimental values of WN(ω) in the proposed scheme are: WN(0) = 9367, WN(1) = 617, WN(2) = 16 and WN(ω) = 0 for ω = 3, 4, …, 16 respectively. The distribution of the number of ASCII characters with the same value at the same location in the hash value is displayed in Fig. 1.
Uniform distribution on hash space
In order to check the distribution capacity in hash space, similar to that in ref. 18, we generated two hash values according to the method described in previous subsection and then counted the number of the changed bits at each location. The minimum, maximum and mean of changed bit numbers are 4072, 5689 and 4973.5, respectively for N = 10,000. The statistical results for N = 10,000 are shown in Supplementary Fig. S4 online. The mean of the changed bit number 4973.5 is very close to the ideal value 5000, which accounts for half of the test times. It can be concluded that the hash value is distributed uniformly in the hash space as all the changed bit numbers are around the ideal value. Obviously, this demonstrates the resistance against statistical attack.
Resistance to birthday attack
Similar to collision resistance, the birthday attack is mainly aimed to find two messages with identical hash values with less than 2n/2 trials (n is the size of hash value). According to the current computing power, the size of hash value should be greater than 128 to ensure the birthday attack complexity is greater than 264. In our proposed hash scheme, the length of hash value is 128-bit and it can be easily extended to 256-bit or 512-bit. So the attack difficulty is at least 264, which is huge enough to resist brute force attack and birthday attack. Also in the proposed algorithm, in order to analyze the security, several tests including the SP800-22 test and the collision tests were applied. Therefore, the results of the tests, the size of the hash value and the collision resistance of the proposed algorithm suggest that the birthday attack is almost impossible and that the proposed algorithm is resistant against this type of attack.
Speed analysis
Our proposed hash algorithm does not need to pad bits. The time required to generate a hash value is closely related to the length of the message. The algorithm is simulated in MATLAB on a PC with Intel(R) Core(TM) i3-2370M CPU 2.40 GHz 2 GB RAM running on Windows 7 professional OS. The average speed of our algorithm is 0.2 Mbit/s. Although the speed of the proposed algorithm is lower than the traditional hash functions such as SHA-1 and MD519, it is acceptable for practical use. At the same time, the algorithm is so flexible since the length of hash value can be 128, 256, or 512 bits. Moreover, because of the excellent properties of quantum parallel computing, the speed of the proposed algorithm will increase exponentially in the quantum computing environment. For example, finding the prime factorization of an n-bit integer is thought to require  operations using the best classical algorithm. In contrast, a quantum algorithm can accomplish the same task using
operations using the best classical algorithm. In contrast, a quantum algorithm can accomplish the same task using  operations20. That is, a quantum computer can factor a number exponentially faster than the best known classical algorithms.
operations20. That is, a quantum computer can factor a number exponentially faster than the best known classical algorithms.
Flexibility
Our hash scheme is based on the QW model. Although the proposed hash function is constructed as a keyed one, we can also regard it as an unkeyed one if the initial parameters of the coin state of QHF act as the constants. Besides we can also get a 256-bit or 512-bit hash function with a slight change in the original version, similar to refs 21,22.
Resistance to meet-in-the-middle attack
The meet-in-the-middle attack is valid for the block cipher encryption mode. Block cipher mode allows the use of a cipher key for encrypting more than one block of data. In contrast, in our proposed algorithm, we use just the nonlinear quantum map to construct the hash function, so the attack is useless for the proposed algorithm.
Resistance to forgery attack
Most of the parallel hash function algorithms have a mixing section in their structure which usually uses the XOR operation for preventing forgery attack. Unfortunately, some of these algorithms are broken by such an attack23,24. In the proposed algorithm, the state evolution of the total quantum system can be implemented by repeating the sequence of the coin flipping operator and the conditional shift operator step by step according to the message(so-called discrete time). That is, the nth bit of the message controls the nth step of the walk, i.e., applying the Grover operator  16 or the coin operator
16 or the coin operator  17 on the coin state. This leads to high complexity in mixture and can resist forgery attack in any section of the proposed algorithm.
17 on the coin state. This leads to high complexity in mixture and can resist forgery attack in any section of the proposed algorithm.
Security analyses of the QHF-based pseudo-random number generator (PRNG)
QHF can also be used for pseudo-random number generation due to its inherent chaotic dynamics. To analyze the pseudo-randomness of the QHF-based PRNG, we analyzed its statistical properties and some quantifiers were proposed. The quantifiers are mainly classified into two classes: (i) quantifiers based on information theory25,26,27, (ii) quantifiers based on recurrence plots28,29.
Statistical complexity measure
Complexity is a measure of off-equilibrium ‘order’. Statistical complexity measures (SCM) were proposed as quantifiers of the degree of physical structure in a signal25,30,31. Based on the method of Ref. 32, we analyzed the statistical complexity of the QHF-based PRNG. The intensive SCM (CJ[P]) can be considered as a quantity that characterizes the probability distribution P associated with the time series generated by the dynamical system32. It quantifies not only randomness but also the presence of correlational structures31,32. The measure of statistical complexity CJ[P] is defined as32:

where the normalized entropic measure  is associated with the probability distribution P, with
is associated with the probability distribution P, with 
 for the equilibrium distribution Pe and S is the Shannon entropy. The disequilibrium QJ is defined in terms of the Jensen-Shannon divergence26,32 by
for the equilibrium distribution Pe and S is the Shannon entropy. The disequilibrium QJ is defined in terms of the Jensen-Shannon divergence26,32 by

with Q0 being the normalization constant  . Thus, the disequilibrium QJ is an intensive quantity. Following the methodology proposed by Bandt and Pompe33, the comparisons between our proposal and the QW-based PRNG14 in terms of the normalized entropy HS and the intensive statistical complexity CJ as functions of the number of 8 bits and 16 bits-words are shown in Figs 2 and 3 respectively. When the number of words of the analyzed sequence increases, the statistical complexity and the normalized entropy tend to 0 and 1 respectively. It is shown that given the same words, our scheme has better statistical complexity and normalized entropy than the QW-based PRNG14.
. Thus, the disequilibrium QJ is an intensive quantity. Following the methodology proposed by Bandt and Pompe33, the comparisons between our proposal and the QW-based PRNG14 in terms of the normalized entropy HS and the intensive statistical complexity CJ as functions of the number of 8 bits and 16 bits-words are shown in Figs 2 and 3 respectively. When the number of words of the analyzed sequence increases, the statistical complexity and the normalized entropy tend to 0 and 1 respectively. It is shown that given the same words, our scheme has better statistical complexity and normalized entropy than the QW-based PRNG14.
Comparisons in terms of Normalized Shannon entropy HS.
The black and red curves denote the Normalized Shannon entropy HS for the number of 8 bits and 16 bits-words respectively in our proposal, while the blue and green curves represent the Normalized Shannon entropy of the QW-based scheme14 for the number of 8 bits and 16 bits-words respectively. (see text in the section entitled Results).
Comparisons in terms of intensive statistical complexity measure CJ respectively.
The black and red curves denote the intensive statistical complexity measure CJ for the number of 8 bits and 16 bits-words respectively in our proposal, while the blue and green curves represent the intensive statistical complexity measure CJ of the QW-based scheme14 for the number of 8 bits and 16 bits-words respectively. (see text in the section entitled Results).
Recurrence plots
Recurrence is a fundamental property of dynamical systems, which can be exploited to characterize the system’s behavior in phase space. In 1987, Eckmann et al. introduced a powerful tool for visualization and analysis of recurrences called recurrence plot (RP)28. RP is a two-dimensional representation in which both axes are time ones. The recurrence of a state appearing at two given times ti, tj is pictured in the two-dimensional graph by means of a black dot.
To visualize the recurrences of states of a dynamical system, the RP of a trajectory  can be formally expressed by the matrix
can be formally expressed by the matrix

where N is the number of measured points  , ε is a threshold distance,
, ε is a threshold distance,  is the Heaviside function (i.e.
is the Heaviside function (i.e.  , if x < 0 and
, if x < 0 and  otherwise) and
otherwise) and  is a norm.
is a norm.
RPs for various values of the message exhibit visually the recurrences of the QHF-based PRNG (Supplementary Fig. S5 online). We used an embedding dimension m = 2 and the delay τ = 1. The threshold distance ε is set to be 10% of the mean phase space radius σ. It is shown that the QHF-based PRNG with different messages causes a rather homogeneous RP with numerous single points and some short, diagonal or vertical lines.
Because the visual impact produced by the RP is insufficient to demonstrate the quality of the QHF-based PRNG because of the ‘small-scale’ structures29, several measures of complexity which quantify the small scale structures in RPs, have been proposed34,35,36 and are known as recurrence quantification analysis (RQA). In this paper, these measures based on the recurrence point density and the diagonal and vertical line structures are considered.
Measures based on the recurrence density
The simplest measure of the RQA is the recurrence rate (RR)

which is a measure of the density of recurrence points in the RP. Furthermore, in the limit N → ∞, RR is the probability that a state recurs to its ε-neighbourhood in phase space. For PRNGs, the ideal value would be RR = 0. But in practice, in order that the quantifier may make sense, a larger ε should be adopted to avoid the situation in which no points are found in the recurrence plot. It is shown that the value of the RR ranges from 0.00595 to 0.00662 for different messages (see Supplementary Fig. S6 online). It exhibits the good randomness of the QHF-based PRNG.
Measures based on diagonal lines
The measures are related to the histogram  of the diagonal line lengths l, given by
of the diagonal line lengths l, given by

Supplementary Fig. S7 online shows the histogram of the diagonal line lengths of the RP in Supplementary Fig. S5 online with the parameter message = 50. It is shown that the diagonal line lengths are mainly very short exhibiting the good randomness.
Processes with uncorrelated or weakly correlated behaviors cause none or very short diagonals, whereas deterministic processes cause longer diagonals and less single, isolated recurrence points. Therefore, the ratio of recurrence points that form diagonal structures (of at least length lmin) to all recurrence points

is introduced as a measure for determinism (or predictability) of the system. The threshold lmin excludes the diagonal lines which are formed by the tangential motion of the phase space trajectory.
A diagonal line of length l means that a segment of the trajectory is rather close during l time steps to another segment of the trajectory at a different time; thus these lines are related to the divergence of the trajectory segments. The average diagonal line length

is the average time that two segments of the trajectory are close to each other and can be interpreted as the mean prediction time.
Another RQA measure considers the length Lmax of the longest diagonal line found in the RP,

where  is the total number of diagonal lines. These measures are related to the exponential divergence of the phase space trajectory. The faster the trajectory segments diverge, the shorter the diagonal lines are.
is the total number of diagonal lines. These measures are related to the exponential divergence of the phase space trajectory. The faster the trajectory segments diverge, the shorter the diagonal lines are.
The measure entropy refers to the Shannon entropy of the probability  to find a diagonal line of exactly length l in the RP, where
to find a diagonal line of exactly length l in the RP, where  is the total number of diagonal lines.
is the total number of diagonal lines.

ENTR reflects the complexity of the RP in respect of the diagonal lines, e.g. for uncorrelated noise the value of ENTR is rather small, indicating its low complexity, as shown in Supplementary Fig. S8 online.
Measures based on vertical lines
The total number of the vertical lines of the length v in the RP is then given by the histogram

Supplementary Fig. S9 online shows the histogram of vertical line lengths of the RP in Supplementary Fig. S5 with the parameter message = 50. It is shown that the vertical line lengths are mainly very short exhibiting the good randomness.
Analogous to the definition of the determinism in equation (15), the ratio between the recurrence points forming the vertical structures and the entire set of recurrence points can be computed,

The computation of LAM is realized for those v that exceed a minimal length vmin in order to decrease the influence of the tangential motion. LAM will decrease if the RP consists of more single recurrence points than vertical structures.
The average length of vertical structures is given by

and is called trapping time. TT estimates the mean time that the system will abide at a specific state or how long the state will be trapped.
Finally, the maximal length of the vertical lines in the RP

can be defined, analogously to the standard measure Lmax (Nv is the absolute number of vertical lines).
Figures 4, 5, 6 give some selected RQA measures for different values of the message and demonstrates the good statistical properties of the QHF-based PRNG.
Degree of non-periodicity
In order to study the non-periodicity in the QHF-based PRNG, the scale index analysis (SIA) is carried out which is introduced by Benìtez et al.37. The SIA method is often used as a framework to enhance the general performance of cryptosystems in designing new chaos-based cryptosystems and PRNGs. For example, recently Akhshani et al. proposed a new scheme for generating good PRNGs based on quantum logistic map38. They used the SIA technique to assess the degree of non-periodicity of the chaotic sequences of the quantum map. The SIA technique is based on the continuous wavelet transform (CWT) and the wavelet multi-resolution analysis39. To study the non-periodicity of the QHF-based PRNG40, we assumed that the key sequence f generated by QHF is compactly supported and is defined over a finite time interval T = [a, b]. The CWT of f at time u and scale s is defined as39:

and it provides the frequency component (or details) of f corresponding to the scale s and time location t. Supplementary Fig. S10 online shows the time frequency decomposition of f in the time-frequency plane which provided by the wavelet transform given in equation (23).
The wavelet transform given in equation (23), provides a time frequency decomposition of f in the time-frequency plane.
The scalogram of f is defined as follows:

where  is the energy of the CWT of f at scale s. The scalogram is a useful tool for studying a signal, since it allows the detection of its most representative scales or frequencies37,40. The innerscalogram of f at a scale s can be defined by:
is the energy of the CWT of f at scale s. The scalogram is a useful tool for studying a signal, since it allows the detection of its most representative scales or frequencies37,40. The innerscalogram of f at a scale s can be defined by:

where  is the maximal subinterval in T for which the support of
is the maximal subinterval in T for which the support of  is included in T for all
is included in T for all  . As the length of J(s) depends on the scale s, the values of the inner scalogram at different scales cannot be compared. Therefore, the inner scalogram should be normalized as follows37:
. As the length of J(s) depends on the scale s, the values of the inner scalogram at different scales cannot be compared. Therefore, the inner scalogram should be normalized as follows37:

Supplementary Fig. S11 online shows that the normalized inner scalogram can be a valuable tool for detecting the non-periodicity of the signals, where a signal with details at every scale is non-periodic.
The scale index of f in the scale interval [s0, s1] can be defined by:

where smax is the smallest scale such that  for all
for all  and smin the smallest scale such that
and smin the smallest scale such that  for all
for all  . The scale index will be zero or close to zero for periodic sequences and close to one for highly non-periodic sequences37.
. The scale index will be zero or close to zero for periodic sequences and close to one for highly non-periodic sequences37.
In Fig. 7, the SIA of the QHF-based key sequence is presented. It can be concluded that the best value of the scale index is up to 0.98. Thus, the key sequence in this state is highly non-periodic and it can be used for any PRNG purposes.
The scale index of the QHF-based key sequence for different messages.
It can be concluded that, the value of the scale index is larger than 0.7 and the best value of the scale index is up to 0.98. Thus, the key sequence in this state is highly non-periodic and it can be used for any PRNG purposes. (see text in the section entitled Results).
The application of the QHF-based PRNG to image encryption
The proposed image encryption algorithm consists of the following major steps:
Step 1: Initialization step
In this step we choose the parameters (n, (α, β, χ, δ)) and the message, then generate a random sequence S by running our proposed PRNG given by

Each value of the sequence S is a floating-point number ranging from 0 to 1.
Step 2: Encryption procedure
-
1
Divide the original image I with size M × N into four parts with the same size and determine the encryption order of four image blocks according to the size of the first four values of the sequence S. For example,
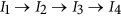 if
if  . Here we take Buddha image as an example (see Supplementary Fig. S12 online).
. Here we take Buddha image as an example (see Supplementary Fig. S12 online). -
2
The encryption process is a two round one (Supplementary Fig. S13 online) i.e.,

Then we describe the encrypt function  by taking I2 as an example.
by taking I2 as an example.
1. Sum the gray values of EI1 to produce a binary sequence V, use V as the message to generate a new random sequence S1 as follows.

where pixeli,j represents the gray value of the pixel in the ith row and jth column of EI1.

where dec2bin is a function to convert the decimal to binary sequence.
2. Do the tensor product of S and S1 to obtain a new sequence and transform it into a two-dimensional matrix of size  .
.

where  is tensor product operator.
is tensor product operator.
3. Multiply all values in the P matrix by 108 modulo 256 to form a new matrix P′.

4. Make P′ exclusive-OR (XOR) with I2 and get

5. Sort the elements in P′ in ascending order and obtain the index vector.

where sortedP is the sorted matrix and index is the index vector, i.e.,  .
.
6. Shuffle the elements in temp_I2 and get encrypted image block EI2 for the first round.

At last we can get the final encrypted image by executing the encrypt function as the order shown in Step 2.
Step 3: Decryption procedure
In the decryption process, we use the secret key to determine the decryption order, shown as follows.

Here,  represents the decryption operation and it is the reverse of the encryption process.
represents the decryption operation and it is the reverse of the encryption process.
Experimental simulations
Experiments are performed on a laptop with Intel(R) Core(TM) i3-2370M CPU 2.40 GHz 2 GB RAM running on Windows 7 professional equipped with the MATLAB R2012a environment and the Python 2.7.8. To test our encryption method for security and robustness, we choose a group of images with size 512 × 512, which were taken by Yu-Guang Yang and list them and their corresponding encrypted images and decrypted images in Supplementary Figs S12–S18.
Key space analysis
A desirable encryption scheme should have a sufficiently large key space to resist brute-force attacks. Here the encryption key can be represented by (n, (α, β, χ, δ), message), where n denotes the number of nodes in a circle. α, β, χ, δ are complex numbers and also control parameters of the coin state satisfying the normalization constraint:  . Message is a binary string as an input of the proposed QHF, which can have an infinite length theoretically. Although there is an infinite key space theoretically, because of finite precision of digital computers, the key space actually turns out to be finite. Considering that the calculation precision is 10−14, the size of key space for initial conditions and control parameters would be roughly 2325, which is large enough for any encryption purposes and is also large enough to resist all kinds of brute-force attacks.
. Message is a binary string as an input of the proposed QHF, which can have an infinite length theoretically. Although there is an infinite key space theoretically, because of finite precision of digital computers, the key space actually turns out to be finite. Considering that the calculation precision is 10−14, the size of key space for initial conditions and control parameters would be roughly 2325, which is large enough for any encryption purposes and is also large enough to resist all kinds of brute-force attacks.
Histogram analysis
Histogram is a very important security measure for evaluating the security of an image encryption algorithm. The histograms of seven images and the corresponding cipher images are shown in Supplementary Figs S12–S18 online. It is shown that the histograms of the cipher images are nearly uniform and significantly different from the ones of the original images. Therefore they provide no clue for attackers in a statistical analysis attack.
Correlation analysis
A desirable encryption scheme should generate the cipher image with rather low correlation between adjacent pixels. By randomly selecting 10000 pairs (in horizontal, vertical and diagonal directions respectively) of adjacent pixels from the original image and the cipher image, respectively, we test the correlation between adjacent pixels and draw the correlation distribution of adjacent pixels in the Buddha image and its cipher image in Supplementary Fig. S21 online, respectively. It is shown that the original image has strong correlation, but the cipher image is quite random. The encryption scheme improves the security of the test images greatly.
We also calculate the correlation coefficient rxy of adjacent pixels of the original image and the cipher image given by

where E(x) and D(x) are the expectation and variance of variable x, respectively.
We compute the correlation coefficients of the seven images and their cipher images. From Supplementary Table S2 online, we can see that the average correlation coefficients of the encrypted images are 0.0010, 0.0012, 0.0023 and they are very close to zero. The result demonstrates that our scheme is effective.
Comparison with other image encryption techniques
Experimental results of the proposed image encryption scheme were compared with six typical image encryption techniques, i.e., chaos-based image encryption41, optics-based image encryption42, hash-based image encryption43, quantum image encryption44, the QW-based image encryption14 and the image encryption based on quantum logistic map45, respectively. From Supplementary Tables S3–S8 online, we can see that the images encrypted by our algorithm have lower correlation compared with the six image encryption schemes14,41,42,43,44,45. In addition, we also compared our algorithm with two recently published schemes46,47 and see Supplementary Tables S9 and S10 online for details.
Differential attack analysis
In general, two common performance measures are used to test the influence of a little change in the original image on the cipher image, i.e., the number of pixels change rate (NPCR) and the unified average changing intensity (UACI). NPCR is expressed by

where

and c1 and c2 are two cipher images with size m × n.
UACI is defined by

In our tests, we just put the gray value of grid (100,100) minus one in the seven images in Supplementary Figs S12–S18 with size 512 × 512, respectively. From Supplementary Table S11 online, we can see that NPCR is 99.61% and UACI is 33.46% in our algorithm which implies that it is highly sensitive to the original image and is robust against differential attacks. In addition, we also compared our proposal with other image encryption schemes41,43,45,46,47 and see Supplementary Tables S12–S17 online for details. From these tables, it is indicated that the proposed algorithm can resist the differential attack. The secret key in our algorithm is related to the image self. So it makes a good performance in this field.
Key sensitivity analysis
First, we encrypted Buddha image with the key n = 1, [α, β, χ, δ] = [0, 0, 0, 1], message = [1, 0, 1, 0, …, 1, 0, 1, 0…] and obtained the cipher image in Supplementary Fig. S22(a). Then we encrypted Buddha image by making a little change of the message and got the cipher image in Supplementary Fig. S22(b). We also draw the differential image of Supplementary Fig. S22(a) and S22(b) in Supplementary Fig. S22(c). By calculation, we got that the difference (NPCR) between Supplementary Fig. S22(a) and Supplementary Fig. S22(b) is 99.59%(see Supplementary Tables S18 online), which implies the encryption process is quite sensitive to the encryption key.
Second, we encrypted Buddha image by the key n = 1, [α, β, χ, δ] = [0, 0, 0, 1], message = [1, 0, 0, 1, …, 1, 0, 1, 1…] and then decrypted the resulting cipher image with the correct key (see Supplementary Fig. S22(d)) and the wrong key with a little change of the message = [1, 0, 0, 1, …, 1, 1, 1, 1…] (see Supplementary Fig. S22(e)), respectively. We calculated out the difference (NPCR) between Supplementary Fig. S22(d) and Fig. S22(e) is 99.61% (see Supplementary Tables S18 online). Therefore, the decryption process is also highly sensitive to the decryption key.
In the same way, we also calculated the NPCR of other test images from Supplementary Figs S12–S18 and listed the results in Supplementary Table S18 online. It is found that the results are approximately 99.60%, which shows that the proposed algorithm is of good key sensitivity to images.
Information entropy analysis
The information entropy is often used to measure the randomness of the cipher images. The entropy H(x) of a message source m is given by

where p(xi) represents the probability of the occurrence of symbol xi.
From Supplementary Table S19 online, we can see the average information entropy of our cipher images is very close to the theoretical value 8. We also compared our algorithm with the algorithm based on quantum logistic map45 in terms of information entropy(Supplementary Table S20 online). This implies that the information leakage in the encryption process is negligible and the proposed algorithm is stable and secure against information entropy attack.
Randomness test analysis
Next, we used NIST SP800-22 and TestU0148 tools to test the randomness of the cipher images. Each test produces a P-value in [0, 1]. If the P-value is higher than a preset threshold α, it means that the cipher image passes the test. In our tests, we set α = 0.01 and Buddha’s cipher image with size 1024 × 1024. α = 0.01 implies that the cipher image can be inferred to be random with 99% probability if it passes the test. From Supplementary Table S21 online, we can judge that our proposed algorithm passes the NIST SP800-22 tests.
However, when we applied the most stringent test by TestU0148 on the cipher images, surprisingly, the TestU01 test cannot be done successfully. Maybe the coin flipping operators were not chosen properly. Therefore, the future work will focus on the improvement of our proposal.
Speed performance analysis
Speed is an important factor for evaluating the performance of an image encryption algorithm. For the proposed image encryption algorithm, we measured the time cost in the operating environment: Windows 7, Matlab R2012a, Intel(R) Core(TM) i3-2370M CPU 2.40 GHz 4 GB RAM. In our algorithm, the time is mainly spent on shuffling pixels, we can figure out that the time complexity of our algorithm is  and the average time cost for encrypting images of size 512 × 512 is 0.015 seconds or so. Therefore, our algorithm is fast enough for practical applications.
and the average time cost for encrypting images of size 512 × 512 is 0.015 seconds or so. Therefore, our algorithm is fast enough for practical applications.
Discussion
The main contribution of the work is to construct a hash function used for the privacy amplification process of QKD systems with higher security by means of the physical principles of quantum mechanics. As a byproduct, QHF can also be used for pseudo-random number generation due to its inherent chaotic dynamics and further we propose a novel QHF-based image encryption algorithm.
The QHF is in fact constructed in the quantum context. Because the practical quantum computation device is unavailable, we have to do the simulations by MATLAB software on a classical computer in order to demonstrate the performance of the constructed QHF. However, in fact the properties of quantum parallel computation cannot be simulated precisely on a classical computer. So both randomness and speed of the proposed scheme seem not acceptable for cryptographic purpose. Fortunately, with the rapid development of the field of quantum computation, maybe the practical quantum computer is possible in the future. When the QHF operates on a practical quantum computer, the computation speed will be increased exponentially because of the properties of quantum parallel computation.
Methods
The construction of a QHF by modifying the one-dimensional two-particle discrete-time QW on a circle
A one-dimensional two-particle discrete-time QW on a circle describes the QW of two walkers whose motions are restricted to the circle. The operators  and
and  of two-particle QW on circles becomes
of two-particle QW on circles becomes

Here  is similar to
is similar to  . The total conditional sift operator
. The total conditional sift operator  is denoted as
is denoted as  .
.
When the ith bit of the message is 0(1), the ith step of the walk executes with the interaction  . For example, if the message, m is ‘0100110’, then the final state evolves
. For example, if the message, m is ‘0100110’, then the final state evolves

where  and
and  . The initial state of the total quantum system
. The initial state of the total quantum system  is given by
is given by

Here

where  .
.
Additional Information
How to cite this article: Yang, Y.-G. et al. Quantum Hash function and its application to privacy amplification in quantum key distribution, pseudo-random number generation and image encryption. Sci. Rep. 6, 19788; doi: 10.1038/srep19788 (2016).
References
Bennett, C. H., Brassard, G., Crépeau, C. & Maurer, U. M. Generalized privacy amplification. IEEE Trans. Inf. Theory 41, 1915–1923 (1995).
Bennett, C. H. & Brassard, G. Quantum cryptography: public key distribution and coin tossing. In: Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, IEEE, New York, pp. 175-179 (1984).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Tamaki, K., Koashi, M. & Imoto, N. Unconditionally secure key distribution based on two nonorthogonal states. Phys. Rev. Lett. 90, 167904 (2003).
Elías, S. & Andraca, V. Quantum walks: a comprehensive review. Quantum Inf. Process. 11, 1015–1106 (2012).
Ambainis, A. Quantum walk algorithm for element distinctness. SIAM J. Comput. 37, 210–239 (2007).
Magniez, F., Santha, M. & Szegedy, M. Quantum algorithms for the triangle problem. SIAM J. Comput. 37, 413–424 (2007).
Li, Q., He, Y. & Jiang, J.-P. A hybrid classical-quantum clustering algorithm based on quantum walks. Quantum Inf. Process. 10, 13–26 (2011).
Babatunde, A. M., Cresser, J. & Twamley, J. Using a biased quantum random walk as a quantum lumped element router. Phys. Rev. A 90, 012339 (2014).
Tamascelli, D. & Zanetti, L. A quantum-walk-inspired adiabatic algorithm for solving graph isomorphism problems. J. Phys. A-Math. Theor. 47, 325302 (2014).
Childs, A. M. & Ge, Y. M. Spatial search by continuous-time quantum walks on crystal lattices. Phys. Rev. A 89, 052337(2014).
Izaac, J. A. & Wang, J. B. pyCTQW: A continuous-time quantum walk simulator on distributed memory computers. Comput. Phys. Commun. 186, 81–92 (2015).
Zhan, X., Qin, H., Bian, Z. H., Li, J. & Xue, P. Perfect state transfer and efficient quantum routing: A discrete-time quantum-walk approach. Phys. Rev. A 90, 012331 (2014).
Yang, Y. G., Pan, Q. X., Sun, S. J. & Xu, P. Novel image encryption based on quantum walks. Sci. Rep. 5, 7784 (2015).
Li, D., Zhang, J., Guo, F.-Z., Huang, W. & Wen, Q.-Y. Discrete-time interacting quantum walks and quantum Hash schemes. Quantum Inf. Process. 12, 1501–1513 (2013).
Shenvi, N., Kempe, J. & Whaley, K. B. Quantum random-walk search algorithm. Phys. Rev. A 67, 052307 (2003).
Štefaňák, M., Barnett, S. M., Kollár, B., Kiss, T. & Jex, I. Directional correlations in quantum walks with two particles. New J. Phys. 13, 033029 (2011).
Zhang, J., Wang, X. & Zhang, W. Chaotic keyed hash function based on feed forward-feedback nonlinear digital filter. Phys. Lett. A 362, 439–448 (2007).
Rivest, R. The MD5 message-digest algorithm. RFC 1321 http://www.fourmilab.ch/hotbits (1992) (29/6/2015).
Nielsen, M. & Chuang, I. Quantum Computation and Quantum Information. Cambridge University Press, New York, 2000.
Akhavan, A., Samsudin, A. & Akhshani, A. A novel parallel hash function based on 3D chaotic map. EURASIP J. Adv. Signal Process. 2013, 126 (2013).
Akhshani, A. et al. Hash function based on hierarchy of 2D piecewise nonlinear chaotic maps. Chaos, Solitons and Fractals 42, 2405–2412 (2009).
Wei, G., Wang, X. M., He, D. K. & Cao, Y. Cryptanalysis on a parallel keyed hash function based on chaotic maps. Phys. Lett. A 373, 3201–3206 (2009).
Wang, X.-Y. & Zhao, J.-F. Cryptanalysis on a parallel keyed hash function based on chaotic neural network. Neurocomputing 73, 3224–3228 (2010).
López-Ruiz, R., Mancini, H. L. & Calbet, X. A statistical measure of complexity. Phys. Lett. A 209, 321–326 (1995).
Lamberti, P. W., Martin, M. T., Piastino, A. & Rosso, O. A. Intensive entropy non-triviality measure. Physica A 334, 119–131 (2004).
Rosso, O. A., Larrondo, H. A., Martin, M. T., Plastino, A. & Fuentes, M. A. Distinguishing noise from chaos. Phys. Rev. Lett. 99, 154102 (2007).
Eckmann, J. P., Oliffson Kamphorst, S. & Ruelle, D. Recurrence plots of dynamical systems. Europhys. Lett. 4, 973–977 (1987).
Marwan, N., Romano, M. C., Thiel, M. & Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 438, 237–329 (2007).
Shiner, J. S., Davison, M. & Landsberg, P. T. Simple measure for complexity. Phys. Rev. E 59, 1459–1464 (1999).
Martin, M. T., Plastino, A. & Rosso, O. A. Statistical complexity and disequilibrium. Phys. Lett. A 311, 126–132 (2003).
Larrondo, H. A., González, C. M., Martin, M. T., Plastino, A. & Rosso, O. A. Intensive statistical complexity measure of pseudorandom number generators. Physica A 356, 133–138 (2005).
Bandt, C. & Pompe, B. Permutation Entropy: A natural complexity measure for time series. Phys. Rev. Lett. 88, 174102 (2002).
Marwan, N., Wessel, N., Meyerfeldt, U., Schirdewan, A. & Kurths, J. Recurrence plot based measures of complexity and its application to heart rate variability data. Phys. Rev. E 66, 026702 (2002).
Zbilut, J. P. & Webber, C. L. Embeddings and delays as derived from quantification of recurrence plots. Phys. Lett. A 171, 199–203 (1992).
Webber, C. L. & Zbilut, J. P. Dynamical assessment of physiological systems and states using recurrence plot strategies. J. Appl. Physiol. 76, 965–973 (1994).
Benítez, R., Bolós, V. J. & Ramírez, M. E. A wavelet-based tool for studying non-periodicity. Comput. Math. Appl. 60, 634–641 (2010).
Akhshani, A., Akhavan, A., Mobaraki, A., Lim, S.-C. & Hassan, Z. Pseudo random number generator based on quantum chaotic map. Commun. Nonlinear Sci. Numer. Simulat. 19, 101–111 (2014).
Mallat, S. A wavelet tour of signal processing. Academic Press: London, (1999).
Chandre, C., Wiggins, S. & Uzer, T. Time-frequency analysis of chaotic systems. Physica D 181, 171–196 (2003).
Gao, T. & Chen, Z. A new image encryption algorithm based on hyper-chaos. Phys. Lett. A 372, 394–400 (2008).
Refregier, P. & Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 20, 767–769 (1995).
Cheddad, A., Condell, J., Curran, K. & McKevitt, P. A hash-based image encryption algorithm. Opt. Commun. 283, 879–893 (2010).
Yang, Y.-G., Xia, J., Jia, X. & Zhang, H. Novel image encryption/decryption based on quantum Fourier transform and double phase encoding. Quantum Inf. Process. 12, 3477–3493 (2013).
Akhshani, A., Akhavan, A., Lim, S.-C. & Hassan, Z. An image encryption scheme based on quantum logistic map. Commun Nonlinear Sci. Numer. Simulat. 17, 4653–4661 (2012).
Huang, X. L. & Ye, G. D. An image encryption algorithm based on hyper-chaos and DNA sequence. Multimed. Tools Appl. 72, 57–70 (2014).
Shahram, E. G. & Mohammad, E. Chaotic image encryption system using phase-magnitude transformation and pixel substitution. Telecommun. Syst. 52, 525–537 (2013).
L’Ecuyer, P. & Simard, R. J. TestU01: A C library for empirical testing of random number generators. ACM Trans. Math. Soft. 33, 22 (2007).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No.61572053); The Importation and Development of High-Caliber Talents Project of Beijing Municipal Institutions (No.CIT&TCD201304039); The Scientific Research Common Program of Beijing Municipal Commission of Education (No.KM201510005016); The Basic Research Foundation of Beijing University of Technology (Nos.X4007999201501,007000514315501); Jing-Hua Talents Project of Beijing University of Technology(2014-JH-L06); Beijing Natural Science Foundation (Grant No.4152038).
Author information
Authors and Affiliations
Contributions
Y.-G.Y. proposed the theoretical method and wrote the main manuscript text. P.X. made the numerical simulations. R.Y., Y.-H.Z. and W.-M.S. reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Yang, YG., Xu, P., Yang, R. et al. Quantum Hash function and its application to privacy amplification in quantum key distribution, pseudo-random number generation and image encryption. Sci Rep 6, 19788 (2016). https://doi.org/10.1038/srep19788
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep19788
This article is cited by
-
QBIoV: a secure data sharing scheme for the Internet of vehicles based on quantum-enabled blockchain
Quantum Information Processing (2024)
-
Quantum hash function based on controlled alternate lively quantum walks
Scientific Reports (2023)
-
Quantum color image encryption based on controlled two-particle quantum walks
Multimedia Tools and Applications (2023)
-
A discrete cosine transform-based intelligent image steganography scheme using quantum substitution box
Quantum Information Processing (2023)
-
Controlled alternate quantum walk-based block hash function
Quantum Information Processing (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


 . n is the node number of a circle.
. n is the node number of a circle.






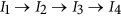 if
if  . Here we take Buddha image as an example (see
. Here we take Buddha image as an example (see