Introduction

Quantum criticality and topology are two of the main impetuses of modern condensed matter physics. Self-similarity of many-electron wave-functions associated with quantum criticality1,2,3 unveils emergent universality of physical observables and topology of the electronic wave-functions manifests itself as various fascinating topological insulators and associated quantized responses4,5,6,7. The two striking characteristics of the wave-function are naturally and inevitably intertwined at topological quantum phase transitions.

Long-range Coulomb interaction between electrons induces striking screening effects near the topological phase transitions. Electronic critical modes and the Coulomb interaction are intrinsically correlated, so non-trivial quantum criticality usually appears8,9,10,11,12,13. For example, quasi-particles lose their stability due to the Coulomb interaction and the ground state becomes quantum critical non-Fermi liquid with emergent full rotational symmetry in quadratic band touching semimetals, which is near three dimensional (3d) topological insulator8.

In two dimensions (2d), the Coulomb interaction becomes more special. It is because the Coulomb potential originally lives in 3d but electrons are confined in 2d. Thus the electrons in 2d feels the dimensionally different interaction, originating from 3d. Since correlation and fluctuation are enhanced in lower dimensions, one may expect stronger interplay between the Coulomb interaction and critical modes in a topological phase transition and indeed we find the novel quantum criticality in a class of 2d topological quantum phase transitions.

Conventional 2d topological phase transitions between two topologically distinct insulators are described by the pseudo-relativistic Dirac fermion theory with Pauli matrices in band index spinor space. Here the topological nature of the transition is captured by the change in the Berry curvature of the wave-function depending on the sign of M and different patterns of opening up band gaps at separate Dirac points represent different topological insulator phases when supplemented with proper symmetries. The long-range Coulomb interaction at the critical point induces intriguing logarithmic modification of the Dirac velocities, so not only rotational symmetry at the critical point emerges but also important interaction effects appear whose structure has been extensively studied in literature14,15 in connection with charge-neutral mono-layer graphenes. We emphasize that the isotropic Coulomb interaction dominates microscopic anisotropy of electrons in this case.

Here we focus on a different class of the topological phase transitions whose electronic Hamiltonian is

With a tuning parameter m, energy spectrum of is . The two phases are determined by the sign of the tuning parameter. With a positve A and , energy spectrum is gapped, so the ground state is an insulator. On the other hand, with , the zero-energy points appear at two points in momentum space, . By expanding the Hamiltonian (1) near these points, we obtain around the point with . Thus the ground state is a 2d Dirac semimetal. Thus, it is clear that our model Hamiltonian describes a phase transition between a (either topological or trivial) insulator and a Dirac semimetal in 2d.

The Hamiltonian (1) has been suggested in various physical systems, ranging from TiO2-VO2 oxide heterostructures16,17,18 and the organic material α-(BEDT-TTF)2I3 under pressure19,20,21 to optical lattice systems22,23,24. For example, in the oxide heterostructure TiO2-VO2 layers16,17,18, there is a metal-insulator transition as the number of layers is changed. At the certain number of layers, the first-principle band structure calculation16,17,18 reveals that there should be the anisotropic semimetal (1). Furthermore, the structure of the Hamiltonian (1) is similar to that of the notorious quantum criticality problem with Fermi surfaces in 2d25,26,27,28,29,30 whose scaling of the dispersion along the radial direction to the Fermi surface is linear in momentum while that along the perpendicular direction is quadratic in momentum. Due to the similarity in dispersions, we expect that our analysis might shed some light on understanding the quantum criticality with Fermi surfaces despite of the finite density of states in the Fermi surface case.

In this work, we show, by using the systematic renormalization group (RG) method, that the long range interaction strongly changes the nature of the eigenstates of the non-interacting Hamiltonian. We find a novel quantum criticality characterized by both anisotropically renormalized and marginal Coulomb interactions which is in sharp contrast to other quantum criticalities. The anisotropic marginal quantum criticality is out of intricate interplay between the long range Coulomb interaction in 2d and the critical electron modes and we emphasize its striking properties by calculating physical observables.

Models with Coulomb Interaction

We start with the theory incorporating the electron Hamiltonian with the long-range Coulomb interaction,

where mediates Coulomb interaction between electrons . The short-hand writing is used. Hereafter, all integrations are defined with the short-distance (or high-energy) ultra-violet (UV) cutoff. is the Fourier transformation of (1) and the bare gauge boson propagator represents the long-range Coulomb interaction. For future convenience, we introduce a dimensionless coupling constant, the fine structure constant , which measures the “strength” of Coulomb interaction.

We investigate the stability of the theory by the lowest order perturbation calculation, in particular, by calculating the bosonic self-energy whose Feynman diagram representation is in Fig. 1(a),

Figure 1
figure 1

Diagrams for (a) the boson self-energy Π(q) and (b) the fermion self-energy .

Here the dotted line represents the boson propagator and the solid line represents the fermion propagator .

Full size image

is used. It is straightforward to evaluate the integral (see the supplementary information I for detail) and we find that

where is the function of the dimensionless parameter . Hereafter, we drop the frequency dependence in the boson self-energy since we are only interested in the instantaneous Coulomb interaction. The full functional form of is not important. Thus we will not present it here and plot it only in the supplementary information I. Instead, the asymptotic behavior of in each direction is extracted

with the numeric constants . Notice that the boson self-energy is independent of the UV cutoff which signal a novel quantum criticality in our system.

It is clear that the perturbation becomes more important than the original bare term along ,

in the limit . Thus we conclude that the action (2) is unstable under the fermion-gauge boson coupling.

The instability from the perturbative calculation often indicates the presence of the stable strong-coupling fixed point which can be accessed by large- analysis with the number of fermion flavors . The large- analysis starts with adding the bosonic self-energy to the boson bare term,

The schematic representation of the inverse of the corrected boson propagator is

The limit recovers the unstable bare action (2) and we investigate the opposite limit where we drop the bare term .

Using this corrected boson propagator, we calculate the fermion self-energy in Fig. 1(b)

obtained by expanding the self-energy near with the UV and IR cutoffs, . Straightforward calculation gives

with the two dimensionless constants, (see supplementary information III for detail). We notice that the instantaneous nature of the Coulomb propagator enforces no vertex correction through the Ward identity.

Therefore, the RG flow equations, i.e., beta functions, for v and α can be derived by changing the ratio, ,

near the strong-coupling fixed point. It is clear from the RG equations that the fine structure constant α decreases with the anomalous dimension of the velocity, . This concludes that the strong-coupling fixed point is unstable.

Our controlled analysis near the two extreme limits (standard perturbation and large- analysis) clearly shows that both the fixed points are unstable. Then it is obvious that the stable fixed point should be in the intermediate regime, which is difficult to access in a fully controlled way. Thus, we study the fixed point with the standard momentum-shell RG and check a posteriori its validity by self-consistency.

In the momentum-shell RG analysis, we remark that the non-analytic dependence of the Coulomb interaction does not receive correction from integrating out higher-momentum modes. Thus, we first keep the seemingly irrelevant term in the boson action,

It turns out that the following three dimensionless parameters determine the RG flows

Evaluating Feynman diagrams in Fig. 1 gives the renormalized action . Here, we use the cutoff scheme such that we integrate along the -directional momentum with after integrating out the -direction momentum and frequency. On integrating out the higher-momentum modes, three parameters are renormalized as

We find that the functions are non-negative near whose specific forms are illustrated in supplementary information IV. The RG flow equations of are

The two fixed points are, and it is easy to show that the former is unstable and the latter is stable. At the stable fixed point , the boson propagator receives a large anomalous scaling dimension, which can be understood as (because is the scaling factor of . Such large anomalous dimension indicates that the momentum-shell RG is not controlled and a priori not reliable.

At the stable fixed point, the effective bosonic action becomes

which is very similar to the large- calculation with one important difference; a new coupling constant with UV cutoff scale naturally enters in contrast to the large- calculation where the coefficient of is (see equation (4)) which depends on the other parameters . Here the new dimensionful parameter appears in the bosonic part at the intermediate coupling regime.

With this intuition in hand, we investigate the stability of the new fixed point by taking equation (8) as the bare boson action and performing the momentum-shell RG near this fixed point. Remarkably, we find that the velocity v and inverse mass A receives the same corrections at the fixed point

The same correction is another evidence for our fixed point to be stable since the ratio appearing in the boson self-energy becomes constant. Notice that the remarkable same correction also appears in Fermi surface quantum criticalities with very different physical reasons which also supports stability of our fixed point26. It is manifest that the gapless excitation structure of our system is completely different from that of Fermi surfaces (lines) in 2d. Only nodal point excitation appears in our system. However, the low energy scaling structures of the two systems are same considering the patch theory of Fermi surfaces in 2d ; one momentum direction has linear scaling while the other one has quadratic scaling. We believe this unexpected similarity is the source of the similar behaviors in the beta functions. It would be very intriguing to find more similarity and difference of two systems’ quantum criticalities, which we leave for future work.

The beta functions around the novel fixed point are

where calculated in the supplementary information V.

We remark that the hard momentum cutoff scheme is only used for simplicity and illustration. It is shown that our results are independent of cutoff schemes in the supplementary information VIII.

The above RG flow structure (9) is unique to this fixed point. The beta functions contain the fine structure constant α in contrast to those of the large- calculation (5) in which α is absent and here both receive the same logarithmic corrections, which are proportional to α. Thus, the fine structure constant α decreases and the fermion only receives the logarithmic corrections, which indicates the fixed point is stable. Naturally, as in mono-layer graphene, marginal Fermi liquid behaviors are expected with higher order corrections31.

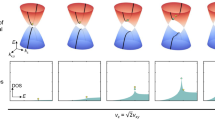
Based on the calculations and intuitions, a schematic RG flow can be deduced as in Fig. 2 which summarizes our main results. Our controlled calculation shows the non-interacting critical point (Non-Int.) and the strong coupling fixed point (S) are unstable and the RG flow comes out of the both points and flow into the intermediate fixed point (QC), which is characterized by the definite anisotropic scaling of bosons and electrons and the single logarithmic corrections to velocity and inverse mass.

Figure 2
figure 2

Proposed RG flow.

The horizontal axis is for the tuning parameter m of the quantum criticality equation (1) and the vertical axis is for the strength of Coulomb interaction. There are two stable fixed points, insulators (‘Ins’) and Dirac semimetal (‘Dirac’). The two unstable critical points are illustrated with dashed circles, non-interacting (‘Non-Int.’) and strong-coupling fixed point (‘S’). And the stable critical point is the filled circle (‘QC’). The critical point is characterized by the definite anisotropic scaling and the logarithmic corrections to mass and velocity. Near the fixed points (Ins, Dirac, QC), one-particle spectrum with the Coulomb interaction is illustrated.

Full size image

Experimental Signatures

We now investigate the physical consequences of both the anisotropy and marginal irrelevance of the renormalized Coulomb potential at the novel intermediate critical point.

First of all, with the beta functions of v and A (9), we can find logarithmic corrections to all physical quantities. The parameters at the temperature scale T are

Here is the bandwidth or the UV cutoff of the theory (1). and are the bare parameters at the highest energy scale . The logarithmic corrections in may be observed in quasi-particle experiments as in graphene, for example, angle resolved photo-emission spectroscopy (ARPES)32 or quantum oscillation.

Furthermore, thermodynamic quantities such as specific heat and compressibility also show logarithmic corrections. Specific heat and compressibility of the unstable free electron fixed point are and in which is the (thermal-averaged) energy density per volume as the function of temperature T and is the density of the electron per volume as the function of chemical potential μ and temperature T. But at the novel fixed point, the logarithmic corrections give

at the temperature T by following the reference14.

Secondly, we can see the effect of the anisotropic renormalization of the gauge boson via the screening charge when a single impurity charge Z is introduced at . At the level of the linear response theory, the screening charge is , in which is the propagator of the gauge boson. We are interested in the directional behaviors of the screening charge and hence define the integrated screening charges and along and . Here we will contrast the extremely different behaviors of the screening charges between the free fixed point and the non-trivial fixed point.

At the free fixed point, we ignore the corrections to the gauge boson propagator and use . Following the straightforward calculation in supplementary information VI, we find whose sign is the opposite of the impurity charge Z.

On the other hand, at the non-trivial anisotropic fixed point in which we use the renormalized boson propagator , we find the asymptotic behaviors of the screening charges

where is the UV cutoff. Here the sign of the screening charge is the same as the impurity charge Z, which is reminiscent of graphene case33.

From the above calculations, we see that the asymptotic scaling behaviors of the screening charges in distance from the impurity along and are surprisingly isotropic. The isotropic scaling in both the directions is originated from the facts that the scaling of is identical to that of and that at the energy scale μ receive the same logarithmic corrections as (9). Hence this isotropic scaling behaviors are truly from the effects of interactions between the electrons and the gauge boson.

Discussion and Conclusion

The presence of the novel fixed point implies that the electrons and gauge bosons are strongly correlated. At low energy, electrons and gauge bosons affect each other, so the Coulomb interaction mediated by the bosons becomes anisotropic and electrons receive back-reaction from the renormalized anisotropic Coulomb interaction. Thus, the Coulomb interaction behaves differently from that of most critical systems where it enforces low-energy isotropy of electronic modes8,14,31,34. Also, notice that the ground state of our fixed point has marginally well-defined quasi-particles as those in graphene, which is in contrast to non-Fermi liquids with non-zero anomalous dimensions. In Table 1, the comparison with other quantum criticality associated with topological phase transitions is summarized.

Table 1 Comparison with the quantum criticalities in various semimetallic systems.
Full size table

Our novel quantum criticality can be experimentally tested in the systems such as VO2-TiO2 heterostructure. Near the critical point, optical conductivity shows anisotropy inherited from the electron band structure. Straightforward calculation with current operators gives

upto logarithmic corrections from the Coulomb interaction (see the supplementary information VII). However, as shown in the previous section, the screening charge due to the charged impurity, which can be measured in principle by scanning tunneling microscopy (STM), shows qualitatively isotropic behaviors. Such discrepancy between the two experiments is a smoking gun of the novel quantum criticality in addition to thermodynamics quantities such as specific heat.

It is worth to mention that disorder scattering in the non-interacting electrons (1) is relevant35, so our results work better for cleaner samples. We expect that there will be an intriguing interplay between the anisotropic Coulomb interaction and impurity scattering at the novel critical point, which we leave for the future problem.

In conclusion, we have investigated the quantum criticality of the anisotropic semimetal which can be thought as the critical point between topological insulators and Dirac semimetal in two spatial dimensions. At the low-energy limit, we found the novel fixed point out of the interplay between critical electron modes and the long-range Coulomb interaction. The non-trivial anisotropic renormalization of the Coulomb interaction and the logarithmic corrections manifest at various physical quantities including screening charge when the impurity charge is introduced. Surprisingly we have shown that the scaling behavior of the screening charge in distance from the impurity is isotropic despite of the underlying anisotropic nature of the system.

Note added : After the completion of the paper, we became aware of the independent work by H. Isobe, B.-J. Yang, A. Chubukov, J. Schmalian and N. Nagaosa [ref. (36)]. Similarity and differences between our work and theirs are discussed in supplementary information.

Additional Information

How to cite this article: Cho, G. Y. and Moon, E.-G. Novel Quantum Criticality in Two Dimensional Topological Phase transitions. Sci. Rep. 6, 19198; doi: 10.1038/srep19198 (2016).