Abstract
Quantum spin Hall (QSH) insulators feature edge states that topologically protected from backscattering. However, the major obstacles to application for QSH effect are the lack of suitable QSH insulators with a large bulk gap. Based on first-principles calculations, we predict a class of large-gap QSH insulators in ethynyl-derivative functionalized stanene (SnC2X; X = H, F, Cl, Br, I), allowing for viable applications at room temperature. Noticeably, the SnC2Cl, SnC2Br and SnC2I are QSH insulators with a bulk gap of ~0.2 eV, while the SnC2H and SnC2F can be transformed into QSH insulator under the tensile strains. A single pair of topologically protected helical edge states is established for the edge of these systems with the Dirac point locating at the bulk gap and their QSH states are confirmed with topological invariant Z2 = 1. The films on BN substrate also maintain a nontrivial large-gap QSH effect, which harbors a Dirac cone lying within the band gap. These findings may shed new light in future design and fabrication of large-gap QSH insulators based on two-dimensional honeycomb lattices in spintronics.
Similar content being viewed by others
Introduction
Topological insulators (TIs)1,2,3,4 have generated intensive research and engineering activities in recent years, because they give an alternative and robust platform for obtaining relativistic and spin-polarized Fermions in the condensed matter system. One of the most interesting phenomena in this realm is the quantum spin Hall (QSH) effect in two-dimensional (2D) structures1,2, characterized by an insulating bulk and gapless edge states at its boundaries due to time-reversal symmetry (TRS), thus providing enticing concepts for novel quantum devices with low energy dissipation3,4. The prototypical concept of QSH effect is first proposed by Kane and Mele in graphene5,6, in which the spin-orbit coupling (SOC) opens a band gap at the Dirac point. However, the associated gap due to rather weak SOC is too small (~10–3 meV), which makes the QSH state in graphene only appear at an unrealistically low temperature. To date, quantized conductance through QSH state has only been experimentally observed in HgTe/CdTe7,8 and InAs/GaSb9,10 quantum wells at the ultralow temperature, which greatly obstructs further experimental studies and possible applications in spintronics.
Generally, a good QSH insulator should be easily synthesized and have a large bulk band gap to realize the spin transport at high temperatures. Controlling the chemical bonding at atomic levels to induce the band inversion by orbital selection3,4 is an efficient way to realize QSH effect8,11,12,13,14,15. 2D materials are advantageous in this respect as their bonding character is relatively easy to modify in post synthesis processes, for example, by surface adsorption. Recently, group-IV honeycomb lattices such as functionalized germanene and stanene16,17 have been reported, with a bulk-gap as large as 0.2–0.3 eV, sufficiently large for practical applications at room temperature. Besides, the strong SOC effect can also be sufficed by group-V heavy elements such as bismuth, which drives nontrivial QSH states18,19. On the other hand, group III-V materials GaAs and GaBi have also reported to be large-gap QSH insulators20,21. Unfortunately, the experiments22 reveal that plasma fluorination and hydrogenation generally increase defects and lattice disorder even under short plasma exposures. Thus, the achievement of these systems with high quality is rather challengeable, demonstrating the detection of QSH effect is difficult in experiments. More recently, an approach to design a large-gap QSH state on a semiconductor surface by a substrate orbital filtering process is also proposed23,24. These large-gap QSH insulators are essential for realizing many exotic phenomena and for fabricating new quantum devices that can operate at room temperature.
Recently, the small molecule functionalization has been the focus to enhance the geometric stability and nontrivial band gap of new 2D films. For instance, Methyl (CH3), another organic molecule, has also been suggested as a promising tool to stabilize 2D systems, such as methyl-functionalized germanane (GeCH3)25 and bismuth (BiCH3)26, to realize large gap QSH insulators. Experimentally, GeCH3 film has been synthesized in recent work27. This raises an interesting question: can the methyl be applied to stabilize group IV and V films and whether their band gap can be enhanced significantly in QSH phase? Motivated by recent works on stanene by zhang et al.17, in our previous works28, we have found that the organic molecule ethynyl (C2H) can be applied to stabilize stanene by decoration on its surface and its band gap in TI states reaches up to 0.3 eV. However, the QSH phase is not intrinsic, but driven by the external strain, thus is unfavorable for practical applications in spintronics. Here, we extend these into ethynyl-derivative functionalized films (SnC2X; X = F, Cl, Br, I), making the experimental observation facile. The SnC2Cl, SnC2Br and SnC2I are all QSH insulators with a bulk gap of ~0.2 eV, while the SnC2H and SnC2F can be transformed into QSH insulator under the tensile strains. The topological characteristic of these films is attributed to s-pxy band inversion related to the honeycomb symmetry, while the effect of SOC is only to open up a large gap. We also propose high-dielectric BN as an ideal substrate for the experimental realization of these films, maintaining its nontrivial topology. These results have potential applications in low-power quantum electronics and may enable topological quantum computing based on Majorana fermions29.
Results and Discussion
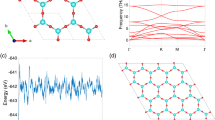
We have performed first-principles calculations of electronic structures and band topology of 2D hexagonal lattices functionalized with ethynyl-derivatives. We first discuss in detail the results of SnC2H and SnC2Br as representative examples. Figure 1(a) shows the geometric structure of 2D SnC2X, which prefers a buckled configuration, with C2X bonding on both sides of stanene in an alternating way (Fig. 1(b)), in analogy to hydrogenated germanene and stanene16,17. In comparison to the pristine stanene, the lattice constant of SnC2X increase slightly by 0.19 ~ 0.06 Å, along with the buckling height between Sn planes decreasing by about 0.14 ~ 0.07 Å, the details as listed in Table 1. The buckling plays a crucial role in the engineering of the band structures in this structure. To confirm the structural stability, we calculate the phonon spectrum along the highly symmetric directions, as shown in Fig. 1(c). One can see that all branches of the phonon dispersion curves have positive frequencies and no imaginary phonon modes are found, confirming the stability of SnC2H film.
To get a preliminary insight into the topological properties, we present the calculated band structures of SnC2H including SOC. At equilibrium state in Fig. 2(a), which shows a semiconductor nature with a direct band gap located at Γ point. By projecting the bands onto different atomic orbitals, we find that the valence band maximum (VBM) at Γ point near the Fermi level is mainly composed of px,y orbitals from Sn atoms with the features of binding states, whereas the conduction band minimum (CBM) is the anti-binding s state. Thus, no inverted band order is observed, suggesting that it is a trivial TI phase. However, if applying the tensile strain (ε = 4%), the s-p band inversion appears, with an indirect-gap of 0.22 eV opened under SOC effect, as illustrated in Fig. 2(b). To demonstrate the 2D TI phase, we calculate the Z2 invariants v, as listed in Table 2. Obviously, the products of the parity eigenvalues at these three symmetry points: Γ (0.0, 0.0), M1 (0.5, 0.0) and M2 (0.0, 0.5) are both 1, while at the M3 (0.5, 0.5) shows −1, which give Z2 = 1. Therefore, it directly confirms the existence of QSH insulator state.
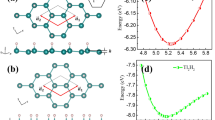
The buckled configuration generally sustain a larger mechanical strain than planner one, thus we explore the variations of electronic structure with respect to the mechanical strain30,31,32,33,34. Here, we employ an external strain on SnC2H maintaining the crystal symmetry by changing its lattices as ε = (a − a0)/a0, where a (a0) is the strained (equilibrium) lattice constants. In what follows, we systematically investigate the effects of both uniaxial and biaxial strains on topological properties of SnC2H. Figure 3(a) presents the variation of nontrivial QSH gap (direct, EΓ) at Γ point and bulk gap (indirect, Eg) as a function of the biaxial strain. One can see that, both the direct and indirect band gaps in TI phase decrease steadily with respect to strain, especially Eg and EΓ being equal to strain beyond 30%. Remarkably, for ε = 3%, we find the largest gap of ~0.33 eV opened at Γ point, along with a global indirect band gap of ~0.22 eV, which is significantly greater than kBT (~26 meV). While the biaxial strain is compressed to ε = −4%, we find that no inverted band order is observed, suggesting that it is a trivial QSH insulator (Fig. 2(c)). On the other hand, we explore the effect of uniaxial strain on the electronic properties, as displayed in Fig. 3(c). Interestingly, we obtain a larger SOC-induced bulk gap as large as ~0.46 eV (ε = 18%), which is almost twice the one of biaxial strain. Further analysis of the parity eigenvalue gives Z2 = 1, which suggests that the uniaxial strain is also efficient way to tune QSH state in these films.
Now, we wish to point out that the ethynyl functionalization in stanene is not the only way to achieve the large-gap QSH state, the same results can be obtained by decorating the surface with otherwise ethynyl-derivatives, such as -C2F, -C2Cl, -C2Br and -C2I. We thus perform calculations for SnC2X (X = F, Cl, Br, I) films to check their topological properties. Table 1 summarizes their lattice constants, Sn-Sn bond lengths and nontrivial gaps at their equilibrium states. Similar to the case of SnC2H, for SnC2F, it is a trivial QSH phase at the equilibrium state, but can be driven to QSH phase at the biaxial tensile strain ε > 2%. However, for the other SnC2X (X = Cl, Br, I) films, they are TI phases at the equilibrium state with Z2 = 1, as listed in Table 2. The global QSH gaps of SnC2Cl, SnC2Br and SnC2I are 0.19, 0.20 and 0.23 eV, respectively, (see Table 1 and supplemental information in Fig. S1), which are sufficiently large for practical application at high temperature.
The calculated band structures of SnC2Br film are presented in Fig. 2(d–f) as a typical model. Obviously, the s-pxy band inversion are still exist, in analogy to the strain-induced QSH phase in SnC2H. Similar results for SnC2F, SnC2Cl and SnC2I films are also observed, as illustrated in Fig. S1. From Fig. 3(b), we also find that the biaxial-strain range of QSH phase is rather large (from −3% to 30%). Interestingly, there are two peaks in the region of the topology phase, in which one peak is 0.34 eV for Eg under 3% strain and another higher peak is 0.61 eV at 28%. Such robust topology makes it easier for experimental realization in spintronics. For uniaxial strain (Fig. 3(c–d)), we consider the effects of uniaxial strain along x direction for SnC2H and SnC2Br. In addition, the detailed evolution of band structure for SnC2H under the uniaxial strain is added into Fig. S2. Band structure calculations indicate that it is still in QSH phase, with a larger bulk gap of ~0.42 eV (ε = 16%). Also, as can be seen in Fig. S3, the systematically investigate the effects of both uniaxial and biaxial strains on topological properties of SnC2F, SnC2Cl and SnC2I, respectively, which are sufficiently tunable ranges of strain for practical applications at high temperature.
The QSH phase should support topologically protected conducting edge states that are helical with the spin-momentum locked by TRS. To demonstrate these edge states explicitly, we take SnC2H and SnC2Br with the external strain ε = 2% and ε = 0%, respectively, to introduce edges on stanene by forming the zigzag-type nanoribbons, as shown in Fig. 4(a). The edge Sn atoms are passivated by hydrogen atoms to eliminate the dangling bonds. The width of the nanoribbon is large enough to avoid interactions between the edge states of the two sides. Figure 4(b,c) show the zigzag-type edge states of SnC2X (X = H, Br) films, where a Dirac point at the Γ point is located inside the band gap with a high velocity of ~1.0 × 105 m/s and ~2.0 × 105 m/s, comparable to that of 5.5 × 105 m/s in HgTe/CdTe quantum well35, both of which are larger than that of 3.0 × 104 m/s in InAs/GaSb quantum well36. Helical edge states are very useful for electronics and spintronics owning to their robustness against scattering. The similar results for the remaining edge states of SnC2X (X = F, Cl, I) are also displayed in Fig. S4. All these band structures maintain topologically protected conducting edge states that are helical, thus providing enticing concepts for novel quantum electronic devices with low energy dissipation.
It is known that GGA method usually underestimates the band gap, we thus carried out test computations based on the hybrid functional HSE0637,38 to assess the robustness of our results within the PBE. The calculated band structures of SnC2X (X = Cl, Br, I) films under the critical strain are presented in Fig. S3 in supplementary information. One can see that the band gap of these films are indeed enhanced. However, the s-px,y band order is not changed and in agreement with those obtained from PBE, indicating the PBE results are qualitatively reasonable and reliable.
To better understand the physical origin of QSH states, we next do an orbital analysis around the Fermi level for SnC2X films. Figure 5 presents the band evolution at Γ point, in which the energy levels near the Fermi level are mainly composed of Sn-5s and Sn-5px,y orbitals. Thus, the chemical bonding between Sn-Sn atoms makes them split into the bonding and antibonding states, i.e., s± and px,y±, where the superscripts + and − represent the parities of corresponding states, respectively. At zero strain in Fig. 5(a), the bands near the Fermi level are contributed by the px,y+ and s−, with the s− being above the px,y+, indicating a normal band order, as shown in SnC2H. When considering the tensile strain, as seen in Fig. 5(b), the enlarged lattice constant weakens the interaction between Sn atoms, decreasing the splitting between the bonding and antibonding states, which lowers s− level and raises px,y+ level accordingly. Thus, depending on the strength of interatomic coupling, the band gap of SnC2H can be continuously reduced, with the band order being reversed at critical point, making it a topological insulator with Z2 = 1. Taken together, the level crossing leads to a parity exchange between occupied and unoccupied bands, inducing a TI phase transition. While for SnC2Br, the lattice constant at equilibrium state is equal to strain-induced SnC2H (ε = 4%), thus it is a QSH insulator. As a result, the s-p band inversion39 is a strong indication of the existence of topologically nontrivial phases. Herein, we must point out that, although the s-px,y band inversion is caused mainly by the strength of interatomic coupling, the SOC is still indispensable because it makes the px,y+ orbital split into p+x + iy, ↑ & p+x−iy, ↓ and p+x−iy, ↑ & p+x+iy, ↓, opening a larger band gap. In previous works, the topological states are usually originated from pz system such as graphene and silicene of which the nontrivial gaps are often very small40. but in our cases, the topological states with larger gaps are obtained due to the contribution of px,y orbitals on Sn atoms, where the large SOC is from the on-site SOC, instead of the next-nearest-neighbor SOC in the pz cases40. These results emphasize the importance of orbital selection for topological materials.
On the experimental side, choosing the suitable substrate material is a key factor in device application, since a free-standing film must eventually be deposited or grown on a substrate. It is known that the QSH features in pristine graphene and germanene12,13,14,15,16,17 are easily destroyed by the substrate. In contrast, although the TI phase of SnC2X films are obtained in free-standing structure, their nontrivial QSH would be robust when they are on the substrate, because their band inversion occurs at Γ point rather than at K point, as well as the full saturation of Sn-pz orbitals ensures a weak interaction with the substrate. Here, we select h-BN as a possible substrate to form SnC2Br@BN heterostructure (HTS), where the lattice mismatch is only about 1.19% (SnC2Br) in comparison to h-BN(2 × 2) sheet, showing that they are feasible to grown on the h-BN substrate. To correctly describe the effect of van der Waals (vdW) interaction, we employ a dispersion-corrected DFT method (optB88-vdW)41,42, which has been demonstrated to reliably describe 2D HTSs. Thus, the optimized distance (d) between adjacent layers is 3.278 Å. The calculated binding energy is found to be −71 meV, suggesting a typical vdW HTS. In Fig. 6(c), we present the corresponding band structure for SnC2Br film. Bader analysis43 indicates no charge transfer between adjacent layers, thus the states near the Fermi level are mainly determined by SnC2Br film. In comparison to the free-standing film, little difference is observed between them. As a result, it is indeed a robust QSH insulator with band inversion not being affected by the h-BN substrate. Similar electronic properties of SnC2X@BN (X = H, F, Cl, I) HTSs are obtained, as shown in Fig. S6.
To conclude, on the basis of first-principles calculations, we predict a class of new QSH insulator of SnC2X films with sizable bulk gaps, making the experimental observation facile. Noticeably, the SnC2Cl, SnC2Br and SnC2I are all QSH insulators with global gaps of ~0.2 eV, while the SnC2H and SnC2F can be transformed into QSH insulator under the tensile strains. This large-gap opening is mainly attributed to the result of the strong SOC related to the px and py orbitals of Sn atoms at Γ point, significantly different from that of the pz orbital as in pristine group IV ones. A single pair of topologically protected helical edge states are established for the edge of these systems with the Dirac point locating at the bulk band gap and their QSH states are also confirmed with Z2 = 1. Also, these films on h-BN substrate are observed to support a nontrivial large-gap QSH, which harbors a Dirac cone lying within the band gap. These findings may shed new light in future design and fabrication of large-gap QSH insulators based on 2D honeycomb lattice in spintronics.
Methods
To study the structural and electronic properties of SnC2X films, we employed state-of-the-art ab initio simulations, based on density functional theory (DFT) as implemented in VASP44,45. We used the generalized gradient approximation for the exchange and correlation potential, as proposed by Perdew-Burk-Ernzerhof (PBE)46, the projector augmented wave potential (PAW)47 to treat the ion-electron interactions. The energy cutoff of the plane waves was set to 500 eV with the energy precision of 10−6 eV. The Brillouin zone was sampled by using a 21 × 21 × 1 Gamma-centered Monkhorst-Pack grid. The vacuum space was set to 20 Å to minimize artificial interactions between neighboring slabs. SOC was included by a second vibrational procedure on a fully self-consistent basis. With the optimized structures, the more sophisticated HSE06 hybrid functional37,38 was used to check the corresponding results of the systems. The phonon spectra were calculated using a supercell approach within the PHONON code48. To determine the Z2 index of the inversion symmetric 2D materials, the invariants v can be derived from the parities of wave function at the four TRIM points Ki, namely one Γ point and three equivalent M points in the Brillouin zone. The topological invariant ν was determined based on the Fu-Kane’s formula49:

where δ is the product of parity eigenvalues at the TRIM points, ξ = ±1 are the parity eigenvalues and N is the number of the occupied bands. According to the Z2 classification, ν = 1 characterizes a QSH insulator, whereas ν = 0 represents a trivial band topology.
Additional Information
How to cite this article: Zhang, R.-w. et al. Room Temperature Quantum Spin Hall Insulator in Ethynyl- Derivative Functionalized Stanene Films. Sci. Rep. 6, 18879; doi: 10.1038/srep18879 (2016).
References
Yan, B. & Zhang, S. Topological Materials. Rep. Prog. Phys. 75, 096501 (2012).
Moore, J. E. Majorana’s Wires. Nat. Nanotechnol 8, 194 (2013).
Song, Z. et al. Quantum spin Hall insulators and quantum valley Hall insulators of BiX/SbX (X = H, F, Cl and Br) monolayers with a record bulk band gap. NPG Asia Mater. 6, e147 (2014).
Qi, X. & Zhang, S. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011).
Kane, C. L. & Mele, E. J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 95, 226801 (2005).
Kane, C. L. & Mele, E. J. Z2 Topological Order and the Quantum Spin Hall Effect. Phys. Rev. Lett. 95, 146802 (2005).
Bernevig, B. A., Hughes, T. L. & Zhang, S. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science. 314, 1757 (2006).
König, M. et al. Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science 318, 766 (2007).
Du, L., Knez, I., Sullivan, G. & Du, R. Robust Helical Edge Transport in Gated InAs/GaSb Bilayers. Phys. Rev. Lett. 114, 096802 (2015).
Liu, C. et al. Quantum Spin Hall Effect in Inverted Type-II Semiconductors. Phys. Rev. Lett. 100, 236601 (2008).
Qi, X. & Zhang, S. The quantum spin Hall effect and topological insulators. Rhys. Today 63, 33 (2010).
Fu, L., Kane, C. L. & Mele, E. J. Topological Insulators in Three Dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438 (2009).
Wu, S., Shan, G. & Yan, B. Prediction of Near-Room-Temperature Quantum Anomalous Hall Effect on Honeycomb Materials. Phys. Rev. Lett. 113, 256401 (2014).
Tang, P. et al. Stable two-dimensional dumbbell stanene: A quantum spin Hall insulator. Phys. Rev. B 90, 121408 (2014).
Si, C. et al. Functionalized Germanene as a Prototype of Large-gap Two-dimensional Topological Insulators. Phys. Rev. B 89, 115429 (2014).
Xu, Y. et al. Large-Gap Quantum Spin Hall Insulators in Tin Monolayers. Phys. Rev. Lett. 111, 136804 (2013).
Liu, C. et al. Topological Phase Transitions in Half-hydrogenated Bi Honeycomb Monolayers. Phys. Rev. B 90, 085431 (2014).
Jin, K. H. & Jhi, S. H. Quantum Anomalous Hall and Quantum Spin-Hall Phases in Flattened Bi and Sb Bilayers. Sci. Rep. 5, 8426 (2015).
Li, L., Zhang, X., Chen, X. & Zhao, M. Giant Topological Nontrivial Band Gaps in Chloridized Gallium Bismuthide. Nano Lett. 15, 1296 (2015).
Zhao, M., Chen, X., Li, L. & Zhang, X. Driving a GaAs Film to a Large-gap Topological Insulator by Tensile Strain. Sci. Rep. 5, 8441(2015).
Wu, J. et al. Controlled Chlorine Plasma Reaction for Noninvasive Graphene Doping. J. Am. Chem. Soc. 133, 19668 (2011).
Zhou, M. et al. Formation of quantum spin Hall state on Si surface and energy gap scaling with strength of spin orbit coupling. Sci. Rep. 4, 7102 (2014).
Zhou, M. et al. Epitaxial growth of large-gap quantum spin Hall insulator on semiconductor surface. PNAS 111, 14378 (2014).
Ma, Y. et al. Strain-induced quantum spin Hall Effect in methyl-substituted germanane GeCH3 . Sci. Rep. 4, 7297 (2014).
Ma, Y. et al. Robust Two-Dimensional Topological Insulators in Methyl-Functionalized Bismuth, Antimony and Lead Bilayer Films. Nano Lett. 15(2), 1083 (2015).
Jiang, S. et al. Improving the stability and optical properties of germanane via one-step covalent methyl-termination. Nat. Commun. 5, 3389 (2014).
Zhang, R. et al. Ethynyl-functionalized stanene film: a promising candidate as large gap quantum spin Hall insulator. New J. Phys. 17, 083036 (2015).
Tsai, W. et al. Gated Silicene as a Tunable Source of Nearly 100% Spin-Polarized Electrons. Nat. Commun. 4, 1500 (2013).
Zhu, Z., Cheng, Y. & Schwingenschlögl, U. Topological phase transition in layered GaS and GaSe. Phys. Rev. Lett. 108, 266805 (2012).
Li, Y. & Wu, C. High-dimensional topological insulators with quaternionic analytic Landau levels. Phys. Rev. Lett. 110, 216802 (2013).
Murakami, S., Nagaosa. N. & Zhang, S. Dissipationless quantum spin current at room temperature. Science 301, 1348 (2003).
Zhao, L., Liu, J. W., Tang, P. Z. & Duan, W. H. Design of Strain-engineered Quantum Tunneling Devices for Topological Surface States. Appl. Phys. Lett. 100, 131602 (2012).
Ma, Y., Dai, Y., Yu, L., Niu, C. & Huang, B. Engineering a Topological Phase Transition β-InSe via Strain. New J. Phys. 15, 073008 (2013).
Konig M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 1148047 (2007).
Du, L., Knez, I., Sullivan, G. & Du, R. R. Robust Helical Edge Transport in Gated InAs/GaSb Bilayers. Phys. Rev. Lett. 114, 096802 (2015).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. J. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207 (2003).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. J. Erratum: Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 124, 219906 (2006).
Zimmermann, H., Keller, R. C., Meisen, P. & Seelmann-Eggebert, M. Growth of Sn Thin Films on CdTe (111). Surf. Sci. 904, 377 (1997).
Qiao, Z. et al. Quantum anomalous Hall effect in graphene proximity coupled to an antiferromagnetic insulator. Phys. Rev. Lett. 112, 116404 (2014).
Klimeš, J., Bowler, D. R. & Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter. 22, 022201 (2010).
Klimeš, J., Bowler, D. R. & Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 83, 195131 (2011).
Bader, R. F. W. A quantum theory of molecular structure and its applications. Chem. Rev. 91, 893 (1991).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Zimmermann, H., Keller, R. C., Meisen, P. & Seelmann-Eggebert, M. Growth of Sn thin films on CdTe (111). Surf. Sci. 904, 377 (1997).
Fu, L. & Kane, C. L. Topological Insulators with Inversion Symmetry. Phys. Rev. B 76, 045302 (2007).
Acknowledgements
We would like to thank Dr. Hongbin Zhang for useful discussions. This work was supported by the National Natural Science Foundation of China (Grant No. 11274143, 11434006, 61172028 and 11304121) and Research Fund for the Doctoral Program of University of Jinan (Grant no. XBS1433).
Author information
Authors and Affiliations
Contributions
R.Z. and C.Z. conceived the study and wrote the manuscript. R.Z. and S.L. performed the first-principles calculations. S.Y. gave us further discussion. W.J. and S.H. calculated the phonon spectrum. P.L. prepared Figures 1–3, P.W. and F.L. prepared Figures 4–6. All authors read and approved the final manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhang, Rw., Zhang, Cw., Ji, Wx. et al. Room Temperature Quantum Spin Hall Insulator in Ethynyl-Derivative Functionalized Stanene Films. Sci Rep 6, 18879 (2016). https://doi.org/10.1038/srep18879
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep18879
This article is cited by
-
Stanene: A good platform for topological insulator and topological superconductor
Frontiers of Physics (2020)
-
Asymmetric hydrogenation-induced ferromagnetism in stanene nanoribbons considering electric field and strain effects
Journal of Materials Science (2018)
-
First-Principles Calculations of van der Waals and Spin Orbit Effects on the Two-Dimensional Topological Insulator Stanene and Stanene on Ge(111) Substrate
Journal of Superconductivity and Novel Magnetism (2018)
-
Two-Dimensional Large Gap Topological Insulators with Tunable Rashba Spin-Orbit Coupling in Group-IV films
Scientific Reports (2017)
-
Quasiparticle and optical properties of strained stanene and stanane
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.