Abstract
Experimental investigation of electron-ion coupling and electron heat capacity of copper in warm and dense states are presented. From time-resolved x-ray absorption spectroscopy, the temporal evolution of electron temperature is obtained for non-equilibrium warm dense copper heated by an intense femtosecond laser pulse. Electron heat capacity and electron-ion coupling are inferred from the initial electron temperature and its decrease over 10 ps. Data are compared with various theoretical models.
Similar content being viewed by others
Introduction
Under extreme temperature and pressure conditions, normal matters behave abnormally and often regulates physical processes in the stars and large planets1, inertial confinement fusion2 as well as the applied processes of laser machining and ablation3. As an example of such extreme conditions, the warm dense matter (WDM) regime represents the state between condensed matter and plasma, where the thermal energy is comparable to the Fermi energy and the ions are strongly coupled4. As an intermediate state of matter between the well-defined disciplines of condensed matter and plasmas, investigation of the WDM regime provides key understanding of non-equilibrium phase transitions and energy relaxation processes in the extreme conditions. However, the complicated interplay of the physical processes in WDM creates difficulty for theoretical description. In addition, the extremely high temperature and pressure conditions associated with WDM create significant challenges for detailed experimental studies5.
Most experimental methods for generating WDM put energy into either the electrons or ions. The material then evolves toward equilibrium. Femtosecond laser excitation or laser generated proton beam heating of thin metal foils are widely used techniques6,7,8,9,10,11,12,13,14. Initially, a strongly non-equilibrium state is created and then energy is transferred from the hot electrons to the cold lattice. However, the fast relaxation dynamics (typically on a ps time scale) makes the measurement of WDM thermophysical properties, such as heat capacity and electron-ion coupling, extremely difficult. Instead, well-known thermodynamic data or theoretical descriptions based on either plasmas or solids have often been adopted without rigorous experimental validation6,7,8.
For strongly heated fluid / plasma systems, the energy relaxation processes are often modeled through direct two-particle scattering or ion acoustic modes15,16. Generally, the relaxation times estimated by such models taking into account the collective behavior of coupled modes are much longer than early predictions17,18 and strong indications of such longer relaxation times are found in some experiments19,20. On the other hand, Lin et al. presented the computational study of the temperature - dependent thermophysical properties of various metals irradiated by an intense femtosecond laser pulse21,22. In this work, it was included a high temperature Fermi distribution and electron density-of-states (DOS) to calculate electron heat capacities, the electron-phonon couplings and chemical potentials of high-temperature metals showed large deviations from the widely used free-electron models21. A series of investigations have used Lin et al.’s calculations to interpret experimental data for optical conductivity and electron diffraction in WDM regime10,12,14. However, applying these results requires caution because they assume the DOS of solid-state materials and the room temperature phonon spectra. The consideration of non-equilibrium electron distributions is also lacking. Therefore, direct measurements of thermodynamic properties in the WDM regime are required.
In this paper, we present an experimental investigation of the electron heat capacity and the electron-ion relaxation of copper in warm and dense conditions. With the strong femtosecond optical excitation of a tamped copper nano foil, the initial non-equilibrium warm dense copper (WDCu) states are created and then advance toward equilibrium via energy exchange between the two sub-systems at a constant density. Utilizing picosecond x-ray absorption spectroscopy, the temporal evolution of electron temperatures of WDCu is determined. From the initial value and the decrease of the electron temperature, the electron heat capacity and the electron-ion coupling are inferred. The experimental results are compared with Lin’s model as well as with new calculations using the high-temperature liquid DOS.
Experimental Setup
For the experiment performed at the beamline 6.0.2 of the Advanced Light Source (ALS), we employed the femtosecond laser pump - picosecond x-ray probe technique [Fig. 1]. Details of setup are described in the references23. The sample is a 70 nm thick foil of copper coated with 100 nm silicon-dioxide layers on both sides. Reflection and transmission measurements of the Ti:sapphire laser pulse (800 nm, 150 fs) in the experimental geometry indicate that 80 ~ 95% of incident laser energies are transmitted through the silicon-dioxide layer and the absorbed laser fluences to copper sample are estimated to be 0.32 ~ 0.60 J/cm2 depending on the pulse energies. Since the femtosecond pulse heats the sample isochorically, corresponding energy densities Ed are 3.5 ~ 6.5 × 106 J/kg.
Under these conditions, the temperature of the sample will be of the order of an electron volt (eV), which is higher than the melting and boiling points. The high temperature fluid will undergo expansion dynamics and the expansion speed of the surfaces of bare sample is estimated to be an order of sound speed (~103 m/s). This hydromotion poses a challenge to the experiment that requires a well-defined density. Previous experiment showed that after ~10 ps, isochoric conditions no longer hold and expansion may affect the sample temperature12. Therefore, the sample is “tamped” in order to delay the expansion of the foil24. The tamping silicon dioxide layers have a large band gap and prevent the copper foil from expanding on a time scale 2d/v ~ 30 ps, where d = 100 nm is the thickness of the tamping layer and v ~ 6000 m/s is the sound speed in SiO2 at ambient conditions. This delay of the expansion allows us to observe the equilibration dynamics of warm dense copper at a constant volume and density.
X-ray Absorption Near Edge Spectroscopy (XANES) at the copper L edge is performed using broadband 70 ps x-ray pulses from an undulator source. Transmitted x-rays are dispersed by a spectrometer and detected by an x-ray streak camera. Spectral and temporal resolutions are 1 eV and 2 ps, respectively. The streak camera records a series of XANES spectra during the x-ray pulse duration.
Results
TR-XANES and electron temperature measurement
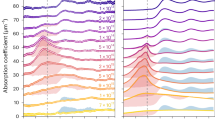
Figure 2(a,b) exhibit typical time-resolved (TR) XANES spectra measured at different energy densities. For comparison, the ambient spectrum is also presented. The strong red shift of the L edge for WDCu is a consequence of the elevated electron temperature. For Cu, the high-energy edge of the 3d band is located 2 eV below the Fermi level. Therefore, Fermi distributions of 1 ~ 2 eV electron temperatures can generate significant unoccupied states in the 3d band and 2p → 3d photo-absorption is allowed. The peaks at 930 and 950 eV represent these transitions with different initial angular momentums, 3/2 and 1/2. Note that the pre-edge peaks are very prominent in this work compared to the data in the previous work12. In this work, much stronger laser pulses created higher temperature conditions and more unoccupied d-states. In addition, an improved spectral resolution allows us to resolve clearly peaks and structures near the absorption edge for both ambient and warm dense spectra.
XANES and electron temperature.
Determination of electron temperature of WDCu by comparison of the experimental XANES (black solid curve) and calculations (blue). 6.5 MJ/kg at 2 ps (a) and 3.5 MJ/kg at 4 ps (b). For comparison, the ambient Cu spectrum is also shown (double dotted line). (c) Calculated warm dense XANES at various electron temperatures. (d) High temperature liquid and ambient solid Cu density of states used to calculate the Fermi distribution functions, which in turn, were used to calculate the XANES in c. (e) Evolution of electron temperatures in WDCu. Three different laser fluencies are irradiated on 70 nm copper foils. In the two temperature description, electrons and ions are equilibrated after ~10 ps. Final temperatures are approximately 13,000 K, 11,850 K and 6,400 K, respectively.
Using the electron DOS of high temperature liquid copper12, warm dense XANES spectra are calculated at various electron temperatures and presented in Fig. 2(c). Details of the calculations are described in the Method section. The series of spectra reproduce the essential changes at the L edges observed in the experiment. The higher the electron temperature, the stronger is the absorption seen near 930 and 950 eV. The height and width of these peaks are sensitive to the electron temperature. Hence, with the proper adjustment of electron temperature and corresponding Fermi distribution in the liquid DOS, good agreement between the calculated and experimental XANES spectra can be obtained [Fig. 2(a,b)].
From XANES spectra at different delays, we determine how the electron temperature of warm dense copper evolves at various energy densities [Fig. 2(e)]. Although the initial energy deposition (3.5 ~ 6.5 MJ/kg) happens at t = 0, due to the time response of detector, the peak temperatures are always observed at 2 ps, which is the temporal resolution of the experiment. At t = 0, the observed temperatures represent a sampling of both the ambient (t < 0) and warm dense (t > 0) states.
The sample thickness is matched with the electron mean-free-path at the Fermi level (70 nm)25. It is considered that the thermal gradient across the thickness is minimal and the heat transfer scenario is simplified. The decreasing electron temperature is primarily due to the energy transfer from the hot electrons to the initially cold ions. Figure 2(e) shows that for all three energy densities, equilibrium is obtained within a time scale of 10 ps. The importance of isochoric conditions obtained with the tamping layers is seen in the bottom panel of Fig. 2(e) by the comparison with data from the reference12. Whilst the initial dynamics up to ~6 ps are similar, at longer time delays, the electron temperature in the previous work decreases further. A temperature of ~4,000 K was reached, which is ~30% lower than in the present experiment. Hydrodynamic expansion might have caused this additional cooling.
Electron and ion heat capacities
From the data in Fig. 2(e) and the framework of the two-temperature model (TTM), which is widely used to describe the non-equilibrium systems created by femtosecond laser pulses, we attempt to determine the electron heat capacity and electron-ion coupling at high temperatures.
The time scale of the energy deposition by the laser pulse, ~150 fs is much shorter than the time resolution of the streak camera and the time scale of electron – ion equilibration. Thus, we assume the initial energy from a delta-function like laser pulse is deposited into only electrons creating a high temperature Fermi distribution instantly. At this stage, energy deposition to the lattice is not considered. Without a good prior knowledge of energy relaxation in this regime, the electron temperature is considered to decrease exponentially. The temperature data in Fig. 2(e) are fit with a causal exponential function (0, for t < 0 and a × exp(–t/τ) + b, for t > 0) convolved with the detector response. Figure 3(a) shows an example of such a fit for the 5.3 MJ/kg energy density. The initial electron temperature (a + b), is determined as 19,800 K. For three different energy densities, all fitting results are summarized in the Table 1. The initial electron temperatures for three cases are shown in the Fig. 3(b) [red circle]. For comparison, the initially absorbed energy density in the electron system, Ed(Te) = ∫ f(ε,μ,Te)g(ε)εdε, is calculated using both the WDM and ambient density of states, where f, g, ε, μ are the electron distribution, density of states, electron energy and chemical potential, respectively. It is noted that the WD Cu is in the liquid phase. Overall, with a given Ed, the electron temperatures calculated with the WDM DOS are lower than with the ambient DOS and in closer agreement to the experiment.
Electron and ion heat capacities.
(a) Fitting of electron temperatures with a causal exponential function for the energy density 5.3 MJ/kg. (b) Initial electron temperatures vs. absorbed energy densities. Experiments (red hexagons) and approximations based on WDM and solid DOS. Final temperatures vs. absorption energy densities (blue squares) are also shown. (c) Electron heat capacity at around 20,000 K (red hexagon). Electron heat capacities calculated based on WDM, solid DOS and free electron model. Ion heat capacity vs. temperature (blue square) at around 10,000 K is also determined.
The theoretical predictions of the temperature dependent electron heat capacity are also presented in the Fig. 3(c). The Sommerfeld expansion Ce(Te) = γTe and Ce(Te) = ∫ ∂f/∂Teg(ε)εdε with solid Cu DOS are from the refs 21,26. In addition, we also calculated Ce(Te) with the liquid DOS. Experimentally, it is hard to determine a temperature dependent heat capacity function with the three data points in Fig. 3(b). Instead, we made a linear fit in the temperature range of 15,000–23,000 K and determined Ce at around 20,000 K to be 380 ± 80 J/kg·K. The result is clearly several-fold larger than the linear dependence, γTe and validates the argument of Lin et al. that the details of a material’s electronic structure should be included in a model of the high temperature heat capacity21.
The predicted heat capacity based on the liquid DOS provides a good agreement with the experimental data. But within the present uncertainty, the ambient DOS curve cannot be excluded. Further investigations with improved time resolution will be required.
The analysis presented above describes the transient non-equilibrium dynamics and electronic heat capacity in the vicinity of 20,000 K. We note that the thermally equilibrated electron-ion state reached after 10 ps (Fig. 2(e) and the third column of Table 1) can be independently used to determine the total heat capacity in the temperature range around 10,000 K (blue squares in Fig. 3(b)). From a linear fit of equilibrium temperatures and deposited energy densities, we obtain a specific heat of 440 ± 100 J/kg·K at around 10,000 K. A common assumption in equation of state modeling is that the heat capacity is the sum of electronic Ce and ionic Ci contributions. By using the model electronic heat capacity of Lin at 10,000 K as shown in Fig. 3(c), the ionic heat capacity, Ci = 170 ± 100 J/kg·K is obtained. For reference, it corresponds to an ionic heat capacity 1.3 kB/atom, near ideal gas heat capacity and lower than Dulong-Petit. Due to possible heat loss and expansion in the scale of 10 ps, the obtained value might be an underestimation of the heat capacity. This result, however, can be important to constrain the thermodynamic models of dense liquids in this largely unexplored range of temperatures27.
Electron – ion coupling
The temperature dependent electron-ion coupling is also determined from the electron temperature, Te(t) = a exp(−t/τ) + b and temperature-dependent electron heat capacity, Ce. For the three energy densities, 3.5, 5.3 and 6.5 MJ/kg, the time constants, τ are 2.8 ± 0.4, 3.4 ± 0.7 and 3.3 ± 1.0 ps respectively. Placing Te(t) into the set of TTM equations, the time-dependent electron-ion coupling can be obtained as followings

where εi(t) = ∫ Ce[Te(t)]/ρ a/τ exp(−t/τ) dt and ρ are the ion energy density and the mass density respectively.
For the electron temperature, the measured values in the Fig. 2(e) are used. Here, we note that G is proportional to the derivative of Te. Within the given experimental accuracy, the small temperature variation after 8 ps is insufficiently determined. Therefore, the electron temperatures and their change at 2, 4 and 6 ps are used. For the electron heat capacity, Ce(Te) is required over the temperature range of the cooling sample. In the previous section, we determined Ce near 20,000 K and validated the DOS dependent heat capacity. Here we adopt the calculated Ce(Te) based on the WDM DOS.
For three energy densities, the G values for electron temperatures at 2, 4 and 6 ps are plotted in the Fig. 4. The electron-ion couplings are strongly dependent on electron temperature in 6,000 ~ 10,000 K range, but relatively unchanged in 10,000 ~ 20,000 K. Overall, they are found to be 4 ~ 6 × 1017 W m−3 K−1, which are a factor of 4 ~ 6 greater than the known electron-phonon coupling of solid copper, G0 = 1017 W m−3 K−1 28.
Electron – ion couplings of warm dense copper.
(a) The G obtained by Eq. (1) at 2, 4 and 6 ps for three different energy densities are displayed at the corresponding electron temperatures together with electron-phonon coupling calculations using Eq. (2) with both liquid DOS and ambient solid DOS21. For comparison, the electron-phonon coupling constant of solid Cu is also shown28.
We have calculated the electron-ion coupling parameter using the following relation from the ref. 21 with both the ambient and liquid density of states.

where G0 is  . In this expression,
. In this expression,  is the second moment of the phonon spectrum29 and λ is the electron –phonon mass enhancement parameter30. Overall, both curves show a similar trend, that in the range of 5,000~ 10,000 K, G(Te) rapidly increases and then varies slowly in >10,000 K.
is the second moment of the phonon spectrum29 and λ is the electron –phonon mass enhancement parameter30. Overall, both curves show a similar trend, that in the range of 5,000~ 10,000 K, G(Te) rapidly increases and then varies slowly in >10,000 K.
Compared with the experiment in the high temperature range (>10,000 K), the WDM calculations provide a good agreement with the data (~ 5 × 1017 W m−3 K−1). The ambient DOS predicts about 20% higher coupling than the measurement and WDM DOS. In the lower temperature range (<10,000 K), a strong temperature dependency is well reproduced, but both calculations show lower values than the measurement.
Two points should be noted here. First, the experimental time resolution, 2 ps, is slower than a typical time scale of lattice disordering. Therefore experimental data at 2 ps may include multiple phases i.e. solid, liquid and their mixtures. In particular for the case of <10,000 K, the contributions from lower temperature phases would be greater. For the proper description of this complicate regime, accurate knowledge about non-equilibrium melting process would be required. Second, for the Eq. (2), the room temperature lattice and a relevant phonon spectrum are assumed21. A good agreement with our interpretation of experimental data using a single exponential fitting may indicate that the coupling between the electrons and low-temperature phonon are still a major pathway of energy exchange even for warm dense condition of copper. Future research with higher time resolution would allow high precision measurements of the electron heat capacity and election-ion coupling at various temperatures.
Discussion
In this paper, we have presented the experimentally determined electron heat capacity and electron-ion relaxation of warm dense copper heated by an intense femtosecond laser pulse. The evolution of electron temperature was measured using the picosecond x-ray absorption spectroscopy technique. The electron heat capacity and electron-ion relaxation were determined from the initial electron temperatures and their decrements. Comparisons with the thermal properties of ambient copper and various theoretical predictions confirmed that these properties are sensitive to electron temperature and details of electronic structure. Both quantities exhibited the best agreement with the calculations including high temperature electron distributions and the liquid density of state, albeit the ambient DOS could not be excluded. Finally, it is noted that recent x-ray free electron laser (XEFL) based experiments have demonstrated the possibility to study the lattice disorder and ion temperature in warm dense conditions31,32 and to perform ultrafast XANES measurements33,34. Combining ultrafast x-ray spectroscopy and diffraction/scattering, future investigations utilizing XFELs would be able to reveal the detailed dynamics of both the electronic and ionic systems.
Method
DFT-MD and XANES calculations of high temperature liquid Cu
In order to determine the electron temperature from the XANES measurement, first principle density functional theory - molecular dynamic (DFT-MD) simulations and ab-initio derived dipole-matrix elements calculation for liquid copper at the ionic temperature of 3800 K were performed. The atomic configurations for Cu were generated first principles using the quantum-espresso package35. A supercell containing 32 Cu atoms was used and several picoseconds of MD simulations were performed after the equilibration process. A plane wave expansion was performed with Ecut = 40 Ry and an ultrasoft pseudopotential was used to describe the electron-ion interaction. The Perdew-Burke-Ernzerhof generalized gradient approximation (PBEGGA) exchange correlation functional was used to approximate the many-body exchange correlation effect.
For selected uncorrelated atomic configurations, dipole matrix elements were calculated using the prescription described in ref. 36. An average was taken over the matrix elements for different Cu atoms in the supercell. As was discussed in the previous study, the profile of Cu L-edge dipole-matrix is not very sensitive to the ionic temperature in the range of this work, reflecting the metallic bonding of copper. However, the XANES, which is a product of dipole matrix and the Fermi distribution function, is sensitive to the electron temperature near the absorption edge reflecting the change of the Fermi distribution. In particular, at higher Te (>1 eV), where electrons in d-bands are excited (partially unoccupied), x-ray excitations of the Cu 2p electrons into the d-bands become possible, leading to the development of a sharp absorption peak near the edge.
Additional Information
How to cite this article: Cho, B. I. et al. Measurement of Electron-Ion Relaxation in Warm Dense Copper. Sci. Rep. 6, 18843; doi: 10.1038/srep18843 (2016).
References
Daligault, J. & Gupta, S. Electron–Ion Scattering in Dense Multi-Component Plasmas: Application to the Outer Crust of an Accreting Neutron Star. Astrophys. J. 703, 994 (2009).
Glenzer, S. H. et al. Symmetric Inertial Confinement Fusion Implosions at Ultra-High Laser Energies. Science 327, 1228–1231 (2010).
Chan, J. W., Huser, T. & Risbud, S. Structural changes in fused silica after exposure to focused femtosecond laser pulses. Opt. Lett. 26, 1726 (2001).
Lee, R. W. et al. Plasma-based studies with intense X-ray and particle beam sources. Laser Part. Beams 20, 527–536 (2002).
Basic Research Needs for High Energy Density Laboratory Physics (ed. E. Rothman). Ch 6, 85 (US DOE report 2010).
Ng, A., Ao, T., Perrot, F., Dharma-Wardana, M. W. C. & Foord, M. E. Idealized slab plasma approach for the study of warm dense matter. Laser Part. Beams 23, 527–537 (2005).
Ao, T. et al. Optical Properties in Nonequilibrium Phase Transitions. Phys. Rev. Lett. 96, 055001 (2006).
Ping, Y. et al. Broadband Dielectric Function of Nonequilibrium Warm Dense Gold. Phys. Rev. Lett. 96, 255003 (2006).
Dyer, G. M. et al. Equation-of-State Measurement of Dense Plasmas Heated With Fast Protons. Phys. Rev. Lett. 101, 015002 (2008).
Ernstorfer, R. et al. The Formation of Warm Dense Matter: Experimental Evidence for Electronic Bond Hardening in Gold. Science 323, 1033–1037 (2009).
Mančić, A. et al. Picosecond Short-Range Disordering in Isochorically Heated Aluminum at Solid Density. Phys. Rev. Lett. 104, 035002 (2010).
Cho, B. I. et al. Electronic Structure of Warm Dense Copper Studied by Ultrafast X-Ray Absorption Spectroscopy. Phys. Rev. Lett. 106, 167601 (2011).
White, T. G. et al. Observation of inhibited electron-ion coupling in strongly heated graphite. Sci. Rep. 2, 889 (2012).
Chen, Z. et al. Evolution of AC Conductivity in Nonequilibrium Warm Dense Gold. Phys. Rev. Lett. 110, 135001–135001 (2013).
Dharma-wardana, M. W. C. & Perrot, F. Energy relaxation and the quasiequation of state of a dense two-temperature nonequilibrium plasma. Phys. Rev. E 58, 3705–3718 (1998).
Vorberger, J., Gericke, D. O., Bornath, T. & Schlanges, M. Energy relaxation in dense, strongly coupled two-temperature plasmas. Phys. Rev. E 81, 046404 (2010).
Spitzer Jr., L. Physics of Fully Ionized Gases. Ch 5, 65 (Wiley 1956).
Reimann, U. & Toepffer, C. Collision times in plasmas. Laser Part. Beams 8, 763–770 (1990).
Ng, A., Celliers, P., Xu, G. & Forsman, A. Electron-ion equilibration in a strongly coupled plasma. Phys. Rev. E 52, 4299–4310 (1995).
Riley, D. et al. X-Ray Diffraction from a Dense Plasma. Phys. Rev. Lett. 84, 1704–1707 (2000).
Lin, Z., Zhigilei, L. V. & Celli, V. Electron-phonon coupling and electron heat capacity of metals under conditions of strong electron-phonon nonequilibrium. Phys. Rev. B 77, 075133 (2008).
Zhigilei, L. V. Electron-Phonon Coupling and Electron Heat Capacity in Metals at High Electron Temperatures. “ http://www.faculty.virginia.edu/CompMat/electron-phonon-coupling/, (date of access: 1/11/2015).
Cho, B. I. et al. Picosecond Single-Shot X-ray Absorption Spectroscopy for Warm and Dense Matter. Sync. Rad. News 25, 12 (2012).
Johnson, S. et al. Bonding in Liquid Carbon Studied by Time-Resolved X-Ray Absorption Spectroscopy. Phys. Rev. Lett. 94, 057407 (2005).
Hohlfeld, J., Wellershoff, S., Güdde, J. & Conrad, U. Electron and lattice dynamics following optical excitation of metals. Chem. Phys. 251, 237–258 (2000).
American Institute of Physics Handbook 3rd edn (ed. D. E. Gray ), Ch 4. 105 (McGraw-Hill 1972).
Wallace, D. C. Statistical Physics of Crystals and Liquids: A Guide to Highly Accurate Equations of State. (World Scientific Pub Co Inc 2003).
Elsayed-Ali, H., Norris, T. & Pessot, M. Time-resolved observation of electron-phonon relaxation in copper. Phys. Rev. Lett. 58, 1212 (1987).
McMillan, W. L. Transition Temperature of Strong-Coupled Superconductors. Phys. Rev. 167, 331–344 (1968).
Grimvall, G. The Electron-Phonon Interaction in Metals, Selected Topics in Solid State Physics (ed. E. Wohlfarth ). Ch 10, 245 (North-Holland 1981).
Fletcher, L. B. et al. Ultrabright X-ray laser scattering for dynamic warm dense matter physics. Nat Photon 9, 274–279 (2015).
Gorman, M. G. et al. Direct Observation of Melting in Shock-Compressed Bismuth With Femtosecond X-ray Diffraction. Phys. Rev. Lett. 115, 095701 (2015).
Gaudin, J. et al. Towards simultaneous measurements of electronic and structural properties in ultra-fast x-ray free electron laser absorption spectroscopy experiments. Sci. Rep 4, 4724 (2014).
Dorchies, F. et al. Time evolution of electron structure in femtosecond heated warm dense molybdenum. Phys. Rev. B 92, 144201 (2015).
Paolo, G. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.Condense. Matter 21, 395502 (2009).
Prendergast, D. & Galli, G. X-Ray Absorption Spectra of Water from First Principles Calculations. Phys. Rev. Lett. 96, 215502 (2006).
Acknowledgements
This work was supported by the Institute for Basic Science (Project code: IBS-R012-D1) and the National Research Foundation (NRF-2013R1A1A1007084 and NRF-2015R1A5A1009962) of Korea. Portions of this research were performed at LBNL under the auspices of the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences Division Contracts No. DE-AC03-76SF00098. The work at LLNL was performed under the auspices the U.S. Department of Energy under contract No. DE-AC52-07NA27344. T.O., A.A.C. and Y.P. were supported by DOE HEDLP program.
Author information
Authors and Affiliations
Contributions
B.I.C., R.W.F. and P.A.H. conceived the experiment. B.I.C., K.E., Y.P. and P.A.H. performed the experiment. B.I.C., J.W.L. and L.J.B. analyzed the data. T.O., A.A.C. and D.P. performed the theoretical work. B.I.C., T.O. and P.A.H. wrote the manuscript. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Cho, B., Ogitsu, T., Engelhorn, K. et al. Measurement of Electron-Ion Relaxation in Warm Dense Copper. Sci Rep 6, 18843 (2016). https://doi.org/10.1038/srep18843
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep18843
This article is cited by
-
Single-shot X-ray absorption spectroscopy at X-ray free electron lasers
Scientific Reports (2023)
-
Full-scale ab initio simulations of laser-driven atomistic dynamics
npj Computational Materials (2023)
-
Temperature relaxation in strongly-coupled binary ionic mixtures
Nature Communications (2022)
-
Review of laser-plasma physics research and applications in Korea
Journal of the Korean Physical Society (2022)
-
Probing warm dense matter using femtosecond X-ray absorption spectroscopy with a laser-produced betatron source
Nature Communications (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.