Abstract
Identification of different isomer structures of atomic and molecular clusters has long been a challenging task in the field of cluster science. Here we present a three-dimensional (3D) assignment method, combining the energy (1D) and simulated (2D) spectra to assure the assignment of the global minimum structure. This method is more accurate and convenient than traditional methods, which only consider the total energy and first vertical detachment energies (VDEs) of anion clusters. There are two prerequisites when the 3D assignment method is ultilized. First, a reliable global minimum search algorithm is necessary to explore enough valleys on the potential energy surface. Second, trustworthy simulated spectra are necessary, that is to say, spectra that are in quantitative agreement. In this paper, we demonstrate the validity of the 3D assignment method using Au8M− (M = Si, Ge, Sn) systems. Results from this study indicate that the global minimum structures of Au8Ge− and Au8Sn− clusters are different from those described in previous studies.
Similar content being viewed by others
Introduction
Nanoclusters, including small groups of atoms or molecules, possess an intermediate size range between single atoms and condensed matter. Owing to the unique properties of the clusters in designing new types of nanofunctional materials, many efforts have been devoted to demonstrating that the properties of the clusters depend on their structure and composition1,2. Once low-lying structures are found, their properties can be calculated and compared with measured values to make precise structural assignments. Therefore, it is very important to determine the exact structure and composition of these nanoclusters3,4.
In the past two decades, various techniques have been used to investigate the structures of nanoclusters, such as photoelectron spectroscopy5,6,7,8,9,10, ion mobility11,12, infrared multiphoton dissociation spectroscopy13,14, electron diffraction15, X-ray diffraction16, coulomb explosion17,18,19 and trapped ion electron diffraction20. All of these techniques are quite powerful for obtaining structural information when combined with optimization algorithms and density functional theory (DFT) calculations. So far, the different types of algorithms have been developed to search the low-energy structure on the complicated potential energy surface (PES), such as genetic algorithms (GA)21, simulated annealing (SA)22 and basin hopping (BH)23,24,25,26. These experimental techniques and optimization algorithms are very useful for finding the low-energy structure on PES. However, the assignment of cluster structures remain to be difficult, specifically identifying the structural and energetic close isomers27. Therefore, determining the different isomers and confirming which structure is the global minimal structure in low-lying structures is still a fundamental problem in atomic clusters.
The conventional method used to distinguish the global minimum from other isomers is to calculate their relative energies and compare the calculated vertical detachment energies (VDEs) with the experimental value28. This methodology is not very effective at recognizing the lowest energy structure and the energetically close isomers27 because the relative energy calculations depend on the method and basis set. The different method and basis set can lead to a change of energy order. On the other hand, normally the vertical detachment energy differences of different isomers, especially for the low energy isomers, are very small. Therefore, it is difficult to distinguish the lowest energy structure from different isomers only by the relative energy and VDE values. To more reliably identify the global minimum from all of the isomers, we present a three-dimensional (3D), including energy (1D) and density of state (DOS) (2D), assignment method for effectively analyzing different low-energy structures of anion clusters. The simulated DOS spectra are based on a generalized Koopmann’s theorem29. It can effectively simulate the photoelectron spectra obtained by experiment to make the structure assignment. We used Au8M− (M = Si, Ge, Sn) as an example system to illustrate the validity of our method. We then compared the DOS spectra for the isomers of Au8M− (M = Si, Ge, Sn) systems with previous studies, thereby providing considerable credence for the identified isomers of these clusters.
Results
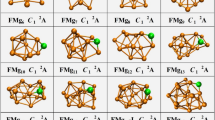
To determine the global minima of the Au8M− (M = Si, Ge, Sn) systems, we searched more than 200 isomeric forms using the BH method23 Table 1 lists the relative energies of the top 5 isomers of Au8M− (M = Si, Ge, Sn) systems at several levels of theory (see the table titles). All the coordinates of the top 5 low energy structures of the Au8M− (M = Si, Ge, Sn) systems can be found in the Supporting Information. The first VDEs of each species are calculated at the PBE0/CRENBL (SO) level of theory (using the NWChem software package30) and compared with the experimental values obtained by Wang et al.31 in Table 1. The simulated spectra of the primary structures of the Au8M− (M = Si, Ge, Sn) systems are depicted in Fig. 1. The top 5 lowest-energy structures of the Au8M− (M = Si, Ge, Sn) systems, together with their simulated PES spectra, are depicted in Figure S1 in the Supporting Information. The experimental spectra of the Au8M− (M = Si, Ge, Sn) systems are showed in Fig. 2a~c.
The experimental (left) and simulated (right) photoelectron spectra of Au8M− (M = Si, Ge, Sn).
with the permission ref. 31. Copyright 2009 American Chemical Society.
Table 1 shows that the results calculated from different theoretical levels lead to different energy values. Therefore, it is difficult for us to distinguish which isomer is the global minimum by their total energy and first VDEs. To accurately obtain the lowest energy structure, we compared their total energy and DOS spectra with the experimental results. The simulated spectrum of isomer 1 for the Au8Si− cluster agrees well with the experimental data (Fig. 2a) obtained by Wang, et al.31 and should be the lowest-energy structure by our calculation. Due to the spin-orbit effects included for the Au atom, our simulated spectrum is better than previous studies (Fig. 2d)31, which had not considered the spin-orbit effects for the Au atom. The experimental spectra (Fig. 2b,c) of Au8Ge− and Au8Sn− clusters are very similar to the literature31, which suggests that their primary structures should be similar with each other. Based on the comparison of the total energy and DOS spectra of isomers 1 and 2 for the Au8Sn− cluster, we confirmed that the primary structure of Au8Sn− should be isomer 2. The simulated spectrum of isomer 2 agrees well with the experimental spectra (Fig. 2c) and suggests that isomer 2 is more likely to exist under real conditions. Comparing experimental and theoretical spectra for the Au8Ge− cluster31, the simulated spectrum of isomer 4 (Figure. S1i in the Supporting Information) together with isomer 3 (Figure. S1h in the Supporting Information) has good agreement with the experimental spectrum (Fig. 2b). However, isomer 4 has a relatively higher energy than the other structures at several different theoretical levels (Table 1). Due to the similar experimental spectra of the Au8Ge− and Au8Sn− clusters, we believe that isomer 4 should be a primary structure of the Au8Ge− cluster. To further verify those structures analyzed by our method, the distributions of conformational populations were calculated at the MP2/ Def2-TZVPPD level of theory (using Gaussian09 software package, revision D.02, Gaussian, Inc.) and the results are summarized in Table 2. The conformational populations depending on temperature can be found in Figure S2. The results show those primary structures of the Au8M− (M = Si, Ge, Sn) system obtained by our method hold a high percentage in the range of 1 to 500 K. For the structure analysis, the contrast of multi-dimensional characters, including energy, PES and infrared spectra, can more accurately distinguish the different isomer configurations and reduce the uncertainty of the structure assignment. Through structure searching, the global minimum structure of MN+1 usually can be found from one of the low-lying isomers of MN using our previous calculations32,33,34. Therefore, we have speculated that some low-lying isomers of the Au8Ge− and Au8Sn− systems may coexist under certain experimental conditions. Two possible evolution routes are presented in Fig. 3 for the Au8Ge− and Au8Sn− systems. The structure evolution routes provide us with another method to analyze the global minimum structure.
Discussion
In this study, we have presented a three-dimensional structural assignment method based on energies and DOS spectra to distinguish different isomers. The method first involves exploring the PES using an optimization algorithm and obtaining sufficient isomers. Secondly, the DOS spectra of the low energy structures were simulated based on a generalized Koopmann’s theorem. The three-dimensional characteristics of cluster structure can be seen as the fingerprint of different isomers. This method will be more effective to determine which structures exist under real conditions. Applying the method to the Au8M− (M = Si, Ge, Sn) systems, we found that the primary structures of Au8Ge− and Au8Sn− cluster are different from previous studies. The three-dimensional structure assignment method is simple and effective for different types of clusters to distinguish their structures.
Methods
The basin hopping (BH) algorithm combined with density functional theory has been used to search the potential energy surface (PES). Generalized gradient approximation in the Perdue-Burke-Ernzerhof (PBE) functional and the double-numerical polarized (DNP) basis set with effective core potentials (ECPs), implemented in the DMol3 code35, were chosen for structure optimization of the Au8M− (M = Si, Ge, Sn) system. More than 200 possible structures were produced by the BH method for the Au8M− (M = Si, Ge, Sn) systems. The top 5 isomers were chosen based on their relative energies. The top 5 isomers were re-optimized using the functional PBEPBE and a scalar relativistic effective core potential Stuttgart/Dresden (SDD) basis set for all of elements in the Gaussian 09 software package (revision D.02, Gaussian, Inc.). The DOS spectra for all candidate isomers were calculated using PBE0 functional and CRENBL basis set for Si, Ge and Sn, CRENBL basis set for Au with spin-orbit effects included in the NWChem software package30.
The DOS spectra were calculated using the following steps: (i) calculate the first vertical detachment energies (VDEs) of anion clusters, which was defined as the energy difference between the optimized anion isomer and the neutral at the corresponding anion geometry, (ii) add the binding energies of deeper orbitals of the anion cluster to the first VDEs to approximate the higher binding energy detachment features and (iii) fit each peak with a 35-meV-wide Gaussian curve. Each peak can be seen as a molecular orbital. Therefore, we can obtain the approximate electronic structures of the anion cluster using this method. Because each anion cluster has a unique electronic structure, we can easily distinguish the difference of each isomer by their DOS spectra. This method is very effective for anion clusters and we used this method to study the pure Au or doped-Au anion clusters in previous studies33,34,36,37,38,39,40.
Additional Information
How to cite this article: Liu, Y.-R. et al. Three-Dimensional Assignment of the Structures of Atomic Clusters: an Example of Au8M (M=Si, Ge, Sn) Anion Clusters. Sci. Rep. 5, 17738; doi: 10.1038/srep17738 (2015).
References
Shao N. et al. Structural Evolution of Medium-Sized Gold Clusters Aun–(n = 36, 37, 38): Appearance of Bulk-Like Face Centered Cubic Fragment. J Phys Chem C 118, 6887–6892 (2014).
Shao N. et al. Probing the Structural Evolution of Medium-Sized Gold Clusters: Aun−(n = 27−35). J Am Chem Soc 132, 6596–6605 (2010).
Zhai H.-J. et al. Observation of an all-boron fullerene. Nat Chem 6, 727–731 (2014).
Ferrando R., Jellinek J. & Johnston R. L. Nanoalloys: from theory to applications of alloy clusters and nanoparticles. Chem Rev 108, 845–910 (2008).
Müller‐Dethlefs K. & Schlag E. W. Chemical applications of zero kinetic energy (ZEKE) photoelectron spectroscopy. Angew Chem Int Edit 37, 1346–1374 (1998).
Grant E. R. & White M. G. ZEKE threshold photoelectron spectroscopy. Nature 354, 249–250 (1991).
Li W.-L. et al. The B35 Cluster with a Double-Hexagonal Vacancy: A New and More Flexible Structural Motif for Borophene. J Am Chem Soc 136, 12257–12260 (2014).
Li W. L., Zhao Y. F., Hu H. S., Li J. & Wang L. S. [B30]−: A Quasiplanar Chiral Boron Cluster. Angew Chem Int Edit 126, 5646–5651 (2014).
Kiran B. et al. Planar-to-tubular structural transition in boron clusters: B20 as the embryo of single-walled boron nanotubes. Proc Natl Acad Sci USA 102, 961–964 (2005).
Li J., Li X., Zhai H.-J. & Wang L.-S. Au20: A tetrahedral cluster. Science 299, 864–867 (2003).
Weis P. Structure determination of gaseous metal and semi-metal cluster ions by ion mobility spectrometry. Int J Mass Spectrom 245, 1–13 (2005).
Lanucara F., Holman S. W., Gray C. J. & Eyers C. E. The power of ion mobility-mass spectrometry for structural characterization and the study of conformational dynamics. Nat Chem 6, 281–294 (2014).
Fielicke A. et al. Structure determination of isolated metal clusters via far-infrared spectroscopy. Phys Rev Lett 93, 023401 (2004).
Gruene P. et al. Structures of neutral Au-7, Au-19 and Au-20 clusters in the gas phase. Science 321, 674–676 (2008).
Ihee H. et al. Direct imaging of transient molecular structures with ultrafast diffraction. Science 291, 458–462 (2001).
Schotte F., et al. Watching a protein as it functions with 150-ps time-resolved X-ray crystallography. Science 300, 1944–1947 (2003).
Kanter E. et al. Role of excited electronic states in the interactions of fast (MeV) molecular ions with solids and gases. Phys Rev A 20, 834 (1979).
Légaré F. et al. Imaging the time-dependent structure of a molecule as it undergoes dynamics. Phys Rev A 72, 052717 (2005).
Wu C., et al. Nonsequential and Sequential Fragmentation of CO23+ in Intense Laser Fields. Phys Rev Lett 110, 103601 (2013).
Xing X., Yoon B., Landman U. & Parks J. H. Structural evolution of Au nanoclusters: From planar to cage to tubular motifs. Phys Rev B 74, 165423 (2006).
Deaven D. M. & Ho K. M. Molecular geometry optimization with a genetic algorithm. Phys Rev Lett 75, 288–291 (1995).
Kirkpatrick S. & Vecchi M. Optimization by simmulated annealing. Science 220, 671–680 (1983).
Wales D. J. & Doye J. P. Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms. J Phys Chem A 101, 5111–5116 (1997).
Brooks C. L., Onuchic J. N. & Wales D. J. Taking a Walk on a Landscape. Science 293, 612–613 (2001).
Wales D. J. & Scheraga H. A. Global optimization of clusters, crystals and biomolecules. Science 285, 1368–1372 (1999).
Oakley M. T., Johnston R. L. & Wales D. J. Symmetrisation schemes for global optimisation of atomic clusters. Phys Chem Chem Phys 15, 3965–3976 (2013).
Huang W., Pal R., Wang L.-M., Zeng X. C. & Wang L.-S. Isomer identification and resolution in small gold clusters. J Chem Phys 132, 054305 (2010).
Fischer D. et al. Chemisorption on small clusters: can vertical detachment energy measurements provide chemical information? H on Au as a case study. Chem Phys Lett 361, 389–396 (2002).
Koopmans T. Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den einzelnen Elektronen eines Atoms. Physica 1, 104–113 (1934).
Kendall R. A. et al. High performance computational chemistry: An overview of NWChem a distributed parallel application. Comput Phys Commun 128, 260–283 (2000).
Pal R., Wang L.-M., Huang W., Wang L.-S. & Zeng X. C. Structural Evolution of Doped Gold Clusters: MAu x−(M = Si, Ge, Sn; x = 5−8). J Am Chem Soc 131, 3396–3404 (2009).
Liu Y.-R. et al. Structural Exploration of Water, Nitrate/Water and Oxalate/Water Clusters with Basin-Hopping Method Using a Compressed Sampling Technique. J Phys Chem A 118, 508–516 (2013).
Xu K.-M. et al. A density functional study of phosphorus-doped gold clusters: AunP−(n = 1–8). RSC Adv 3, 24492–24502 (2013).
Huang W., Bulusu S., Pal R., Zeng X. C. & Wang L.-S. Structural Transition of Gold Nanoclusters: From the Golden Cage to the Golden Pyramid. ACS Nano 3, 1225–1230 (2009).
Delley B. et al. An All-Electron Numerical-Method for Solving the Local Density Functional for Polyatomic-Molecules. J Chem Phys 92, 508–517 (1990).
Yan L.-L. et al. Structure, stability and electronic property of carbon-doped gold clusters AunC−(n = 1–10): A density functional theory study. J Chem Phys 139, 244312 (2013).
Wen H. et al. Observation of linear to planar structural transition in sulfur-doped gold clusters: AuxS−(x = 2–5). J Chem Phys 138, 174303 (2013).
Huang W. et al. A concentric planar doubly π-aromatic B19− cluster. Nat Chem 2, 202–206 (2010).
Huang W. & Wang L.-S. Probing the 2D to 3D Structural Transition in Gold Cluster Anions Using Argon Tagging. Phys Rev Lett 102, 153401 (2009).
Huang W. et al. Relativistic effects and the unique low-symmetry structures of gold nanoclusters. ACS Nano 2, 897–904 (2008).
Acknowledgements
The study was supported by grants from the National Natural Science Foundation of China (Grant No. 21403244, 21133008, 21573241 and 41527808), the National High Technology Research and Development Program of China (863 Program) (Grant No. 2014AA06A501), the program of Formation Mechanism and Control Strategies of Haze in China (Grant No. XDB05000000) and “Interdisciplinary and Cooperative Team” of CAS. Acknowledgement is also made to the “Thousand Youth Talents Plan”. The computation was performed in EMSL, a national scientific user facility sponsored by the department of Energy’s Office of Biological and Environmental Research and located at Pacific Northwest National Laboratory (PNNL). PNNL is a multiprogram national laboratory operated for the DOE by Battelle. Part of the computation was performed at the Supercomputing Center of the Chinese Academy of Sciences and Supercomputing Center of USTC.
Author information
Authors and Affiliations
Contributions
Y.R.L. and W.H. analyzed the results and wrote the manuscript. T.H. and Y.B.G. prepared Figures 1–3. Y.Z. and Y.J.F. prepared Tables 1–2. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Liu, YR., Huang, T., Gai, YB. et al. Three-Dimensional Assignment of the Structures of Atomic Clusters: an Example of Au8M (M=Si, Ge, Sn) Anion Clusters. Sci Rep 5, 17738 (2015). https://doi.org/10.1038/srep17738
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep17738
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.