Abstract
We report on the integration of inkjet-printed graphene with a CMOS micro-electro-mechanical-system (MEMS) microhotplate for humidity sensing. The graphene ink is produced via ultrasonic assisted liquid phase exfoliation in isopropyl alcohol (IPA) using polyvinyl pyrrolidone (PVP) polymer as the stabilizer. We formulate inks with different graphene concentrations, which are then deposited through inkjet printing over predefined interdigitated gold electrodes on a CMOS microhotplate. The graphene flakes form a percolating network to render the resultant graphene-PVP thin film conductive, which varies in presence of humidity due to swelling of the hygroscopic PVP host. When the sensors are exposed to relative humidity ranging from 10–80%, we observe significant changes in resistance with increasing sensitivity from the amount of graphene in the inks. Our sensors show excellent repeatability and stability, over a period of several weeks. The location specific deposition of functional graphene ink onto a low cost CMOS platform has the potential for high volume, economic manufacturing and application as a new generation of miniature, low power humidity sensors for the internet of things.
Similar content being viewed by others
Introduction
Humidity sensors are employed today in a wide range of applications, including in environmental monitoring, automotive, industrial process, healthcare, agriculture and increasing indoor air quality in smart buildings. Over the years, a variety of transduction techniques has been reported for humidity sensors, including the use of surface acoustic wave (SAW)1,2,3, resistive4,5, capacitive6, optical fibre7, field effect transistor8,9 and quartz crystal microbalance10. Sensors based on some of these transduction techniques are available on the market, such as the SHTC1 digital humidity sensor11. Among these approaches, capacitive technique is the most widely used for humidity sensing because of its linear response to humidity over a wide range12. Capacitive sensing makes use of a thin dielectric layer, typically a polymer, to adsorb/desorb water molecules and thus detect changes in the capacitance (i.e. electrical permittivity) for humidity sensing12. However, hysteresis is a major drawback in polymer-based capacitive humidity sensors. This is due to the cluster of water adsorbed inside bulk polymers that may cause deformation and instability of the sensing polymer layer, eventually reducing the lifetime of the sensor12. In addition, most of the current generation of chemical, gas and humidity sensors uses semi-automated manufacturing, increasing the overall production cost13. On the other hand, resistive humidity sensors are easier to read out with basic circuitry compared to other types of sensors. Indeed, resistive sensors with integrated CMOS on a single silicon chip can reduce the production cost significantly. In recent years, various materials have been studied as sensing materials for resistive humidity sensors such as polymers1,14, metal oxides8, carbon nanotubes15,16 and graphene oxide-based polymer/polyelectrolyte nanocomposites5,17. Among these, nanomaterials are particularly attractive because of their high surface area to volume ratio, promising high sensitivity and fast response times.
Sensors available on the market are typically bulky or usually have high power consumption18. CMOS is suitable as an underlying platform for the development of economic, compact and low power sensing devices. It is a mature, reliable technology and most importantly, it makes integration of sensors with electronics possible. However, to take advantage of CMOS miniaturization and single chip solution, their small active sensing areas need to exploit high sensitivity materials. Nanomaterials are therefore an ideal candidate for a low cost CMOS sensing platform.
With its 2-dimensional (2d) structure, high specific surface area and in particular, sensitivity of its electrical properties to environmental perturbations, graphene has attracted significant attention in various sensing applications including humidity5 and gas sensing19,20,21,22,23. Graphene can be prepared via various methods, the most widely exploited ones being mechanical cleavage24 and chemical25 and shear force assisted exfoliation of graphite26 and chemical vapour deposition (CVD)27. Among these, micromechanical cleavage24 produces the highest quality flakes, although at extremely low yield28. It is thus only widely used in fundamental studies of graphene and related 2d materials28. Though CVD has, in recent years, been scaled up to produce large area, high quality graphene29, the high temperature growth process is not ideal for device fabrication and integration. In addition, CVD grown mono- or few-layer graphene has limited exposed surface area and edges (i.e. active area) compared to graphene produced by solution processing, a key requirement for sensing applications. Solution based strategies, such as ultrasonic assisted liquid phase exfoliation (UALPE) produces high quality, defect free, pristine graphene nanoflakes at room temperature30. The lateral size of the graphene nanoflakes is typically several hundred nanometres, offering high surface area and edges, making them ideal active materials for sensors. Thus far, the demonstrations of sensors based on graphene or graphene oxide (GO) are mostly based on non-CMOS platform such as on glass/ZnO1, glass6, polyamide substrate17, ceramic substrate31 and polyethylene naphthalate32.
Here, we demonstrate resistive CMOS MEMS devices, fully integrated with an inkjet-printed chemically pristine graphene-polyvinyl pyrrolidone (PVP) composite sensing layer for humidity sensing. Our graphene ink formulation allows selective area deposition and room temperature curing after printing. The conductive graphene flakes, interspersed inside the insulating, hygroscopic PVP form a 3-dimensional (3d) percolating network that responds to adsorbed moisture by the polymer with a change in electrical resistivity, allowing humidity sensing.
Results
Microhotplate design and fabrication
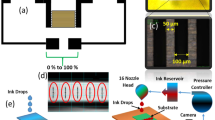
A key component of our resistive humidity sensor is the CMOS MEMS based microhotplate (μHP) structure. Details of the μHP structure are reported elsewhere33,34. A cross section view of the sensor structure is shown in Fig. 1(a). An optical microscope image of the fabricated device is shown in Fig. 1(b). The silicon die measures 1 mm × 1 mm. It is designed using a 1.0 μm Silicon on Insulator (SOI) CMOS process technology and fabricated in a commercial foundry, followed by deep reactive ion etching (DRIE) to release the thin membrane. The processing employs SOI wafers with 1 μm buried oxide, 0.25 μm SOI layer and 3 metallization layers. The μHP structure typically consists of an embedded, 0.3 μm thick, resistive tungsten microheater (metal layer 1), 0.3 μm thick heat spreader plate (metal layer 2) and a top gold layer for interdigitated sensing electrodes (IDEs). The diameters of the circular heater and membrane structures are 250 and 600 μm, respectively. The heater is fabricated during the CMOS process while the top gold electrodes and corresponding tracks are deposited as a post CMOS process in the same commercial foundry. The tungsten heater controls the operating temperature of the membrane and graphene-based sensing layer. The IDEs underneath the sensing layer are used to measure the change in resistance due to humidity exposure. Use of tungsten in the heater allows the device to operate at a very high temperature (up to 750 °C), if required, for example, when oxide-based sensing materials are used. Gold is used as the electrode material because of its chemical inertness (and hence, unchanged conductivity over prolonged use under various temperature and humidity conditions) compared to commonly used aluminum in this SOI process. The silicon underneath the μHP is etched away, using the dioxide layer as the etch stopper, at a wafer level by DRIE technique. This forms a 4.5 μm silicon dioxide: SiO2 (4 μm)/silicon nitride: Si3N4 (0.5 μm) membrane structure onto which the microheater and electrodes are suspended. The membrane structure reduces DC power consumption of the sensing device to <5 mW when used for humidity sensing in this work. The heating temperature is uniformly confined over the microheater region, due to the buried heat spreader33. The temperature decreases rapidly away from the heater region and is at close to room temperature at the membrane rim, allowing reliable temperature independent on-chip circuit performance35.
The characteristic power versus temperature plot (up to 217 °C) of the μHP device is given in Fig. 2. To calculate the power consumption, the resistive μHPs are first calibrated to up to 300 °C using a computer controlled high temperature chuck (Signatone S-1060R-6TG). Two temperature coefficients of resistance (α, β) are calculated from the measured value using the relationship:  , where
, where  is the resistance of the heater at room temperature
is the resistance of the heater at room temperature  and
and  is the temperature increase. The values of α (2.05 × 10−3 K−1) and β (0.2 × 10−6 K−2) are very closely matched to the values provided by the CMOS foundry. A constant current is supplied to the
is the temperature increase. The values of α (2.05 × 10−3 K−1) and β (0.2 × 10−6 K−2) are very closely matched to the values provided by the CMOS foundry. A constant current is supplied to the  HP and the voltage is measured across the heater. From the constant current and measured voltage, the power supplied to the devices is calculated. The corresponding heater temperature is calculated from the change in resistance using
HP and the voltage is measured across the heater. From the constant current and measured voltage, the power supplied to the devices is calculated. The corresponding heater temperature is calculated from the change in resistance using  ,
,  values estimated during the calibration. Over small temperature changes, a linear function is fitted through the experimental points of power versus temperature plot, yielding an electrothermal transduction efficiency of 8.46 °C/mW; Fig. 2.
values estimated during the calibration. Over small temperature changes, a linear function is fitted through the experimental points of power versus temperature plot, yielding an electrothermal transduction efficiency of 8.46 °C/mW; Fig. 2.
Formulation of graphene-polymer ink
The first step towards ink formulation is exfoliation of graphite into graphene flakes. UALPE starts with mixing bulk graphite crystals into a solvent. The ultrasound causes high-frequency pressure variations and formation of microcavities in the solvent. Collapse of these microcavities produces high shear forces, exfoliating mono-, bi- and few-layer flakes from the bulk crystals by overcoming the interlayer van der Waals forces36. Since the UALPE process does not involve chemical pre- or post-treatment, the dispersed graphene flakes are chemically pristine. Note that, when experimental parameters such as sonication vessel and solvent volume are kept fixed37, solvent viscosity plays an important role in cavitation (higher viscosity requires higher acoustic pressure to create cavitation38) and hence, the UALPE process. However, in reality, a large majority of common solvents have a viscosity ranging from 1 to 5 mPa.s at room temperature, which have no strong effect on the exfoliation. Instead, the dispersability and stability of graphene in the solvents are largely governed by their intermolecular interactions. This has been explained through matching the degree of the Hansen solubility parameters  of graphene and solvents, where
of graphene and solvents, where  ,
,  and
and  are the dispersive, polar and hydrogen-bonding components, respectively39. It was experimentally observed that effective solvents for the exfoliation and stabilization of graphene should possess Hansen solubility parameters close to
are the dispersive, polar and hydrogen-bonding components, respectively39. It was experimentally observed that effective solvents for the exfoliation and stabilization of graphene should possess Hansen solubility parameters close to  = 18 MPa1/2,
= 18 MPa1/2,  = 9.3 MPa1/2 and
= 9.3 MPa1/2 and  = 7.7 MPa1/2. N-methyl-2-pyrrolidone (NMP) is an example of such effective solvents30 (with
= 7.7 MPa1/2. N-methyl-2-pyrrolidone (NMP) is an example of such effective solvents30 (with  = 18 MPa1/2,
= 18 MPa1/2,  = 12.3 MPa1/2 and
= 12.3 MPa1/2 and  = 7.2 MPa1/2 )40. However, the surface tension of the solvents (
= 7.2 MPa1/2 )40. However, the surface tension of the solvents ( NMP has a surface tension of ~40.7 mNm−1) suitable for graphene typically poses a challenge for inkjet printing on low energy surfaces26 such as the
NMP has a surface tension of ~40.7 mNm−1) suitable for graphene typically poses a challenge for inkjet printing on low energy surfaces26 such as the  HP membrane (the surface energy of Si3N4 is estimated as ~40 mNm−1)41. This results in poor wetting of the substrates42 and inconsistent coating43, leading to non-uniform deposition of graphene and ‘coffee-ring effect’ after solvent evaporation.
HP membrane (the surface energy of Si3N4 is estimated as ~40 mNm−1)41. This results in poor wetting of the substrates42 and inconsistent coating43, leading to non-uniform deposition of graphene and ‘coffee-ring effect’ after solvent evaporation.
It is thus required to develop graphene inks with low surface tension solvents to allow for good wetting. Alcohols, in particular, are attractive for this purpose. In addition, their low boiling point allows rapid drying of ink after deposition, ensuring uniform coating of graphene flakes. Indeed, they are commonly used as the primary or secondary solvent in the majority of graphics and functional inks44. Among the common alcohols, isopropyl alcohol (IPA) can exfoliate graphene, but with meta-stable dispersion45. This is primarily due to its mismatched Hansen solubility parameters ( = 15.8 MPa1/2,
= 15.8 MPa1/2,  = 6.1 MPa1/2 and
= 6.1 MPa1/2 and  = 15.4 MPa1/2) with graphene. Therefore, pure IPA based graphene dispersion cannot be used for inkjet printing. UALPE with ionic surfactants and nonionic polymers are commonly used strategies to stabilize graphene46,47. This is typically achieved through steric hindrance and favourable enthalpic interactions with graphitic surface48. Here, we use PVP as the stabilizer. Indeed, PVP is a polymer analog to NMP with the N-substituted pyrrolidone rings similar to that of NMP49,50 and has been used before to stabilize carbon nanostructures, such as nanotubes in different solvents49,51,52. In addition, PVP is highly hygroscopic, swelling when absorbing moisture in humid environments53. PVP is also an electrically insulating polymer but can be made conductive by addition of graphene through percolation54. The hygroscopic nature and moisture-induced swelling with conductivity change in graphene-PVP composites make our formulated graphene-PVP-IPA ink (henceforth, we use the term ‘graphene ink’) very attractive for humidity sensing.
= 15.4 MPa1/2) with graphene. Therefore, pure IPA based graphene dispersion cannot be used for inkjet printing. UALPE with ionic surfactants and nonionic polymers are commonly used strategies to stabilize graphene46,47. This is typically achieved through steric hindrance and favourable enthalpic interactions with graphitic surface48. Here, we use PVP as the stabilizer. Indeed, PVP is a polymer analog to NMP with the N-substituted pyrrolidone rings similar to that of NMP49,50 and has been used before to stabilize carbon nanostructures, such as nanotubes in different solvents49,51,52. In addition, PVP is highly hygroscopic, swelling when absorbing moisture in humid environments53. PVP is also an electrically insulating polymer but can be made conductive by addition of graphene through percolation54. The hygroscopic nature and moisture-induced swelling with conductivity change in graphene-PVP composites make our formulated graphene-PVP-IPA ink (henceforth, we use the term ‘graphene ink’) very attractive for humidity sensing.
We ultrasonicate 100 mg of graphite (Sigma-Aldrich, 100 mesh flakes) with 1.5 mg PVP (Sigma-Aldrich, average molecular weight 10,000 Da) in 10 mL IPA for 12 hours at ~15 °C. This starting PVP concentration enables stabilization as well as desired ink rheological properties specific to our inkjet printer nozzle discussed below. The resultant dispersion is centrifuged for 1 hour at 4,030 rpm (~1540 g), sedimenting the unexfoliated graphite. The upper 70% of the dispersion, enriched with mono- and few-layer graphene nanoflakes, is decanted for analysis and experiment.
Optical absorption spectroscopy is used to estimate the concentration of the dispersed graphene using the Beer-Lambert law ( ), where
), where  is the graphene concentration (gL−1) and
is the graphene concentration (gL−1) and  is the distance the light passes through the dispersion (m).
is the distance the light passes through the dispersion (m).  and
and  are the absorption (a.u.) and material dependent optical absorption coefficient (Lg−1m−1) at wavelength
are the absorption (a.u.) and material dependent optical absorption coefficient (Lg−1m−1) at wavelength  (nm), respectively. Figure 3 shows the optical absorption spectrum of the dispersion diluted to 10 vol% to avoid scattering losses during absorption measurement55. The inset of Fig. 3 shows a photograph of a cuvette containing the undiluted graphene dispersion. The spectrum is mostly featureless as expected, due to the linear dispersion of Dirac electrons56,57. The peak in the UV region is a signature of the van Hove singularity in the graphene density of states58. Using α660 nm = 2460 Lg−1m−1 47, we estimate the concentration of graphene in the undiluted dispersion as 0.40 gL−1. We note that the graphene ink is stable, without forming any visible aggregation over several months.
(nm), respectively. Figure 3 shows the optical absorption spectrum of the dispersion diluted to 10 vol% to avoid scattering losses during absorption measurement55. The inset of Fig. 3 shows a photograph of a cuvette containing the undiluted graphene dispersion. The spectrum is mostly featureless as expected, due to the linear dispersion of Dirac electrons56,57. The peak in the UV region is a signature of the van Hove singularity in the graphene density of states58. Using α660 nm = 2460 Lg−1m−1 47, we estimate the concentration of graphene in the undiluted dispersion as 0.40 gL−1. We note that the graphene ink is stable, without forming any visible aggregation over several months.
The graphene flakes are characterized with Atomic Force Microscopy (AFM). The sample for AFM is prepared by dip-coating a Si/SiO2 wafer into a graphene dispersion diluted to 2 vol% by pure IPA. Though the concentration of PVP in this diluted dispersion is ~3.8 × 10−4 wt%, the residual polymer prevents accurate measurement of the flake dimensions. The sample is therefore annealed at 400 °C for 30 min. This temperature is chosen because PVP starts to decompose at this temperature in air59 while the exfoliated graphene flakes remain stable60,61. The annealed sample is imaged with a Bruker Dimension Icon AFM in ScanAsystTM mode, using a silicon cantilever with a Si3N4 tip. Micrographs of typical flakes are shown in Fig. 4(a,b), along with the height variations across the samples; Fig. 4(c,d). The thickness distribution of flakes is also measured; Fig. 4(e). This shows that 63% of the flakes have thicknesses <5 nm, corresponding to <13 layers, assuming ~0.7 nm measured thickness for the bottom layer and ~0.35 nm increase in thickness for each additional layer62. The average flake lateral dimension is ~204 nm. Note that the number of layers obtained in IPA/PVP is higher than what is typically obtained by UALPE of graphite in water/SDC, with ~26% mono- and ~22% bi-layer and with 300–600 nm average lateral dimension from similar experimental parameters47.
Inkjet printing of graphene
We next consider deposition of our graphene ink to form a graphene-PVP thin film composite as the active sensing layer over the IDEs of the 250 μm diameter CMOS  HP. For this, large area techniques such as spray-, spin- or dip-coating are unsuitable, as they do not offer selective area deposition directly on to the IDEs. We use drop-on-demand inkjet printing technique for the deposition of active materials on to the IDEs. It is a digital printing technique, where single ink droplets are ejected from an ink chamber in response to individual electrical impulses26. Inkjet printing also offers selective area deposition across the X-Y plane of a substrate. The inkjet printer used in this work is a DMP-2831 Dimatix Printer. The printing nozzle has a diameter of 22 μm. The volume of individual droplets from this nozzle is ~10 pL. We achieve printing resolutions of ~100 μm with this set-up onto the IDEs without any surface modification. By controlling the number of droplets and the area of deposition, inkjet printing thus enables us to deposit a well defined volume of ink for humidity sensing only onto the IDEs.
HP. For this, large area techniques such as spray-, spin- or dip-coating are unsuitable, as they do not offer selective area deposition directly on to the IDEs. We use drop-on-demand inkjet printing technique for the deposition of active materials on to the IDEs. It is a digital printing technique, where single ink droplets are ejected from an ink chamber in response to individual electrical impulses26. Inkjet printing also offers selective area deposition across the X-Y plane of a substrate. The inkjet printer used in this work is a DMP-2831 Dimatix Printer. The printing nozzle has a diameter of 22 μm. The volume of individual droplets from this nozzle is ~10 pL. We achieve printing resolutions of ~100 μm with this set-up onto the IDEs without any surface modification. By controlling the number of droplets and the area of deposition, inkjet printing thus enables us to deposit a well defined volume of ink for humidity sensing only onto the IDEs.
A stable drop generation (single droplet generation for each electrical impulse, without the formation of satellite droplets) and jetting of ink (avoiding deviation of droplet trajectory) is of primary importance for high quality inkjet printing. Otherwise, unstable jetting may lead to uncontrolled amount of ink deposition on to undesired locations. In inkjet printing, a figure of merit,  , is commonly used to consider the printability of inks and is defined as:
, is commonly used to consider the printability of inks and is defined as:  , where
, where  is surface tension of the ink (mNm−1),
is surface tension of the ink (mNm−1),  is the density of ink (gcm−3),
is the density of ink (gcm−3),  is the viscosity of the ink (mPa.s) and
is the viscosity of the ink (mPa.s) and  is the nozzle diameter (μm). As a rule of thumb, it is commonly accepted that
is the nozzle diameter (μm). As a rule of thumb, it is commonly accepted that  value should be <14 for the case of drop-on-demand inkjet printing to avoid secondary or satellite droplets26,63. Meanwhile, it should be >1 to optimize droplet formation or ejection to avoid long-lived filament formation, which may result in poor positional accuracy and printing resolution26,63,64. The value of
value should be <14 for the case of drop-on-demand inkjet printing to avoid secondary or satellite droplets26,63. Meanwhile, it should be >1 to optimize droplet formation or ejection to avoid long-lived filament formation, which may result in poor positional accuracy and printing resolution26,63,64. The value of  typically falls within 1–10 for commercial inkjet printable inks65. We stress that the acceptable range of
typically falls within 1–10 for commercial inkjet printable inks65. We stress that the acceptable range of  values should be established by experiments and numerical simulations and should be considered as a guide only. Indeed, inks with values outside this range may also be printable, in particular, by controlling the shape and intensity of the electrical pulses for droplet generation. To determine the Z value of our graphene ink, we use pendant drop measurement and parallel plate rheometry to measure
values should be established by experiments and numerical simulations and should be considered as a guide only. Indeed, inks with values outside this range may also be printable, in particular, by controlling the shape and intensity of the electrical pulses for droplet generation. To determine the Z value of our graphene ink, we use pendant drop measurement and parallel plate rheometry to measure  and
and  , respectively at room temperature. We measure
, respectively at room temperature. We measure  ~ 28.0 mNm−1 and
~ 28.0 mNm−1 and  ~ 2.34 mPa.s. The density is measured as
~ 2.34 mPa.s. The density is measured as  ~ 0.8 gcm−3. With a = 22 μm, we calculate Z ~ 9.48, falling into the recommended range for stable jetting. This indicates the formulated ink is suitable for inkjet printing. A stable jetting without the formation of satellite droplet or long filament is thus expected. This is experimentally confirmed by high speed jetting sequence images presented in Fig. 5(a).
~ 0.8 gcm−3. With a = 22 μm, we calculate Z ~ 9.48, falling into the recommended range for stable jetting. This indicates the formulated ink is suitable for inkjet printing. A stable jetting without the formation of satellite droplet or long filament is thus expected. This is experimentally confirmed by high speed jetting sequence images presented in Fig. 5(a).
(a) Stable jetting sequence of graphene ink, the scale bar is 100 μm; (b) Dark field optical microscope image of the IDEs on CMOS μHP (b) without graphene (c) with graphene-PVP deposited on to IDEs, with the targeted printing area marked by dashed lines, the scale bar is 100 μm; (d) SEM image of a small area on the CMOS μHP with graphene-PVP deposited; the IDEs are marked by dashed lines and the scale bar is 3 μm.
The drying process of the deposited ink is critical to ensure uniform coverage after the carrier solvent is evaporated. After impacting the substrate, the wettability of the ink droplets carrying stably dispersed nanoparticles ( graphene) defines consistency of the particle coating on to the substrate43. During the drying process of a droplet, a finite contact edge is formed at the edge of the solid-solvent interface. This enhances the transport of the solvent, promoting faster evaporation at the edges than in the central area of the droplet. Meanwhile, the difference in evaporation speeds results in a convective flow within the droplet from the center towards the edges (Marangoni effect)66. This transports the dispersed materials to be deposited at these edges. These deposited dried materials prevent the contact edge from receding, ‘pinning’ it at its original position. This further promotes the deposition of particles as the solvent evaporates, leading to a non-uniform coating at the edges, commonly termed as the ‘coffee ring effect’67,68. The low surface tension of our ink ensures a good wetting and the low boiling point of IPA (82.6 °C) guarantees a quick evaporation at room temperature, leading to a consistent and uniform coverage of graphene flakes across the printed area. Figure 5(c) shows the dark field optical microscope images of the CMOS device with graphene deposited. The bright spots in Fig. 5(c) indicate graphene flakes in the PVP matrix, demonstrating an even deposition of graphene across the IDEs. We also investigate the structure of the deposited graphene-PVP using scanning electron microscopy (SEM); showing evenly interspersed graphene flakes (darker spots) on the CMOS
graphene) defines consistency of the particle coating on to the substrate43. During the drying process of a droplet, a finite contact edge is formed at the edge of the solid-solvent interface. This enhances the transport of the solvent, promoting faster evaporation at the edges than in the central area of the droplet. Meanwhile, the difference in evaporation speeds results in a convective flow within the droplet from the center towards the edges (Marangoni effect)66. This transports the dispersed materials to be deposited at these edges. These deposited dried materials prevent the contact edge from receding, ‘pinning’ it at its original position. This further promotes the deposition of particles as the solvent evaporates, leading to a non-uniform coating at the edges, commonly termed as the ‘coffee ring effect’67,68. The low surface tension of our ink ensures a good wetting and the low boiling point of IPA (82.6 °C) guarantees a quick evaporation at room temperature, leading to a consistent and uniform coverage of graphene flakes across the printed area. Figure 5(c) shows the dark field optical microscope images of the CMOS device with graphene deposited. The bright spots in Fig. 5(c) indicate graphene flakes in the PVP matrix, demonstrating an even deposition of graphene across the IDEs. We also investigate the structure of the deposited graphene-PVP using scanning electron microscopy (SEM); showing evenly interspersed graphene flakes (darker spots) on the CMOS  HP; see Fig. 5(d).
HP; see Fig. 5(d).
Humidity sensing
Evaporation of IPA forms a graphene-PVP composite sensing layer on to the IDEs. Within the graphene-PVP composite, the graphene flakes are randomly distributed. The electrical behaviour of randomly arranged conducting objects in an insulating thin film matrix can be described by percolation theory in 3d 69. When continuous pathways of the conducting objects are not formed, the conductivity of the matrix is zero. As the conductive pathways start building up, electrical conductivity becomes non-zero and increases with an increasing number of conducting pathways following the relation:

where ϕ is the conductivity,  is the critical density of the conducting objects above which the density of the objects
is the critical density of the conducting objects above which the density of the objects  results in conductivity and
results in conductivity and  is the percolation coefficient. For a 3d composite with conductive filler materials distributed in an insulating matrix (such as the graphene-PVP composite), the equation can be rewritten in terms of volume fractions:
is the percolation coefficient. For a 3d composite with conductive filler materials distributed in an insulating matrix (such as the graphene-PVP composite), the equation can be rewritten in terms of volume fractions:

where  and
and  are the volume fraction and the critical volume fraction of the conducting objects, respectively70. Since this relation does not take into account of particle size, shape, orientation and their distribution uniformity inside a composite matrix,
are the volume fraction and the critical volume fraction of the conducting objects, respectively70. Since this relation does not take into account of particle size, shape, orientation and their distribution uniformity inside a composite matrix,  and
and  are empirically derived for a given system70. Modelling the graphene flakes as thin, circular, 2d conductive platelets and considering their 3d random distribution within the composite, it can be shown that70:
are empirically derived for a given system70. Modelling the graphene flakes as thin, circular, 2d conductive platelets and considering their 3d random distribution within the composite, it can be shown that70:

where  and
and  are the diameter and thickness of the platelets, respectively and
are the diameter and thickness of the platelets, respectively and  is the interplatelet distance. If
is the interplatelet distance. If  is shorter than the electron hopping distance through the non-conducting matrix, electron hopping takes place, facilitating formation of conductive pathways. The limit for single-step electron hopping is ~10 nm 71. Multistep electron hopping may take place for >10 nm. A critical value of ~1 μm has been reported for some polymers with conductive fillers71,72. With ~4.5 nm average flake thickness and ~204 nm average lateral dimension estimated from AFM measurements and considering d* ~ 10 nm-1 μm, we get v0 ~ 0.486–0.003. This requires
is shorter than the electron hopping distance through the non-conducting matrix, electron hopping takes place, facilitating formation of conductive pathways. The limit for single-step electron hopping is ~10 nm 71. Multistep electron hopping may take place for >10 nm. A critical value of ~1 μm has been reported for some polymers with conductive fillers71,72. With ~4.5 nm average flake thickness and ~204 nm average lateral dimension estimated from AFM measurements and considering d* ~ 10 nm-1 μm, we get v0 ~ 0.486–0.003. This requires  > 0.486 to ensure a conductive graphene-PVP composite. Bulk density of graphite is ~2.3 gcm−3. However, exfoliated graphene flakes can have a significantly lower density. Commercial graphene samples are typically quoted to have a density ranging from 0.03–0.4 gcm−3 73. Assuming 0.4 gcm−3 for our UAPLE graphene, a >0.047 gL−1 concentration of graphene ink is required to form a conductive graphene-PVP composite. We stress that this estimation is dependent on further experimental determination of
> 0.486 to ensure a conductive graphene-PVP composite. Bulk density of graphite is ~2.3 gcm−3. However, exfoliated graphene flakes can have a significantly lower density. Commercial graphene samples are typically quoted to have a density ranging from 0.03–0.4 gcm−3 73. Assuming 0.4 gcm−3 for our UAPLE graphene, a >0.047 gL−1 concentration of graphene ink is required to form a conductive graphene-PVP composite. We stress that this estimation is dependent on further experimental determination of  of PVP and the density of UALPE graphene. The graphene-PVP composite (v ~ 0.889) formed from this graphene ink (c ~ 0.40 gL−1) is therefore predicted to be conductive. This is experimentally confirmed with resistance measurement between the IDEs at room temperature, 40 °C and 70 °C, as shown in Fig. 6(a). The linear relationship confirms good Ohmic contact between the graphene-PVP composite and the gold IDEs. A control experiment is conducted by inkjet printing pure PVP solution, which shows negligible electrical conductivity, as expected.
of PVP and the density of UALPE graphene. The graphene-PVP composite (v ~ 0.889) formed from this graphene ink (c ~ 0.40 gL−1) is therefore predicted to be conductive. This is experimentally confirmed with resistance measurement between the IDEs at room temperature, 40 °C and 70 °C, as shown in Fig. 6(a). The linear relationship confirms good Ohmic contact between the graphene-PVP composite and the gold IDEs. A control experiment is conducted by inkjet printing pure PVP solution, which shows negligible electrical conductivity, as expected.
(a) Current versus voltage of humidity sensor at three different temperatures; (b)Humidity sensing response at room temperature with eight different  levels; (c) Sensing response under three different temperature conditions (room temperature, 40 °C and 70 °C); (d) Humidity sensing varies with the amount of deposited graphene.
levels; (c) Sensing response under three different temperature conditions (room temperature, 40 °C and 70 °C); (d) Humidity sensing varies with the amount of deposited graphene.
The sensors are next tested using different relative humidity (RH) levels inside a stainless steel chamber. Initially the sensors are kept in dry air before they are exposed to eight different humidity levels (10–80%  ). In typical experiments, the sensors are exposed to humid air for 20 minutes, followed by dry air purging for 30 minutes. Note that our set-up allows a maximum of 80%
). In typical experiments, the sensors are exposed to humid air for 20 minutes, followed by dry air purging for 30 minutes. Note that our set-up allows a maximum of 80%  above which condensation of water vapor inside the test chamber starts to appear. The sensor response is defined as:
above which condensation of water vapor inside the test chamber starts to appear. The sensor response is defined as:

where  and
and  are the measured resistances exposed to humid conditions and dry air, respectively. Typical response of the sensor with the inkjet-printed graphene-PVP composite sensing layer when exposed to different
are the measured resistances exposed to humid conditions and dry air, respectively. Typical response of the sensor with the inkjet-printed graphene-PVP composite sensing layer when exposed to different  levels at room temperature is plotted in Fig. 6(b). We see an increased response with an increased
levels at room temperature is plotted in Fig. 6(b). We see an increased response with an increased  . The sensitivity (defined as: Response/RH) achieved from the sensor varies from 0.3%/%
. The sensitivity (defined as: Response/RH) achieved from the sensor varies from 0.3%/% to 0.21%/%
to 0.21%/% as
as  increases from 10% to 80%. We also observe a drift in the response baseline in the lower humidity levels (10–20%). This could be due to trapped water molecules within the sensing layer during the recovery from pre-exposures74.
increases from 10% to 80%. We also observe a drift in the response baseline in the lower humidity levels (10–20%). This could be due to trapped water molecules within the sensing layer during the recovery from pre-exposures74.
To investigate the effect of temperature on the response, we have tested the sensors at three temperatures (room temperature, 40 °C and 70 °C). The temperature rise is achieved by using the on-chip microheater. The result is plotted in Fig. 6(c). We observe a reduced response with increasing temperature. We note that the baseline drift shown in Fig. 6(b) reduces with increase in temperature as the trapped water molecules desorb from the sensing layer faster. We further add that 40 °C and 70 °C are sufficiently low not to induce any discernible thermal stress on to the CMOS  HP or the graphene-PVP film and affect the measurements.
HP or the graphene-PVP film and affect the measurements.
To further investigate the influence of graphene volume fraction on the sensing layer, a series of 5 inks with 0.40, 0.32, 0.24, 0.16 and 0.08 gL–1 graphene concentration is prepared while keeping the PVP concentration constant. This gives the volume fraction  as 0.889, 0.865, 0.828, 0.762 and 0.615, respectively. With this v > 0.486, the deposited graphene-PVP composites after evaporation of IPA are predicated to be conductive. Sensors with these inks are then exposed to 40–60%
as 0.889, 0.865, 0.828, 0.762 and 0.615, respectively. With this v > 0.486, the deposited graphene-PVP composites after evaporation of IPA are predicated to be conductive. Sensors with these inks are then exposed to 40–60%  . We observe an increased response with the increase of graphene concentration under all the
. We observe an increased response with the increase of graphene concentration under all the  conditions; Fig. 6(d). We suggest that the graphene-PVP composite with more percolating pathways shows a larger change in resistance, leading to a higher response. The larger change may be subject to that more percolating pathways are broken due to the polymer swelling effect. However, this is yet to be conclusive, requiring further experimental work to understand the electrical conduction and percolation behavior of our graphene-PVP composite sensing layer.
conditions; Fig. 6(d). We suggest that the graphene-PVP composite with more percolating pathways shows a larger change in resistance, leading to a higher response. The larger change may be subject to that more percolating pathways are broken due to the polymer swelling effect. However, this is yet to be conclusive, requiring further experimental work to understand the electrical conduction and percolation behavior of our graphene-PVP composite sensing layer.
The sensor with 0.40 gL−1 graphene ink exhibits the highest response and is used to further investigate typical response and recovery times (defined as the time needed to reach 63% of the maximum response and to recover to the baseline, respectively). The response and recovery times measured at room temperature are reasonably fast, varying from ~6–16 s and ~60–300 s, respectively; Fig. 7(a,b). The slower recovery time at higher  could be attributed to the presence of higher partial pressure of water vapour close to the surface of the sensing layer when the sensor recovers through the desorption of water molecules. It should be noted that long (humidity)
could be attributed to the presence of higher partial pressure of water vapour close to the surface of the sensing layer when the sensor recovers through the desorption of water molecules. It should be noted that long (humidity)  and
and  times were used to ensure that the device response reaches its saturated limit without any noticeable drift.
times were used to ensure that the device response reaches its saturated limit without any noticeable drift.
Reproducibility of a sensor at different sensing cycles and of sensing over a long period are also investigated. We measure response of different sensors with the same design to investigate performance variations between the devices. All the sensors use 0.40 gL−1 ink and are tested at room temperature. The reproducibility of response is demonstrated at 50%  for five cycles; Fig. 8(a). The long-term stability of the sensor is investigated over a 4-week period. We do not observe a significant variation (~4%) of response at 30, 40, 50 and 60%
for five cycles; Fig. 8(a). The long-term stability of the sensor is investigated over a 4-week period. We do not observe a significant variation (~4%) of response at 30, 40, 50 and 60%  during this period; Fig. 8(b). The performance variation is investigated by measuring the response for three separate but identical sensors when exposed to different
during this period; Fig. 8(b). The performance variation is investigated by measuring the response for three separate but identical sensors when exposed to different  conditions, with a maximum variation of ~13%; Fig. 8(c). Figure 8(c) also shows a linear response of the sensors. We believe the variation could be further improved by optimizing the sensing layer and graphene flake dimensions for the development of reliable, reproducible, low power and compact sensors.
conditions, with a maximum variation of ~13%; Fig. 8(c). Figure 8(c) also shows a linear response of the sensors. We believe the variation could be further improved by optimizing the sensing layer and graphene flake dimensions for the development of reliable, reproducible, low power and compact sensors.
Discussion
The adsorbed water molecules on graphene surface may disassociate to H+ and OH− ions at the edges of graphene, similar to what is observed for graphene oxide samples6. These H+ ions may tunnel from one water molecule to another through hydrogen bonding, reducing the overall electrical resistance of the sensing layer6. On the other hand, the adsorbed water molecules on graphene surface act as electron donors5. As the electron density increases, the normally  -type graphene becomes more resistive. This p-type semiconductor nature of carbon materials is in agreement with reported results75,76. Meanwhile, PVP is a hygroscopic, electrically insulating polymer, absorbing up to 25% moisture at 75%
-type graphene becomes more resistive. This p-type semiconductor nature of carbon materials is in agreement with reported results75,76. Meanwhile, PVP is a hygroscopic, electrically insulating polymer, absorbing up to 25% moisture at 75%  , swelling the polymer53. We propose that moisture absorption and subsequently polymer swelling increases the distance between the graphene flakes, leading to a reduction of electrically percolating pathways through single hopping. We note this change in polymer volume and corresponding increase in distance between the adjacent graphene flakes may also depend on other factors such as chemical composition and graft density of the polymer film77. Among the two opposing effects on resistance, we suggest that effect of the
, swelling the polymer53. We propose that moisture absorption and subsequently polymer swelling increases the distance between the graphene flakes, leading to a reduction of electrically percolating pathways through single hopping. We note this change in polymer volume and corresponding increase in distance between the adjacent graphene flakes may also depend on other factors such as chemical composition and graft density of the polymer film77. Among the two opposing effects on resistance, we suggest that effect of the  -type semiconductor nature of graphene and the swelling and consequent reduction of percolating pathways dominate. This results in increased electrical resistance of the graphene-PVP composite sensing layer, enabling humidity sensing through the IDEs.
-type semiconductor nature of graphene and the swelling and consequent reduction of percolating pathways dominate. This results in increased electrical resistance of the graphene-PVP composite sensing layer, enabling humidity sensing through the IDEs.
In summary, we have integrated functional graphene inks with CMOS MEMS technology to fabricate a resistive humidity sensor. Our formulation of the ink using a blend of hygroscopic, electrically insulating polymer with chemically pristine, conducting graphene nanoflakes offers an ideal sensing layer for use with an economic, compact and low power CMOS sensing platform. Through 3d percolation theory, we show that our ink formulation produces a conductive sensing layer. Upon humidity exposure, reduction in percolating networks in the sensing layer leads to an increased resistivity for humidity sensing. The response of the sensors are reproducible, with a maximum of ~13% variation among sensors at different  levels with stable performance (<4%) over a period of few weeks. The combination of CMOS and inkjet printing platform, with graphene and potentially, other nanomaterial based functional inks, opens exciting opportunities for mass produced CMOS based sensor systems for a tremendous variety of highly commercially valuable applications.
levels with stable performance (<4%) over a period of few weeks. The combination of CMOS and inkjet printing platform, with graphene and potentially, other nanomaterial based functional inks, opens exciting opportunities for mass produced CMOS based sensor systems for a tremendous variety of highly commercially valuable applications.
Additional Information
How to cite this article: Santra, S. et al. CMOS integration of inkjet-printed graphene for humidity sensing. Sci. Rep. 5, 17374; doi: 10.1038/srep17374 (2015).
References
Li, Y., Deng, C. & Yang, M. A novel surface acoustic wave-impedance humidity sensor based on the composite of polyaniline and poly(vinyl alcohol) with a capability of detecting low humidity. Sensors Actuators, B Chem . 165, 7–12 (2012).
Xuan, W. et al. Fast response and high sensitivity ZnO/glass surface acoustic wave humidity sensors using graphene oxide sensing layer. Sci. Rep . 4, 7206 (2014).
Guo, Y. et al. Graphene/LiNbO3 surface acoustic wave device based relative humidity sensor. Optik. 125, 5800–5802 (2014).
Mogera, U., Sagade, A. A., George, S. J. & Kulkarni, G. U. Ultrafast response humidity sensor using supramolecular nanofibre and its application in monitoring breath humidity and flow. Sci. Rep . 4, 4103 (2014).
Zhang, D., Tong, J. & Xia, B. Humidity-sensing properties of chemically reduced graphene oxide/polymer nanocomposite film sensor on layer-by-layer nano self-assembly. Sensors Actuators B Chem . 197, 66–72 (2014).
Bi, H. et al. Ultrahigh humidity sensitivity of graphene oxide. Sci. Rep . 3, 2714 (2013).
Wong, W. C. et al. Polyvinyl alcohol coated photonic crystal optical fiber sensor for humidity measurement. Sensors Actuators B Chem . 174, 563–569 (2012).
Kuang, Q., Lao, C., Wang, Z. L., Xie, Z. & Zheng, L. High-sensitivity humidity sensor based on a single SnO2 nanowire. J. Am. Chem. Soc. 129, 6070–6071 (2007).
Hu, P. et al. Carbon nanostructure-based field-effect transistors for label-free chemical/biological sensors. Sensors 10, 5133–5159 (2010).
Wang, X., Ding, B., Yu, J., Wang, M. & Pan, F. A highly sensitive humidity sensor based on a nanofibrous membrane coated quartz crystal microbalance. Nanotechnology 21, 055502 (2010).
Humidity & temperature sensor SHTC1. Available at: http://www.sensirion.com/en/products/humidity-temperature/humidity-temperature-sensor-shtc1/ (Accessed: 14th June 2015).
Farahani, H., Wagiran, R. & Hamidon, M. Humidity sensors principle, mechanism and fabrication technologies: A comprehensive review. Sensors 14, 7881–7939 (2014).
Simon, I., Bârsan, N., Bauer, M. & Weimar, U. Micromachined metal oxide gas sensors: Opportunities to improve sensor performance. Sensors Actuators B Chem . 73, 1–26 (2001).
Fei, T., Zhao, H., Jiang, K., Zhou, X. & Zhang, T. Polymeric humidity sensors with nonlinear response: Properties and mechanism investigation. J. Appl. Polym. Sci. 130, 2056–2061 (2013).
Chen, W.-P., Zhao, Z.-G., Liu, X.-W., Zhang, Z.-X. & Suo, C.-G. A capacitive humidity sensor based on multi-wall carbon nanotubes (MWCNTs). Sensors 9, 7431–7444 (2009).
Han, J.-W., Kim, B., Li, J. & Meyyappan, M. A carbon nanotube based ammonia sensor on cellulose paper. RSC Adv . 4, 549–553 (2014).
Zhang, D., Tong, J., Xia, B. & Xue, Q. Ultrahigh performance humidity sensor based on layer-by-layer self-assembly of graphene oxide/polyelectrolyte nanocomposite film. Sensors Actuators B Chem . 203, 263–270 (2014).
HUMICAP“ humidity and temperature transmitter series HMT310. Available at: http://www.vaisala.com/en/products/humidity/Pages/HMT310.aspx. (Accessed: 4th May 2015).
Fowler, J. D. et al. Practical chemical sensors from chemically derived graphene. ACS Nano 3, 301–306 (2009).
Leenaerts, O., Partoens, B. & Peeters, F. M. Adsorption of H2O, NH3, CO, NO2 and NO on graphene: A first-principles study. Phys. Rev. B 77, 6 (2007).
Schedin, F. et al. Detection of individual gas molecules adsorbed on graphene. Nat. Mater. 6, 652–655 (2007).
Some, S. et al. Highly sensitive and selective gas sensor using hydrophilic and hydrophobic graphenes. Sci. Rep. 3, 1868 (2013).
Zhang, J. et al. A UV light enhanced TiO2/graphene device for oxygen sensing at room temperature. RSC Adv . 3, 22185 (2013).
Novoselov, K. S. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Stankovich, S. et al. Synthesis of graphene-based nanosheets via chemical reduction of exfoliated graphite oxide. Carbon 45, 1558–1565 (2007).
Howe, R. C. T., Hu, G., Yang, Z. & Hasan, T. Functional inks of graphene, metal dichalcogenides and black phosphorus for photonics and (opto)electronics. SPIE Nanosci. + Eng . 95530R (2015).
Li, X. et al. Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 324, 1312–1314 (2009).
Bonaccorso, F. et al. Production and processing of graphene and 2d crystals. Mater. Today 15, 564–589 (2012).
Bae, S. et al. Roll-to-roll production of 30-inch graphene films for transparent electrodes. Nat. Nanotechnol . 5, 574–578 (2010).
Hernandez, Y. et al. High-yield production of graphene by liquid-phase exfoliation of graphite. Nat. Nanotechnol . 3, 563–568 (2008).
Ghosh, R., Midya, A., Santra, S., Ray, S. K. & Guha, P. K. Chemically reduced graphene oxide for ammonia detection at room temperature. ACS Appl. Mater. Interfaces 5, 7599–7603 (2013).
Borini, S. et al. Ultrafast graphene oxide humidity sensors. ACS Nano 7, 11166–11173 (2013).
Ali, S., Udrea, F., Milne, W. & Gardner, J. Tungsten-based SOI microhotplates for smart gas sensors. J. Microelectromechanical Syst. 17, 1408–1417 (2008).
Guha, P. et al. Novel design and characterisation of SOI CMOS micro-hotplates for high temperature gas sensors. Sensors Actuators B Chem . 127, 260–266 (2007).
Santra, S., Guha, P. K., Ali, S. Z., Haneef, I. & Udrea, F. Silicon on insulator diode temperature sensor-A detailed analysis for ultra-high temperature operation. IEEE Sens. J. 10, 997–1003 (2010).
Nicolosi, V., Chhowalla, M., Kanatzidis, M. G., Strano, M. S. & Coleman, J. N. Liquid exfoliation of layered materials. Science 340, 1226419–1226419 (2013).
Yi, M., Shen, Z., Zhang, X. & Ma, S. Vessel diameter and liquid height dependent sonication-assisted production of few-layer graphene. J. Mater. Sci. 47, 8234–8244 (2012).
Mason, T. J. & Lorimer, J. P. Applied sonochemistry: Uses of power ultrasound in chemistry and processing (Wiley-VCH, 2002).
Hernandez, Y., Lotya, M., Rickard, D., Bergin, S. D. & Coleman, J. N. Measurement of multicomponent solubility parameters for graphene facilitates solvent discovery. Langmuir 26, 3208–3213 (2010).
Hansen, C. M. Hansen solubility parameters: A user’s handbook 2nd edn (CRC Press, 2007).
Luo, S., Harris, T. & Wong, C. Study on surface tension and adhesion for flip chip packaging. In Proc. Int. Symp. Adv. Packag. Mater. Process. Prop. Interfaces (IEEE Cat. No.01TH8562), 299–304 (IEEE, 2001).
Zisman, W. A. In Contact angle, wettability and adhesion, Vol. 43 of Advances in Chemistry, Ch. 1, 1–51 (American Chemical Society, 1964).
Aleeva, Y. & Pignataro, B. Recent advances in upscalable wet methods and ink formulations for printed electronics. J. Mater. Chem. C 2, 6436 (2014).
Wansbrough, H. Printing ink technology and manufacture. Available at: http://nzic.org.nz/ChemProcesses/polymers/10E.pdf. (Accessed: 22nd June 2015).
O’Neill, A., Khan, U., Nirmalraj, P. N., Boland, J. & Coleman, J. N. Graphene dispersion and exfoliation in low boiling point solvents. J. Phys. Chem. C 115, 5422–5428 (2011).
Hasan, T. et al. Nanotube-polymer composites for ultrafast photonics. Adv. Mater. 21, 3874–3899 (2009).
Hasan, T. et al. Solution-phase exfoliation of graphite for ultrafast photonics. Phys. status solidi 247, 2953–2957 (2010).
Torrisi, F. et al. Inkjet-printed graphene electronics. ACS Nano 6, 2992–3006 (2012).
O’Connell, M. J. et al. Reversible water-solubilization of single-walled carbon nanotubes by polymer wrapping. Chem. Phys. Lett. 342, 265–271 (2001).
Bourlinos, A. B. et al. Aqueous-phase exfoliation of graphite in the presence of polyvinylpyrrolidone for the production of water-soluble graphenes. Solid State Commun. 149, 2172–2176 (2009).
Hasan, T. et al. Stabilization and ‘debundling’ of single-wall carbon nanotube dispersions in N-Methyl-2-pyrrolidone (NMP) by polyvinylpyrrolidone (PVP). J. Phys. Chem. C 111, 12594–12602 (2007).
Hasan, T. et al. Polymer-assisted isolation of single wall carbon nanotubes in organic solvents for optical-quality nanotube-polymer composites. J. Phys. Chem. C 112, 20227–20232 (2008).
Bhattacharya, S. et al. Plasticization of poly(vinylpyrrolidone) thin films under ambient humidity: Insight from single-molecule tracer diffusion dynamics. J. Phys. Chem. B 117, 7771–7782 (2013).
Huang, L., Li, C. & Shi, G. High-performance and flexible electrochemical capacitors based on graphene/polymer composite films. J. Mater. Chem. A 2, 968–974 (2014).
Bohren, C. E. & Wiley, D. R. H. Absorption and scattering of light by small particles (Wiley-VCH, 1998).
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009).
Mak, K. F. et al. Measurement of the optical conductivity of graphene. Phys. Rev. Lett. 101, 196405 (2008).
Kravets, V. G. et al. Spectroscopic ellipsometry of graphene and an exciton-shifted van Hove peak in absorption. Phys. Rev. B 81, 155413 (2010).
Chou, K.-S. & Chen, C.-C. Fabrication and characterization of silver core and porous silica shell nanocomposite particles. Microporous Mesoporous Mater . 98, 208–213 (2007).
Li, J. et al. Efficient inkjet printing of graphene. Adv. Mater. 25, 3985–3992 (2013).
Secor, E. B., Prabhumirashi, P. L., Puntambekar, K., Geier, M. L. & Hersam, M. C. Inkjet printing of high conductivity, flexible graphene patterns. J. Phys. Chem. Lett. 4, 1347–1351 (2013).
Gupta, A., Chen, G., Joshi, P., Tadigadapa, S. & Eklund, P. C. Raman scattering from high-frequency phonons in supported n-graphene layer films. Nano Lett. 6, 2667–2673 (2006).
Jang, D., Kim, D. & Moon, J. Influence of fluid physical properties on ink-jet printability. Langmuir 25, 2629–2635 (2009).
Derby, B. Inkjet printing of functional and structural materials: Fluid property requirements, feature stability and resolution. Annu. Rev. Mater. Res. 40, 395–414 (2010).
van den Berg, A. M. J. et al. Inkjet printing of polyurethane colloidal suspensions. Soft Matter 3, 238–243 (2007).
Zeytounian, R. Kh . In Interfacial phenomena and the Marangoni effect, Vol. 428 of CISM International Centre for Mechanical Sciences, Ch. 4, 123–190 (Springer: Vienna,, 2002).
Singh, M., Haverinen, H. M., Dhagat, P. & Jabbour, G. E. Inkjet printing-process and its applications. Adv. Mater. 22, 673–685 (2010).
Deegan, R. D. et al. Contact line deposits in an evaporating drop. Phys. Rev. E 62, 756–765 (2000).
Finn, D. J. et al. Inkjet deposition of liquid-exfoliated graphene and MoS2 nanosheets for printed device applications. J. Mater. Chem. C 2, 925–932 (2014).
Li, J. & Kim, J.-K. Percolation threshold of conducting polymer composites containing 3D randomly distributed graphite nanoplatelets. Compos. Sci. Technol . 67, 2114–2120 (2007).
Dani, A. Electrical percolation behavior of short-fiber composites: Experimental characterization and modeling. Compos. Sci. Technol . 56, 911–920 (1996).
Wang, S. & Ogale, A. Continuum space simulation and experimental characterization of electrical percolation behavior of particulate composites. Compos. Sci. Technol . 46, 93–103 (1993).
Graphene nanoplatelets. Available at: http://www.strem.com/uploads/resources/documents/graphene_nanoplatelets.pdf. (Accessed: 23rd June 2015).
Tai, H., Li, X., Jiang, Y., Xie, G. & Du, X. The enhanced formaldehyde-sensing properties of P3HT-ZnO hybrid thin film OTFT sensor and further insight into its stability. Sensors 15, 2086–2103 (2015).
Lu, G., Ocola, L. E. & Chen, J. Gas detection using low-temperature reduced graphene oxide sheets. Appl. Phys. Lett. 94, 083111 (2009).
Yuan, W. & Shi, G. Graphene-based gas sensors. J. Mater. Chem. A 1, 10078 (2013).
Galvin, C. J., Dimitriou, M. D., Satija, S. K. & Genzer, J. Swelling of polyelectrolyte and polyzwitterion brushes by humid vapors. J. Am. Chem. Soc. 136, 12737–12745 (2014).
Acknowledgements
S.S. acknowledges Department of Science and Technology (DST), India for Ramanujan Fellowship to support the work (project no. SR/S2/RJN-104/2011). This work was (partly) supported through the EU FP7 project MSP (611887). T.H. acknowledges support from the Royal Academy of Engineering through a fellowship (Graphlex).
Author information
Authors and Affiliations
Contributions
S.S. and T.H. conceived the experiments. S.S., P.K.G., G.H. and R.C.T.H. conducted the experiments. S.S., G.H., R.C.T.H. and T.H. analysed the results. A.D.L., S.Z.A., F.U., J.W.G. and S.K.R. provided guidance on microhotplate design and device characterization. S.S., G.H. and T.H. wrote the manuscript. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Santra, S., Hu, G., Howe, R. et al. CMOS integration of inkjet-printed graphene for humidity sensing. Sci Rep 5, 17374 (2015). https://doi.org/10.1038/srep17374
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep17374
This article is cited by
-
Tetrazine-based 1D polymers for the selective chemiresistive sensing of nitrogen dioxide via the interplay between hydrogen bonding and n-heteroatom interactions
Polymer Journal (2022)
-
Porous nanocarbon particles drive large magnitude and fast photomechanical actuators
Journal of Nanostructure in Chemistry (2022)
-
The electrical conductivity of solution-processed nanosheet networks
Nature Reviews Materials (2021)
-
Inkjet-printed CMOS-integrated graphene–metal oxide sensors for breath analysis
npj 2D Materials and Applications (2019)
-
Inkjet-printed MXene micro-scale devices for integrated broadband ultrafast photonics
npj 2D Materials and Applications (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.