Abstract
Geometric frustration, in which competing interactions give rise to degenerate ground states, potentially induces various exotic quantum phenomena in magnetic materials. Minimal models comprising triangular units, such as triangular and Kagome lattices, have been investigated for decades to realize novel quantum phases, such as quantum spin liquid. A pentagon is the second-minimal elementary unit for geometric frustration. The realization of such systems is expected to provide a distinct platform for studying frustrated magnetism. Here, we present a spin-1/2 quantum pentagonal lattice in the new organic radical crystal α-2,6-Cl2-V [=α-3-(2,6-dichlorophenyl)-1,5-diphenylverdazyl]. Its unique molecular arrangement allows the formation of a partially corner-shared pentagonal lattice (PCPL). We find a clear 1/3 magnetization plateau and an anomalous change in magnetization in the vicinity of the saturation field, which originate from frustrated interactions in the PCPL.
Similar content being viewed by others
Introduction
Closed loop lattice systems with an odd number of antiferromagnetic (AFM) bonds induce frustration through competing exchange interactions that cannot be simultaneously satisfied. Pentagonal lattices can therefore induce frustration in analogy with systems based on triangular lattice, which have been investigated extensively1,2,3,4,5,6,7. Quantum pentagonal systems have yet to be realized experimetaly however. Regular pentagons cannot tile a plane because of the crystallographic restriction theorem, such that distortion and/or additional shapes are necessary8,9,10,11. The Cairo pentagonal lattice—a two-dimensional plane consisting of distorted pentagons with two inequivalent sites8—has attracted considerable attention since its recent realization in iron-based compounds with classical spins12,13. Although the lattice systems in iron-based compounds differ somewhat from the regular Cairo pentagonal lattice, their realizations have inspired further theoretical studies on quantum cases14,15,16,17, where the emergence of a spin-nematic phase and a 1/3 magnetization plateau are predicted. These specific quantum phases originate from the two types of inequivalent sites and the six spins in the magnetic unit cell, important characteristics that are common to the Cairo pentagonal lattice and the partially corner-shared pentagonal lattice (PCPL) investigated here.
Here, we introduce the basic properties of the PCPL. It contains two inequivalent sites, α and β, with coordination numbers 2 and 4, respectively, as shown in Fig. 1(a). The α site has two β neighbors, whereas each β site is connected to one α and three β sites. One ferromagnetic (FM) interaction J1 and two AFM interactions J2 and J3 form a twisted pentagonal unit consisting of J1-J3-J2-J3-J1 and induce frustration. The unit cell of the PCPL contains two α and four β sites (see Supplementary Information). The six spins in the unit cell and the observed 1/3 magnetization plateau suggest the existence of a nonmagnetic singlet state with an excitation energy gap formed by the AFM interactions J2 and/or J3 between the β sites. The residual α-site spins interact with one another through the triplet excited states of such singlet state.
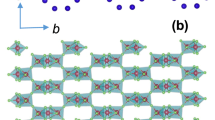
Magnetic and crystal structures of α-2,6-Cl2-V.
(a) Partially corner-shared pentagonal lattice (PCPL) of the α-2,6-Cl2-V crystal. The blue sphere and the three types of solid lines denote spin-1/2 and intermolecular interactions J1, J2 and J3, respectively. There are two inequivalent sites, α and β, with coordination numbers 2 and 4, respectively. The two J1-J1-J2 chains are running along the a + b and a − b directions and J3 corresponds to the interchain interaction. Thus, the unit cell includes six sites consisting of two α and four β sites. (b) Molecular structure of 2,6-Cl2-V. The central verdazyl ring with four nitrogen atoms and three phenyl rings are labeled R1, R2, R3 and R4, respectively. The Cl atoms introduced at the 2,6-position induces a relatively large dihedral angle (>80°) only in R1-R3 owing to the electrostatic repulsion between the Cl and N atoms. (c) Crystal structure of the twisted-plane pentagonal unit. The hydrogen atoms are omitted for clarity. The non-planar structure of the molecules inhibits simple stacking, resulting in the formation of an unconventional pentagonal unit.
The symmetry and shape of electron orbitals make crystals based on pentagonal lattices difficult to form in inorganic materials. In fact, there are few examples in the history of condensed matter physics. Unconventional lattice system should however be realizable with organic radical materials in diverse molecular arrangements. We recently established synthetic techniques for the preparation of high-quality verdazyl radical crystals18. In contrast to other conventional radicals such as nitroxide and nitronyl nitroxide, the π-electron spin density of verdazyl radicals can be delocalized even in non-planar molecular structures. This makes the molecular orbitals (MOs) associated with exchange interactions flexible in shape and enables the design of lattice systems by chemical modification, thereby facilitating the synthesis of new materials forming unconventional lattice systems18,19,20,21. Here, we present the successful synthesis of a new verdazyl radical crystal, α-2,6-Cl2-V. Ab initio MO calculations indicate the formation of an S = 1/2 quantum pentagonal lattice consisting of one FM and two AFM interactions.
Results and Discussion
Figure 1(b) shows the molecular structure of 2,6-Cl2-V. The crystallographic parameters at room temperature are as follows22: orthorhombic, space group Fdd2, a = 42.759(3) Å, b = 15.5551(12) Å, c = 16.6127(13) Å, V = 11049.4(15) Å3, Z = 24, R = 0.0346 and Rw = 0.0846. Furthermore, there is no indication of a structural phase transition down to around 23 K (see Supplementary Table S1). The central verdazyl ring with four nitrogen atoms and three phenyl rings are labeled R1, R2, R3 and R4, respectively [Fig. 1(b)]. The crystals contain two crystallographically independent molecules, in which the large ionic radius of the Cl atom, introduced at the 2,6-position, induces a relatively large dihedral angle (>80°) at R1-R3 owing to electrostatic repulsion between the Cl and N atoms [Fig. 1(b)]. This non-planar structure inhibits molecular stacking and the overlap of singly occupied MOs, resulting in the formation of the PCPL.
Ab initio MO calculations on the basis of the crystallographic arrangement at 23 K show that one FM and two AFM exchange interactions, labeled as J1, J2 and J3 (see Supplementary Fig. S2), are dominant. They are evaluated as J1/kB = −1.6 K, J2/kB = 3.9 K and J3/kB = 3.3 K, which are defined in the Heisenberg spin Hamiltonian given by  , where
, where  denotes the sum over the neighboring spin pairs. The three evaluated interactions form a twisted pentagonal unit consisting of J1-J3-J2-J3-J1, as shown in Fig. 1(c). The pentagonal units are connected to one another by sharing a corner, resulting in the formation of the S = 1/2 PCPL, as shown in Fig. 1(a).
denotes the sum over the neighboring spin pairs. The three evaluated interactions form a twisted pentagonal unit consisting of J1-J3-J2-J3-J1, as shown in Fig. 1(c). The pentagonal units are connected to one another by sharing a corner, resulting in the formation of the S = 1/2 PCPL, as shown in Fig. 1(a).
Figure 2(a) shows the temperature dependence of the magnetic susceptibilities (χ = M/H) at 0.1 T. At temperature above 50 K, the Curie-Weiss law is followed, χ = C/(T − θW). The estimated Curie constant is about C = 0.362 emu· K/mol, which is close to the expected value for noninteracting S = 1/2 spins and the Weiss temperature is estimated to be θW = −0.85(5) K. Considering the mean-field approximation expressed as  , this small absolute value of θW indicates a weak internal field due to competition between the FM and AFM interactions. We observe a shoulder and corresponding two-step decrease in χΤ at about 1 K [inset of Fig. 2(a)] , which indicate the contribution of two or more types of AFM interactions.
, this small absolute value of θW indicates a weak internal field due to competition between the FM and AFM interactions. We observe a shoulder and corresponding two-step decrease in χΤ at about 1 K [inset of Fig. 2(a)] , which indicate the contribution of two or more types of AFM interactions.
Temperature dependence of the magnetization and specific heat of α-2,6-Cl2-V.
(a) Temperature dependence of the magnetic susceptibility (χ = M/H) of α-2,6-Cl2-V at 0.1 T . A shoulder appears in χ at about 1 K with a corresponding two-step decrease in χΤ. The solid line indicates the Curie-Weiss law. (b) Temperature dependence of the total specific heat (Cp) of α-2,6-Cl2-V at zero-field. The inset shows Cp up to 300 K. A peak characteristic of Schottky-like behavior appears at about 1.4 K. The arrow indicates a sharp peak associated with the phase transition to an ordered state at about 0.07 K.
Figure 2(b) shows the temperature dependence of the total specific heat, Cp, at zero-field. A clear broad peak appears at about 1.4 K, which is characteristic of a Schottky-like behavior associated with an energy gap between excited states. Consistent with such Schottky-like Cp behavior, a clear 1/3 magnetization plateau is observed from 0.4 to 1.3 T, indicating an energy gap between the excited states, as shown in Fig. 4. The six spins in the unit cell and the 1/3 magnetization plateau suggest the existence of a nonmagnetic singlet state with an excitation energy gap formed by the AFM interactions J2 and/or J3 between the β sites. If such is the case, residual α-site spins interact with one another through the excited states of the singlet state as discussed later. The magnetization curve indeed increases less steeply than the Brillouin function for free S = 1/2 spins up to the plateau phase, highlighting the presence of non-negligible AFM internal fields. In this context, a sharp peak of the specific heat observed at about 0.07 K is explained by a zero-field phase transition to long-range AFM order of the α-site spins. In the 1/3 plateau phase, these spins are fully polarized along the external field direction such that the ordered state disappears. The phase transition actually disappears in the specific heat at 1.0 T, while the Schottky-like behavior is shifted to around 0.5 K in response to the decrease of the energy gap, as shown in Fig. 3. In the case of the higher field region above the plateau phase, the field derivative of the magnetization curve (dM/dH) indicates linear behavior in H near the saturation field from 3.3 to 4.0 T, as shown in Fig. 4. This behavior is in clear contrast to the magnetization curve of conventional quantum spin systems, in which external field suppresses quantum fluctuations, which results in an upward curvature of the magnetization curve and a sharp dH/dH peak at the phase transition to fully polarized state23,24. The upturn observed in Cp at 4.0 T should therefore be attributed to unconventional magnetic behavior near the saturation field.
Low-temperature magnetization curve of α-2,6-Cl2-V.
Magnetization curve and its field derivative for α-2,6-Cl2-V at 0.1 K. The illustration describes the predicted magnetic state in the 1/3 plateau phase, where spins on the α and β sites are fully polarized state and singlet dimer, respectively. The colored region between about 3.3 and 4.0 T indicates an unconventional phase with the relation of H ∝ M near the saturation field.
Low-temperature specific heat of α-2,6-Cl2-V under various magnetic fields.
Temperature dependence of the total specific heat (Cp) of α-2,6-Cl2-V below 1.0 K under various magnetic fields. At these low-temperatures, Cp can be regarded as that from magnetic contribution. For clarity, the Cp for 1.0, 2.0, 3.0, 4.0 and 5.0 T have been shifted upward by 1.0, 2.2, 3.3, 4.2 and 5.3 J/mol K, respectively. The black arrow at zero-field indicates the temperature of the phase transition to the ordered state. At 1.0 T, the phase transition disappears and Schottky-like behavior appears at about 0.5 K. The red arrow shows a clear upturn in the 4.0 T data, suggesting some kind of field-induced phase transition at lower temperatures.
In order to identify the contribution of abovementioned AFM interaction, we assumed a simple situation in which the fully polarized α-site spin works only as an internal field  for each β-site spin in the high-field region above the 1/3 magnetization plateau. Accordingly, we considered a lattice system consisting of only J2 and J3 with an effective internal field
for each β-site spin in the high-field region above the 1/3 magnetization plateau. Accordingly, we considered a lattice system consisting of only J2 and J3 with an effective internal field  , where Hext is the external magnetic field. In the extreme case where
, where Hext is the external magnetic field. In the extreme case where  , the two spins connected by the J2 interaction form a nonmagnetic singlet dimer with an excitation energy gap. In gapped cases such as this, the magnetization curve near the critical field—the end of the 1/3 plateau phase in the present case—increases with the square root of the applied field. For
, the two spins connected by the J2 interaction form a nonmagnetic singlet dimer with an excitation energy gap. In gapped cases such as this, the magnetization curve near the critical field—the end of the 1/3 plateau phase in the present case—increases with the square root of the applied field. For  in contrast, the AFM interaction J3 forms a well-known S = 1/2 uniform AFM chain with a Tomonaga-Luttinger liquid ground state and the energy gap disappears. The 1/3 plateau phase and sharp dM/dH peak that are observed here therefore indicate a singlet state arising from the AFM interaction J2 with
in contrast, the AFM interaction J3 forms a well-known S = 1/2 uniform AFM chain with a Tomonaga-Luttinger liquid ground state and the energy gap disappears. The 1/3 plateau phase and sharp dM/dH peak that are observed here therefore indicate a singlet state arising from the AFM interaction J2 with  , as described in Fig. 4. Accordingly, the effective interactions between the residual α-site spins are caused through the triplet excited states of the J2 singlet dimer22,25,26. They are roughly evaluated from the second-order and third-order perturbation treatment of the J2 term in the spin Hamiltonian (see Supplementary Information). We can consider that α-site spins form a uniform AFM chain with weak interchain interactions in the low-field region. These interactions should cause the phase transition to long-range AFM order of the α-site spins.
, as described in Fig. 4. Accordingly, the effective interactions between the residual α-site spins are caused through the triplet excited states of the J2 singlet dimer22,25,26. They are roughly evaluated from the second-order and third-order perturbation treatment of the J2 term in the spin Hamiltonian (see Supplementary Information). We can consider that α-site spins form a uniform AFM chain with weak interchain interactions in the low-field region. These interactions should cause the phase transition to long-range AFM order of the α-site spins.
Finally, concerning the unconventional behavior near the saturation field, a plausible explanation is that this reflects a hidden order of spin multipoles caused by correlations between multi-magnon bound states, such as those in a spin-nematic phase27. The presence of such a phase is expected in the high-field region (near the saturation field) in S = 1/2 frustrated spin systems with FM interactions27,28, but has not been verified experimentally to date. In the PCPL, the three spins connected by the J1 FM interaction may stabilize the three-magnon bound state in the vicinity of the saturation field, resulting in multipole spin order. Additional experimental techniques, notably neutron scattering using deuterated samples, should afford a more quantitative description of this field-induced phase and clarify the pentagonal frustration effect.
Methods
We synthesized 2,6-Cl2-V using a conventional procedure similar to that used for preparing the typical verdazyl radical 1,3,5-triphenylverdazyl29. The crystal structure was determined on the basis of intensity data collected using a Rigaku AFC-8R Mercury CCD RA-Micro7 diffractometer with Japan Thermal Engineering XR-HR10K. The magnetizations were measured using a commercial SQUID magnetometer (MPMS-XL, Quantum Design) and a capacitive Faraday magnetometer down to about 70 mK. The experimental results were corrected for diamagnetic contribution (−2.57 × 10−4), which is determined to become almost χΤ = const. above about 200 K and close to the value calculated by Pascal's method. The specific heat was measured using a hand-made apparatus by a standard adiabatic heat-pulse method down to about 50 mK. Considering the isotropic nature of organic radical systems, all experiments were performed using small randomly oriented single crystals. The ab initio MO calculations were performed using the UB3LYP method as broken-symmetry hybrid-density functional theory calculations. All the calculations were performed using the Gaussian 09 program package and the basis functions used were 6–31G. To estimate the intermolecular magnetic interaction of the molecular pairs within 4.0 Å, we applied our previously presented evaluation scheme30.
Additional Information
How to cite this article: Yamaguchi, H. et al. Experimental Realization of a Quantum Pentagonal Lattice. Sci. Rep. 5, 15327; doi: 10.1038/srep15327 (2015).
References
Coldea, R., Tennant, D. A., Tsvelik, A. M. & Tylczynski, Z. Experimental realization of a 2D fractional quantum spin liquid. Phys. Rev. Lett. 86, 1335–1338 (2001).
Fortuen, N. A. et al. Cascade of magnetic-field-induced quantum phase transitions in a spin-1/2 triangular-lattice antiferromagnet. Phys. Rev. Lett. 102, 257201 (2009).
Shirata, Y., Tanaka, H., Matsuo, A. & Kindo, K. Experimental realization of a spin-1/2 triangular-lattice Heisenberg antiferromagnet. Phys. Rev. Lett. 108, 057205 (2012).
Okamoto, Y., Yoshida, H. & Zenji, H. Vesignieite BaCu3V2O8(OH)2 as a candidate spin-1/2 kagome antiferromagnet. J. Phys. Soc. Jpn. 78, 033701 (2009).
Matan, K. et al. Pinwheel valence-bond solid and triplet excitations in the two-dimensional deformed kagome lattice. Nature Phys. 6, 865–869 (2010).
Han, T. H. et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 492, 406–410 (2012).
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
Urumov, V. Exact solution of the Ising model on a pentagonal lattice. J. Phys. A: Math. Gen. 35, 7317–7321 (2002).
Bhaumik, U. & Bose, I. Collinear Néel-type ordering in partially frustrated lattices. Phys. Rev. B 58, 73–76 (1998).
Levine, D. & Steinhardt, P. J. Quasicrystals: A new class of ordered structure. Phys. Rev. Lett. 53, 2477–2480 (1984).
Tsunetsugu, H., Fujiwara, T., Ueda, K. & Tokihiro, T. Electronic properties of the Penrose lattice. I. Energy spectrum and wave functions. Phys. Rev. B 43, 8879–8891 (1990).
Ressouche, E., Simonet, V., Canals, B., Gospodinov, M. & Skumryev, V. Magnetic frustration in an iron-based Cairo pentagonal lattice. Phys. Rev. Lett. 103, 267204 (2009).
Abakumov, A. M. et al. Frustrated pentagonal Cairo lattice in the non-collinear antiferromagnet Bi4Fe5O13F. Phys. Rev. B 87, 139902 (2013).
Arnaud, R. Phase diagram of the Cairo pentagonal XXZ spin-1/2 magnet under a magnetic field. Phys. Rev. B 84, 184434 (2011).
Rousochatzakis, I., Läuchli, A. M. & Moessner, R. Quantum magnetism on the Cairo pentagonal lattice. Phys. Rev. B 85, 104415 (2012).
Nakano, H., Isoda, M. & Sakai, T. Magnetization process of the S = 1/2 Heisenberg antiferromagnet on the Cairo pentagon lattice. J. Phys. Soc. Jpn. 83, 053702 (2014).
Isoda, M., Nakano, H. & Sakai, T. Frustration-induced magnetic properties of the spin-1/2 Heisenberg antiferromagnet on the Cairo pentagon lattice. J. Phys. Soc. Jpn. 83, 084710 (2014).
Iwase, K. et al. Crystal structure and magnetic properties of the verdazyl biradical m-Ph-V2 forming a ferromagnetic alternating double chain. J. Phys. Soc. Jpn. 82, 074719 (2013).
Yamaguchi, H. et al. Unconventional magnetic and thermodynamic properties of S = 1/2 spin ladder with ferromagnetic legs. Phys. Rev. Lett. 110, 157205 (2013).
Yamaguchi, H. et al. Various regimes of quantum behavior in an S = 1/2 Heisenberg antiferromagnetic chain with fourfold periodicity. Phys. Rev. B 88, 174410 (2013).
Yamaguchi, H. et al. Fine-tuning of magnetic interactions in Organic spin ladders. J. Phys. Soc. Jpn. 83, 033707 (2014).
Crystallographic data have been deposited with Cambridge Crystallographic Data Centre: Deposition No. CCDC 1403881 for room temperature and CCDC 1403882 for 23 K.
Griffiths, R. B. Magnetization curve at zero temperature for the antiferromagnetic Heisenberg linear chain. Phys. Rev. 133, A768–A775 (1964).
Zhitomirsky, M. E. & Nikuni, T. Magnetization curve of a square-lattice Heisenberg antiferromagnet. Phys. Rev. B 57, 5013–5016 (1998).
Masuda, T. et al. Cooperative ordering of gapped and gapless spin networks in Cu2Fe2Ge4O13 . Phys. Rev. Lett. 93, 077202 (2004).
Hase, M. et al. Direct observation of the energy gap generating the 1/3 magnetization plateau in the spin-1/2 trimer chain compound Cu3(P2O6OD)2 by inelastic neutron scattering measurements. Phys. Rev. B 76, 064431 (2007).
Shanon, N., Momoi, T. & Sindzingre, P. Nematic order in square lattice frustrated ferromagnets. Phys. Rev. Lett. 96, 027213 (2006).
Hikihara, T., Kecke, L., Momoi, T. & Furusaki, A. Vector chiral and multipolar orders in the spin-1/2 frustrated ferromagnetic chain in magnetic field. Phys. Rev. B 78, 144404 (2008).
Kuhn, R. Über verdazyle und verwandte Stickstoffradikale. Angew. Chem. 76, 691 (1964).
Shoji, M. et al. A general algorithm for calculation of Heisenberg exchange integrals J in multispin systems. Chem. Phys. Lett. 432, 343–347 (2006).
Acknowledgements
We thank T. Kawakami, H. Nakano and T. Tonegawa for valuable discussions. We also thank A. Matsuo for specific heat measurement. This research was partly supported by a Grant for Basic Science Research Projects from the Sumitomo Foundation, KAKENHI (Nos. 24540347 and 24340075), the Strategic Programs for Innovative Research (SPIRE), MEXT and the Computational Materials Science Initiative (CMSI), Japan. This work was partly performed under the interuniversity cooperative research program of the joint-research program of the ISSP (University of Tokyo) and the Institute for Molecular Science.
Author information
Authors and Affiliations
Contributions
H.Y., K.I., N.A., T.O. and Y.H. carried out sample preparation and characterization. H.Y. and T.O. discussed the results. S.K., T.S. and K.A. performed the magnetic and thermodynamic measurements.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Yamaguchi, H., Okubo, T., Kittaka, S. et al. Experimental Realization of a Quantum Pentagonal Lattice. Sci Rep 5, 15327 (2015). https://doi.org/10.1038/srep15327
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep15327
This article is cited by
-
Randomness-induced quantum spin liquid on honeycomb lattice
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.