Abstract
The laws of thermodynamics put limits to the efficiencies of thermal machines. Analogues of these laws are now established for quantum engines weakly and passively coupled to the environment providing a framework to find improvements to their performance. Systems whose interaction with the environment is actively controlled do not fall in that framework. Here we consider systems actively and locally coupled to the environment, evolving with a so-called boundary-driven Lindblad equation. Starting from a unitary description of the system plus the environment we simultaneously obtain the Lindblad equation and the appropriate expressions for heat, work and entropy-production of the system extending the framework for the analysis of new and some already proposed, quantum heat engines. We illustrate our findings in spin 1/2 chains and explain why an XX chain coupled in this way to a single heat bath relaxes to thermodynamic-equilibrium while and XY chain does not. Additionally, we show that an XX chain coupled to a left and a right heat baths behaves as a quantum engine, a heater or refrigerator depending on the parameters, with efficiencies bounded by Carnot efficiencies.
Similar content being viewed by others
Introduction
Considerable experimental progress in various physical systems has been achieved toward the goal of controlling the dynamics of open quantum systems and their interactions with the environment1,2,3. For quantum computations or digital coherent quantum simulations, one may wish to have a system that is well isolated from the environment. For dissipative variants of quantum computations4 or creating new scenarios for non-equilibrium many-body systems, one would need to engineer the coupling to the environment. Recently, a setting in which the quantum system of interest interacts at its boundaries with an external quantum probe such that their coupling can be localized and can be switched on and off repeatedly with a controlled and well-defined state for the probe prior to the interaction has been experimentally realized5. This repeated interaction scheme has also been theoretically studied6,7. Importantly, the dynamics in an appropriate limit is a boundary-driven Lindblad equation. In this article, we explore the question of what is the thermodynamic cost of having such operations on an open quantum system and what are the thermodynamical quantities, such as heat and work that will determine the efficiency of quantum engines operating in this manner. Boundary-driven Lindblad equations have been intensively studied theoretically, particularly for one-dimensional quantum chains7,8,9,10,11,12,13,14,15,16,17,18,19 and powerful techniques have been developed to find their non-equilibrium steady states (NESS)12,13,14,15,16,17,18,19. These equations are also frequently used to describe quantum engines20,21,22,23 and other complex open quantum systems coupled to one or several environments24,25,26,27 because they are easy to implement. Nevertheless, a boundary driven Lindblad equation does not correctly describe a quantum system passively and weakly coupled to a heat-bath as often occurs in natural systems. It was pointed out recently28 that inconsistencies with the second law of thermodynamics may arise in this case and a careful examination of the coupling between a quantum refrigerator and the heat-baths29 reveals why boundary driven models are inappropriate for these situations. For a system passively and weakly coupled to one or several heat-baths the master equation derived in the Born-Markov-secular approximation30 yields a proper description of the system and the correct balance of heat flows and irreversible entropy production.
Thus, for our study, we consider explicitly the active (time-dependent) type of interaction between the system and the environment implemented in5 and the model developed in6,7. We apply the results of31,32 to derive the appropriate thermodynamical quantities and, in particular, we focus in the limit where the system is described by a boundary driven Lindblad equation.
Our main result is that driving at the boundaries, even though it looks like a work-free operation, actually might bring work to the system. We illustrate our findings on boundary-driven spin 1/2 chains coupled to one or two heat baths. We show that an XX spin 1/2 chain coupled in this way to a single heat bath relaxes to thermodynamic equilibrium while an XY does not because it is driven out of equilibrium by the power produced by the coupling to the heat bath. When two baths are connected to the chain, we observe that for different parameters, the chain operates as a quantum heat engine, refrigerator or heater and we determine their efficiencies in the simple case of a chain of two sites. The rest of the paper is organized as follows. We start by reviewing first the thermodynamics of Markovian open quantum systems in the weak coupling limit33,34,35,36 and second a formulation31 where the “universe”, system plus the environment, evolves unitarily. After that, we consider the repeated interaction scenario for the system and the environment from which the boundary-driven Lindblad equation and the appropriate thermodynamical quantities for the open system are obtained. Then we illustrate our results in XX and XY spin 1/2 chains and offer our conclusions. Finally we have collected in section Methods some details of the calculations.
Thermodynamics of open quantum systems
Open system weakly and passively coupled to the environment
Let us briefly review the usual formulation of thermodynamics in open quantum systems33,34,35,36. Consider an open system described by a master equation in the Lindblad form

where the environment consists of several heat-baths r whose action on the system is represented by the dissipator

with  the commutator and
the commutator and  the anti-commutator. The operators
the anti-commutator. The operators  are system operators and represent the action of the environment over the system. When this equation is obtained from the weak coupling limit for a time independent system, one finds global Lindblad operators
are system operators and represent the action of the environment over the system. When this equation is obtained from the weak coupling limit for a time independent system, one finds global Lindblad operators  that are eigen-operator of the Hamiltonian HS30. For simplicity, we consider that the system can only exchange energy and no particles with the environment.
that are eigen-operator of the Hamiltonian HS30. For simplicity, we consider that the system can only exchange energy and no particles with the environment.
Now consider the internal energy  and the entropy
and the entropy 
 . The first law of thermodynamics
. The first law of thermodynamics  splits the rate of change of internal energy in two, power
splits the rate of change of internal energy in two, power  and heat flow
and heat flow  with one contribution per heat-bath. For system passively and weakly coupled to the heat-baths, these quantities are defined as
with one contribution per heat-bath. For system passively and weakly coupled to the heat-baths, these quantities are defined as

In section Methods: Heat from a given reservoir in the weak-coupling limit we justify these definitions. Note that if the Hamiltonian of the system is time independent, no work can be performed on the system and only heat is exchanged with the baths. In that case the system will typically reach a steady state. Consider now this to be the situation. The second law states the positivity of the entropy production  , which is the difference between the time-derivative of the entropy
, which is the difference between the time-derivative of the entropy  and the entropy flow from the environment to the system
and the entropy flow from the environment to the system  ,
,

The canonical distribution  appears in the last equality of Eq. (3) due to the definition of heat that we plug in the first equality in Eq. (3). The second law
appears in the last equality of Eq. (3) due to the definition of heat that we plug in the first equality in Eq. (3). The second law  in Eq. (3) holds if for every r,
in Eq. (3) holds if for every r,  relaxes towards the unique equilibrium state
relaxes towards the unique equilibrium state  . This is the local-detailed-balance condition37 i.e. if a single heat-bath is in contact with the system detailed balance as defined in34,38 holds. This property of the dissipators
. This is the local-detailed-balance condition37 i.e. if a single heat-bath is in contact with the system detailed balance as defined in34,38 holds. This property of the dissipators  is satisfied in quantum master equations obtained in the weak-coupling and with the Born-Markov-secular approximation (global Lindblad equation). This framework has been applied successfully to the study of thermodynamic properties and efficiencies of engines29,39,40,41.
is satisfied in quantum master equations obtained in the weak-coupling and with the Born-Markov-secular approximation (global Lindblad equation). This framework has been applied successfully to the study of thermodynamic properties and efficiencies of engines29,39,40,41.
In boundary-driven systems the Lindblad operators  act locally on the boundaries of the system and in general the corresponding Lindblad equation does not satisfy local-detailed-balance. We come back to this point later. Following recent developments in the physics of non-equilibrium systems that have emphasized the importance of time reversal symmetry at the microscopic level of description42, a formulation of quantum thermodynamics in which the system plus the environment evolves unitarily has been proposed31. We consider this framework to analyze boundary driven systems.
act locally on the boundaries of the system and in general the corresponding Lindblad equation does not satisfy local-detailed-balance. We come back to this point later. Following recent developments in the physics of non-equilibrium systems that have emphasized the importance of time reversal symmetry at the microscopic level of description42, a formulation of quantum thermodynamics in which the system plus the environment evolves unitarily has been proposed31. We consider this framework to analyze boundary driven systems.
“universe” under unitary evolution
Let a system and an environment with Hamiltonians  and HE (time independent), respectively, coupled by an interaction potential V(t) evolve with total Hamiltonian
and HE (time independent), respectively, coupled by an interaction potential V(t) evolve with total Hamiltonian  . The environment might consists of several heat baths
. The environment might consists of several heat baths  with
with  the initial density matrix for the reservoir r. Initially, the system and heat baths are uncorrelated
the initial density matrix for the reservoir r. Initially, the system and heat baths are uncorrelated  . For arbitrary strength coupling between the system and environment31, the internal energy is defined by
. For arbitrary strength coupling between the system and environment31, the internal energy is defined by  and the first law relates its changes to work and heat
and the first law relates its changes to work and heat  with the work
with the work  performed on the system in the time interval [0, t], which is also given by
performed on the system in the time interval [0, t], which is also given by

and the total heat flow  split in reservoir contributions
split in reservoir contributions

given by minus the change in energy of the r-reservoir.
Considering  as the thermodynamic entropy of the system and
as the thermodynamic entropy of the system and  , it is found that
, it is found that  with the entropy flow
with the entropy flow  determined by the heat flows in Eq. (5) and the entropy production31
determined by the heat flows in Eq. (5) and the entropy production31

with  . Unitarity, expressed through the invariance of
. Unitarity, expressed through the invariance of  under the time evolution of the full system, plays a crucial role in the splitting of entropy change in the entropy flow and a positive entropy production. In the weak-coupling limit
under the time evolution of the full system, plays a crucial role in the splitting of entropy change in the entropy flow and a positive entropy production. In the weak-coupling limit  and assuming that the open system satisfies a Lindblad equation obtained from the Born-Markov-secular approximation30, the rate of entropy production
and assuming that the open system satisfies a Lindblad equation obtained from the Born-Markov-secular approximation30, the rate of entropy production  and the above expressions for work and heat take the standard form given in Eq. (3) and Eq. (2) respectively. This is shown in section methods by considering the method of full-counting statistics43. However, the Lindblad models investigated in7,8,9,10,12,13,14,15,16,17,18,28 are not obtained from the weak-coupling limit and do not satisfy local-detailed-balance. Thus to obtain the appropriate expressions for the thermodynamical quantities in boundary driven systems we apply in the next section the previous formulation, in particular Eqs (4),(5),(6), to a system plus environment evolving unitarily in which the reduced density matrix for the system satisfy a boundary driven Lindblad equation in an exact limit.
and the above expressions for work and heat take the standard form given in Eq. (3) and Eq. (2) respectively. This is shown in section methods by considering the method of full-counting statistics43. However, the Lindblad models investigated in7,8,9,10,12,13,14,15,16,17,18,28 are not obtained from the weak-coupling limit and do not satisfy local-detailed-balance. Thus to obtain the appropriate expressions for the thermodynamical quantities in boundary driven systems we apply in the next section the previous formulation, in particular Eqs (4),(5),(6), to a system plus environment evolving unitarily in which the reduced density matrix for the system satisfy a boundary driven Lindblad equation in an exact limit.
The repeated interaction scheme
Let us consider a finite system with time-independent Hamiltonian HS and left (L) and right (R) reservoirs composed of an infinite set of identical non-interacting finite systems with Hamiltonian  , i.e.,
, i.e.,  , where r is L or R. Each
, where r is L or R. Each  interacts with the system for a time span τ. This interaction is always of the same form, but to emphasize that interactions occur with different copies
interacts with the system for a time span τ. This interaction is always of the same form, but to emphasize that interactions occur with different copies  in different time intervals, we write it as
in different time intervals, we write it as  if
if  with
with  . At
. At  , the system and reservoirs are decoupled, i.e.,
, the system and reservoirs are decoupled, i.e.,  , with
, with  arbitrary and
arbitrary and  , where
, where  . At
. At  , the system begins to interact with the first copy
, the system begins to interact with the first copy  and after a lapse of time τ, the state of the total system is
and after a lapse of time τ, the state of the total system is  . Then, at t = τ + 0, the interaction with the first copy is replaced by an interaction with the second copy for a time τ and so on. A recursion relation for the state of the system is obtained6,7 by tracing out the nth copy of the environment (denoted as Trn)
. Then, at t = τ + 0, the interaction with the first copy is replaced by an interaction with the second copy for a time τ and so on. A recursion relation for the state of the system is obtained6,7 by tracing out the nth copy of the environment (denoted as Trn)

The unitaries are  . This is the repeated interaction scheme. For simplicity we considered only two heat-baths but the generalization to several reservoirs is straight forward.
. This is the repeated interaction scheme. For simplicity we considered only two heat-baths but the generalization to several reservoirs is straight forward.
Let us consider the change of thermodynamical quantities in the time intervals of length τ. Crucially, due to the resetting of the heat baths, the interaction term is time dependent. According to Eq. (4) for time-independent  , work is performed at the discrete times
, work is performed at the discrete times  where the interaction between the system and the environment changes because the copy in interaction changes. Performing the integral in Eq. (4) between an initial time
where the interaction between the system and the environment changes because the copy in interaction changes. Performing the integral in Eq. (4) between an initial time  and a final time
and a final time  , we obtain
, we obtain  in the limit
in the limit  . We simplify this expression with the standard30 assumption that
. We simplify this expression with the standard30 assumption that  . This condition will be repeatedly used; it allows us to split
. This condition will be repeatedly used; it allows us to split  (we drop the index nτ) with
(we drop the index nτ) with

We use Trr to denote the trace over the r = L or r = R system and Tr to denote the full trace.
The heat flow from the bath to the system in the time interval of length τ where the system interacts with the nth copy is evaluated from Eq. (5)

where  is the density matrix of the nth copy of the environment at the end of the interaction with the system.
is the density matrix of the nth copy of the environment at the end of the interaction with the system.
The entropy production  in the time lapse τ is obtained from Eq. (6) and after some manipulations31,32, it can be written as the sum
in the time lapse τ is obtained from Eq. (6) and after some manipulations31,32, it can be written as the sum

where the mutual information  quantifies the correlations built up between the system and the nth copy after time τ. Note that
quantifies the correlations built up between the system and the nth copy after time τ. Note that  and
and  and vanishing entropy production requires
and vanishing entropy production requires  and the absence of correlations between the system and the copy
and the absence of correlations between the system and the copy  . Note that because before the interaction the state of the system is arbitrary and uncorrelated with the product of thermal states of the copy, the theory of 31,32 applies independently of the correlations built between the system and previous copies.
. Note that because before the interaction the state of the system is arbitrary and uncorrelated with the product of thermal states of the copy, the theory of 31,32 applies independently of the correlations built between the system and previous copies.
Heat, work and boundary-driven Lindblad equation
The index n is associated with the copy that interacts in the interval of time  , but the copies are all identical prior to the interaction (a tensor product of two canonical distributions) and the interaction
, but the copies are all identical prior to the interaction (a tensor product of two canonical distributions) and the interaction  is always of the same form. Because no confusion will arise, we drop the label n and denote the interaction
is always of the same form. Because no confusion will arise, we drop the label n and denote the interaction  , the Hamiltonian of the bath copy Hr and the state
, the Hamiltonian of the bath copy Hr and the state  with
with  . It was shown6,7 that for Vr that satisfies
. It was shown6,7 that for Vr that satisfies  and whose strength is scaled with τ as
and whose strength is scaled with τ as  , the system evolution Eq. (7) in the limit
, the system evolution Eq. (7) in the limit  converges to a Lindblad evolution (see methods)
converges to a Lindblad evolution (see methods)

with  . This equation applied to particular systems provides boundary-driven Lindblad equations.
. This equation applied to particular systems provides boundary-driven Lindblad equations.
Consider now  and
and  with
with  in Eq. (8) and
in Eq. (8) and  in Eq. (9). In the limit
in Eq. (9). In the limit  with
with  , we obtain (see methods)
, we obtain (see methods)

where  . Note the first law
. Note the first law  , where
, where  Finally, we express the entropy production rate as the difference between the time derivative of the von Neumann entropy and the entropy flow
Finally, we express the entropy production rate as the difference between the time derivative of the von Neumann entropy and the entropy flow

where the first term is computed using Eq. (10) with  and the second term is computed from Eq. (11). Eqs (11),(12) provide appropriate thermodynamic expressions for systems evolving with Eq. (10). Now we illustrate our findings in spin 1/2 chains.
and the second term is computed from Eq. (11). Eqs (11),(12) provide appropriate thermodynamic expressions for systems evolving with Eq. (10). Now we illustrate our findings in spin 1/2 chains.
Spin models
Consider an XY spin 1/2 chain with Hamiltonian

In the repeated interaction scheme we consider the couplings

to a left r = L and a right r = R spin 1/2 reservoir copy with Hamiltonians  and we take hL = h1 and hR = hN. To obtain the boundary-driven Lindblad model, we scale
and we take hL = h1 and hR = hN. To obtain the boundary-driven Lindblad model, we scale  . The canonical density matrices
. The canonical density matrices  are fully characterized by the magnetization
are fully characterized by the magnetization  .
.
Evaluating the second term on the right-hand side of Eq. (10) yields the dissipator in the Lindblad from  with
with  and
and  where
where  . Note that
. Note that  .
.
This system does not satisfy local-detailed-balance with respect to the Gibbs state, i.e.  is not the solution of
is not the solution of  with r either R or L because
with r either R or L because  . What can be shown is that these dissipators thermalize the single spin in the boundary if we disconnect it from the rest of the chain. Indeed let us consider the L dissipator
. What can be shown is that these dissipators thermalize the single spin in the boundary if we disconnect it from the rest of the chain. Indeed let us consider the L dissipator

upon evaluation we see that  . This is the generic situation in boundary driven Lindblad systems.
. This is the generic situation in boundary driven Lindblad systems.
The expression for power and heat Eq. (11) can be evaluated using the system hamiltonian Eq. (13), the coupling Eq. (14), the bath hamiltonian  and the corresponding
and the corresponding  . One obtain (we take
. One obtain (we take 

and

Replacing the indices {L, 1, 2} by  in Eqs (15),(16) one has the corresponding
in Eqs (15),(16) one has the corresponding  and
and  . To compute this quantities, we obtain
. To compute this quantities, we obtain  by solving the Lindblad equation44.
by solving the Lindblad equation44.
Consider the case in which the system interacts with one bath (for instance the left bath, but we drop the label L). In general, two situations can occur: the system relaxes to thermodynamic equilibrium in which all current vanishes or the system reaches a NESS if it is externally driven.
XX chain coupled to one bath
An XX spin chain (Jx = Jy) in a uniform magnetic field hi = h coupled to a single bath relaxes to equilibrium: the entropy production rate, heat flows and power vanish. The equilibrium density matrix is not generally a canonical distribution but rather, as one can prove, is given by a generalized Gibbs state  with
with  , which is a conserved quantity, i.e.,
, which is a conserved quantity, i.e.,  . This state is a product state of the canonical density matrices ωβ for each spin of the chain and all equal to the one of the reservoir copy. Therefore,
. This state is a product state of the canonical density matrices ωβ for each spin of the chain and all equal to the one of the reservoir copy. Therefore,  and
and  , i.e.,
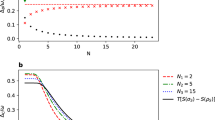
, i.e.,  . Figure 1 illustrates the relaxation to this equilibrium state by depicting the decaying power, heat flow and entropy production rate.
. Figure 1 illustrates the relaxation to this equilibrium state by depicting the decaying power, heat flow and entropy production rate.
As a function of time t plots of  (blue),
(blue),  (black) and diS/dt (red) for an XX (Jx = 1 = Jy) and
(black) and diS/dt (red) for an XX (Jx = 1 = Jy) and  (blue, dashed),
(blue, dashed),  (back, dashed) and −diS/dt (red, dashed) for an XY (Jx = 1 = 0.5Jy) chain. In both cases, the chain has N = 5 sites with hi = 1, i = 1,5 coupled with λ = 1 to a single left bath of β = 1 and h = 1.
(back, dashed) and −diS/dt (red, dashed) for an XY (Jx = 1 = 0.5Jy) chain. In both cases, the chain has N = 5 sites with hi = 1, i = 1,5 coupled with λ = 1 to a single left bath of β = 1 and h = 1.
XY chain coupled to a single bath
For an XY chain, we found that the system reaches a driven NESS. In this NESS, entropy production is strictly positive and constant and because  , the first law gives
, the first law gives  . Furthermore, by combining the first and second laws, we have that
. Furthermore, by combining the first and second laws, we have that  because in NESS,
because in NESS,  . See Fig. 1.
. See Fig. 1.
XX chain coupled to two baths
Consider a hot left and a cold right heat baths  connected by an XX spin 1/2 chain with the Hamiltonian in Eq. (13) with Jx = Jy = J. The NESS in the special case of a uniform magnetic field was analyzed in7. The power and heat from the reservoir to the system are given by Eqs (15),(16). In Fig. 2, we plot
connected by an XX spin 1/2 chain with the Hamiltonian in Eq. (13) with Jx = Jy = J. The NESS in the special case of a uniform magnetic field was analyzed in7. The power and heat from the reservoir to the system are given by Eqs (15),(16). In Fig. 2, we plot  ,
,  ,
,  and
and  in the NESS as functions of hL. We observe that the heat flows can change sign and that for hR = hL, they have opposite signs, i.e.,
in the NESS as functions of hL. We observe that the heat flows can change sign and that for hR = hL, they have opposite signs, i.e.,  , which means that
, which means that  . We also observe in Fig. 2 that
. We also observe in Fig. 2 that  and vanishes only when
and vanishes only when  , that is, the second law holds even when heat flows from cold to hot, as is the case for
, that is, the second law holds even when heat flows from cold to hot, as is the case for  , a situation that would appear to be a contradiction to the Clausius statement of the second law if we do not realize the presence of
, a situation that would appear to be a contradiction to the Clausius statement of the second law if we do not realize the presence of  .
.
The previous numerical study of boundary-driven spin chains can be complemented with exact results for power and heat in a two-site boundary-driven spin chain obtained from a full analytical solution of the NESS (see methods). In the NESS, the expression for power Eq. (16) and heat Eq. (15) can be written in terms of the spin current44

as  ,
,  and
and  . Thus, for
. Thus, for  , there is no power, but as the previous expression shows, this does not mean that the spin current vanishes. Moreover, the entropy production rate in the NESS is
, there is no power, but as the previous expression shows, this does not mean that the spin current vanishes. Moreover, the entropy production rate in the NESS is

i.e., the spin current js and the affinity  characterize the rate of entropy production in the NESS and because
characterize the rate of entropy production in the NESS and because  , the sign of the entropy production rate is given by
, the sign of the entropy production rate is given by  , where the equality holds only if
, where the equality holds only if  . Let us end this analysis by noting that for
. Let us end this analysis by noting that for  , this system behaves as a heat engine for
, this system behaves as a heat engine for  with efficiency
with efficiency  , as a refrigerator for
, as a refrigerator for  with efficiency
with efficiency  and as a heater for
and as a heater for  . Note that the efficiencies are independent of temperature. These are steady-state operating engines analogous to those in45.
. Note that the efficiencies are independent of temperature. These are steady-state operating engines analogous to those in45.
Discussion
In conclusion, the repeated interaction scheme provides a physical description of a system interacting with an environment that, in an appropriate limit, provides a boundary-driven Lindblad equation for the system. The Lindblad operators that appear in this equation are determined by the interaction of the system with the environment, the Hamiltonian of the copies that form the bath and, importantly, by the fact that it is refreshed constantly. By computing the thermodynamical quantities for the full system plus the environment, one can derive the corresponding expressions for the boundary-driven model. One important observation is that due to the refreshing of the reservoir, work is done or extracted by the external agent in charge of this refreshing. This power drives the system out of equilibrium. Note that this power appears even if the system Hamiltonian and Lindblad operators are time independent. We applied our results to spin chains. In the single bath case, we found that an XX spin chain with a homogeneous magnetic field relaxes to thermal equilibrium, i.e., a state with zero entropy production, while an XY spin chain reaches a driven NESS, a state with a non-zero entropy production  In the two heat bath case, the XX chain for different temperatures
In the two heat bath case, the XX chain for different temperatures  and a homogeneous magnetic field reaches a non-driven
and a homogeneous magnetic field reaches a non-driven  NESS and an equilibrium state for
NESS and an equilibrium state for  where the entropy production rate, power, heat flows and spin currents vanish. For inhomogeneous magnetic fields, the chain reaches a driven
where the entropy production rate, power, heat flows and spin currents vanish. For inhomogeneous magnetic fields, the chain reaches a driven  NESS. Jumping to a broader context, this work shows that the knowledge of a Lindblad equation for an open system does not determine the heat flows or other thermodynamical quantities. These quantities also depend on the properties of the environment and how the system is coupled to it. Here, we have obtained appropriate expressions for heat flows and power for interactions with an environment of a type recently implemented in a laboratory5. But when the reservoir is weakly and passively coupled to the system, i.e. there is no work cost in achieving the coupling, the system is appropriately described by a global28 Lindblad equation and the thermodynamical quantities by Eq. (2). Finally, this work is also an extension of quantum thermodynamics to a class of open quantum systems without local-detailed-balance.
NESS. Jumping to a broader context, this work shows that the knowledge of a Lindblad equation for an open system does not determine the heat flows or other thermodynamical quantities. These quantities also depend on the properties of the environment and how the system is coupled to it. Here, we have obtained appropriate expressions for heat flows and power for interactions with an environment of a type recently implemented in a laboratory5. But when the reservoir is weakly and passively coupled to the system, i.e. there is no work cost in achieving the coupling, the system is appropriately described by a global28 Lindblad equation and the thermodynamical quantities by Eq. (2). Finally, this work is also an extension of quantum thermodynamics to a class of open quantum systems without local-detailed-balance.
Methods
We provide here some details of the calculations mentioned in the main text.
Work, heat and boundary-driven Lindblad equation from the repeated interaction scheme
For completeness we derive Eq. (10) and Eq. (11) of the main text. Consider 
 . We have from Eq. (7) of the main text that
. We have from Eq. (7) of the main text that

where we have dropped the label n from U and ρn in Eq. (7) because the copies are identical and the interaction  is always of the same form. The trace Trn over the state
is always of the same form. The trace Trn over the state  is denoted TrE. The unitary
is denoted TrE. The unitary  in (17) is expanded for small τ considering the scaling
in (17) is expanded for small τ considering the scaling  and
and 

Now, because  the leading order in the right hand side of (17) is
the leading order in the right hand side of (17) is  . Thus, we divide by τ and take the limit
. Thus, we divide by τ and take the limit  and
and  such that
such that  and obtain
and obtain

where the equality  was used.
was used.
Now we use Trr to denote the trace over the r = L or r = R system and Tr the full trace. Because  and
and  , it is possible to split the last two terms in contributions for each reservoir giving Eq. (10) in the text:
, it is possible to split the last two terms in contributions for each reservoir giving Eq. (10) in the text:

with  .
.
We continue with the derivation of Eq. (11) of the main text. Let us start from  , i.e. Eq. (9), where
, i.e. Eq. (9), where  . Dropping as before the label n, in the limit
. Dropping as before the label n, in the limit  and
and  we can replace U by (18). The leading order of
we can replace U by (18). The leading order of  is
is 

or 

Consider Eq. (8) now i.e.  . As before we drop the label n. The leading order is also
. As before we drop the label n. The leading order is also  but we need U up to
but we need U up to  because V is
because V is  ,
,  and
and  . We obtain
. We obtain

or 

Expressions (20) and (21) correspond to those in Eq. (11) from the main text.
The two spin XX chain with inhomogeneous magnetic field
Consider a XX two sites spin chain and the corresponding Lindblad dynamics Eq. (1) with HS given by Eq. (13) main text (with Jx = Jy = J, h1 = hL and h2 = hR) and the Lindblad dissipator

with  and
and  where
where  . This system is fully characterized by the correlation functions
. This system is fully characterized by the correlation functions  ,
,  ,
,  and
and  where
where  . They satisfy a close system of equations:
. They satisfy a close system of equations:




From Eqs (15,16) in the main text we note that  , while the first term in the right hand side of (23) is
, while the first term in the right hand side of (23) is  and the corresponding term in (24) is
and the corresponding term in (24) is  . Moreover the spin current44 is
. Moreover the spin current44 is  . In the steady state the left-hand-side of the system (22),(23),(24),(25) vanishes and
. In the steady state the left-hand-side of the system (22),(23),(24),(25) vanishes and  ,
,  and
and  . The current given in the main text is obtained by solving the full system in the NESS.
. The current given in the main text is obtained by solving the full system in the NESS.
Heat from a given reservoir in the weak-coupling limit
Consider a system coupled to several reservoirs as discussed in “universe” under unitary evolution. The heat that comes from one of them, for instance the r = L reservoir is  . The methods developed in full counting statistics43 gives
. The methods developed in full counting statistics43 gives  where
where  is a modified evolution super-operator with
is a modified evolution super-operator with  . When this modification is done for a system in the weak coupling Born-Markov-secular approximation one obtain46,47
. When this modification is done for a system in the weak coupling Born-Markov-secular approximation one obtain46,47  where only the dissipator associated to the r = L reservoir depends on λ as
where only the dissipator associated to the r = L reservoir depends on λ as

Here  are system eigen-operators obtained from the coupling of the system to the left reservoir30,46,47 and
are system eigen-operators obtained from the coupling of the system to the left reservoir30,46,47 and  . A slow time dependence of the system can be included, see46. From Eq. (26) we obtain
. A slow time dependence of the system can be included, see46. From Eq. (26) we obtain

Thus  where we used that in this limit the dynamics is Markovian. We have to compare this with the heat flow defined in section “open system weakly and passively coupled to the environment”,
where we used that in this limit the dynamics is Markovian. We have to compare this with the heat flow defined in section “open system weakly and passively coupled to the environment”,  , where the dissipator
, where the dissipator  in the same weak coupling Born-Markov-secular approximation is given by
in the same weak coupling Born-Markov-secular approximation is given by  , from which we compute
, from which we compute

To obtain this we used  30. Taking the trace in Eq. (27) and in Eq. (28) the desired equality
30. Taking the trace in Eq. (27) and in Eq. (28) the desired equality  is found. Now, since the heat flow to a system weakly and passively coupled to the L heat-bath is given by
is found. Now, since the heat flow to a system weakly and passively coupled to the L heat-bath is given by  , the corresponding definition for work follows and the entropy production given in Eq. (3) as well.
, the corresponding definition for work follows and the entropy production given in Eq. (3) as well.
Additional Information
How to cite this article: Barra, F. The thermodynamic cost of driving quantum systems by their boundaries. Sci. Rep. 5, 14873; doi: 10.1038/srep14873 (2015).
References
Maze, J. R. et al. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 455, 644–647 (2008).
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).
Hanson, R., Kouwenhoven, L. P., Petta, J. R., Tarucha, S. & Vandersypen, L. M. K. Spins in few-electron quantum dots. Rev. Mod. Phys. 79, 1217 (2007).
Verstraete, F., Wolf, M. M. & Cirac, J. I. Quantum computation and quantum-state engineering driven by dissipation. Nature Physics 5, 633–636 (2009).
Schindler, P. et al. Quantum simulation of dynamical maps with trapped ions. Nature Physics 9, 361–367 (2013).
Attal, S., & Pautrat, Y. From repeated to continuous quantum interactions. Ann. Inst. Henri Poincaré 7, 59–104 (2006).
Karevski D. & Platini, T. Quantum Nonequilibrium Steady States Induced by Repeated Interactions. Phys. Rev. Lett. 102, 207207 (2009).
Prosen, T. & Pižorn, I. Quantum Phase Transition in a Far-from-Equilibrium Steady State of an XY Spin Chain. Phys. Rev. Lett. 101, 105701 (2008).
Prosen, T. & Žunkovič, B. Exact solution of Markovian master equations for quadratic Fermi systems: thermal baths, open XY spin chains and non-equilibrium phase transition. New J. Phys. 12, 025016 (2010).
Žunkovič, B. & Prosen, T. Explicit solution of the Lindblad equation for nearly isotropic boundary driven XY spin 1/2 chain. J. Stat. Mech. 2010, P08016 (2010).
Wichterich, H., Henrich, M. J., Breuer, H-P., Gemmer, J. & Michel, M. Modeling heat transport through completely positive maps. Phys. Rev. E 76, 031115 (2007).
Prosen, T. Exact Nonequilibrium Steady State of a Strongly Driven Open XXZ Chain. Phys. Rev. Lett. 107, 137201 (2011).
Ilievski, E. & Žunkovič, B. Quantum group approach to steady states of boundary-driven open quantum systems. J. Stat. Mech. P01001 (2014).
Prosen, T. Matrix product solutions of boundary driven quantum chains. E-print arXiv:1504.00783 (2015).
Karevski, D., Popkov V., & Schütz, G. M. Exact Matrix Product Solution for the Boundary-Driven Lindblad XXZ Chain. Phys. Rev. Lett. 110, 047201 (2013).
Prosen, T., Ilievski E. & Popkov, V. Exterior integrability: Yang-Baxter form of nonequilibrium steady state density operator. New J. Phys. 15, 073051 (2013).
Žnidarič, M. A matrix product solution for a nonequilibrium steady state of an XX chain. J. Phys. A 43, 415004 (2010).
Žnidarič, M. Exact solution for a diffusive nonequilibrium steady state of an open quantum chain. J. Stat. Mech. L05002 (2010).
Popkov, V. & Livi, R. Manipulating energy and spin currents in non-equilibrium systems of interacting qubits. New J. Phys. 15, 023030 (2013).
Mari, A. & Eisert, J. Cooling by Heating: Very Hot Thermal Light Can Significantly Cool Quantum Systems. Phys. Rev. Lett. 108, 120602 (2012).
Linden, N., Popescu, S. & Skrzypczyk, P. How small can thermal machines be? The smallest possible refrigerator. Phys. Rev. Lett. 105, 130401 (2010).
Restrepo, J., Ciuti, C. & Favero, I. Single-Polariton Optomechanics. Phys. Rev. Lett. 112, 013601 (2014).
Brunner, N., Huber, M., Linden, N., Popescu, S., Silva, R. & Skrzypczyk, P. Entanglement enhances cooling in microscopic quantum refrigerators. Phys. Rev. E 89, 032115 (2014).
Boukobza, E. & Ritsch, H. Breaking the Carnot limit without violating the second law: A thermodynamic analysis of off-resonant quantum light generation. Phys. Rev. A 87, 063845 (2013).
Ajisaka, S. & Barra, F. Nonequilibrium mesoscopic Fermi-reservoir distribution and particle current through a coherent quantum system Phys. Rev. B 87, 195114 (2013).
Ajisaka, S., Barra, F., Mejia-Monasterio, C. & Prosen, T. Nonequlibrium particle and energy currents in quantum chains connected to mesoscopic Fermi reservoirs. Phys. Rev. B 86, 125111 (2012).
Ajisaka, S., Barra, F., Mejia-Monasterio, C. & Prosen, T. Current in coherent quantum systems connected to mesoscopic Fermi reservoirs. Phys. Scr. 86, 058501 (2012).
Levy, A. & Kosloff, R. The local approach to quantum transport may violate the second law of thermodynamics. EPL 107, 20004 (2014).
Correa, L. A., Palao, J. P., Adesso, G. & Alonso, D. Performance bound for quantum absorption refrigerators. Phys. Rev. E 87, 042131 (2013).
Breuer, H.-P. & Petruccione, F. The Theory of Open Quantum Systems (Oxford University Press, Oxford), 2002.
Esposito, M., Lindenberg, K. & Van den Broeck, C. Entropy production as correlation between system and reservoir. New J. Phys. 12, 013013 (2010).
Reeb, D. & Wolf, M. M. An improved Landauer principle with finite-size corrections. New J. Phys. 16, 103011 (2014).
Alicki, R. The quantum open system as a model of the heat engine. J. Phys. A: Math. Gen. 12, L103 (1979).
Spohn, H. Entropy production for quantum dynamical semigroups. Journal of Mathematical Physics 19, 1227 (1978).
Spohn, H. & Lebowitz, J. Irreversible thermodynamics for quantum systems weakly coupled to thermal reservoirs. Adv. Chem. Phys. 109, 38 (1978).
Kosloff, R. Quantum thermodynamics: A dynamical viewpoint. Entropy 15, 2100 (2013).
Esposito, M. Stochastic thermodynamics under coarse graining. Phys. Rev. E 85, 041125 (2012).
Alicki R. On the detailed balance condition for non-hamiltonian systems. Rep. Math. Phys. 10, 249–258 (1976).
Correa, L. A., Palao, J. P., Alonso, D. & Adesso, D. Quantum-enhanced absorption refrigerators. Sci. Rep. 4, 3949 (2014).
Levy, A. & Kosloff, R. Quantum absorption refrigerator. Phys. Rev. Lett. 108, 070604 (2012).
Geva, E. & Kosloff, R. The quantum heat engine and heat pump: An irreversible thermodynamic analysis of the three-level amplifier. J. Chem. Phys. 104, 7681 (1996).
Campisi, M., Hänggi, P. & Talkner, P. Colloquium: Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 83, 771 (2011).
Esposito, M., Harbola, U. & Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems and counting statistics in quantum systems. Rev. Mod. Phys. 81, 1665 (2009).
Prosen, T. Third quantization: a general method to solve master equations for quadratic open Fermi systems. New J. Phys. 10, 043026 (2008).
Campisi, M., Pekola, J. & Fazio, R. Nonequilibrium fluctuations in quantum heat engines: theory, example and possible solid state experiments. New J. Phys. 17, 035012 (2015).
Yuge, T., Sagawa, T., Sugita, A. & Hayakawa, H. Geometrical Excess Entropy Production in Nonequilibrium Quantum Systems. J. Stat. Phys. 153, 412 (2013).
Silaev, M., Heikkilä, T. T. & Virtanen, P. Lindblad-equation approach for the full counting statistics of work and heat in driven quantum systems. Phys. Rev. E 90, 022103 (2014).
Acknowledgements
This research is funded by Fondecyt grant 1151390.
Author information
Authors and Affiliations
Contributions
F.B. conceived and conducted the research and wrote the manuscript.
Ethics declarations
Competing interests
The author declares no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Barra, F. The thermodynamic cost of driving quantum systems by their boundaries. Sci Rep 5, 14873 (2015). https://doi.org/10.1038/srep14873
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep14873
This article is cited by
-
Perturbation Analysis of Quantum Reset Models
Journal of Statistical Physics (2021)
-
Reversing the direction of heat flow using quantum correlations
Nature Communications (2019)
-
Non-Markovian Dynamics of Macroscopic Quantum Systems in Interaction with Non-equilibrium Environments
Journal of Statistical Physics (2019)
-
On the General Definition of the Production of Entropy in Open Markov Quantum Systems
Journal of Mathematical Sciences (2019)
-
Out of time ordered quantum dissipation
Journal of High Energy Physics (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



 ,
,  and
and  as a function of hL = h1.
as a function of hL = h1. , all quantities vanish (equilibrium state). At
, all quantities vanish (equilibrium state). At  ,
,  and thus
and thus  (non-driven steady state).
(non-driven steady state).