Abstract
The boundary layer at solid-liquid interfaces is a unique reaction environment that poses significant scientific challenges to characterize and understand by experimentation alone. Using ab initio molecular dynamics (AIMD) methods, we report on the structure and dynamics of boundary layer formation, cation mobilization and carbonation under geologic carbon sequestration scenarios (T = 323 K and P = 90 bar) on a prototypical anorthite (001) surface. At low coverage, water film formation is enthalpically favored, but entropically hindered. Simulated adsorption isotherms show that a water monolayer will form even at the low water concentrations of water-saturated scCO2. Carbonation reactions readily occur at electron-rich terminal Oxygen sites adjacent to cation vacancies that readily form in the presence of a water monolayer. These results point to a carbonation mechanism that does not require prior carbonic acid formation in the bulk liquid. This work also highlights the modern capabilities of theoretical methods to address structure and reactivity at interfaces of high chemical complexity.
Similar content being viewed by others
Introduction
A large number of important chemical phenomena happen at solid-liquid interfaces relevant to geochemistry1,2,3,4, atmospheric phenomena5 and catalysis6,7,8,9. Critical scientific questions arise regarding the species present at the boundary layer, the impact of the dynamics and structure of this layer on surface reconstruction, reactivity and adsorbed molecular states. Unlike solid-gas interfaces, solid liquid interfaces are buried in condensed media and pose a stringent challenge to characterize by experimentation alone. Advances in computational methods have afforded us with the unique opportunity to address these issues at the molecular level at different length and time scales. Classical molecular dynamics (MD) has been used as a tool to understand the thermodynamics of interfaces and surface adsorption10,11,12,13,14. These methods although extremely valuable, are highly reliant on predetermined intermolecular potentials, which may not necessarily be transferrable from the bulk liquid to the interfacial environments, or able to reproduce surface reactivity. Ab initio molecular dynamics (AIMD)15 on the other hand, is in principle more transferrable, but is more limited in its ability to represent models of the requisite chemical complexity, size and time scale. Nevertheless, recent advances in linear scaling density functional theory methods have allowed us to approach realistic interfacial models16,17,18. This work addresses surface adsorption and reactivity in a prototypical mineral/water/scCO2 system, in the context of carbon management, with strong implications for CO2 sequestration strategies and general interfacial phenomena.
Feldspars are abundant in cap rock formations targeted for sequestration where permanent CO2 trapping in the form of carbonates is aided by the presence and dissolution of cations such as Na+, K+ or Ca2+ 19,20. Anorthite, the Ca-end member of the feldspar group, is present in many geologic formations and is of particular interest because of fast dissolution that may significantly affect cap rock stability and porosity21,22. However, the higher charge cations in anorthite carry the potential of more efficient CO2 sequestration and carbonate precipitation. Recent advances in experimental instrumentation, for example X-ray scattering and reflectivity studies22,23,24,25 have allowed the unprecedented in situ characterization of mineral-water interactions. In addition, surface microanalysis techniques have allowed a closer view of the local structure and concomitant changes at the interface of feldspar minerals with water under different conditions and different compositions25. While these studies provide a unique dataset to benchmark our ability to represent and quantify structure, dynamics and reactivity in these complex systems via simulation, they cannot reveal the intimate details of molecular level reactivity. When in contact with minerals, the water response is often film assembly at the interface with various degrees of structure, e.g. ice-like layers26 or liquid boundary layers25, controlled by hydrophilic or hydrophobic effects27,28. Remarkably, the structural effects have significant impact in the structure of water or other liquids away from the immediate vicinity of the interface29,30,31,32. Reactivity in water-bearing scCO2 has received scant attention, in spite of unique mechanistic details of corrosion33,34 and mineralization35 reactions occurring under sequestration conditions.
The relative energetics of water and CO2 adsorption as well as their impact on surface reconstruction, cation mobilization and carbonate formation are discussed in terms of enthalpic and entropic contributions. These insights are used to understand the structure and dynamics of the scCO2 mineral interface as a function of hydration state and temperature effects. We show that Ca dissolution is enthalpically favorable in the presence of just a water monolayer. Carbonate formation adjacent to cation vacancies is shown to be facile by direct activation of CO2, even on the picosecond time scale of this study. Finally, the free energy profile for water adsorption and monolayer nucleation and growth is used to de-convolute the role of energy and entropy in water film formation in the presence of wet scCO2.
Results
Energetics of H2O and CO2 adsorption
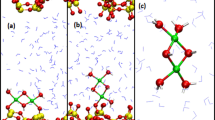
Here, we consider the energetics of water and carbon dioxide adsorption by examining the first layer of molecules adjacent to the Ca-rich anorthite surface as extracted from the AIMD simulations with water and scCO2 molecules over the mineral, respectively. The extracted structures are optimized to obtain the structure of a stand-alone monolayer of H2O and CO2, see Supplementary Figs 1 and 2 Table 1, we summarize the adsorption energies per molecule at full-monolayer coverage on the Ca-rich face of the anorthite (001) surface and compare to single-molecule adsorption. For the estimation of the energies, the following formulae were used:






where Emol is the energy of gas phase molecule, Etot is the total energy of any combined system, Eslab is the energy for the slab, Elayer/Eliq is the energy of the H2O or CO2 layer, or a box of water or scCO2, CE is the cohesion energy and n is the number of molecules in the simulation. Equation (1) estimates the binding energy of a single, gas-phase molecule to the surface. Equation (2) provides an estimate of the average binding energy to the surface per H2O or CO2 molecule, including both molecule/surface and molecule/molecule interactions. To de-convolute these energy terms, we introduce equations (3) and (4), where the former provides estimates of the average layer-surface interaction energy, while the latter provides the average molecule-molecule interaction within the layer. Equation (5) estimates the cohesion energy in the pure liquids to juxtapose with the binding energy of the layer to the surface. Equation (6), gives BE4, the difference between BE1 and CE, which is a measure of the energetic preference of a molecule being adsorbed on the surface, as opposed to being solvated in the pure liquid phase. Figure 1 describes how the above quantities are related in a thermodynamic cycle.
Based on the computed values of adsorption energies, the following conclusions can be drawn regarding water film formation. When a full monolayer of water is formed on the surface, the adsorption energy (−97 kJ/mol) only mildly decreases compared to the adsorption of a monomer (−103 kJ/mol). This is a result of strong H2O-surface interactions (−82 kJ/mol) and comparatively weak H2O-H2O interactions within the layer (−15 kJ/mol). The surface-H2O interaction can be mainly attributed to the 8 coordination bonds between the 4 top-most Ca cations and H2O. These interactions are very similar in magnitude to the hydration energy of the Ca (H2O)62+ species36, which provides an average energy per Ca-water coordination bond of 164 kJ/mol. Using this quantity as guideline, we extrapolate that 8 Ca-H2O bonds provide an estimated −93 kJ/mol each. This is slightly higher than the computed quantity BE2 and suggests that the surface Ca-H2O interactions are weaker than those in the fully-solvated Ca2+. Similarly, the cohesion energy CE of bulk water (−57 kJ/mol) arises from approximately 3.5 H-bonds per H2O molecule, averaging −16.3 kJ/mol each.
In the case of CO2, the average binding energy of a CO2 in the monolayer is lower (−17 kJ/mol) than that of a single CO2 molecule (−34 J/mol). More specifically, while the Ca-OCO217, or Osurf-CCO2 interactions have a stabilizing effect37,38, the OH-OCO2 interactions are only mildly stabilizing39. Thus, CO2-CO2 interactions in the monolayer provide only a small stabilization of −4 kJ/mol and the CO2 layer is only weakly bound. Overall, there is a stronger enthalpic driving force for H2O adsorption on the mineral surface than the appreciably weaker one for the CO2, suggesting that in carbon sequestration scenarios, water saturated CO2 will likely undergo preferential segregation, with H2O gravitating towards the surface forming a water film. However, as we will see shortly, entropic considerations may radically influence the speciation at the interface.
Finite Temperature Effects
We assess the impact of the hydration level on mineral dissolution and carbonate formation. For the analysis, we consider the progression of systems ranging from: pure scCO2, scCO2 with one, two and three water layers and pure water, snapshots shown in Fig. 2. A summary of cell parameters and simulation times for all the systems can be found in Supplementary Table 1.
In Fig. 3, we show the molecular density profiles of Ca, H2O and CO2 along the direction of the surface normal. The top two panels show the distribution of CO2 (sc-CO2) and H2O (Water) for the surface/pure liquid systems. For pure scCO2, we observe a liquid-like layer (calculated density ~ 0.6 g/ml) that is consistent with a super-critical CO2 medium. Higher density peaks, at ~2 Å from the surface, are indicative of a denser CO2 layer, also observed in the case of other minerals38. The bottom 4 panels in Fig. 3 show distinct water layer features with or without scCO2. At the H2O/scCO2 interface, we still observe a higher density CO2 layer, however it is less ordered compared to the pure scCO2 system. In all cases, diffusion in and out of the CO2 layer is evident on the ps time scale. On the Ca-deficient surface, within 5 ps of simulation, formation of carbonates (CO32−) is observed from reaction of CO2 with surface oxygens O2− adjacent to Ca2+ vacancies. Conversely, on the Ca-rich face, neither carbonate formation nor strong Ca2+/CO2 interactions are observed on the simulation time scale. However, as we will discuss later, carbonates can be formed when Ca vacancies occur near the surface.
The water-only system (Water) shows a striation of the molecular density, with a pronounced maximum adjacent to the surface. The water monolayer (1W) is stable at finite temperature and perturbed only slightly by the presence of the scCO2 component (1W/CO2). Within this layer, water exhibits a diffusion coefficient D ~ 10−6 cm2/s only an order of magnitude smaller than water self-diffusion in water (22 × 10−6 cm2/s)40, indicating a mobile water layer. Although water molecules diffuse within this layer, they do not diffuse out of it. Within the layer, each H2O is bound to an average of 1.4/1.4 (w/wo scCO2) waters and 1.0/1.0 surface oxygens via hydrogen bonds. Each Ca2+ is bound to an average of 1.5 water molecules through direct Ca-Ow coordination bonds. Compared to the 1W system, the water coordination environment changes in the 2W and 3W systems. Within the first layer, each H2O is bound to an average of 2.0/2.0/2.0 (2W/3W/Water systems) waters and 0.2/0.1/0.2 surface oxygens via hydrogen bonds. Each Ca2+ is bound to an average of 1.6/1.1/1.1 waters through Ca-Osurf bonds. The 2nd and 3rd water layers show a distinctly different intermolecular structure, very similar to that of the bulk water. For instance, the 2nd water layer shows a broader density maxima than the first, even exhibiting a double peak in the 2W system similar to other studies11. The 3rd water layer shows progressively lower density maxima, indicating that a finite percentage of waters, ca 2%, reside in a 4th layer. Diffusion coefficients and densities for all these systems are summarized in Supplementary Table 2.
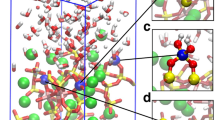
The presence of a water layer, adjacent to the surface, induces large disorder in the Ca positions such that these atoms exhibit finite populations up to 1 Å above their normal lattice positions, see Fig. 3. To examine this further, we performed a simulation with a single Ca atom extracted from the surface into the first water layer of the 1W system. The resulting structure (Fig. 4a and Supplementary Fig. 4) consists of a water-solvated Ca2+ species within the 1W film as an outer sphere complex. Using the Blue-Moon sampling method41, we examined the free energetics of the dissolution process by computing the potential of mean force (PMF) along the reaction coordinate defined by the Ca2+ z-coordinate, i.e. height above the surface plane. We find that the free-energy barrier for dissolution is 30 kJ/mol indicating that at 323 K this process will be relatively fast. The change of Helmholtz free energy, ΔA, between the two minima is 14 kJ/mol demonstrating that at this temperature there will be an equilibrium between inner and outer sphere Ca2+ complexes with a Keq = exp(−ΔA/kBT) ~ 10−3. Note that this complex shows a positive increase in free energy as it moves out into the scCO2 layer, as long as the first coordination sphere of Ca2+ consists only of water. However, complexes with mixed coordination (H2O and CO2) may further enhance Ca transport away from the surface17,42.
Ca2+ dissolution results in Ca-vacancies where carbonate formation is expected to be spontaneous, in a process similar to sulfite formation35. To verify this, we computed a PMF by moving a CO2 from the scCO2 liquid across the water layer towards the Ca vacancy to estimate the free energy of carbonate formation. As can be seen in Fig. 4b, this process is effectively barrier-less and exergonic by 17 kJ/mol, implying that carbonation can readily occur and is limited only by diffusion and the available population of Ca-vacancy sites. This emphasizes the paramount importance of a stable water monolayer in establishing the nucleation sites for carbonate formation.
Water adsorption/desorption to/from Anorthite
We now will focus on extracting information about water transport to, from and across these interfaces. This phenomenon is particularly relevant to reactivity under geologic sequestration conditions, as water-saturated scCO2 can lead to unexpected events, such as steel corrosion in water-lean scCO233,34 or preferential sulfite formation in carbonate minerals35. We computed the PMF for moving a single H2O from the middle of the liquid slab through the box, such that its immediate environment changes from being solvated in the scCO2 to being bound on the Ca-rich surface41. This process was repeated for the following systems: 1H2O/scCO2, 2H2O/scCO2, 3H2O/scCO2, 10H2O/scCO2, 14H2O/scCO2 (1W), 15H2O/scCO2 (1W+1H2O) and 28H2O/scCO2 (2W). Supplementary Section S4 provides details on the PMF convergence. The associated changes in the Helmholtz free energy, ΔA, are given in Fig. 5 and the computed coverage dependent adsorption free energy, ΔA(θ), is presented in Fig. 6a.
The free energy landscape for the 1H2O/scCO2 system is essentially flat, up until H2O is ca 5 Å away from the anorthite surface, see Fig. 5 and Supplementary Fig. 6. This distance corresponds to the water approaching the periphery of the high density CO2 layer. The free energy decreases monotonically up to 1.7 Å above the surface where the water is stabilized by forming both Ca-Ow and hydrogen bonds with the O atoms of the mineral surface, ΔA = −34 kJ/mol. The simulations with 2 and 3 H2O molecules were started with a pre-formed water dimer and trimer in the scCO2 liquid, see panel 2H2O in Supplementary Fig. 6. Because the constrain is imposed on only one of the waters, the density and free energy profiles are very similar to those for 1 H2O, with the other H2O molecule(s) moving freely. Adsorption occurs step-wise with the H2O dimer/trimer breaking apart along the way and with the constrained water molecule adsorbing first. Subsequently, in both the dimer and trimer simulations, the remaining molecules gravitate towards the surface adsorbed H2O: once the additional waters become engulfed in the scCO2 layer, they adsorb to the surface adjacent to the constrained H2O molecule without any additional constraints. These simulations imply that water film growth begins with a single water molecule as a nucleation site followed by the addition of subsequent molecules, to form an island.
To quantify this observation, we focus on the ΔA(θ) of the reactions:

The resulting free energy ΔA(θ), as a function of coverage θ (θ = n/14), is plotted in Fig. 5a. We note that in order to directly compare the ΔA(θ) values obtained from the PMF for the n = 2 and 3 simulations (which are relative to solvated clusters) with those of the n = 1, 7, 10 and 14 (which are relative to solvated monomers) we adjust the free energy of the cluster in the solvated phase to be relative to n solvated water monomers at infinite dilution, see Supplementary Section S6 for details. In accord with our above conclusion regarding H2O-H2O interactions, the computed ΔA(θ) values grow steadily from n = 2–14 by about −20 kJ/mol. Note that this value is on the order of the molecule-molecule interaction energy (BE3 = −15 kJ/mol) reported in Table 1.
We proceed by de-convoluting ΔA(θ) = ΔE(θ) − TΔS(θ) into its entropic (TΔS(θ)) and energetic (ΔE(θ)) components in order to understand the role played by the H2O-H2O interactions in driving film formation. To assess ΔE(θ), we consider that adsorption of water at the anorthite surface involves replacing adsorbed CO2 molecules with adsorbing waters at a ratio of 9CO2/14H2O based on the full coverage of the of CO2 and H2O monolayers:

This process can be subdivided into the sum of two half reactions:


The energy ΔE(θ) of (9) and (10) can be easily estimated based on arguments similar to those discussed earlier. As shown in the thermodynamic cycle of Fig. 1, for H2O, the energy of (9) can be decomposed utilizing the binding energies of Table 1, while introducing an intermediate state (H2O(g)) and the solvation energy of water in scCO2 (estimated to be −20 kJ/mol39). Neglecting the molecule-molecule interaction term (BE3) and using only the average surface-molecule adsorption energy (BE2) we obtain:

In an analogous manner, the energy for (10) is found to be ΔE = 6 or 4 kJ/mol, with or without CO2-CO2 interactions. As such, the energy for (8) can be estimated to be approximately −57 kJ/mol neglecting H2O-H2O interactions. To include the latter term, we note that an H-bond between waters in the 1W system was estimated to have an average energy of 15 kJ/mol and the number of hydrogen bonds per bound H2O molecule increases steadily from 0.5–1.4 between n = 2–14 as estimated from the number of H-bonds/water obtained from the AIMD simulations. Assuming an average stabilization energy directly proportional to the number of H-bonds, ΔE(θ) smoothly evolves from −57 kJ/mol (n = 1) to −78 kJ/mol (n = 14) as shown in Fig. 6a.
The relationship ΔE(θ) − ΔA(θ) = TΔS(θ) allows us to estimate the entropy change during adsorption, which agree fairly well with values obtained using quasiharmonic approximation43, see Supplementary section S7 for detailed method and results. In all cases, the entropy of adsorption (Fig. 6a) is negative due to a loss of the degrees of freedom of the scCO2-solvated H2O upon adsorption. The function TΔS(θ) becomes more negative by −27 kJ/mol between the adsorption of a monomer and a dimer, then remains relatively flat as the cluster of adsorbed waters increases in size up to a full monolayer. This occurs because addition of water molecules to a surface-bound cluster requires an increase in entropy of adsorption due to the restriction of the number and locality of binding sites. This factor is roughly unchanged for n = 2–14 and hence TΔS(θ) is relatively constant as the layer forms. As such, ΔA(θ) decreases roughly at the same rate as ΔE(θ) and is proportional to the increase in the H-bonding. Our simulations indicate that the barrier for nucleation of a 1W water layer, via an island growth mechanism, arises due to the entropic considerations and has the strongest influence at n = 2–3 where the number of H-bonds are relatively few.
Finally, our results also suggest that water layer formation will be kinetically hindered due to the lack of a strong thermodynamic driving force at low θ. To assess this quantitatively, we have computed an adsorption isotherm44 employing the θ -dependent equilibrium constants, K(θ) = exp(−ΔA(θ)/kBT), see Fig. 6b. From this isotherm, we solve the equation to estimate the expected water coverage as a function of water concentration. We find that water concentrations below 10−5%mol result in very low surface coverage (θ < 0.1), while for water concentrations above 10−3%mol, a full coverage water monolayer is expected. In the intermediate concentration range of 10−5−10−3, consistent with the average 10−4%mol concentration of water in wet scCO2 at P = 90 bar, T = 323 K45, the non-monotonic behavior of ΔA(θ) leads to multiple solutions to the equation where both a high and low coverage regions are stable. This is interpreted as the likely occurrence of an equilibrium distribution of high and low coverage patches on the surface. In the context of Ca2+ extraction and carbonate formation, this implies that the partial water layer formation will impact the population of Ca2+ vacancies and thus be a major kinetic bottleneck for carbonate formation.
Discussions
We have demonstrated that in the case of a prototypical mineral surface, here anorthite, in contact to water-saturated scCO2, a liquid, boundary layer of water will form and facilitate the extraction of Ca2+ cations in the form of stable, hydrated, outer-sphere complexes. This process creates cation vacancies at the top-most layers, which can serve as nucleation sites for carbonate formation limited only by the water layer formation and CO2 diffusion. Water film formation was found to be energetically driven by both Ca2+-H2O and H2O-H2O interactions, but entropic contributions largely override the stabilizing factors. The entropic component arises from H2O adsorption on the surface as well as the availability of binding sites. Our results highlight that the existence of a boundary water layer, significantly different in composition to the bulk liquid phase, can occur at even relatively low concentrations, as in the case of water-bearing scCO2. In the present case, it also points to a novel mechanism for carbonation, distinct from the traditional view that carbonation must begin with CO2 dissolution in the water phase. We have shown that a molecular level understanding of enthalpic and entropic contributions is now achievable through a combination of simple and intuitive chemical arguments and large-scale AIMD simulations. With this capability, we can now access an unprecedented level of qualitative and quantitative molecular scale understanding of structure, dynamics and reactivity at a chemically complex solid-liquid interface which may be difficult to obtain by direct experimental observation alone.
Methods
DFT parameters
Density-functional-theory(DFT) based AIMD simulations were carried out with periodic boundary conditions (3D PBC) with the exchange correlation functional of Perdew, Burke and Ernzerhoff (PBE)46 as implemented in the CP2K package25. Dispersion corrections were accounted for by Grimme’s third generation corrections DFT-D347 that have been evaluated extensively in the literature for both scCO2 and H2O and shown to adequately represent weak interactions in these systems16,17,38,48,49,50. The core electrons were described by the norm-conserving pseudopotentials51, while the valence wavefunctions were expanded in terms of double-zeta quality basis sets optimized for condensed systems to minimize linear dependencies and superposition errors52. An additional auxiliary plane wave basis set with a 350 Ry cutoff was used for the calculation of the electrostatic terms. We used a time-step of 1.0 fs and the Nosé-Hoover thermostat for NVT ensemble calculations at 323 K.
Computational models
Anorthite, with the chemical composition of CaAl2Si2O8, is the calcium end-member of the plagioclase feldspars. A coupled substitution of two Al3+ for two of Si4+, allows the incorporation of one Ca2+ and overall neutrality53. The fully optimized cell parameters at P=90 bar, a = 8.231 Å, b = 12.98 Å, c = 14.15 Å, α = 93.9°, β = 115.4°, γ = 91.3°, are less than 1% different than the crystallographic parameters, a0 = 8.1860 Å, b0 = 12.876 Å, c0 = 14.1820 Å, α = 93.3°, β = 115.8°, γ = 91.12°. Using the optimized parameters, an oxygen-terminated (001) surface model was generated, shown in Supplementary Fig. 1. A 2 × 1 × 1 slab model of the (001) surface (one of the most frequently occurring surfaces in this class of minerals23,54) with 18.3 Å interlayer space was created, including the top-most layer of Ca cations (Ca-rich surface) in order to study Ca-speciation and mobilization. The bottom side of the slab is devoid of Ca cations (Ca-deficient surface) in accordance with known cation vacancies as reported in the literature23. Finally, 8 hydrogens were added to terminal oxygens of the upper surface of the slab for charge compensation.
The mineral-liquid interface was modeled with 2 different simulations of the anorthite slab with 32 CO2 or 84 H2O molecules in the interlayer space, determined by optimization of cell parameters at 90 bar. MD simulations within the NVT statistical ensemble were performed at 323 K, resulting in a pronounced peak near the surface in the density profile plot indicating formation of strong first H2O/CO2 layer near the interface. Based on this analysis, the first layer of H2O/CO2 was determined to contain 14H2O/9CO2 molecules respectively and was used to conduct simulations for stand-alone monolayer properties.
AIMD simulations
Simulations with 1 H2O/32 CO2, 2 H2O/31 CO2 and 3 H2O/30 CO2 molecules were performed to simulate very low hydration states. In addition, simulations with 10/28, 14/28, 15/28 and 28/21 H2O/CO2 molecules were performed to simulate the formation of 1 (1W) and 2 (2W) monolayers. Because 14 was found to be the least number of H2O required to form a full monolayer, the simulation with 15 H2O was performed to provide estimates of H2O binding onto the first stable ad-layer. In all cases, full cell optimizations of the composite systems were performed at 90 bar. Supplementary Table 1 summarizes the optimized simulation cell parameters and simulation times for each system. Estimates of the diffusion coefficients and densities in the liquid slab of each simulation are summarized in Supplementary Table 2. Overall, it was found that the scCO2 layer in our model adequately reproduces the structure, density and dynamics of an scCO2 liquid phase at ~90 bar and T = 323 K.
We have employed the Blue-Moon ensemble method41 to calculate the potential of mean force (PMF) required to move a H2O molecule from the middle of the liquid region towards the Ca-rich face of the anorthite (001) surface. This method is broadly used to compute the free energy profile along a reaction coordinate direction, which is not likely explored with MD simulation due to potentially high barriers. For the initial and final points, we also performed unconstrained MD simulations to locate the thermodynamic minima. The average forces subject to geometric constraints were calculated as ensemble-averages and converted to a PMF based on the Blue-Moon ensemble method41: the z-distance between the surface and the water Oxygen atoms was chosen as the geometric constraint and all other parameters were allowed to vary. This approach allowed the H2O molecule to move laterally over the mineral surface through the liquid boundary layer. Integrating the average force along the reaction coordinate generated the free energy profile. Increments in dz were chosen to be 0.2–0.5 Å apart depending on the steepness of the PMF to better estimate the free-energetics via thermodynamic integration, which resulted in a total of 11–18 simulations per PMF. The force on each point in the PMF was converged to within ±0.0004 a.u. See Supplementary section S4 for details.
Each AIMD trajectory, both constrained and unconstrained, was equilibrated for approximately 5–10 ps and data was collected for analysis from at least 10 ps of well-equilibrated trajectory. The sum total of the overall compiled AIMD trajectories accounts for approximately 2.0 ns of total simulation time (system-specific simulation times are recorded in Supplementary Table 1). This data set represents over 106 DFT configurations for systems of total size of ~500 atoms.
Additional Information
How to cite this article: Lee, M.-S. et al. Structure, dynamics and stability of water/scCO2/mineral interfaces from ab initio molecular dynamics simulations. Sci. Rep. 5, 14857; doi: 10.1038/srep14857 (2015).
References
Chalbaud, C. et al. Interfacial Tension Measurements and Wettability Evaluation for Geological CO2 Storage. Adv. Water Resour. 32, 98–109 (2009).
Jena, K. C. & Hore, D. K. Variation of Ionic Strength Reveals the Interfacial Water Structure at a Charged Mineral Surface. J. Phys. Chem. C 113, 15364–15372 (2009).
Lis, D. et al. Liquid Flow Along a Solid Surface Reversibly Alters Interfacial Chemistry. Science 344, 1138–1142 (2014).
Perez-Blanco, M. E. & Maginn, E. J. Molecular Dynamics Simulations of Carbon Dioxide and Water at an Ionic Liquid Interface. J. Phys. Chem. B 115, 10488–10499 (2011).
Finlayson-Pitts, B. J. Reactions at Surfaces in the Atmosphere: Integration of Experiments and Theory as Necessary (but Not Necessarily Sufficient) for Predicting the Physical Chemistry of Aerosols. Phys. Chem. Chem. Phys. 11, 7760–7779 (2009).
Gaigeot, M.-P., Martinez, M. & Vuilleumier, R. Infrared Spectroscopy in the Gas and Liquid Phase from First Principle Molecular Dynamics Simulations: Application to Small Peptides. Mol. Phys. 105, 2857–2878 (2007).
Arends, I. & Sheldon, R. A. Activities and Stabilities of Heterogeneous Catalysts in Selective Liquid Phase Oxidations: Recent Developments. Appl. Catal., A 212, 175–187 (2001).
Lambert, J. F. Adsorption and Polymerization of Amino Acids on Mineral Surfaces: A Review. Origins Life Evol.B. 38, 211–242 (2008).
Pirkanniemi, K. & Sillanpaa, M. Heterogeneous Water Phase Catalysis as an Environmental Application: A Review. Chemosphere 48, 1047–1060 (2002).
da Rocha, S. R. P., Johnston, K. P., Westacott, R. E. & Rossky, P. J. Molecular Structure of the Water-Supercritical Co2 Interface. J. Phys. Chem. B 105, 12092–12104 (2001).
Kerisit, S., Weare, J. H. & Felmy, A. R. Structure and Dynamics of Forsterite–scCO2/H2O Interfaces as a Function of Water Content. Geochim. Cosmochim. Acta 84, 137–151 (2012).
Krishnan, M., Saharay, M. & Kirkpatrick, R. J. Molecular Dynamics Modeling of CO2 and Poly(Ethylene Glycol) in Montmorillonite: The Structure of Clay–Polymer Composites and the Incorporation of CO2 . J. Phys. Chem. C 117, 20592–20609 (2013).
Morrow, C. P. et al. Structure, Energetics and Dynamics of Smectite Clay Interlayer Hydration: Molecular Dynamics and Metadynamics Investigation of Na-Hectorite. J. Phys. Chem. C 117, 5172–5187 (2013).
Zhao, L. et al. Molecular Dynamics Investigation of the Various Atomic Force Contributions to the Interfacial Tension at the Supercritical CO2–Water Interface. J. Phys. Chem. B 115, 6076–6087 (2011).
Marx, D. & Hutter, J. Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods. (Cambridge University Press, 2012).
Yoon, Y. et al. First-Principles Study of Phenol Hydrogenation on Pt and Ni Catalysts in Aqueous Phase. J. Am. Chem. Soc. 136, 10287–10298 (2014).
Lee, M.-S., McGrail, B. P. & Glezakou, V.-A. Microstructural Response of Variably Hydrated Ca-Rich Montmorillonite to Supercritical CO2 . Environ. Sci. Technol. 48, 8612–8619 (2014).
Glezakou, V.-A. & McGrail, B. P. in Applications of Molecular Modeling to Challenges in Clean Energy Vol. 1133 ACS Symposium Series Ch. 3, 31–49 (American Chemical Society, 2013).
Gauss, I. Role and Impact of CO2–Rock Interactions During CO2 Storage in Sedimentary Rocks. Int. J. Greenh. Gas Control 4, 73–89 (2010).
Smith, J. V. Feldspars and Their Reactions. Vol. 421 (Kluwer Academic Publishers, 1994).
Hangx, S. J. T. & Spiers, C. J. Reaction of Plagioclase Feldspars with CO2 under Hydrothermal Conditions. Chem. Geol. 265, 88–98 (2009).
Sorai, M., Ohsumi, T., Ishikawa, M. & Tsukamoto, K. Feldspar Dissolution Rates Measured Using Phase-Shift Interferometry: Implications to CO2 Underground Sequestration. Appl. Geochem. 22, 2795–2809 (2007).
Fenter, P. et al. Structure of the Orthoclase (001)- and (010)-Water Interfaces by High-Resolution X-Ray Reflectivity. Geochim. Cosmochim. Acta 67, 4267–4275 (2003).
Fenter, P. et al. Orthoclase Dissolution Kinetics Probed by in Situ X-Ray Reflectivity: Effects of Temperature, Ph and Crystal Orientation. Geochim. Cosmochim. Acta 67, 197–211 (2003).
Fenter, P. & Sturchio, N. C. Mineral-Water Interfacial Structures Revealed by Synchrotron X-Ray Scattering. Prog. Surf. Sci. 77, 171–258 (2004).
Meng, S., Xu, L. F., Wang, E. G. & Gao, S. Vibrational Recognition of Hydrogen-Bonded Water Networks on a Metal Surface. Phys. Rev. Lett. 89, 176104 (2002).
Wang, C. et al. Stable Liquid Water Droplet on a Water Monolayer Formed at Room Temperature on Ionic Model Substrates. Phys. Rev. Lett. 103, 137801 (2009).
Wang, C. et al. Critical Dipole Length for the Wetting Transition Due to Collective Water-Dipoles Interactions. Sci. Rep. 2, 358 (2012).
Lee, C. Y., McCammon, J. A. & Rossky, P. J. The Structure of Liquid Water at an Extended Hydrophobic Surface. J. Chem. Phys. 80, 4448–4455 (1984).
Giovambattista, N., Rossky, P. J. & Debenedetti, P. G. Phase Transitions Induced by Nanoconfinement in Liquid Water. Phys. Rev. Lett. 102, 050603 (2009).
Koga, K., Zeng, X. C. & Tanaka, H. Freezing of Confined Water: A Bilayer Ice Phase in Hydrophobic Nanopores. Phys. Rev. Lett. 79, 5262–5265 (1997).
Skipper, N. T., Sposito, G. & Chou Chang, F.-R. Monte Carlo Simulation of Interlayer Molecular Structure in Swelling Clay Minerals. 2. Monolayer Hydrates. Clay. Clay. Miner. 43, 294–303 (1995).
Glezakou, V. A., Dang, L. X. & McGrail, B. P. Spontaneous Activation of CO2 and Possible Corrosion Pathways on the Low-Index Iron Surface Fe(100). J. Phys. Chem. C 113, 3691–3696 (2009).
McGrail, B. P. et al. Water Reactivity in the Liquid and Supercritical CO2 Phase: Has Half the Story Been Neglected? Energy Procedia 1, 3415–3419 (2009).
Glezakou, V.-A., McGrail, B. P. & Schaef, H. T. Molecular Interactions of SO2 with Carbonate Minerals under CO-Sequestration Conditions: A Combined Experimental and Theoretical Study. Geochim. Cosmochim. Acta 92, 265–274 (2012).
Pavlov, M., Siegbahn, P. E. M. & Sandström, M. Hydration of Beryllium, Magnesium, Calcium and Zinc Ions Using Density Functional Theory. J. Phys. Chem. A 102, 219–228 (1998).
Lin, X. et al. Structure and Dynamics of CO2 on Rutile TiO2 (110)-1×1. J. Phys. Chem. C 116, 26322–26334 (2012).
Schaef, H. T. et al. Surface Condensation of CO2 onto Kaolinite. Environ. Sci. Technol. Lett. 1, 142–145 (2013).
Glezakou, V.-A., Rousseau, R., Dang, L. X. & McGrail, B. P. Structure, Dynamics and Vibrational Spectrum of Supercritical CO2/H2O Mixtures from Ab Initio Molecular Dynamics as a Function of Water Cluster Formation. Phys. Chem. Chem. Phys. 12, 8759–8771 (2010).
Marsh, K. N. Recommended Reference Materials for the Realization of Physicochemical Properties. (Oxford Press, 1987).
Carter, E. A., Ciccotti, G., Hynes, J. T. & Kapral, R. Constrained Reaction Coordinate Dynamics for the Simulation of Rare Events. Chem. Phys. Lett. 156, 472–477 (1989).
Criscenti, L. J. & Cygan, R. T. Molecular Simulations of Carbon Dioxide and Water: Cation Solvation. Environ. Sci. Technol. 47, 87–94 (2013).
Carlsson, J. & Åqvist, J. Absolute and Relative Entropies from Computer Simulation with Applications to Ligand Binding. J. Phys. Chem. B 109, 6448–6456 (2005).
Adamson, A. W. & Gast, A. P. Physical Chemistry of Surfaces. Sixth edn, 400–408 (Wiley, 1997).
King, M. B., Mubarak, A., Kim, J. D. & Bott, T. R. The Mutual Solubilities of Water with Supercritical and Liquid Carbon Dioxides. .J. Supercrit. Fluid. 5, 296–302 (1992).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Grimme, S., Hujo, W. & Kirchner, B. Performance of Dispersion-Corrected Density Functional Theory for the Interactions in Ionic Liquids. Phys. Chem. Chem. Phys. 14, 4875–4883 (2012).
Balasubramanian, S., Kohlmeyer, A. & Klein, M. L. Ab Initio Molecular Dynamics Study of Supercritical Carbon Dioxide Including Dispersion Corrections. J. Chem. Phys. 131, 144506 (2009).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Windisch, C. F. Jr. et al. Raman Spectrum of Supercritical C18O2 and Re-Evaluation of the Fermi Resonance. Phys. Chem. Chem. Phys. 14, 2560–2566 (2012).
Goedecker, S., Teter, M. & Hutter, J. Separable Dual-Space Gaussian Pseudopotentials. Phys. Rev. B 54, 1703–1710 (1996).
VandeVondele, J. & Hutter, J. Gaussian Basis Sets for Accurate Calculations on Molecular Systems in Gas and Condensed Phases. J. Chem. Phys. 127, 114105–114113 (2007).
Zhang, L. & Luttge, A. Aluminosilicate Dissolution Kinetics: A General Stochastic Model. J. Phys. Chem. B 112, 1736–1742 (2008).
Kerisit, S., Liu, C. & Ilton, E. S. Molecular Dynamics Simulations of the Orthoclase (0 0 1)- and (0 1 0)-Water Interfaces. Geochim. Cosmochim. Acta 72, 1481–1497 (2008).
Acknowledgements
This work was supported by the US Department of Energy, Office of Fossil Energy (M.-S. L., B. P. M. and V.-A. G.) and the Office of Basic Energy Science, Division of Chemical Sciences, Geosciences and Biosciences (R.R.) and performed at the Pacific Northwest National Laboratory (PNNL). PNNL is a multi-program national laboratory operated for DOE by Battelle. Computational resources were provided by PNNL’s Platform for Institutional Computing (PIC), the W. R. Wiley Environmental Molecular Science Laboratory (EMSL), a national scientific user facility sponsored by the Department of Energy’s Office of Biological and Environmental Research located at PNNL and the National Energy Research Scientific Computing Center (NERSC) at Lawrence Berkeley National Laboratory. The authors are grateful to Dr. S. Kerisit, Dr. D. C. Cantù and Dr. Z. Dohnalek for a critical reading of the manuscript and F. Verdier (NERSC) for technical assistance.
Author information
Authors and Affiliations
Contributions
M.-S.L. performed the calculations. M.-S.L., R.R. and V.-A.G. analyzed the data. M.-S.L., B.P.M., R.R. and V.-A.G. equally contributed to the writing of the manuscript. All authors have given approval to the final version of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Lee, MS., Peter McGrail, B., Rousseau, R. et al. Structure, dynamics and stability of water/scCO2/mineral interfaces from ab initio molecular dynamics simulations. Sci Rep 5, 14857 (2015). https://doi.org/10.1038/srep14857
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep14857
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.