Abstract
Until the early 1990s, incidences of Mycoplasma pneumoniae (MP) infection showed three to five year epidemic cycles in multiple countries, however, the mechanism for the MP epidemic cycle has not been understood. Here, we investigate the determinant of periodicity in MP incidence by employing a mathematical model describing MP transmission dynamics. Three candidates for the determinant of periodicity were evaluated: school-term forcing, minor variance in the duration of immunity and epidemiological interference between MP serotypes. We find that minor variation in the duration of immunity at the population level must be considered essential for the MP epidemic cycle because the MP cyclic incidence pattern did not replicate without it. Minor variation, in this case, is a less dispersed distribution for the duration of immunity than an exponential distribution. Various lengths of epidemic cycles, including cycles typically found in nature, e.g. three to five year cycles, were also observed when there was minor variance in the duration of immunity. The cyclic incidence pattern is robust even if there is epidemiological interference due to cross-immune protection, which is observed in the epidemiological data as negative correlation between epidemics per MP serotype.
Similar content being viewed by others
Introduction
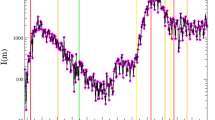
Mycoplasma pneumoniae (MP) is a bacterium that causes bacterial pneumonia in humans and is a common cause of respiratory bacterial infection1. The most distinctive epidemiological feature of MP is its periodicity. In Denmark, the U.S. and Japan, three to five year cycles were observed up to the early 1990s2,3. Especially in Japan, the incidences of MP infection showed a clear four year epidemic cycle until the early 1990s and so was commonly called “Olympic disease” among clinicians (Fig. 1a). These periodicities disappeared for reasons which are currently not well understood. A decline in MP incidence rates were observed with the widespread use of macrolides antibiotics4, but in recent years a macrolides-resistant strain of MP has emerged and macrolides-resistant MP cases have increased drastically5. With the drastic rise in macrolides-resistant MP cases, the need to be able to predict MP prevalence is growing. Understanding the dynamics of MP epidemics in the past is essential to predicting the prevalence in the future. However, the mechanism of oscillation in past MP epidemics has yet to be explained.
MP incidence in Japan.
(a) Time series data of weekly MP cases per sentinel in Japan from 1981 to 2015. The figure shows the number of reported primary atypical pneumonia cases until March 1999 and MP cases after April 1999 due to the change in the law for reporting infectious diseases. The data were collected from nationwide sentinel clinics and integrated by the Infectious Diseases Surveillance Center, National Institute of Infectious Diseases, Japan (http://idsc.nih.go.jp/index.html). (b) Annual detection rate of serotype I among all reported MP cases with the four-year moving average. (c) Time series data of yearly cases per serotype from 1976 to 2005. The data shown in (a) were collected from the whole area of Japan while most data shown in (b,c) were collected from Kanagawa prefecture in Japan.
Many mechanisms of periodicity have been hypothesized to explain the oscillation of MP epidemics6,7,8,9,10,11,12,13. Among them is a seasonally-forced transmission rate. Most MP cases are observed among school children14 and also exhibit complex epidemic cycles as observed in other childhood diseases15,16. Mathematical models demonstrate that school-term forced transmission rates explain multi-annual dynamics in childhood diseases12,15,16. Other candidate mechanisms are the distribution of the infectious period, the distribution of the duration of immunity and the latent period. Most mathematical models describing transmission dynamics of infectious diseases assume that the distribution of the sojourn time between host infection states follows an exponential distribution, however, conclusions and interpretations derived from mathematical modelling would be changed by using different assumptions for the distribution of the sojourn time17,18. Previous studies show that the dynamics become much more complex if the sojourn time follows a distribution pattern which is less dispersed than an exponential distribution19,20,21,22,23. Epidemiological interference is also a candidate mechanism of MP epidemic periodicity. MP is classified into two distinct serotypes with negative correlation between epidemics of different serotypes being observed (see Fig. 2a,b in Kenri et al. 20083). This negative correlation suggests epidemiological interference between serotypes by cross-immune protection. Epidemiological interference itself does not induce sustained oscillation of the epidemic curve24, however, it affects the epidemic dynamics and can change the periodicity of epidemics triggered by other mechanisms15,25. As the effect of cross-immune reactions on the epidemic cycle of MP was not previously understood, we delve into the topic here.
Epidemic cycles with varied infectious periods and latent periods.
Short latent and infectious periods are required for epidemic cycles longer than one year (the periodicity of school terms). The latent and infectious periods for MP are both 2 to 3 weeks. Black denotes annual epidemic cycles and white denotes epidemic cycles longer than one year. To explore the possibility of oscillation the epidemic cycles were calculated with varied b from 1.1 to 17.0 (the estimated b for measles cases in the U.K. is 1.727). Mean duration of immunity is assumed to be 7 years.
In this paper, we assessed whether three mechanisms commonly used in mathematical models to describe the oscillation of the epidemic curve can, in fact, explain the periodicity of MP epidemics. These three mechanisms are: i) school term-forced transmission; ii) epidemiological interference by cross-immune reaction; and iii) minor variation in latent, infectious and immunity periods. We began by analyzing whether i) and ii) are sufficient to explain MP epidemic periodicity within a simple SEIRS model. We then employed an SEIRS model with time delay for the assessment of a special case of iii), in which there is a constant duration for the latent, infectious and immunity periods. Subsequently we assessed a more general case of iii) with individual-based Monte Carlo simulation.
Results
Epidemic periodicity when the sojourn time of each infectious state follows an exponential distribution
In this section, we assumed that the distribution of sojourn time of each infectious state follows an exponential distribution and assessed the effect of cross-immune reaction and seasonal fluctuation of transmission rate on the oscillation of the epidemic curve using a deterministic model whose parameters are described in Table 1. If the transmission rate is constant over time and there is no cross-immune protection, there is no oscillation of the epidemic curve at equilibrium because endemic equilibrium is always stable, if it exists. Even if there is cross-immune protection, oscillation as seen in MP epidemics does not always exist if the transmission rate is constant over time24.
School-term forcing
With respect to seasonality in the transmission rate, one possible explicit mechanism for the MP periodicity is the school term because most MP cases are observed among school children. The difference of behavior in school children, e.g. contact and movement between school terms and school holidays, is proposed as the cause of seasonality in the incidence of infectious diseases. The change in transmission rates between school terms and holidays is commonly referred to as ‘school-term forcing’26. Previous studies show that school-term forcing can explain the seasonality of measles epidemics well16.
So far, studies employing either SIR or SEIR models which take into account host birth and death rates reported that the periodicity of epidemics triggered by seasonally-fluctuating transmission rates is closely related to the basic reproductive number, R0, the length of the infectious period and the amplitude of seasonally-fluctuating transmission rates15,16,25,27. Intermediate values of R0 are required for multi-annual epidemic cycles, while small or large R0 can induce only annual cycles27. Keeling et al. 200116 reported that a short infectious period is required for sustained long-cycle oscillation of the epidemic curve. With respect to the amplitude of seasonally-fluctuating transmission rates, annual cycles are observed when the amplitude is small and multi-annual cycles emerge when the amplitude is sufficiently large15,25.
We examined the effect of school-term forcing on MP epidemics. However, when parameters were set for MP as shown in Table 1 and the amplitude of school-term forcing b = 1.7 as the estimated b for measles in the U.K.27, the four year cycle was not observed. The results of previous studies are not comparable with our results due to the difference in model structure (with vs. without waning immunity), three possibilities can be considered for the reason why school-term forcing cannot explain the MP epidemic cycle; i) R0 of MP is out of range for multi-annual cycles, ii) the infectious period of MP is too long to induce multi-annual cycles and iii) the amplitude of school-term forcing is not large enough to cause multi-annual cycles. With respect to R0, we explored the epidemic cycle using varying R0, from 1.5 to 20.5, however only annual cycles were observed. In terms of latent period and infectious period, we also explored the epidemic cycle with varying latent periods and infectious periods from 3 to 25 days. We observed multi-annual cycles when both the latent and infectious periods were sufficiently short (white regions in Fig. 2c). The length of the epidemic cycle is close to the length of the cycle of the fluctuating transmission rate (an annual cycle) when the latent or infectious periods are large, as observed in MP epidemics (latent period = 2 to 3 weeks and infectious period = 2 to 3 weeks for MP) (Fig. 2c), thus school-term forcing does not explain the periodicity of MP (i.e. four years), which is much larger than the school term cycle (i.e. one year). Regarding the amplitude of school-term forcing, we explored the epidemic cycle when the strength of the school-term forcing, b, was varied from 1.1 to 17 (this range includes realistic b values, as the estimated b for measles in the U.K. is 1.727), however, school-term forcing always produces annual cycles with MP parameter settings, i.e., latent period = 2 to 3 weeks and infectious period = 2 to 3 weeks (Fig. 2).
Epidemiological interference
Epidemiological interference between strains by cross-immune protection is known to change the periodicity of epidemics25. A combination of cross-immune protection and school-term forcing may explain the MP epidemic cycle. We also examined whether the presence of both seasonally-forced transmission rates and cross-immune protection can capture the MP epidemic cycle. By varying the strength of cross-immune protection (with a range from 0 to 1), mean duration of immunity (with the range from two to ten years) and the ratio of transmission rates from school days to holidays, b, (with a range from 0.1 to 20), only annual cycle oscillation was observed. Even when both cross-immune reaction and seasonally-forced transmission rates were taken into account, the four-year epidemic cycle of MP was not explained, nor was it observed within our model.
Epidemic periodicity when the sojourn time of each infectious state follows a non-exponential distribution
Without cross-immune protection
We investigated the contribution of minor variance in three sojourn times, i.e. the latent period, the infectious period and the duration of immunity. For the sake of simplicity, we assumed variance of the sojourn time is either zero (delta) or mean-squared (exponential). Minor variance in the duration of immunity is critical for the oscillation of epidemics (Table 2). On the other hand, variance in the length of the latent and infectious periods is not important for oscillation. Furthermore, the mean of the length of the latent and infectious periods is also not sensitive to the oscillation in long-term MP transmission dynamics (please see Supplemental Information Figure S1a,b for the details). This analysis was conducted using a deterministic model.
To analyze the detailed effect of minor variance in the duration of immunity, we also used a stochastic model to investigate the relationship between the oscillation of the epidemic and non-zero, but small, variance in the duration of immunity. The strength of oscillation of the epidemic curve is measured by the coefficient of variation, CV (see Methods). Weak oscillation shows small CV and strong oscillation shows large CV (top panels in Fig. 3c). Our simulation results show the smaller the variance in the duration of immunity, the larger the CV (bottom panel in Fig. 3c). Threshold-like behavior in the variance of the duration of immunity for the oscillation of epidemics was also observed. Since CV for the MP epidemic in Japan from 1982 to 1990 is 0.73, the intermediate variance in the duration of immunity between zero (constant immunity duration) and the square of its mean (immunity duration following an exponential distribution) can explain MP epidemic dynamics.
The impact of variance in the duration of immunity on MP epidemics.
(a) The distribution of the immunity duration with mean = 6 years and varied variance. We assumed Δt = 1/200 years. (b) The relationship between variance in the duration of immunity and the epidemic cycle. The dashed line shows the 4 year cycle observed in Japan. (c) Variance in the duration of immunity determines the oscillation of the epidemic curve.
Not only sustained oscillation in MP epidemics, but also multi-annual epidemic cycles not explained by school-term forcing, are observed with minor variance in the duration of immunity (Fig. 3b). The epidemic cycle depends on both the mean and the variance in the duration of immunity.
With cross-immune protection
Even if MP serotypes interfere with each other by cross-immune protection, the periodicity of epidemics is determined by variance of the duration of immunity as similar to a stochastic model which disregards cross-immunity; the smaller the variance, the stronger the epidemic oscillation (Fig. 4). Various epidemic cycles, including three to five year cycles observed in Denmark, the U.S. and Japan, were observed. The effect of the mean duration of immunity and the strength of cross-immune protection on the epidemic cycle are less clear than the variance of the immunity period (Fig. 5).
The impact of epidemiological interference by cross-immunity on the oscillation of the epidemic curve.
The strength of the cross-immune reaction is denoted by α; α = 0 means no cross-immune reaction and α = 1 means perfect protection by cross-immune reaction. The coefficient of variation, CV, of the number of people infected with any strain was measured. CV is a measure of the variation in the number of infected individuals over time.
Discussion
In this study, we assessed which assumptions in theoretical studies of childhood diseases are required to explain MP epidemic periodicity. Our results show that minor variation in the duration of immunity is essential to capturing MP epidemic periodicity and also suggest that ordinary differential equations, ODE, are not suitable for describing MP epidemics. Oscillation of the epidemic curve is robust even if there is epidemiological interference due to cross-immune protection, which is observed as negative correlation between epidemics per MP serotype.
Both the epidemic cycle and the shape of the epidemic curve, i.e. the coefficient of variation, are less sensitive to the strength of cross-immune reactions. At the same time, the cycle of dominant strain shift is sensitive to cross-immunity (Fig. 6b–d). Previous studies show that stronger cross-immunity causes longer periodicity for dominant strain shifting12. MP epidemics in Kanagawa prefecture, Japan in 1976–1991 show 16 to 20 year cycles for dominant strain shift (Fig. 1b)3. Long periodicity for dominant strain shift, which takes the duration of four to five MP epidemic cycles, suggests strong cross-immunity between strains. Indeed, our results showed similar tendency for the relationship between strength of cross-immunity and the cycle of dominant strain shift. Short timespan dominant strain shifts (with duration of one to two epidemic cycles) are observed if cross-immunity is weak (Fig. 6b–d). This result suggests that the strength of cross-immunity can be estimated from the time between switching dominant strains.
The impact of epidemiological interference on the cycle for dominant strain shift.
(a) Illustrates the relationship between the cycle for dominant shift and the epidemic cycle on the MP epidemic with mr = 8 years, log10[σr2] = −0.60 and α = 0.6. (b–d) show the cycles for dominant strain shift with varied strength of cross-immune protection α.
A previous study showed positive correlation between the mean duration of immunity and epidemic cycles21. However, this tendency was not clearly visible in our results. This lack of a clear relationship observed in our results may be caused by an occurrence of switching between attractors. Previous theoretical studies show multiple solutions for epidemic cycles with a fixed mean duration of immunity even if there is no epidemiological interference from cross-immune reactions21. Our simulations also confirmed these results of multiple epidemic cycles as shown in Figures S2. This warrants future work on the possible existence of conditions of multiple attractors and transitions between them.
To predict MP prevalence per serotype, the estimation of the immunity duration distribution is essential. However, degeneracy of the epidemic cycle, i.e. the existence of multiple attractors, suggests the difficulty involved in the estimation of the mean duration of immunity solely from prevalence time-series data. In addition to multiple attractors, transmission dynamics are complicated by epidemiological interference between serotypes. The prevalence for each serotype is necessary to fully capture the dynamics, however, serotype information was not reported except for a few studies, as shown in Fig. 1c and Nguipdop-Djomo et al. 201328. A possible strategy for estimating the mean duration of immunity would be to use the age-specific sero-prevalence for each serotype. The simplest catalytic model frequently used for epidemiological parameter estimation from serological data is not applicable for MP because of the periodicity of the epidemics. Extrapolation of time-series data of prevalence may enable us to estimate both the mean and the variance of the duration of immunity.
In this study we did not take into account the realistic age structure of the host population, while a previous theoretical study showed that age structure may explain sustained oscillation of the epidemic curve24. Age structure is unlikely to be essential for MP epidemic periodicity, because disappearances of oscillation in MP prevalence were observed at similar timing in different countries. Synchronization of similar changes of age structure in different countries at similar timing is required to explain the disappearance of the MP epidemic periodicity, however this is unrealistic. Disappearances of oscillation in MP incidence may be explained better by the change in the distribution for the duration of immunity due to widespread use of macrolide antibiotics in those countries.
Throughout this study we assumed a constant fraction of infections become symptomatic over time. R0 from Nguipdop-Djomo et al. 201328 was used in our analysis as the baseline scenario and is estimated from sero-prevalence. Our results for MP prevalence use the sum of symptomatic and asymptomatic cases. If the proportion of infections that become symptomatic is the same over time, MP periodicity is independent from the symptomatic case rate.
In summary, minor variation in the duration of immunity at the population level is the most likely determinant of the periodicity of MP epidemics. If the distributions of latent, infection and immunity periods follow exponential distribution, epidemic cycles longer than one year were not reproducible, even if both seasonal forcing of transmission (school-term forcing) and cross-immune protection were considered as the driving forces of multi-annual epidemic cycles11,15,16,25,29. In short, only non-exponentially distributed variation in the duration of immunity produced multi-annual epidemic cycles. The cyclic incidence pattern induced by minor variation in the duration of immunity is robust even if there is epidemiological interference due to cross-immune protection. Since small variance in the duration of immunity can induce complex dynamics, more detailed analysis is required to understand MP epidemic dynamics; even though the analysis of the compartmental model with non-exponential distributed sojourn time is an analytically challenging issue.
Methods
From MP clinical observations, symptoms appear two to three weeks after infection and continue for an additional two to three weeks30. The latent period may be different from the incubation period, but as the latent period is not known, we assumed the latent period to be the same duration as the incubation period (me = 3 weeks). Based on the natural history of MP, the whole population can be classified by infection state: susceptible s, exposed e, infectious i, recovered r. Re-infection with Mycoplasma pneumoniae is frequently observed, suggesting waning acquired immunity, so we employed the SEIRS model.
The age distribution of MP infection peaks in children and young adults14. For the sake of simplicity, we focused only on the prevalence among the populations of children and young adults. We also assumed a constant host population; the rate of birth and outflow of host by death or aging are the same, μ. As a result, we focused on a 15 year range for the high risk age group (1/μ = 15 years).
Compartmental models in epidemiology, such as the SIR model, are described by ordinary differential equations which assume the sojourn time in each compartment follows an exponential distribution. To relax this strong assumption, we assume that the sojourn time in infection state x, τx, follows a gamma distribution Gx,

where mx and σx2 are the mean and variance of τx and Γ is the gamma function. If σx2 = mx2, the distribution of τx is equal to the exponential distribution and the system is equivalent to a system described by ordinary differential equations. If σx2 = 0, the distribution of τx is equal to the delta distribution and the system is equivalent to a system described by delay differential equations with a fixed delay. To analyze the impact of σx2 on the dynamics of MP epidemics, we explored the system with varying σe2, σi2 and σr2 with ranges from 0 to me2, mi2 and mr2, respectively. When τe, τi and τr follow an exponential distribution (σe2 = me2, σi2 = mi2, σr2 = mr2), the time series change of each compartment is described as follows:

where each prime denotes a time derivative. Each variable represents the population fraction so that S(t) + e(t) + i(t) + r(t) = 1 holds for t > 0. When τe and τi follow exponential distributions (σe2 = me2, σi2 = mi2) and τr follows a gamma distribution, the time series change of each compartment is described as follows:

The integral term in equation (3) describes the proportion of those who lose immunity per unit time at time t; namely, the transition from compartment r to compartment s at time t. When the sojourn time follows a non-exponential distribution, the transition rate to the next compartment depends on the sojourn time at the current compartment. To calculate the transition to the next compartment (compartment s), it is necessary to calculate the transition of individuals per elapsed sojourn time at the current compartment (compartment r). The proportion of individuals belonging to compartment r with elapsed sojourn time at compartment r, τr, is given by the product of the initial proportion of transition from compartment i,  , the transition probability per unit time to compartment s at sojourn time τr, Gr(τr) and the survival probability at the sojourn time τr, exp(−μτr). The parameter values used in this paper are summarized in Table 1. The transmission rate, β, is derived by solving R0 = 1.7 for each parameter set. The basic reproduction number, R0, is given by
, the transition probability per unit time to compartment s at sojourn time τr, Gr(τr) and the survival probability at the sojourn time τr, exp(−μτr). The parameter values used in this paper are summarized in Table 1. The transmission rate, β, is derived by solving R0 = 1.7 for each parameter set. The basic reproduction number, R0, is given by

R0 of the SEIRS model is defined by the expected number of secondary cases from a single exposed individual in a fully susceptible population31 and can be decomposed to the product of the transmission rate β, the survival probability of initially exposed individuals exp(−μa) and the probability that an initially exposed individual has infectiousness after a unit time elapsed since the infection (here τ can be interpreted as the elapsed time since the infection when the initially exposed individual leaves compartment e and enters compartment i), i.e., belongs to compartment i,  . For the analysis utilizing the assumption that the sojourn time follows an intermediate distribution between delta and exponential distributions, i.e., 0 < σx2 < mx2, we employed individual-based Monte Carlo simulation (IBM), the details of which are shown in the “Cross-immunity” section under Methods.
. For the analysis utilizing the assumption that the sojourn time follows an intermediate distribution between delta and exponential distributions, i.e., 0 < σx2 < mx2, we employed individual-based Monte Carlo simulation (IBM), the details of which are shown in the “Cross-immunity” section under Methods.
School-term forcing transmission
The school year in Japan is divided into three terms: the first trimester is from 7 April to 18 July, the second trimester is from 1 September to 22 December and the third trimester is from 7 January to 24 March for 2014. The length of semesters is similar between different years. As with previous mathematical models for school-term forcing26, we assumed transmission rates during semesters, βschool days, are constant over time and higher than that on other days, βholidays. To determine βschool days and βholidays, we introduce a parameter, b, describing the ratio of transmission rate between school days and holidays (i.e., b = βschool days/βholidays) and a parameter, β, describing the annual average of βschool days and βholidays (i.e., β = ([number of holidays in a year]βholidays + [number of school days in a year]βschool days)/[length of a year]). Using β and b, βschool days and βholidays are given by

Cross-immunity
To clarify the impact of cross-immunity on the epidemic dynamics of MP we expand the above model to incorporate a reduction of susceptibility due to previous MP infection. We assumed that acquired immunity from the infection with a strain reduces susceptibility to other strains and this immune cross-protection decays with waning acquired immunity. When the prevalence of multiple strains interferes with one another via cross-immune protection, compartments for all combinations of infection states against all strains are required to capture the epidemic dynamics using deterministic models. For example, there are two serotypes and four infection states for each serotype (s, e, i and r), therefore 42, or 16, compartments are required. Furthermore, when the sojourn time in each compartment does not follow an exponential distribution, many more compartments are required and the model structure becomes much more complicated. To avoid complexity, we constructed an IBM describing co-circulation of two serotypes.
We considered a host population of two million and tracked the timing of transition between the infection states. The sojourn time in each infection state is determined using a gamma random number generator with the parameters σx2 and mx2. Transition of the infection state occurs after the lapse of determined sojourn time. Transmission probability is determined by the current infection state of each individual. If the individual does not have immunity to any strain, the transmission probability of strain x per unit time Δt is

where Ix is the number of infected individuals with strain x and N is total number of hosts. In this study we set Δt = 1/200 year (≈1.8 days). The transmission probability of a strain for an individual is reduced by α if he has immunity against another strain. For the analysis of a model disregarding cross-immunity with arbitral σx2 having a range of 0 < σx2 < mx2, IBM was used with α = 0. Birth, death and outflow of hosts from the population by aging occur randomly with a given rate, μ.
Analysis of IBM results
In all analyses the IBM results during the first 200 years were discarded and the number of infected individuals during the next 500 years were recorded. The epidemic cycle and the cycle of dominant strain shift was measured by power spectral analysis with Fourier transformation. The epidemic cycle, in the presence of epidemiological interference by cross-immune protection, was measured based on field data regarding the number of people infected with any MP serotype. The strength of oscillation of the epidemic curve was measured by the coefficient of variation (CV) for the number of infected individuals over time, CV = [standard deviation]/[mean].
Additional Information
How to cite this article: Omori, R. et al. The determinant of periodicity in Mycoplasma pneumoniae incidence: an insight from mathematical modelling. Sci. Rep. 5, 14473; doi: 10.1038/srep14473 (2015).
References
Jacobs, E. Mycoplasma pneumoniae: now in the focus of clinicians and epidemiologists. Euro Surveill. 17, 2–4 (2012).
Waites, K. B. & Talkington, D. F. Mycoplasma pneumoniae and its role as a human pathogen. Clin. Microbiol. Rev. 17, 697–728 (2004).
Kenri, T. et al. Genotyping analysis of Mycoplasma pneumoniae clinical strains in Japan between 1995 and 2005: type shift phenomenon of M-pneumoniae clinical strains. J. Med. Microbiol. 57, 469–475 (2008).
Ito, I. et al. Culturally verified Mycoplasma pneumoniae pneumonia in Japan: a long-term observation from 1979–99. Epidemiol. Infect. 127, 365–367 (2001).
Morozumi, M. et al. Increased macrolide resistance of Mycoplasma pneumoniae in pediatric patients with community-acquired pneumonia. Antimicrob. Agents Chemother. 52, 348–350 (2008).
Martinez-Bakker, M., Bakker, K. M., King, A. A. & Rohani, P. Human birth seasonality: latitudinal gradient and interplay with childhood disease dynamics. P. Roy. Soc. B-Biol. Sci. 281, 20132438 (2014).
Altizer, S. et al. Seasonality and the dynamics of infectious diseases. Ecol. Lett. 9, 467–484 (2006).
Althouse, B. M. & Hebert-Dufresne, L. Epidemic cycles driven by host behaviour. J. R. Soc. Interface 11, 20140575 (2014).
Olsen, L. F. & Schaffer, W. M. Chaos versus noisy periodicity - alternative hypotheses for childhood epidemics. Science 249, 499–504 (1990).
Arinaminpathy, N., Lavine, J. S. & Grenfell, B. T. Self-boosting vaccines and their implications for herd immunity. P. Natl. Acad. Sci. USA 109, 20154–20159 (2012).
Adams, B. et al. Cross-protective immunity can account for the alternating epidemic pattern of dengue virus serotypes circulating in Bangkok. P. Natl. Acad. Sci. USA 103, 14234–14239 (2006).
Keeling, M. J. & Rohani, P. Modeling infectious diseases in humans and animals. (Princeton University Press, 2008).
Pascual, M. & Dobson, A. Seasonal patterns of infectious diseases. Plos Med. 2, 18–20 (2005).
Foy, H. M. Infections caused by Mycoplasma pneumoniae and possible carrier state in different populations of patients. Clin. Infect. Dis. 17 Suppl 1, S37–46 (1993).
Rohani, P., Earn, D. J., Finkenstadt, B. & Grenfell, B. T. Population dynamic interference among childhood diseases. P. Roy. Soc. B-Biol. Sci. 265, 2033–2041 (1998).
Keeling, M. J., Rohani, P. & Grenfell, B. T. Seasonally forced disease dynamics explored as switching between attractors. Physica D 148, 317–335 (2001).
Feng, Z. Final and peak epidemic sizes for SEIR models with quarantine and isolation. Math. Biosci. Eng. 4, 675–686 (2007).
Feng, Z. L., Xu, D. S. & Zhao, H. Y. Epidemiological models with non-exponentially distributed disease stages and applications to disease control. B. Math. Biol. 69, 1511–1536 (2007).
Lloyd, A. L. Realistic distributions of infectious periods in epidemic models: Changing patterns of persistence and dynamics. Theor. Popul. Biol. 60, 59–71 (2001).
Hethcote, H. W. & Levin, S. A. Periodicity in epidemiological models. Applied mathematical ecology (eds Levin, S. A., Hallam, T. G. & Gross, L. J. ) 193–211 (Springer, 1989).
Goncalves, S., Abramson, G. & Gomes, M. F. C. Oscillations in SIRS model with distributed delays. Eur. Phys. J. B 81, 363–371 (2011).
Krylova, O. & Earn, D. J. D. Effects of the infectious period distribution on predicted transitions in childhood disease dynamics. J. R. Soc. Interface 10, 20130098 (2013).
Blyuss, K. B. & Kyrychko, Y. N. Stability and bifurcations in an epidemic model with varying immunity period. B. Math. Biol. 72, 490–505 (2010).
Castillo-Chavez, C., Hethcote, H. W., Andreasen, V., Levin, S. A. & Liu, W. M. Epidemiological models with age structure, proportionate mixing and cross-immunity. J. Math. Biol. 27, 233–258 (1989).
Kamo, M. & Sasaki, A. The effect of cross-immunity and seasonal forcing in a multi-strain epidemic model. Physica D 165, 228–241 (2002).
Grassly, N. C. & Fraser, C. Seasonal infectious disease epidemiology. P. Roy. Soc. B-Biol. Sci. 273, 2541–2550 (2006).
Earn, D. J. D., Rohani, P., Bolker, B. M. & Grenfell, B. T. A simple model for complex dynamical transitions in epidemics. Science 287, 667–670 (2000).
Nguipdop-Djomo, P., Fine, P. E., Halsby, K. D., Chalker, V. J. & Vynnycky, E. Cyclic epidemics of Mycoplasma pneumoniae infections in England and Wales from 1975 to 2009: time-series analysis and mathematical modelling. The Lancet 382, S78 (2013).
Recker, M. et al. Immunological serotype interactions and their effect on the epidemiological pattern of dengue. P. Roy. Soc. B-Biol. Sci. 276, 2541–2548 (2009).
Clyde, W. A. Clinical overview of typical Mycoplasma-Pneumoniae infections. Clin. Infect. Dis. 17, S32–S36 (1993).
Allen, L. J., Brauer, F., Van den Driessche, P. & Wu, J. Mathematical epidemiology. (Springer, 2008).
Lind, K., Benzon, M. W., Jensen, J. S. & Clyde, W. A. A seroepidemiological study of Mycoplasma pneumoniae infections in Denmark over the 50-year period 1946-1995. Eur. J. Epidemiol. 13, 581–586 (1997).
Acknowledgements
We thank Dr. Tsuyoshi Kenri for providing the epidemiological data shown in Fig. 1. This research was supported by CREST, Japan Science and Technology Agency (JST) to RO, MEXT Grant-in-Aid for Young Scientists (B) Grant Number 15K19217 to RO, JST RISTEX program for Science of Science, Technology and Innovation Policy to YN, grant from the Ministry of Health, Labour and Welfare of Japan (H24-Shinkou-Ippan 010) to SS and KS. YN was supported by JSPS Fellows, No.268448 of Japan Society for the Promotion of Science.
Author information
Authors and Affiliations
Contributions
R.O. conceived the study, R.O. and Y.N. developed the mathematical model and performed the analyses. R.O., Y.N., H.T., S.S. and K.S. contributed to the interpretation of the results and drafting of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Omori, R., Nakata, Y., Tessmer, H. et al. The determinant of periodicity in Mycoplasma pneumoniae incidence: an insight from mathematical modelling. Sci Rep 5, 14473 (2015). https://doi.org/10.1038/srep14473
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep14473
This article is cited by
-
Asthma incidence can be influenced by climate change in Italy: findings from the GEIRD study—a climatological and epidemiological assessment
Scientific Reports (2023)
-
An Explicit Periodic Solution of a Delay Differential Equation
Journal of Dynamics and Differential Equations (2020)
-
Evidence for a link between the Atlantic Multidecadal Oscillation and annual asthma mortality rates in the US
Scientific Reports (2019)
-
Positively interacting strains that co-circulate within a network structured population induce cycling epidemics of Mycoplasma pneumoniae
Scientific Reports (2019)
-
Epidemiological characterization of respiratory tract infections caused by Mycoplasma pneumoniae during epidemic and post-epidemic periods in North China, from 2011 to 2016
BMC Infectious Diseases (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.