Abstract
This work reports the dynamical thermal behavior of lasing microspheres placed on a dielectric substrate while they are homogeneously heated-up by the top-pump laser used to excite the active medium. The lasing modes are collected in the far-field and their temporal spectral traces show characteristic lifetimes of about 2 ms. The latter values scale with the microsphere radius and are independent of the pump power in the studied range. Finite-Element Method simulations reproduce the experimental results, revealing that thermal dynamics is dominated by heat dissipated towards the substrate through the medium surrounding the contact point. The characteristic system scale regarding thermal transport is of few hundreds of nanometers, thus enabling an effective toy model for investigating heat conduction in non-continuum gaseous media and near-field radiative energy transfer.
Similar content being viewed by others
Introduction
Whispering gallery mode (WGM)-based lasing cavities can enhance the high sensitivity of passive WGM cavities1,2 and achieve extremely low detection limits thanks to their narrow linewidths3,4,5. Furthermore, coupled schemes in which bus-waveguides are used to inject light inside the cavity are not needed since simple far-field pumping configurations can be used. Regarding signal collection, the high intensity of the emitted laser light allows for either standard far-field detection or for coupled configurations using bus-waveguides6,7. Made of semiconducting or dielectric materials, high-quality WGM cavities are prone to thermally-induced changes due to the thermo-optic (TO) effects, i.e., thermo-refractive mechanisms and thermal expansion, which often limit their sensitivity5. Moreover, a wide range of thermally induced nonlinear phenomena such as hysteretic wavelength response and oscillatory instability have been reported experimentally in such cavities8,9,10.
Although usually considered detrimental features, TO effects can be exploited in time-resolved experiments to determine heat exchange rates between the cavity and the external environment10,11,12. Despite the lack of large sensitivities, these are calibration-free techniques that allow extracting quantitative information of the medium surrounding the cavity. Heat transfer dynamics using WGM passive cavities has been successfully studied to measure adsorbed water layer thickness and desorption rates11 and to obtain absolute values of thermal accommodation coefficients of different gases at low pressures12. In particular, wide interest has been reported in predicting heat transfer to a surface when immersed in a gas in the non-continuum limit, when the characteristic length scale of the system is comparable to the gas mean free path. This limit can be used to describe the gas environment in a variety of applications, ranging from MEMS devices (low dimensions) to semiconductor manufacturing or spacecraft aerodynamics (low pressures)13.
Standard investigation of dynamical thermal behavior of passive WGM cavities is performed by in-coupling laser light through the evanescent field of a tapered fiber. Under such conditions, the transmitted light is monitored while the WGM cavity is out of thermal equilibrium in response to non-adiabatic heating11,12. Conversely, the coupled light can be used both to test the thermal dynamics and as a heating source localized within the WGM volume10. However, this approach complicates the dynamics of the system since: i) the heating efficiency is modulated by the shape of the resonance and ii) the cavity takes some time to thermalize internally.
In this work, we present an alternative approach that combines high-power laser emission and narrow spectral linewidths with excitation-detection in the far field, enabling a straightforward investigation of the thermal dynamics of the cavity with all-optical means.
The investigated WGM lasing cavity is a Nd-doped Barium-Titanium-Silicate (BTS)7 microsphere fabricated with the method reported in ref. 14 (see Methods) placed on top of a 2.7 micron thick SiO2 layer deposited over a Si substrate. A free space laser is used to resonantly excite the Nd3+ ions and homogeneously heat the cavity, while the signal of a lasing WGM is collected in the far-field to monitor the thermal dynamics of the cavity. The sphere-plate geometry has been the object of deep investigation during the last years in the context of local thermal transfer between non-planar geometries15,16,17 mainly driven by their promising application in nanoscale heat stamps18,19. We demonstrate that, at ambient conditions, thermal dynamics is governed by heat conduction to the substrate, mediated by the medium surrounding the contact point. Given that the characteristic dimensions of thermal transport are of few hundred nanometers, i.e., substantially lower than the thermal wavelength and comparable to the gas mean free path, we propose lasing microspheres as a simple and versatile scheme to investigate radiative thermal conduction and non-continuum gas thermal behaviors.
Results and Discussion
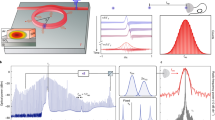
The measurement setup for the optical experiment is schematically shown in Fig. 1. A continuous wave (CW) laser at 808 nm was focused on a single microsphere (radius between 20 and 25 μm) by means of a microscope objective20, the spot size being large enough to fit the microspheres dimensions. Heat generation can be approximated to be spatially homogeneous within the microspheres since: i) the spatial inhomogeneity of the pump power density provoked by their focusing ability is not very pronounced (the focus lies several microns below the substrate surface), ii) the spatial profile of the PL emission looks homogeneous (see bottom-right panel of Fig. 1) and iii) the internal thermal dynamics is much faster than the dissipation to the surrounding. The PL signal associated to WGMs contained in a plane close to the microsphere equator (parallel to the substrate) and coming out from a lateral edge was collected by a second microscope objective. It was then focused on the input slit of a monochromator and recorded either by a charge-coupled-device (CCD) detector or by a photomultiplier tube (PMT). Time-resolved experiments were made by modulating the pump with a mechanical chopper and by registering the PMT output with a digital oscilloscope (see Methods for further details of the experiment).
Schematic diagram of the experimental set-up.
Dimensions are not to scale. The bottom-right panel illustrates a spatial profile of the emitted PL below lasing threshold, which has been taken by placing the focus of the collection objective at the sphere center and widely opening the pinhole. The sphere contour is highlighted for clarity. The bright spot is probably associated to a scattering region within the sphere. The figure has been drawn by J. M. Ramirez.
The Nd3+ excitation process is described in Fig. 2a. Under external excitation, Nd3+ ions are promoted from the ground state (4I9/2) up to the 4F5/2 and 2H9/2 levels, from where a rapid non-radiative thermalization to the 4F3/2 transition takes place. Subsequently, another radiative de-excitation occurs from this level down to the 4I11/2 state. The final thermalization to the ground state is through non radiative scattering. Nd3+ effective dynamics can be modeled by a four-level rate equation system, where N4, N3, N2 and N1 correspond to the number of ions excited in transitions 4F5/2, 4F3/2, 4I11/2 and 4I9/2, respectively. Laser action at around 1064 nm occurs provided that N3 > N2 and internal gain compensates passive losses.
(a) Schematic diagram of Nd3+ energy levels under excitation at 808 nm. (b) 2D color-map of the PL intensity (in color) as a function of the wavelength (y-axis) and the pump photon flux (x-axis). (c) Intensity of a lasing resonance (left y-axis scale) and wavelength shift relative to the value of the cold-cavity resonance wavelength (right y-axis scale) as a function of the incident photon flux. Dashed lines mark the values of the incident photon flux at which time-resolved measurements were performed (see Fig. 4).
Figure 2b shows a 2D color-map displaying the measured PL intensity of a microsphere with radius R = 25 μm as a function of the observation wavelength (λc, y-axis scale) and the pump photon flux (Φp, x-axis scale). Multimode lasing is observed at various wavelengths within the Nd3+ emission band at around 1064 nm. A typical spectrum taken at the maximum used photon flux (Φp = 5.5 × 1023 ph/cm2 s) is reported on the right hand side of Fig. 2b. The two most intense lasing peaks have been numbered as 1 and 2, respectively.
In the same figure, a red-shift associated to the TO effect is observed for all lasing modes when Φp is increased. In a first order approximation it is possible to correlate the spectral shift of the lasing mode (Δλ = λs − λini, where λs and λini are the stationary lasing wavelength for a given temperature and the cold-cavity resonance wavelength respectively) with the temperature difference between the volume where the mode is localized and the surrounding environment as:

where a is the TO coefficient, accounting for both physical dilatation and refractive index changes10. Figure 2c shows that, for a microsphere with radius R = 25 μm, while laser emission is inherently nonlinear (superlinear at first and then saturating for high Φp (left y-axis scale)), Δλ follows Φp linearly (right y-axis scale). This indicates that the dominant heating mechanism is partial absorption of the incident pump power radiation ( , where σp, λp and V are the absorption cross section, pump wavelength and sphere volume respectively), which is to some extent released into heat through the non-radiative decay of the excited ions described above. This result allows us to neglect localized heating within the cavity mode and, therefore, to consider spatially homogeneous heating of the whole sphere. The offset of the linear spectral shift curve corresponds to the cold-cavity resonance (λini), which is λini = 1065.0 nm for the measured sphere.
, where σp, λp and V are the absorption cross section, pump wavelength and sphere volume respectively), which is to some extent released into heat through the non-radiative decay of the excited ions described above. This result allows us to neglect localized heating within the cavity mode and, therefore, to consider spatially homogeneous heating of the whole sphere. The offset of the linear spectral shift curve corresponds to the cold-cavity resonance (λini), which is λini = 1065.0 nm for the measured sphere.
The thermal dynamics of the microsphere can be described by the following heat equation:

which reflects the balance between the incoming heat due to partial absorption of the incident pump power radiation minus the heat dissipated to the surrounding. Cp is the heat capacity of the microsphere (Cp = ρVcp, ρ and cp being the mass density and the specific heat of the BTS glass respectively) and can be directly calculated, since both the glass intrinsic properties and the dimensions of the spheres are known. γ is the efficiency at which Pabs is converted into heat and k is the heat transfer rate per unit temperature. In order to extract an analytic solution of the previous equation we assume that the dynamics governing the ion level population has achieved a stationary regime, making the heat absorbed rate time-independent. Under such condition and using Eq. 1, the temporal evolution of Δλ can be written as follows:

The exponential fit of the dynamical Δλ evolution allows extracting the transitory characteristic time  . This scales linearly with R, since Cp and k are proportional to the sphere volume and surface respectively (the heat leaking through the contact point is neglected). Then, the stationary spectral shift is given by:
. This scales linearly with R, since Cp and k are proportional to the sphere volume and surface respectively (the heat leaking through the contact point is neglected). Then, the stationary spectral shift is given by:

The experimental linear evolution of Δλ with Φp reported in Fig. 2c agrees with the theoretical analysis, giving support to the hypothesis of considering k as a temperature-independent parameter. This is confirmed by the large stability of thermal conductivity of air for the particular experimental conditions (50% relative humidity), with a 10% variation over hundred degrees above ambient temperature21.
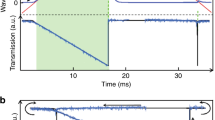
Time-resolved measurements of the laser emission spectral shift were carried out in phase with the modulated pump. Different λc were collected, accordingly to the monochromator filtering. A transitory signal was detected when the lasing resonance aligned with λc on its pathway from λini towards λs as a consequence of the thermal-induced red-shift. The red-shift delay time (Δt) was then extracted taking the chopper as an absolute reference that marks the beginning of the microsphere excitation process. A complete temporal evolution of the lasing wavelength spectral shift was obtained by subsequent recording of Δt for a complete sweep of λc from λini to λs in small steps (0.01 nm). Figure 3 explains the followed methodology by illustrating three different situations:
-
- In panel a) (λc ≈ λini) the time-resolved signal (red solid line at the bottom of the panel) shows a sharp signal overshoot that is detected when the laser pump switches on.
-
- Panel b) (λini < λc < λs) shows an intermediate situation in which an asymmetric overshoot signal is captured. This is ascribed to a decrease of the red-shift rate during the measurement, i.e., the resonance wavelength shifts faster when entering into the detection range than when coming out.
-
- Panel c) (λc ≈ λs) shows that a stationary signal appears and persists for the entire excitation period until the pumping is switched off again. This corresponds to a full thermalization of the microsphere, the stationary lasing wavelength being that measured with CW excitation.
(Top panels in (a–c)) Schematic diagram of the relative position between collection wavelength (red dashed rectangle) and lasing wavelength shift range.
Dotted resonances depict the cold-cavity resonance wavelength and solid resonances the stationary wavelength for a given photon flux. Bottom panels in (a–c) detail the observed line-shape of the time-resolved signal under three different wavelengths of detection: (a) at λc ≈ λini, (b) at λini < λc < λs and (c) at λc ≈ λs. Notice that Δt1 < Δt2 < Δt3.
The 2D color-map plot of Fig. 4a illustrates a particular case obtained by pumping a sphere of R = 25 μm with Φp = 5.5 × 1023 ph/cm2 s. The spectrum covers the full temporal trace of lasing mode 1 and the last part of that of lasing mode 2 (see the corresponding CW spectrum in Fig. 1b). Both curves follow the same exponential law, reaching λs after about 10 ms. From this point on, stable thermal equilibrium is maintained.
(a) Time-resolved 2D color-map of the wavelength red-shift of lasing mode 1 (and part of mode 2) under an incident photon flux of 5.5 × 1023 ph/cm2 s. Colors refer to detected PL intensity, being the legend the same as in Fig. 1b, y-axis scale represents the collection wavelength and the x-axis scale is the excitation time, its origin taken at tini. (b) Temporal behavior of the laser spectral position of mode 1 for low (2.5 × 1023 ph/cm2 s) and high (5.5 × 1023 ph/cm2 s) incident photon fluxes, respectively. (c) Normalized wavelength shift for low and high photon fluxes together with a fit using Eq. 3. (d) Inverted normalized wavelength shift for low and high photon fluxes represented in logarithmic scale.
Figure 4b shows the temporal traces of the spectral position of lasing mode 1 upon low and high Φp (2.5 × 1023 ph/cm2 s and 5.5 × 1023 ph/cm2 s, respectively). As expected, Δλmax scales with Φp, in accordance with Eq. 4 and with the previously reported values in Fig. 2c (marked with dashed lines). When normalizing Δλ to Δλmax for the specific value of Φp, the obtained curves overlap (Fig. 4c). In fact, a characteristic lifetime of τ (R = 25 μm) = 2.4 ms is extracted for both curves, which, according to Eq. 4, allows us to conclude that also Cp can be assumed independent of the temperature of the cavity. Indeed, it has been previously demonstrated that although ΔT can reach a few hundreds of degrees in extreme cases22, Cp in BTS is almost unresponsive to temperature variations23. The pure exponential behavior of the thermal dynamics can be further inspected in Fig. 4d, given that, when represented in log scale, 1 − Δλ/Δλmax shows a linear behavior with negative slope.
Finally, in Fig. 5a we have compared the thermal dynamics of a sphere of R = 25 μm (τ (R = 25 μm) = 2.4 ms, black dots), with that of a smaller radius (R = 20 μm, green dots). As expected, the characteristic lifetime scales with R, the value obtained for the latter case being τ (R = 20 μm) = 1.8 ms. It is worth noting that an equivalent trend was observed in several lasing spheres of similar radii, denoting high consistency and reproducibility.
(a) Normalized experimental traces of the dynamic spectral shift (normalized temperature in the graph) obtained for microspheres of R = 20 μm (black dots) and R = 25 μm (green dots). Solid curves correspond to FEM simulations of the normalized thermal dynamics of the microsphere under different conditions. The red (blue) curve show the case of R = 20 μm (R = 25 μm) surrounded by air and leaning on the substrate. The cyan (orange) curve shows the case of R = 25 μm leaning on the substrate under vacuum (surrounded by moist air with no substrate). (b) Stationary temperature profile along the horizontal (black) and vertical (red) directions. The inset shows a 2D color scaled graph of the local temperature across a vertical plane passing through the sphere center. Both profiles have been normalized to the maximum temperature within the simulation volume, which is found at the north-pole of the microsphere (c) Bottom view of the stationary normalized heat flux across the microsphere surface (R = 25 μm). The contact point is highlighted with a cyan cross.
In order to get more insight on the origin of the observed thermal dynamics we have performed Finite-Element Method (FEM) simulations on a system consisting of a BTS glass microsphere that is heated up by a homogenous source distributed along the sphere volume. The used FEM module solves Fourier’s heat conduction law just by considering conductive heat transfer mechanisms through purely diffusive processes. We have neglected convection on the basis of the small dimensions of the spheres24 and radiation since it only becomes significant with respect to conduction at gas pressures below 10−2 mb17. On the basis of the high relative humidity of the ambient, we have considered a temperature independent air thermal conductivity, as discussed previously. The temperature has been monitored within the sphere with two probes. The first is the whole sphere domain, while the second is a much smaller spherical region (radius = 1 μm). The normalized thermal dynamics extracted from the two probes are equivalent, regardless the position of the small one. We have first solved the problem of a sphere fully surrounded by air (orange solid curve of Fig. 5a). The obtained result is a spatially homogenous output heat flux along the sphere surface, but with a much slower thermal dynamics than that observed experimentally. The second case of study was that of a sphere under vacuum deposited on a substrate such as that of the experiment, which leads to an even slower dynamics (cyan solid curve of Fig. 5a). This is an expected result, as the released heat can only be dissipated through the contact point between the sphere and the substrate. The direct combination of both cases, i.e., microsphere surrounded by air on top of a substrate, successfully reproduces the experimental results for the two microsphere radii under analysis (R1 = 20 μm and R2 = 25 μm). It is worth noting the absence of free parameters in these simulations, the input values being only the geometric dimensions and the intrinsic properties of the materials involved. Figure 5b shows the corresponding stationary ΔT profiles along the horizontal (r, parallel to the substrate surface) and vertical (z, perpendicular to the substrate surface) directions passing through the center of the sphere, i.e. r = 0 and z = 0. The inset shows the bidimensional distribution along a cross section of the whole system geometry. In the horizontal direction (along the r-axis) the temperature profile (black curve of Fig. 5b) is isotropic. Starting from r = 0, a subtle decrease in ΔT is observed when approaching the surface of the sphere, followed by a steep decay for r values beyond the radius of the sphere (r > 25 μm in this case). On the contrary, along the vertical direction, the profile is strongly affected by the substrate, providing a highly asymmetric feature. In the upper semisphere, ΔT is much higher while it gets very close to zero at the contact point with the substrate. This spatial distribution is better understood by analyzing the output heat flux across the microsphere surface (Fig. 5c), which reveals that most of the heat dissipates through its lower part. It is thus possible to conclude that the main heat loss mechanism is thermal conduction towards the substrate through the region surrounding the substrate contact point. In fact, temperature gradients increase towards it, given that the substrate remains very close to ambient temperature. As described above, we monitor lasing modes that come out from one of the lateral edges of a microsphere, i.e., they circulate on planes close to the equator of the microsphere. Thus, given that there is an azimuthal symmetry in the temperature spatial distribution and that the mode is confined in the outer part of the sphere, it is a good approximation to assume that the temperature along the volume mode is spatially homogeneous. The characteristic length scale of the system, which is the distance between the lower part of the sphere surface around the contact point and the substrate (Δz = R(1 − cosθ), where θ is the angle with respect to the z axis pointing downwards), remains below 400 nm in the region dissipating 90% of the heat (being θ < 11°).
In conclusion, we have performed an experimental characterization of the thermal dynamics of Nd-doped BTS laser microspheres deposited on a glass substrate when they are homogeneously heated up by a pump laser. By using a lasing cavity, we overcome the stringent requirements for characterizing passive WGM cavities, i.e., near-field excitation of the optical modes, hence allowing for far-field pumping and detection. Heating characteristic lifetimes of about 2 ms were determined by tracing the dynamic spectral behavior of the lasing modes. Those were dominated by the heat exchange towards the substrate through the medium in the close surrounding of the contact point (moist air in our case).
Provided that the heat transfer occurs on distance scales on the hundreds of nanometers, we believe that this system and technique could become an interesting tool for studying thermal transport dynamics in non-continuum regimes. For the same reason, it would be possible to shine some light in the yet not fully understood enhancement of the radiative heat transfer17 by performing a similar characterization below 10−3 mb, in which it becomes dominant over thermal conduction16.
Methods
For the optical measurements, a continuous wave laser diode at 808 nm is modulated at a frequency of 11 Hz through a mechanical chopper. After spatial filtering by means of a pinhole it is shined into an infrared objective (Mitutoyo 20X, NA = 0.4). The resulting focused beam has a spot with an area of 1.5 × 10−5 cm2, where the power is ensured to be within 90% of the maximum value. A single microsphere can be aligned with the pump beam using a xyz micro-precision stage. The PL is collected by an objective placed in front of the microsphere. A long-pass filter with a cut-off wavelength of 950 nm is used to filter out the laser beam excitation. The output beam is directed towards a second pinhole that removes the scattered signal. The diameter of the microspheres is far greater than the spatial resolution of the collection system (about 5 μm)20, hence the collected PL emission comes out of localized volumes within the microsphere. In the current work we align the collection objective focal plane with the center of the microsphere and collect the signal from a region around one of its lateral edges, where the signal associated to WGMs is well-defined and not masked by the Nd3+ bulk emission20. Moreover, those are the modes experiencing less radiative losses due to the presence of the substrate. Collected light is then focused at the entrance slit of a 750 mm monochromator. For signal detection, a CCD is placed at one of the monochromator output ports and directly connected to a computer. An infrared PMT (H10330-25) is placed at the other output port of the monochromator and used in time-resolved measurements at various wavelengths. In the latter case, the signal is monitored by a digital oscilloscope using the TTL signal of the chopper as a reference. The best attainable temporal resolution is roughly 1 μs and the maximum spectral resolution is 0.01 nm. The dimensions of the microspheres have been quantified using the collection objective and forming the device image in the CCD. Using a structure of known size as calibration, we achieved a spatial resolution of about 1 μm20.
The microspheres were fabricated from BTS glass doped with Nd3+ ions with the composition of 40%BaO–20%TiO2–40%SiO2 and doped with 1.5% Nd2O3 (in the molar ratio). The glass is reduced to dust by means of a mortar and is heated up to its fusion temperature, which is around 900 °C. Most of the splinters melt and, when the temperature decreases, solidify in a spherical shape of several micrometer radii14.
Additional Information
How to cite this article: Ramírez, J. M. et al. Far-field characterization of the thermal dynamics in lasing microspheres. Sci. Rep. 5, 14452; doi: 10.1038/srep14452 (2015).
References
Vollmer, F. & Arnold, S. Whispering-gallery-mode biosensing: label-free detection down to single molecules. Nat. Methods 5, 591 (2008).
Zhang, X. et al. Coupled optofluidic ring laser for ultrahigh-sensitive sensing. Opt. Express 19, 22242–22247 (2011).
He, L., Özdemir, Ş. K. & Yang, L. Whispering gallery microcavity lasers. Laser Photon. Rev. 7, 60–82 (2013).
Yang, J. & Guo, L. J. Optical sensors based on active microcavities. IEEE J. Sel. Top. Quantum Electron. 12, 143–147 (2006).
Vollmer, F. & Yang, L. Review Label-free detection with high-Q microcavities: a review of biosensing mechanisms for integrated devices. Nanophotonics 1, 267–291 (2012).
Murugan, G., Zervas, M., Panitchob, Y. & Wilkinson, J. Integrated Nd-doped borosilicate glass microsphere laser. Opt. Lett. 36, 73–75 (2011).
Martín, L. L. et al. Laser emission in Nd3+ doped barium–titanium–silicate microspheres under continuous and chopped wave pumping in a non-coupled pumping scheme. Laser Phys. 23, 75801 (2013).
Rokhsari, H., Spillane, S. M. & Vahala, K. J. Loss characterization in microcavities using the thermal bistability effect. Appl. Phys. Lett. 85, 3029–31 (2004).
Fomin, A. E., Gorodetsky, M. L., Grudinin, I. S. & Ilchenko, V. S. Nonstationary nonlinear effects in optical microspheres. J. Opt. Soc. Am. B 22, 459–65 (2005).
Carmon, T., Yang, L. & Vahala, K. J. Dynamical thermal behavior and thermal selfstability of microcavities. Opt. Express 12, 4742–50 (2004).
Ganta, D., Dale, E. B. & Rosenberger, A. T. Measuring sub-nm adsorbed water layer thickness and desorption rate using a fused-silica whispering-gallery microresonator. Meas. Sci. Technol. 25, 055206 (2014).
Ganta, D., Dale, E. B., Rezac, J. P. & Rosenberger, A. T. Optical method for measuring thermal accommodation coefficients using a whispering-gallery microresonator. J. Chem. Phys. 135, 084313 (2011).
Rader, D. J., Grasser, T. W., Castaneda, J. N., Trott, W. M. & Torczynski, J. R. Measurements of thermal accommodation coefficients. Sandia National Laboratories Report, SAND2005-6084 (2005).
Elliott, G. R., Hewak, D. W., Murugan, G. S. & Wilkinson, J. S. Chalcogenide glass microspheres; their production, characterization and potential. Opt. Express 15, 17542–17553 (2007).
Otey, C. & Fan, S. Numerically exact calculation of electromagnetic heat transfer between a dielectric sphere and plate. Phys. Rev. B 84, 245431 (2011).
Narayanaswamy, A. & Chen, G. Near-field radiative heat transfer between a sphere and a substrate. Phys. Rev. B 78, 115303 (2008).
Rousseau, E. et al. Radiative heat transfer at the nanoscale. Nature Photon. 3, 514–517 (2009).
Volokitin, A. I. & Persson, B. N. Near-field radiative heat transfer and noncontact friction. Rev. Mod. Phys. 79, 1291 (2007).
Cahill, D. G. et al. Nanoscale thermal transport. II. 2003–2012, Appl. Phys. Rev. 1, 011305 (2014).
Navarro-Urrios, D. et al. Local characterization of rare-earth doped single microspheres by combined microtransmission and microphotoluminescence techniques. J. Opt. Soc. Am. B 29, 3293–3298 (2012).
Tsilingiris, P. T. Thermophysical and transport properties of humid air at temperature range between 0 and 100 C. Energy Conv. Manag. 49, 1098–1110 (2008).
Martin, L. L., Perez-Rodriguez, C., Haro-Gonzalez, P. & Martin, I. R. Whispering gallery modes in a glass microsphere as a function of temperature. Opt. Express 19, 25792–8 (2011).
Shen, C. et al. Investigations on the thermal and piezoelectric properties of fresnoite Ba2TiSi2O8 single crystals. J. Appl. Phys. 116, 044106 (2014).
Mahony, J. J. Heat Transfer at Small Grashof Numbers. Proc. R. Soc. London, Ser. A 238, 412 (1957).
Acknowledgements
This work was supported by the EU through the Advanced Grant SOULMAN (ERC-FP7-321122) and the Spanish Ministry of Economy and Competitiveness through the project LEOMIS (TEC2012-38540-C02-01). JMR acknowledges the financial support of Secretariat for Universities and Research of Generalitat de Catalunya through the program FI-DGR 2013. We acknowledge A. Toncelli for fruitful discussions.
Author information
Authors and Affiliations
Contributions
J.M.R., D.N.-U. and Y.B. performed the experiments and analyzed the data. J.M.R., D.N.-U., N.E.C. and A.P. developed the model and performed the simulations. N.E.C. fabricated the microspheres. D.N.-U., B.G. and A.T. designed the experiment. All authors contributed to the discussion and writing of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ramírez, J., Navarro-Urrios, D., Capuj, N. et al. Far-field characterization of the thermal dynamics in lasing microspheres. Sci Rep 5, 14452 (2015). https://doi.org/10.1038/srep14452
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep14452
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.