Abstract
We present a quantum mechanical memristive Nb/Al/Al2O3/NbxOy/Au device which consists of an ultra-thin memristive layer (NbxOy) sandwiched between an Al2O3 tunnel barrier and a Schottky-like contact. A highly uniform current distribution for the LRS (low resistance state) and HRS (high resistance state) for areas ranging between 70 μm2 and 2300 μm2 were obtained, which indicates a non-filamentary based resistive switching mechanism. In a detailed experimental and theoretical analysis we show evidence that resistive switching originates from oxygen diffusion and modifications of the local electronic interface states within the NbxOy layer, which influences the interface properties of the Au (Schottky) contact and of the Al2O3 tunneling barrier, respectively. The presented device might offer several benefits like an intrinsic current compliance, improved retention and no need for an electric forming procedure, which is especially attractive for possible applications in highly dense random access memories or neuromorphic mixed signal circuits.
Similar content being viewed by others
Introduction
Memristive devices have emerged as promising candidates in the field of non-volatile data storage for future information technology where the device resistance depends on the history of the applied voltage1,2,3,4. Due to their simple two terminal capacitor-like layer sequence (metal-insulator-metal), highly scalable crossbar arrays and multilevel memory structures have been proposed where memristive devices might overcome technical and physical scaling limits of modern semiconductor devices5,6,7. Their binary and analog properties qualify them as promising building blocks for in-situ-computing8. Apart from memory and logic applications, the use of memristive devices as artificial synapses in neuromorphic circuits is intensively discussed, focusing on bio-inspired artificial neuronal networks9,10. In general, today’s research on memristive devices and networks is characterized by numerous elegant system concepts for novel memories, programmable logic units and neuromorphic circuits limited only by a lack of reliable devices and a thorough understanding of the involved switching mechanisms. Nevertheless, the steady progress in memristive device performance in recent years could close the gap between promising computing concepts and the hardware realizations in the near future.
Although the underlying physical mechanism is often unclear, the majority of memristive devices involve the random creation of one or more conductive filaments, resulting in a poor switching reproducibility and a high device-to-device variability6,11,12,13. Moreover, most memristive devices require an initial and individual electrical forming step, additionally complicating their use in crossbar architectures and complex mixed-signal circuits.
Interface-based devices may overcome these restrictions, because uniform interface effects lead to a homogeneous change in resistance, avoiding the randomness generated by electroforming or filament growth14,15,16,17,18,19,20. Most of the investigated interfacial devices are oxide-metal junctions, where the resistive switching mechanism results from changes at a Schottky-like contact15,21. A less common approach uses junctions consisting of a tunnel barrier and a memristive layer, where the change in resistance results from a varying electron tunneling probability17,18,22,23. To explain the not completely understood resistance change in interface-based devices, two rather different models are usually considered: The first model is related to the concept of charge injection, where traps within the memristive layer or at the metal interface are charged and discharged, resulting in a high- and low-resistances state, respectively14,24,25,26,27,28. In the second model, the applied electric field is sufficient to move ions within the memristive layer, leading to a change in interfacial properties and consequently changing the overall device resistance. Besides interface effects, contributions from the memristive layer itself (e.g. local chemical bounds, oxide phases, doping, local heating effects and so on) may affect or oppose the resistive switching, making a thorough analysis of the underlying mechanism more complicated. Therefore, scaling down the thickness of the memristive layer to the length scale of a single electron wave may provide an opportunity to avoid the stated contributions of the memristive layer, while the use of a second barrier might restrict switching effects to interfacial contributions and to derive a physical model of the resistance switching mechanisms.
Here, a double barrier device with an ultra-thin memristive layer sandwiched between a tunnel barrier and a Schottky-like contact is presented. The layer sequence of the device is Al/Al2O3/NbxOy/Au, with a thickness of 1.3 nm for the Al2O3 tunnel barrier and 2.5 nm for the NbxOy layer. In order to get a deeper understanding of the particular interfacial contributions to the observed switching characteristics, single barrier devices were fabricated, i.e. an Al/Al2O3/NbxOy/Nb tunnel junction excluding the Schottky contact and an Nb/NbxOy/Au Schottky contact without the tunneling barrier. Based on the experimental results an equivalent circuit model was developed, which shows evidence that the NbxOy layer may act as an ionic/electronic (mixed) conductor, where the switching mechanism is related to mobile ions within the NbxOy. This might offer several benefits. For example, the properties of the Al2O3 tunnel barrier could define the lower resistance boundary (i.e. the LRS) of the junction. In particular, amorphous Al2O3 is known to be a “good” tunnel barrier (i.e., elastic electron tunnelling dominates the transport) where the barrier thickness can be effectively controlled during growth29. The tunnel barrier thickness acts as a current limiter and represents an essential design parameter as will be explained in detail. The tunnel barrier and the gold electrode define chemical barriers for the ionic species, confining them within the NbxOy. A saturation of the ion density (number of ions per area) at either interface will define the LRS and HRS. No current compliance is needed, due to the self-limited ion assembly at either interface. The finite activation energies of the ionic species will lead to a frozen (memory) resistance state in case of zero bias and will therefore improve the data retention compared to a purely electronic switching mechanism, which face a voltage-time dilemma30.
Results
Device structure
Figure 1 shows the cross-section of the double barrier Al/Al2O3/NbxOy/Au memristive device. The thickness of the Al2O3 tunnel barrier is 1.3 nm and that of the NbxOy layer 2.5 nm. In general, two rather different physical mechanisms may describe the memristive characteristics of this double barrier device. In Fig. 1(a), NbxOy acts as a trapping layer for electrons, where localized electronic states within the NbxOy layer are filled or emptied depending on the applied bias voltage polarity. Therefore, the amount of charge within this layer depends on the history of the applied bias voltage, where charged traps and discharged traps will represent the high- and low-resistances state, respectively. The first charge trapping model, originally used to describe resistive switching in metal-insulator-metal (MIM) Al/SiO (20 nm–300 nm)/Au junctions, was developed from Simmons and Verderber31.
Two models to describe the memristive double barrier tunnel junctions.
(a) Simplified cross-sectional view of the memristive tunnel junctions. Here, trap states within the NbxOy are assumed. The filling and emptying of traps by injected electrons varies the amount of charge in the NbxOy layer and therefore the resistance. (b) An alternative model to (a). Under forward bias voltages Vbias oxygen ions (orange circles) can move inside the NbxOy layer, where their diffusion region is confined by the Al2O3 layer and the NbxOy/Au interface. Both, the model in (a) as well as the model in (b) describe the memristive I–V characteristics.
In contrast to the charge injection model of Fig. 1(a), NbxOy acts as an ionic/electronic (mixed) conductor in the model shown in Fig. 1(b). Here, NbxOy represents a solid state electrolyte, while Al2O3 serves as a tunnel barrier. By applying a bias voltage, oxygen ions (within the NbxOy) drift towards the tunnel barrier or Au interface in dependence on their charge and mobility. The redistribution of the ionic species will affect essential interfacial parameters (e. g. density of states, local barrier height, barrier thickness and so on) at the Al2O3/NbxOy and the NbxOy/Au (Schottky) interface simultaneously. By applying an opposite bias, the original ion distribution should be obtained. As a consequence, the electronic transport, i.e. the device resistance, will be altered in accordance to the local ion distribution leading to memristive I–V characteristics. We would like to emphasize that the charge injection and the mobile ion model (Fig. 1(a,b)) will be discussed below with respect to the experimental findings.
Resistive switching behaviour
A representative current-voltage (I–V) characteristic of the double barrier memristive device is depicted in Fig. 2(a). Neither an initial forming procedure nor a current compliance was used. Instead, a linear voltage sweep was applied to the Au electrode, while the current was measured simultaneously. In particular, the voltage was ramped linearly from 0 V to 2.8 V in order to set the device from the high resistance state (HRS) to the low resistance state (LRS), as marked by arrows in Fig. 2(a). To set the device resistance back to the initial HRS the voltage was ramped linearly from 2.8 V to −2 V and afterwards increased to 0 V. As a result, a pinched hysteresis loop of a bipolar memristive device was obtained. The fluctuations for small currents under negative bias indicate the current resolution of our set-up rather than physically relevant mechanisms. The most apparent feature of the memristive hysteresis is the asymmetry between positive and negative bias, which can be attributed to the Schottky-like NbxOy/Au contact. Moreover, an important feature of our double barrier memristive device is the gradual resistance change rather than abrupt resistance jumps. An abrupt jump in the device resistance during voltage sweeps may indicate a filamentary-driven resistance switching effect, while gradual changes may result from homogeneously changed interface properties14,16. This suggestion is supported by the R × A vs. A plot shown in Fig. 2(b). For junctions with areas ranging from 70 μm2 to 2300 μm2, R × A for the high and low resistance states is independent of the device area, which suggests a homogeneous switching mechanism.
Resistive switching characteristics of the memristive double barrier device.
(a) Absolute current density |J| as function of the applied bias voltage. (b) The area-resistance product vs. junction-area curve of the double barrier device measured at 0.5 V indicates a homogeneous area dependent charge transport. The error bars are obtained from 5 cells of each area. Junction areas were confirmed with optical microscopy.
Interface barrier contributions
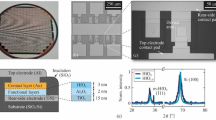
For interface-based memristive behavior, the charge transport through the tunneling barrier has to be dominated by elastic tunneling rather than trap induced tunneling or interfacial trap states within the Al2O3 barrier. This requires a nearly defect free, highly stable and electrically high-quality tunnel barrier. Additionally, it requires that the memristive behavior originates from changes in the NbxOy layer, while the Al2O3 layer is stable under a changed contact resistance at the NbxOy interface. In particular, Al2O3 ranks among the best tunnel barriers for this purpose. In the field of superconductivity, Al2O3 is intensively used as a tunnel barrier in Josephson junctions, where the Nb/Al/Al2O3 technology is the prevailing technology29. Moreover, the sputtered NbxOy has been found to be amorphous by using X-ray diffraction measurements. Therefore, the Al2O3 can be assumed to be of higher quality than the NbxOy.
To get a deeper understanding of the transport mechanism, two additional devices were investigated to separate the particular interfacial contributions. Therefore, Al/Al2O3/NbOx tunnel junctions excluding the Schottky contact, as well as Nb/NbxOy/Au Schottky contacts without the tunnel barrier were prepared, as shown in Fig. 3. Here, Nb is used as the electrode to keep the difference in work function between the electrode and NbxOy layer low. The obtained I–V curves are compared in Fig. 3(a,b). While memristive behavior is clearly visible for the Nb/NbxOy/Au contact, no change in the device resistance behavior was observed for Al/Al2O3/NbxOy tunnel junctions (Fig. 3(a)). This indicates that the NbxOy/Au Schottky-like interface contributes to the resistive switching observed in the double-barrier device. Memristive devices with oxide-metal Schottky contacts have been studied extensively and the origin of the resistive switching is supposed to be the modulation of the Schottky barrier height15. Nonetheless, the aforementioned observations indicate that the two interfaces Al2O3/NbxOy and NbxOy/Au cannot be treated as separate entities and involve a very strong mutual interdependence. However, the following analysis considers the influence of both interfaces individually, while taking into account that both mechanisms should be treated simultaneously.
In order to study the influence of the Schottky interface, the thermionic emission theory was employed to get information from I–V data (cf. Fig. 4(b)). In this theory, a Schottky contact is described by a set of analytical expressions, where the Schottky diode current for forward bias voltages is defined as32,33
Schematic of the electronic band structure variations.
(a) I–V characteristics of the LRS and HRS branch of the double barrier device in the reverse voltage regime of the Schottky contact (device area is normalized to 1 μm2). Solid lines are data fits according to Equation 1 to extract the Schottky barrier height ϕB. (b) Comparison between the Schottky contact resistance at the LRS and HRS branch and the tunnelling resistance. Inset: Shift of the diode forward current onset. (c) Schematic electronic band diagram of the double barrier structure for the LRS (red line) and HRS (blue line). During the transition from the HRS to LRS, moving oxygen ions cause an decrease of the interfacial potential VI by a down shift of the interfacial band in NbxOy (dashed line). Further, the effective barrier tunnel width deff and the apparent barrier heights ϕAl and ϕAu of ,respectively, the Al electrode and Au contact are decreased.

Where kB and T are the Boltzmann constant and temperature, respectively, while n is the ideality factor which describes the derivation from the ideal current. The reverse current IRis given by

where ϕB is the Schottky barrier height, A the junction area and A* the effective Richardson constant, which is 1.20173 106 Am−2K−2. The reverse current is dominated by the lowering of the Schottky barrier. If, however, the apparent barrier height ϕB at the Schottky interface is reasonably smaller than the conductive band gap of the insulator, the reverse current decreases gradually with the applied negative bias and it follows from Equations 1, 2 that32

Here, αr denotes a device dependent parameter which is used to describe the experimentally observed reverse voltage dependence. By using ϕB and n as fit parameters, Equation 1 is fitted in the low forward bias voltage regime (V < 1 V) to the LRS and HRS branches of the measured I–V curve. The resulting fit curves are shown in Fig. 4(a). The apparent Schottky barrier height decreases from 0.62 eV to 0.54 eV and the ideality factor from 4.1 to 3.5 when the device resistance is decreased. In particular, the decrease of the ideality factor with increasing forward current suggests surface effects at the NbxOy/Au interface, which could be the reason for the observed lowering of the apparent Schottky barrier height20,19 in agreement with recent findings15.
Besides the Schottky interface, contributions arising from the tunnelling barrier have to be taken into account to better understand the charge transport in the device. The internal electrical field distribution is of particular interest, since this determines the effective interfacial potentials within the NbxOy layer. Figure 4(b) compares the contact resistance of the Schottky interface for the HRS (blue line) and LRS (red line) to the tunneling resistance of the Al2O3 layer. For the calculation of the tunnelling resistance, we used the tunneling current formula from Simmons34:

where  ,
,  , K = 6.32 1010 V/s, Φ is the apparent barrier height of the tunnelling oxide (Φ = (ϕAl + ϕNbO)/2 = 3.1 eV), A the normalized device area (A = 1 μm2) and
, K = 6.32 1010 V/s, Φ is the apparent barrier height of the tunnelling oxide (Φ = (ϕAl + ϕNbO)/2 = 3.1 eV), A the normalized device area (A = 1 μm2) and  (m: free electron mass; ћ Planck’s constant divided by 2π). VI is the resulting voltage across the Al2O3 tunnel barrier and dtox is the thickness of the Al2O3 layer (dtox = 1.3 nm). As a result, most of the applied voltage drops across the Schottky barrier for bias voltages below 0.5 V (LRS) and 1.0 V (HRS), while the tunnelling resistance of the Al2O3 layer is getting more important for voltages above 0.5 V (LRS) and 1.0 V (HRS). The inset in Fig. 4(b) shows the state dependent diode forward voltages, VHRS = 0.65 V and VLRS = 0.255 V, at a forward current of 1 nA. Thus, the electron transport at low voltages is limited by the Schottky barrier and at higher voltages by the tunnelling barrier. Figure 4(b) shows a comparison for a constant tunnelling distance. However, due to the small thickness of the Al2O3 and the NbxOy layer, the properties of both interfaces, Al2O3/NbxOy and NbxOy/Au cannot be considered independent. Any change in the electronic distribution within the NbxOy layer will affect both interfaces simultaneously. Thus, the device can be only described by taking the properties of both interfaces into account, since both interfaces are interwoven via the NbxOy layer. Our experimental data indicates a homogeneous area-dependent charge transport mechanism. This might be especially important in the case where mobile oxygen-ions are involved in the resistance switching process, as described in the model in Fig. 1(b). A variation of the oxygen concentration in the NbxOy solid state electrolyte layer affects interfacial properties of both the Al2O3/NbxOy as well as the NbxOy/Au boundary. The macroscopically measured memristive I–V curve of a junction is a result of a delicate superposition of electronic and ionic effects at both interfaces. One obvious possibility is the change of the effective tunnelling thickness in accordance to the oxygen concentration at the Al2O3/NbxOy contact:
(m: free electron mass; ћ Planck’s constant divided by 2π). VI is the resulting voltage across the Al2O3 tunnel barrier and dtox is the thickness of the Al2O3 layer (dtox = 1.3 nm). As a result, most of the applied voltage drops across the Schottky barrier for bias voltages below 0.5 V (LRS) and 1.0 V (HRS), while the tunnelling resistance of the Al2O3 layer is getting more important for voltages above 0.5 V (LRS) and 1.0 V (HRS). The inset in Fig. 4(b) shows the state dependent diode forward voltages, VHRS = 0.65 V and VLRS = 0.255 V, at a forward current of 1 nA. Thus, the electron transport at low voltages is limited by the Schottky barrier and at higher voltages by the tunnelling barrier. Figure 4(b) shows a comparison for a constant tunnelling distance. However, due to the small thickness of the Al2O3 and the NbxOy layer, the properties of both interfaces, Al2O3/NbxOy and NbxOy/Au cannot be considered independent. Any change in the electronic distribution within the NbxOy layer will affect both interfaces simultaneously. Thus, the device can be only described by taking the properties of both interfaces into account, since both interfaces are interwoven via the NbxOy layer. Our experimental data indicates a homogeneous area-dependent charge transport mechanism. This might be especially important in the case where mobile oxygen-ions are involved in the resistance switching process, as described in the model in Fig. 1(b). A variation of the oxygen concentration in the NbxOy solid state electrolyte layer affects interfacial properties of both the Al2O3/NbxOy as well as the NbxOy/Au boundary. The macroscopically measured memristive I–V curve of a junction is a result of a delicate superposition of electronic and ionic effects at both interfaces. One obvious possibility is the change of the effective tunnelling thickness in accordance to the oxygen concentration at the Al2O3/NbxOy contact:

Here, δ denotes the maximum variation of the effective distance and x(t) is the state variable of the memristive process, which ranges between 0 and 1. Figure 4(c) shows a schematic electronic band diagram for the double barrier device, which assumes an effective tunneling distance and a varying Schottky barrier height. In particular, the HRS (blue line) and LRS (red line) band profiles are shown, which differ due to the changed contact resistance at the NbxOy/Au interface. This leads to a variation of the band structure, which itself influences the tunnelling process.
Device model
Although the fabricated devices and electrical characterizations fit the scenario described above, the experimental results can be explained by both models, i.e. charging and discharging of interfacial trap states and mobile oxygen ions. Moreover, by considering the local electric field and possible distribution of ions with respect to the electron tunneling transport, the electrical properties of the device and their interdependencies are not obvious at all and require a closer look from a theoretical point of view. Therefore, equivalent circuit models for the devices are often developed, which provides a more thorough understanding of the device functionality35,36,37,38,39,40,41.
Figure 5(a) shows the equivalent circuit which was used to model the scenario from Fig. 1(a), where both, mobile oxygen ions and interfacial trap states, are responsible for the observed resistive switching mechanism. The calculated I–V curve shown in Fig. 5(b) contains the main experimental recorded characteristics, such as an asymmetric pinched hysteresis, a high resistance at small voltages and the current saturation at higher voltages. In contrast, Fig. 5(c) shows the simulated I–V curve for a constant effective tunneling distance deff. In agreement with our experimental findings (cf. Fig. 3(b,c)) this decoupling of the particular interfacial interactions reduces the width of the memristive hysteresis, indicating that mobile oxygen-ions are involved in the resistance switching process and that the two interfaces cannot be treat separately.
Device model.
(a) Equivalent circuit model of a double barrier memristive device. The tunnelling current is defined by a current source supplying the current according to Equation 4. The Schottky barrier is taken into account as a diode according to Equation 1. The capacitance of the tunnelling barrier is CT, while CI represents the capacitance of the NbxOy layer. The oxygen-ion migration, which changes the interfacial potential VI, is expressed in the model as a variable resistance RI(x) parallel to the NbxOy layer capacitance CI. The local electrical field strength ES, EI and ET due to the applied voltage are indicated as a red line. (b) Calculated I–V curve for a variable tunneling distance and (c) for a constant tunneling distance.
For the device model, the capacitances of the NbxOy/Au interface CI and the tunnelling barrier CT are modelled in a capacitive divider. The values of CI and CT have been estimated from capacitance measurements. Therefore, devices with an NbxOy layer thickness ranging from 1 nm to 20 nm were fabricated and the total capacitance was measured. By using a linear regression and extrapolating to 0 nm NbxOy, the values CT = 2.07 × 10−14 F/μm2 and CI = 1.74 × 10−14 F/μm2 were found. The electron tunnelling is implemented in the model by a voltage driven current source, which depends on the effective tunnelling distance deff (see Equation 5) and the interfacial potential VI. The potential change of the NbxOy resistance is taken into account by the resistance RI(x), which depends on the memristive state variable x(t). Additionally, the Schottky contact resistance is accounted for by using a Schottky diode DS described by Equations 1, 2, 3. This diode defines the potential VS(ϕB, n), which is a function of the memristive state dependent Schottky barrier height (ϕHRSB = 0.62 eV and ϕLRSB = 0.54 eV) and the ideality factors (nHRS = 4.1 and nLRS = 3.5). At negative bias voltages, the Schottky contact induced potential VS(ϕB, n) is strongly influenced by the reverse current (cf. Equation 3), so that we assume a state variable dependent reset of ϕB according to ϕB = x/xmaxϕLRSB + (1 − x/xmax) ϕHRSB, where xmax is the maximal value of x during the set process and x varied between 0 and 1. For the set process we are using ϕHRSB and ϕLRSB estimated from Fig. 4(a).
The interfacial potential VI is used as the reference potential of the equivalent circuit, so that the total capacitance of the device is Ctot = CT + CI (since they are in parallel according to the reference potential) and VI thus reads

where Vin is the external applied bias voltage. Hence, the specific value of the interfacial potential VI modulates the tunnelling current and is responsible for the electron injection and the local field strength. The profile of the electrical field is sketched in Fig. 5(a) (red curve). Here, ET, EI and ES are, respectively, the local electrical field strengths at the tunnelling barrier, across the NbxOy layer and at the Schottky contact at the Au interface. While ET depends on the effective tunnelling distance according to ET = VI/deff, we assume that the NbxOy layer thickness dNbO defines the region EI = (VI − VS)/dNbO. In addition, EI depends on the Schottky potential VS. For our device model we assume that mobile oxygen ions are involved in the resistance switching mechanisms by calculating the memristive state variable x(t) using the simple one-dimensional voltage driven memristor model of Ref. 4,

where kon = 35 × 102 (As)−1 and koff = 37 × 104 (As)−1 are constants for positive and negative bias voltages, while f(x) is the window function defined in Ref. 42. Therefore, the resistance change within the NbxOy layer can be calculated by  , where RI-HRS = 7 MΩ and RI-LRS = 6 MΩ are the interface resistances for the HRS and LRS, respectively and x changes between 0 and 1.
, where RI-HRS = 7 MΩ and RI-LRS = 6 MΩ are the interface resistances for the HRS and LRS, respectively and x changes between 0 and 1.
Discussion
The most important feature of our device is the double barrier separated by the ultra-thin solid state electrolyte NbxOy, which restricts the resistive switching to interface effects. The use of homogenous, interface effects as the origin of memristive switching avoids the formation of active current paths (conductive filaments) through the device. This avoids the drawbacks of initial electroforming steps and allows the targeted development of memristive devices by a controlled modification of interfacial potentials. Therefore, the interplay between electron tunneling, oxygen ion diffusion inside the NbxOy layer and interfacial state variations at the Schottky contact must be balanced by the local electrical fields.
Figure 6 shows the calculated electric field strengths for positive bias voltages across the tunneling barrier ET, the interfacial layer of the double barrier device EI and the Schottky contact ES. At low bias voltages the electrical field across the interfacial layer (Fig. 6(b)) and the tunneling layer (Fig. 6(c)) is nearly zero, since the current is blocked by the Schottky contact (Fig. 6(a)). In other words, the Schottky diode defines a threshold voltage for our device, which has to be exceeded to change the resistance of the device. This can be seen from the inset of Fig. 6(a), which shows the change of the effective tunneling distance as a function of the applied external voltage. Here, the resulting electrical field across the NbxOy layer is too small to affect either ion diffusion or electron injections in the reverse diode regime. It is worth to mention that the device threshold additionally depends on the particular resistance state of the device, as marked by blue and red dotted lines in Fig. 6(a–c) for the HRS and LRS, respectively. This opens the possibility to adjust the device threshold by the memristive state of the device, which may be of interest in neuromorphic circuits to emulate threshold dependent plasticity processes, or for ultra dense packet crossbar memory arrays to suppress sneak-path leakage currents43.
Local electrical field strengths.
Calculated electrical fields across the Schottky contact ES, the NbyOx layer EI (b) and across the tunnelling barrier ET (b) during a positive voltage sweep. The onset current of the Schottky diode for the LRS and HRS are marked in red and blue, respectively. The black arrows show the direction of the voltage sweep. Inset: Corresponding change in effective tunneling distance.
If the applied bias voltage is increased in the forward regime of the Schottky diode DS, the electric field ET increases exponentially. While ET saturates at higher voltages, EI shows no saturation effects. Moreover, EI exhibits memristive behavior in a way that the field strength with increasing voltage is always smaller than on the way back, while ET decreases and crosses itself at 1.1 V, when the external voltage is ramped back to zero (cf. Fig. 5(c)). Regarding the device model shown in Fig. 5(a), we can explain the observed saturation from the interplay between the effective tunneling distance and the interfacial potential VI. In particular, the increase of the tunneling current stems from the decrease of the tunneling resistance due to the reduced effective tunneling distance (cf. inset Fig. 5(a)). Since the interfacial potential VI is increasing according to Equation 6 with a rising tunnelling current Itun and a decreasing Schottky contact voltage VS, the field strength EI is increasing too, according to EI = (VI − VS)/dNbO. However, since ET is decreasing with an increasing VI, the tunneling interface acts as an intrinsic current compliance. Thus, no external current compliance has to be set, as it is typically the case for filamentary based memristive devices to protect the device from a dielectric breakdown. It is worth to mention that thin insulating layers as tunneling barriers have been used already to incorporate memristive cells into high density cross-type array structures44. Due to their non-linear I–V characteristic, tunneling barriers act as access devices, where an intrinsic current compliance improves the device endurance by suppressing a too high device current during voltage application.
However, by referring to the two initially described microscopic models of trap charging and discharging (Fig. 1(a)) versus mobile ions (or oxygen vacancies, Fig. 1(b)), the inner field strength EI is in the order of 10−1 V/nm and consequently allows filling and emptying of traps as well as the drift of oxygen-ions within the NbxOy layer as realistic scenarios. While the developed equivalent circuit models shows evidence that oxygen-ion diffusion are involved in the switching mechanisms, the impact of interfacial trap states cannot be ruled out. A closer look at the retention characteristic might be helpful to gain further insight. In Fig. 7 the retention characteristic of the memristive double barrier device is compared to the retention characteristic of the single Schottky barrier memristive device presented in Fig. 3(b). For the retention time measurements the devices were first set to their LRS by ramping the bias voltage to 2.9 V and 2.0 V for the memristive double barrier device and memristive Schottky contact, respectively. Afterwards the resistance was recorded by applying voltage pulses of 0.5 V for 2 s every 60 s and measuring the current. The double barrier device shows an increase in resistance in the first 500 s (black data points in Fig. 7), while afterwards the resistance increase is significantly less pronounced and shows an Ron/Roff ratio of more than one order of magnitude after one day. In contrast to the retention characteristic of the double barrier memristive device, the Schottky barrier device exhibited virtually no increase in the device resistance up to 700 s (gray data points in Fig. 7) but increased drastically afterwards. Hence, the introduction of the Al2O3 barrier led to a significantly improved retention characteristic.
Retention characteristics.
Time dependence of the LRS (data points) compared to the HRS (blue dashed line) for the NbxOy/Au Schottky contact of Fig. 2(a) (gray data points) and the double barrier device (black data points). For the readout of the resistance state read pulses of 0.5 V every 60 s were applied. Red lines are data fits used to extrapolate retention times. Inset: retention characteristic for the double barrier device within the first 500s.
These obviously different retention behaviours can be quantitatively determined by fitting the experimental data to a tβ power law (red lines in Fig. 7), a procedure typically used to characterise high k-dielectrics44. While the resistance ratio Ron/Roff of the Schottky barrier device follows a power law of the form t3.56, the double barrier device follows for the first 600 s a t0.65 power law and then changes to t0.18. Although we cannot give a final explanation for the long retention time in case of the double barrier device, possibly both initially referred effects (cf. Fig. 1) are essential to explain the observed retention characteristics. However, from our investigation, the following picture seems to be the most likely: Right after switching the device resistance to the low resistance state, previously emptied traps are filled by electronic charge carriers, leading to an increase in resistance. After approximately 100 s this mechanism fades out and is followed by a second, independent, ionic driven process. During switching, oxygen vacancies are pushed towards the Au interface and lower the contact resistance. The further increase towards the high resistance state can be explained by a partial back-diffusion of oxygen vacancies, leading nevertheless to a considerably longer retention time in comparison to the Schottky barrier device. Nonetheless, further investigations are necessary to clarify the relevance of electronic and ionic effects in ultrathin double barrier devices.
For possible applications of the presented device, we see interesting possibilities in the field of neuromorphic computing9,10, where high resistances are desired in order to reduce the overall power consumption of the whole system. Moreover, the extremely high resistance at low voltages (<1V) make our device in particular interesting for crossbar-architectures, since it requires no selector device43, as already mentioned above. However, we would like to mention that the scalability of the device is restricted by the relative high device resistances, which results from the Au (Schottky) contact. Here, the use of other electrode materials might lead to lower resistances without affecting the presented double barrier device mechanism.
In conclusion, a double barrier memristive device was realized with a highly uniform current distribution for the high and low resistance states, which indicates a non-filamentary based resistive switching mechanism. We have shown evidence that the use of an ultra-thin NbxOy solid state electrolyte layer of 2.5 nm sandwiched between an Au (Schottky) contact and an Al2O3 tunneling barrier restricts the resistive switching mechanism to interfacial effects where both barriers are involved. This may lead to the observed drastically improved retention characteristic compared to the single barrier Schottky contact devices and may be based on confined oxygen ion diffusion within the sandwiched NbxOy layer. An equivalent circuit model of the device was developed, which confirms our experimental findings and shows evidence that mobile oxygen-ions are involved in the resistance switching process. In order to come to a quantitative description of the resistance switching process, further investigation is necessary to study the influence of the second claimed scenario of charged traps within the NbxOy layer. However, we showed that the controlled modification of interfacial potentials allows the development of homogenous resistive switching mechanisms, which is essential for a wider application of memristive devices in future digital and complex analog memory circuits.
Methods
Sample preparation
Memristive tunneling junctions were fabricated on 4-inch Si wafers with 400 nm of SiO2 (thermally oxidized) using a standard optical lithography process. The junctions are arranged in 1 mm × 1 mm cells across the wafer, containing 6 different contact sizes ranging from 70 μm2 to 2300 μm2. The devices were fabricated using the following procedure: First of all, the multilayer (including top- and bottom-electrode) is deposited without breaking the vacuum using DC magnetron sputtering. The Al2O3 tunnel barrier was fabricated by depositing Al which was afterwards partially oxidized in-situ, the NbxOy layer was deposited by reactive sputtering in an O2/Ar-atmosphere. Following the subsequent lift-off, the junction area was defined by etching the top electrode using wet etching (potassium iodide, for Au) and dry etching (reactive ion etching with SF6, for Nb). The etched parts were then covered with thermally evaporated SiO to insulate the bottom electrode from the subsequently deposited Nb-wiring to contact the top electrode.
I–V measurements
All measurements were performed using an Agilent E5260 source measurement unit. Current-voltage measurements (I–V curves) were obtained by sweeping the applied voltage and measuring the device current simultaneously.
Capacitance measurements
In order to determine the layer capacitance for the Al2O3 tunneling barrier and NbxOy solid state electrolyte, capacitance measurements were done using a precision HP4284A LCR meter. The measurements were performed at room temperature using a bias voltage of 0.5 V and a sinusoidal signal of 0.3 V (peak-to-peak) at 50 kHz. To determine the capacities of the Al2O3 and NbxOy-layers, 5 samples with NbxOy thicknesses ranging from 1 to 20 nm were fabricated. For each of these samples, the capacity was measured for all contact areas (70 μm2 to 2300 μm2). From each contact size, about 20 devices were measured. The spread in capacity for each area was typically in the order of few percents (which already includes the device-specific variance). To calculate the total capacitance for each sample, the slope of the C vs. area plot was taken, which always showed perfect area dependence and a negligible linear offset.
Additional Information
How to cite this article: Hansen, M. et al. A double barrier memristive device. Sci. Rep. 5, 13753; doi: 10.1038/srep13753 (2015).
References
Hickmott, T. W. Low‐frequency negative resistance in thin anodic oxide films. J. Appl. Phys. 33, 2669 (1962).
Dearnaley, G., Stoneham, A. M. & Morgan, D. V. Electrical phenomena in amorphous oxide films. Rep. Prog. Phys. 33, 1129 (1970).
Beck, A., Bednorz, J. G., Gerber, J. G., Rossel, C. & Widmer, D. Reproducible switching effect in thin oxide films for memory applications. Appl. Phys. Lett. 77, 139 (2000).
Strukov, D. B., Snider, G. S., Stewart, D. R. & Williams, R. S. The missing memristor found. Nature 453, 80 (2008).
Strukov, D. B. & Kohlstedt, H. Resistive switching phenomena in thin films: materials, devices and applications. MRS Bull. 37, 108 (2012).
Ha, S. D. & Ramanathan, S. Adaptive oxide electronics: a review. J. Appl. Phys. 110, 071101 (2011).
Adamatzky, A. & Chua, L. in Memristor Networks (Eds. Adamatzky, A. & Chua, L. ) (Springer, 2014).
Kavehei, O., Skafidas, E. & Eshraghian, K. Memristive in Situ Computing in Memristor Networks (Eds. Adamatzky, A. & Chua, L. ) 413 (Springer, 2014).
Jeong, D. S., Kim, I., Ziegler, M. & Kohlstedt, H. Towards artificial neurons and synapses: a materials point of view. RSC Adv. 3, 3169–3183 (2013)
Kozma, R., Pino, R. E. & Paziena, G. E. in Advances in Neuromorphic Memristors Science and Applications (Eds. Kozma, R., Pino, R. E. & Paziena, G. E. ) (Springer, 2012).
Szot, K., Speier, W., Bihlmayer, G. & Waser, R. Switching the electrical resistance of individual dislocations in single-crystalline SrTiO3 . Nat. Mater. 5, 312 (2006).
Waser, R., Dittmann, R., Staikov, G. & Szot, K. Redox-Based Resistive Switching Memories—nanoionic mechanisms, prospects and challenges. Adv. Mater. 21, 2632 (2009).
Yang, J. J., Strukov, D. B. & Stewart, D. R. Memristive devices for computing. Nat. Nanotechnol. 8, 13 (2013).
Sawa, A. Resistive switching in transition metal oxides Mater. Today 11, 28 (2008).
Mikheev, E., Hoskins, B. D., Strukov, D. B. & Stemmer, S. Resistive switching and its suppression in Pt/Nb:SrTiO3 junctions. Nat. Commun. 5, 3990 (2014).
Aoki, Y. et al. Bulk mixed ion electron conduction in amorphous gallium oxide causes memristive behaviour. Nat. Commun. 5, 3473 (2014).
Baik, S. J. & Lim, K. S. Bipolar resistance switching driven by tunnel barrier modulation in TiOx/AlOx bilayered structure. Appl. Phys. Lett. 97, 072109 (2010).
Jeong, D. S., Cheng, B. & Kohlstedt, H. Pt/Ti/Al2O3/Al tunnel junctions exhibiting electro forming-free bipolar resistive switching behaviour. Solid-State Electron. 63, 1 (2011).
Hu, J. et al. Impact of fixed charge on metal-insulator-semiconductor barrier height reduction. Appl. Phys. Lett. 99, 252104 (2011).
Park, C., Seo, Y., Jung, J. & Kim, D.-W. Electrode-dependent electrical properties of metal/Nb-doped SrTiO3 junctions. J. Appl. Phys. 103, 054106 (2008).
Baikalov, A. et al. Field-driven hysteretic and reversible resistive switch at the Ag–Pr0.7Ca0.3MnO3 interface. Appl. Phys. Lett. 83, 957 (2003).
Kohlstedt, H., Kuriki, S. & Gundlach, K.-H. Electro forming and telegraph noise in Pb/Bi/InOx/Pb/Bi tunnel junctions. J. Appl. Phys. 73, 2564 (1993).
Meyer, R. et al. Oxide dual-layer memory element for scalable non-volatile cross-point memory technology. NVMTS 9, 1–5 (2008).
Fujii, T. et al. Hysteretic current-voltage characteristics and resistance switching at an epitaxial oxide Schottky junction SrRuO3/SrTi0.99Nb0.01O3. . Appl. Phys. Lett. 86, 012107 (2005).
Hovel, H. J. & Urgell, J. J. Switching and Memory Characteristics of ZnSe—Ge Heterojunctions. J. Appl. Phys. 42, 5076–5083 (1971).
Odagawa, A. et al. Colossal electroresistance of a Pr0.7Ca0.3MnO3 thin film at room temperature. Phys. Rev. B 70, 224403 (2004).
Kim, C. J. & Chen, I.-W. Effect of top electrode on resistance switching of (Pr, Ca)MnO3 thin films. Thin Solid Films 515, 2726–2729 (2006).
Pearson, C. et al. Electronic memory device based on a single-layer fluorene-containing organic thin film. Appl. Phys. Lett. 91, 123506 (2007).
Gurvitch, M., Washington, M. A. & Huggins, H. A. High quality refractory josephson tunnel junctions utilizing thin aluminium layers. Appl. Phys. Lett. 42, 472–474 (1983).
Schroeder, H., Zhirnov, V. V., Cavin, R. K. & Waser, R. Voltage-time dilemma of pure electronic mechanisms in resistive switching memory cells. J. Appl. Phys. 107, 054517 (2010).
Simmons, J. G. & Verderber, R. R. New conduction and reversible memory phenomena in thin insulating films . Proc. R. Soc. Lond. A 301, 1464 (1967).
Sze, S. M. & Ng, K. K. Physics of Semiconductor Devices (Wiley, 2007).
Tung, R. T. The physics and chemistry of the schottky barrier height. Appl. Phys. Rev. 1, 011304 (2014).
Simmons, G., Generalized formula for the electric tunnel effect between similar electrodes separated by a thin insulating film. J. Appl. Phys. 34, 1793 (1963).
Pickett, M. D. et al. Switching dynamics in titanium dioxide memristive devices. J. Appl. Phys. 106, 074508 (2009).
Hur, J. H., Lee, M.-J., Lee, C. B., Kim, Y.-B. & Kim, C.-J. Modeling for bipolar resistive memory switching in transition-metal oxides. Phys. Rev. B 82, 155321 (2010).
Hur, J. H. et al. Modeling for multilevel switching in oxide-based bipolar resistive memory. Nanotechnology 23, 225702 (2012).
Menzel, S., Tappertzhofen, S., Waser, R. & Valov, I. Switching kinetics of electrochemical metallization memory cells. PCCP 15, 6945–6952 (2013).
Blasco, J., Ghenzi, N., Suñé, J., Levy, P. & Miranda, E. Modeling of the hysteretic I–V characteristics of TiO2-based resistive switches using the generalized diode equation. IEEE Electron Device Lett. 35, 390–392 (2014).
Blasco, J., Ghenzi, N., Suñé, J., Levy, P. & Miranda, E. Equivalent circuit modeling of the bistable conduction characteristics in electroformed thin dielectric films. Microelectronics Reliab. 55, 1–14 (2015).
Linn, E., Siemon, A., Waser, R. & Menzel, S. Applicability of well-established memristive models for simulations of resistive switching devices. IEEE Trans. Circuits Syst. I: Reg. Papers 61, 2402–2410 (2014).
Biolek, Z., Biolek, D. & Biolková, V. SPICE model of memristor with nonlinear dopant drift. Radioengineering 18, 210 (2009).
Burr, G. W. et al. Access devices for 3D crosspoint memory J. Vac. Sci. Technol. B 32, 040802 (2014).
Westerlund, S. & Ekstam, L. Capacitor theory. IEEE Trans. Dielectr. Electr. Insul. 1, 5 (1984).
Acknowledgements
Financial support by the Deutsche Forschungsgemeinschaft through FOR 2093 is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
M.H. prepared the samples, performed the measurements, analysed the experimental results and co-wrote the manuscript. M.Z. and L.K., supported the measurements and data interpretation and developed the simulation model. The simulation results were discussed and interpreted between M.Z., S.D, T.M., M.H. and H.K. H.K. and M.Z. conceived the idea, initiated and supervised the experimental research. R.S. carefully read the manuscript and gave important suggestions to improve the overall quality of the manuscript. M.H., M.Z. and H.K. discussed the experimental results and contributed to the refinement of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Hansen, M., Ziegler, M., Kolberg, L. et al. A double barrier memristive device. Sci Rep 5, 13753 (2015). https://doi.org/10.1038/srep13753
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep13753
This article is cited by
-
Linear and symmetric synaptic weight update characteristics by controlling filament geometry in oxide/suboxide HfOx bilayer memristive device for neuromorphic computing
Scientific Reports (2023)
-
Emerging Memory Technologies for Data Storage and Brain-Inspired Computation: A Global View with Indian Research Insights with a Focus on Resistive Memories
Proceedings of the National Academy of Sciences, India Section A: Physical Sciences (2023)
-
Physics inspired compact modelling of \(\hbox {BiFeO}_3\) based memristors
Scientific Reports (2022)
-
Multilayer redox-based HfOx/Al2O3/TiO2 memristive structures for neuromorphic computing
Scientific Reports (2022)
-
Concept and modelling of memsensors as two terminal devices with enhanced capabilities in neuromorphic engineering
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.