Abstract
Stimulated Raman backscattering in plasma is potentially an efficient method of amplifying laser pulses to reach exawatt powers because plasma is fully broken down and withstands extremely high electric fields. Plasma also has unique nonlinear optical properties that allow simultaneous compression of optical pulses to ultra-short durations. However, current measured efficiencies are limited to several percent. Here we investigate Raman amplification of short duration seed pulses with different chirp rates using a chirped pump pulse in a preformed plasma waveguide. We identify electron trapping and wavebreaking as the main saturation mechanisms, which lead to spectral broadening and gain saturation when the seed reaches several millijoules for durations of 10’s – 100’s fs for 250 ps, 800 nm chirped pump pulses. We show that this prevents access to the nonlinear regime and limits the efficiency and interpret the experimental results using slowly-varying-amplitude, current-averaged particle-in-cell simulations. We also propose methods for achieving higher efficiencies.
Similar content being viewed by others
Introduction
High power, short pulse laser systems have become valuable tools with significant scientific and societal value1. Considerable international effort is being focused on developing the next generation of ultra-high power systems capable of realizing exawatt powers2. These systems are based on chirped pulse amplification (CPA)3 and utilise solid state media, but the next step is very challenging because the low damage threshold of optical elements results in very large amplifiers and compressors. This constraint has led to the suggestion of stimulated Raman backscattering (SRBS) in plasma4 as an alternative amplification method5 suitable for high field intensities, where energy is directly transferred from a pump beam to a short seed beam. SRBS amplification is achieved through the generation of a plasma density echelon, which acts as a transient grating that scatters the pump pulse into the seed, without requiring a temporally stretched seed pulse or storing the energy of the pump. Resonant excitation of the plasma wave occurs when ω0 = ω1 + ωp and k0 = k1 + kp, where (ω0, k0), (ω1, k1), (ωp, kp) are the respective frequencies and wave-vectors of the pump, seed and plasma waves. SRBS has potential to significantly reduce the size and cost of laser systems, however, its feasibility has not yet been demonstrated and energy transfer efficiencies have been limited to a few percent for seed energies of a few mJ6,7,8,9,10,11,12,13,14, which contrasts with current theoretical predictions5,15,16,17,18. While plasma has no damage threshold, several phenomena can lead to the saturation of the gain. In the fluid regime, where a wave description is sufficient to describe the interaction, electrostatic decay instability and/or modulational instability are important19. In the kinetic regime, where wave-particle interaction becomes important, the dominant saturation mechanisms are detuning due to the Bohm-Gross shift20, wavebreaking and particle trapping21/nonlinear Landau damping, which arise from the plasma finite temperature, as will be discussed in this paper. Control of the plasma kinetic behaviour is crucial for the development of an efficient amplifier and, therefore, an in-depth understanding of these physical processes is required.
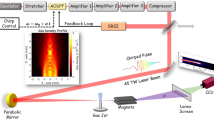
While significant progress has been made in this direction14,22,23,24,25,26,27, here we provide a comprehensive investigation of the saturation processes supported by experimental and numerical results in long, homogeneous plasma channel. Raman amplification is experimentally studied in a hydrogen-filled capillary discharge waveguide28 using a long duration, frequency chirped pump, which leads to a spatio-temporal distribution of the gain that enables amplification of the whole seed spectrum13,29. In addition, the chirped pump helps reduce spontaneous Raman scattering16,30 and is useful for counteracting the time dependent increase in the plasma frequency due to heating31. The experiments have been carried out using the TOPS Ti:sapphire laser system32; details of the experimental setup can be found in the Supplementary Information section. The pump is a ~250 ps duration chirped pulse, with a central wavelength of 800 nm and an energy of 1 J. The seed pulse has a minimum duration of 70 fs, an energy of up to ~2 mJ and a central wavelength of 817 nm, apart from one set of data obtained at low pump power in Fig. 1 where the central wavelength is 836 nm (see Methods and Supplementary Information). The two beams are focused to a waist of ~60 μm onto opposite sides of a 4 cm long, 300 μm diameter plasma-filled hydrogen discharge capillary waveguide. This enables interaction over the full duration of the pump in uniform plasma densities of 1–2 × 1018 cm−3. After interaction, the seed pulse properties are measured using three diagnostic systems: i) an imaging system consisting of a 4× microscope objective and a 12 bit CCD camera (Point Grey, Flea2), which is used to measure the relative energy gain, ii) a spectrometer (OceanOptics, USB4000) connected to an optical fiber to observe spectral changes and iii) a frequency resolved optical gating (FROG) based diagnostic system, which monitors phase and temporal profile modifications. Consistent series of measurements have been taken for various seed and pump energies, seed durations and chirps. The main results from three typical runs are summarized in Fig. 1, where seed energies range from 0.4 mJ to 2 mJ, seed durations from 75 fs (fully compressed) to 330 fs (positive chirp) and pump energies from 100 mJ to 880 mJ. Figure 1a presents the measured amplification factor, together with the theoretically expected amplification factor for both cold and warm (30 eV) plasma, as function of pump power. The theoretical values are calculated making two observations: i) for a chirped pump, the amplification factor of the seed amplitude in the linear regime is given by G = exp(πγ2/2α)13,29 with the resonant energy transfer rate (growth rate in the small signal regime)4
Main experimental results.
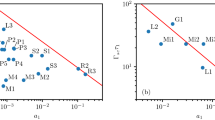
Initial seed properties: (◀) 200 fs, 400 μJ, (■) 75 fs, 1 mJ, ( ) 110 fs, 2 mJ, (
) 110 fs, 2 mJ, ( ) 140 fs, 2 mJ, (▲) 160 fs, 560 μJ, (
) 140 fs, 2 mJ, (▲) 160 fs, 560 μJ, ( ) 275 fs, 560 μJ, (
) 275 fs, 560 μJ, ( ) 330 fs, 560 μJ. Circles represent simulation outputs for direct comparison with experiment: (
) 330 fs, 560 μJ. Circles represent simulation outputs for direct comparison with experiment: ( ) 275 fs, a1 = 2.86 × 10−3, (
) 275 fs, a1 = 2.86 × 10−3, ( ) 275 fs, a1 = 5.72 × 10−3. (a) Measured amplification factor as function of pump power. The 2 theoretical lines are derived from Eq. (1). (b) Seed spectral bandwidth change as function of
) 275 fs, a1 = 5.72 × 10−3. (a) Measured amplification factor as function of pump power. The 2 theoretical lines are derived from Eq. (1). (b) Seed spectral bandwidth change as function of  . (c) Seed spectral mean wavelength change as function of
. (c) Seed spectral mean wavelength change as function of  . (d) Seed transverse profile images at the capillary output: (left) without pump, (right) with pump present. (e) Spectra related to images in (d). Dashed (black) line: initial spectrum, solid (red) line: spectrum after amplification. (f) FROG traces showing retrieved temporal profiles and phases. Dashed/solid (blue) line: temporal profile before/after interaction. Dashed/solid (green) line: phases before/after interaction. As shown in this measurement, seed duration is mainly conserved and increase in the spectral bandwidth leads to a larger chirp rate. In (b,c) dashed lines are guides for the eyes.
. (d) Seed transverse profile images at the capillary output: (left) without pump, (right) with pump present. (e) Spectra related to images in (d). Dashed (black) line: initial spectrum, solid (red) line: spectrum after amplification. (f) FROG traces showing retrieved temporal profiles and phases. Dashed/solid (blue) line: temporal profile before/after interaction. Dashed/solid (green) line: phases before/after interaction. As shown in this measurement, seed duration is mainly conserved and increase in the spectral bandwidth leads to a larger chirp rate. In (b,c) dashed lines are guides for the eyes.

which has been extended to finite temperature plasma. a0 is the normalized vector potential of the pump, α is the pump linear frequency chirp rate defined as Δω/τ where Δω is the pump frequency bandwidth and τ its duration, both given as full width half maximum.  is the cold plasma frequency and βth is the electron thermal velocity normalized to c, the speed of light in vacuum; and ii) the pump power is halved to account for the fraction of energy concentrated in the beam waist (determined experimentally). The initial plasma temperature is 3–5 eV33, which is estimated to increase to ~30 eV towards the end of its propagation for our highest pump power, due to inverse bremsstrahlung heating. Apart from the run at low pump powers, resonance is only satisfied at the rear of the pump, where the plasma is warm, which is the main reason for gain reduction, as can be seen from equation (1). For pump powers up to 2.5 GW, the measured amplification factors are in good agreement with the linear Raman theory, for plasma temperature up to 30 eV. For higher powers (data points labeled A and B in Fig. 1a–c), the measured amplification factors, of up to ~7.5 for a 275 fs, 560 μJ seed (see Fig. 1d–f), are lower than expected and thus other saturation mechanisms must be identified.
is the cold plasma frequency and βth is the electron thermal velocity normalized to c, the speed of light in vacuum; and ii) the pump power is halved to account for the fraction of energy concentrated in the beam waist (determined experimentally). The initial plasma temperature is 3–5 eV33, which is estimated to increase to ~30 eV towards the end of its propagation for our highest pump power, due to inverse bremsstrahlung heating. Apart from the run at low pump powers, resonance is only satisfied at the rear of the pump, where the plasma is warm, which is the main reason for gain reduction, as can be seen from equation (1). For pump powers up to 2.5 GW, the measured amplification factors are in good agreement with the linear Raman theory, for plasma temperature up to 30 eV. For higher powers (data points labeled A and B in Fig. 1a–c), the measured amplification factors, of up to ~7.5 for a 275 fs, 560 μJ seed (see Fig. 1d–f), are lower than expected and thus other saturation mechanisms must be identified.
Important information is obtained from studying the seed spectral characteristics after interaction. Figure 1b,c show that the spectral bandwidth and the mean wavelength change as function of  , with a1 the seed normalized vector potential. To evaluate
, with a1 the seed normalized vector potential. To evaluate  the initial peak amplitude of the pump and the maximum peak amplitude of the seed after interaction are used. This is chosen as an indication of the ponderomotive amplitude driving the plasma wave. For low values of
the initial peak amplitude of the pump and the maximum peak amplitude of the seed after interaction are used. This is chosen as an indication of the ponderomotive amplitude driving the plasma wave. For low values of  , the spectral bandwidth of the seed initially reduces by 20%, suggesting spectral gain narrowing. But, as the values of
, the spectral bandwidth of the seed initially reduces by 20%, suggesting spectral gain narrowing. But, as the values of  increases, the seed spectral bandwidth quickly broadens, up to +30%. In addition, the mean wavelength of the seed is pushed towards shorter wavelengths when
increases, the seed spectral bandwidth quickly broadens, up to +30%. In addition, the mean wavelength of the seed is pushed towards shorter wavelengths when  increases. As the plasma wave is driven more strongly, the seed spectra become broader, extending mainly on the high frequency side. This is attributed to particle trapping (or equivalently nonlinear Landau damping) and has been generally observed in several experiments, however such a scaling has never been presented. Particle trapping occurs when kpλD is large34, where λD is the Debye length. Because the wave traps electrons, the wave frequency decreases35. Wave-particle mechanisms are the principal nonlinear processes for driven plasma waves with kpλD > 0.29 (ref. 34). Under our experimental conditions the plasma temperature is 30 eV, at maximum pump power, kpλD ≥ 0.6 indicating operation in the kinetic regime, which is consistent with our experimental findings. Particle trapping is expected to play an important role in the saturation of SRBS. However, proper quantification has previously been difficult because existing models are only valid for kpλD ≤ 0.4 (ref. 36).
increases. As the plasma wave is driven more strongly, the seed spectra become broader, extending mainly on the high frequency side. This is attributed to particle trapping (or equivalently nonlinear Landau damping) and has been generally observed in several experiments, however such a scaling has never been presented. Particle trapping occurs when kpλD is large34, where λD is the Debye length. Because the wave traps electrons, the wave frequency decreases35. Wave-particle mechanisms are the principal nonlinear processes for driven plasma waves with kpλD > 0.29 (ref. 34). Under our experimental conditions the plasma temperature is 30 eV, at maximum pump power, kpλD ≥ 0.6 indicating operation in the kinetic regime, which is consistent with our experimental findings. Particle trapping is expected to play an important role in the saturation of SRBS. However, proper quantification has previously been difficult because existing models are only valid for kpλD ≤ 0.4 (ref. 36).
An important observation from our experimental studies is the indirect effect of the seed chirp on the amplification process. An experimental run has been conducted using different pump energies and different seed durations with positive chirp (PC) and negative chirp (NC), respectively. The energy of the seed is maintained at 750 μJ. Figure 2 illustrates the results obtained for three different pump energies 230, 400 and 940 mJ and five seed durations from 400 fs, with a positive chirp, to 375 fs, with a negative chirp. Apart for the lowest pump energy where the plasma wave is not strongly excited, the use of fully compressed or PC seeds consistently results in a higher amplification factor, usually by a factor ~2. It has been theoretically shown that the sign of the seed chirp can be chosen to take advantage of the group velocity dispersion (GVD)37, but for our experimental parameters GVD is negligible and we attribute the difference in amplification to wavebreaking, which is understood as the maximum (or breaking) plasma wave amplitude for warm plasma. Coffey has shown, using a simplified model, that strong adiabatic heating rapidly limits the electrostatic field amplitude, which decreases as the ratio  increases, where vth is the electron thermal velocity and vϕ the phase velocity of the plasma wave21. The maximum field amplitude, fmax, normalized to the cold limit value, is given by:
increases, where vth is the electron thermal velocity and vϕ the phase velocity of the plasma wave21. The maximum field amplitude, fmax, normalized to the cold limit value, is given by:

Due to the large seed chirp rate, the beat-wave excites a plasma wave with a rapidly varying phase velocity along the seed temporal envelope, with vϕ increasing (decreasing) for negative (positive) chirps respectively. As will be illustrated later, for our parameters, equation (2) shows that the plasma wave is heavily damped at the front of the negatively chirped seed because vϕ is lower than the thermal velocity. The plasma wave amplitude has therefore less time to grow, leading to saturation. In the case of the positively chirped seed, the plasma wave is excited initially from the front of the pulse, which extends the period of growth, even when damping of the plasma wave occurs at later times because of the reduction in vϕ.
Our experimental results indicate that thermal effects play a key role in the SRBS saturation mechanism. Heating not only leads to a reduction in the growth rate but also to particle trapping that enhances saturation through the change in the plasma frequency and limitation of the plasma wave amplitude.
To obtain further insight into the dynamics of the amplification process, SRBS is numerically studied using the 1D slowly-varying-amplitude, current-averaged particle-in-cell code, aPIC38. The pump parameters are as follows: central wavelength 805 nm, bandwidth at FWHM 35 nm, duration 230 ps (flat profile, positive chirp). a0 values of 1.93 × 10−3, 2.73 × 10−3 and 3.86 × 10−3 are used, representing powers of 1, 2 and 4 GW, respectively. The seed spectra are centered at 817 nm and have a 10 nm FWHM bandwidth. The temporal profile is Gaussian with a FWHM of 275 fs and a positive chirp. A a1 of 2.86 × 10−3 (corresponding to ≈0.5 mJ) is used in conjunction with each pump power value and a1 of 5.72 × 10−3.(≈2 mJ) is used only for the highest a0. The plasma density is set to 1 × 1018 cm−3. aPIC is a collisionless code, therefore the time-dependent plasma temperature is evaluated beforehand from the ion-electron collision rate and fresh plasma electrons enter the moving window with the corresponding thermal velocity distribution (see Supplementary Information). Because of ωp/ω0 ≪ 1 a dispersionless solver is used38, which has been previously checked to ensure that dispersion has no effect.
The simulation results are summarized in Fig. 1 together with the experimental results. The amplification factors are in good agreement with the theoretical values for warm plasma, except for the simulation with large a1. Spectral bandwidth narrowing followed by broadening as function of  and spectral shifts towards high frequencies are also observed, which are consistent with measurements. Figure 3 illustrates, in detail, the amplification process for positively and negatively chirped seeds with a1 = 2.86 × 10−3 and a pump of highest intensity. Figure 3g,h show the amplification factor and mean wavelength shift as a function of time for PC and NC seeds, respectively. It is clearly observed that i) the amplification factor for the PC seed is three times larger than the amplification factor for the NC seed, confirming our experimental findings, ii) spectral shift towards high frequencies (indicating the onset of particle trapping) occurs when an amplification factor of 3–4 is reached, corresponding to the few mJ seeds for our parameters. To illustrate this, snapshots of the temporal and spectral profiles for PC and NC seeds at t = 0, 105 and 120 ps are shown in Fig. 3a,c and Fig. 3b,d, respectively. The difference in gain is explained by comparing, in Fig. 3e,f, the electron phase-space plots at t = 105 ps extracted at the front, peak and back of the pulse and plotting them together with the corresponding electrostatic field amplitudes. In agreement with our argument using Coffey’s theory, the plasma wave amplitude is larger by more than a factor two for the PC case, when compared with the NC case. To be more quantitative, the calculated plasma wave velocity and maximum amplitude (from equation (2)) are plotting in Fig. 4c,d for positive and negative chirp respectively. A plasma wave with an amplitude of 20% of the cold limit amplitude can be excited from the front of the PC seed, while the plasma wave is suppressed when considering the negative chirp case. Also, particle trapping is clearly locally observed in Fig. 3e,f with the full electron phase space maps presented in Fig. 4a,b. Trapped electron fractions of up to 8% (PC) and 3% (NC) are obtained. Strong trapping is observed at the peak of the seed beam, with the fraction of trapped particles remaining constant at the back of the pulse. The fraction of trapped electrons increases by up to 15% for the run with a1 = 5.72 × 10−3, leading to a large plasma frequency shift that explains the drop in the amplification factor.
and spectral shifts towards high frequencies are also observed, which are consistent with measurements. Figure 3 illustrates, in detail, the amplification process for positively and negatively chirped seeds with a1 = 2.86 × 10−3 and a pump of highest intensity. Figure 3g,h show the amplification factor and mean wavelength shift as a function of time for PC and NC seeds, respectively. It is clearly observed that i) the amplification factor for the PC seed is three times larger than the amplification factor for the NC seed, confirming our experimental findings, ii) spectral shift towards high frequencies (indicating the onset of particle trapping) occurs when an amplification factor of 3–4 is reached, corresponding to the few mJ seeds for our parameters. To illustrate this, snapshots of the temporal and spectral profiles for PC and NC seeds at t = 0, 105 and 120 ps are shown in Fig. 3a,c and Fig. 3b,d, respectively. The difference in gain is explained by comparing, in Fig. 3e,f, the electron phase-space plots at t = 105 ps extracted at the front, peak and back of the pulse and plotting them together with the corresponding electrostatic field amplitudes. In agreement with our argument using Coffey’s theory, the plasma wave amplitude is larger by more than a factor two for the PC case, when compared with the NC case. To be more quantitative, the calculated plasma wave velocity and maximum amplitude (from equation (2)) are plotting in Fig. 4c,d for positive and negative chirp respectively. A plasma wave with an amplitude of 20% of the cold limit amplitude can be excited from the front of the PC seed, while the plasma wave is suppressed when considering the negative chirp case. Also, particle trapping is clearly locally observed in Fig. 3e,f with the full electron phase space maps presented in Fig. 4a,b. Trapped electron fractions of up to 8% (PC) and 3% (NC) are obtained. Strong trapping is observed at the peak of the seed beam, with the fraction of trapped particles remaining constant at the back of the pulse. The fraction of trapped electrons increases by up to 15% for the run with a1 = 5.72 × 10−3, leading to a large plasma frequency shift that explains the drop in the amplification factor.
Numerical results for a positively (a,c,e,g) and negatively (b,d,f,h) chirped seed with a1 = 2.86 × 10−3 counter-propagating with the pump with a0 = 3.86 × 10−3.
The seed is positioned at the front of the 750 µm long moving window and travels to the right in the laboratory frame. (a,b) temporal seed profiles at 0, 105 and 120 ps for PC/NC seed, (c,d) spectral seed intensities at 0, 105 and 120 ps for PC/NC seed, (e,f) electrostatic field amplitude and electron phase space extracted at time t = 105 ps and position 500, 600 and 650 μm for PC/NC seed, (g,h) amplification factor (square) and mean spectral wavelength (circle) as function of interaction time for PC/NC seed.
Electron thermal velocity distribution maps with superimposition of the seed amplitude (solid line) for (a) positive chirp, (b) negative chirp.
The color scale indicates the ratio of electrons at a given position and velocity. Also presented, the calculation of the plasma wave velocity (dashed-dotted line) and maximum amplitude derived from equation (2) (solid line) for (c) positive chirp, (d) negative chirp.
Reaching amplification factors beyond the limit governed by the observed saturation mechanisms requires operation in a regime where thermal effects are either compensated for or can be neglected. In the former case autoresonance occurs when the increase in the plasma density in the direction of propagation of the plasma wave partly (or fully) compensates the nonlinear frequency shift39. For the waves to become phase-locked a spatial parabolic density profile is required, which is experimentally difficult to achieve. However, a promising approach proposed by Malkin and Fisch40, is to amplify as close as possible to wavebreaking in the pump depletion regime and in the hydrodynamic limit. While their 3-wave interaction description includes the relativistic electron nonlinearity for determining the optimum amplification time before energy flow slows down or reverses, it does not take into account thermal effects as described in our paper, nor a pump chirp.
To establish whether growth can be maintained in the kinetic regime, 1D aPIC simulations, which include dispersion, have been performed with parameters obtained from the analytical formulae in ref. 40: a0 = 4.35 × 10−3 (4 × 1013 Wcm−2), pump central wavelength λ0 = 800 nm, pump duration τp = 300 ps, a1 = 0.01, seed central wavelength λ1 = 850 nm, seed duration τs = 50 fs. The plasma density is chosen to be 5 × 1018 cm−3 for an experiment to be feasible using a capillary or gas cell over an extended length. This has the advantage of avoiding Brillouin scattering and laser beam filamentation because the formation time τfil ≈ 60 ns ≫ τp,s. The plasma temperature is set to ~5 eV at the beginning of interaction, increasing to ~85 eV when interaction finishes. From our parameter choice, the best attainable results are: a maximum seed intensity Imax = 9 × 1016 Wcm−2 (fluence ~4.5 kJ cm−2), a minimum seed duration τmin = 50 fs for an optimum interaction time tM = 85 ps. The plasma temperature increase results in a change in plasma frequency of up to 22% at tM, which is sufficient to avoid strong amplification from noise40. Table 1 summarizes the characteristics of the amplified seed obtained from different numerical studies, mainly comparing results between fluid and aPIC simulations, different temperatures and use of a chirped/unchirped pump. Intensities reached in the fluid/unchirped runs at 0, 25 and 50 eV show good agreement with the expected values, seemingly providing a robust amplification scheme because temperature changes do not strongly affect the seed output. In contrast, the seed intensity obtained in the aPIC simulation is half that expected from the 3-wave model. However, extending the interaction duration leads to continuous amplification to an intensity of 2.8 × 1017 Wcm−2 and pulse duration of 15 fs at time tF = 147 ps. At this intensity, while longitudinal instabilities should be properly accounted for, transverse instabilities, that cannot be modeled here, would need to be considered. However, this still demonstrates that high energy transfer efficiencies should be possible. The use of a chirped pump is useful for avoiding Raman backward and forward amplification from noise and, as previously mentioned, to keep the three waves resonant by compensating for changes in the plasma frequency due to heating. Numerical studies with a positive pump chirp with Δω/ω of 1% and 3.8% (the value for our current experimental pump beam) have been performed. While for the former the gain is not drastically reduced in the aPIC simulation, for the latter, the gain reduction is appreciable (also when considering the fluid simulation). Figure 5 shows the seed at times tM and tF for each aPIC simulation and at time tM for the fluid simulation with a monochromatic pump. Inset of Fig. 5 illustrates that the seed depletes the monochromatic pump at t = 136 ps.
aPIC seed snapshots at t = tM (dashed line) and t = tF (solid line) for different pump bandwidths:
(green) 3.8%, (red) 1%, (blue) quasi-monochromatic. The (gray) dashed-dot line represents the seed snapshot at t = tM from the fluid simulation for a monochromatic pump. (inset) seed and pump snapshots at t = 136 ps, showing pump depletion.
In conclusion, we have experimentally studied SRBS saturation mechanisms in the kinetic regime and compared our results with 1D simulations. We find that the pump chirp and finite plasma temperature significantly reduce the amplification factor. Moreover, the electron thermal distribution not only affects the growth rate γ, but also leads to particle trapping, which further reduces the growth through saturation of the plasma wave amplitude and to a nonlinear frequency shift, which increases as  increases. To reduce this deleterious effect, it is necessary to choose vϕ ≫ vth, which requires high densities, which are susceptible to filamentation. To numerically find a promising amplification regime we have followed Malkin and Fisch40 and have selected a plasma density of 5 × 1018 cm−3, which can be relatively easily obtained in capillaries or gas cells to produce a long interaction region. In 1D, this scheme seems to be robust to heating, kinetic effects and small pump chirp. Seed intensities of ~3 × 1017 Wcm−2 and pulse compression could be achievable for very moderate pump intensities.
increases. To reduce this deleterious effect, it is necessary to choose vϕ ≫ vth, which requires high densities, which are susceptible to filamentation. To numerically find a promising amplification regime we have followed Malkin and Fisch40 and have selected a plasma density of 5 × 1018 cm−3, which can be relatively easily obtained in capillaries or gas cells to produce a long interaction region. In 1D, this scheme seems to be robust to heating, kinetic effects and small pump chirp. Seed intensities of ~3 × 1017 Wcm−2 and pulse compression could be achievable for very moderate pump intensities.
Methods
Experimental setup
The general schematic of the experimental set-up is presented in Supplementary Figure 1. The seed and pump originate from the same laser beam, therefore care must be taken to prevent transmission of the beams back into the laser chain. The initial beam polarization is horizontal and polarisers and quarter wave plates are used in each beam line to first change the polarization to circular in the region of interaction and, then, to vertical to reflect the beams out of the initial path after interaction, acting as a discriminator. Single-stack dielectric coated mirrors are used to minimize polarization changes after reflection.
Gas-filled capillary discharge waveguide
The plasma channel waveguide is formed by ionizing H2 with a high voltage discharge formed by applying a potential difference of 15 kV across a pre-filled alumina capillary41. Thermal conduction results in an inhomogeneous temperature distribution. The plasma cools against the capillary wall to form a parabolic radial density distribution, with n(r) = n0 + Δn(r/rm)2. n0 is the on-axis density, Δn the density increase at the capillary wall and rm is the capillary radius. The laser beam couples to the fundamental mode of the waveguide provided the beam waist (radius at 1/e2 in intensity)  , where re is the electron radius. An approximate value is given by
, where re is the electron radius. An approximate value is given by  , where namb is the ambient or unperturbed electron density. For a density of 1 × 1018 cm−3, wM ≈ 57 μm. The capillary and electrodes are embedded in a perspex housing mounting on a 5-axis stage (linear XYZ stage for translation motion and a gimbal mount for rotation).
, where namb is the ambient or unperturbed electron density. For a density of 1 × 1018 cm−3, wM ≈ 57 μm. The capillary and electrodes are embedded in a perspex housing mounting on a 5-axis stage (linear XYZ stage for translation motion and a gimbal mount for rotation).
White light generation
White light generation in a noble gas is used to either entirely shift the laser spectrum to lower frequencies or to broaden it before filtering out the higher frequencies. White light generation is due to filamentation in a gas. Argon is chosen as a good compromise between the requirement of a high ionization threshold and a large nonlinear refractive index. Supplementary Figure 2 presents the detailed experimental arrangement while supplementary Figure 3 gives an example of the optical characteristics of the seed. The main challenge in using a white light generator is reproducibility, which is also the reason for only using the compressor as a cut-off filter for most experiments.
FROG technique
The amplitude and phase of probe pulses with and without amplification are measured using the second-harmonic generation frequency-resolved optical gating (SHG-FROG) technique42. The pulse to be characterised is mixed with a delayed replica in a nonlinear crystal. The up-converted signal is conveyed to an imaging spectrometer (Oriel MS127i) connected to a 8 bit CCD camera, which records the 2D spectrogram of the signal intensity versus wavelength and time delay. The amplitude and phase of the electric field is retrieved using commercial software from Swamp Optics43. Inversion of a SHG trace is ambiguous in the direction of time and therefore the sign of the chirp cannot be determined. Therefore, an additional measurement is performed with the input beam passing through a glass window, to add positive dispersion, which changes the pulse duration. Thus, positively chirped pulses are stretched and negatively chirped pulses are compressed.
Analysis of experimental results
For each measurement, ten data acquisitions are recorded with and without the pump. Because of fluctuations in measurements mainly due to laser pointing and capillary discharge jitter, for each data set, only the analysis of the single best acquisition for the amplified seed is kept. Extracted beam characteristics are compared with the averaged characteristics of the 3 best guided shots without pump. Standard deviation of the spectrum is used as a measure of the spectral bandwidth and the central wavelength is obtained through the weighted arithmetic mean.
Simulations
aPIC is a 1-dimensional, averaged particle-in-cell (PIC) code developed for the simulation of Raman amplification in plasma38. It employs envelope equations for the two laser pulses and a particle description for the plasma, where motion on fast time scales is eliminated. The simulation time step does not resolve the laser period and, as a result, simulations are faster than a full PIC code by a factor of ω/ωp, where ω is the laser frequency. A moving window, which defines the simulation domain, is implemented to improve computational efficiency. Modifications have been made to the original code, which include implementation of chirped laser pulses, single-pulse ponderomotive contributions (which drive Raman forward scattering and wakefield generation), a dispersive model for the laser solver and a time-dependent temperature function.
The aPIC numerical model is polarization independent, therefore, input values for the normalized vector potentials of the beams are given as root-mean-square (rms) values, such that  , with −e and m the electron charge and mass, Irms the rms value of the beam intensity, ε0 the vacuum permittivity.
, with −e and m the electron charge and mass, Irms the rms value of the beam intensity, ε0 the vacuum permittivity.
Data availability
The data associated with this research is available at doi: 10.15129/a55d0576-fdff-4a0f-b0da-70e025523c7a.
Additional Information
How to cite this article: Yang, X. et al. Chirped pulse Raman amplification in warm plasma: towards controlling saturation. Sci. Rep. 5, 13333; doi: 10.1038/srep13333 (2015).
References
Zetta-Exawatt Science and Technology. Eur. Phys. J. ST. 223, 979–1242 (2014).
WHITEBOOK ELI Extreme Light Infrastructure, Science and Technology with Ultra-Intense Lasers (CNRS, Paris, 2011).
Strickland, D. & Mourou, G. Compression of amplified chirped optical pulses. Opt. comm. 56, 219 (1985).
Kruer, W. The Physics of Laser Plasma Interaction (Addison-Wesley, Reading, MA, 1988).
Malkin, V. M., Shvets, G. & Fisch, N. J. Fast compression of laser beams to highly overcritical powers. Phys. Rev. Lett. 82, 4448 (1999).
Ping, Y., Geltner, I., Fisch, N. J., Shvets, G. & Suckewer, S. Demonstration of ultrashort laser pulse amplification in plasmas by a counterpropagating pumping beam. Phys. Rev. E 62, R4532 (2000).
Ping, Y., Geltner, I., Morozov, A., Fisch, N. J. & Suckewer, S. Raman amplification of ultrashort laser pulses in microcapillary plasmas. Phys. Rev. E 66, 046401 (2002).
Ping, Y., Geltner, I. & Suckewer, S. Raman backscattering and amplification in a gas jet plasma. Phys. Rev. E 67, 016401 (2003).
Ping, Y., Cheng, W., Suckewer, S., Clark, D. S. & Fisch, N. J. Amplification of ultrashort laser pulses by a resonant Raman scheme in a gas-jet plasma. Phys. Rev. Lett. 92, 175007 (2004).
Balakin, A. A. et al. Laser pulse amplification upon Raman backscattering in plasma produced in dielectric capillaries. JETP Lett. 80, 12 (2004).
Cheng, W. et al. Reaching the nonlinear regime of Raman amplification of ultrashort laser pulses. Phys. Rev. Lett. 94, 045003 (2005).
Ren, J., Cheng, W., Li, S. & Suckewer, S. A new method for generating ultraintense and ultrashort laser pulses. Nat. Phys. 3, 732 (2007).
Vieux, G. et al. Chirped pulse Raman amplification in plasma. New J. Phys. 13, 063042 (2011).
Turnbull, D., Li, S., Morozov, A. & Suckewer, S. Possible origins of a time-resolved frequency shift in Raman plasma amplifiers. Phys. Plasmas 19, 073103 (2012).
Shvets, G., Fisch, N. J., Pukhov, A. & Meyer-ter Vehn, J. Superradiant amplification of an ultrashort laser pulse in a plasma by a counterpropagating pump. Phys. Rev. Lett. 81, 4879 (1998).
Malkin, V. M., Shvets, G. & Fisch, N. J. Ultra-powerful compact amplifiers for short laser pulses. Phys. Plasmas 7, 2232 (2000).
Malkin, V. M. & Fisch, N. J. Quasitransient backward Raman amplification of powerful laser pulses in dense plasmas with multicharged ions. Phys. Plasmas 17, 073109 (2010).
Trines, R. M. G. M. et al. Simulations of efficient Raman amplification into the multipetawatt regime. Nat. Phys. 7, 87 (2011).
Robinson, P. A. Nonlinear wave collapse and strong turbulence. Rev. Mod. Phys. 69, 507 (1997).
Bohm, D. & Gross, E. P. Theory of plasma oscillations. a. Origin of medium-like behavior. Phys. Rev. 75, 1851 (1949).
Coffey, T. P. Breaking of large amplitude plasma oscillations. Phys. Fluids 14, 1402 (1971).
Ren, J. et al. A compact double-pass Raman backscattering amplifier/compressor. Phys. Plasmas 15, 056702 (2008).
Yampolsky, N. A. et al. Demonstration of detuning and wavebreaking effects on Raman amplification efficiency in plasma. Phys. Plasmas 15, 113104 (2008).
Ersfeld, B., Farmer, J., Raj, G. & Jaroszynski, D. A. The role of absorption in Raman amplification in warm plasma. Phys. Plasmas 17, 083301 (2010).
Farmer, J. P., Ersfeld, B. & Jaroszynski, D. A. Raman amplification in plasma: Wavebreaking and heating effects. Phys. Plasmas 17, 113301 (2010).
Yampolsky, N. A. & Fisch, N. J., Limiting effects on laser compression by resonant backward Raman scattering in modern experiments. Phys. Plasmas 18, 056711 (2011).
Turnbull, D., Li, S., Morozov, A. & Suckewer, S. Simultaneous stimulated Raman, Brillouin and electron-acoustic scattering reveals a potential saturation mechanism in Raman plasma amplifiers. Phys. Plasmas 19, 083109 (2012).
Butler, A., Spence, D. J. & Hooker, S. M. Guiding of high-intensity laser pulses with a hydrogen-filled capillary discharge waveguide. Phys. Rev. Lett. 89, 185003 (2002).
Ersfeld, B. & Jaroszynski, D. A. Superradiant linear Raman amplification in plasma using a chirped pump pulse. Phys. Rev. Lett. 95, 165002 (2005).
Nuter, R. & Tikhonchuk, V. Prepulse suppression and optimization of backward Raman amplification with a chirped pump laser beam. Phys. Rev. E 87, 043109 (2013).
Berger, R. L., Clark, D. S., Solodov, A. A., Valeo, E. J. & Fisch, N. J. Inverse bremsstrahlung stabilization of noise in the generation of ultrashort intense pulses by backward Raman amplification. Phys. Plasmas 11, 1931 (2004).
Jaroszynski, D. A. et al. The Strathclyde Terahertz to Optical Pulse Source (tops). Nucl. Instr. and Meth. in Phy. Res. A 445, 317 (2000).
Abuazoum, S. et al. Linearly tapered discharge capillary waveguides as a medium for a laser plasma wakefield accelerator. Appl. Phys. Lett. 100, 014106 (2012).
Kline, J. L. et al. Different kλD regimes for nonlinear effects on Langmuir waves. Phys. Plasmas 13, 055906 (2006).
Morales, G. J. & O’Neil, T. M. Nonlinear frequency shift of an electron plasma wave. Phys. Rev. Lett. 28, 417 (1972).
Lindberg, R. R., Charman, A. E. & Wurtele, J. S. Reduced kinetic description of weakly-driven plasma waves. Phys. Plasmas 15, 055911 (2008).
Toroker, Z., Malkin, V. M. & Fisch, N. J. Seed laser chirping for enhanced backward Raman amplification in plasmas. Phys. Rev. Lett. 109, 085003 (2012).
Hur, M. S., Penn, G., Wurtele, J. S. & Lindberg, R. Slowly varying envelope kinetic simulations of pulse amplification by Raman backscattering. Phys. Plasmas 11, 5204 (2004).
Chapman, T. et al. Driven spatially autoresonant stimulated Raman scattering in the kinetic regime. Phys. Rev. Lett. 108, 145003 (2012).
Malkin, V. & Fisch, N. Key plasma parameters for resonant backward Raman amplification in plasma. Eur. Phys. J. ST 223, 1157 (2014).
Wiggins, S. M. et al. Note: Femtosecond laser micromachining of straight and linearly tapered capillary discharge waveguides. Rev. Sci. Instrum. 82, 096104 (2011).
DeLong, K. W., Kohler, B., Wilson, K., Fittinghoff, D. N. & Trebino, R. Pulse retrieval in frequency-resolved optical gating based on the method of generalized projections. Opt. Lett. 19, 2152 (1994).
Swamp Optics website www.swampoptics.com. Date of access: 17/05/2015.
Acknowledgements
We acknowledge support of the U.K. EPSRC (grant no. EP/J018171/1), the EC’s LASERLAB-EUROPE (grant no. 284464), EuCARD-2 (grant no. 312453) and the Extreme Light Infrastructure (ELI) European Project.
Author information
Authors and Affiliations
Contributions
The project was initiated by D.A.J. The experiment was conceived by G.V., X.Y. and D.A.J. The experiments and equipment calibration were undertaken by X.Y., G.V., E.B., R.C.I., S.M.W. and G.H.W. Experimental data were processed and analysed by X.Y. and G.V. Theoretical analysis, interpretation and simulations were carried out by B.E., M.S.H., G.V., X.Y., J.P.F., G.R., S.Y. and D.A.J. The manuscript was mainly written by G.V., X.Y., B.E. and D.A.J.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Yang, X., Vieux, G., Brunetti, E. et al. Chirped pulse Raman amplification in warm plasma: towards controlling saturation. Sci Rep 5, 13333 (2015). https://doi.org/10.1038/srep13333
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep13333
This article is cited by
-
The role of transient plasma photonic structures in plasma-based amplifiers
Communications Physics (2023)
-
Review of laser-plasma physics research and applications in Korea
Journal of the Korean Physical Society (2022)
-
New criteria for efficient Raman and Brillouin amplification of laser beams in plasma
Scientific Reports (2020)
-
An ultra-high gain and efficient amplifier based on Raman amplification in plasma
Scientific Reports (2017)
-
Plasma optical modulators for intense lasers
Nature Communications (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.




 ) 400 mJ, (
) 400 mJ, ( ) 944 mJ. The top scale indicates the seed duration for a given chirp rate.
) 944 mJ. The top scale indicates the seed duration for a given chirp rate.

