Abstract
Physical unclonable functions (PUFs) exploit the intrinsic complexity and irreproducibility of physical systems to generate secret information. The advantage is that PUFs have the potential to provide fundamentally higher security than traditional cryptographic methods by preventing the cloning of devices and the extraction of secret keys. Most PUF designs focus on exploiting process variations in Complementary Metal Oxide Semiconductor (CMOS) technology. In recent years, progress in nanoelectronic devices such as memristors has demonstrated the prevalence of process variations in scaling electronics down to the nano region. In this paper, we exploit the extremely large information density available in nanocrossbar architectures and the significant resistance variations of memristors to develop an on-chip memristive device based strong PUF (mrSPUF). Our novel architecture demonstrates desirable characteristics of PUFs, including uniqueness, reliability and large number of challenge-response pairs (CRPs) and desirable characteristics of strong PUFs. More significantly, in contrast to most existing PUFs, our PUF can act as a reconfigurable PUF (rPUF) without additional hardware and is of benefit to applications needing revocation or update of secure key information.
Similar content being viewed by others
Introduction
The earliest known lock, resembling the mechanical locks of this century, is estimated to be 4,000 years old—a large wooden lock and key from the palace of Khorasabad in Niveveh. Modern security systems still keep valuables under lock and key in order to ensure the safety and authenticity of goods, information or identities. Locks now, however, can refer to electronic security systems with keys that are coded in, for example, magnetic strips or silicon chips.
Since the invention of locks and keys—physical, electronic or combined—the essence of keeping a good security system effective is protecting the key. This is one of the reasons we keep the physical key to our offices on a personal key chain, our electronic access cards on lanyards and never reveal our computer passwords. Whilst physical locks can be picked, in the digital and electronic worlds hackers have developed both invasive and non-invasive physical tampering methods, such as micro-probing, laser cutting and power analysis1, in order to extract digitised secret information from the integrated circuits (ICs) imprinted on devices such as credit cards. Even tamper proofing techniques used in smartcards—such as cutting power or tripping tamper-sensitive circuitry that clears out the secret information—to protect secret keys have been shown to be vulnerable to physical attack1. Therefore, the problem is storing digital information in a device in such a way that is resistant to physical attacks.
Recently, the growing new area of PUFs is receiving increased attention because a PUF offers a solution by extracting secret key information from a complex physical system. Therefore, unlike conventional applications, more randomness is a desirable property for building PUFs. They are favourable because they are easy to build but practically impossible to duplicate. This latter strength comes from the use of a micro-structure that is bound to tiny variations in physical properties resulting from numerous random features that occur during manufacturing to generate secret keys. When a PUF is physically stimulated, i.e., challenged, a response is generated by a complex interaction of the challenge with many or all of the random micro-structure features. Therefore, the use of PUFs for security is, extremely appealing, since the simple process of fabrication equips them with a unique and unclonable features for extracting secret keys. Besides cryptographic key generation, PUFs can be used for more complicated cryptographic protocols such as oblivious transfer (OT), bit commitment (BC), key exchange (KE), device authentication and identification2,3,4,5,6,7,46.
Conventional PUFs such as Ring Oscillator PUF (ROPUF)2, Arbiter PUF (APUF)9,10, SRAM (Static Random Access Memory) PUF (SRAM PUF)11,12 exploit uncontrollable process variations in conventional CMOS fabrication technology—a comprehensive overview of PUFs can be found in13,14. Although technological developments in CMOS devices such as the FinFET extend the life of microelectronics, such developments are still expected to confront physical limitations imposed by the continuing trend towards smaller feature sizes. Consequently, CMOS based PUF designs will also face a roadblock in terms of providing secure physical unclonable functions in the future15. Furthermore, contemporary PUF designs also face challenges, such as exhaustive CRP access attacks to PUFs that possess a limited number of CRPs, model building attacks16,47, reliability deterioration due to device aging or extreme environment conditions. Strong PUFs14,16 address the first two issues because they are capable of producing huge number of CRPs and are resistant to model building attacks. Reconfigurable rPUFs17 overcome the last two issues because they endow appealing features such as key renewal and a revocation ability by updating itself as a new PUF instance. Here, for the first time, we exploit the unique properties of nanoelectronics rather than CMOS technology to provide an opportunity for building a PUF design possessing integrated strong PUF and rPUF characteristics in one single PUF architecture. More significantly we are able to achieve reconfigurability that is impossible to reverse.
The nanocrossbar is in principle the simplest functional electrical circuit holding great promise in nanoelectronics due to its attractive, regular structure and simple implementation. The nanocrossbar array (Fig. 1a) consists of parallel horizontal wires on top and perpendicular vertical wires at the bottom. Nanocrossbars are usually combined with a passive two-terminal resistive device such as a memristor (in the literature, the terms memristor and memristive device are used interchangeably)18,19,20 shown in Fig. 1b at the cross-point aimed for data storage, computing and neuromorphic applications. Together with nanocrossbar structures the unique properties of memristors such as non-volatility, switching behaviour and nanoscale dimensions present new opportunities for realizing ultra high density memory arrays21.
Nanocrossbar array and a memristive device.
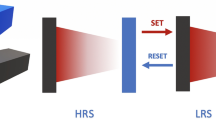
(a) Nanocrossbar array of memristive devices, where each memristive device is located at the crosspoint of a top and a bottom electrode as shown in (b). (c) Illustrates the operation principles of a memristive device. There is a concentration gradient of ions which can be moved back and forth using an applied electric field. The memristive device switches from HRS (High Resistance State) to LRS (Low Resistance State) with a positive potential difference between the bottom electrode and top electrode corresponding to SET switching as one or more conductive filaments grow or form, while it switches from LRS to HRS with a negative potential difference between the bottom electrode and top electrode corresponding to RESET switching as the filaments are disrupted. Once a memristive device has been programmed its memristance does not change even if its power supply is disconnected unless a voltage higher than threshold voltage is applied across the device. Note that this is a very simple illustration of the memristive switching and does not cover all device-physics aspects of the switching. (d) An interconnection model of one memristive device in the array where rw is the segment nanowire resistance and Ri,j is the resistance of the memristive device at the crosspoint of the i-th bottom and j-th top electrode. (e) Reading scheme. When reading a targeted memristive device (selected cell), reading voltage is applied to the selected word line and the current passing through the selected bit line is sensed to determine the state of the memristive device. For other unselected word and bit lines, they can be connected to ground or to a high impedance (floating). During reading it is important to note that there also exists many sneak path currents (purple dashed line) besides the desired read current (green dashed line).
It has been shown that the memristor can be used to store digital states by utilizing its two distinct resistance values Fig. 1c,d namely the ON resistance and OFF resistance, referred to as RON and ROFF. However, memristors have inherent randomness at both the memristor device level—due to the cycle to cycle programming variations of the device—as well as the fabrication process level (such as thickness and cross-sectional area variations)22,23. These resistances are random variables with log-normal distribution values19. In Figs 2 and 3, we illustrate the distribution of these resistances after an initial programming step of randomly selected binary values in a nanocrossbar array. Undesirable resistance variation will deteriorate the ability to distinguish RON and ROFF states during reading the state of a memristor in a nanocrossbar array (Fig. 1e). However, this large resistance variation is very desirable for constructing a PUF architecture. In addition, the large information density in the nanocrossbar enables strong PUF characteristics. Moreover, the unique C2C (Cycle-to-Cycle) programming variation of memristance allows building PUF architectures with reconfigurable characteristics. Furthermore, our mrSPUF in this report realizes a potentially low cost security primitive because the memristor-based nanocrossbar is easy to fabricate and compatible with CMOS fabrication processes. All aforementioned advantages motivate the design of our mrSPUF.
Resistance variation in a nanocrossbar.
Programming variation across a 40 × 40 nanocrossbar. Each crosspoint is a memristor that can be accessed and programmed using a top electrode and a bottom electrode. Memristors are randomly programmed into RON and ROFF state. Experimental data is obtained from19.
Histogram of resistance variation distribution.
Experimental resistance variation distribution extracted from a 40 × 40 nanocrossbar array with 1600 memristors obtained from experimental data in19. Note that data for this graph was extracted by reading each crosspoint resistance (current sensing) in the crossbar, therefore, resistance of an individually isolated device may be higher.
The proposed mrSPUF architecture that combines nanocrossbar and current mirror controlled ring oscillators to realize a strong and reconfigurable PUF is unique and has not been considered in the past to the best of our knowledge. Our architecture allows the extraction of secret information by exploiting the abundant and readily available variations in nanodevices. We summarize our contributions as: i) A novel PUF architecture that exploits the fabrication variations inherent in nano-electronic devices. In particular we exploit the significant variations in the resistance values in a nanocrossbar structure based resistive memory to build mrSPUF; ii) We evaluate mrSPUF and demonstrate its superior performance with respect to fundamental performance metrics: uniformity; diffuseness; uniqueness; and reliability by conducting extensive studies; iii) We demonstrate the capability of the proposed structure in generating a significantly large number of CRPs and, consequentially, we show that mrSPUF is a candidate of strong PUF. vi) We demonstrate that mrSPUF can act as a rPUF relying on C2C programming variations of memristors and, which has never been exploited in memristor based PUFs, to the best of our knowledge. Moreover, the architecture integrates nanocrossbar array with current mirror-controlled ring oscillators is also unique.
Results
mrSPUF Architecture
Our proposed mrSPUF architecture aims to exploit the substantial variations in individual memristors that can be realized in high density with minimal area overhead using a nanocrossbar shown in Fig. 4. To capture variations of memristors and increase the number of CRPs, we employ multiple individual memristors to control the oscillation frequency of a CM-RO that translates analog variations to digital frequency counts (see Fig. 4d). To enable reconfigurability and generate responses to challenges, our mrSPUF architecture also includes key circuits to both program and re-program the nanocrossbar (see programming control circuitry shaded in Fig. 4), apply challenges using the decoder block and the analog MUXs block and extract digital responses using the CM-RO, counter and comparator in Fig. 4.
mrSPUF architecture.
(a) Simplified mrSPUF architecture. All the memristors are in the ON state. The shaded programming control circuit comprises of the row programming control circuitry in (b) and column programming control circuitry in (c) which is employed to program memristors in nanocrossbar array before it acts as a PUF and facilitates reconfigurability of mrSPUF by subsequent reprogramming to refresh CRPs of mrSPUF to transform it into a new PUF instance. In contrast to the programing control circuit, the top decoder block and left analog multiplexers block, CM-ROs and counters enables the stimulation by a challenge and the extraction of a corresponding response. A challenge encoded as a vector of binary values (bits) is used to provide the address bits for both the analog multiplexers block and the decoder block. (d) CM-RO. Each current mirror starves only an inverter in the RO structure, where the bias memristor for each current mirror, Mi, is selected from the nanocrossbar array. Although variation in the oscillation frequency of each RO is slight influenced by the threshold voltage variation in the CMOS transistor composing the starved inverter and current mirror structures, the overall variation in the oscillation frequency is primarily determined by the variations in memresistance of Mi if the supply voltage, VDD, is kept constant.
Although the nanocrossbar offers promising low area overhead circuitry for storing high-density information, the main problem it faces is the presence of sneak path currents19. A memristive device is read from the nanocrossbar by applying a voltage to the selected word line of the nanocrossbar array. This will result in a current that flows through the selected device. The current through the selected bit line is then sensed to read the analog/digital state of the memristor. In a practical implementation of such nanocrossbar architecture, in addition to the current through the targeted memristor, there exists a number of other current paths that are commonly referred to as sneak path currents that result in an inaccurate reading of the targeted memristor device value (see Fig. 1e). This effect is illustrated in Fig. 5. It should be noted that sneak path current in the nanocrossbar array mitigates the effect of process variations (reduces the standard deviation) in individual memristors during readout. A larger standard deviation is desirable for PUF that derives its security by exploiting process variation. To suppress sneak path currents and therefore maintain the readout resistance variations of memristors in crossbar, a number of techniques can be used19. Three of the leading techniques at the centre of attention in today’s industry and academic research community to suppress sneak path currents are: i) an intrinsic current-rectifying behaviour19,24 that is translated into an extremely high current-voltage nonlinearity as shown in Fig. 6; ii) using a highly nonlinear series element with a transistor-like or a diode-like behaviour; and iii) using a complementary resistive switches (CRS) to replace a single memristor in nanocrossbar array25,26. Presently, the first solution appears more promising than the other two approaches due to its ability to maintain competing memory features such as high density and the highly nonlinear self-rectifying effects in these solid-state devices. As for CRS, the read operation is destructive and multilevel capability of memristive devices cannot be used.
The effect of sneak path currents.
The solid lines show resistance distribution of individual isolated memristors in ON and OFF state while the dashed lines show the readout resistance distribution after isolated memristors integrated in the crossbar array. The sneak path current will reduce the mean value of RON slightly and ROFF significantly resulting in narrowed difference between ON and OFF resistance. Besides that, the sneak path current also reduces the standard deviation of resistance distribution in ON and OFF states.
Current-voltage (I-V) characteristic for a memristor.
The curves show the I-V relationship of a memristor with intrinsic diode characteristics. The red dotted line is obtained from experimental data19,44 and the dashed line depicts the simulated results produced by our memristor model written in Verilog-A language and used in simulations in our study. For the SET operation (Fig. 1c) a positive voltage higher than 2 V (positive threshold voltage) is applied. For the RESET operation (Fig. 1c) a negative voltage lower than −3.5 V (negative threshold voltage) is applied.
The mrSPUF operation comprises a Programming Phase and a Response Generation Phase.
Programming phase
The resistance variation is more prevalent in the RON state than in the ROFF state due to the thickness of memristors demonstrated in23. Furthermore, in27 it is demonstrated that resistance is resilient to temperature and telegraph noise in the RON state more than in the ROFF state. For these reasons only the RON state is used to construct the mrSPUF architecture (i.e. we initially program the entire nanocrossbar to store the logic value ‘1’) to reduce susceptibility to both temperature fluctuations and telegraph noise and consequently increase the reliability of the PUF architecture.
The programming control circuitry is shown in Fig. 4b,c. In programming phase, we set P = 1 to disconnect rows and columns from the analog multiplexers block and decoder block. Programming a memristor into the RON is carried out by a SET operation (Fig. 1c) achieved by applying S = VSET, a voltage that is higher than a memristor’s positive threshold voltage (Fig. 6), to the selected row (word line) and applying R = 0 to the selected column (bit line). All other unselected rows and columns are floating to reduce power consumption.
Response generation phase
Once all the memristors in the nanocrossbar array are programmed into ON state, we set P = 0 to connect rows with analog multiplexers block and columns with decoder block. And simultaneously, set rows and columns connected to programming control circuitry to floating (Fig. 4b,c). Then mrsPUF is configured to generate responses to given challenges.
The decoder block selects one column of the nanocrossbar array. The analog multiplexers block selects a set of 2 × i rows acting as bit lines. In our mrSPUF design, ten memristors (2 × i, i = 5) in the same column are selected. Each selected memristor is then used to control the current in a single current mirror and consequently to starve the current in each inverter in the ring oscillator, to achieve a current starved ring oscillator structure (Fig. 4a,d) refereed to current mirror controlled ring oscillator (CM-RO). Therefore, the oscillation frequency of a CM-RO is predominantly a function of current through the memristor that in turn is related to the resistance of the memristor. Consequently, the oscillation frequency of each oscillator is a function of the selected memristors and measured using a counter. Subsequently, a response bit is generated by comparing the outputs from the two counters.
In general mrSPUF has two CM-ROs, each RO has i inverters, 2 × i memristors are randomly selected. So the total CRPs (NTCRP) in this configuration can be estimated as:

where N is the number of columns, M is the number of rows. Therefore, the number of inverters in CM-RO or the nanocrossbar array size or all of the design parameters can be altered according to the desirable number of CRPs.
The average frequency observed by using 5 inverters configured by 5 memristors is in the vicinity of 25 MHz. Therefore, an advantage of using the current starved ring oscillator is that the frequency is sufficiently low that an accurate counter is not required to measure the frequency of CM-RO.
Fundamental PUF characteristics of mrSPUF
We evaluate the fundamental PUF characteristics of mrSPUF using uniformity, diffuseness, uniqueness and reliability metrics. Detailed definitions of these metrics can be found in the Methods section. Generally, A PUF generates multiple bits responses. However, A single mrSPUF only produces a single response bit. To obtain multiple response bits, there are two solutions. First, one can duplicate mrSPUF architecture on the same chip with the same challenge as the input. Second, one can query a single mrSPUF with a set of challenges (multiple challenges) and concatenate the response. Here, we use the later approach for saving chip area.
Uniformity and diffuseness
Uniformity captures the proportion of ‘1’ and ‘0’ in responses of a PUF. Ideally, the proportion is 50% for truly random response. A PUF is expected to output different responses to different challenges and these responses can be treated as IDs of a PUF. Diffuseness is the degree of difference among different responses to different challenges for the same PUF. The expected diffuseness is 50%.
In order to evaluate uniformity and diffuseness we randomly apply 100 different challenge sets to one mrSPUF. Each challenge set has 128 challenges, subsequently, the 128 single response bits are concatenated to form a 128 multiple bits response. Each 128 bits response vector acts as an identifier (ID) of a given mrSPUF instance. The distribution of ‘1’ and ‘0’ among all response vectors is calculated representing uniformity. From Fig. 7a, it can be seen that both the probability of ‘1’ and ‘0’ are nearly 50%, which are 50.76% and 49.24% respectively. We calculate Hamming Distance (HD) between responses of these IDs to determine diffuseness. The diffuseness is 49.96% that is close to the ideal value of 50%, as shown in Fig. 7b.
Uniformity and diffuseness.
(a) Uniformity or randomness of mrSPUF: probability of output logic ‘1’ and ‘0’ are near 50% (50.76% and 49.24% for logic ‘1’ and logic ‘0’ respectively). (b) Hamming distance distribution for evaluating diffuseness: mean of HD is 63.9 bits out of 128 bits (49.96%). Standard deviation is 5.65 bits (3.63%).
Uniqueness
When the same challenge sets are applied to different PUF instances, the output responses are expected to be different. Uniqueness represents the ability to uniquely distinguish a particular PUF instance among a group of instances. Ideally, the HD between the responses to a same challenge from different PUF instances should be 50%.
We use 100 different mrSPUF instances to evaluate uniqueness and the result is shown in Fig. 8. The mean of HD of mrSPUF is 64.1 bits out of the 128 bits response and this value agrees with ideal value of 64 bits.
Reliability
Reliability measures the consistency with which a given PUF reproduces a response to repeated application of a given challenge. Ideally, a PUF reproduces the same responses corresponding to the same challenges for the same PUF. The reliability can also be assessed by Bit Error Rate (BER) measuring the percentage of flipped (error) bits in responses. Reliability and BER are complementary metrics. From a practical implementation point of view there is a need to evaluate reliability under different temperature and supply voltages.
We evaluate the reliability of 20 mrSPUFs. The results obtained are shown in Fig. 9. Response vector of 500 bits generated by using a set of 500 randomly selected challenges is collected by repeatedly testing each mrSPUF instances using four different supply voltages, namely, 0.9 V, 0.95 V, 1.05 V and 1.1 V. Here we use BER. The worst mean BER (Bit Error Rate) is 1.5% under −10% deviation from the nominal value of 1 V, while the circuit core temperature is kept at 27 °C.
The resistance temperature coefficient of a memristive device in ON state is similar to a metallic resistor28,29. So we use temperature coefficients obtained from metallic resistors to conduct reliability evaluation under different core temperature settings. Temperature reliability tests were repeated for four different ambient temperatures (−20 °C, 0 °C, 50 °C, 85 °C) under a constant power supply voltage of 1.0 V. The worst mean BER observed is 4.9% when the temperature is 85 °C.
We also conducted a corner test in four combinations: (0.9 V, −20 °C); (0.95 V, −20 °C); (1.0 V, 27 °C); (1.05 V, 85 °C) and (1.1 V, 85 °C). The worst case occurs when the supply voltage is 0.9 V and temperature was reduced to −20 degree Celsius where the mean BER is 7.5%.
It is impractical to directly use the raw responses of mrSPUF as cryptographic keys. On one hand, output response to a given challenge slightly differ at times applied to the same PUF instance due to temperature and supply voltage fluctuations. However, cryptographic primitive requires that every bit of the key remains unchanged. On the other hand, cryptographic primitive such as RSA requires the key to meet specific mathematical properties unavailable from mrSPUF randomly responses2.
To generate cryptographic keys based on PUF responses that overcomes the aforementioned limitations, two steps should be followed. Firstly, ECC (Error Correction Code) like BCH code can be used to generate syndromes from stable PUF responses to subsequently correct erroneous bits in PUF responses. After correction, the corrected response can be directly used for cryptographic primitives such as AES (Advanced Encryption Standard) requiring no specific properties after simply hashing down to a desired length. Secondly, if specific mathematical properties are needed for cryptographic primitives, the corrected PUF output can be used as a seed to generate required cryptographic keys with the desired mathematical properties.
Strong PUF characteristics of mrSPUF
Before delving into specifics, we first outline the characteristics expected from a strong PUF model14,16:
-
Impossible to build a duplicate or clone of a PUF instance physically,
-
Generate a huge number of CRPs to prevent exhaustive measurement of responses to all possible challenges—full characterization of the PUF—within a limited time period, several days or weeks, demonstrated ideally by exponential CRPs in the number of challenge bits,
-
Resilient to model building attacks when an adversary aims to build a complete model to predict responses to hitherto unseen challenges given a polynomial number of CRPs.
Similar to silicon PUFs the proposed mrSPUF meets the first feature since it exploits significant abundant and uncontrollable process variation in fabrication of nano devices, even manufacturer can not fabricate two identical mrSPUFs. The number of CRPs generated by a given nanocrossbar array size and the number of inverters stages in one CM-RO is calculated using Eq. (1) is described in Fig. 10. For example, using a nanocrossbar array with equal number of rows and columns (N = M = 100) and a 5-stage (i = 5) CM-RO, we can acquire 2.1811 × 1017 CRPs. Assuming a readout speed of 107 bits/s for mrSPUF, it will take over 690 years for an attacker to fully readout all possible CRPs. In reality it will be greatly slower because CM-ROs average frequency is around 25 MHz and therefore it will take longer to accurately measure frequencies even if a high accuracy counter is used. Moreover, the starting period before RO frequency is stable will prolong the time for each measurement. Therefore our mrSPUF meets the second characteristic of strong PUFs. Furthermore, we also investigate model building attacks and demonstrate that mrSPUF is resistant to model building attacks (see section Additional Information). So the mrSPUF is a candidate strong PUF.
Reconfigurability of mrSPUF
The concept of a reconfigurable PUF, first articulated in30, is the idea of imparting on to the same PUF realization the ability to change its behaviour to the same challenge. Instead of exhibiting static challenge-response behaviour, updatability of challenge-response behavior of reconfigurable PUF is desirable for some practical applications including the revocation or update of ‘secrets’ in PUF-based key storage and cryptographic primitives based on PUFs31. Since then a stronger definition of a reconfigurable PUFs has been proposed to ensure that the reconfiguration is difficult to reverse, even by an invasive attack measure32. Therefore the reconfiguration should not depend on a hidden device or parameter that can be influenced by an attacker, for example, part of the challenge or the location of the PUF structure in reconfigurable FPGA logic33.
Ideally, a rPUF is a PUF that can be updated using a methodology to alter the PUF into a new instance such that:
-
The CRPs of rPUF are unpredictable after reconfiguration even if the CRPs of a rPUF before reconfiguration are known.
-
The security properties of the rPUF are preserved after reconfiguration.
-
Reconfiguration is uncontrollable and should not rely on updating a hidden parameter.
In32, authors present two rPUFs concepts. The first is a reconfigurable optical PUF, when this PUF is irradiated with a laser beam beyond normal operating conditions, the structure will change its internal configuration and subsequently refreshed CRPs can be obtained while the security properties are preserved. The second is PCM (Phase Change Memory) based rPUF. The PCM is a resistive device with a lower endurance characteristic because the switching (analog or digital) is a result of small area (≈1 nm) melt-down of device structure and switching between amorphous and crystalline material states. Although the authors in32 did not consider the significant problem of resistance drift in PCMs, the reconfigurability of the PCM-based PUF comes from the ‘long-lived random state that can be reconfigured at will’, precisely what is needed for an rPUF. A reconfigurable optical PUF is not practical for lightweight cryptographic primitives because its implementation especially the measurement part is expensive. In17 the authors further investigate the conceptual PCM-based rPUF32 and show its feasibility. However, the hash function and fuzzy extractor45 are always used since the uniqueness, reliability is unsatisfactory leading to a great overhead.
The internal change in ionic concentration gradient within nonionic memristors during switching (see Fig. 1c) results in different resistance values for RON and ROFF. This variation is referred to as C2C variation. Figure 11 illustrates the C2C variation in resistance values for 5000 reprogramming cycles. It is worth highlighting that components of this source of variation, as oppose to conventional CMOS, is a unique spatiotemporal source of variation. By utilizing this property, we can implement a reconfigurable PUF using mrSPUF because after reprogramming the memristors in the nanocrossbar, their resistances in RON will change randomly and therefore will meet the requirements for a rPUF.
Cycle to Cycle (C2C) variations.
ROFF and RON variation of an individual memristor for 5000 cycles, experimental data is adopted from24.
Reconfigurable phase
Additional circuitry is not needed to enable the mrSPUF acts as an rPUF other than switching the memristor from ON state to OFF by applying R = |VRESET|, a voltage that is higher than absolute value of negative threshold voltage, to the selected column (bit line) and applying S = 0 to the selected row (word line). Then switching it back from OFF to ON state again by applying S = VSET to the selected row and R = 0 to the selected column using the programming control circuitry shown in Fig. 4.
The advantage of using mrSPUF-based rPUF is low-cost overhead requiring no additional circuitry and unlimited configuration space—the number of times that rPUF can be evolved into a new PUF instance—as opposed to other rPUFs. More significantly, the reconfiguration is nearly impossible to reverse!
Discussion
In contrast to ROPUF that uses an array of ROs, the proposed mrSPUF efficiently uses two i-stage CM-ROs which are re-configured using the nanocrossbar and consequently leads to a significant area reduction and ease of reading as the output frequency is substantially reduced to facilitate accurate counting. Also unlike the memristor-based PUF in34 where the goal is to sense the value of the resistance to determine the binary value (in RON or ROFF state) of a target memristor in nanocrossbar array, we translate analog memristance value (here only RON state is used) into a frequency through CM-RO. The advantages of this implementation include: i) Use of significantly smaller number of ROs and only i inverter stages (in the demonstrated case, i = 5) to build each RO. ii) Generate a significantly improved number of CRPs. iii) Mitigate some of the undesirable variations in responses caused by power supply and temperature fluctuations as we employ a differential structure to generate a response bit. vi) Unlike the proposed structure in34 we do not need complex circuitry to readout a memory cell and we do not directly expose full physical information—binary value in memory—at each junction of a nanocrossbar array.
Besides our proposed memristor based PUF, there are some initial works addressed the feasibility of building up a memristor based PUF34,35,36,37. Both of these two studies34,35 employ a time and voltage constrained write mechanism (weak-write) to force each memristor to an undefined logic region (neither logic ‘1’ or ‘0’). Subsequently, these memristors attain an unpredictable logic state due to process variations that influence memristance. Similar to SRAM PUF, a memristor PUF34,35 is only capable of producing a limited number of CRPs. More significantly, the memristor based PUFs in34,35 require a calibration procedure to determine the weak-write parameters (time and voltage) to force a memristor into undefined logic region before it can be used. The proposed PUFs exploit static randomness from process variations. However, it should be noted that the memristor has large C2C variations, which means reprogramming it using the same pulse period or voltage amplitude will cause unstable responses (dynamic randomness) for the same challenge with respect to the same PUF for the aforementioned memristor based PUFs. This C2C variations is not taken into account in the aforementioned memristor based PUF designs.
In38 the authors leveraged sneak path currents inherent in memristor-based nanocrossbars and bidirectional features to build up a nano PPUF (Public Physical Unclonable Function). Unlike PUFs, the security of the nano PPUF no longer relies on the secrecy of its physical parameters that define its uncontrollable variations and the model of a PPUF that exactly matches the PPUF hardware behaviour is publicly known to every one. The security of a PPUF is based on the time difference (several orders of magnitude) between fast execution time on PPUF hardware to acquire correct response and the much longer time required to compute the response correctly using the PPUF model. In fact, PUFs and PPUFs are hardware primitives with different requirements for authentication and other security services. Since nano PPUF always need accurate measurements of its physical model parameters to create the model of nano PPUF that is inconvenient and expensive. Although PPUFs provide an alternatives securely storing challenge response pairs, the high reliability requirement of PPUF designs still need to be addressed. We refer readers to39 for a more comprehensive overview.
Here we compare mrSPUF with other memristor based PUFs. However, comparison with the nano PPUF is not conducted because the nano PPUF has different application protocols and the most difference is that building a model of nano PPUF requires a very high accuracy measurement in provisioning phase.
In Table 1, whether nanocrossbar is used or not determines the circuit’s density. Since all the PUF performance data in Table 1 are from simulation, so the uniqueness and uniformity are all close to ideal value of 50%. We do not compare reliability and diffuseness performance because there is no such information in other PUFs listed in the table. M and N mean number of rows and columns in nanocrossbar array respectively for the proposed mrSPUF and the PUF structure in34. In this PUF structure35, M means the number of memristors used since there is no nanocrossbar used. In general, the number of CRPs is equal to the number of memristors in these two PUF designs34,35. It can be seen our proposed mrSPUF can significantly expand the number of CRPs. Proposed memristor based mrSPUF distinguish from other memristor based PUFs in terms of reconfigurability and has the qualities of strong PUF. We propose the concept of exploiting the inherent C2C variations of memristor to build rPUF for the first time.
Methods
Simulation set-up
We conduct extensive simulations based on experimental data to evaluate our proposed PUF architecture. The simulation study was carried out at the device level using Cadence tools. In these simulations the mrSPUF was built using a 40 × 40 nanocrossbar array with rw = 1.25 Ω segment resistance for nano-wires and two 5-stage ROs as shown in Fig. 4. Each nano device is a memristor that is programmed to RON where the value of RON is randomly selected from a log-normal distribution, shown in Fig. 3 via Monte Carlo command in Cadence. It should be noted here that the log-normal distribution values are from extracted fabricated experimental data in19. Readout is achieved using a 1 V supply voltage to ensure the device memristance does not alter with respect to time as a result of the operation is below memristor’s threshold voltage. In these simulations, we use a standard CMOS 90 nm technology with a 1.0 V supply voltage. The memristor model is adapted from40,41 written by Verilog-A language. The simulated results of memristor model with a large rectification ratio for minimizing sneak path currents shown in Fig. 6 agrees well with the experimental results.
Fundamental PUF performance metrics
To assess the fundamental PUF performance of mrSPUF, metrics consist of uniformity, diffuseness, uniqueness and reliability are evaluated. More detailed definitions of these metrics can be found in42,43.
∂ Uniformity. Uniformity is an indicator of the balance of ‘0’ and ‘1’ in the response vector. An ideal PUF should show that a ‘0’ or ‘1’ response is equiprobable. The uniformity is defined as:

Where ri,j is the j-th binary bit of an n bit response from a response vector i.
∂ Diffuseness. Diffuseness measures the difference between response vectors for different challenges applied to the same PUF. Diffuseness is measured by calculating the mean of HD for all the possible response vectors generated by the PUF. In reality, a random sample of response vectors are evaluated if the number of CRPs is too large. Diffuseness of ideal value is half of response vector length, ideally 50% in percentage. Diffuseness quantifies the information content that can be extracted from a PUF, in another words, how many IDs that this PUF has. If one PUF takes m IDs to evaluate its diffuseness, Ri and Rj (i ≠ j), have n bit responses, are two different response vectors corresponding to 2 different IDs. Then diffuseness is defined as:

∂ Uniqueness. When applying the same challenge to different PUFs, the response vectors from different PUFs are expected to be different due to intrinsic variations of each PUF. This is a highly desirable characteristic that measures the amount of unique information that can be extracted from a PUF. Uniqueness is measured by inter-HD. If two PUFs, i and j (i ≠ j), have n bit responses, produce Ri and Rj response vectors corresponding to the same challenge, The uniqueness of k PUFs is defined as:

∂ Reliability. Reliability or steadiness indicates stability of PUF output bits, i.e. the ability to consistently generate the same response to a corresponding challenge. Reliability of an ideal value should be strong (100%) without. However, because noise (environmental variations, instabilities in circuit, aging) are unavoidable, there are always uncertain factors affecting the response.
A reference response Refi is recorded at normal operating condition (27 °C and 1.0 V supply voltage for our simulation), then a response vector  is extracted at a different operating condition but using the same challenge as before. After samples of
is extracted at a different operating condition but using the same challenge as before. After samples of  are collected, the HD between Refi and
are collected, the HD between Refi and  is calculated named intra-HD. The ideal value of intra-HD should be 0. Intra-HD can also be described by Bit Error Rate (BER), which is the percentage of flipped (error) bits out of response bits due to noise. If the same n-bit response is collected at a different operating condition with a value
is calculated named intra-HD. The ideal value of intra-HD should be 0. Intra-HD can also be described by Bit Error Rate (BER), which is the percentage of flipped (error) bits out of response bits due to noise. If the same n-bit response is collected at a different operating condition with a value  . Note that m samples of
. Note that m samples of  are collected. Then the average intra-chip HD or BER is defined as:
are collected. Then the average intra-chip HD or BER is defined as:

Where  is the t-th sample of
is the t-th sample of  . The reliability of a PUF is defined as:
. The reliability of a PUF is defined as:

Additional Information
How to cite this article: Gao, Y. et al. Memristive crypto primitive for building highly secure physical unclonable functions. Sci. Rep. 5, 12785; doi: 10.1038/srep12785 (2015).
References
Kömmerling, O. & Kuhn, M. G. Design principles for tamper-resistant smartcard processors. In Proc. USENIX Workshop on Smartcard Technology, vol. 12, 9–20 (1999).
Suh, G. E. & Devadas, S. Physical unclonable functions for device authentication and secret key generation. In Proc. 44th annual Design Automation Conference, 9–14 (2007).
Maes, R., Van Herrewege, A. & Verbauwhede, I. PUFKY: A fully functional PUF-based cryptographic key generator. In Cryptographic Hardware and Embedded Systems, 302–319 (Springer, 2012).
van Dijk, M. & Rührmair, U. Physical unclonable functions in cryptographic protocols: Security proofs and impossibility results. IACR Cryptology ePrint Archive 2012, 228 (2012).
Zhang, L., Kong, Z. H. & Chang, C.-H. PCKGEN: A phase change memory based cryptographic key generator. In Proc. IEEE Int. Symp. Circuits and Systems (ISCAS), 1444–1447 (2013).
Ruhrmair, U. & van Dijk, M. PUFs in security protocols: Attack models and security evaluations. In Proc. IEEE Symp. Security and Privacy, 286–300 (2013).
Kang, H., Hori, Y., Katashita, T., Hagiwara, M. & Iwamura, K. Cryptographic key generation from PUF data using efficient fuzzy extractors. In Proc. IEEE 16th Int. Conf. Advanced Communication Technology (ICACT), 23–26 (2014).
Gao, M., Lai, K. & Qu, G. A highly flexible ring oscillator PUF. In Proc 2014 51st ACM/EDAC/IEEE Design Automation Conference, (DAC), San Francisco, CA (2014), 10.1145/2593069.2593072.
Lee, J. W. et al. A technique to build a secret key in integrated circuits for identification and authentication applications. In Proc. IEEE Symp. VLSI Circuits, 176–179 (2004).
Gassend, B., Lim, D., Clarke, D., Van Dijk, M. & Devadas, S. Identification and authentication of integrated circuits. Concurrency and Computation: Practice and Experience 16, 1077–1098 (2004).
Holcomb, D. E., Burleson, W. P. & Fu, K. Initial SRAM state as a fingerprint and source of true random numbers for RFID tags. In Proc. Conf, on RFID Security, vol. 7, Malaga, Spain, art. no. 1.2 (2007).
Holcomb, D. E., Burleson, W. P. & Fu, K. Power-up SRAM state as an identifying fingerprint and source of true random numbers. IEEE Trans. Comp. 58, 1198–1210 (2009).
Roel, M. Physically Unclonable Functions: Constructions, Properties and Applications. Ph.D. thesis, Dissertation, University of KU Leuven (2012).
Herder, C., Yu, M.-D., Koushanfar, F. & Devadas, S. Physical unclonable functions and applications: A tutorial. Proc. IEEE 102, 1126–1141 (2014).
Rostami, M., Wendt, J. B., Potkonjak, M. & Koushanfar, F. Quo vadis, PUF? Trends and challenges of emerging physical-disorder based security. In Proceedings of Design, Automation and Test in Europe Conference and Exhibition (DATE), 352 (2014).
Rührmair, U. et al. Modeling attacks on physical unclonable functions. In Proc. 17th ACM Conference on Computer and Communications Security. 237–249 (ACM, 2010).
Zhang, L., Kong, Z. H., Chang, C.-H., Cabrini, A. & Torelli, G. Exploiting process variations and programming sensitivity of phase change memory for reconfigurable physical unclonable functions. IEEE Trans. Information Forensics and Security 9 921–932 (2014).
Strukov, D. B., Snider, G. S., Stewart, D. R. & Williams, R. S. The missing memristor found. Nature 453, 80–83 (2008).
Kim, K.-H. et al. A functional hybrid memristor crossbar-array/CMOS system for data storage and neuromorphic applications. Nano Letters 12, 389–395 (2011).
Kavehei, O., Al-Sarawi, S., Cho, K.-R., Eshraghian, K. & Abbott, D. An analytical approach for memristive nanoarchitectures. IEEE Trans. Nanotech. 11, 374–385 (2012).
Kavehei, O. et al. An associative capacitive network based on nanoscale complementary resistive switches for memory-intensive computing. Nanoscale 5, 5119–5128 (2013).
Chen, A. & Lin, M.-R. Variability of resistive switching memories and its impact on crossbar array performance. In Proc. 2011 IEEE International Reliability Physics Symposium, MY-7 (2011).
Rajendran, J., Karri, R. & Rose, G. S. Improving tolerance to variations in memristor-based applications using parallel memristors. IEEE Trans. Computers. 64, 733–746 (2105).
Wu, S. et al. Bipolar resistance switching in transparent ITO/LaAlO3/SrTiO3 memristors. ACS Appl. Mat. & Interfaces 8575–8579 (2014).
Linn, E., Rosezin, R., Kügeler, C. & Waser, R. Complementary resistive switches for passive nanocrossbar memories, Nature Mat. 5 403–406 (2010).
van den Hurk, J., Havel, V., Linn, E., Waser, R. & Valov, I. Ag/GeSx/Pt-based complementary resistive switches for hybrid CMOS/nanoelectronic logic and memory architectures. Sci. Rep. 3, 2856 (2013).
Choi, S., Yang, Y. & Lu, W. Random telegraph noise and resistance switching analysis of oxide based resistive memory. Nanoscale 6, 400–404 (2014).
Borghetti, J. et al. Electrical transport and thermometry of electroformed titanium dioxide memristive switches. J. Appl. Phys. 106, 124504 (2009).
Kwon, D.-H. et al. Atomic structure of conducting nanofilaments in TiO2 resistive switching memory. Nature Nanotech. 5, 148–153 (2010).
Lim, D. Extracting Secret Keys From Integrated Circuits. Ph.D. thesis, Massachusetts Institute of Technology (2004).
Katzenbeisser, S. et al. Recyclable PUFs: Logically reconfigurable PUFs. Journal of Cryptographic Engineering 1, 177–186 (2011).
Kursawe, K., Sadeghi, A., Schellekens, D., Skoric, B. & Tuyls, P. Reconfigurable physical unclonable functions-enabling technology for tamper-resistant storage. In IEEE International Workshop on Hardware-Oriented Security and Trust, 22–29 (2009).
Majzoobi, M., Koushanfar, F. & Potkonjak, M. Techniques for design and implementation of secure reconfigurable PUFs. ACM Transactions on Reconfigurable Technology and Systems (TRETS) 2, 5 (2009).
Koeberl, P., Kocabaş, Ü. & Sadeghi, A.-R. Memristor PUFs: a new generation of memory-based physically unclonable functions. In Proceedings of the Conference on Design, Automation and Test in Europe, 428–431 (EDA Consortium, 2013).
Rose, G. S., McDonald, N., Yan, L.-K. & Wysocki, B. A write-time based memristive PUF for hardware security applications. In IEEE/ACM International Conference on Computer-Aided Design (ICCAD), 830–833 (2013).
Kavehei, O., Hosung, C., Ranasinghe, D. & Skafidas, S. mrPUF: A memristive device based physical unclonable function. arXiv preprint arXiv:1302.2191 (2013).
Rajendran, J. et al. Nanoelectronic solutions for hardware security. IACR Cryptology ePrint Archive 2012, 575 (2012).
Rajendran, J., Rose, G. S., Karri, R. & Potkonjak, M. Nano-PPUF: A memristor-based security primitive. In 2012 IEEE Computer Society Ann. Symp. VLSI (ISVLSI). 84–87 (2012).
Potkonjak, M. & Goudar, V. Public physical unclonable functions. Proc. IEEE 102, 1142–1156 (2014).
Vourkas, I., Batsos, A. & Sirakoulis, G. C. SPICE modeling of nonlinear memristive behavior. Int. J. Circuit Theory and Applications (2013), 10.1002/cta.1957.
Kvatinsky, S. et al. Verilog-A for memristor models. Technical Report 801, Center for Communication and Information Technlogies (CCIT), Technion, Israel, (2011).
Maiti, A., Gunreddy, V. & Schaumont, P. A systematic method to evaluate and compare the performance of physical unclonable functions. In Embedded Systems Design with FPGAs. 245–267 (Springer, 2013).
Hori, Y., Yoshida, T., Katashita, T. & Satoh, A. Quantitative and statistical performance evaluation of arbiter physical unclonable functions on FPGAs. In Proc. IEEE Int. Conf. on Reconfigurable Computing and FPGAs (ReConFig), 298–303 (2010).
Kim, K.-H., Jo, S. H., Gaba, S. & Lu, W. Nanoscale resistive memory with intrinsic diode characteristics and long endurance. Appl. Phys. Lett. 96, 053106 (2010).
Dodis, Y., Reyzin, L. & Smith, A. Fuzzy extractors: How to generate strong keys from biometrics and other noisy data. In Advances in Cryptology-Eurocrypt 2004. 523–540 (Springer, 2004).
Lim, D. et al. Extracting secret keys from integrated circuits. IEEE Transactions on Very Large Scale Integration (VLSI) Systems 13, 1200–1205 (2005).
Mahmoud, A., Rührmair, U., Majzoobi, M. & Koushanfar, F. Combined modeling and side channel attacks on strong PUFs. IACR Cryptology ePrint Archive 2013, 632 (2013).
Acknowledgements
This research was supported by a grant from the Australian Research Council (DP140103448). The authors also appreciate sponsorship from the China Scholarship Council.
Author information
Authors and Affiliations
Contributions
Y.G. wrote the paper; Y.G. performed experiments; Y.G., D.C.R. and O.K. analyzed the data; D.C.R., S.F.A., O.K. and D.A. supervised the study; Y.G., D.C.R., S.F.A., O.K. and D.A. discussed and interpreted the results; D.C.R., S.F.A., O.K. and D.A. proofed the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Gao, Y., Ranasinghe, D., Al-Sarawi, S. et al. Memristive crypto primitive for building highly secure physical unclonable functions. Sci Rep 5, 12785 (2015). https://doi.org/10.1038/srep12785
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep12785
This article is cited by
-
Memristor-based PUF for lightweight cryptographic randomness
Scientific Reports (2022)
-
Twin physically unclonable functions based on aligned carbon nanotube arrays
Nature Electronics (2022)
-
Nanoscale physical unclonable function labels based on block copolymer self-assembly
Nature Electronics (2022)
-
Laser fabrication and evaluation of holographic intrinsic physical unclonable functions
Scientific Reports (2022)
-
Reconfigurable physical unclonable cryptographic primitives based on current-induced nanomagnets switching
Science China Information Sciences (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.