Abstract
The recent development in the fabrication of artificial oxide heterostructures opens new avenues in the field of quantum materials by enabling the manipulation of the charge, spin and orbital degrees of freedom. In this context, the discovery of two-dimensional electron gases (2-DEGs) at LaAlO3/SrTiO3 interfaces, which exhibit both superconductivity and strong Rashba spin-orbit coupling (SOC), represents a major breakthrough. Here, we report on the realisation of a field-effect LaAlO3/SrTiO3 device, whose physical properties, including superconductivity and SOC, can be tuned over a wide range by a top-gate voltage. We derive a phase diagram, which emphasises a field-effect-induced superconductor-to-insulator quantum phase transition. Magneto-transport measurements show that the Rashba coupling constant increases linearly with the interfacial electric field. Our results pave the way for the realisation of mesoscopic devices, where these two properties can be manipulated on a local scale by means of top-gates.
Similar content being viewed by others
Introduction
The interplay between superconductivity and spin-orbit coupling (SOC) is at the centre of intensive research efforts as it can generate a variety of unique phenomena such as the occurrence of triplet superconductivity, for instance1. Recently, hybrid nanostructures involving a superconductor in proximity to a semiconducting nanowire with a strong SOC have been proposed as an ideal system to observe a topological superconducting phase, which accommodates pairs of Majorana fermions2,3. Following this idea, the first signatures of Majorana Fermions were obtained in devices made with indium antimonide in contact with niobium titanium nitride4. However, the realisation of such devices remains a challenge because (i) the intrinsic value of the SOC in semiconductors is weak and cannot be tuned (ii) it is difficult to control the spin state at the interface between very different materials. For this reason, the discovery of a two-dimensional electron gas (2-DEG) at the interface between two insulating oxides such as LaAlO3/SrTiO3 or LaTiO3/SrTiO3 raised a considerable interest5. Indeed, this 2-DEG displays both superconductivity6,7 and a strong SOC which is expected to be Rashba-type8,9, a combination of properties which is rarely observed in the same material.
The 2-DEG whose typical extension in the SrTiO3 substrate is of order ~10 nm10,12 is confined in an interfacial quantum well buried under an few unit cells thick insulating LaAlO3 layer. By adjusting the Fermi level with a gate voltage, the conductivity of the 2-DEG can be modulated from insulating to superconducting11,12. In addition, the Rashba SOC, which is dominated by the local electric field at the interface, can also be controlled with a gate voltage8. The combination of these two effects enables the realisation of nanostructures, where the very same material can be turned into different states by applying a local electric field-effect. Thus far, controlling the superconductivity and SOC have been demonstrated almost exclusively with gates deposited at the back of thick SrTiO3 substrates. Because of the very high value of the SrTiO3 dielectric constant at low temperatures ( )13, the electric field-effect can significantly modulate the carrier density with gate voltages on the order of 100 V11,12,14. However, in such geometry, it is not possible to control the properties of the 2-DEG on a scale much smaller than the typical thickness of the substrate (500 μm), making it impossible to realise devices with dimensions comparable to lengths that are characteristic of quantum orders (such as the superconducting coherence length and the spin diffusion length). To overcome this problem, field-effect control of the superconductivity and Rashba SOC needs to be achieved by means of local top-gates. Forg et al. fabricated field-effect transistors in a LaAlO3/SrTiO3 heterostructures using the insulating LaAlO3 layer as the gate dielectric and the YBa2Cu3O7 layer as the top-gate electrode15. Hosoda et al. achieved top-gate control of the normal state properties using a metallic gate directly deposited on the LaAlO3 layer16. More recently, a first attempt to modulate the superconductivity with a top-gate gave promising results17, despite the leaky insulating LaAlO3 layer. In this article, the realisation of a top-gated field-effect device is reported. The properties of the 2-DEG could be tuned over a wide range, from a superconducting to an insulating state. In addition, the control of the Rashba SOC by means of a top-gate is also demonstrated.
)13, the electric field-effect can significantly modulate the carrier density with gate voltages on the order of 100 V11,12,14. However, in such geometry, it is not possible to control the properties of the 2-DEG on a scale much smaller than the typical thickness of the substrate (500 μm), making it impossible to realise devices with dimensions comparable to lengths that are characteristic of quantum orders (such as the superconducting coherence length and the spin diffusion length). To overcome this problem, field-effect control of the superconductivity and Rashba SOC needs to be achieved by means of local top-gates. Forg et al. fabricated field-effect transistors in a LaAlO3/SrTiO3 heterostructures using the insulating LaAlO3 layer as the gate dielectric and the YBa2Cu3O7 layer as the top-gate electrode15. Hosoda et al. achieved top-gate control of the normal state properties using a metallic gate directly deposited on the LaAlO3 layer16. More recently, a first attempt to modulate the superconductivity with a top-gate gave promising results17, despite the leaky insulating LaAlO3 layer. In this article, the realisation of a top-gated field-effect device is reported. The properties of the 2-DEG could be tuned over a wide range, from a superconducting to an insulating state. In addition, the control of the Rashba SOC by means of a top-gate is also demonstrated.
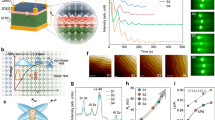
A ten-μm-wide superconducting Hall bar was first fabricated with an amorphous LaAlO3 template method and then covered by a Si3N4 dielectric layer and a metallic top gate (see Fig. 1a,b)18. More information on the fabrication processes is given in the Methods section. The sample was anchored to the mixing chamber of a dilution refrigerator with a base temperature of 16 mK. Figure 1c shows the superconducting transition of the device at the critical temperature  , which is similar to an unprocessed LaAlO3/SrTiO3 heterostructure. The current-voltage (I-V) characteristics of the device abruptly switches from the superconducting state (R = 0) to the resistive state (R ≠ 0) at the critical current Ic = 460 nA which corresponds to a critical current density of approximately 500 μA/cm.
, which is similar to an unprocessed LaAlO3/SrTiO3 heterostructure. The current-voltage (I-V) characteristics of the device abruptly switches from the superconducting state (R = 0) to the resistive state (R ≠ 0) at the critical current Ic = 460 nA which corresponds to a critical current density of approximately 500 μA/cm.
Device structure and superconducting transition.
(a) Schematic of the LaAlO3/SrTiO3 device with a 500 nm thick Si3N4 dielectric layer (scheme drawn by N. B.). (b) Dark-field optical picture of the device showing the Hall bar covered by a top-gate. (c) Sheet resistance as a function of temperature showing a superconducting transition at a critical transition temperature Tc ≈ 250 mK. Inset) Current-voltage characteristics of the device indicating the critical current Ic = 460 nA. The arrows indicate the direction of the current sweep.
Electrostatic Control of the Carrier Density
After the sample was cooled, the top-gate voltage VTG was first increased to +110 V, beyond the saturation threshold of the resistance. During this operation, electrons are added in the quantum well, increasing the Fermi energy to its maximum value (i.e., the top of the well)19. In comparison with back-gate experiments where the relationship between the carrier density (n) and the back-gate voltage VBG is not trivial owing to the electric-field-dependent dielectric constant of SrTiO313, here, the carrier density is expected to increase linearly with VTG. Figure 2 shows the sheet carrier density  , extracted from the Hall effect measurements performed up to B = 4 T as a function of the top-gate voltage VTG, for two different back-gate voltages (VBG = 0 V and VBG = −15 V). For VBG = 0 V, the linear increase in n is observed with VTG only for negative VTG. The non-physical decrease in n with VTG for positive gate voltages is caused by the incorrect determination of the carrier density at low magnetic fields. It was shown that at the LaAlO3/SrTiO3 interface, the Hall voltage is no longer linear with the magnetic field for strong filling of the quantum well because of multi-band transport12,20,21. To reach a doping regime where the one-band approximation is valid, a negative back-gate VBG = −15 V was applied producing a depletion of the highest energy sub-bands that accommodate the highly-mobile carriers, responsible of the decrease of the Hall number at positive VTG. Figure 2 shows that in this case, the linear dependence of
, extracted from the Hall effect measurements performed up to B = 4 T as a function of the top-gate voltage VTG, for two different back-gate voltages (VBG = 0 V and VBG = −15 V). For VBG = 0 V, the linear increase in n is observed with VTG only for negative VTG. The non-physical decrease in n with VTG for positive gate voltages is caused by the incorrect determination of the carrier density at low magnetic fields. It was shown that at the LaAlO3/SrTiO3 interface, the Hall voltage is no longer linear with the magnetic field for strong filling of the quantum well because of multi-band transport12,20,21. To reach a doping regime where the one-band approximation is valid, a negative back-gate VBG = −15 V was applied producing a depletion of the highest energy sub-bands that accommodate the highly-mobile carriers, responsible of the decrease of the Hall number at positive VTG. Figure 2 shows that in this case, the linear dependence of  with VTG can be recovered. The linear fit of slope
with VTG can be recovered. The linear fit of slope  is obtained from numerical simulations of the electric field-effect by a finite elements method assuming a dielectric constant
is obtained from numerical simulations of the electric field-effect by a finite elements method assuming a dielectric constant  for the Si3N4 layer (see the inset in Fig. 2). Finally, the following relationship between the carrier density and top-gate voltage is deduced: n = 5.0 × 1010 VTG + 1.69 × 1013 e- .cm-2.
for the Si3N4 layer (see the inset in Fig. 2). Finally, the following relationship between the carrier density and top-gate voltage is deduced: n = 5.0 × 1010 VTG + 1.69 × 1013 e- .cm-2.
Hall effect and carrier density.
Carrier density (n) extracted from the slope of the Hall voltage (VH) at 4 T as a function of VTG for two different back-gate voltages (VBG). The curve at VBG = −15 V is offset to match the curve at VBG = 0 V at negative top-gate voltages. The dashed line was obtained from numerical simulations on the carrier density, assuming a dielectric constant  for the Si3N4 layer. Inset: example of a numerical simulation of the charge carrier distribution in the device for VBG = 0 V and VTG = 10 V.
for the Si3N4 layer. Inset: example of a numerical simulation of the charge carrier distribution in the device for VBG = 0 V and VTG = 10 V.
Superconductivity and Phase Diagram
In the following, the back gate voltage VBG was always set to 0 V unless otherwise stated. Figure 3a shows the sheet resistance of the device as a function of temperature measured for different top-gate voltages in the range [−110 V, +110 V], where the leakage gate current is negligible (<0.1 nA). The variation in VTG induces a modulation in the normal state resistance by two orders of magnitude. Figure 3b summarises the variations of the normalised resistance R/R(T = 350 mK) as a function of temperature (T) and top-gate voltage VTG on a phase diagram. The corresponding n is also indicated on the top axis. The device displays a gate-dependent superconducting transition, whose critical temperature Tc describes a partial dome as a function of VTG, similar to that observed with a back-gate11,12,14. The maximum Tc, corresponding to optimal doping, is around 250 mK. In the underdoped region, a decrease in the gate voltage causes Tc to continuously decrease from its maximum value to zero. A superconductor-to-insulator quantum phase transition takes place around VTG = −90 V. The critical sheet resistance at the transition is  , which is close to the quantum of resistance of bosons with 2e charges,
, which is close to the quantum of resistance of bosons with 2e charges,  . For large negative voltages, corresponding to low electron densities, the sheet resistance increases strongly when approaching the insulating state. In the overdoped region, the addition of electrons into the quantum well with the top-gate produces a small decrease in Tc whose origin is currently under debate. Such behaviour has also been observed in doped bulk SrTiO322 and could be reinforced by the two-dimensionality of the interface23. The current-voltage characteristics of the device for different top-gate voltages are shown in Supplementary Material.
. For large negative voltages, corresponding to low electron densities, the sheet resistance increases strongly when approaching the insulating state. In the overdoped region, the addition of electrons into the quantum well with the top-gate produces a small decrease in Tc whose origin is currently under debate. Such behaviour has also been observed in doped bulk SrTiO322 and could be reinforced by the two-dimensionality of the interface23. The current-voltage characteristics of the device for different top-gate voltages are shown in Supplementary Material.
Field-effect control of the superconductivity.
(a) Sheet resistance of the device as a function of temperature for different VTG. (b) Sheet resistance normalised by its value at T = 350 mK plotted with a colour scale as a function of temperature (left axis) and top-gate voltage. The carrier densities corresponding to the top-gate voltages have been added in the top axis. The sheet resistance at T = 350 mK is plotted as a function of top-gate voltage on the right axis. The critical temperature Tc is plotted as function of the top-gate voltage on the left axis for the different criteria: drop of 10%, 50% and 90% of the normal resistance taken at T = 350 mK.
Rashba Spin-orbit Coupling
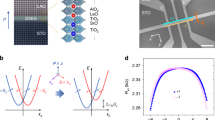
In LaAlO3/SrTiO3 heterostructures, the accumulation of electrons in the interfacial quantum well generates a strong local electric field Ez perpendicular to the motion of the electrons, which translates into a magnetic field in their rest frame. It is expected that the coupling of the electrons spin to this field gives rise to a Rashba-type SOC described by the Hamiltonian  , where
, where  is the electron wave vector,
is the electron wave vector,  is a unit vector perpendicular to the interface and σ are the Pauli matrices24. The constant α represents the strength of the SOC and has to be directly proportional to the interfacial electric field Ez. In electronic transport measurements, the presence of a spin-orbit coupling results in an additional spin relaxation mechanism characterised by the relaxation time τSO. Caviglia et al. reported a τSO roughly proportional to the inverse of the elastic scattering time τe in agreement with a D’Yakonov-Perel mechanism characteristic of a Rashba interaction8. However, to confirm experimentally the Rashba-type SOC, it is also important to establish the linear dependance of α with Ez (α ∝ Ez) when the filling of the quantum well is varied by gating.
is a unit vector perpendicular to the interface and σ are the Pauli matrices24. The constant α represents the strength of the SOC and has to be directly proportional to the interfacial electric field Ez. In electronic transport measurements, the presence of a spin-orbit coupling results in an additional spin relaxation mechanism characterised by the relaxation time τSO. Caviglia et al. reported a τSO roughly proportional to the inverse of the elastic scattering time τe in agreement with a D’Yakonov-Perel mechanism characteristic of a Rashba interaction8. However, to confirm experimentally the Rashba-type SOC, it is also important to establish the linear dependance of α with Ez (α ∝ Ez) when the filling of the quantum well is varied by gating.
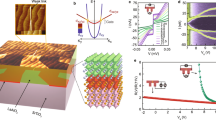
The weak localization corrections to the conductance of a two-dimensionnal system at low temperatures are modified by the presence of an additional spin relaxation mechanism due to SOC25,26 whose strength can therefore be determined by properly analysing the magnetoconductance Δσ(B) = σ(B) − σ(0). Δσ(B) was measured in the normal state at different temperatures and top-gate voltages. For negative VTG a positive magnetoconductance was observed beyond 1 T. This is characteristic of a weak localization regime with small SOC (Fig. 4). As VTG is increased, an inversion of the sign of the magnetoconductance is observed and at large positive gate voltages the magnetoconductance remains always negative. The experimental data in Fig. 4 were fitted with the Maekawa-Fukuyama formula in a diffusive regime that describes the change in the conductivity with magnetic field with negligible Zeeman splitting25,
Magnetotransport measurements.
(a) Magnetoconductance of the device at T = 3.5 K for different VTG. The experimental data (open symbols) are fitted with the Maekawa-Fukuyama formula (1). (b) Evolution of the fitting parameters BSO, Bϕ and AK as a function of the gate voltage. Inset) Variations in BSO and Bϕ as a function of temperature for VTG = 0.

where Ψ is the digamma function,  is the quantum of conductance and the parameters Btr, BΦ, BSO are the effective fields related to the elastic, inelastic and spin-orbit relaxation times respectively. BΦ and BSO, which are measured here by a transport experiment, are related to the relaxation times τΦ and τSO by the expressions
is the quantum of conductance and the parameters Btr, BΦ, BSO are the effective fields related to the elastic, inelastic and spin-orbit relaxation times respectively. BΦ and BSO, which are measured here by a transport experiment, are related to the relaxation times τΦ and τSO by the expressions  and
and  respectively, where D is the diffusion constant25,26. Finally, to account for the orbital magnetoconductance, we have added in Eq. (1) a B2 term with a Kohler coefficient AK which increases quadratically with the mobility27,28. Good agreement is obtained between the experimental data and the theory over the whole electrostatic doping range.
respectively, where D is the diffusion constant25,26. Finally, to account for the orbital magnetoconductance, we have added in Eq. (1) a B2 term with a Kohler coefficient AK which increases quadratically with the mobility27,28. Good agreement is obtained between the experimental data and the theory over the whole electrostatic doping range.
The evolution of the fitting parameters as a function of the top-gate voltage and equivalent carrier density is shown in Fig. 4b. Bϕ varies only weakly over the whole range of gate voltage, indicating that the number of inelastic collisions does not depend on the carrier density. In the framework of the weak localisation theory the temperature dependence of the inelastic scattering time is given by τΦ ∝ T−p and therefore BΦ ∝ Tp, where p depends on the inelastic mechanism. The same fitting procedure was performed at different temperatures, giving a linear relationship between BΦ and T (Fig. 4b inset and Supplementary Material). This is consistent with p = 1, which indicates that the inelastic scattering is dominated by electron-electron interactions6,29.
Spin-splitting Energy
The spin-orbit term (BSO) increases with top-gate voltage and, correspondingly, with the carrier density. The analysis of this dependence can shed light on the origin of the SOC at the LaAlO3/SrTiO3 interface. If we assume that the spin relaxation is dominated by the D’Yakonov-Perel mechanism, based on a Rashba spin-orbit interaction,  26,30. We then obtain the relationship between the coupling constant and the spin-orbit effective field
26,30. We then obtain the relationship between the coupling constant and the spin-orbit effective field  . Integrating the Maxwell-Gauss equation in the direction perpendicular to the interface gives the interfacial electric field
. Integrating the Maxwell-Gauss equation in the direction perpendicular to the interface gives the interfacial electric field  where
where  is the dielectric constant of Si3N4 at the interface and nt is the carrier density of non-mobile charges trapped in the SrTiO3 substrate. The coupling constant being proportional to Ez, it is therefore expected to vary with carrier density with the form α = an + b, which is well satisfied experimentally for a wide range of electrostatic doping (Fig. 5). This confirms experimentally that the D’Yakonov-Perel mechanism in the presence of Rashba spin-orbit interaction is dominant in these 2-DEGs.
is the dielectric constant of Si3N4 at the interface and nt is the carrier density of non-mobile charges trapped in the SrTiO3 substrate. The coupling constant being proportional to Ez, it is therefore expected to vary with carrier density with the form α = an + b, which is well satisfied experimentally for a wide range of electrostatic doping (Fig. 5). This confirms experimentally that the D’Yakonov-Perel mechanism in the presence of Rashba spin-orbit interaction is dominant in these 2-DEGs.
Assuming a Fermi energy of 100 meV and an effective mass m = 0.7m0 for the dxy light subbands mainly occupied, we can estimate the characteristic spin-splitting energy ΔSO = 2kFα where kF is the electron wave vector at Fermi energy. The order of magnitude of a few meV, which is much larger than in most semiconductors, is in agreement with previous studies8,9. Neglecting the small changes in kF with doping, we can plot the variation of ΔSO with VTG and correspondingly, n (Fig. 5). ΔSO is independent of the temperature below 10 K as the shape of the quantum well and Ez do not change in this temperature range (see the inset in Fig. 5 and Supplementary Material). The Kohler term (parameter AK) is proportional to the square of the mobility. For positive gate voltages where the 2-DEG has a rather large mobility, this term dominates the magnetoconductance and must be taken into account in Eq. (1). As shown in the Supplementary Figure S4, fitting the data without this term leads to an incorrect determination of the SOC in a large range of positive gating.
In summary, LaAlO3/SrTiO3 -based field-effect devices were fabricated using the amorphous LaAlO3 template method. The superconductivity can be electrostatically modulated over a wide range by a top-gate voltage, without any leakage. A superconductor-to-insulator quantum phase transition is induced when the quantum well is strongly depleted. By analysing the magnetotransport measurements, the presence of strong spin-orbit coupling that could be controlled with the top-gate voltage was demonstrated. The spin-spliting energy on the order of a few meV was found to increase linearly with the interfacial electric field in agreement with the Rashba mechanism. These results represent an important step toward the realisation of new mesoscopic devices, where the interaction between superconductivity and the Rasba SOC could give rise to non-conventional electronic states.
Methods
Device fabrication
Starting with a TiO2 -terminated -oriented SrTiO3 commercial substrate (Crystec), the template of a Hall bar with contact pads was defined by evaporating an amorphous LaAlO3 layer through a resist patterned by optical lithography. After a lift-off process, a thin layer of crystalline LaAlO3 (8 u.c) was grown on the amorphous template by Pulse Laser Deposition, such that only the areas directly in contact with the substrate (Hall bar and contact pads) were crystalline. A KrF excimer (248 nm) laser was used to ablate the single-crystalline LaAlO3 target at 1 Hz, with a fluence between 0.6 and 1.2 J/cm2 under an O2 pressure of 2 × 10−4 mbar31. The substrate was typically kept at 650 °C during the growth of the film, monitored in real-time by reflection high-energy electron diffraction RHEED. As the growth occurs layer-by-layer, the thickness can be controlled at the unit cell level. After the growth of the film, the sample was cooled down to 500 °C under a O2 pressure of 10−1 mbar, which was increased up to 400 mbar. To reduce the presence of oxygen vacancies (in both the substrate and the film), the sample was kept under these conditions for 30 minutes before it was cooled to room temperature. The 2-DEG forms at the interface between the crystalline LaAlO3 layer and the SrTiO3 substrate. Such method has already been used to fabricate ungated 500 nm wide channels without noticeable alteration of the 2DEG properties18. Once the channel is defined, a 500 nm thick Si3N4 dielectric layer was deposited on the Hall bar by a lift-off process. After this step, a gold top-gate layer was deposited and lifted-off forming and appropriate geometry to cover the Hall bar. A metallic back gate was added at the end of the process.
Additional Information
How to cite this article: Hurand, S. et al. Field-effect control of superconductivity and Rashba spin-orbit coupling in top-gated LaAlO3\SrTiO3 devices. Sci. Rep. 5, 12751; doi: 10.1038/srep12751 (2015).
References
Gorkov, L. P. & Rashba, E. I. Superconducting 2D System with Lifted Spin Degeneracy: Mixed Singlet-Triplet State. Phys. Rev. Lett. 87, 037004 (2001).
Lutchyn, R. M., Sau, J. D. & Das Sarma, S. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Oreg, Y., Refael, G. & von Oppen, F. Helical Liquids and Majorana Bound States in Quantum Wires. Phys. Rev. Lett. 105, 177002 (2010).
Mourik, V. et al. Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices. Science 336, 1003 (2012).
Ohtomo, A. & Hwang, H. Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004).
Biscaras, J. et al. Two-dimensional superconductivity at a Mott insulator/band insulator interface LaTiO3/SrTiO3 . Nature Commun. 1, 89 (2010).
Reyren, N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196–1199 (2007).
Caviglia, A. D., Gabay, M., Gariglio, S., Reyren, Cancellieri, C. & Triscone, J.-M. Tunable Rashba Spin-Orbit Interaction at Oxide Interfaces. Phys. Rev. Lett. 104, 126803 (2010).
Ben Shalom, M., Sachs, M., Rakhmilevitch, D., Palevski, A. & Dagan, Y. Tuning Spin-Orbit Coupling and Superconductivity at the SrTiO3/LaAlO3 Interface: A Magnetotransport Study. Phys. Rev. Lett. 104, 126802 (2010).
Copie, O. et al. Towards Two-Dimensional Metallic Behavior at LaAlO3/SrTiO3 Interfaces. Phys. Rev. Lett. 102, 216804 (2009).
Caviglia, A. D. et al. Electric field control of the LaAlO3/SrTiO3 interface ground state. Nature 456, 624 (2008).
Biscaras, J. et al. Two-dimensional superconductivity induced by high-mobility carrier doping in LaTiO3/SrTiO3 heterostructures. Phys. Rev. Lett. 108, 247004 (2012).
Neville, R. C., Hoeneisen, B. & Mead, C. A. Permittivity of Strontium Titanate. J. Appl. Phys. 43, 2124 (1972).
Bell, C. et al. Dominant Mobility Modulation by the Electric Field Effect at the LaAlO3/SrTiO3 Interface. Phys. Rev. Lett. 103, 226802 (2009).
Forg, B., Richter, C. & Mannhart, J. Field-effect devices utilizing LaAlO3/SrTiO3 interfaces. Appl. Phys. Lett. 100, 053506 (2012).
Hosoda, M., Hikita, Y., Hwang, H. Y. & Bell, C. Transistor operation and mobility enhancement in top-gated LaAlO3/SrTiO3 heterostructures. Appl. Phys. Lett. 103, 103507 (2013).
Eerkes, P. D., van der Wiel, W. G. & Hilgenkamp, H. Modulation of conductance and superconductivity by top-gating in LaAlO3/SrTiO3 2-dimensional electron systems. Appl. Phys. Lett. 103, 201603 (2013).
Stornaiuolo, D. et al. In-plane electronic confinement in superconducting LaAlO3/SrTiO3 nanostructures. Appl. Phys. Lett. 101, 222601 (2012).
Biscaras, J. et al. Limit of the electrostatic doping in two-dimensional electron gases of LaXO3(X = Al,Ti)/SrTiO3 . Sci. Rep. 4, 6788 (2014).
Kim, J. S. et al. Nonlinear Hall effect and multichannel conduction in LaTiO3/SrTiO3 superlattices. Phys. Rev. B 82, 201407 (2010).
Ohtsuka, R., Matvejeff, M., Nishio, N., Takahashi, R. & Lippmaa, M. Transport properties of LaTiO3/SrTiO3 heterostructures. Appl. Phys. Lett. 96, 192111 (2010).
Takada, Y. Theory of Superconductivity in Polar Semiconductors and Its Application to N-Type Semiconducting SrTiO3 . J. Phys. Soc. Jpn. 49, 1267 (1980).
Klimin, S. N., Tempere, J., Devreese, J. T. & van der Marel, D. Interface superconductivity in LaAlO3 - SrTiO3 heterostructures. Phys. Rev. B 89, 184514 (2014).
Bychkov, Y. A. & Rashba, E. I. Oscillatory effects and the magnetic susceptibility of carriers in inversion layers. J. Phys. C 17, 6039 (1984).
Maekawa, S. & Fukuyama, H. Magnetoresistance in Two-Dimensional Disordered Systems: Effects of Zeeman Splitting and Spin-Orbit Scattering. J. Phys. Soc. Jpn. 50, 2516–2524 (1981).
Hikami, S., Larkin, A. I. & Nagaoka, Y. Spin-Orbit interaction and magnetoresistance in the 2 dimensional random system. Prog. Theor. Phys. 63, 707 (1980).
Sommerfeld, A. & Frank, N. H. The Statistical theory of thermoelectric, galvano- and thermomagnetic phenomena in metals. Rev. Mod. Phys. 3 1 (1931).
Macdonald, D. K. C. & Sarginson, K. Galvanomagnetic effects in conductors. Rep. Prog. Phys. 15 249 (1952).
Lee, P. A. & Ramakrishnan, T. V. Disordered electronic systems. Rev. Mod. Phys. 57, 2873317 (1985).
D’yakonov, M. I. & Perel, V. I. Spin relaxation of conduction electrons in non-centrosymmetric semiconductors. Sov. Phys. Solid State 13, 3023 (1972).
Lesne, E. et al. Suppression of the critical thickness threshold for conductivity at the LaAlO3/SrTiO3 interface. Nature Commun. 5, 4291 (2014).
Acknowledgements
This work was supported by the french ANR, the DGA the CNRS PICS program and the Région Ile-de-France through CNano IdF and Sesame programs.
Author information
Authors and Affiliations
Contributions
J.L. and N.B. supervised the project. E.L. and N.R. fabricated the LaAlO3/SrTiO3 heterostructures by PLD under the supervision of A.B. and M.B. S.H. and A.J. made the top-gate devices with the help of C.F.-P., X.L, C.U. and M.P.-L. S.H., A.J. and G.S performed and analysed the measurements. C.F.-P. performed the Comsol simulations. All authors contributed to the interpretation of the results. S.H., J.L. and N.B. wrote the manuscripts with inputs of J.B., S.C. and M.G.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Hurand, S., Jouan, A., Feuillet-Palma, C. et al. Field-effect control of superconductivity and Rashba spin-orbit coupling in top-gated LaAlO3/SrTiO3 devices. Sci Rep 5, 12751 (2015). https://doi.org/10.1038/srep12751
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep12751
This article is cited by
-
Gate-tunable pairing channels in superconducting non-centrosymmetric oxides nanowires
npj Quantum Materials (2022)
-
Anomalous Josephson coupling and high-harmonics in non-centrosymmetric superconductors with S-wave spin-triplet pairing
npj Quantum Materials (2022)
-
Oxide spin-orbitronics: spin–charge interconversion and topological spin textures
Nature Reviews Materials (2021)
-
Transition from a uni- to a bimodal interfacial charge distribution in \(\hbox {LaAlO}_3\)/\(\hbox {SrTiO}_3\) upon cooling
Scientific Reports (2020)
-
Planar Hall effect and anisotropic magnetoresistance in polar-polar interface of LaVO3-KTaO3 with strong spin-orbit coupling
Nature Communications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.