Abstract
We studied two BaFe2−xNixAs2 (Ni-doped Ba-122) single crystals at two different doping levels (underdoped and optimally doped) using an optical spectroscopic technique. The underdoped sample shows a magnetic phase transition around 80 K. We analyze the data with a Drude-Lorentz model with two Drude components (D1 and D2). It is known that the narrow D1 component originates from electron carriers in the electron-pockets and the broad D2 mode is from hole carriers in the hole-pockets. While the plasma frequencies of both Drude components and the static scattering rate of the broad D2 component show negligible temperature dependencies, the static scattering rate of the D1 mode shows strong temperature dependence for the both samples. We observed a hidden quasi-linear temperature dependence in the scattering rate of the D1 mode above and below the magnetic transition temperature while in the optimally doped sample the scattering rate shows a more quadratic temperature dependence. The hidden non-Fermi liquid behavior in the underdoped sample seems to be related to the magnetic phase of the material.
Similar content being viewed by others
Introduction
The FeAs high temperature superconductors have been attracted much attention and have been studied intensively since their first discovery in 2006 and 20081,2. These compounds are of several different types. Those types are a “1111” type (LaFePO, SmFeAsO, PrFeAsO, LaFeAsO etc.), a “122” type (BaFe2As2, SrFe2As2, CaFe2As2 etc.), a “111” type (LiFeAs, NaFeAs, LiFeP etc.), a “11” type (Fe(Te, Se)) and so on. Each type except “11” has a different layered structure consisting of an alternating a charge transport layer and a charge reservoir layer; “11” type consists of only charge transfer layers. Each type shows a similar phase diagram as that of cuprates3 even though the details are quite different; undoped parent compounds are antiferromagnetic metals while cuprates are antiferromagnetic Mott insulators. The superconducting mechanism in this material has not yet been figured out. Researchers in this field believe that its mechanism may have a common origin with that of the cuprates. Density functional theory calculation shows the electronic structure of FeAs compounds is multiband with three hole-like bands at the Γ point and two electron-like bands at the Brillouin zone corners4. The FeAs-compounds also show multigap superconductivity5 compared with the cuprates which have a single d-wave superconducting gap. Since this material has the multiband channels an analysis of the optical data may need to include two different types of free-carrier contributions6. This material also shows quite strong correlations among charge carriers; electronic many-body effects seem to be important7.
Recent optical study on Ba0.6K0.4Fe2As2 with two Drude modes shows interesting hidden temperature-dependent properties of the two Drude modes8. It is observed that the two Drude modes show significantly different temperature-dependent trends; only one of the Drude modes shows a strong temperature dependence. The approach used is a similar to the so-called two-component analysis introduced in an earlier paper on Bi2Sr2CaCu2O8+δ cuprates9. In the earlier paper they also introduced a so-called one-component analysis, which is also known as an extended Drude model10,11. Since FeAs-compounds have multibands the compounds can be analyzed approximately with two Drude components as in Dai et al. paper8, which corresponds to the two-component analysis for cuprates. The one-component (or extended Drude model) analysis has been applied to Fe-pnictide systems12,13,14 with a single band approximation even though the material systems have multiband characteristics. To resolve the multiband issue one should develop a new method including the multiband nature. Another issue for the direct application of the extended Drude model to the Fe-pictides is that the system has low-energy interband transitions15, which need to be considered. Because of those nontrivial issues associated with application of the one-component analysis we applied a two-component analysis to analyze our optically measured spectra.
In this paper we investigate Ni-doped Ba-122 type Fe-pnictide samples (BaNixFe2−xAs2) at two different doping levels: an underdoped x = 0.05 with the superconducting transition temperature, Tc = 10 K and an optimally doped x = 0.10 with Tc = 17 K. The underdoped compound shows magnetic and structure transitions near 80 K. We applied the two-component analysis to understand our optical data of BaFe2−xNixAs2 (x = 0.05 and 0.10). For the analysis we use a model with two Drude components for the two electron- and hole- pockets on the Fermi surface. We found that one of the two Drude modes is quite narrow compared to the other as in a reported paper8. We denote the narrow as D1 and the broad D2. Other studies show that D1 (D2) come from the contribution of the electron-pocket (hole-pocket)8,16,17. From this analysis we can expose hidden transport properties. We found that in the underdoped sample the magnetic transition affects transport properties of electron carriers. We observed that the underdoped and optimally doped samples show different temperature dependent hidden transport properties; the optimally doped sample shows a Fermi-liquid behavior while the underdoped one shows a non-Fermi liquid behavior.
Results and Discussion
The measured reflectance spectra of our two Ni-doped Ba-122 crystal samples (see Methods section) at various temperatures are shown in Fig. 1(a,b). In the insets we display magnified views to show the data better in low frequency region. While the optimally doped sample (x = 0.10) shows a monotonic temperature evolution the underdoped one (x = 0.05) shows non-monotonic temperature evolution below ~1000 cm−1; reflectance increases initially as temperature decreases down to ~100 K and then below this temperature it decreases as shown in the inset of the upper panel. The non-monotonic behavior with temperature seems to be related to the magnetic phase transition of the system. Both sets of data show two characteristic crossing points near 1000 cm−1 and 4000 cm−1. We analyzed further the reflectance spectra using a Kramers-Kronig relation (see Methods section) to obtain optical constants including the optical conductivity and the dynamic dielectric function.
In Fig. 2(a,b) we display the real part of the optical conductivity (σ1(ω)) of our two samples obtained using the Kramers-Kronig process described in Methods section. As we expected from the reflectance data we can see a conductivity inversion at low frequency in the conductivity of the underdoped sample while the optimally doped sample shows a monotonic increase as temperature decreases. We also display the measured DC resistivity data obtained by using a four-probe measurement technique in the insets. The DC resistivity of the underdoped sample shows an anomaly near 80 K marked with a red arrow as shown in the inset of the upper panel where the magnetic phase transition takes place. To study the frequency dependent spectral weight redistribution we calculated the accumulated conductivity (or partial sum), which is defined as  . We note that Ws(∞) is proportional to the number density of total electrons in a material, i.e.
. We note that Ws(∞) is proportional to the number density of total electrons in a material, i.e.  where Ni is the electron density of the ith band, e is the unit charge and
where Ni is the electron density of the ith band, e is the unit charge and  is the effective mass (or band mass) of electron in the ith band. We display the partial sums of our two samples at various temperatures in Fig. 3(a,b). We can see spectral weight redistributions as a function of temperature. Our optimally doped sample (in Fig. 3b) shows monotonic temperature dependence; as temperature decreases the spectral weight increases in the low frequency region and then the spectral weights at all measured temperatures merge together at high frequency. We display the optical conductivity in low frequency region below 700 cm−1 in the inset to show the temperature dependent behavior more clearly. Our underdoped sample (in Fig. 3a) shows a dramatic change across the magnetic transition temperature; below the transition temperature a significant spectral weight loss in low frequency region is observed and the spectral weight loss seems to be transferred to high frequency region above our measurement range. We also display the optical conductivity in the low frequency region below 700 cm−1 in the inset to show the non-monotonic temperature dependent behavior in the spectral weight.
is the effective mass (or band mass) of electron in the ith band. We display the partial sums of our two samples at various temperatures in Fig. 3(a,b). We can see spectral weight redistributions as a function of temperature. Our optimally doped sample (in Fig. 3b) shows monotonic temperature dependence; as temperature decreases the spectral weight increases in the low frequency region and then the spectral weights at all measured temperatures merge together at high frequency. We display the optical conductivity in low frequency region below 700 cm−1 in the inset to show the temperature dependent behavior more clearly. Our underdoped sample (in Fig. 3a) shows a dramatic change across the magnetic transition temperature; below the transition temperature a significant spectral weight loss in low frequency region is observed and the spectral weight loss seems to be transferred to high frequency region above our measurement range. We also display the optical conductivity in the low frequency region below 700 cm−1 in the inset to show the non-monotonic temperature dependent behavior in the spectral weight.
(a,b) The extracted conductivity spectra of BaFe2−xNixAs2 (x = 0.05 and 0.10) at various temperatures using the Kramers-Kronig analysis. In the insets we display measured DC resistivity data. The red arrow in the inset of the upper panel indicates the onset temperature of the magnetic phase transition.
We display two representative real parts of the optical conductivity data of our two samples at 150 K and their Drude-Lorentz fits (see Methods section) in Fig. 4(a,b). For the fitting we used two Drude modes (D1: one narrow and D2: the other broad) and two Lorentz modes (L1: one is strong at high and L2: the other weak at low frequency). While the narrow Drude component (D1) is known as contribution from electron carriers in the electron-pocket, the broad one (D2) from hole carriers8,16,17. The Lorentz component (L1) at high frequency shows negligible temperature dependence. The Lorentz component (L2) at low frequency is the interband transition at 1300 cm−1 which was reported recently by Marsik et al.18. For the fitting we used the reported temperature and doping dependent amplitudes of the low-energy Lorentz component. We note that the low-energy component is quite weak in terms of the spectral weight. Therefore we expect that it will have negligible impact on overall fits. We display temperature dependent fitting parameters of the two Drude components of the underdoped and optimally doped samples in Fig. 5(a,b) and Fig. 6(a,b), respectively.
(a,b) Two representative Drude-Lorentz fits and optical conductivity data of BaFe2−xNixAs2 (x = 0.05 and 0.10) at T = 150 K. We used two Drude components (D1 and D2) and also included a low-energy interband transition observed by Marsik et al.18.
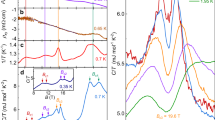
(a,b) The fitting parameters (ΩDi,p and 1/τDi) of two Drude components (i = 1, 2) of BaFe1.90Ni0.10As2. In the inset we display the static scattering rate of D1 mode as a function of T2. (c,d) We also display the calculated DC conductivities (σdc(T)) and DC resistivity data(ρ(T)) including the total resistivity as functions of temperature, T.
In Fig. 5(a–d) we show four quantities of two Drude modes (D1 and D2) in the underdoped sample at various temperatures below and above the magnetic transition temperature (~80 K) obtained from the fitting. The four quantities are the plasma frequency (ΩDi,p), the static scattering rate (1/τDi), the DC conductivity (σdc) and the DC resistivity (ρ) of the two Drude modes. Both plasma frequencies (in panel (a)) show negligible temperature dependencies. While the static scattering rate of the D1 Drude mode shows strong temperature dependence that of the D2 mode shows negligible temperature dependence (in panel (b)). These are similar behaviors to what was observed by Dai et al.8; only the scattering rate of the D1 shows significant temperature dependence. We note that their sample was an optimally hole-doped (or K-doped) Ba-122 sample. Here we observed that our underdoped sample shows an interesting upturn below the magnetic transition temperature (marked with a red arrow), which is absent in both optimally hole-doped Ba0.6K0.4Fe2As2 sample in Dai et al. paper8 and our optimally electron-doped one. As shown in panel (b) the static scattering rate of the D1 mode decreases linearly down to the magnetic transition temperature from 300 K and then it increases linearly below this temperature. This linear temperature dependent behavior indicates that the hidden transport property is the non-Fermi-liquid above and below the transition temperature. The linear temperature dependent behavior seems to be similar to that in non-Fermi liquid phase of cuprates19. Here we point out that the magnetic phase transition in the underdoped sample is closely associated with the D1 mode or electron carriers in the electron-pocket. It seems to be consistent with earlier angle-resolved photoemission study of detwinned single crystals of electron-doped Ba(Fe1−xCox)2As220. We observe similar temperature dependent non-trivial behavior in the other two quantities [ and
and  ] shown in the right panels (c, d). In panel (d) we also display the total DC resistivity (open star symbols) which can be calculated using a relation, 1/ρD1+D2 = 1/ρD1 + 1/ρD2.
] shown in the right panels (c, d). In panel (d) we also display the total DC resistivity (open star symbols) which can be calculated using a relation, 1/ρD1+D2 = 1/ρD1 + 1/ρD2.
In Fig. 6(a–d) we display the four quantities of our optimally doped sample at various temperatures. We can see that only the static scattering rate of D1 shows significant temperature dependence as we have seen previously in the underdoped sample. In panel (a) we observe that the plasma frequency of the D2 mode (the hole carrier density) is reduced and that of the D1 (the electron carrier density) is slightly enhanced as we expected; the system is more electron-doped. In panel (b) we do not observe the non-monotonic and non-Fermi liquid behavior in the static scattering rate of D1 mode which we observed in the underdoped sample (see Fig. 5b). The D1 scattering rate decreases monotonically as temperature decreases. We do not see the T linear dependence which was observed in the optimally doped Ba0.6K0.4Fe2As2 by Dai et al.8 instead our data show a rapid decrease down to 200 K and then a less rapid decrease below this temperature. The different hidden temperature dependent trends might be related to different temperature dependencies in the measured DC resistivity data of two materials with different doping types: one in the inset of Fig. 2b and the other in the inset of Fig. 1 of Ref. [8]In the inset we display the D1 scattering rate as a function of T2; its temperature dependence is near quadratic, which is similar to that of near optimally electron-doped (Co- and Ni-doped) samples reported by Barisic et al.21. Here we note that the optimally electron-doped sample seems to show different hidden transport property from that of the hole-doped sample in Ba-122 material Fe-pnictide systems. We also display σdc(T) and ρ(T) in Fig. 6(c,d), respectively. In panel (d) we show the total DC resistivity (solid star symbols) to compare it with the measured DC resistivity in the inset of Fig. 2b; even though the two data sets show similar temperature dependence they also show different residual resistivities, which we do not know clearly yet.
Conclusion
We studied two different Ni-doped (or electron-doped) Ba-122 single crystal samples, BaFe2−xNixAs2 (x = 0.05: underdoped and x = 0.10: optimally doped), using an optical spectroscopic technique. The DC resistivity of our underdoped sample shows a magnetic phase transition near 80 K. We applied the so-called two-component approach9, which is also called the Drude-Lorentz analysis, to disclose their hidden transport properties. The underdoped sample shows significantly different transport properties below and above the transition temperature. Above the transition temperature the static scattering of the D1 mode (or the narrow mode) shows a quasi-linear temperature behavior which is different from that of the optimally doped sample (x = 0.10). The optimally doped sample shows near Fermi-liquid (quadratic temperature dependent) behavior in the measured temperature range. Below the magnetic transition temperature the underdoped sample shows completely different transport properties; we observed an increase linear law on lowering the temperature for the static scattering rate of the D1 Drude mode (see Fig. 5b). We also found that the magnetic phase transition influences only electron carriers of the electron-pocket on the Fermi surface; as the system enters into the ordered magnetic phase the D1 static scattering increases linearly with temperature. The holes in the hole-pocket seems not to be affected by the magnetic ordering in the system. The scattering rate of D1 mode in the optimally doped sample shows near quadratic temperature dependence, which is consistent with those of near optimally electron-doped samples reported by Barisic et al.21. However, this temperature dependent transport behavior is different from that of optimally hole-doped sample investigated by Dai et al.8. This indicates that the electron- and hole-doped samples show different hidden D1 transport properties. We believe that these new findings may help to figuring out the superconducting mechanism of relatively new high temperature superconductors, Fe-pnictides.
Methods
Samples and reflectance measurement technique
High quality single crystal BaNixFe2−xAs2 (x = 0.05 and 0.10) samples were grown using a high-temperature self-flux method22,23,24. The areas of samples are roughly 2 × 2 mm2 with a thickness ≤ 200 μm. We had to add a thin metal plate between the sample and a sample cone to support and prevent bending of the sample caused by an epoxy contraction when the temperature was reduced. The transition temperatures were determined using magnetic susceptibility and DC-transport measurements. The DC transport resistivity data of two samples are shown in insets of Fig. 1. We obtained accurate reflectance spectra of our samples at various temperatures using an in-situ metallization method25 and a continuous liquid Helium flow system. We used a commercial FTIR-type spectrometer, Bruker Vertex 80 v to take the reflectance spectra in far- and mid-infrared range (80–8000 cm−1 or 10 meV–1.0 eV).
Kramers-Kronig analysis
To get the optical constants from the measured reflectance spectra we performed a Kramers-Kronig analysis method26. To do the analysis we have to have data in a complete frequency range from zero to infinity. Practically we can have measured data only in a finite spectral range because of experimental limitations. We need to extrapolate the measured data to both directions: zero and infinity. We used the well-known Hagen-Rubens relation for the low frequency extrapolations. For the high frequency extrapolations we took advantage of existing data of similar materials (BaFe1.85Co0.15As2)27 for the higher frequencies up to 25,000 cm−1. Above the frequency up to 106 cm−1 we used R(ω) = R(ωmax)ω−DE, where R(ω) is reflectance, ωmax is the highest frequency in the measured data file and DE can be selected between 0 and 2. Above 106 cm−1, where we are in the free electron region, we used R(ω) = ω−P, where P can be selected between 2 and 426,28.
Two-component analysis: Drude-Lorentz model with two Drude modes
We applied the two-component analysis to the optical conductivity as in a published literature8. We used two Drude components (one is narrow and the other is comparatively broad) and one Lorentz component and a low-energy interband transition located near 1300 cm−1 as reported recently18 to fit the conductivity data up to 6500 cm−1. The complex dielectric function ( ) can be written in a Drude-Lorentz model as:
) can be written in a Drude-Lorentz model as:

where εH is the background dielectric function, which comes from contribution of the high frequency absorption. D1 (D2) stands for a narrow Drude component (a broad Drude component), ΩDi,p is the Drude plasma frequency,  is the (average) elastic scattering rate among free charge carriers. Ωj,p, ωj and γj are the plasma frequency, the center frequency and the width of the jth Lorentz component, respectively. The optical conductivity can be related to the dielectric function as
is the (average) elastic scattering rate among free charge carriers. Ωj,p, ωj and γj are the plasma frequency, the center frequency and the width of the jth Lorentz component, respectively. The optical conductivity can be related to the dielectric function as  .
.
Additional Information
How to cite this article: Lee, S. et al. Hidden non-Fermi liquid behavior caused by magnetic phase transition in Ni-doped Ba-122 pnictides. Sci. Rep. 5, 12156; doi: 10.1038/srep12156 (2015).
Change history
22 September 2015
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has been fixed in the paper.
References
Kamihara, Y. et al. Iron-based layered superconductor: LaOFeP. J. Am. Chem. Soc. 128, 10012 (2006).
Kamihara, Y., Watanabe, T., Hirano, M. & Hosono, H. Iron-based layered superconductor La[O1−xFx]FeAs (x = 0.05-0.12) with Tc = 26 K. J. Am. Chem. Soc. 130, 3296 (2008).
Basov, D. N. & Chubukov, A. V. Manifesto for a higher Tc . Nat. Phys. 7, 272 (2011).
Subedi, A., Zhang, L., Singh, D. J. & Du, M. H. Density functional study of FeS, FeSe and FeTe: Electronic structure, magnetism, phonons and superconductivity. Phys. Rev. B 78, 134514 (2008).
Ding, H. et al. Observation of fermi-surface-dependent nodeless superconducting gaps in Ba0.6K0.4Fe2As2 . Europhys. Lett. 83, 47001 (2008).
Wu, D. et al. Optical investigations of the normal and superconducting states reveal two electronic subsystems in iron pnictides. Phys. Rev. B 81, 100512(R) (2010).
Qazilbash, M. M. et al. Electronic correlations in the iron pnictides. Nat. Phys. 5, 647 (2009).
Dai, Y. M. et al. Hidden T-linear scattering rate in Ba0.6K0.4Fe2As2 revealed by optical spec-troscopy. Phys. Rev. Lett. 111, 117001 (2013).
Quijada, M. A. et al. Anisotropy in the ab-plane optical properties of Bi2Sr2CaCu2O8 single-domain crystals. Phys. Rev. B 60, 14917 (1999).
Puchkov, A. V., Basov, D. N. & Timusk, T. The pseudogap state in high-Tc superconductors: an infrared study. J. Phys.: Cond. Matter 8, 10049 (1996).
Hwang, J., Timusk, T. & Gu, G. D. High-transition-temperature superconductivity in the absence of the magnetic-resonance mode. Nature (London) 427, 714 (2004).
Yang, J. et al. Optical spectroscopy of superconducting Ba0.55K0.45Fe2A2: Evidence for strong coupling to low-energy bosons. Phys. Rev. Lett. 102, 187003 (2009).
Wu, D. et al. Eliashberg analysis of optical spectra reveals a strong coupling of charge carriers to spin uctuations in doped iron-pnictide BaFe2As2 superconductors. Phys. Rev. B 82, 144519 (2010).
Hwang, J., Carbotte, J. P., Min, B. H., Kwon, Y. S. & Timusk, T. Electron-boson spectral density of lifeas obtained from optical data. J. Phys. Condens. Matter 27, 055701 (2015).
Benfatto, L., Cappelluti, E., Ortenzi, L. & Boeri, L. Extended drude model and role of interband transitions in the midinfrared spectra of pnictides. Phys. Rev. B 83, 224514 (2011).
Fang, L. et al. Roles of multiband effects and electron-hole asymmetry in the superconductivity and normal-state properties of Ba(Fe1−xCox)2As2 . Phys. Rev. B 80, 140508 (2009).
Shen, B. et al. Transport properties and asymmetric scattering in Ba1−xKxFe2As2 single crystals. Phys. Rev. B 84, 184512 (2011).
Marsik, P. et al. Low-energy interband transitions in the infrared response of Ba(Fe1−xCox)2As2 . Phys. Rev. B 88, 180508 (2013).
Ito, T., Takenaka, K. & Uchida, S. Systematic deviation from T-linear behavior in the in-plane resistivity of YBa2Cu3O7−y: Evidence for dominant spin scattering. Phys. Rev. Lett. 70, 3995 (1993).
Yi, M. et al. Symmetry-breaking orbital anisotropy observed for detwinned Ba(Fe1−xCox)2As2 above the spin density wave transition. PNAS 108, 6878 (2011).
Barisic, N. et al. Electrodynamics of electron-doped iron pnictide superconductors: Normal-state properties. Phys. Rev. B 82, 054518 (2010).
Canfield, P. C. & Fisk, Z. Growth of single crystals from metallic uxes. Phil. Mag. 65, 1117 (1992).
Wang, X. F. et al. Anisotropy in the electrical resistivity and susceptibility of superconducting BaFe2As2 single crystals. Phys. Rev. Lett. 102, 117005 (2009).
Ni, N. Structural/magnetic phase transitions and superconductivity in Ba(Fe1−xTMx)2As2 (TM = Co, Ni, Cu, Co/Cu, Rh and Pd) single crystals. Ph.D. thesis, Iowa State University (2009).
Homes, C. C., Reedyk, M. A., Crandles, D. A. & Timusk, T. Technique for measuring the reectance of irregular, submillimeter-sized samples. Appl. Opt. 32, 2976 (1993).
Wooten, F. Optical Properties of Solids (Academic, New York, 1972).
Tu, J. J. et al. Optical properties of the iron arsenic superconductor BaFe1.85Co0.15As2 . Phys. Rev. B 82, 174509 (2010).
Poter, C. D. & Tanner, D. B. Datan. http://www.phys.ufl.edu/~tanner/datan.html (1985). Accessed: 25/02/2013.
Acknowledgements
J.H. is supported by the National Research Foundation of Korea (NRFK grant No. 20100008552 and NRFK Grant No. 2013R1A2A2A01067629), K.C. by the Basic Science Research Program (2012-008233) funded by the Korean Federation of Science and Technology Societies and T.P. by a NRF grant funded by the Ministry of Science, ICT and Future Planning (No. 2012R1A3A2048816).
Author information
Authors and Affiliations
Contributions
J.H. wrote the main manuscript, S.L. took the optical data and analyzed them. K.C. grew the single crystals, E.J. and S.R. contributed to the taking and analyzing of the optical data, S.S. and T.P. took the transport data. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Lee, S., Choi, KY., Jung, E. et al. Hidden non-Fermi liquid behavior caused by magnetic phase transition in Ni-doped Ba-122 pnictides. Sci Rep 5, 12156 (2015). https://doi.org/10.1038/srep12156
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep12156
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.