Abstract
Low-dimensional materials such as graphene provide an ideal platform to probe the correlation between thermal transport and lattice defects, which could be engineered at the molecular level. In this work, we perform molecular dynamics simulations and non-contact optothermal Raman measurements to study this correlation. We find that oxygen plasma treatment could reduce the thermal conductivity of graphene significantly even at extremely low defect concentration (∼83% reduction for ∼0.1% defects), which could be attributed mainly to the creation of carbonyl pair defects. Other types of defects such as hydroxyl, epoxy groups and nano-holes demonstrate much weaker effects on the reduction where the sp2 nature of graphene is better preserved. With the capability of selectively functionalizing graphene, we propose an asymmetric junction between graphene and defective graphene with a high thermal rectification ratio of ∼46%, as demonstrated by our molecular dynamics simulation results. Our findings provide fundamental insights into the physics of thermal transport in defective graphene and two-dimensional materials in general, which could help on the future design of functional applications such as optothermal and electrothermal devices.
Similar content being viewed by others
Introduction
Graphene features a superior phononic thermal conductivity κ = ∼5300 W/mK, which is attributed to both its high group velocities of acoustic phonons, v = 23.6, 15.9 m/s for LA, TA branches and long phonon mean free path lMFP = 240 nm1,2,3,4. Moreover, the two-dimensional monatomic structure of graphene allows every carbon atom to be engineered, which suggests an ideal test-bed for the study of thermal transport in solids by considering the disorder and imperfection. In the previous work, it has been reported that defects such as vacancies, isotopic doping and chemically functional groups at low concentration act as localized phonon scatters, which reduce the thermal conductivity5,6,7. Experimental studies show that ∼1% 13C isotope atoms reduce κ by ∼25%7. Theoretical and computational studies suggest that vacancy-like and sp3-type defects can reduce the thermal conductivity up to tens of times at a certain areal coverage8,9,10. As the concentration further increases, the material then becomes more like an amorphous solid, or phonon glass, with a reduced mean free path for the heat carrier on the order of a few interatomic spacings11 and the limit of minimum of thermal conductivity is reached. In this situation, heat is conducted via hopping between localized atomic vibrations12,13,14. Graphene oxide with oxygen-rich functional groups, which can be tuned upon chemical treatments, pushes for this amorphous limit of thermal conduction at high defect concentration4,10,15,16. However, the knowledge about thermal transport between the crystal and amorphous limits is still very limited. To bridge the gap between graphene and its amorphous counterparts, it is crucial to understand the mechanism of heat transport in defective graphene (DG), e.g. how is the reduction in conductivity related to the type and concentration of defects? How could the defect engineering of heat transport be implemented for functional devices with the capability of modulating heat flow? Answering these questions could further enable relevant technical applications.
In this work, we study the thermal conduction in graphene with the presence of a broad spectrum of defects by performing molecular dynamics (MD) simulations. We find that carbonyl pairs and vacancies lead to more significant reduction in the conductivity than hydroxyl, epoxy groups and nano-holes. This conclusion is confirmed by our non-contact opto-thermal Raman measurements, where defects are introduced through oxygen plasma irradiation and a huge reduction of κ = ∼83% is characterized at an extremely low defect concentration of ∼0.1%. We then explore the possibility to manipulate 2D heat conduction and flow by patterning defects into grapehene by performing MD simulations and demonstrate a remarkable thermal rectification ratio of ∼46% through a junction between pristine and DG with carbonyl pairs.
Results
The effectiveness of defects in reducing the thermal conductivity of graphene
Defects could be created in graphene by exotic treatments such as oxygen plasma irradiation or chemical functionalization. Typical defects that have been characterized in oxidized graphene include hydroxyl, epoxy groups, carbonyl pairs, vacancies, as well as nanoholes17,18,19,20,21. Here, to explore their effects in modifying thermal transport behaviors in graphene, we firstly adopt MD simulations to calculate the in-plane thermal conductivities of graphene containing four different types of defects (Fig. 1a), which will be compared with our opto-thermal Raman measurements. The thermal conductivities are calculated using the Green-Kubo formula, which relate the thermal conductivity of materials with the auto-correlation function of heat flux operators (see Methods for details). In general, our simulation results in Fig. 1b demonstrate that these defects can be categorized into two sub-groups as proposed in the Lerf-Klinowski model for graphene oxide22. The hydroxyl and epoxy groups do not break the underlying hexagonal lattice and preserve relatively well the lattice symmetry of carbon atoms and integrity, thus disturb the thermal transport weakly. In contrast, the presence of carbonyl pairs (CP) and vacancies reduce the thermal conductivity of graphene significantly as they break the in-plane network of sp2 carbon bonds.
(a) Typical defect types characterized in DG that include hydroxyl, epoxy groups, carbonyl pairs and mono-vacancies. Isolated defects of these types and their clusters (except for the carbonyl pair clusters that are unstable) are both considered in the simulations. (b) Thermal conductivities of DG (κDG) measured in the unit of κG for the pristine graphene sheet with various types of defects. The ones with mono-vacancies and carbonyl pairs are singled out in the inset, along with the experiment results. (c) The reduction factor r calculated for various types of defects with the concentration of 0.1% measured in the simulations and experiments following the effective medium theory.
To quantify the concentration dependence, we fit our MD simulation results empirically by using the effective medium theory (EMT)9, where the thermal conductivity of DG κDG is related to the thermal conductivity of defects κd, pristine graphene κG and the areal defect concentration f as:

By rewriting Eq. 1 into κDG/κG = 1/(1 + rf), we can define a reduction factor r = κG/κd −1 that quantifies the strength of reduction in thermal conductivity, or equivalently an effective size of the defect a = lG − ld = rlG/(r + 1), where lG and ld are the mean free paths by considering the phonon-phonon scattering processes in pristine graphene and defect scattering in DG, respectively. The results summarized in Fig. 1c indicate that strong perturbation from the carbonyl pairs and mono-vacancies reduce κDG significantly (with a one-order higher values of r), in stark contrast to the much weaker effects of hydroxyl and epoxy groups that are uniformly distributed in the samples. We also find that once the hydroxyl and epoxy groups clustered into groups, the reduction in κ is almost unchanged. In contrast, the scattering of mono-vacancies is significantly weakened by their coalescence into nano-holes, where scattering occurs at the edges of nanoholes instead of discrete point defects. These results provide an argument that the defects breaking in-plane sp2 bonds are more effective in reducing the thermal conductivity of graphene.
Thermal conductivity in a solid can in general be expressed in the form of kinetic theory, which is expressed as:

where c is the specific heat, v, l = vτ, τ are the average phonon group velocity, mean free path, relaxation time and d is the dimension of problem. The scattering sources arising from defects in graphene include mass difference, local strain and boundaries. If we assume that the relaxation times for all these scattering processes are independent, the phonon relaxation or scattering time τ can be calculated by the Matthiessen’s rule τ−1 = Σiτi−1, where the relaxation time τi characterize all scattering mechanisms including the phonon-phonon scattering and defect scattering23. The previous work suggests that the absorption of oxygen groups does not significantly change the group velocities and thus the thermal conductivity is mainly reduced by the shortening of mean free path in the regime of defect scattering4. However, defects that break the in-plane sp2 lattice integrity not only introduce stronger scattering centers for propagating phonons, but also reduce the group velocities by softening the lattice9. This contrast explains why carbonyl pairs and vacancies lead to higher reduction of the thermal conductivity in graphene.
Thermal conductivity of oxygen-plasma-treated graphene
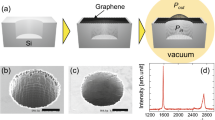
To verify our simulation results, the thermal conductivity of oxygen-plasma-treated graphene was measured by using a non-contact optothermal Raman technique. Oxygen plasma irradiation creates oxygen-containing functional groups and a certain amount of vacancies in graphene24. The basic setup of thermal conductivity measurement is illustrated in Fig. 2a1,25. The Raman spectrum of pristine CVD monolayer graphene26 presents an intense peak at ∼1580 cm−1, namely the G peak27. Raman mapping integrated from G peak intensity confirms the graphene film across the 3.0 μm hole is homogenous and continuous without any visible wrinkles or broken holes, as shown in the inset of Fig. 2a. Plasma-treated graphene possesses additional D and D’ peaks (Fig. 2b), which originate from the double resonant Raman process with the presence of defects28. The intensity ratio between the D and G peaks, ID/IG, is commonly used to estimate the defect concentration29. It can be clearly seen that the ID/IG increases with the plasma power density (Stage 1) and decreases after a certain point (Stage 2). Here, Stage 1 indicates the structural transition from high quality graphene to defective graphene and Stage 2 refers to the transition from defective graphene to amorphous carbon30. To estimate the density of defects, the inter-defect distance LD follows the relation of Eq. 3 in Stage 129,30,31:
(a) Schematic of the experiment, where graphene film is covered on the 50 nm-gold-coated silicon nitride membrane with a 3.0 μm diameter hole. Inset is Raman mapping of the intensities of G peak, scale bar is 1 μm. (b) Raman spectra of monolayer defective graphene after oxygen plasma irradiation. The LD stands for inter-defect distance in graphene. (c) Raman spectra of oxygen plasma treated graphene under different absorbed laser power. (d) Thermal conductivities of oxygen plasma treated graphene with different defect concentration. The inset is the G peak frequency shift as a function of the absorbed laser power.

where CA ∼4.2 is a parameter given by previous experiment results29. rS ∼1 nm determines the radius of the structurally disordered area and rA ∼3.1 nm is defined as the radius of the area where the D peak scattering takes place29. In our case, the ID/IG of oxygen plasma treated sample is about ∼0.4, ∼1.8, ∼2.3, ∼3.0 and ∼2.2 (Stage 2) when the absorbed laser power is 0.1 mW, corresponding to an average defect distance of ∼17.7, ∼7.5, ∼6.3, ∼5.1 and ∼2 nm (based on Ref. 31), respectively. Accordingly, the concentration of oxygen-containing defects is ∼0.1, ∼0.4, ∼0.6,∼1.0 and ∼6.6‰.
In our opto-thermal Raman experiments, the increase in local temperature at the laser spot causes a redshift of Raman peaks (Fig. 2c)32,33, because of the thermal expansion and 3- and 4-phonon scattering processes27. Therefore, local temperature at the measured spot can be plotted as the function of absorbed laser power of graphene and adopted to extract the thermal conductivity κ25. Typical results for G frequency shift as a function of the absorbed laser power for samples with different oxygen defect concentration are plotted in the inset of Fig. 2d. Larger frequency shift indicates a higher temperature at the laser spot and hence a lower thermal conductivity of the sample. It can be clearly seen that the temperature of samples with higher defect concentrations rises much faster compared to those with lower defect concentrations under the same laser power. According to the thermal transport model in Cai et al.’s work25, the temperature distribution in suspended graphene T(r) is:

where T1 is the temperature at the boundary of suspended graphene, i.e. the part in contact with the gold film, which is assumed to keep at room temperature. Q is the absorbed laser power in total and R = 1.5 μm is the radius of suspended graphene. t = ∼0.34 nm is thickness of graphene and r is radial position from the laser beam’s center. Ei(x) is exponential integral and r0 = 0.15 μm is the radius of measured laser beam. In this work, the thermal coefficient for G peak of 4.05 ± 0.2 × 10−2 cm−1/K is adopted for the thermal conductivity data fitting25 and we find that the thermal coefficients of DG are similar to that of pristine graphene and almost independent on the defect concentration. As shown in Fig. 2d, the pristine graphene has a thermal conductivity of 3.50 ± 0.32 × 103 W/mK at 350 K, which is comparable to previously reported values1,7,25. On the other hand, the thermal conductivities of oxygen-plasma-treated graphene drop to 2.06 ± 0.27, 1.48 ± 0.06, 0.93 ± 0.09, 0.59 ± 0.05 and 0.16 ± 0.06 × 103 W/mK with the increase of defect concentration. The calculated reduction factor r from experimental results is comparable to the values predicted for lattice vacancy and carbonyl pair by our MD simulations, as shown in Fig. 1b,c. It is then suggested that the above two types of defects (the vacancy and carbonyl pair) could be the main contributors to the great reduction of thermal conductivity in oxygen plasma treated graphene.
It is interesting to find that in experiments, with the defect concentration of 0.1%, the thermal conductivity of graphene has dropped by ∼83%. While as suggested by our MD simulation results, such a reduction requires for a much higher defect concentration when the defect type being hydroxyl, epoxy groups, as well as nano-holes34. This reduction is also more significant compared to those observed in experiments by considering the effect of substrates35, isotope doping7, organic residues36 and metal nanoparticles attachment37, which reduce κ much more gently. It should be mentioned that the measured thermal conductivity of graphene could be differed by experimental details, such as the effects of absorptance on graphene, the temperature coefficient of G peak1,7,25,38 and techniques of measurement36,37. However, the reduction factor r should be a reliable measurement since all graphene samples are measured under same condition and the influence of absorptance and temperature coefficient is minimized via the calculation of κDG/κG.
Self-repairing of vacancy-like defects
In order to verify whether the vacancy-like defects play an important role in thermal conductivity reduction in our experiment, we study the sample treated by Ar + plasma, which is believed to introduce vacancy-like defects in graphene only. Previous work has demonstrated that the intensity ratio between the Raman D and D’ peaks (ID/ID’) can be used to distinguish the nature of defects in graphene, e.g. ID/ID’ is much higher for sp3-like defects (∼13) than vacancy-like defects (∼7)39. Figure 3a shows Raman spectra of Ar + - and oxygen-plasma-treated graphene and ID/ID’ for these two samples (∼7.3 and ∼13.0) agree quite well with the above signature. With the increase of absorbed laser power, the ID/IG for Ar+-plasma-treated-graphene dramatically decreases, as shown in Fig. 3b, indicating the decrease in defect concentration. In comparison, we plot the ID/IG of Ar+- and oxygen-plasma-treated graphene as a function of the absorbed laser power in Fig. 3c. When the absorbed laser power increases to ∼0.2 mW, the ID/IG of oxygen-plasma-treated-graphene dropped by ∼25% (from ∼4 to ∼3) only, while that of Ar+-plasma-treated-graphene dropped by ∼75% (from ∼4 to ∼1).
(a) Raman spectra of Ar + and oxygen plasma treated graphene. (b) Raman spectra of Ar + plasma treated sample under different absorbed laser power. (c) ID/IG of Ar + and oxygen plasma treated graphene as a function of absorbed laser power. (d) The G peak frequency shift of Ar + and oxygen plasma treated graphene as a function of the absorbed laser power.
The above phenomena could be related to the self-repairing of vacancy-like defects. Previous work has shown that the vacancy-like defects tend to self-heal while being annealed in vacuum, which is attributed to the mechanisms of mobile carbon adatoms recombination with vacancies40 and the reconstruction of graphene lattice by forming non-hexagonal rings as topological defects41. For example, the mono-vacancy could reconstruct to form a five-membered and a nine-membered ring, while a di-vacancy could dissociate into two pentagons and one octagon. The self-repairing of vacancy-like defects could more complicated for laser heating in air (as in our experiments) compared to vacuum annealing40,41, e.g. nanoholes could be formed. Further work is required to elucidate the detailed atomic structures and reconstruction regimes.
The frequency shifts of Ar + - and oxygen-plasma-treated graphene with the increase in the absorbed laser power are plotted in Fig. 3d. According to the simulation results in Fig. 1c, the vacancy in lattice is an effective phonon scatterer23 and the frequency shift of Ar + -plasma-treated graphene should be larger than the oxygen-plasma-treated one. However, Fig. 3d suggest the opposite result – the average thermal conductivity of Ar + -plasma-treated graphene is ∼0.77 × 103 W/mK, that is higher than the value of oxygen-plasma-treated graphene (∼0.55 × 103 W/mK). Based on the above analysis, vacancy-like defects might not be the major source for the huge thermal conductivity reduction in our oxygen-plasma-treated graphene because of its strong self-repairing effect at high temperature. We suggest that oxygen groups leading to significant modification of the in-plane carbon-bonding network, such as the carbonyl pairs, are the main source of thermal conductivity reduction.
Thermal rectifier using patterned graphene
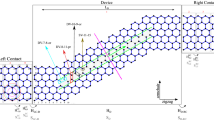
As we have discussed, thermal transport in graphene can be controllably tuned by defect engineering, which offers a promising route to design functional devices with the capability of modulating the heat flow, e.g. the design of thermal rectification. Thermal rectifier is a two terminal device with a thermal conductance depending on the direction of heat flow, which has broad applications for heat control/management in the future42. Most experimentally reported thermal rectifiers require asymmetric shape43, mass density mismatch41 or interface between dissimilar materials44, which result in the sophisticated fabrication process and strongly limit the system stability. This aporia might be conquered by using functionalized or defective graphene45. Here, we propose an asymmetric junction by selectively introducing different types of defects or functional groups on one side and forming a graphene-defective graphene junction (G-DG junction). Our MD simulations show that for oxygen plasma treated graphene with carbonyl pair defects, the thermal rectification factor defined by Rth = (κG-DG – κDG-G)/κDG-G could reach 46% at defect concentration f = 1% (Fig. 4), where κG-DG and κDG-G are the effective thermal conductivities when heat flux is directed from G to DG and the opposite. This value of Rth converges with f after the peak is reached and is significantly higher than the measured ratio of ∼7% obtained by coating boron-nitride nanotubes asymmetrically with metal particles and the predicted ratio of ∼10% for asymmetrical graphene nanoribbons from MD simulations42,46. Similarly, the G-DG junction with other types of defects also demonstrate high rectification factors that is ∼27% for hydrogenated graphene and ∼36% for hydroxyl group functionalized graphene. However, the peak values are reached at a much higher defect concentration, due to the fact that their effects in modifying the thermal conduction in graphene are much weaker, which makes them less effective in practical applications compared to the carbonyl pair defects. From the results in Fig. 4b, we can see that the rectification ratio of CP features a significant drop at the defect concentration of 5%, which is different from other types of defects. This discrepancy may be attribute to the following fact. As the defect concentration approaches 5%, the CP defects that break C-C bonds and perturb the graphene lattice strongly could lead to lattice instability when they are located closely or overlap, which leads to the observed drop of rectification ratio. Previous works on G-DG junction as thermal rectifiers also consider vacancies, silicon substitutions, Stone-Wales defects47 or hydrogenation48 as manipulating means, while these types of defects are either not thermally stable or difficult to create. The origin of strong rectifying process of G-DG junction could be attributed to the fact that the vibrational density of states in graphene and DG is asymmetric43 and the low-frequency modes are more dominating in defective graphene due to the presence of defects and decrease in the stiffness4,9,49. As a result, the high-frequency vibrational modes carrying heat in pristine can propagate into DG more efficiently than their excitation by the energy flow from modes with lower frequencies and thus the thermal conductivity from pristine graphene to the DG is higher than the reversed direction. It should be noted that even though the rectification factor is very high, this G-DG junction may still not be an ideal thermal rectifier, as heat flux in the low heat flux direction is not zero. Anyhow, this work sheds light on the single component system, which avoids the issue of interface thermal resistance and sophisticated fabrication process and may open up its important applications in thermal management.
(a, b) Thermal rectification in a graphene-defective graphene junctions, where graphene is selectively functionalized by hydrogen, hydroxyl and carbonyl pairs with various concentration. The asymmetric in graphene and functionalized graphene induce difference in the thermal conductivity when the temperature gradient applied to the junctions is reversed (a) which yields a concentration-dependent rectification factor up to 46% (b).
Discussion
We have demonstrated using atomistic simulations and non-contact optothermal Raman technique that the carbonyl pairs in oxygen-plasma-treated graphene could lead to a huge reduction of thermal conductivity of graphene, with ∼83% at defect coverage of only ∼0.1% compared to pristine one. Such a great reduction could not be explained by commonly considered defects in oxidized graphene with oxygen-rich groups such as the hydroxyl and epoxy groups. Moreover, we have also shown that, vacancy like defects, although predicted to greatly reduce the thermal conductivity, might not be the major contributor either because the strong self-repairing effect. The significant reduction of the thermal conductivity could be attributed mainly to the creation of carbonyl pair defects. With the ability to control the selective functionalization of graphene (e.g. introducing carbonyl pairs by oxygen plasma), we propose a thermal rectifier with high rectification ratio ∼46%, at only 1% defect concentration. Our results could also help on the better understanding of mechanism of thermal conductivity reduction in graphene-based materials and also provide an efficient way to tune the local thermal conductivity for the future design of graphene based devices, e.g. optothermal, electrothermal devices.
Methods
Experimental Section
Graphene synthesis and treatment
Monolayer graphene was synthesized on a copper foil (25 μm) by means of chemical vapor deposition (CVD) in a vacuum chamber, with a gas mixture of methane and hydrogen (60 and 90 sccm, respectively, total pressure of ∼300 Pa) at 1045 °C for 10 min26. A 3 × 3 array of 3.0 μm diameter holes was pre-fabricated in the 50 nm-gold-coated silicon nitride membrane using focused ion beam. The graphene film was transferred onto the membrane to form suspended structure. Defective graphene samples were fabricated via oxygen or Ar + plasma treatment (commercial 13.56 MHz RF source). The defect concentration can be modulated by fixing the plasma power (15 W, 5 s for oxygen plasma and 40 W, 60 s for Ar + plasma) and changing the gas pressure (from 5 Pa to 40 Pa, to change the plasma density).
Opto-thermal Raman measurement
Raman spectra were taken by a Witec alpha 300 R confocal Raman system with an excitation laser of 532 nm (2.33 eV). A 100x objective lens with numerical aperture of 0.9 is used and the spot size of the laser is estimated to be ∼300 nm by scanning across a smooth cleaved edge of Au25. The Raman mapping of graphene is acquired with the step size of 100 nm and the result confirms that graphene are free from wrinkles or broken holes1,25,50. As informed from Ref. 1, the heat wave generated over the suspended portion of graphene on the 3.0 μm diameter hole continues to propagate all the way out. The variation in the heating power Q on the sample surface leads to the shift in the G peak position, which corresponds to change in the temperature at laser spot.
Molecular Dynamics Simulations
Atomic structures
The molecular structure of DG consists of hydroxyl, epoxy and carbonyl groups on the basal plane, as well as defective sites and open edges22. In this work, we construct models of DG containing hydroxyl, epoxy groups, as well as carbonyl pairs and mono-vacancies17. Their concentration f is defined as nD/nC where nD is number of the defective atom site and nC is the number of carbon atoms in the pristine graphene lattice. The distribution of defects in DG is sampled randomly.
Molecular dynamics simulations
Classical MD simulations are performed using the large-scale atomic/molecular massively parallel simulator (LAMMPS)51. The all-atom optimized potential for liquid simulations (OPLS-AA) is used for DG, which can capture essential many-body terms in inter-atomic interactions, including bond stretching, bond angle bending, van der Waals and electrostatic interactions52. This force field was successfully applied in predicting thermal transport in graphene or carbon nanotubes53,54,55,56. Periodic boundary conditions are applied to a 9.82 × 8.52 nm2 supercell of graphene and DG, which are verified to capture the thermal conduction in G and DG structures57,58. The periodic box and atomic structures are relaxed in the simulations before investigating thermal transport.
Calculation of thermal conductivities
To compute the thermal conductivity κ of pristine and defective graphene from MD simulations, we use the Green-Kubo method based on the linear response theory59, which applies for systems in thermal equilibrium where heat flux fluctuates around zero. κ could thus be expressed as an integration of the heat flux operator multiplied by a prefactor

where T is the temperature of system, kB is the Boltzmann constant and V is the system volume that is defined here as the area of graphene or DG multiplied by a nominal thickness (the inter layer distance of graphite, 3.4 Å). The upper limit of time integration τc needs to be long enough so the current-current correlation function decays to zero, Jx and Jy are the heat current operators in the x and y directions and the angular bracket represents the ensemble average, namely the heat flux autocorrelation function (HFACF). The heat flux J of the system is computed from the expression J = (Σieivi – ΣiSivi)/V, where ei, vi and Si are the total energy, velocity vector and stress tensor of each atom i, respectively. We first integrate HFACF with an integration time τ following Eq. 5, then obtained the relation between κ and τ. The decorrelation time for the heat flux is typically on the scale 100 ps for our models and thus converged results for κ could be extracted when τ > τc in the simulations. The advantage of Green-Kubo method, compared to the non-equilibrium molecular dynamics (NEMD) simulations with thermal gradient built up across the material that is used in our investigation on the non-equilibrium processes, is that it does not need to perturb the simulated system out of equilibrium, where nonlinearity arises60. Moreover, the Green-Kubo approaches demonstrates a weaker size dependence60,61. Due to the hexagonal symmetry of graphene lattice and random distribution of defects, the thermal conductivity of is isotropic. We thus evaluate κ as the mean value of κxx and κyy that may differ in the finite system under simulation though, where the maximum difference between κxx and κyy in our simulations is less than 0.1κ.
In the MD simulations, the atomic structures of graphene or DG are firstly equilibrated at the same temperature as the experimental condition (T = 350 K, where the quantum nuclear effect is weak) under a Nosé-Hoover thermostat for 200 ps, in which the time step is 0.1 fs. The stress is released by coupling with a barostat. The structure is further equilibrated in a NVE ensemble for 50 ps before the thermal conductivity is calculated. In the equilibrium Green-Kubo calculations, the system is simulated in a microcanonical ensemble as well. The atomic positions and velocities are collected during the simulations to evaluate the heat flux and its autocorrelation functions. The thermal conductivity is finally obtained by following the Green-Kubo formula. The results are calculated by averaging over five different runs for the same DG sample at a certain defect concentration.
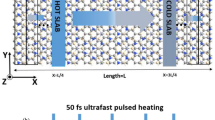
Simulations for the thermal rectification
In simulating the thermal rectification in a G-DG junction, we construct a graphene strip with length of 19.6 nm and width of 5.2 nm with in-plane periodic boundary conditions applied and half of the strip along the length direction is functionalized by uniformly distributed hydrogen, hydroxyl groups or carbonyl pairs with various concentrations. The thermal conductivity is calculated by following Müller-Plathe’s NEMD approach in a NVE ensemble62. The strip is partitioned axially into slabs for temperature recording and control, after heat flux J is induced by exchanging the momentum between the ‘hottest’ atom in sink slab and the ‘coldest’ atom in the source slab. The effective thermal conductivity in both directions of the junction is calculated by following the Fourier’s law63

The cross-sectional area A is calculated by considering the thickness of graphene and DG as 3.4 Å. We assume that the temperature gradient dT/dx is ΔT/d, where ΔT and d are the temperature difference and distance between heat source and heat sink, respectively.
Additional Information
How to cite this article: Zhao, W. et al. Defect-Engineered Heat Transport in Graphene: A Route to High Efficient Thermal Rectification. Sci. Rep. 5, 11962; doi: 10.1038/srep11962 (2015).
References
Balandin, A. A. et al. Superior thermal conductivity of single-layer graphene. Nano Lett. 8, 902–907 (2008).
Klemens, P. G. & Pedraza, D. F. Thermal conductivity of graphite in the basal plane. Carbon 32, 735–741 (1994).
Ghosh, S. et al. Extremely high thermal conductivity of graphene: Prospects for thermal management applications in nanoelectronic circuits. Appl. Phys. Lett. 92, 151911 (2008).
Mu, X. et al. Thermal transport in graphene oxide--from ballistic extreme to amorphous limit. Sci. Rep. 4, 3909 (2014).
Yang, P. et al. Numerical investigation on thermal conductivity and thermal rectification in graphene through nitrogen-doping engineering. Appl. Phys. A 112, 759–765 (2013).
Bagri, A., Kim, S. P., Ruoff, R. S. & Shenoy, V. B. Thermal transport across twin grain boundaries in polycrystalline graphene from nonequilibrium molecular dynamics simulations. Nano Lett. 11, 3917–3921 (2011).
Chen, S. et al. Thermal conductivity of isotopically modified graphene. Nat. Mater. 11, 203–207 (2012).
Sreeprasad, T. S. & Berry, V. How do the electrical properties of graphene change with its functionalization? Small 9, 341–350 (2013).
Hao, F., Fang, D. & Xu, Z. Mechanical and thermal transport properties of graphene with defects. Appl. Phys. Lett. 99, 041901 (2011).
Kim, J. Y., Lee, J. H. & Grossman, J. C. Thermal transport in functionalized graphene Acsnano 6, 9050–9057 (2012).
Holland, M. G. Analysis of lattice thermal conductivity. Phys. Rev. 132, 2461 (1963).
Cahill, D., Watson, S. & Pohl, R. O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 46, 6131 (1992).
Trushin, M. & Schliemann, J. Minimum Electrical and Thermal Conductivity of Graphene: A Quasiclassical Approach. Phys. Rev. Lett. 99, 216602 (2007).
Kittel, C. Interpretation of the thermal conductivity of glasses. Phys. Rev. 75, 972 (1949).
Zhang, H., Fonseca, A. F. & Cho, K. Tailoring Thermal Transport Property of Graphene through Oxygen Functionalization. J Phys. Chem. C 118, 1436–1442 (2014).
Lin, S. & Buehler, M. J. Thermal Transport in Monolayer Graphene Oxide: Atomistic Insights into Phonon Engineering through Surface Chemistry. Carbon 77, 351–359 (2014).
Zhou, S. & Bongiorno, A. Origin of the chemical and kinetic stability of graphene oxide. Sci. Rep. 3, 2484 (2013).
Li, Z. et al. How graphene is cut upon oxidation? J. Am. Chem. Soc. 131, 6320–6321 (2009).
Bagri, A. et al. Structural evolution during the reduction of chemically derived graphene oxide. Nat. Chem. 2, 581–587 (2010).
Mao, S., Pu, H. & Chen, J. Graphene oxide and its reduction: modeling and experimental progress. RSC Adv. 2, 2643–2662 (2012).
Pan, D., Zhang, J., Li, Z. & Wu, M. Hydrothermal Route for Cutting Graphene Sheets into Blue-Luminescent Graphene Quantum Dots. Adv. Mater. 22, 734–738 (2010).
Lerf, A., He, H. Y., Forster, M. & Klinowski, J. Structure of graphite oxide revisited. J Phys. Chem. B 102, 4477–4482 (1998).
Onn, D., Witek, A., Qiu, Y., Anthony, T. & Banholzer, W. Some aspects of the thermal conductivity of isotopically enriched diamond single crystals. Phys. Rev. Lett. 68, 2806–2809 (1992).
Zandiatashbar, A. et al. Effect of defects on the intrinsic strength and stiffness of graphene. Nat. Commun. 5, 3186 (2014).
Cai, W. et al. Thermal transport in suspended and supported monolayer graphene grown by chemical vapor deposition. Nano Lett. 10, 1645–1651 (2010).
Li, X. et al. Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 324, 1312–1314 (2009).
Ferrari, A. C. & Basko, D. M. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Nanotech. 8, 235–246 (2013).
Chen, J. et al. Defect Scattering in Graphene. Phys. Rev. Lett. 102, 236805 (2009).
Eckmann, A. et al. Raman study on defective graphene: Effect of the excitation energy, type and amount of defects. Phys. Rev. B 88, 035426 (2013).
Lucchese, M. M. et al. Quantifying ion-induced defects and Raman relaxation length in graphene. Carbon 48, 1592–1597 (2010).
Cancado, L. G. et al. Quantifying defects in graphene via Raman spectroscopy at different excitation energies. Nano Lett. 11, 3190–3196 (2011).
Calizo, I. et al. Variable temperature Raman microscopy as a nanometrology tool for graphene layers and graphene-based devices. Appl. Phys. Lett. 91, 071913 (2007).
Calizo, I. et al. Temperature dependence of the Raman spectra of graphene and graphene multilayers. Nano Lett. 7, 2645–2649 (2007).
Erickson, K. et al. Determination of the local chemical structure of graphene oxide and reduced graphene oxide. Adv. Mater. 22, 4467–4472 (2010).
Seol, J. H. et al. Two-dimensional phonon transport in supported graphene. Science 328, 213–216 (2010).
Pettes, M. T., Jo, I., Yao, Z. & Shi, L. Influence of polymeric residue on the thermal conductivity of suspended bilayer graphene. Nano Lett. 11, 1195–1200 (2011).
Wang, J. et al. Suppressing thermal conductivity of suspended tri-layer graphene by gold deposition. Adv. Mater. 25, 6884–6888 (2013).
Lee, J. U. et al. Thermal conductivity of suspended pristine graphene measured by Raman spectroscopy. Phys. Rev. B 83, 081419 (2011).
Eckmann, A. et al. Probing the nature of defects in graphene by Raman spectroscopy. Nano Lett. 12, 3925–3930 (2012).
Chen, J. et al. Self healing of defected graphene. Appl. Phys. Lett. 102, 103107 (2013).
Banhart, F., Kotakoski, J. & Krasheninnikov, A. V. Structural Defects in Graphene. Acsnano 5, 26–41 (2011).
Chang, C. W., Okawa, D., Majumdar, A. & Zettl, A. Solid-state thermal rectifier. Science 314, 1121–1124 (2006).
Tian, H. et al. A novel solid-state thermal rectifier based on reduced graphene oxide. Sci. Rep. 2, 523 (2012).
Hu, M., Goicochea, J. V., Michel, B. & Poulikakos, D. Thermal rectification at water/functionalized silica interfaces. Appl. Phys. Lett. 95, 151903 (2009).
Hu, J., Ruan, X. & Chen, Y. P. Thermal conductivity and thermal rectification in graphene nanoribbons: a molecular dynamics study. Nano Lett. 9, 2730–2735 (2009).
Wang, Y. et al. Phonon Lateral Confinement Enables Thermal Rectification in Asymmetric Single-Material Nanostructures. Nano lett. 14, 592–596 (2014).
Wang, Y., Chen, S. & Ruan, X. Tunable thermal rectification in graphene nanoribbons through defect engineering: A molecular dynamics study. Appl. Phys. Lett. 100, 163101 (2012).
Rajabpour, A., Allaei, S. V. & Kowsary, F. Interface thermal resistance and thermal rectification in hybrid graphene-graphane nanoribbons: a nonequilibrium molecular dynamics study. Appl. Phys. Lett. 99, 051917 (2011).
Chien, S. K. & Yang, Y. T. Influence of hydrogen functionalization on thermal conductivity of graphene: Nonequilibrium molecular dynamics simulations. Appl. Phys. Lett. 98, 033107 (2011).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 117, 1–16 (1995).
Chen, S. et al. Thermal conductivity measurements of suspended graphene with and without wrinkles by micro-Raman mapping. Nanotech. 23, 365701 (2012).
Shih, C.-J. et al. Understanding the pH-dependent behavior of graphene oxide aqueous solutions: a comparative experimental and molecular dynamics simulation study. Langmuir 28, 235–241 (2011).
Mortazavi, B. et al. Combined molecular dynamics-finite element multiscale modeling of thermal conduction in graphene epoxy nanocomposites. Carbon 60, 356–365 (2013).
Huxtable, S. T. et al. Interfacial heat flow in carbon nanotube suspensions. Nat. Mater. 2, 731–734 (2003).
Nika, D. L. et al. Lattice thermal conductivity of graphene flakes: Comparison with bulk graphite. Appl. Phys. Lett. 94, 203103 (2009).
Nika, D. L. et al. Phonon thermal conduction in graphene: Role of Umklapp and edge roughness scattering. Phys. Rev. B 79, 155413 (2009).
Zhang, H., Lee, G. & Cho K. Thermal transport in graphene and effects of vacancy defects. Phys. Rev. B 84, 115460 (2011).
Hao, F., Fang, D. & Xu, Z. Mechanical and thermal transport properties of graphene with defects. Appl. Phys. Lett. 99 041901 (2011).
Wang, Y., Song, Z. & Xu, Z. Characterizing phonon thermal conduction in polycrystalline graphene. J. Mater. Res. 29, 362–372 (2014).
Schelling, P. K., Phillpot, S. R. & Keblinski, P. Comparison of atomic-level simulation methods for computing thermal conductivity. Phys. Rev. B 65, 144306 (2002).
Sellan, D. P. et al. Size effects in molecular dynamics thermal conductivity predictions. Phys. Rev. B 81, 214305 (2010).
Müller-Plathe, F. A. simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. chem. Phys. 106, 6082–6085 (1997).
Xu, Z. & Buehler, M. J. Strain controlled thermomutability of single-walled carbon nanotubes. Nanotechnol. 20, 185701 (2009).
Acknowledgements
This work was supported by NSFC (61376104, 61422503 and 11222217), National Basic Research Program of China (2011CB707605), Research Fund for the Doctoral Program of Higher Education of China (No. 20110092120032), the open research fund of Key Laboratory of MEMS of Ministry of Education, Southeast University.
Author information
Authors and Affiliations
Contributions
Z.N., Z.X. and Y.C. conceived and supervised the project. W.Z., Z.W., W.W. and Z.L. performed experiments and data analysis. Y.W. and Z.X. performed MD calculations. K.B. and J.Y. contributed to data analysis. W.Z., Y.W., Z.N. and Z.X. co-wrote the paper. All authors discussed the results and commented on the manuscript. Correspondence and requests for materials should be addressed to Z.N. or Y.C. for general aspects of the paper and to Z.X. for DFT calculations.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhao, W., Wang, Y., Wu, Z. et al. Defect-Engineered Heat Transport in Graphene: A Route to High Efficient Thermal Rectification. Sci Rep 5, 11962 (2015). https://doi.org/10.1038/srep11962
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep11962
This article is cited by
-
Simultaneous optimization of phononic and electronic transport in two-dimensional Bi2O2Se by defect engineering
Science China Information Sciences (2023)
-
A review of the mechanical, thermal and tribological properties of graphene reinforced polymer nanocomposites: a molecular dynamics simulations methods
Polymer Bulletin (2023)
-
Spatially mapping thermal transport in graphene by an opto-thermal method
npj 2D Materials and Applications (2022)
-
Graphene-based SiC Van der Waals heterostructures: nonequilibrium molecular dynamics simulation study
Journal of Molecular Modeling (2022)
-
Tunable thermal conductivity of single layer MoS2 nanoribbons: an equilibrium molecular dynamics study
Journal of Computational Electronics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.