Abstract
The ease of travelling between cities has contributed much to globalization. Yet, it poses a threat on epidemic outbreaks. It is of great importance for network science and health control to understand the impact of frequent journeys on epidemics. We stress that a new framework of modelling that takes a traveller’s viewpoint is needed. Such integrated travel network (ITN) model should incorporate the diversity among links as dictated by the distances between cities and different speeds of different modes of transportation, diversity among nodes as dictated by the population and the ease of travelling due to infrastructures and economic development of a city and round-trip journeys to targeted destinations via the paths of shortest travel times typical of human journeys. An example is constructed for 116 cities in China with populations over one million that are connected by high-speed train services and highways. Epidemic spread on the constructed network is studied. It is revealed both numerically and theoretically that the traveling speed and frequency are important factors of epidemic spreading. Depending on the infection rate, increasing the traveling speed would result in either an enhanced or suppressed epidemic, while increasing the traveling frequency enhances the epidemic spreading.
Similar content being viewed by others
Introduction
Controlling an epidemic, e.g. severe acute respiratory syndrome (SARS), H1N1 swine influenza and Ebola, in the midst of frequent movements of infected persons via cars, trains and aeroplanes poses a challenging problem. In network science, much effort and progress has been made on understanding epidemics in single-layered networks1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 and multi-layered networks21,22,23,24,25,26,27,28. In single-layered static networks with an immobile agent at each node, for example, no finite epidemic threshold exists for scale-free (SF) networks and a tiny initial infection eventually spreads11. A delicate balance between the number of high degree nodes and the topological distance between them29 is shown to be crucial. The same result holds for reaction-diffusion models with random diffusion of agents among nodes with infections only among the agents momentarily on the same node6. Recently, how human dynamics affects an epidemic has become the focus of research14,18,30,31,32,33, but the diversity of links and the time spending on journeys are largely ignored. Real-life networks, e.g. power grids and the internet, are often multi-layered networks34,35, with their mutual influence and cascades being hot research topics36,37. Epidemics in two-layered networks also received much attention21,22,23,24,25,26 and the layer for infection processes actually shares the same set of nodes with the layer for information exchanges.
For diseases spreading through human contacts, it is most important to understand the impact of frequent journeys. There exist many single and multi-layered transportation network models38,39,40,41,42,43, with the layers representing networks of airports, railways, highways, etc. coupled together. To incorporate epidemics, however, random diffusion of people on such networks will be an oversimplification, as a journey involves a planned route to a destination using mixed modes of transportation. These directed movements should be incorporated in studying epidemics.
The ease and speed of inter-city travels offered by the growth in the airline and high-speed train44 industries and better highways has contributed to making our Earth a global village. These inter-city travels readily spread a disease to different places. However, the big populations in major cities and densely packed travellers on multiple means of transportation of various speeds add further complications. A reliable framework for studying the effects of travelling on epidemics has yet to be constructed. Earlier works on epidemics in airport and railway networks often modelled journeys as random diffusion of agents4,5,45. The obvious shortcomings are: (i) real journeys typically involve multiple means of transportation instead of agents all travelling the same way; (ii) neighboring stations have different distances that affect the chance of infection instead of identical distance between adjacent nodes; (iii) real journeys are round-trip with an destination instead of random diffusion. It should be noted that intra-city travel is also inhomogeneous. It is, therefore, of fundamental importance to construct a framework incorporating the differences in travelling means and distances between cities. We propose here such a framework to incorporate inhomogeneity among the links and round-trip journeys with intended destination. It is found that infections at the links greatly affect the epidemic threshold and the traveling speed and frequency are key factors in determining the extent of an epidemic.
Results
An integrated travel network (ITN) model
Our integrated travel network (ITN) model accounts for different means of transportation by different kinds of links. Figure 1(a) shows schematically an inter-city transportation network emphasizing its link inhomogeneity: Links of faster transportation (dashed lines), e.g. airlines and high-speed trains, connecting major cities and links of slower transportation (solid lines), e.g. highways, connecting to surrounding cities (blue nodes) via part of a highway network.
Schematic illustration of transportation networks.
(a) Schematic inter-city transportation network illustrating the inhomogeneity in the links, e.g. dashed lines for higher speed transportation such as a part of an airport network or high-speed railway network and other cities (in blue) are connected through a part of the highway network. (b) Schematic intra-city transportation illustrating the link inhomogeneity, e.g. nodes (filled) connected by subways (dashed lines) and other nodes (open) connected by bus routes (solid lines).
A journey starts from a city i to an intended destination j through intermediate places along the path that takes the shortest time, which necessarily invoke the actual distance between two cities and the mode of transportation. The return journey could follow the same path or an alternative path, as depicted in Fig. 2(a,b). The ITN aims to incorporate the key features of how human travel, namely round-trip journeys of shortest time through multiple means of transportation. Here, we invoke the travel time, which depends on the distance and the means of transportation, as the key factor, instead of the effective distance43. Instead of emphasizing the multi-layered network structure as in previous works, ITN takes a traveller’s viewpoint that journeys take place in a single-layered undetachable network with a diversity of links connecting cities representing an inhomogeneous transportation network, see Methods for details. It aims to provide a step closer to a realistic description of human journeys and an alternative platform for studying epidemics on which finer and further details on local area transportation could be added.
Epidemic spreading on ITN
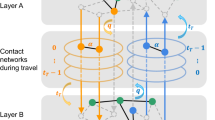
Contacts during journeys are important for epidemics. An example is the 2009 H1N1 cases in a Singapore’s hospital that 116 of 152 patients in two months were classified as air travel-associated imported cases46. The time that travellers meet becomes a crucial factor. It is related to the length of a link and how fast agents travel on it. As a minimum model, we consider two speeds vs and vf with vs < vf (see solid and dashed lines in Fig. 1) representing slower and faster transportation. An agent starts a round-trip journey from a node (home) to a destination chosen randomly (upper Fig. 3) through intermediate (middle) nodes along the path of shortest travel time18. Let rij be the distance between neighbouring nodes i and j. The time travelling on the link is
Schematic illustration of the key points in ITN.
An agent starts a round-trip journey from his home city (Host) via the path of shortest travel time (Forward path) towards the destination via many other cities (Middle) along the path. After remaining at the destination for some time steps, he takes a return trip (Backward) back home. Other agents may join or leave. A link is divided into segments (red circles) according to the travel time between stations. During a journey, an agent would encounter passengers who are infected (red open circles) or susceptible to an infection (black open circles).

with v = vs or vf depending on the type of transportation. To account for travel time, a link from node i to node j is divided into τij segments, with τij = tij if mod(rij,v) = 0 and τij = int(tij) + 1 if mod(rij,v) ≠ 0 (lower Fig. 3), where mod(x,y) represents the modulo operation and int(x) taking the integral part of x.
For epidemic on ITN, we invoke the susceptible-infected-susceptible (SIS) model6,9,10,11,12,13,14,15,16,17. A susceptible agent will be infected if it contacts an infected agent, with an infectious rate β. There are travelling and non-travelling agents in a population. Generally, people travelling are in closer contact and have a higher infectious rate β2 than the non-travelling agents with β147. An infected agent recovers and becomes susceptible with a recovery rate μ. For travelling agents, we assume that infections take place only among agents in the same segment kr (1 ≤ kr ≤ τij) of a link. For non-travelling agents, the SIS process is confined to non-travelling agents at the same node. Explicitly, a non-travelling susceptible agent at node i has a probability 1−(1−β1)ni,I to be infected at a time step, when there are ni,I infected non-travelling agents at the node. Similarly, a susceptible agent at a segment of a link has a probability  to be infected when there are
to be infected when there are  infected agents at that section kr.
infected agents at that section kr.
An example of ITN: China’s big city network
Buses on highways and high-speed trains in China together provide an example of ITN. To include a large population and to reduce the number of nodes, we consider 116 cities with population over one million (see Table S1 in Supplementary Information (SI)). From high-speed train schedule, 61 cities are served by routes of high-speed trains. For the remaining 55 cities, we construct the highway links as follows. A highway link is added between two cities in the same province or two neighbouring provinces when there is a highway between them. Finally, highway links are added to connect neighboring highway and high-speed railway nodes in the same province. Figure 4 shows the resulting ITN of 116 cities with two types of links. We give the structural properties in SI. It has a mean degree 〈k〉 = 4.25 and a high clustering coefficient of C = 0.35. The degree distribution is shown in Fig. S1(a) in SI. Table S2 in SI gives the lengths of the links.
An example of ITN.
An integrated travel network (ITN) constructed based on high-speed railway services (red links) and highway network (black lines) in China for 116 cities with a population larger than one million. The cities are represented by nodes of different sizes according to the populations. This figure was generated by R.
Typically, travels between major cities and/or nearby cities are more frequent. This was modelled by assigning weights  to a link, where Ni denotes the population at node i and rij the distance between nodes i and j48,49. To incorporate factors including transportation infrastructure and convenience, we modified the weight in ITN to
to a link, where Ni denotes the population at node i and rij the distance between nodes i and j48,49. To incorporate factors including transportation infrastructure and convenience, we modified the weight in ITN to

where Sij represents the daily services of high-speed trains between nodes i and j and thus an indication of how convenient it is and Sij = 0 for highway links. Values of Sij as obtained by train schedules are listed in Table S2 in SI. Summing Wij for the ki links give the weight Wi of node i as

To set up a model for simulations, we measure population in units of 5000 and distance rij in kilometers. Thus cities of Ni ≥ 200 are considered and Ni is  of the real population. The corresponding weight distribution is shown in Fig. S1(b) in SI. Sensitivity to the choice of measuring populations in lots of 5000 is tested in Fig. S2 in SI. In each time step,
of the real population. The corresponding weight distribution is shown in Fig. S1(b) in SI. Sensitivity to the choice of measuring populations in lots of 5000 is tested in Fig. S2 in SI. In each time step,  agents starts a round-trip journey from node i, where the parameter pT is chosen so that
agents starts a round-trip journey from node i, where the parameter pT is chosen so that  , i.e., people travelling are fewer than a city’s residents. It is related to the small fraction f of the total population
, i.e., people travelling are fewer than a city’s residents. It is related to the small fraction f of the total population  starting a journey every time step by
starting a journey every time step by

An agent from node i picks a destination j according to the probability

and follows the path of shortest travel time. An agent typically travels on slower transportation in the local area before transferring to high-speed train followed by local transportation to the destination. ITN captures the inhomogeneous means of travelling better than multi-layered networks. An agent spends some time at the destination before the return trip begins, which is taken to be 5 time steps corresponding to 5 hours50,51. Returning to home city, an agent becomes a non-traveller until the next journey. Figure 3 shows a schematic journey. The travelling dynamics leads to a steady state in which  residents among
residents among  are non-travellers at node i. The number of all non-travellers
are non-travellers at node i. The number of all non-travellers  depends on f (see Fig. S2 in SI) linearly for f ≤ 0.01. We thus take f = 0.01. The values of ni and
depends on f (see Fig. S2 in SI) linearly for f ≤ 0.01. We thus take f = 0.01. The values of ni and  for the 116 cities are shown in Fig. S3 in SI.
for the 116 cities are shown in Fig. S3 in SI.
Epidemic spreading on China’s ITN network
Let vs = 100 (km/h) be the highway traffic speed and vf> vs be speed of high-speed train. The speeds and rij determine the time τij of each link. After the travelling population reaches the steady state, the SIS process is initialized by assigning  agents randomly as infected at t = 0. Practically, uniformly distributed initial infection speeds up the approach to the steady state. The recovery rate is fixed at μ = 0.1. Let ρI be the fraction of infected agents. Figure 5(a) shows ρI(t) for β1 = 2 × 10−5 and β2 = 0.004, for two values of vf = 250 and 500. An epidemic steady state is reached quickly. As a higher
agents randomly as infected at t = 0. Practically, uniformly distributed initial infection speeds up the approach to the steady state. The recovery rate is fixed at μ = 0.1. Let ρI be the fraction of infected agents. Figure 5(a) shows ρI(t) for β1 = 2 × 10−5 and β2 = 0.004, for two values of vf = 250 and 500. An epidemic steady state is reached quickly. As a higher  shortens the time on the links that the infection rate is higher, ρI is smaller for higher vf. Figure 5(b) shows the steady state ρI for β1 = β2. There exists a threshold β1c ≈ 4 × 10−5 above which ρI ≠ 0.
shortens the time on the links that the infection rate is higher, ρI is smaller for higher vf. Figure 5(b) shows the steady state ρI for β1 = β2. There exists a threshold β1c ≈ 4 × 10−5 above which ρI ≠ 0.
Effect of different parameters on infected density.
(a) Time evolution of ρI with β1 = 2 × 10−5 and β2 = 0.004, for two values of train speed vf = 250 and 500. (b) ρI as a function of the parameter β1 with β1 = β2, for two values of train speed vf = 250 (squares) and 500 (dots). (c) ρI as a function of the parameter β2 with β1 = 2 × 10−5 < β1c ≈ 4 × 10−5, for two values of train speed vf = 250 and 500. (d) ρI as a function of the parameter β2 with vf = 250, for three different values of β1 = 1 × 10−5 (squares), 2 × 10−5 (dots) and 3 × 10−5 (triangles).
As β2> β1 generally, Fig. 5(c) shows ρI (β2) after setting β1 = 2 × 10−5 < β1c, for two values of vf. Figure 5(d) shows ρI(β2) for three different values of β1 < β1c. It is found that β2c remains unchanged for different β1 < β1c. It is reasonable in that when the outbreaks come from infections in journeys, the infection rate β1 of non-travellers is irrelevant to the threshold β2c. However, for β2> β2c, a higher β1 leads to a higher ρI.
Next, we set β1 = 10−4> β1c and Fig. 6(a) shows that ρI(β2) increases monotonically with β2, for vf = 250 and 500. Here, ρI ≠ 0 for all β2. There exists a value β2c′ (β2c′ = 0.0025 for the case in Fig. 6(a) below (above) which ρI for vf = 250 is lower (higher) than that for vf = 500.
To summarize the findings in a physical picture, for β2 < β2c′, infections among non-travellers at the nodes dominate the epidemic process. A higher vf (e.g. vf = 500) reduces the time that agents spent on journeys and thus promotes infection. For β2 > β2c′, infections among travellers on journeys dominate the epidemic process. A higher vf shortens the journey and suppresses infection.
For β1 = 2 × 10−5 < β1c and β2 = 0.006> β2c, infections during journeys dominate. Figure 6(b) shows that ρI increases monotonically with the fraction of travellers f, with ρI for vf = 500 smaller than that for vf = 250 due to the shorter journey time.
Discussion
We stressed the necessity of establishing a new framework for modelling journeys in modern times and their effects on epidemics. We illustrated the key ideas by presenting an integrated travel network constructed by considering geographic data, population data and transportation infrastructures in China. An example using only the high-speed trains and highways among the 116 cities of over a million population suffices for stressing the points. An ITN should include: (i) diversity among the links due to different distances and different speeds of transportation; (ii) diversity among the cities due to different population sizes and transportation services often reflecting their economic growth; (iii) round-trip journeys to targeted destination via paths of shortest time; and (iv) different infection rates for travellers and non-travellers. The ITN can readily be extended to include details on local area transportation, multiple means of transportation and journeys among different countries. For example, Fig. 1(b) shows schematically a local transportation network with stations (nodes) served by a subway network (dashed lines) and a bus network (solid lines). A journey includes generally travelling in both Fig. 1(a,b). Effects such as traffic congestion naturally emerge. As far as epidemics are concerned, faster and more convenient inter-city journeys would reduce the travel time during which passengers are crowded and thus suppress the chance of being infected, but they would also induce people to make more journeys and to farther places and thus spread a diseases more readily. Our ITN would serve as a good starting point for exploring the interplay of travelling and infection dynamics for many further work.
Methods
Degree and weight distributions of ITN
Highway buses and high-speed trains are the major means of transportation in China. After constructing ITN (see Fig. 4) based on high-speed trains and highways data, the number of links ki is recorded for each node and the degree distribution P(k) is obtained (Fig. S1(a) in SI). The average degree  and the clustering coefficient
and the clustering coefficient  are calculated, where Ei is the number of links connecting the ki neighbors of node i52.
are calculated, where Ei is the number of links connecting the ki neighbors of node i52.
For the weights in Eq. (2), we record the actual populations in each node and reduce them to Ni in units of 5000 and the distances rij between pairs of nodes in km according to the China official website. The frequency of high-speed trains Sij is obtained based on the routes and schedules of all high-speed trains. For each route that originates from a city A and terminates at a city B, we record the cities, say A, C1, C2, C3, B, served along the route and the number of services ms per day. Then, all Sij, i.e. SA,C1, SC1,C2, CC2,C3 and SC3, B, are augmented by ms. Data for all routes give the final Sij that go into Eq. (2) for the weights of the links Wij and Eq. (3) for the weights of the nodes Wi (see Table S1 in SI).
Journeys on ITN
For a journey that starts from the home city, the path of the shortest travel time to the destination is chosen. For a single type of links, i.e., vs = vf, the path of shortest travel time coincides with the shortest path. In ITN with vs < vf, the shortest paths are generally different from the paths of shortest time. As vf > vs, selected paths will involve railways as much as possible. It is convenient to discretize the journeys. The distance rij between two neighboring nodes i and j are divided into τij time steps. At each time step,  agents at node i become travellers. The destinations are chosen according to Eq. (5). The journeys are carried out as follows:
agents at node i become travellers. The destinations are chosen according to Eq. (5). The journeys are carried out as follows:
-
1
For every path between the home city i and destination j, the sum of τij along the path is obtained. The path of shortest time is the one with the smallest sum.
-
2
Paths originated from different cities to different destinations may partially overlap. Therefore, in the intermediate nodes (cities) in a journey, some travellers may come in and other travellers may leave.
-
3
Upon arrival at the destination, an agent stays 5 time steps before the return journey begins.
Initially, the segments 1 ≤ kr ≤ τij on the links are empty and they will be occupied only when agents travel. For a node i, there are  new travellers starting their journeys in the steady state, making a total
new travellers starting their journeys in the steady state, making a total  new travellers. Each of them has the chance
new travellers. Each of them has the chance  of choosing node i as the destination, giving a total
of choosing node i as the destination, giving a total  agents arriving per time step in the steady state.
agents arriving per time step in the steady state.
Epidemic spreading measurement on ITN
In the SIS dynamics, we distinguish infections among non-travellers in the cities and among travellers in the same segment of a link with infectious rates β1 and β2, respectively. As travellers on trains/buses are densely packed, β2> β147. An agent is a traveller and non-traveller at different times. When he is a non-traveller in a city, he is exposed to an infectious rate of β1. Once he is on a journey, he is exposed to an infectious rate of β2 during each segment of his journey, regardless of the segment being in the middle of a link or a passing-by city. Only travelling agents in the same segment kr (1 ≤ kr ≤ τij) towards the same direction can infect each other. Thus, SIS on ITN accounts for the continual exchanges of agents on trains and buses due to partial overlaps of agents’ journeys and the spread of a diseases through journeys. A susceptible non-traveller at node i will be infected by the rate 1−(1−β1)ni,I when he is in contact with ni,I infected agents. A susceptible traveller at a segment kr of a link will be infected by the rate  when he is in contact with
when he is in contact with  infected agents. Each infected agent recovers with a rate μ. The fraction ρI of infected agents is obtained by
infected agents. Each infected agent recovers with a rate μ. The fraction ρI of infected agents is obtained by  , where
, where  is over all the segments in all links in both travelling directions and Ntot is the total population.
is over all the segments in all links in both travelling directions and Ntot is the total population.
An approximate theoretical analysis
We make a qualitative analysis of the key behavior and illustrate that the dependence of ρI on the model parameters in ITN can be captured by mean-field considerations. Let there be M cities. There are  pairs of cities that the journey between which is all on high-speed trains. The mean number of sections 〈τ〉 in a link is τs = int(s/vs) + 1 for highway links and τf = int(s/vf) + 1 for railway links, where
pairs of cities that the journey between which is all on high-speed trains. The mean number of sections 〈τ〉 in a link is τs = int(s/vs) + 1 for highway links and τf = int(s/vf) + 1 for railway links, where  is the mean distance between neighbouring nodes. There are altogether
is the mean distance between neighbouring nodes. There are altogether

sections on the links, with d being the mean shortest path length between two nodes. It follows that Nmid decreases with m.
There are two processes in one time step: infection and motion. For the step t → (t + 1), SIS processes take place in the time interval t+ → (t + 1)− and the motion occurs at (t + 1). At a node  , there are ni,s susceptible and ni,I infected agents and ni = ni,S + ni,I. Similarly, there are nα,S susceptible and nα,I infected agents at a section α of a link, with
, there are ni,s susceptible and ni,I infected agents and ni = ni,S + ni,I. Similarly, there are nα,S susceptible and nα,I infected agents at a section α of a link, with  and
and  . The dynamics of the infected agents can be described by
. The dynamics of the infected agents can be described by

where XI accounts for infected agents arriving at the destination or at home, YI represents infected agents starting a journey, kstation are nodes where agents switch means of transportation and  is over the ki links to node i.
is over the ki links to node i.
The time evolution of ρI is given by  and thus
and thus

where Ntot is the total population. The set of equations can be iterated in time for the steady state. Further generalizations of ITN can be treated accordingly.
Based on Eq. (8), we make the following observations:
1. For β1 = β2: As ni >> nα, we readily have ni,I >> nα,I and the second term in Eq. (8) dominates. Thus, ρI in Fig. 5(b) comes mostly from infections at the nodes.
2. For β1 ≠ β2 and β1 > β1c: Infections at the nodes give ρ ≠ 0, but the third term in Eq. (8) becomes important when β2 > β1 and β2 > β2c. This gives the behaviour in Fig. 6(a).
3. For β1 ≠ β2 with β1 < β1c: Infections at the nodes alone cannot sustain ρI. Infections on journeys dominate and ρI becomes finite at β2 = β2c, independent of β1 (see Fig. 5d). It follows from the equation for nα,I((t + 1)−) that

indicating that β2c is inversely proportional to the mean number of agents travelling in a segment of a link nα.
4. For different m: The third term in Eq. (8) indicates that ρI ∝ Nmid. As Nmid decreases with m (see Eq. 6), ρI also drops with increasing m and high-speed railways tend to prevent epidemics by shortening travel times. One should note that this captures one effect of having faster transportation. However, an opposite effect of inducing more travellers poses a risk.
Additional Information
How to cite this article: Ruan, Z. et al. Integrated travel network model for studying epidemics: Interplay between journeys and epidemic. Sci. Rep. 5, 11401; doi: 10.1038/srep11401 (2015).
References
Liljeros, F., Edling, C. R., Amaral, L. A. N., Stanley, H. E. & Aberg, Y. The web of human sexual contacts. Nature 411, 907–908 (2001).
Ferguson, N. M. et al. Planning for smallpox outbreaks. Nature 425, 681–685 (2003).
Neumann, G., Noda T. & Kawaoka, Y. Emergence and pandemic potential of swine-origin H1N1 influenza virus. Nature 459, 931–939 (2009).
Meloni, S., Arenas, A. & Moreno, Y. Traffic-driven epidemic spreading in finite-size scale-free networks. Proc. Natl. Acad. Sci. USA 106, 16897–16902 (2009).
Balcan, D. et al. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc. Natl. Acad. Sci. USA 106, 21484–21489 (2009).
Colizza, V., Pastor-Satorras, R. & Vespignani, A. Reaction-diffusion processes and metapopulationmodels in heterogeneous networks. Nature Phys. 3, 276–282 (2007).
Kitsak, M. et al. Identification of influential spreaders in complex networks. Nature Phys. 6, 888–893 (2010).
Perra, N., Goncalves, B., Pastor-Satorras R. & Vespignani, A. Activity driven modeling of time varying networks. Sci. Rep. 2, 469–21489 (2012).
Moore C. & Newman, M. E. J. Epidemics and percolation in small-world networks. Phys. Rev. E 61, 5678–5682 (2002).
Kuperman M. & Abramson, G. Small World Effect in an Epidemiological Model. Phys. Rev. Lett. 86, 2909–2912 (2001).
Pastor-Satorras R. & Vespignani, A. Epidemic Spreading in Scale-Free Networks. Phys. Rev. Lett. 86, 3200–3203 (2001).
Pastor-Satorras R. & Vespignani, A. Epidemic dynamics and endemic states in complex networks. Phys. Rev. E 63, 066117 (2001).
Moreno, Y., Gomez, J. B. & Pacheco, A. F. Epidemic incidence in correlated complex networks. Phys. Rev. E 68, 035103 (2003).
Liu, Z. Effect of mobility in partially occupied complex networks. Phys. Rev. E 81, 016110 (2010).
Newman, M. E. J. Threshold Effects for Two Pathogens Spreading on a Network. Phys. Rev. Lett. 95, 108701 (2005).
Serrano, M. A. & Boguna, M. Percolation and Epidemic Thresholds in Clustered Networks. Phys. Rev. Lett. 97, 088701 (2006).
Parshani, R., Carmi, S. & Havlin, S. Epidemic Threshold for the Susceptible-Infectious-Susceptible Model on Random Networks. Phys. Rev. Lett. 104, 258701 (2010).
Tang, M., Liu, Z. & Li, B. Epidemic spreading by objective traveling. Europhys. Lett. 87, 18005 (2009).
Masuda, N. Effects of diffusion rates on epidemic spreads in metapopulation networks. New J. Phys. 12, 093009 (2010).
Wang, W. et al. Epidemic spreading on complex networks with general degree and weight distributions. Phys. Rev. E 90, 042803 (2014).
Ruan, Z., Tang, M. & Liu, Z. Epidemic spreading with information-driven vaccination. Phys. Rev. E 86, 036117 (2012).
Ruan, Z., Hui, P., Lin, H. & Liu, Z. Risks of an epidemic in a two-layered railway-local area traveling network. Eur. Phys. J. B 86, 13 (2013).
Granell, C., Gomez, S. & Arenas, A. Dynamical Interplay between Awareness and Epidemic Spreading in Multiplex Networks. Phys. Rev. Lett. 111, 128701 (2013).
Funk, S. & Jansen, V. A. A. Interacting epidemics on overlay networks. Phys. Rev. E 81, 036118 (2010).
Saumell-Mendiola, A., Serrano, M. A. & Boguna, M. Epidemic spreading on interconnected networks. Phys. Rev. E 86, 026106 (2012).
Funk, S., Gilad, E., Watkins, C. & Jansen, V. A. A. The spread of awareness and its impact on epidemic outbreaks. Proc. Natl. Acad. Sci. USA 106, 6872–6877 (2009).
Dickison, M., Havlin, S. & Stanley, H. E. Epidemics on interconnected networks. Phys. Rev. E 85, 066109 (2012).
Wang, W. et al. Asymmetrically interacting spreading dynamics on complex layered networks. Sci. Rep. 4, 5097 (2014).
Boguñá, M., Castellano, C. & Pastor-Satorras, R. Nature of the Epidemic Threshold for the Susceptible-Infected-Susceptible Dynamics in Networks. Phys. Rev. Lett. 111, 068701 (2013).
Wang, L., Li, X. Spatial epidemiology of networked metapopulation: An overview. Chin. Sci. Bull. 59, 3511–3522 (2014).
Meloni, S. et al. Modeling human mobility responses to the large-scale spreading of infectious diseases. Sci. Rep. 1, 62 (2011).
Wang, L., Wang, Z., Zhang, Y. & Li, X. How human location-specific contact patterns impact spatial transmission between populations? Sci. Rep. 3, 1468 (2013).
Wang, L., Zhang, Y., Wang, Z. & Li, X. The impact of human location-specific contact pattern on the SIR epidemic transmission between populations. Int. J. Bifurcat. Chaos 23, 1350095 (2013).
Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. & Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature (London) 464, 1025–1028 (2010).
Gao, J., Buldyrev, S. V., Stanley, H. E. & Havlin, S. Networks formed from interdependent networks. Nat. Phys. 8, 40–48 (2012).
Baxter, G. J., Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Avalanche Collapse of Interdependent Networks. Phys. Rev. Lett. 109, 248701 (2012).
Li, W., Bashan, A., Buldyrev, S. V., Stanley, H. E. & Havlin, S. Cascading Failures in Interdependent Lattice Networks: The Critical Role of the Length of Dependency Links. Phys. Rev. Lett. 108, 228702 (2012).
Gu, C. et al. Onset of cooperation between layered networks. Phys. Rev. E 84, 026101 (2011).
Morris, R. G. & Barthelemy, M. Transport on Coupled Spatial Networks. Phys. Rev. Lett. 109, 128703 (2012).
Tan, F., Wu, J., Xia, Y. & Tse, C. K. Traffic congestion in interconnected complex networks. Phys. Rev. E 89, 062813 (2014).
Halu, A., Mukherjee, S. & Bianconi, G. Emergence of overlap in ensembles of spatial multiplexes and statistical mechanics of spatial interacting network ensembles. Phys. Rev. E 89, 012806 (2014).
Han, X., Hao, Q., Wang, B. & Zhou, T. Origin of the scaling law in human mobility: Hierarchy of traffic systems. Phys. Rev. E 83, 036117 (2011).
Brockmann, D., Helbing, D. The Hidden Geometry of Complex, Network-Driven Contagion Phenomena. Science 342, 1337–1342 (2013).
Saltzstein, D. Japan Plans Worlds’s Fastest Train. 14/02/2011. http://intransit.blogs.nytimes.com/2011/02/14/japan-plans-worlds-fastest-train/.
Ruan, Z., Tang, M. & Liu, Z. How the contagion at links influences epidemic spreading. Eur. Phys. J. B 86, 149 (2013).
Mukherjee, P. et al. Epidemiology of Travel-associated Pandemic (H1N1) 2009 Infection in 116 Patients, Singapore. Emer. Infe. Dise. 16, 21 (2010).
DeNoon, D. J. Travel Health Risks You Can—and Can’t Avoid. 1/10/2006. http://www.webmd.com/cold-and-flu/features/disease-prevention-traveling.
Jung, W., Wang, F. & Stanley, H. E. Gravity model in the Korean highway. Europhys. Lett. 81, 48005(2008).
Barthelemy, M. Spatial networks. Phys. Rep. 499, 1–101 (2011).
Poletto, C., Tizzoni, M. & Colizza, V. Heterogeneous length of stay of hosts’ movements and spatial epidemic spread. Sci. Rep. 2, 476 (2012).
Poletto, C., Tizzoni, M. & Colizza, V. Human mobility and time spent at destination: Impact on spatial epidemic spreading. J. Theor. Biol. 338, 41 (2013).
Albert, R. & Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002).
Acknowledgements
This work was partially supported by the NNSF of China under Grant Nos. 11135001 and 11375066 and 973 Program under Grant No. 2013CB834100.
Author information
Authors and Affiliations
Contributions
Z.L. and Z.R. conceived the research project. Z.R., Z.L. and C.W. performed research. Z.L., Z.R. and P.M.H. analyzed the results. Z.L. and P.M.H. wrote the paper. All authors reviewed and approved the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ruan, Z., Wang, C., Ming Hui, P. et al. Integrated travel network model for studying epidemics: Interplay between journeys and epidemic. Sci Rep 5, 11401 (2015). https://doi.org/10.1038/srep11401
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep11401
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.









 as a function of the parameter β2 with β1 = 10−4> β1c, for two values of train speed vf = 250 (squares) and 500 (dots). (b) ρI as a function of f with β1 = 2 × 10−5 < β1c and β2 = 0.006> β2c, for vf = 250 (squares) and 500 (dots).
as a function of the parameter β2 with β1 = 10−4> β1c, for two values of train speed vf = 250 (squares) and 500 (dots). (b) ρI as a function of f with β1 = 2 × 10−5 < β1c and β2 = 0.006> β2c, for vf = 250 (squares) and 500 (dots).