Abstract
The global minimum structure of borospherene (B40) is a cage, comprising two hexagonal and four heptagonal rings. Born-Oppenheimer Molecular Dynamics simulations show that continuous conversions in between six and seven membered rings take place. The activation energy barrier for such a transformation is found to be 14.3 kcal·mol−1. The completely delocalized σ- and π-frameworks, as well as the conservation of the bonding pattern during rearrangement, facilitate the dynamical behavior of B40. B40 is predicted to act as a support-free spherical two-dimensional liquid at moderate temperature. In other words, B40 could be called as a nanobubble.
Similar content being viewed by others
Introduction
Is it possible to build a buckyball comprising only boron atoms? Boron is an electron deficient atom with only three valence electrons. So, a perfect boron buckminsterfullerene (B60) is not expected to be stable owing to the absence of the fourth electron, which is essential for the π-stabilization of a spherical shell. A fullerene-like boron cluster, B80, was predicted in silico, which has structural similarity with C60 but with an additional boron atom at the center of each hexagon1. However, several unsymmetrical B80 structures were found to be more stable than the fullerene-like geometry2,3,4,5,6.
Quite recently, Zhai et al.7 reported the experimental detection of B40− by photoelectron spectroscopy. Density functional theory (DFT) computations revealed that the most stable structure includes a quasi-planar arrangement with two adjacent hexagonal holes. However, a cage structure is also viable as the relative energy to the global minimum is only 1.7 kcal·mol−1. In contrast, the lowest energy structure of the neutral B40 cluster possesses a perfect cage-like shape containing two hexagonal and four heptagonal holes (1, see Fig. 1) and it is more stable than the corresponding quasi-planar form by approximately 27 kcal·mol−1. The bonding network in B40 is completely delocalized via σ– and π-type multicenter bonds. The structure gains its stability due to its very high HOMO-LUMO energy gap (3.13 eV), which is comparable to that of C60 (3.02 eV). So, B40 represents the first pure boron buckyball (borospherene). Very recently, a couple of boron buckyballs (B38 and B39−) were also reported in the literature8,9.
Four years ago, the B19− cluster was reported to have a perfect planar structure with a central filled pentagonal unit inside a B13 ring. Some of us subsequently found a remarkable fluxional behavior in the B19− cluster10,11. B19− exhibits an almost free rotation of the internal pentagon-shaped hub within the co-planar B13 ring akin to a Wankel motor, which is evident from the Born-Oppenheimer Molecular Dynamics (BO-MD) simulations. In fact, the zero-point energy is sufficient to overcome the barrier that allows the inner and outer rings to rotate independent of each other. The presence of various multicenter bonds between the outer-ring and the inner-ring, that could easily migrate from one position to another during rotation, facilitates such a dynamical feature12. This fluxional behavior is not limited to B19− only, B13+,13,14,15 B182−,16,17 and B20− also show similar dynamical features18,19. As B40 has a similar multicenter bonding pattern, there arises the compelling question, “Is B40 also fluxional?” and that prompted us to explore the probable dynamical behavior of B40. Indeed, a fluxional behavior of a cage would correspond to a nanobubble — a molten, hollow pure boron object, which is unprecedented to our knowledge and thus is of immense interest concerning its chemical and physical properties.
In order to explore the dynamical behavior of B40, we carried out a series of BO-MD simulations at the PBE/DZVP20 level in deMon2K (deMon2k v. 3, the deMon developers, Cinvestav, Mexico City 2011). The simulations are launched from the equilibrium geometry of B40 (1) with random velocities assigned to the atoms, employing a Hoover thermal bath, for a simulation time of 25 ps with 0.5 fs time steps. During the MD computations, we keep the total angular momentum of the cluster as zero, thereby suppressing the cluster rotation. The behavior of the mean square displacement (msd) as a function of time easily allows us to differentiate between a solid-like and a liquid-like behavior. The mean-square displacement at time t is given by

where ri(t) is the position vector of the i-th atom at the time t and N is the total number of atoms in the system.
During the BO-MD simulations at 1000 K, the cluster maintains its connectivity pattern and cage-like structure as was reported by Zhai et al.7 But at 1200 K and 1500 K, a continuous transformation between the seven membered rings (7-MRs) and six membered rings (6-MRs) is perceived (see movie files in the electronic supporting information). The structure of the rear 7-MR first gets distorted by moving one B atom towards the adjacent 6-MR and then it becomes a 6-MR, which transforms the contiguous 6-MR into a 7-MR. But still the near 7-MR does not show any significant structural change. Thereafter, the rear 6-MR is again transformed into 7-MR and the near 7-MR starts to have a structural deformation. Therefore, the boron cage certainly shows a series of transformation in which the ring sizes continuously get changed during the simulations.
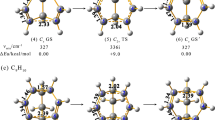
Figure 1 depicts the minimum energy structures and the transition state involved in the structural change of B40 (see the Cartesian coordinates in the Supplementary Information), which were optimized at the PBE0/6-311+G(d)21 level using Gaussian 09 program (Gaussian 09 Revision D.1, Wallingford CT, 2009). The global minimum corresponds to a D2d structure, such that the 6-MRs are in front of each other. The transition state (TS1) related to the transformation between a 7-MR and a 6-MR has a Cs geometry (υmin = 117i cm−1). It is only 14.3 kcal·mol−1 higher in energy (including the zero-point energy correction) than 1. The change comprises a B5 fragment located in between a 6-MR and a 7-MR, which contains a quasi-planar tetracoordinate boron atom. The result of this alteration is the intermediate cage 2 (with Cs symmetry), which possesses two adjacent 6-MRs. The relative energy between 1 and 2 is only 11.1 kcal·mol−1.
Structure 2 can return to 1 via the same transition state. In Fig. 1, two boron atoms are labeled as B1 and B2 in order to follow the transformations. These atoms form part of the B5 fragment, which suffers the relevant changes. Originally B1 and B2 belong to a 7-MR. After the transformation into 2, B1 becomes a part of a 6-MR and B2 is moving to form a new 7-MR. Note that there are four B5 fragments surrounding the two 6-MRs and all of them are suitable for such a structural reorganization. If the central B5 moiety changes, the original structure is recovered. In contrast, if any of the other B5 fragments switches, then four boron atoms will change their positions to form a 7-MR from a 6-MR.
Real-temperature simulations on realistic time scales are computationally impossible for quantum-mechanical systems to date. As a typical time step is about one fs (10−15 s), 1015 MD steps would be required. Given that it is unrealistic from the computational point of view, the standard procedure to overcome this problem is to run simulations at higher temperature, what essentially serves as a time lapse. In our case, the rare event is overcoming a barrier of 14.3 kcal/mol. Using Boltzmann’s law, our 25 ps simulation at 1200 K corresponds roughly to 0.5 ms in reality. Thus, with in this – admittedly crude – approximation we do observe fluxionality at chemically relevant time scales. In other words, it does not mean that the transformation occurs at 1200 K, it is only that at this temperature, the molecule has the enough kinetic energy to cross the barrier in a 25 ps time frame.
The extraordinary dynamical behavior of B40 is also reflected in the 〈msd〉 values (Fig. 2). In a solid-like system, one would expect the 〈msd〉 to be essentially a constant close to zero, whereas a liquid-like system should exhibit a nearly linear increase in 〈msd〉 with respect to time22. At 1000 K, clearly B40 behaves like a solid-like system, where the structure remains almost the same during the MD simulation, but the behavior of <msd> changes drastically at 1200 K and 1500 K. As a result of the nuclear mobility, B40 can be described as a surface or two-dimensional liquid-like system at these temperatures. Thus, B40 is a system that behaves like a support-free spherical two-dimensional liquid.
Fluxionality in carboranes is common, but no such interchange in the sizes of the rings occurs there. On the other hand, the classical carbon cages like C60 do not show such type of transformations. A somewhat similar process is the formation of Stone-Wales (SW) defects23 in fullerenes or nanotubes. However, particularly for C60, this isomerization is restricted due to a very high activation energy barrier (approximately 7 eV in fullerenes). So, the barrier in B40 is significantly lower than that in the SW defects formation in carbon systems. In other words, B40 is the first boron cluster that shows an interesting dynamical behavior with a moderate barrier (less than 15 kcal/mol), which allows that the ring sizes get changed continuously.
The bonding situation in B40 is intriguing. Zhai et al.7 studied in detail the nature of bonding in 1 using the adaptive natural density partitioning (AdNDP) analysis24 and showed that a strong delocalization of the σ- and π-system is present in 1. 48 pairs of valence electrons are delocalized via σ-bonds and the remaining electrons are delocalized via π-bonds. Zhai et al.7 also computed the nucleus independent chemical shift (NICS)25 to determine whether B40 could be classified as an aromatic system. NICS indicates that the system is indeed aromatic in nature. However, there are some details about delocalization that were not explored previously and could provide some insight into the fluxional behavior of 1. Here we use the induced magnetic field, particularly the z-component of the induced magnetic field (Bindz)26,27, in order to understand delocalization.
Figure 3 shows the profiles of Bindz for external fields applied perpendicular to the 6-MRs. An external magnetic field in this direction can induce a current around the cage. The magnetic response at the cage center is very high (Bindz = −47.1 ppm) and diatropic in nature. This value is even larger than those computed in other spherenes28,29,30. The intensity of Bindz in B40 diminishes gradually along the center to surface of the cage. The radius of B40 is approximately 2.5 Å. At this distance, the |Bindz| values are around 20 ppm lower than that computed at the cage center. However, at both 6-and 7-MRs, the magnitudes are still appreciable (Bindz ≈ −20 ppm), indicating a strong delocalization in the σ-framework.
The Bindz profile, which is mathematically equivalent to NICSzz, shows a long-range shielding cone above the 6-MRs with an extension of nearly 10 Å, which is even more intense than that computed at C60. In contrast, the magnetic response is different on the 7-MRs. In this case, the Bindz values become positive at around 3.5 Å above, implying a decrease in delocalization above the 7-MRs. Hence, these results indicate a strong π-delocalization at the 6-MRs, which is much higher than those at the 7-MRs.
The Bindz profiles of TS1 and 2 show essentially the same magnetic responses in both, shape and intensity as that in 1 (see Fig. 1-SI). Thus, during the rearrangement process, the changes in the σ- and π-delocalizations are not significant. This is the main difference compared to the carbon cages like C60, where the changes in the connectivity (as Stone-Wales defects) modify the σ- and π-frameworks drastically and accordingly the delocalization and stability.
In summary, BO-MD simulations reveal that B40, the first pure all-boron buckyball, shows a fascinating dynamical behavior in which the ring sizes continuously get changed during simulation. The transformation between 6- and 7-MRs occurs through an activation energy barrier of 14.3 kcal·mol−1. The electronic structure of B40 favors such transformation as the σ- and π-delocalizations are properly maintained in both the minimum energy structures (1 and 2) as well as in the corresponding transition state (TS1). During the rearrangement, the changes around the multicenter B-B bonds are almost negligible, thus unlike in the carbon cages the barrier is not prohibitive. This is also related to the fact that a B-B bond is weaker than the C-C one. So, the dynamic behavior of B40 is a consequence of the strong delocalization existing around the multicenter B-B bonds. The msd supports that B40 is a nanobubble that behaves like a support-free spherical two-dimensional liquid.
Additional Information
How to cite this article: Martínez-Guajardo, G. et al. Dynamical behavior of Borospherene: A Nanobubble. Sci. Rep. 5, 11287; doi: 10.1038/srep11287 (2015).
References
Szwacki, N. G., Sadrzadeh, A. & Yakobson, B. I. B80 fullerene: An ab initio prediction of geometry, stability and electronic structure. Phys. Rev. Lett. 98, 166804–166807 (2007).
Li, H. et al. Icosahedral B12-containing core-shell structures of B80 . Chem. Commun. 46, 3878–3880 (2010).
Wang, X.-Q. Structural and electronic stability of a volleyball-shaped B80 fullerene. Phys. Rev. B 82, 153409–153412 (2010).
Zhao, J., Wang, L., Li, F. & Chen, Z. B80 and other medium-sized boron clusters: core shell structures, not hollow cages. J. Phys. Chem. A 114, 9969–9972 (2010).
De, S. et al. Energy landscape of fullerene materials: A comparison of boron to boron nitride and carbon. Phys. Rev. Lett. 106, 225502–225505 (2011).
Li, F. et al. B80 and B101–103 clusters: Remarkable stability of the core-shell structures established by validated density functionals. J. Chem. Phys. 136, 074302–074309 (2012).
Zhai, H.-J. et al. Observation of an all-boron fullerene. Nature Chem 6, 727–731 (2014).
Lv, J., Wang, Y., Zhu, L. & Ma, Y. B38: An all-boron fullerene analogue. Nanoscale 6, 11692–11696 (2014).
Chen, Q. et al. Experimental and theoretical evidence of an axially chiral borospherene. ACS Nano 9, 754–760 (2015).
Huang, W. et al. A concentric planar doubly p-aromatic B19- cluster. Nature Chem. 2, 202–206 (2010).
Jimenez-Halla, J. O. C., Islas, R., Heine, T. & Merino, G. B19-: An aromatic Wankel motor. Angew. Chem., Int. Ed. Engl. 49, 5668–5671 (2010).
Sergeeva, A. P. et al. Understanding boron through size-selected clusters: Structure, chemical bonding and fluxionality. Acc. Chem. Res. 47, 1349–1358 (2014).
Martinez-Guajardo, G. et al. Unravelling phenomenon of internal rotation in B13+ through chemical bonding analysis. Chem. Commun. 47, 6242–6244 (2011).
Merino, G. & Heine, T. And yet it rotates: The starter for a molecular Wankel motor. Angew. Chem., Int. Ed. Engl. 51, 10226–10227 (2012).
Zhang, J., Sergeeva, A. P., Sparta, M. & Alexandrova, A. N. B13+: A photodriven molecular Wankel engine. Angew. Chem., Int. Ed. Engl. 51, 8512–8515 (2012).
Moreno, D. et al. B182–: A quasi-planar bowl member of the Wankel motor family. Chem. Commun. 50, 8140–8143 (2014).
Sergeeva, A. P., Averkiev, B. B., Zhai, H.-J., Boldyrev, A. I. & Wang, L.-S. All-boron analogues of aromatic hydrocarbons: B17– and B18–. J. Chem. Phys. 134, 224304 (2011).
Tai, T. B., Ceulemans, A. & Nguyen, M. T. Disk aromaticity of the planar and fluxional anionic boron clusters B20−. Chem. Eur. J. 18, 4510–4512 (2012).
Kiran, B. et al. Planar-to-tubular structural transition in boron clusters: B20 as the embryo of single-walled boron nanotubes. Proc. Natl. Acad. Sci. U. S. A. 102, 961–964 (2005).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Adamo, C. & Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 110, 6158–6170 (1999).
Haile, J. M. in Molecular Dynamics Simulation: Elementary Methods, 1–487 (Wiley-Interscience, 1992).
Stone, A. J. & Wales, D. J. Theoretical-studies of icosahedral C60 and some related species. Chem. Phys. Lett. 128, 501–503 (1986).
Zubarev, D. Y. & Boldyrev, A. I. Developing paradigms of chemical bonding: adaptive natural density partitioning. Phys. Chem. Chem. Phys. 10, 5207–5217 (2008).
Chen, Z. F., Wannere, C. S., Corminboeuf, C., Puchta, R. & Schleyer, P. v. R. Nucleus-independent chemical shifts (NICS) as an aromaticity criterion. Chem. Rev. 105, 3842–3888 (2005).
Merino, G., Heine, T. & Seifert, G. The induced magnetic field in cyclic molecules. Chem. Eur. J. 10, 4367–4371 (2004).
Islas, R., Heine, T. & Merino, G. The induced magnetic field. Acc. Chem. Res. 45, 215–228 (2012).
Castro, A. C. et al. Scalar and spin-orbit relativistic corrections to the NICS and the induced magnetic field: The case of the E122– spherenes (E = Ge, Sn, Pb). J. Chem. Theory Comput. 6, 2701–2705 (2010).
Cui, L.-F., Huang, X., Wang, L.-M., Li, J. & Wang, L.-S. Pb122−: Plumbaspherene. J. Phys. Chem. A 110, 10169–10172 (2006).
Cui, L. F. et al. Sn122–: Stannaspherene. J. Am. Chem. Soc. 128, 8390–8391 (2006).
Acknowledgements
COZCyT, UACQ-UAZ, REA-FP7-IRSES TEMM1P (GA 295172) and Moshinsky Foundation supported this project. The CGSTIC (Xiuhcoalt) at Cinvestav is gratefully acknowledged for generous allocation of computational resources. P.K.C thanks DST, New Delhi for the J.C. Bose National Fellowship. S.P. thanks CSIR for his fellowship.
Author information
Authors and Affiliations
Contributions
G.M., J.L.C., A.D. and R.I. performed all the computations. S.P. and P.K.C. helped in analyzing the results and in writing the manuscript. T.H. and G.M. analyzed the results and wrote the manuscript. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Martínez-Guajardo, G., Luis Cabellos, J., Díaz-Celaya, A. et al. Dynamical behavior of Borospherene: A Nanobubble. Sci Rep 5, 11287 (2015). https://doi.org/10.1038/srep11287
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep11287
This article is cited by
-
Probing the Structural Evolution and Stabilities of LiBn− (n=2–12) Clusters
Journal of Cluster Science (2024)
-
LiB13: A New Member of Tetrahedral-Typed B13 Ligand Half-Surround Cluster
Scientific Reports (2020)
-
Probing the structure and electronic properties of beryllium doped boron clusters: A planar BeB16− cluster motif for metallo-borophene
Scientific Reports (2019)
-
Structures, stabilities and spectral properties of borospherene B44− and metalloborospherenes MB440/− (M = Li, Na, and K)
Scientific Reports (2017)
-
Computational prediction of the endohedral metalloborofullerenes Ti n @B40 (n = 1, 2)
Theoretical Chemistry Accounts (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.