Abstract
Strongly interacting one-dimensional quantum systems often behave in a manner that is distinctly different from their higher-dimensional counterparts. When a particle attempts to move in a one-dimensional environment it will unavoidably have to interact and ‘push’ other particles in order to execute a pattern of motion, irrespective of whether the particles are fermions or bosons. A present frontier in both theory and experiment are mixed systems of different species and/or particles with multiple internal degrees of freedom. Here we consider trapped two-component bosons with short-range inter-species interactions much larger than their intra-species interactions and show that they have novel energetic and magnetic properties. In the strongly interacting regime, these systems have energies that are fractions of the basic harmonic oscillator trap quantum and have spatially separated ground states with manifestly ferromagnetic wave functions. Furthermore, we predict excited states that have perfect antiferromagnetic ordering. This holds for both balanced and imbalanced systems and we show that it is a generic feature as one crosses from few- to many-body systems.
Similar content being viewed by others
Introduction
The interest in one-dimensional (1D) quantum systems with several interacting particles arguably began back in 1931 when Bethe solved the famous Heisenberg model of ferromagnetism1, but it was only in the 1960 s that people realized that the techniques invented by Bethe could be used to solve a host of different many-body models2,3,4,5,6. It was subsequently realized that many 1D systems have universal low-energy behaviour and can be described by the paradigmatic Tomonaga-Luttinger-Liquid (TLL) theory7,8,9. This opened up the field of one-dimensional physics, which has remained a large subfield of condensed-matter physics ever since9,10. Recently, there has been a great revival of interest in 1D systems due to the realization of 1D quantum gases in highly controllable environments using cold atomic gases11,12,13,14,15,16,17. This development implies that one may now experimentally realize 1D systems with bosons or fermions and explore the intricate nature of their quantum behaviour.
A recent frontier is the realization of multi-component systems18 in order to study fundamental 1D effects such as spin-charge separation19. While this effect is usually associated with spin 1/2 fermions, it turns out that it can also be explored in Bose mixtures (two-component bosonic systems) where the phenomenon can be even richer as there can be interactions between the two components (inter-species) and also within each component separately (intra-species)10,20,21. The latter is strongly suppressed for fermions due to the Pauli principle. In the case where the intra- and inter-species interactions are identical it has been shown that a ferromagnetic ground state occurs22,23. Generalizing to the case of unequal intra- and inter-species interactions may be possible, but since the proofs and techniques rely on spin algebra and representation theory, they cannot be used to obtain the full spatial structure of general systems and other approaches are therefore needed. Here we consider the limit where the inter-species dominates the intra-species interactions. This regime has been explored in recent years for small systems using various few-body techniques24,25,26,27,28,29 and behaviour different from strongly interacting fermions or single-component bosons can be found already for three particles29. From the many-body side, the system is known to have spin excitations with quadratic dispersion,30,31,32,33 which can be shown to be a generic feature of the ‘magnon’ excitations above a ferromagnetic ground state34,35. This goes beyond the TLL theory and it has been conjectured that a new universality class (‘ferromagnetic liquid’) emerges in this regime36,37,38,39,40.
Here we provide a particularly clean realization of a ‘ferromagnetic’ system confined in a harmonic trap. Using numerical and newly developed analytical techniques we obtain and analyze the exact wave function. This allows us to explore the crossover between few- and many-body behaviour and to demonstrate that the strongly interacting regime realizes a perfect ferromagnet in the ground state, while particular excited states will produce perfect antiferromagnetic order. In the extremely imbalanced system, with one strongly interacting ‘impurity’, we find both numerically and analytically that the impurity will always move to the edge of the system. This is in sharp contrast to fermionic systems where the impurity is mainly located at the center41. Our work provides a rare and explicit example of perfect ferro- or antiferromagnetism using the most fundamental knowledge of a quantum system as given by the full wave function.
Results
Energetics and wave functions
Our two-component bosonic system has  particles split between
particles split between  and
and  identical bosons of two different kinds. All
identical bosons of two different kinds. All  particles have mass
particles have mass  and move in the same external harmonic trapping potential with single-particle Hamiltonian
and move in the same external harmonic trapping potential with single-particle Hamiltonian  , where
, where  and
and  denote the momentum and position of either an
denote the momentum and position of either an  or
or  particle and
particle and  is the common trap frequency. The trap provides a natural set of units for length,
is the common trap frequency. The trap provides a natural set of units for length,  and energy,
and energy,  , which we will use throughout (here
, which we will use throughout (here  is Planck’s constant divided by
is Planck’s constant divided by  ). We assume short-range interactions between
). We assume short-range interactions between  and
and  particles that we model by a Dirac delta-function parameterized by an interaction strength,
particles that we model by a Dirac delta-function parameterized by an interaction strength,  , i.e.
, i.e.

where  and
and  denote the coordinates of
denote the coordinates of  and
and  particles, respectively. The intraspecies interaction strengths are assumed to be much smaller than
particles, respectively. The intraspecies interaction strengths are assumed to be much smaller than  and we will therefore neglect such terms. To access the quantum mechanical properties of our system we must solve the
and we will therefore neglect such terms. To access the quantum mechanical properties of our system we must solve the  -body Schrödinger equation. This will be done using novel analytical tools and using exact diagonalization. In the latter case we have adapted an effective interaction approach that has recently been succesfully applied to fermions in harmonic traps42,41 (see the Methods section for further details). The analytical and numerical methods allow us to address up to ten particles, which is larger than most previous studies not based on stochastic or Monte Carlo techniques.
-body Schrödinger equation. This will be done using novel analytical tools and using exact diagonalization. In the latter case we have adapted an effective interaction approach that has recently been succesfully applied to fermions in harmonic traps42,41 (see the Methods section for further details). The analytical and numerical methods allow us to address up to ten particles, which is larger than most previous studies not based on stochastic or Monte Carlo techniques.
The simplest non-trivial case is the three-body system which has two  and one
and one  particle. The energy spectrum is shown in Fig. 1 as a function of
particle. The energy spectrum is shown in Fig. 1 as a function of  . The most interesting feature to notice is the ground state behaviour as
. The most interesting feature to notice is the ground state behaviour as  . Here, an odd and an even state become degenerate at an energy of
. Here, an odd and an even state become degenerate at an energy of  . This should be contrasted to the behaviour of single-component bosons or two-component fermions which will always have energies that are an integer times
. This should be contrasted to the behaviour of single-component bosons or two-component fermions which will always have energies that are an integer times  when
when  . Furthermore, we notice how the two states that merge at
. Furthermore, we notice how the two states that merge at  become two excited state branches on the attractive side of the resonance but the even parity state remains the lower one. This is opposite to the behaviour of fermions43 where the hierarchy of states is inverted at
become two excited state branches on the attractive side of the resonance but the even parity state remains the lower one. This is opposite to the behaviour of fermions43 where the hierarchy of states is inverted at  . The ground state for large and negative
. The ground state for large and negative  is very different as it contains deeply bound molecules, which we will not consider further. The fractional energies in the spectrum can be explained by a schematic three-body model and in stochastic variational calculations29. This provides a hint that larger systems could also display fractional energy states in the strongly interacting limit and begs the question as to what spatial configurations such states correspond to.
is very different as it contains deeply bound molecules, which we will not consider further. The fractional energies in the spectrum can be explained by a schematic three-body model and in stochastic variational calculations29. This provides a hint that larger systems could also display fractional energy states in the strongly interacting limit and begs the question as to what spatial configurations such states correspond to.
Three-body spectral flow.
The energy spectrum of two  and one
and one  particle as a function of interaction strength,
particle as a function of interaction strength,  , obtained by numerical calculations. In the limit
, obtained by numerical calculations. In the limit  , the ground state becomes doubly degenerate and has half-integer energy. The contribution from center-of-mass motion has been removed. For visibility, we have dimmed states from the attractive side that diverge to large negative energies close to
, the ground state becomes doubly degenerate and has half-integer energy. The contribution from center-of-mass motion has been removed. For visibility, we have dimmed states from the attractive side that diverge to large negative energies close to  .
.
We will now show that the fractional energy states are generic for strongly interacting two-component bosons in 1D and, importantly, for the ground state they realize perfect ferromagnetic behaviour irrespective of whether the system is balanced ( ) or not. The term perfect ferromagnetic behaviour implies that we have a full spatial separation of the two components in the exact ground state wave function of the system, i.e. the probability to find only
) or not. The term perfect ferromagnetic behaviour implies that we have a full spatial separation of the two components in the exact ground state wave function of the system, i.e. the probability to find only  on one side and only
on one side and only  on the other side of the system is not just dominant, it is exactly unity. The ground state has only a single ‘domain wall’ at which an
on the other side of the system is not just dominant, it is exactly unity. The ground state has only a single ‘domain wall’ at which an  and a
and a  particle are neighbours. As a consequence, imagine that you detect an
particle are neighbours. As a consequence, imagine that you detect an  particle on the left (right) side of the system, then you can immediately conclude that all the
particle on the left (right) side of the system, then you can immediately conclude that all the  particles reside to the right (left) of this
particles reside to the right (left) of this  particle.
particle.
Balanced systems
We first consider a four-body system that has two  and two
and two  particles. The energy spectrum for
particles. The energy spectrum for  is shown in Fig. 2a). A striking feature is the two-fold degenerate ground state for
is shown in Fig. 2a). A striking feature is the two-fold degenerate ground state for  that has a non-integer energy similar to the three-body problem. In this strongly repulsive limit, the system realizes a perfect spatially ferromagnetic quantum state as we will now demonstrate analytically.
that has a non-integer energy similar to the three-body problem. In this strongly repulsive limit, the system realizes a perfect spatially ferromagnetic quantum state as we will now demonstrate analytically.
Balanced four-body system. a) Energy spectrum for  for two
for two  and two
and two  particles. The
particles. The  limits are analytically known and indicated by triangles. Even parity states are in blue solid while odd parity states are in red (dot-dashed). b) Three-dimensional representation of the coordinate space on which the four-body wave function is defined when the center-of-mass position is removed. The specific Jacobi coordinates used are shown at the bottom. The solid coloured circular planes indicate the planes where an
limits are analytically known and indicated by triangles. Even parity states are in blue solid while odd parity states are in red (dot-dashed). b) Three-dimensional representation of the coordinate space on which the four-body wave function is defined when the center-of-mass position is removed. The specific Jacobi coordinates used are shown at the bottom. The solid coloured circular planes indicate the planes where an  pair overlap. The wave function must vanish on these planes in the limit where
pair overlap. The wave function must vanish on these planes in the limit where  . The checkerboard coloured circular planes are reflection planes for a pair of identical particles (
. The checkerboard coloured circular planes are reflection planes for a pair of identical particles ( and
and  ). The red region has twice the volume of the green region and four times that of the yellow region. The smaller figures in the middle show the same regions viewed from different angles for clarity.
). The red region has twice the volume of the green region and four times that of the yellow region. The smaller figures in the middle show the same regions viewed from different angles for clarity.
First we note that the center-of-mass motion of the four-body system can be separated and thus ignored. This leaves three Jacobi coordinates to describe the system. The details of these reductions can be found in the Methods section below. In Fig. 2b) we show the space of the Jacobi coordinates and highlight all the planes at which an  (solid planes), an
(solid planes), an  or a
or a  (checkerboard planes) pair of particles overlap. The main observation is that as
(checkerboard planes) pair of particles overlap. The main observation is that as  , the wave function must vanish on all the solid planes in Fig. 2b) and we arrive at the disconnected regions shown with different colours. The particles become effectively impenetrable and we may characterize the wave function by specifying the amplitudes of all possible spatial configurations of the four particles. These regions correspond to specific orderings on a line of the four particles. In particular, the large (red) region dominating the figure corresponds to spatial configurations
, the wave function must vanish on all the solid planes in Fig. 2b) and we arrive at the disconnected regions shown with different colours. The particles become effectively impenetrable and we may characterize the wave function by specifying the amplitudes of all possible spatial configurations of the four particles. These regions correspond to specific orderings on a line of the four particles. In particular, the large (red) region dominating the figure corresponds to spatial configurations  or
or  . The green region occupies half the spatial volume of the red and corresponds to
. The green region occupies half the spatial volume of the red and corresponds to  or
or  , while the yellow region has one-fourth the volume of the red region and corresponds to
, while the yellow region has one-fourth the volume of the red region and corresponds to  or
or  configurations. A wave function that vanishes on all
configurations. A wave function that vanishes on all  interfaces may now be constructed in each of these regions. However, it is immediately clear that it will have lower energy when it can spread over a larger volume. We thus conclude that the doubly degenerate ground state at
interfaces may now be constructed in each of these regions. However, it is immediately clear that it will have lower energy when it can spread over a larger volume. We thus conclude that the doubly degenerate ground state at  has the structure
has the structure  (taking into account the parity invariance of the Hamiltonian).
(taking into account the parity invariance of the Hamiltonian).
As discussed in the Methods section, one may solve a simple wave equation in the red region and obtain the ground state energy to arbitrary precision. The triangles at the  line in Fig. 2a) show the energies obtained in this manner. We reproduce both the ground state and a set of excited states. All of these have fractional energies and all of them are perfectly ferromagnetically ordered. The remaning states of the spectrum can be obtained by solving in the other regions of Fig. 2b). Note that states with amplitude exclusively in the yellow regions are perfectly spatial antiferromagnetic,
line in Fig. 2a) show the energies obtained in this manner. We reproduce both the ground state and a set of excited states. All of these have fractional energies and all of them are perfectly ferromagnetically ordered. The remaning states of the spectrum can be obtained by solving in the other regions of Fig. 2b). Note that states with amplitude exclusively in the yellow regions are perfectly spatial antiferromagnetic,  and have energies (n + 1/2)
and have energies (n + 1/2)  with integer
with integer  . They are the only parts of the spectrum which can be constructed by starting from identical fermions using Girardeau’s mapping techniques44. The arguments presented here are neither restricted to
. They are the only parts of the spectrum which can be constructed by starting from identical fermions using Girardeau’s mapping techniques44. The arguments presented here are neither restricted to  nor to a harmonic trapping potential and hold for any
nor to a harmonic trapping potential and hold for any  and any shape of the external confinement. They hinge only on the fact that the
and any shape of the external confinement. They hinge only on the fact that the  or
or  configurations occupy the largest volume. For instance, for
configurations occupy the largest volume. For instance, for  the four regions
the four regions  ,
,  ,
,  and
and  are adjacent regions and are connected by Bose symmetry of each component, thus they make up the connected upper red region (
are adjacent regions and are connected by Bose symmetry of each component, thus they make up the connected upper red region ( ) of the coordinate space in Fig. 2b). For
) of the coordinate space in Fig. 2b). For  one finds that only
one finds that only  and
and  are adjacent and connected. This implies that the volume for
are adjacent and connected. This implies that the volume for  is half as large.
is half as large.
In order to further study the correlation between the  and
and  particle subsystems, one can use the pair-correlation function. The pair-correlation function measures the probability of finding a particle from one subsystem (say of type
particle subsystems, one can use the pair-correlation function. The pair-correlation function measures the probability of finding a particle from one subsystem (say of type  ) at position
) at position  given that we know the position,
given that we know the position,  , of a particle in the other subsystem (say of type
, of a particle in the other subsystem (say of type  ). The pair-correlation function for the balanced
). The pair-correlation function for the balanced  case is shown in Fig. 3a) for the case where
case is shown in Fig. 3a) for the case where  is zero and therefore no separation and hence no specific ordering is present, but as
is zero and therefore no separation and hence no specific ordering is present, but as  becomes strongly repulsive evidence of separation is seen as illustrated in Fig. 3b,c). In particular, Fig. 3c) shows that if we have a given particle from one subsystem situated on the negative
becomes strongly repulsive evidence of separation is seen as illustrated in Fig. 3b,c). In particular, Fig. 3c) shows that if we have a given particle from one subsystem situated on the negative  -axis (
-axis ( ) then a particle from the other subsystem is most likely to be found on the positive
) then a particle from the other subsystem is most likely to be found on the positive  -axis (
-axis ( ) and vice versa. These numerical calculations are also supported by our analytical method for the four-body system at
) and vice versa. These numerical calculations are also supported by our analytical method for the four-body system at  . Fig. 3d) shows the analytical result that is virtually identical to the numerical results of Fig. 3c.
. Fig. 3d) shows the analytical result that is virtually identical to the numerical results of Fig. 3c.
Pair-correlation function for ground state of the balanced four-body system. a) The non-interacting case where  . b) and c) Numerically calculated pair-correlation function at
. b) and c) Numerically calculated pair-correlation function at  and
and  . The phase separation starts slowly at
. The phase separation starts slowly at  and the magnetic ordering is fully present at
and the magnetic ordering is fully present at  . d) Analytically calculated pair-correlation function for
. d) Analytically calculated pair-correlation function for  . Notice how c) and d) are virtually indistinguishable.
. Notice how c) and d) are virtually indistinguishable.
Larger systems may in principle be handled in similar fashion by solving wave equations with proper boundary conditions and obtaining the fractional energies in the limit  . However, the increase in dimension of the problem makes this very difficult in practice. In order to further demonstrate that balanced systems have perfect ferromagnetic ground states irrespective of particle number, we have numerically computed the ground state densities for systems with
. However, the increase in dimension of the problem makes this very difficult in practice. In order to further demonstrate that balanced systems have perfect ferromagnetic ground states irrespective of particle number, we have numerically computed the ground state densities for systems with  as shown in Fig. 4. Evidence of the separation of
as shown in Fig. 4. Evidence of the separation of  and
and  can be seen in the total density already in Fig. 4a) for
can be seen in the total density already in Fig. 4a) for  as
as  increases (note the perfect agreement with the analytical result in the limit
increases (note the perfect agreement with the analytical result in the limit  ). We expect the two degenerate ground states to have structure
). We expect the two degenerate ground states to have structure  . In order to prove this perfect ferromagnetic behaviour, we consider the odd and even superposition of the two degenerate states which we expect will yield states with exclusively
. In order to prove this perfect ferromagnetic behaviour, we consider the odd and even superposition of the two degenerate states which we expect will yield states with exclusively  or
or  particles on either side of the system (corresponding to
particles on either side of the system (corresponding to  or
or  ). The corresponding densities are shown in Fig. 4b) and Fig. 4c) and beautifully confirm our expectations.
). The corresponding densities are shown in Fig. 4b) and Fig. 4c) and beautifully confirm our expectations.
Ground state densities of balanced systems. a) Total density for  and different values of
and different values of  . Dotted (red) line corresponds to
. Dotted (red) line corresponds to  while the solid (black) line is for
while the solid (black) line is for  . The dots show the analytical solution for
. The dots show the analytical solution for  . b) and c) Densities for an equal superposition (sum) of the (nearly) two-fold degenerate ground state at
. b) and c) Densities for an equal superposition (sum) of the (nearly) two-fold degenerate ground state at  for
for  , 3, 4 and 5. b) shows
, 3, 4 and 5. b) shows  particles and c) shows
particles and c) shows  particles. d) Rescaled plot of the total density at
particles. d) Rescaled plot of the total density at  . For
. For  the density has been rescaled to a total density with
the density has been rescaled to a total density with  . The dashed line corresponds to the density expected in the many-body limit
. The dashed line corresponds to the density expected in the many-body limit  .
.
As the ground state for  is spatially separated, one may speculate that it can be understood physically as two ideal Bose gases or ‘condensates’ sitting on either side of the system even in this strongly interacting limit. In Fig. 4d) we plot the densities in a rescaled fashion where we multiply by
is spatially separated, one may speculate that it can be understood physically as two ideal Bose gases or ‘condensates’ sitting on either side of the system even in this strongly interacting limit. In Fig. 4d) we plot the densities in a rescaled fashion where we multiply by  ,
,  and
and  on the
on the  ,
,  and
and  densities respectively. The convergence of the results toward the
densities respectively. The convergence of the results toward the  case indicates that the system does behave as two ideal Bose gases as the particle number grows. In the limit
case indicates that the system does behave as two ideal Bose gases as the particle number grows. In the limit  , we would expect the overlap of the two gases to vanish as the energy cost of overlap goes to infinity. We therefore expect that the occupied mode in this large system limit is the first excited state of the harmonic trap which vanishes at the center. The dashed line in Fig. 4d) shows this state rescaled to
, we would expect the overlap of the two gases to vanish as the energy cost of overlap goes to infinity. We therefore expect that the occupied mode in this large system limit is the first excited state of the harmonic trap which vanishes at the center. The dashed line in Fig. 4d) shows this state rescaled to  . This analytical guess displays the same features as the numerical densities and we conclude that already for ten particles the many-body properties are emerging.
. This analytical guess displays the same features as the numerical densities and we conclude that already for ten particles the many-body properties are emerging.
Imbalanced systems
The extremely imbalanced limit, where  and
and  varies, provides a realization of a strongly interacting Bose polaron in 1D, i.e. an impurity that interacts strongly with an ideal Bose gas. In Fig. 5 we plot the densities of systems with
varies, provides a realization of a strongly interacting Bose polaron in 1D, i.e. an impurity that interacts strongly with an ideal Bose gas. In Fig. 5 we plot the densities of systems with  and
and  or
or  . We see that the impurity sits at the edge of the system (Fig. 5a), while the majority component tends to occupy the center (Fig. 5d). We confirm the numerical results by employing an analytical model, which shows excellent agreement. The details can be found in the Methods section. To confirm that the wave function of the strongly interacting ground state has intrinsic phase separation, i.e. has the form
. We see that the impurity sits at the edge of the system (Fig. 5a), while the majority component tends to occupy the center (Fig. 5d). We confirm the numerical results by employing an analytical model, which shows excellent agreement. The details can be found in the Methods section. To confirm that the wave function of the strongly interacting ground state has intrinsic phase separation, i.e. has the form  , we plot the densities for a sum of the nearly degenerate ground states in Fig. 5b,c). As in the balanced case above, we find a perfectly separated ground state behaviour. For instance, if we locate the single
, we plot the densities for a sum of the nearly degenerate ground states in Fig. 5b,c). As in the balanced case above, we find a perfectly separated ground state behaviour. For instance, if we locate the single  particle on one side of the trap, we would thus immediately know that all the
particle on one side of the trap, we would thus immediately know that all the  particles reside on the other side and vice versa. This behaviour is opposite to the case where the
particles reside on the other side and vice versa. This behaviour is opposite to the case where the  particles are identical fermions where the impurity resides mainly in the center of the system41. We have confirmed that this structure is also present for
particles are identical fermions where the impurity resides mainly in the center of the system41. We have confirmed that this structure is also present for  with
with  and it is therefore a generic feature that the two species are perfectly spatially separated (ferromagnetic) in the ground state for strong interactions.
and it is therefore a generic feature that the two species are perfectly spatially separated (ferromagnetic) in the ground state for strong interactions.
Ground state densities of imbalanced systems. a) Impurity density in an  (green) or
(green) or  (purple) systems with
(purple) systems with  . The analytical results for
. The analytical results for  are shown as triangles. b) and c) as in Fig. 4b) and c) but for
are shown as triangles. b) and c) as in Fig. 4b) and c) but for  with
with  or
or  . d) The density of the majority component (
. d) The density of the majority component ( ). All numerical results have been obtained with
). All numerical results have been obtained with  .
.
A remarkable feature of the densities in Fig. 5b,c) is the movement of the centroids of the peaks with particle number. We clearly see the majority moving into the center and the impurity being pushed toward the edge. This demonstrates how an ideal condensate is being built in the center. For large  the energy per particle goes to
the energy per particle goes to  , which implies a single-mode condensate that is becoming macroscopically occupied (see Methods section for details). The relative deviation between numerical and analytical energies is below three percent for
, which implies a single-mode condensate that is becoming macroscopically occupied (see Methods section for details). The relative deviation between numerical and analytical energies is below three percent for  . We thus have an analytic model for the crossover between the few- and many-body limit for the bosonic polaron in one dimension. This includes the external trap that is a reality of most experiments.
. We thus have an analytic model for the crossover between the few- and many-body limit for the bosonic polaron in one dimension. This includes the external trap that is a reality of most experiments.
Discussion
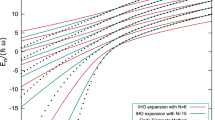
We have shown that a mixture of two ideal Bose systems in one dimension has unusual properties when the inter-species interactions is strong. The systems have energies that are non-integer multiples of  . In Fig. 6 we show the ground state energies for
. In Fig. 6 we show the ground state energies for  in systems with ten particles or less relative to a ground state with only
in systems with ten particles or less relative to a ground state with only  particles. Driving an
particles. Driving an  to
to  transition via radiofrequency spectroscopy would be a possible way to confirm the predicted energies in Fig. 6. This technique has been demonstrated for fermions in recent few-body experiments in 1D17. The results in Fig. 6 show that the energy per particle tends to saturate for large systems and that this happens faster the more imbalanced the system is. We also see that the balanced case has an almost linear energy dependence.
transition via radiofrequency spectroscopy would be a possible way to confirm the predicted energies in Fig. 6. This technique has been demonstrated for fermions in recent few-body experiments in 1D17. The results in Fig. 6 show that the energy per particle tends to saturate for large systems and that this happens faster the more imbalanced the system is. We also see that the balanced case has an almost linear energy dependence.
Ground state energies for .
.
The filled circles show the ground state energy for  relative to the zero-point energy as given by a single-component system of the same size. Each point is marked with the number of particles using the notation
relative to the zero-point energy as given by a single-component system of the same size. Each point is marked with the number of particles using the notation  . The diamonds are the results of the analytical method for the polaron case described in the Methods section. The dashed lines are quadratic interpolations for fixed number of
. The diamonds are the results of the analytical method for the polaron case described in the Methods section. The dashed lines are quadratic interpolations for fixed number of  particles, while the solid line is an interpolation of the energy for the balanced systems.
particles, while the solid line is an interpolation of the energy for the balanced systems.
The ferro- and antiferromagnetic states can also be detected by measuring momentum distributions. In Fig. 7a,d) we show the distributions for  with
with  and
and  , respectively. The purple solid line is the even parity ground state while the solid green line is the excited state with antiferromagnetic ordering. The striking difference of the two distributions implies that they should be easily identifiable in experiments. For comparison, the solid black line with a multi-peak structure shows the distribution for a system of identical fermions. Comparing the solid green and black curves in Fig. 7a,d) clearly demonstrates that, in spite of the fact that these two states have equal energy, the correlations are very different. In Fig. 7a) the dashed black line corresponds to the Tonks-Girardeau hard-core boson state44, which is also seen to be very different from the states discussed here. For imbalanced systems, we find that measuring the impurity momentum distribution, Fig. 7b), yields information about the parity of the state. On the other hand, the majority distributions in Fig. 7c) are identical in the two opposite parity ground states. A characteristic feature seen in Fig. 7b) is the development of oscillatory structure as the number of majority particles increases and pushes the impurity further out in the trap, see also Fig. 5b). A third technique for experimentally addressing the systems we study is controlled tunneling as the trap is gradually lowered16 (see Methods below).
, respectively. The purple solid line is the even parity ground state while the solid green line is the excited state with antiferromagnetic ordering. The striking difference of the two distributions implies that they should be easily identifiable in experiments. For comparison, the solid black line with a multi-peak structure shows the distribution for a system of identical fermions. Comparing the solid green and black curves in Fig. 7a,d) clearly demonstrates that, in spite of the fact that these two states have equal energy, the correlations are very different. In Fig. 7a) the dashed black line corresponds to the Tonks-Girardeau hard-core boson state44, which is also seen to be very different from the states discussed here. For imbalanced systems, we find that measuring the impurity momentum distribution, Fig. 7b), yields information about the parity of the state. On the other hand, the majority distributions in Fig. 7c) are identical in the two opposite parity ground states. A characteristic feature seen in Fig. 7b) is the development of oscillatory structure as the number of majority particles increases and pushes the impurity further out in the trap, see also Fig. 5b). A third technique for experimentally addressing the systems we study is controlled tunneling as the trap is gradually lowered16 (see Methods below).
Momentum distributions. a)  system. The even parity ground state is shown in purple, while the lowest excited state with antiferromagnetic structure is shown in green. For comparison the four-peak black curve represents identical fermions while the narrow peak dashed black curve shows hard-core bosons. b) Ground state impurity distributions for the even (blue) and odd (red) ground states with
system. The even parity ground state is shown in purple, while the lowest excited state with antiferromagnetic structure is shown in green. For comparison the four-peak black curve represents identical fermions while the narrow peak dashed black curve shows hard-core bosons. b) Ground state impurity distributions for the even (blue) and odd (red) ground states with  (solid) and
(solid) and  (dashed). c) Ground state majority distributions for
(dashed). c) Ground state majority distributions for  (solid) and
(solid) and  (dashed). The even and odd parity results coincide for the majority. d) The same as in a) for
(dashed). The even and odd parity results coincide for the majority. d) The same as in a) for  . All curves in the plot have been obtained for
. All curves in the plot have been obtained for  .
.
The separation of components in the ground state for strong interactions is intrinsic to both balanced and imbalanced mixtures, as is the presence of other spatial configurations in specific excited states. Furthermore, the magnetic behaviour discussed above is not connected to the harmonic confinement and should be seen in an arbitrary confining geometry. While we have studied the balanced and the extremely imbalanced limits here, we have checked numerically that the spatial separation of components is an intrinsic feature of the system for systems with ten or less particles. We therefore infer that this will hold also for larger systems, regardless of the population ratio. A simple physical picture can be given in terms of domain walls, i.e. points at which the two components interface. The system tends to minimize the number of domain walls and this principle can be used to understand the ferromagnetic ground state and predict the ordering in energy of other configurations.
In the paradigmatic two-component (spin 1/2) Fermi system, the ground state is never purely ferro- or antiferromagnetic for strong interactions43 and Bose mixtures therefore provide a unique set of quantum ground states for exploring and exploiting magnetic behaviour. The description of these systems clearly goes beyond the famous Bose-Fermi mappings44,45] and we provide not only numerical but also new analytical tools to fill this gap. Importantly, we demonstrate that the crossover from few- to many-body physics can be studied already at the level of ten particles.
Methods
Numerical method
We solve numerically the many-body Schrödinger equation by exact diagonalization with the full Hamiltonian projected onto a finite basis constructed from harmonic oscillator single-particle states. Each many-body basis state is written as a product of symmetrized states of  and
and  particles. The model space truncation is defined by an upper limit of the total energy.
particles. The model space truncation is defined by an upper limit of the total energy.
Instead of the bare zero-range interaction in (1), we consider an effective two-body interaction in order to speed up the convergence of the eigenstates with respect to the size of the many-body basis. The effective potential is constructed in a truncated two-body space and is designed such that its solutions correspond to exact two-body solutions given by the Busch formula46. As explained in detail in Refs. 41,42, this is achieved using a unitary transformation that involves the lowest eigensolutions given by the Busch formula. By construction, this unitary transformation approach will reproduce exact bare Hamiltonian results for the many-body system (both energy spectrum and wave functions) in the limit of infinite model space.
The excellent convergence property of this effective-interaction approach was demonstrated in Ref. 41 and is key to the quality of our numerical results and to our conclusions. In the construction of the effective interactions we benefit from having access to the exact two-body solutions for short-range interactions in harmonic traps. However, we stress that using numerical two-body solutions this approach can be generalized to study many-body systems in higher dimensions with finite-range interactions and in any trapping potential.
Density and pair-correlation profiles
In the second quantization formalism the density profile is calculated by taking the expectation value of the number operator,  at position
at position  , where
, where  creates a particle at position
creates a particle at position  and
and  annihilates it. In other words,
annihilates it. In other words,  , where
, where  is the many-body basis state written as a product of symmetrized states of
is the many-body basis state written as a product of symmetrized states of  or
or  particles. In the same manner the pair-correlation profile is calculated between two particles from different subsystems. It is defined as the expectation value of two number operators,
particles. In the same manner the pair-correlation profile is calculated between two particles from different subsystems. It is defined as the expectation value of two number operators,  and
and  , one from each subsystem, i.e.
, one from each subsystem, i.e.  .
.
In our analytical results we use the following expressions to obtain the density and pair-correlation from the  -body wave function,
-body wave function,  . To get the density of
. To get the density of  particles in the system we need to calculate
particles in the system we need to calculate

Likewise, to obtain the density of a  particle we integrate over all variables except
particle we integrate over all variables except  instead of
instead of  . The
. The  pair-correlation is obtained by calculating
pair-correlation is obtained by calculating

Analytics for balanced systems
Here we outline the calculational procedures required to obtain the exact solutions for the  four-body system in the
four-body system in the  limit. The method can in principle be extended to larger systems, but it becomes increasingly difficult. In the next subsection we provide an alternative method that works well for larger systems in the imbalanced case.
limit. The method can in principle be extended to larger systems, but it becomes increasingly difficult. In the next subsection we provide an alternative method that works well for larger systems in the imbalanced case.
Denote the  coordinates by
coordinates by  and the
and the  coordinates by
coordinates by  , see Fig. 2b). The Hamiltonian is
, see Fig. 2b). The Hamiltonian is

with  the
the  interacting coupling constant and we assume that the
interacting coupling constant and we assume that the  and
and  interactions vanish. We now perform an orthogonal coordinate transformation
interactions vanish. We now perform an orthogonal coordinate transformation

where  are as shown at the bottom of in Fig. 2b) while
are as shown at the bottom of in Fig. 2b) while  denotes the center-of-mass coordinate. The quadratic kinetic and harmonic oscillator terms in
denotes the center-of-mass coordinate. The quadratic kinetic and harmonic oscillator terms in  retain their form under this transformation and one may immediately separate the center-of-mass,
retain their form under this transformation and one may immediately separate the center-of-mass,  , which can be ignored from now on. For the remaining three coordinates we switch to the usual spherical coordinate system, i.e.
, which can be ignored from now on. For the remaining three coordinates we switch to the usual spherical coordinate system, i.e.  ,
,  ,
,  and
and  . Carrying out these transformation we arrive at the relative motion Hamiltonian
. Carrying out these transformation we arrive at the relative motion Hamiltonian

where the sum in the interaction term runs over the four combinations of signs in the argument of the delta function. The first two terms constitute a 3D harmonic oscillator with the well-known regular solution  , where
, where  and
and  is the generalized Laguerre polynomial.
is the generalized Laguerre polynomial.
When  , the angular functions,
, the angular functions,  , are the usual spherical harmonic functions with
, are the usual spherical harmonic functions with  the total and
the total and  the projection angular momentum quantum number. However, in the limit
the projection angular momentum quantum number. However, in the limit  we have to enforce non-trivial boundary conditions whenever
we have to enforce non-trivial boundary conditions whenever  and
and  particles overlap. Let us focus on the region
particles overlap. Let us focus on the region  by restricting to
by restricting to  (solutions for
(solutions for  may be obtained by symmetry arguments or by considering instead
may be obtained by symmetry arguments or by considering instead  ). The arguments of the Dirac delta-functions in Eq. (6) vanish when
). The arguments of the Dirac delta-functions in Eq. (6) vanish when

If we define  , we have
, we have  and
and  . The regions defined by these conditions are illustrated in Fig. 2b). The solid red planes show exactly where the arguments of the interaction Dirac delta-functions have to vanish.
. The regions defined by these conditions are illustrated in Fig. 2b). The solid red planes show exactly where the arguments of the interaction Dirac delta-functions have to vanish.
We now make the simple transformation  and
and  . In these new
. In these new  variables, the boundaries are simply
variables, the boundaries are simply  and
and  , i.e. the function must vanish on the boundary of a square. Finally, one must transform the angular part of the Laplacian into the new variables which yields
, i.e. the function must vanish on the boundary of a square. Finally, one must transform the angular part of the Laplacian into the new variables which yields

By the procedure outlined above we have transformed the problem of solving a harmonic oscillator problem in a non-trivial geometry, i.e. the red region in Fig. 2b), into solving a very simple boundary value problem

with  for
for  . We write the eigenvalue in this way so it matches the usual 3D angular eigenvalue
. We write the eigenvalue in this way so it matches the usual 3D angular eigenvalue  . The equation for
. The equation for  may be straighforwardly solved by using a two-dimensional Fourier expansion of the wave function. This will produce some spurious solutions as we must also impose bosonic symmetry among the two
may be straighforwardly solved by using a two-dimensional Fourier expansion of the wave function. This will produce some spurious solutions as we must also impose bosonic symmetry among the two  and two
and two  particles separately. This translates to the requirement that the solution be symmetric when reflected across the two diagonals. Notice that for each eigenvalue of this problem,
particles separately. This translates to the requirement that the solution be symmetric when reflected across the two diagonals. Notice that for each eigenvalue of this problem,  , we obtain a whole class of solutions with energies
, we obtain a whole class of solutions with energies  as we may add radial excitations.
as we may add radial excitations.
The low-lying solutions of Eq. (9) are given in Table. 1. State number 1, 4, 6, 11, 13 and 15 have the required bosonic symmetries for the balanced system. A number of doubly degenerate states in the spectrum may be used to construct eigenfunctions for a four-body system with  and
and  (or vice versa). In this case the wave function must vanish on the diagonal of the
(or vice versa). In this case the wave function must vanish on the diagonal of the  square domain which is achievable by taking proper linear combinations. The states marked ‘fermions’ in Table. 1 are antisymmetric across the two diagonals in the
square domain which is achievable by taking proper linear combinations. The states marked ‘fermions’ in Table. 1 are antisymmetric across the two diagonals in the  square and provide allowed states for all four-body two-component Fermi systems, i.e. 2+2, 3+1 or four identical fermions. The eigenenergies of the fermionic states have the exact values 7.5, 10.5 and 11.5. Our results differ by
square and provide allowed states for all four-body two-component Fermi systems, i.e. 2+2, 3+1 or four identical fermions. The eigenenergies of the fermionic states have the exact values 7.5, 10.5 and 11.5. Our results differ by  which attests to the accuracy of our method. All states in Table. 1 have been obtained using a modest 400 Fourier basis states. Notice that even though the lowest perfectly antiferromagnetic state for
which attests to the accuracy of our method. All states in Table. 1 have been obtained using a modest 400 Fourier basis states. Notice that even though the lowest perfectly antiferromagnetic state for  bosons is at the same energy as the fermionic state number 5 in Table. 1, they are not related since states with the configurations
bosons is at the same energy as the fermionic state number 5 in Table. 1, they are not related since states with the configurations  or
or  solve a different boundary value problem (corresponding to the yellow regions in Fig. 2b).
solve a different boundary value problem (corresponding to the yellow regions in Fig. 2b).
 for bosons. See the text for details.
for bosons. See the text for details.The energies obtained using this (semi)-analytical approach for the  system are given in Fig. 2a) as triangles at
system are given in Fig. 2a) as triangles at  . The two lowest triangles correspond to the angular ground state (lowest
. The two lowest triangles correspond to the angular ground state (lowest  value) with
value) with  and
and  . The two upper triangles are the first and second excited angular solutions both with
. The two upper triangles are the first and second excited angular solutions both with  . All four solutions have the spatial structure
. All four solutions have the spatial structure  . The blue dots in Fig. 4a) show the ground state density obtained by the transformation method discussed here. The rest of the spectrum at
. The blue dots in Fig. 4a) show the ground state density obtained by the transformation method discussed here. The rest of the spectrum at  can be obtained by solving the boundary value problem in the green (
can be obtained by solving the boundary value problem in the green ( ) and yellow areas (
) and yellow areas ( ). In the latter case a fermionized (totally antisymmetric) wave function is a solution. Our main interest here is to understand the ground state so we leave the remaining states and regions for future investigations.
). In the latter case a fermionized (totally antisymmetric) wave function is a solution. Our main interest here is to understand the ground state so we leave the remaining states and regions for future investigations.
Analytics for imbalanced systems
The analytics provided here is applied for the Bose polaron,  and
and  arbitrary, but can be extended to other systems. The Hamiltonian can be written
arbitrary, but can be extended to other systems. The Hamiltonian can be written

where  is a 1D harmonic oscillator. The
is a 1D harmonic oscillator. The  coordinate denotes the single
coordinate denotes the single  particle, the ‘impurity’, while
particle, the ‘impurity’, while  denotes the coordinates of the majority
denotes the coordinates of the majority  particles. We introduce an adiabatic decomposition of the total wave function of the form
particles. We introduce an adiabatic decomposition of the total wave function of the form

where  is a normalized eigenstate of the eigenproblem
is a normalized eigenstate of the eigenproblem  which depends parametrically on
which depends parametrically on  . This expansion can be related to the Born-Oppenheimer approximation in which case one may consider
. This expansion can be related to the Born-Oppenheimer approximation in which case one may consider  the ‘slow’ variable (typically the nuclear coordinate in molecular physics). In the limit of interest
the ‘slow’ variable (typically the nuclear coordinate in molecular physics). In the limit of interest  , we impose the condition that the total wave function vanishes for
, we impose the condition that the total wave function vanishes for  ,
,  . This implies that
. This implies that  whenever
whenever  . Since there are no intra-species interactions among the
. Since there are no intra-species interactions among the  particles, we can write
particles, we can write

where  denotes the symmetrization operator and
denotes the symmetrization operator and  is the
is the  th normalized eigenstate of
th normalized eigenstate of  which satisfies the condition
which satisfies the condition  . The index
. The index  on
on  denotes the many different ways to distribute the
denotes the many different ways to distribute the  particles among the eigenstates of
particles among the eigenstates of  with the appropriate boundary condition. The Schrödinger equation for
with the appropriate boundary condition. The Schrödinger equation for  can now be written
can now be written

where.


The subscript  on the brackets denote integration over all
on the brackets denote integration over all  . Note that
. Note that  and
and  Ref. 47.
Ref. 47.
As we are interested in the ground state, we assume that all the  particles are in the same state,
particles are in the same state,  , that we specify below. Since the nearest excited states are obtained by promoting one of the
, that we specify below. Since the nearest excited states are obtained by promoting one of the  particles into a single-particle excited orbital, one can show that for large
particles into a single-particle excited orbital, one can show that for large  we can neglect all but the
we can neglect all but the  terms48. Furthermore, in the ground state we expect to find all the
terms48. Furthermore, in the ground state we expect to find all the  particles on one side of the impurity. If we assume that all
particles on one side of the impurity. If we assume that all  particles are to the left of the impurity, we can write the single-particle wave function,
particles are to the left of the impurity, we can write the single-particle wave function,  for
for  , as
, as

for  or
or  and
and  , while for
, while for  and
and  we write
we write

Here  is a normalization factor,
is a normalization factor,  and
and  are the Tricomi and Kummer confluent hypergeometric functions and we have used
are the Tricomi and Kummer confluent hypergeometric functions and we have used  as the unit of length. Here
as the unit of length. Here  is a function that is chosen to satisfy the requirement
is a function that is chosen to satisfy the requirement  . This is equivalent to finding the ground state solution of
. This is equivalent to finding the ground state solution of  for
for  with the condition that the wave function must vanish at
with the condition that the wave function must vanish at  .
.
Once we have determined the functions  and
and  , we can compute the adiabatic potential for the ground state. We have
, we can compute the adiabatic potential for the ground state. We have

Furthermore,  by additivity. The Schrödinger equation for
by additivity. The Schrödinger equation for  is then
is then

Note that the energy  provides a variational upper bound to the exact energy.
provides a variational upper bound to the exact energy.
The energies computed via this method for the polaron are shown in Fig. 6 and agree with the numerical results to within a few percent for the largest particle numbers in the figure. We expect the agreement to become better for even larger particle numbers. Furthermore, since we obtain the full wave function in an analytical form we may also compute the densities of both impurity and majority components. In Fig. 5a) we show the impurity densities for  and
and  , while Fig. 5d) shows the corresponding majority density. We see a striking agreement between the numerical results and the analytically tractable model presented here. The model presented here can be extended to excited states and also to systems with
, while Fig. 5d) shows the corresponding majority density. We see a striking agreement between the numerical results and the analytically tractable model presented here. The model presented here can be extended to excited states and also to systems with  .
.
Tunneling experiments
For 1D few-body systems it is now possible to experimentally access the ratio of tunnelling probabilities for particles with different spins16. For strongly interacting fermionic systems this ratio can be obtained in a rather simple way without knowing the parameters of the experiment (e.g. height of the barrier), as it is determined solely by the probability for the particle to be at the edge of the trap43. For strongly interacting bosonic systems this is unfortunately no longer the case and the detailed parameters of the experiment are needed. To illustrate this consider a system with one impurity in a sea of  majority bosons. For
majority bosons. For  we have shown that for the ground state the impurity is pushed to the edge of the trap whereas the
we have shown that for the ground state the impurity is pushed to the edge of the trap whereas the  bosons can be accurately described using only the lowest energy level of the harmonic trap. Let us assume that the trap is lowered on one side. If the impurity sits on this side we will detect an impurity after some time
bosons can be accurately described using only the lowest energy level of the harmonic trap. Let us assume that the trap is lowered on one side. If the impurity sits on this side we will detect an impurity after some time  which may be very short, since the impurity is very close to the barrier. If, on the contrary, the impurity sits on the other side of the trap we will detect a majority particle after time
which may be very short, since the impurity is very close to the barrier. If, on the contrary, the impurity sits on the other side of the trap we will detect a majority particle after time  . This time may be exponentially enhanced since tunnelling is from the ground state of the trap and the barrier is consequently large. The only system where the ratio of probabilities does not depend on the geometry of the experiment is the
. This time may be exponentially enhanced since tunnelling is from the ground state of the trap and the barrier is consequently large. The only system where the ratio of probabilities does not depend on the geometry of the experiment is the  system where symmetry dictates that one will detect
system where symmetry dictates that one will detect  particles as frequently as
particles as frequently as  particles. As the perfectly antiferromagnetic state is only present for
particles. As the perfectly antiferromagnetic state is only present for  or
or  , its tunneling signature is similar to many other states in the spectrum and detection of the state via tunneling would be quite difficult. For the excited states the ratio of probabilities is again very dependent on the parameters of the experiment. For example for the impurity and
, its tunneling signature is similar to many other states in the spectrum and detection of the state via tunneling would be quite difficult. For the excited states the ratio of probabilities is again very dependent on the parameters of the experiment. For example for the impurity and  bosons system if the experiment is constructed such that only one particle can tunnel then there generally will be many states where only majority particles will be detected. This happens for the states where the impurity sits closer to the center of the trap.
bosons system if the experiment is constructed such that only one particle can tunnel then there generally will be many states where only majority particles will be detected. This happens for the states where the impurity sits closer to the center of the trap.
Additional Information
How to cite this article: Dehkharghani, A. et al. Quantum magnetism in strongly interacting one-dimensional spinor Bose systems. Sci. Rep. 5, 10675; doi: 10.1038/srep10675 (2015).
References
Bethe, H. A. Zur Theorie der Metalle. I. Eigenwerte und Eigenfunktionen der linearen Atomkette. Z. Physik 71, 205–226 (1931).
Lieb, E. H. & Liniger, W. W. Exact analysis of an interacting Bose gas. The general solution and the ground state. Phys. Rev. 130, 1605–1616 (1963).
McGuire, J. B. Interacting Fermions in One Dimension. I. Repulsive Potential. J. Math. Phys. 6, 432–439 (1965).
McGuire, J. B. Interacting Fermions in One Dimension. II. Attractive Potential. 7, 123–132 (1966).
Yang, C. N. Some Exact Results for the Many-Body Problem in one Dimension with Repulsive Delta-Function Interaction. Phys. Rev. Lett. 19, 1312–1315 (1967).
Lieb, E. H. & Wu, F. Y. Absence of Mott Transition in an Exact Solution of the Short-Range, One-Band Model in One Dimension. Phys. Rev. Lett. 20, 1445–1448 (1968).
Haldane, F. D. M. Effective Harmonic-Fluid Approach to Low-Energy Properties of One-Dimensional Quantum Fluids. Phys. Rev. Lett. 47, 1840 (1981).
Haldane, F. D. M. ‘Luttinger liquid theory’ of one-dimensional quantum fluids. I. Properties of the Luttinger model and their extension to the general 1D interacting spinless Fermi gas. J. Phys. C: Solid State Phys. 14, 2585 (1981).
Giamarchi, T. Quantum Physics in One Dimension (Oxford University Press Inc., New York, 2003).
Cazalilla, M. A., Citro, R., Giamarchi, T., Orignac E. & Rigol, M. One dimensional bosons: From condensed matter systems to ultracold gases. Rev. Mod. Phys. 83, 1405 (2011).
Paredes, B. et al. Tonks-Girardeau gas of ultracold atoms in an optical lattice. Nature 429, 277–281 (2004).
Kinoshita, T., Wenger, T. & Weiss, D. S. Observation of a One-Dimensional Tonks-Girardeau Gas. Science 305, 1125–1128 (2004).
Kinoshita, T., Wenger, T. & Weiss, D. S. A quantum Newton’s cradle. Nature 440, 900–903 (2006).
Haller, E. et al. Realization of an Excited, Strongly Correlated Quantum Gas Phase. Science 325, 1224–1227 (2009).
Serwane, F. et al. Deterministic Preparation of a Tunable Few-Fermion System. Science 332, 336–338 (2011).
Zürn, G. et al. Fermionization of Two Distinguishable Fermions. Phys. Rev. Lett. 108, 075303 (2012).
Wenz, A. N. et al. From Few to Many: Observing the Formation of a Fermi Sea One Atom at a Time. Science 342, 457 (2013).
Pagano, G. et al. A one-dimensional liquid of fermions with tunable spin. Nature Phys. 10, 198–201 (2014).
Recati, A., Fedichev, P. O., Zwerger, W. & Zoller, P. Spin-Charge Separation in Ultracold Quantum Gases. Phys. Rev. Lett. 90, 020401 (2003).
Kuklov, A. B. & Svistunov, B. V. Counterflow Superfluidity of Two-Species Ultracold Atoms in a Commensurate Optical Lattice. Phys. Rev. Lett. 90, 100401 (2003).
Duan, L.-M., Demler, E. & Lukin, M. D. Controlling Spin Exchange Interactions of Ultracold Atoms in Optical Lattices. Phys. Rev. Lett. 91, 090402 (2003).
Eisenberg, E. & Lieb, E. H. Polarization of Interacting Bosons with Spin. Phys. Rev. Lett. 89, 220403 (2002).
Nachtergaele, B. & Shannon, S. Ferromagnetic Lieb-Mattis Theorem. Phys. Rev. Lett. 94, 057206 (2005).
Zöllner, S., Meyer, H.-D. & Schmelcher, P. Composite fermionization of one-dimensional Bose-Bose mixtures. Phys. Rev. A 78, 013629 (2008).
Hao, Y. & Chen S. Density-functional theory of two-component Bose gases in one-dimensional harmonic traps. Phys. Rev. A 80, 043608 (2009).
Garcia-March, M. A. & Busch, Th. Quantum gas mixtures in different correlation regimes. Phys. Rev. A 87, 063633 (2013).
Garcia-March, M. A. et al. Sharp crossover from composite fermionization to phase separation in microscopic mixtures of ultracold bosons. Phys. Rev. A 88, 063604 (2013).
Garcia-March, M. A. et al. Quantum correlations and spatial localization in one-dimensional ultracold bosonic mixtures. New J. Phys. 16, 103004 (2014).
Zinner, N. T. et al. Fractional energy states of strongly-interacting bosons in one dimension. Europhys. Lett. 107, 60003 (2014).
Sutherland, B. Further Results for the Many-Body Problem in One Dimension. Phys. Rev. Lett. 20, 98 (1968).
Li, Y.-Q., Gu, S.-J., Ying Z.-J. & Eckern, U. Exact results of the ground state and excitation properties of a two-component interacting Bose system. Europhys. Lett. 61, 368 (2003).
Fuchs, J. N., Gangardt, D. M., Keilmann T. & Shlyapnikov, G. V. Spin Waves in a One-dimensional Spinor Bose Gas. Phys. Rev. Lett. 95, 150402 (2005).
Guan, X., Batchelor, M. T. & Takahashi, M. Ferromagnetic behavior in the strongly interacting two-component Bose gas. Phys. Rev. A 76, 043617 (2007).
Halperin, B. I. & Hohenberg, P. C. Hydrodynamic Theory of Spin Waves. Phys. Rev. 188, 898 (1969).
Halperin, B. I. Dynamic properties of the multicomponent Bose fluid. Phys. Rev. B 11, 178 (1975).
Zvonarev, M. B., Cheianov, V. V. & Giamarchi, T. Spin Dynamics in a One-Dimensional Ferromagnetic Bose Gas. Phys. Rev. Lett. 99, 240404 (2007).
Akhanjee, S. & Tserkovnyak, Y. Spin-charge separation in a strongly correlated spin-polarized chain. Phys. Rev. B 76, 140408 (2007).
Matveev, A. & Furusaki, A. Spectral Functions of Strongly Interacting Isospin-1/2 Bosons in One Dimension. Phys. Rev. Lett. 101, 170403 (2008).
Kamenev, A. & Glazman, L. Dynamics of a one-dimensional spinor Bose liquid: A phenomenological approach. Phys. Rev. A 80, 011603(R) (2009).
Caux, J., Klauser, A. & van den Brink, J. Polarization suppression and nonmonotonic local two-body correlations in the two-component Bose gas in one dimension. Phys. Rev. A 80, 061605 (2009).
Lindgren, E. J., Rotureau, J., Forssén, C., Volosniev, A. G. & Zinner, N. T. Fermionization of two-component few-fermion systems in a one-dimensional harmonic trap. New J. Phys. 16, 063003 (2014).
Rotureau, J. Interaction for the trapped fermi gas from a unitary transformation of the exact two-body spectrum. Eur. Phys. J. D 67, 153 (2013).
Volosniev, A. G., Fedorov, D. V., Jensen, A. S., Valiente, M. & Zinner, N. T. Exact solution of strongly interacting confined quantum systems in one dimension. Nature Communications 5, 5300 (2014).
Girardeau, M. D. Relationship between systems of impenetrable bosons and fermions in one dimension. J. Math. Phys. 1, 516–523 (1960).
Girardeau, M. D. & Olshanii, M. Theory of spinor Fermi and Bose gases in tight atom waveguides. Phys. Rev. A 70, 023608 (2004).
Busch, T., Englert, B.-G., Rzażewski, K. & Wilkens, M. Two cold atoms in a harmonic trap. Found. Phys. 28, 549–559 (1998).
Nielsen, E., Fedorov, D. V., Jensen, A. S. & Garrido, E. The three-body problem with short-range interactions. Phys. Rep. 347, 373–459 (2001).
Dehkharghani, A. S., Volosniev, A. G. & Zinner, N. T. Quantum impurity in a one-dimensional trapped Bose gas. Preprint arXiv:1503.03725 (2014).
Acknowledgements
This work was funded by the Danish Council for Independent Research DFF Natural Sciences and the DFF Sapere Aude program and the European Research Council under the European Community’s Seventh Framework Programme - ERC grant agreement no. 240603.
Author information
Authors and Affiliations
Contributions
N.T.Z. and C.F. devised the project. A.G.V., A.S.D. and N.T.Z. developed the analytical formalism in collaboration with A.S.J. and D.V.F. The numerical method was developed by E.J.L., J.R., C.F. and A.S.D. The calculations were done by A.S.D. under the supervision of D.V.F., A.S.J. and C.F. The initial draft of the manuscript was written by A.S.D., A.G.V. and N.T.Z. and all authors contributed to the revisions that led to the final version.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Dehkharghani, A., Volosniev, A., Lindgren, J. et al. Quantum magnetism in strongly interacting one-dimensional spinor Bose systems. Sci Rep 5, 10675 (2015). https://doi.org/10.1038/srep10675
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep10675
This article is cited by
-
Effects of Interaction Imbalance in a Strongly Repulsive One-Dimensional Bose Gas
Few-Body Systems (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.