Abstract
The search for high-temperature superconductors has been focused on compounds containing a large fraction of hydrogen, such as SiH4(H2)2, CaH6 and KH6. Through a systematic investigation of yttrium hydrides at different hydrogen contents using an structure prediction method based on the particle swarm optimization algorithm, we have predicted two new yttrium hydrides (YH4 andYH6), which are stable above 110 GPa. Three types of hydrogen species with increased H contents were found, monatomic H in YH3, monatomic H+molecular “H2” in YH4 and hexagonal “H6” unit in YH6. Interestingly, H atoms in YH6 form sodalite-like cage sublattice with centered Y atom. Electron-phonon calculations revealed the superconductive potential of YH4 and YH6 with estimated transition temperatures (Tc) of 84–95 K and 251–264 K at 120 GPa, respectively. These values are higher than the predicted maximal Tc of 40 K in YH3.
Similar content being viewed by others
Introduction
The study of hydrogen-rich compounds at hig pressure is mostly motivated by their potential high-tempeature superconducivities at high pressures. In 2004, Ashcroft1 suggested that hydrogen-rich compounds can become metallic and superconducting at lower pressures than hydrogen, preumably because of “chemical compression”. Since then, theoretical studies have revealed a large number of superconducting hydrides (SiH42,3,4, SnH45,6, GeH47, ScH38, YH39, GaH310, H2S11 et al.) at high pressures with predicted Tc ranging from 17 to 86 K. Remarkably, our previously prediction of high Tc (80 K at 160 GPa) in H2S11 has been proven recently from experiments12. Recently, a new type of hydrogen solvated molecular complex SiH4(H2)2 has been synthesized13,14 and was predicted to have a Tc of ~100 K at 250 GPa15, which is much higher than the 17 K observed in SiH42.The experimental and theoretical studies have led to further investigations on hydrides with large hydrogen fraction that may provide a pathway to better superconductors. Using first-principle structure predictions, Zurek et al.16 first predicted three new lithium hydrides (LiH2, LiH6 and LiH8) above 130 GPa, which are stabilized by charge transfer from Li to H. Subsequent studies have revealed a number of hydrides with large hydrogen fractions at high pressures, such as Na-H17, K-H18,19, Rb-H20, Cs-H21, Ca-H22, GeH4-H223 and H2S-H224. Remarkably, some hydrides were predicted to possess high Tc, e.g., ~82 K in LiH6 (300 GPa)25, ~70 K in KH6 (166 GPa)18 and strikingly ~235 K in CaH6 (150 GPa)22.
Among the different hydrides, yttrium hydrides (YHn) are of special interest because each Y atom has three valence electrons and, in principle, could be shared with three H atoms. Experimentally, that during the continuous absorption of H atoms, a reversible transition of YHn between the reflecting YH2 and optically transparent YH3 was observed. This interesting phenomenon offers a great potential for practical application as a “switchable mirror”. Raman26 and infrared27 studies found that the semiconducting YH3 transforms to a metallic fcc structure above 10 GPa. Singnificantly, fcc-YH3 was predicted to be a superconductor with Tc of 40 K at 17.7 GPa, the lowest reported pressure for hydrides to date9. The prediction, however, has not been confirmed by experiment.
At high pressure, it is expected that the valence electronic state of Y atom will change and therefore provides a possibility of bonding with more H atoms. Here, we focus on the formation of Y hydrides with larger H concentration at high pressures of YHn (n = 2, 3, 4, 5, 6, 8). Two new thermodynamically stable hydrides with stoichiometries of YH4 and YH6 were found above 110 GPa. Electron-phonon calculations show both YH4 and YH6 are superconductive with relatively high Tc.
Results
The enthalpies of the candidate structures of YHn found in structure predictions relative to the products of dissociation into Y + solid H2 and YH3 + solid H2 at selected pressures are summarized in Fig. 1 (a,b), respectively. Fig. 1 (a) shows all the stoichiometries considered here possess negative formation enthalpies with respect to Y + solid H2. Among those, YH3 has the lowest energy. Two thermodynamically stable polymorphs, YH4 and YH6, are to be thermodynamically more stable than the decomposition into YH3 + sold H2 were found at 140 and 160 GPa (Fig. 1b). Although YH2, YH5 and YH8 have negative formation enthalpies with respect to Y + solid H2, they are expected to decompose at all pressure. For example, YH2 decomposes into YH3 + Y since the enthalpy is above the tie-line connecting YH3 and Y. Similarly, YH5 and YH8 decompose into YH4 + YH6 and YH6 + H2, respectively (Fig. 1b). Therefore,YH2, YH5 and YH8 are excluded in the discussions hereafter.
Thermodynamical stability of new yttrium hydrides at high pressure.
Formation enthalpies (ΔH) of various Y-H stoichiometries with respect to (Y + solid H2, a) and (YH3 + solid H2, b) at 100, 140 and 160 GPa. ΔH in (a) and (b) were calculated with equations of ΔH = HYHn – (HY + nHH2/2) and ΔH = HYHn – (HYH3 + (n-3)HH2/2, respectively. (c) and (d) present the static enthalpy curves of various structures of YH4 and YH6 relative to (YH3 + solid H2) as functions of pressure without (main figures) and with (insets) zero-point energy corrections, respectively.
So far, YH3 is the only experimentally known yttrium hydrides at high pressure. The structure search readily reproduced the observed fcc structure26,27 at 100 and 150 GPa. As can be seen from Fig. 2 (a), there exist only one type of Y atom occupying the fcc site and two nonequivalent, H1 and H2, atoms at the octahedral and tetrahedral sites. The H-H separation is of 1.9 Å at 120 GPa, clearly indicates no interaction between the H atoms (Fig. 2d). Therefore, the H atoms in fcc-YH3 are monoatomic. fcc-YH3 was previously predicted to be stable in a large pressure region of 20 GPa28 to 197 GPa29 and undergo a superconductor – metal – superconductor transition under pressure9.
High pressure crystal structures of yttrium hydrides.
Crystal structures of fcc-YH3 (a) tI10-YH4 (b) and cI14-YH6 (c). The lattice parameters of tI10-YH4 at 120 GPa are a = 2.87 Å and c = 5.33 Å with Y atom sitting at 2a (0, 0, 0) and two nonequivalent H1 and H2 atoms at 4d (0.5, 0, 0.75) and 4e (0, 0, 0.63), respectively. For cI14-YH6 at 120 GPa, a = 3.7 Å, Y and H atoms occupy 2a (0, 0, 0) and 12d (0, 0.5, 0.25) positions, respectively. (d–f) are three-dimensional charge density difference with isosurface value of 0.01 e/Bohr3 of fcc-YH3, tI10-YH4 and cI14-YH6, respectively. Blue and yellow colors represent losing and gaining electrons, respectively.
Figure 1 (c,d) show the formation enthalpies of YH4 and YH6 with respect to YH3 + solid H2 as functions of pressure. The formation enthalpy of YH4 becomes negative relative to YH3 + solid H2 near 128 GPa (Fig. 1c). It is important to include the quantum nuclear zero-point energies (ZPE) when considering the energetics of systems containing light atoms. We therefore calculated the ZPEs of YH4, YH3 and H2 phases within the quasi-harmonic approximation. When ZPE corrections are included, the predicted pressure for the onset of stability of YH4 is lowered to 112 GPa (inset in Fig. 1c). The stable YH4 has a tetragonal structure (space group I4/mmm, denoted tI10 hereafter, Fig. 2b) with two formula units per unit cell. We found that the tI10-YH4 has the same structure type with tI10-CaH422. The tI10 structure at 120 GPa consists of body-centered arranged Y atoms and two nonequivalent H1 and H2 atoms with H1-H2 and H2-H2 distances of 1.58 and 1.33 Å, respectively. Valence electrons localization was found between the two neighbouring H2 atoms while absent between H1 and H2 atoms (Fig. 2e). This indicates the presence of both molecular “H2” and monoatomic H in tI10-YH4.
YH6 becomes thermodynamically more stable than YH3 + solid H2 above 122 GPa (Fig. 1d). The onset pressure of the stability of YH6 is reduced to 110 GPa when considering the ZPE effect (inset in Fig. 1d). In the thermodynamically stable pressure region, YH6 adopts a cubic structure with space group Im-3m (2 f.u./unit cell, denoted cI14 hereafter, Fig. 2c). The “H6” hexagons are forming a corner-shared sodalite-like cage with a Y atom at the center, the same sodalite structure found in CaH6 above 150 GPa22. In this case, the H-H distance of 1.31 Å at 120 GP is longer than in CaH6. Despite the longer distance, covalent interaction between H atoms is clearly visible from the localized valence electrons between the H atoms (Fig. 2f).
Discussion
We found three types of H species in YHn compounds, monatomic H in YH3, monatomic H+molecular “H2” in YH4 and hexagonal “H6” in YH6. Since molecular H2 has a filled covalent σ bond, the additional electrons donated from Y will occupy the antibonding σ* bond, resulting in a stretched or even dissociated H-H bond. For example, the formation of YH3 can be described by the reaction 2Y + 3H2 → 2YH3. Assuming all 6 valence electrons (3 from each Y atom) were transferred to the H2, then, each H2 would accommodate two additional electrons into the σ* orbital and, thus, breaking the H2 molecule into monatomic H. Integration of the electron density shows that each H1 (H2) atom in fcc-YH3 have accommodated an additional 0.54 (0.47) electrons. A similar description can be used for the formation of YH4. In this the reaction is Y + 2H2 → YH4. There are three electrons available to two H2 molecules. Therefore, one H2 bond is completely broken into two monoatomic H and the remaining electron occupied the σ* one the second H2, thereby weakening the bond and resulted in a longer H-H distance of 1.33 Å. The additional charge of the monatomic H1 in tI10-YH4 is calculated to be 0.42 electrons. Only 0.29 electrons were added to H2 in tI10-YH4. Finally, the formation of YH6 can be described as Y + 3H2 → YH6. In this case only, one electron is added to each H2 and the H-H bond is elongated to 1.31 Å, in close agreement with the “molecular” H2 in YH4. In cI14-YH6, each H atom has accepted 0.25 electrons, which is not enough to dissociate the H2 molecule.
A previous study22 has shown that 4s-3d charge transfer turns Ca from s-dominant into s-d dominant at high pressure, similar to the electronic configuration of Y atom. Therefore, the presence of same structure types in YH4 (YH6) and CaH4 (CaH6) is not accidental. However, the H-H distance of “H2” molecule in YH4 (1.33 Å) is much longer than that (0.81 Å) in CaH4 at 120 GPa as Y transfer one more valence electron to H2 than Ca resulting in a longer H-H distance in YH4 (YH6). The empirical consideration is support from quantitative calculations of the difference of the electron density of tI10-YH4 to that of a hypothetical structure consisting only H sublattice. It is clearly shown in Fig. 3(a,b), that there is no electron density (covalent bond) between the two H2 atoms in the pure H structure. However, when the Y atoms were present, localized electrons are found between two H2 atoms. Therefore, the charge transfer from Y to H2 is responsible to the formation of molecular “H2” in YH4. Similarly, the foramtion of “H6” hexagons in YH6 results from the accommodation by H of excess electrons from Y atom (Fig. 3c,d). For comparison, a survey of molecular “H2” in most hydrogen-rich compounds only show a slightly elongated H-H bond length than pure solid H2. Examples are 0.87 Å in GeH47, 0.79 Å in SnH46, 0.84 Å in SiH2(H2)215, 0.76 Å in LiH216 and 0.8 Å in NaH917.
The electronic properties, lattice dynamical and electron-phonon coupling parameter (EPC) of tI10-YH4 and cI14-YH6 have been calculated. Both tI10-YH4 and cI14-YH6 are found to be metals from the band structures presented in Fig. 4. We found three features common to tI10-YH4 and cI14-YH6: (i) the large densiy of states at the Fermi level (NF), 0.44 eV−1 per f.u. in tI10-YH4 and 0.6 eV−1 per f.u. in cI14-YH6 at 120 GPa; (ii) the concurrence of falt and steep electronic bands near the NF, providing a possibility of the pairing of eletrons at the NF30; (iii) strong Y-H hybridization derived from the significant overlap of Y- and H-DOS. Note that in a preivous study9 it was demonstrated that the Y-H hybridization is responsible for the superconductivity in YH3.
Electronic band structures and projected density of states (PDOS).
Electronic band structures and PDOS (in units of eV−1 per f.u.) of tI10-YH4 (a) and cI14-YH6 (b) at 120 GPa. Dashed red lines in left pannels are the GW-corrected band structures. The horizontal dashed lines represent Fermi level (EF). The numbers (1–6) in (b) label the six bands accrossing the Fermi energy.
Figure 5 shows the calculated phonon dispersions, phonon density of states (PHDOS), Eliashberg spectral function (α2F(ω)/ω)and EPC integrated (λ(ω))for tI10-YH4 and cI14-YH6 at 120 GPa. The absence of any imaginary phonon modes proves the dynamical stabilities of both compounds. As expected, both phonon spectra are separeted into two frequency regions, with the low frequencies (<10 THz) dominated by the vibrations of Y atom while the high end of the spectra by H atoms. In tI10-YH4, the resulting EPC parameter λ is 1.01 at 120 GPa, which is comparable to the maximum value (~1.49) predicted for fcc-YH3. Note that the low-frequency vibrations contribute to 18% of the total λ while the ramaining 82% comes from H vibrations. Circles with radius proportional to the EPC were also plotted in Fig. 6 to illustrate the contributions associated with different phonon modes. One can observe that nearly all phonon modes contribute to the overall λ, reflecting a three-dimensional nature of the structure.
Phonon properties and Eliashberg spectral function.
Phonon dispersions, projected phonon density of states (PHDOS), Eliashberg spectral function α2F(ω)/ω and EPC integration of λ(ω) of tI10-YH4 (a) and cI14-YH6 (b) at 120 GPa. Red circles in the two left pannels indicate the phononline width with a propotional to the strength. (c) The nesting function of cI14-YH6 along several high-symmetry lines of Q calculated at 120 GPa. The present calculation employs 3094 k points and 126 Q points, which result in the evaluaion of energy εk + Q at 390000 points.
Surprisingly, according to the calculation, the EPC parameter λ of cI14-YH6 reaches 2.93 at 120 GPa, even larger than that (2.69 at 150 GPa22) in cI14-CaH6. However, the Eliashberg phonon spectral functions of cI14-CaH6 and cI14-YH6 are quite different. The EPC in cI14-CaH6 was derived primarily from the two phonon modes (T2g and Eg) at the zone center Γ point. However, we observed an overall contribution of different modes to λ along N-P-Γ-N directions. Moreover, 90% of the total λ is contributed by H vibrations. The superconductivity in YH6 is associated with the Kohn anomalies observed in the phonon dispersion of the phonon branch Γ-H and H-N. The calculation of the nesting function (Fig. 5c) confirms this expectation and clearly show strong nesting along Γ-H and H-N directions. Compare to the other 5 bands crossing the Fermi level, the Fermi surface of strongly nested band (Fig. 6c) shows a complex “vase”-like topology with strong nesting along Γ-H.
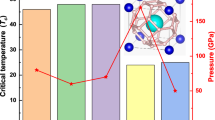
Tc was estimated from the spectral function (α2F(μ)) by numerically solving the Eliashberg equations31 with typical choice of Coulomb pseudopotential μ* = 0.1−0.13. The Coulomb repulsion is taken into account in terms of the μ* scaled to a cutoff frequency32. At 120 GPa, the calculated Tc is 84–95 K for tI10-YH4, much higher than the maximal 40 K predicted for fcc-YH39. Note that tI10-YH4 has a much larger logarithmic average frequency of 1119 K than fcc-YH3 (350 K9) due to the presence of molecular “H2”, which helps to enhance the superconductivity. For cI14-YH6, Tc value of 251–264 K was estimated. This value is comparable to the predicted Tc (220–235 K at 150 GPa) in CaH622. Although, in principle, there is no upper limit to the Tc value within the Midgal-Eliashberg theory, remarks on the very high Tc value of cI14-YH6 must be view with caution. The EPC calculations were based on the harmonic approximation and without the consideration of electron correction effects. A previous study38 had shown that anharmonicity of atomic motion may reduce or even suppress the superconductivity of AlH3 due to the renormalization of the lower vibration modes by anharmonicity33. However, this suggestion is contrary to the observation that anharmonic vibraions will significantly enhance Tc in case of disordered compounds34. Another important, but often neglected, situation is that the Fermi level topology may be altered in improved electronic band structure including corrections to self interaction and electron correlation effects. In AH3, the parallel bands favouring nesting disappeared in the GW calculated band structure35. Here, GW band struture calculations were performed for tI10-YH4 and cI14-YH6. No significant change in the band structures, particularly for the bands near or crossing the Fermi level, was found in both case (Fig. 4). Therefore, the discussion presented above will still be valid and we expect YH4 and YH6 are good superconductors.
Methods
Structure predictions for YHn were performed using the particle swarm optimization technique implemented in the CALYPSO code36,37. In recent studies, it was shown that the approach was successful on the prediction of high pressure structures on both elemental and binary compounds, such as N38, Ca-H22, H2S11 and BeH239. In this work, systematic structure search were performed on six stoichiometries (YH2, YH3, YH4, YH5, YH6 and YH8) at 100 and 150 GPa. Model cells up to 4 formula units (f.u.) for each stoichiometry were used. The structure search was considered converged when~1000 successive structures were generated after a lowest energy structure was found.
ab initio structure relaxations were performed using density functional theory within the Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation (GGA) as implemented in the Vienna ab initio simulation package (VASP)40. The band structures were calculated with both PBE-GGA and GW methods41. The GW interpolated band structures were computed using WANNIER9042. The all-electron projector augmented wave (PAW)43 method was adopted with 1s and 4s24p64d15s2 treated as valence electrons for H and Y, respectively. An energy cutoff of 700 eV and a Monkhorst-Pack Brillouin zone sampling grid with a resolution of 0.5 Å−1 were used in the structure searches. Selected low energy structures were then re-optimized with a denser grid better than 0.2 Å−1 and a higher energy cutoff of 1000 eV. Phonon dispersion and electron-phonon coupling (EPC) calculations were performed with density functional perturbation theory using the Quantum-ESPRESSO package44. Norm-conserving pseudopotentials for Y and H were considered with a kinetic energy cutoff of 140 Ry. 8 × 8 × 8 (59 q-points) and 10 × 10 × 10 (47 q-points) q-meshes in the first Brillouin zones were used in the EPC calculations for YH4 and YH6, respectively. Monkhorst-Pack grids of 32 × 32 × 32 and 40 × 40 × 40 were used to ensure k-points sampling convergence with Gaussians of width 0.03 Ry for YH4 and YH6, respectively, in order to approximate the zero-width limit in the calculations of the EPC parameter, λ.
Conclusion
In conclusion, structure predictions have demonstrated that yttrium atom can react with more than three hydrogens under pressure. Two high-hydride phases, YH4 and YH6, were predicted to be thermodynamically stable relative to YH3 and H2 above 110 GPa. At the stable pressure ranges, YH4 has a bct strucure containing both moniatomic H and molecular “H2” while YH6 adopted a bcc structure with a H sodalite-like cage. Electron-phonon coupling calculations show that both YH4 and YH6 are supercodncutive with Tc higher than YH3. The results presented here support the suggestion that compressing the mixture of elements (compounds) and hydrogen is a way to search high-temperature superconductors. In addition, in principle, YH4 and YH6 can be synthesized by compressing the mixture of YH3 and H2 above 110 GPa.
Additional Information
How to cite this article: Li, Y. et al. Pressure-stabilized superconductive yttrium hydrides. Sci. Rep. 5, 9948; doi: 10.1038/srep09948 (2015).
References
Ashcroft, N. W. Hydrogen Dominant Metallic Alloys: High Temperature Superconductors? Phys. Rev. Lett. 92, 187002 (2004).
Eremets, M. I., et al. Superconductivity in hydrogen dominant materials: silane. Science 319, 1506–1509 (2008).
Chen, X., et al. Superconducting Behavior in Compressed Solid SiH4 with a Layered Structure. Phys. Rev. Lett. 101, 077002 (2008).
Martinez-Canales, M., et al. Novel structures and superconductivity of silane under pressure. Phys. Rev. Lett. 102, 87005 (2009).
Tse, J. S., Yao, Y. & Tanaka, K. Novel Superconductivity in Metallic SnH4 under High Pressure. Phys. Rev. Lett. 98, 117004 (2007).
Gao, G., et al. High-pressure crystal structures and superconductivity of Stannane (SnH4). Proc. Nat. Acad. Sci. U.S.A . 107, 1317–1320 ( 2010).
Gao, G., et al. Superconducting High Pressure Phase of Germane. Phys. Rev. Lett. 101, 107002 (2008).
Kim, D. Y., et al. General trend for pressurized superconducting hydrogen-dense materials. Proc. Nat. Acad. Sci. U.S.A . 107, 2793–2796 (2010).
Kim, D. Y., Scheicher, R. H. & Ahuja, R. Predicted High-Temperature Superconducting State in the Hydrogen-Dense Transition-Metal Hydride YH3 at 40 K and 17.7 GPa. Phys. Rev. Lett. 103, 077002 (2009).
Gao, G., et al. Metallic and superconducting gallane under high pressure. Phys. Rev. B 84, 064118 (2011).
Li, Y., et al. The metallization and superconductivity of dense hydrogen sulfide. J. Chem. Phys. 140, 174712 (2014).
Drozdov, A. P., Eremets, M. I. & Troyan, I. A. Conventional superconductivity at 190 K at high pressures. arXiv preprint arXiv:1412.0460, (2014).
Wang, S., Mao, H., Chen, X. J. & Mao, W. L. High pressure chemistry in the H2-SiH4 system. Proc. Nat. Acad. Sci. U.S.A . 106, 14763–14767 (2009).
Strobel, T. A., Somayazulu, M. & Hemley, R. J. Novel Pressure-Induced Interactions in Silane-Hydrogen. Phys. Rev. Lett. 103, 65701 (2009).
Li, Y., et al. Superconductivity at ~100 K in dense SiH4(H2)2 predicted by first principles. Proc. Nat. Acad. Sci. U.S.A . 107, 15708–15711 (2010).
Zurek, E., et al. A little bit of lithium does a lot for hydrogen. Proc. Nat. Acad. Sci. U.S.A . 106, 17640 (2009).
Baettig, P. & Zurek, E. Pressure-stabilized sodium polyhydrides: NaH n (n>1). Phys. Rev. Lett. 106, 237002 (2011).
Zhou, D., et al. Ab initio study revealing a layered structure in hydrogen-rich KH6 under high pressure. Phys. Rev. B 86, 014118 (2012).
Hooper, J. & Zurek, E. High pressure potassium polyhydrides: a chemical perspective. J. Phys. Chem. C 116, 13322–13328 (2012).
Hooper, J. & Zurek, E. Rubidium Polyhydrides Under Pressure: Emergence of the Linear H3−Species. Chem. Eur. J . 18, 5013–5021 (2012).
Shamp, A., Hooper, J. & Zurek, E. Compressed cesium polyhydrides: and H3–three-connected nets. Inorg. Chem. 51, 9333–9342 (2012).
Wang, H., et al. Superconductive sodalite-like clathrate calcium hydride at high pressures. Proc. Nat. Acad. Sci. U.S.A . 109, 6463–6466 (2012).
Strobel, T. A., Chen, X. J., Somayazulu, M. & Hemley, R. J. Vibrational dynamics, intermolecular interactions and compound formation in GeH4(H)2 under pressure. J. Chem. Phys. 133, 164512 (2010).
Strobel, T. A., et al. Novel Cooperative Interactions and Structural Ordering in H2S-H2 . Phys. Rev. Lett. 107, 255503 (2011).
Xie, Y., Li, Q., Oganov, A. R. & Wang, H. Superconductivity of lithium-doped hydrogen under high pressure. Acta Crystallographica Section C: Structural Chemistry 70, 104–111 (2014).
Kume, T., et al. High-pressure study of YH3 by Raman and visible absorption spectroscopy. Phys. Rev. B 76, 024107 (2007).
Ohmura, A., et al. Infrared spectroscopic study of the band-gap closure in YH3 at high pressure. Phys. Rev. B 73, 104105 (2006).
de Almeida, J. S., et al. On the dynamical stability and metallic behavior of YH3 under pressure. Appl. Phys. Lett. 94, 251913 (2009).
Li, Y. & Ma, Y. Crystal structures of YH3 under high pressure. Solid State Commun. 151, 388–391 (2011).
Simon, A. Superconductivity and Chemistry. Angew. Chem. Int. Ed. 36, 1788–1806 (1997).
Eliashberg, G. Interactions between electrons and lattice vibrations in a superconductor. Sov. Phys. JETP 11, 696 (1960).
Yao, Y., et al. Superconductivity in lithium under high pressure investigated with density functional and Eliashberg theory. Phys. Rev. B 79, 054524 (2009).
Wang, X., et al. Cagelike diamondoid nitrogen at high pressures. Phys. Rev. Lett. 109, 175502 (2012).
Rousseau, B. & Bergara, A. Giant anharmonicity suppresses superconductivity in AlH3 under pressure. Phys. Rev. B 82, 104504 (2010).
Garland, J., Bennemann, K. & Mueller, F. Effect of lattice disorder on the superconducting transition temperature. Phys. Rev. Lett. 21, 1315 (1968).
Shi, H., Zarifi, N., Yim, W. & Tse, J. Electron band structure of the high pressure cubic phase of AlH3 . J. Phys: Conf. Ser. 377, 012093 (2012).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063 (2012).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Wang, Z., et al. Metallization and superconductivity of BeH2 under high pressure. J. Chem. Phys. 140, 124707 (2014).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Aryasetiawan, F. & Gunnarsson, O. The GW method. Rep. Prog. Phys. 61, 237 (1998).
Mostofi, A. A., et al. wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Scandolo, S., et al. First-principles codes for computational crystallography in the Quantum-ESPRESSO package. Z. Kristallogr. 220, 574–579 (2005).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Acknowledgements
Y. L., J. H. and Y. W. acknowledge the funding supports from the National Natural Science Foundation of China under Grant Nos. 11204111, 11404148 and 11404128, the Natural Science Foundation of Jiangsu province under Grant No. BK20130223 and the PAPD of Jiangsu Higher Education Institutions. The charge densities were drawn using the VESTA45 software.
Author information
Authors and Affiliations
Contributions
Y. L. and Y. W. conceived the idea. Y.L., J. H. and H. L. performed the calculations. Y L. and J. T. and Y. M. wrote the manuscript with contribution from all.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Li, Y., Hao, J., Liu, H. et al. Pressure-stabilized superconductive yttrium hydrides. Sci Rep 5, 9948 (2015). https://doi.org/10.1038/srep09948
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep09948
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.