Introduction

Surface plasmon polaritons (SPPs) are evanescent electromagnetic surface waves that propagate along metal-dielectric layer interfaces and continue to be of much practical and fundamental interest1,2,3,4,5,6. Perfect absorption (PA) is another interesting phenomenon that may occur in thin metal films. While PA requires an absorbing layer, it does not necessarily involve SPPs7,8,9,10,11 (see Supplementary Information for more details). Systems containing thin metal or absorbing layers may be coupled with other structures (e.g., nanoparticles, nanoholes, quantum dots, etc.) to achieve an even greater variety of optical phenomena. Examples include negative refraction in metamaterials12, ultra-confined waveguiding13,14, lasing15,16,17, extraordinary field enhancement and non-linear optical effects18,19,20,21,22,23,24, surface plasmon-coupled emission (SPCE)25,26, and, recently, inhomogeneous SPPs27.

The optical response of thin film structures can be understood in terms of resonances that depend on the incident angle and frequency of the excitation source and the material properties and dimensions of the films28,29. The resonant properties of arbitrary thin-film structures can be determined from a generalization of the Fresnel equations for reflection/transmission into the complex plane and the application of boundary conditions that do not involve any incident plane wave sources. The solutions of such equations, termed modes, can be solved either by analytical methods in the case of very simple structures or by numerical methods28,30.

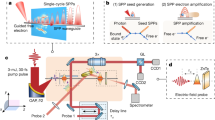
When considering samples composed of metallic films on a glass substrate in air, SPPs may be excited via attenuated total reflection (ATR) experiments. The most common type of ATR experiment is within the Kretschmann-Raether (K-R) configuration2, wherein light at some angle relative to the normal to the film is incident on the metal film from below in the glass side. In such experiments, a very thin germanium layer is often used to promote adhesion of the metal film to the glass prism. SPPs on the metal/air side may be excited with appropriate momentum matching conditions being satisfied. We illustrate a modified setup for performing K-R excitation in Fig. 1a. In this configuration, observation of a strong minimum feature in the reflection as a function of the angle of incidence is most commonly interpreted as a signature of SPP excitation2,3,4,5,31,32,33,34. It is also natural to suspect what is being excited in the system when the reflection is a minimum is something akin to a fully bound modal solution, i.e. a mode that has evanescent character away from the metal film both above and below it. However, several distinct studies have provided a serious challenge to the notion that the SPP is represented by the fully bound modal solution that correlates with a reflection minimum in an attenuated total reflection (ATR) experiment35,36,37,38,39. One important point raised in the early study by Burke, Stegeman and Tamir36 is that SPPs on thin metal films correspond to “leaky modes” that radiate into the high-index substrate at an angle characteristic of the SPP dispersion, θSPP = sin−1(nsub/nSPP), where nSPP is the effective index of the SPP (related to its dispersion) and nsub is the refractive index of the substrate material. In Fig. 1b, we illustrate an experimental configuration for exciting SPPs from the air side of a glass/metal film/air structure that uses metal nanoparticles as scatterers to achieve the momentum matching required for SPP excitation. This configuration allows measurement of the SPP dispersion via the leakage radiation40 without interference from the reflection background. We verified experimentally and by simulation that the nanoparticles have negligible impact on the reflectance spectrum and that they impact the leakage spectrum primarily by broadening the leakage signal about the SPP leakage angle (see Supplementary Information).

Figure 1
figure 1

a) Setup for performing K-R excitation of SPPs.

A microscope objective is used to generate a range of incident wavevector components from a collimated monochromatic light source. The reflected light is collected by a CCD detector, which allows us to observe the characteristic minimum in the K-R experiment as a ring. (b) Setup for measuring leakage radiation of SPPs launched from above. Gold nanoparticles are used to scatter monochromatic incident light providing sufficient momentum to excite SPPs.

Full size image

Results and Discussion

In this work, we consider a four-layer system consisting of a glass prism (layer 1), a 4 nm germanium film (layer 2), a 50 nm gold film (layer 3), with air above (layer 4). We also analyzed 3-layer structures consisting of glass, gold and air and obtained consistent results (see Supplementary Information). The samples were mounted on top of a high numerical aperture (NA = 1.4) objective of an inverted microscope with a laser provided by a broadband supercontinuum source (Fianium). Narrow excitation bandwidth was filtered from the white light using an acousto-optic tunable filter. Thus, our quasi-monochromatic excitation could be tuned across the optical spectral region. In the K-R configuration (Fig. 1a) the light was focused on the sample from the bottom side through the high NA objective and the reflected signal was collected through the same lens. A 50/50 beamsplitter was used to separate the excitation and detection paths and guide the signal to the CCD camera, which served as a 2D detector. In the leakage radiation configuration (Fig. 1b), the laser light was coupled into a multi-mode fiber and its output was loosely focused on the sample from the top side, using a lens with 30 mm focal length. The top illumination excited the localized plasmon modes of ~ 100 nm gold nanoparticles deposited on top of the metal film, which in turn coupled into the propagating SPP modes at the gold/air interface. Leakage radiation from the SPP modes was then collected through the high NA objective from the glass (bottom) side of the sample and sent to the detector using the same path as in the K-R configuration. The strong scattering response of the nanoparticles is important for effective coupling into SPP modes because our metal films lack significant surface roughness and we are using optical frequencies where the absorption losses in the gold film are significant.

In both configurations, a Bertrand lens was inserted in the detection path to image the back-focal (pupil) plane of the objective onto the CCD camera. Representative back-focal plane images for reflection (K-R) and leakage radiation configurations are shown in Fig. 2a and Fig. 2b, respectively. In these images the distance Δx of each pixel from the optical axis determines the reflection (emission) angle, θ = arcsin(Δx/a), where a is the size of the back aperture of the objective41. The angle θ is a direct measure of the transverse wave vector of the emitted light and hence the SPP dispersion. The maximum observable angles (±68°) in our experiments are determined by the NA of the detection objective. The characteristic reflectance dip that is generally associated with SPP excitation is observed in the K-R configuration (Fig. 2a). In the standard interpretation of K-R excitation, the angle of this dip is also understood to be a direct measure of the SPP dispersion, hence the validity of this interpretation requires that the K-R minimum coincide with the SPP leakage angle. The crescent shape of the dip is a consequence of linear polarization of the excitation field. The top illumination configuration (Fig. 2b) features a circular ridge corresponding to the leakage radiation of plasmons propagating in all directions on the glass/air interface. Circular polarization of light was chosen in this configuration to ensure uniform excitation of plasmons in all directions and the distortion of this uniformity seen in Fig. 2b is due to the mixing of the polarization states as light travels through the optical fiber. The bright spot in the central part of the image corresponds to the transmitted light from the loosely focused top illumination beam.

Figure 2
figure 2

a) Experimental back-focal plane images using 690 nm light for a) K-R configuration and b) leakage radiation configuration.

Full size image

K-R and leakage measurements performed on Ge/Au films using 514 nm light show a startling discrepancy between the angle of the K-R minimum and the leakage radiation angle, with the former occurring at 54° and the latter occurring at 47° (see Fig. 3). In this letter, we provide, for the first time to our knowledge, definitive experimental and theoretical evidence that the reflectance minimum in K-R experiments does not signal direct coupling into SPPs, but indicates coupling into a different resonant mode which we call the perfectly absorbing (PA) mode.

Figure 3
figure 3

a) Data from K-R experiment (Reflection) compared to Fresnel R and , showing a significant displacement between reflectance minimum and field maximum.

(b) Data from Leakage experiment (SPP leakage radiation) compared to FDTD simulation of Leakage experiment. (c) Dispersion relations for the SPP and PA modes for the 4-layer structure. Leakage maximum (at 47°), closely matches SPP dispersion (45°) and maximum, while reflection minimum (54°) closely matches PA dispersion. Intensities of experimental and Fresnel quantities are rescaled. see Supplementary Information for details.

Full size image

The modal solutions for thin films provide some insight into this discrepancy. The optical response of the structure in question arises from the frequency-dependent refractive index, Nj(ω) = nj(ω) + ikj(ω), where nj and kj are real numbers. The associated electrical permittivity is . Layers j = 1 and j = 4 can be taken to be semi-infinite in extent and are characterized by real, positive refractive indices, and , for glass and air, respectively. The central layers, germanium (j = 2) and gold (j = 3) have frequency dependent, complex refractive indices, which are taken from Ref. 42 for germanium and Ref. 43 for gold.

The films are homogeneous in the y-direction (see Fig. 1) and we assume p-polarized light so that the relevant tangential electrical field component is with28,30

where the z-component of the wavevector in each layer satisfies , with k0 = ω/c. In the notation above, E1 is in glass, E2 is in Ge, E3 is in Au and E4 is in air. The boundary conditions for satisfying Maxwell's equations require the tangential components of the electric field be continuous across each interface, which leads to28:

(See the Supplementary Information for more detail).

The Fresnel equations for the structure are obtained by setting to 1 and to 0. The complex Fresnel reflection and transmission amplitudes are given by and , respectively. The reflectance is given by and the transmittance is given by , where θ1 represents the incident angle and θ4 represents the angle of refraction of the field in layer 4.

The modal equations that determine the dispersion of the SPPs may be obtained if the incoming wave amplitudes and are set to zero. The solution to Eq. (1), M1,1(β,α) = 0, may be used to find the SPP dispersion, where we use β to denote Re(kx) and α to denote Im(kx). To maintain continuity with the Fresnel equations, we enforce that Re(kz1)> 0 and Im(kz4)> 0 when solving Eq. (1). Consequently, the SPP dispersion corresponds to the location of infinities in R and t in the complex β − α plane.

We propose a new formulation of the modal equations for obtaining the PA dispersion where the wave amplitudes and are set to zero. At odds with the standard modal solution, this mode contains a radiation source in layer 1 as a boundary condition. In this case, Eq. (1) is solved when M2,1(β,α) = 0 and the PA dispersion is seen to depend on the positions of reflectance zeros in the complex β − α plane. Under suitable circumstances, this zero can occur when α is zero. In such cases, because the transmittance is also zero, the mode corresponds to perfect absorption when light is incident at . We note that this mode may also be found from the solution to the ordinary homogeneous equations when Re(kz1) <0 and Im(kz4)> 0, see Supplementary Information for more detail. We also note that 2 additional modes can be found, but for the frequencies considered here, they lie outside the glass light-cone and cannot couple to either the SPP or PA mode.

To complement the K-R experiment, we compute the angle-dependent Fresnel R and amplitudes, where is proportional to the near-field intensity of the surface wave created by K-R excitation2,28. We observe the near-field intensity peaks at 45°, while the reflectance minimum occurs at 54° (Fig. 3a). Results from the leakage radiation experiment show a maximum near 47°, in close agreement to the angle corresponding to the field maximum rather than the angle corresponding reflectance minimum (Fig. 3). The presence of the gold nanoparticles introduces additional loss channels, which can be seen to broaden the leakage signal. This feature is also observed in finite-difference time-domain (FDTD) simulations of the leakage experiment (see Supplementary Information for further information). From examination of the modal solutions, we see that SPP dispersion is in close agreement with the leakage maximum, (near-field), while the PA dispersion is in excellent agreement with the reflectance minimum (Fig. 3c). Measurements and calculations performed on the same system without the 4nm Ge underlayer produce similar results, with slightly less pronounced discrepancy between PA and SPP angles. Hence, we see that the two distinct resonant phenomena have distinct experimentally observable signatures. For SPPs, the signature of resonant coupling is a maximum in the near-field intensity at the metal-dielectric interface, which is proportional to . For the PA mode, the signature of resonant coupling is a minimum in the reflectance. We can understand these experimental signatures on the real wave-vector axis by considering the and R surfaces in the complex wavevector plane (see Figure S4). Evaluating the Fresnel equations at the complex wavevector value that satisfies the SPP modal equations gives an infinity in R and , by definition. Evaluating the Fresnel equations at the complex wavevector value that satisfies the PA modal equations gives a zero in R, by definition. A representative surface in the complex wavevector plane is plotted in Figure S4b and a representative R surface is plotted in Figure S4c. The zero in the R surface has a strong influence on the reflectance curve on the real axis, giving rise to a reflectance minimum. The zero in the R surface also influences the position of the local reflectance maximum that results from the infinity on the R surface. Hence, we find the reflectance minimum to be a reliable predictor of the resonance position of the PA mode, though the local reflectance maximum is not a reliable predictor of the SPP resonance. The infinity in the surface strongly influences the curve on the real axis and gives rise to the maximum in that is an indicator of the resonance position of the SPP mode.

Next, we simulate K-R experiments with 514 nm light resonant with the SPP mode at ≈ 45° (β = 13.1μm−1, Fig. 4a) and with the PA mode at ≈ 54° (β = 14.7μm−1, Fig. 4b) using the FDTD method. A 3 micron region is illuminated from the glass side and the resulting surface wave is allowed to freely propagate in an adjacent 3 micron region in the absence of a light source (denoted the “Driven” and “Propagating” region, respectively, in Fig. 4). We fit the real x-component of the electric field sampled 50 nm above the gold/air interface to the functional form A cos(βx − ωt0)exp(αx). The value of β in the driven region corresponds to the x-component of momentum of the driving field. By contrast, in the propagating region, β agrees closely with the SPP dispersion in both cases. We conclude that the PA mode can only exist under external driving, whereas the SPP mode can exist and propagate without direct interaction from the driving source. The simulations also demonstrate it is possible to excite propagating SPPs guided by the reflectance minimum in a K-R experiment, but in this case, the coupling efficiency is roughly 3.7 times weaker compared to exciting at an angle resonant with the SPP mode as inferred from the near-field intensity (Fig. 3a).

Figure 4
figure 4

FDTD simulation of K-R excitation of SPPs.

The “Driven Region” is directly illuminated with 514 nm light, while in the “Propagating” region, the SPP propagates freely without illumination. In K-R excitation at 44.9°, resonant with the SPP mode (a) (β = 13.1μm−1) and at 54.2°, resonant with the PA mode (b) (β = 14.7μm−1), the field in the propagating region has a value of β in excellent agreement with the SPP dispersion, β = 13.0μm−1. The electric field curves are sampled 10 nm above the gold/air interface in the FDTD simulations.

Full size image

We presented a surprising discrepancy between the leakage radiation patterns of surface plasmon polaritons (SPPs) launched on a layered Ge/Au film compared to the K-R minimum that clearly challenges the belief that the K-R minimum signals direct coupling into SPPs. We provided definitive experimental and theoretical evidence demonstrating that the reflectance dip in K-R experiments does not correspond to the excitation of an SPP mode, but is rather due to a particular type of perfectly absorbing (PA) mode. We showed that the PA mode can only exist under external driving, whereas the SPP mode can propagate freely without direct interaction with the driving source. We also showed that it is possible to excite propagating SPPs guided by the reflectance minimum in a K-R experiment, but the coupling efficiency can be extremely poor. We find that optimal coupling into the SPP can be guided by the square magnitude of the Fresnel transmission amplitude. We believe these results will have important implications for the understanding and design of thin-film systems for devices and applications.