Abstract
The recent development of spin dynamics opens perspectives for various applications based on spin waves, including logic devices. The first important step in the realization of spin-wave-based logics is the manipulation of spin-wave interference. Here, we present the experimental realization of a micrometre-scale spin-wave interferometer consisting of two parallel spin-wave waveguides. The spin waves propagate through the waveguides and the superposition or interference of the electrical signals corresponding to the spin waves is measured. A direct current flowing through a metal wire underneath one of the spin-wave waveguides affects the propagation properties of the corresponding spin wave. The signal of constructive or destructive interference depends on the magnitude and direction of the applied direct current. Thus, the present work demonstrates a unique manipulation of spin-wave interference.
Similar content being viewed by others
Introduction
Many new concepts of information transport using spin waves have been proposed in recent years1,2,3,4,5,6,7,8,9,10. Spin waves can be regarded as the collective spin resonance of electrons in a magnetic material. Interestingly, one can excite spin waves locally and detect them after propagation3,10,11,12,13. These propagating spin waves carry angular momentum like diffusive spin currents in spintronics. Because they are waves, one can use the phase to convey information. Indeed the propagation length of such waves is notably longer than the electron spin diffusion length in semiconductors or metals. Spin waves can thus be applied to long-range propagation of information, as the loss of information per unit propagation length is smaller than that of diffusive spin currents at room temperature.
Spin waves can be generated in various ways3,14,15 and amplified16. Recent reports have shown the possibility of switching the propagation direction at will17,18. The first important step in the development of spin-wave-based devices would be the realization of spin-wave logics. The basic building block of spin-wave logics is the spin-wave interferometer where the interference of two or more spin waves can be manipulated. However, spin-wave-based logics are mainly proposed theoretically down to nanometre scale6,19. Spin-wave interferences have been reported experimentally in micro stripes using rising and falling edges of electrical pulses20,21 and oppositely propagating spin waves22 that do not allow free manipulation of the interference. However, there have been very few reports on Mach–Zehnder-type spin-wave interferometers on millimetre scale with yttrium iron garnet as a magnetic medium14,23.
Herein we demonstrate the manipulation of spin-wave interference using a Mach–Zehnder-type interferometer on a micrometre scale. Like other published results on spin-wave propagation and spin-wave logic gates12,14,17, it is a step towards spin-wave-based logics on micrometre and nanometre scales. In the case of our interferometer, the spin wave propagating through one branch has a shifted dispersion curve compared with the spin wave in the other branch, resulting in a phase difference between them.
Results
Sample characteristics and concept
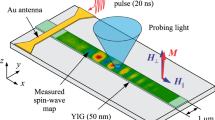
We measure interference signals on various devices. Figure 1 is a sketch of the device layout along with the operating principle. In the present work, under a fixed applied magnetic field (biased field) (H), a continuous radio-frequency (rf) current (Irf) is passed through antenna 1 at frequency (f) to generate an rf magnetic field. This rf magnetic field generates spin waves at the same frequency f in two waveguides (FM1 and FM2) of Co20Fe60B20 above a normal metal, especially under the resonance condition. The resonance condition depends on H, f and the wave vector (k). Spin waves propagate through the two spin-wave waveguides FM1 and FM2. Direct current (Idc) can also be applied through FM2 to change the propagation properties of the spin wave propagating through it. The electrical signal produced inductively by FM1 interferes with that produced by FM2 within antenna 2, where the total interference signal is measured. In the following, we show that the measured interference signal entirely depends on the amplitudes of and relative phase between the spin waves. Thus, even though the spin waves do not actually interfere themselves, we use the term spin-wave interference in the following to remind us that the properties of spin waves are controlled for the realisation of interference. The measurements are carried out with a vector network analyser (VNA). Each antenna consists of two parallel branches or arms with width of 4 μm and edge-to-edge separation of 4 μm. The centre-to-centre separation between the two antennas is of the order of 20 μm. The antennas are electrically isolated from the waveguides by a layer of Al2O3 that is 100 nm thick. The spin-wave waveguides have a width of either 20 or 10 μm and length of 250 μm to avoid spin-wave confinement from the edges along their lengths24,25. To avoid the detection of a spin wave reflected from the edges along the lengths, the antennas are placed at the centre of the waveguides, perpendicular to the length. The centre-to-centre distance between the two waveguides is chosen as 40 μm to minimize dynamic dipolar coupling. H is applied in plane and perpendicular to the spin-wave waveguides (see also Methods). In the following, we concentrate on ferromagnetic waveguides that are 20 μm wide and 20 nm thick with a propagation distance of 20 μm before detection and an applied magnetic field of μ0H = 75 mT. A comparison with other devices is made later in the article.
From the measurement of the reflected spin-wave signal (S11), we obtained a resonance frequency of 9.6 GHz with a k of 0.4 rad.μm−1. This is in agreement with the resonance frequency calculated using the analytical formula for the dispersion relation26,27 given by 
 , with γ/2π = 27.5 GHz/T, μ0MS = 1.45 T, and t being the thickness of the ferromagnetic layer. A typical transmitted signal (S21), from antenna 1 to antenna 2, measured with the VNA at Idc = 0 is presented in Fig. 2(a). The Gilbert damping α is determined as 0.9 × 10−3 ± 0.1 × 10−3. The propagation length is estimated as 11 μm (see also Supplementary Information). Oscillations in the transmitted signals, in phase (Re S21) and out of phase (Im S21) with the excitation signal, are observed. The oscillations in the transmitted signals are the result of exciting several k of propagation with the antenna10,11,13. Indeed, the geometry of our antennas allows us to excite and detect several k as presented in Fig. 2(b). The excited k vectors are a continuous peak centred at k = 0.4 rad.μm−1 (a secondary peak is not observed), which corresponds to the wavelength of 16 μm imposed by the geometry of the antennas. The width of the spectrum of the k vector and the damping α together contribute to the width of the spin-wave spectra. A change in the resonant k arising from the dispersion relation affects the phase of the spin wave after propagation and thus leads to oscillations of the transmission signals (see also Supplementary Information). In the case of our interferometer, for a fixed f and H, Idc applied through FM2 generates an Oersted field that affects the effective magnetic field of FM2. Idc also generates Joule heating that reduces MS. Both the Joule heating and Oersted field contribute to the modification of the wave vector value k from k1 (as in FM1 without Idc) to k2 (as in FM2 with Idc). Thus, the spin waves in the two spin-wave waveguides have different phases when they arrive at the detection antenna. It is worth noting that a change in the k, effective field and/or MS affects the amplitude of the spin wave. The Oersted field is expected to reach 2.0 mT for a Idc of 90 mA, while the measured value is about 2.1 mT. This corresponds to a change in resonance frequency of 130 MHz, while a change of ~250 MHz in resonance frequency is needed to change the phase of the spin wave by 180°. Thus, the Oersted field itself is not strong enough to notably affect the spectrum in Fig. 2(a) to obtain destructive interferences. The increase in temperature due to Joule heating is expected to be around 250–300 °C when a high current density (~1 × 1011 A.m−2) is applied to achieve destructive interference. This would also induce a change in MS which increases the phase of the spin wave by 180°. This leads to the detection of spin-wave generated interferences by antenna 2 as we demonstrate below.
, with γ/2π = 27.5 GHz/T, μ0MS = 1.45 T, and t being the thickness of the ferromagnetic layer. A typical transmitted signal (S21), from antenna 1 to antenna 2, measured with the VNA at Idc = 0 is presented in Fig. 2(a). The Gilbert damping α is determined as 0.9 × 10−3 ± 0.1 × 10−3. The propagation length is estimated as 11 μm (see also Supplementary Information). Oscillations in the transmitted signals, in phase (Re S21) and out of phase (Im S21) with the excitation signal, are observed. The oscillations in the transmitted signals are the result of exciting several k of propagation with the antenna10,11,13. Indeed, the geometry of our antennas allows us to excite and detect several k as presented in Fig. 2(b). The excited k vectors are a continuous peak centred at k = 0.4 rad.μm−1 (a secondary peak is not observed), which corresponds to the wavelength of 16 μm imposed by the geometry of the antennas. The width of the spectrum of the k vector and the damping α together contribute to the width of the spin-wave spectra. A change in the resonant k arising from the dispersion relation affects the phase of the spin wave after propagation and thus leads to oscillations of the transmission signals (see also Supplementary Information). In the case of our interferometer, for a fixed f and H, Idc applied through FM2 generates an Oersted field that affects the effective magnetic field of FM2. Idc also generates Joule heating that reduces MS. Both the Joule heating and Oersted field contribute to the modification of the wave vector value k from k1 (as in FM1 without Idc) to k2 (as in FM2 with Idc). Thus, the spin waves in the two spin-wave waveguides have different phases when they arrive at the detection antenna. It is worth noting that a change in the k, effective field and/or MS affects the amplitude of the spin wave. The Oersted field is expected to reach 2.0 mT for a Idc of 90 mA, while the measured value is about 2.1 mT. This corresponds to a change in resonance frequency of 130 MHz, while a change of ~250 MHz in resonance frequency is needed to change the phase of the spin wave by 180°. Thus, the Oersted field itself is not strong enough to notably affect the spectrum in Fig. 2(a) to obtain destructive interferences. The increase in temperature due to Joule heating is expected to be around 250–300 °C when a high current density (~1 × 1011 A.m−2) is applied to achieve destructive interference. This would also induce a change in MS which increases the phase of the spin wave by 180°. This leads to the detection of spin-wave generated interferences by antenna 2 as we demonstrate below.
Transmitted signal and efficiency of the antenna in excitation of the wave vector.
(a) A typical measurement of the transmission versus the frequency after 20 μm of propagation in 20-μm-wide, 20-nm-thick CoFeB waveguides. The applied magnetic field is μ0H = 75 mT. No direct current is applied through FM2. (b) Normalized Fourier transformation of the power delivered by our antennas (I2rf ) versus the wave vector (k) of the spin wave.
Experimental demonstration of the manipulation of spin-wave interference
To evaluate the efficiency of the interferometer, we measured the transmitted spin-wave signals with a VNA at different f and applied Idc. The f is varied from 9.2 to 10.1 GHz in steps of 10 MHz. For each f, Idc sweeps between −85 and 85 mA. Figures 3(a) and (b) show colour maps of the measured Re S21 and Im S21 signals as functions of Idc and f under a bias magnetic field μ0H = 75 mT. The maps have three important features. First, Re S21 (Fig. 3(a)) and Im S21 (Fig. 3(b)) evolve with Idc in a similar way but with a phase difference of 90°. This is evidence that the spin wave is transmitted. The second feature is the near-perfect symmetry of the maps with respect to the sign of Idc. This can be understood as follows. The Oersted field is added to the bias magnetic field for the determination of the resonant condition. However, this addition depends on the sign of Idc. Thus, for example, when Re S21 is zero for a given frequency without Idc, one would obtain either a positive or negative Re S21 while applying a positive or negative Idc, respectively. The transmitted signal should then have predominantly asymmetric behaviour with respect to the sign of Idc if there is only an Oersted field. However, negligible asymmetry is observed here for real and imaginary components of the transmitted signal at each frequency. Because the contribution from Joule heating ( ) is the same for positive and negative Idc, it tends to generate symmetric curves irrespective of the sign of Idc. Thus, the symmetry in our maps is mainly a consequence of Joule heating and the small asymmetric behaviour is a consequence of the Oersted field. Thus, the effect of the Oersted field on the dispersion is secondary to the effect of Joule heating of the sample under a bias magnetic field of 75 mT and for Idc is sufficiently strong to noticeably affect the transmitted signals. The dominant nature of Joule heating on the modification of the dispersion (resonance) curve is in good agreement with measurements (see Supplementary Information) realised with only one spin-wave waveguide through which Idc flows. The third feature is that the sign of the transmitted signal barely changes with Idc. As the spin wave in FM1 is unaffected by Idc, it creates a baseline around which the transmitted signal oscillates with Idc.
) is the same for positive and negative Idc, it tends to generate symmetric curves irrespective of the sign of Idc. Thus, the symmetry in our maps is mainly a consequence of Joule heating and the small asymmetric behaviour is a consequence of the Oersted field. Thus, the effect of the Oersted field on the dispersion is secondary to the effect of Joule heating of the sample under a bias magnetic field of 75 mT and for Idc is sufficiently strong to noticeably affect the transmitted signals. The dominant nature of Joule heating on the modification of the dispersion (resonance) curve is in good agreement with measurements (see Supplementary Information) realised with only one spin-wave waveguide through which Idc flows. The third feature is that the sign of the transmitted signal barely changes with Idc. As the spin wave in FM1 is unaffected by Idc, it creates a baseline around which the transmitted signal oscillates with Idc.
Maps of interferences at 75 mT.
The sample is the same as that described in Fig. 2(a). The real part of the transmission between antennas 1 and 2 (Re S21) for different frequencies and applied Idc are shown in (a) and the imaginary part (Im S21) in (b). The phase because of spin-wave transmission detected by antenna 2 is presented in (c).
Using Re S21 and Im S21, we calculate the phase of the spin-wave signal detected by antenna 2. As expected, the resulting phase map (Fig. 3(c)) has the same global behaviour as the transmission maps. However, in the phase map, there are four critical points around which the phase can take any possible value in response to a small change in Idc or the applied frequency. The four points are at (9.83 GHz, −45 mA), (9.79 GHz, 61 mA), (9.32 GHz, −52 mA) and (9.27 GHz, 68 mA). To understand this behaviour, we present the transmitted power and corresponding phase for two representative frequencies, 9.57 GHz (Fig. 4(a)) and 9.32 GHz (Fig. 4(b)). The phase varies smoothly with Idc for f = 9.57 GHz, but abruptly for f = 9.32 GHz at Idc = −52 mA. Additionally, in the latter case of f = 9.32 GHz, the transmitted power reaches zero at Idc = −52 mA. Therefore, power associated with the spin-wave propagation also reaches zero. This means that the two spin waves in FM1 and FM2 have opposite phases but equal amplitudes, corresponding to totally destructive interference. This also explains the lack of continuity in the phase (for example, the phase suddenly jumps from −161° to 36° at 9.32 GHz and −52 mA) at the four critical points. Clearly, we cannot define a phase if there is no measurable signal. A consequence is that a slight change in the frequency or current can affect the amplitude and phase of the interference signal. In the case of positive current, a slightly higher current is required to tune k for totally destructive interference at the same frequency because of the competition between the Oersted field and Joule heating. However, the higher current also results in a increment of temperature (via Joule heating). The spin-wave amplitude thus differs from that in the case of negative current. Therefore, a small signal is still transferred and the phase becomes continuous. In this case, the interference is partially destructive. There is totally destructive interference at 9.27 GHz and 68 mA for positive current, against 9.32 GHz and −52 mA for negative current. For frequencies far from frequencies of totally destructive interference (e.g., 9.57 GHz), the amplitude of the spin wave in FM2 is too different from that in FM1 for there to be totally destructive interference, even when the phases are opposite. Thus, in spite of a notable decrease in the received power (which is sufficient for logic devices) arising from partially destructive interference, the phase is continuous with smaller variations than in the case of totally destructive interference.
We note here that no other effects of the direct current on the spin wave, such as a spin-wave Doppler shift28 were observed for our samples (see Supplementary Information for more details). Thus, at fixed frequency, Idc only affects the spin-wave dispersion relation through Joule heating and the Oersted field. Both contribute to the manipulation of the interference by modifying the k of the spin wave propagating through FM2. It is worth noting that the received signal is a wave and not simply a pulse14. Therefore, the signal can be reused especially after amplification16 in more complex spin-wave devices. We can change the number of oscillations or periods of the transmitted signal at Idc = 0, as seen in Fig. 2(a) by changing either the distance between emission and reception11,13 antennae or the thickness of the ferromagnetic layer. In this case, a different value of Idc is required to obtain the required change in phase of 180° in one arm of the interferometer compared with the other arm to achieve destructive interference. However, the physics remains the same.
The application of a stronger magnetic field to any device could be problematic. Thus, last, we present the interference obtained under a lower-bias magnetic field of 10 mT. The colour map of the interference as a function of frequency and current is presented in Fig. 5. Unlike the case for a stronger magnetic field, the map is mainly asymmetric with respect to the sign of Idc. As explained above, this means that the Oersted field dominates the variations in the dispersion relation. The reason is explained as follows. For a weaker magnetic field, the Oersted field leads to greater relative variations in the effective magnetic field. However, we reach totally destructive interference at a frequency around 3.75 GHz and Idc around −70 mA, where the phase is not well defined. The predominance of the Oersted field over Joule heating means that the colour map of interference is less symmetric with respect to the sign of Idc. We can define a threshold current here. Above this threshold current, an increase in positive current modifies the transmission more through Joule heating (where the effect is proportional to Idc2) than through the Oersted field (where the effect is proportional to Idc). This threshold current is around 20–25 mA in Fig. 3. From the dispersion relationship, one would expect the threshold current to be around 45–56 mA in Fig. 5, where it is in fact found to be around 45–50 mA. This good agreement confirms the relative effects of the two contributions. However, the important point is that interference can also be driven from constructive (no current) to destructive under a weak applied magnetic field. A weak magnetic field can be applied by dipolar coupling with a permanent magnet. This consideration has to be taken into account when determining the magnetic field required for spin-wave-based devices in spintronics.
Discussion
We experimentally demonstrated how spin-wave interference can be manipulated with a spin-wave interferometer on the micrometre scale. Unlike previous demonstrations on the millimetre scale14,23, the entire length of the interferometer is used to produce interference. Here, we used direct current to modify dynamically the propagation properties of the spin wave in one of the two branches of our interferometer. We make the most of both Joule heating and the Oersted field produced by the direct current to control the wave vector and hence the phase of the propagating spin wave in one branch compared with that in the other branch for the same excitation frequency. The advantage of controlling the properties of spin-wave propagation with direct current is the ability to freely manipulate the interference. However, to reduce energy consumption, interference can also be manipulated by tuning the resonant conditions of the two arms of the interferometer either by choosing a different width (at smaller width, the width of the spin-wave waveguide also affects the resonant condition) or by choosing different ferromagnetic materials or magnonic crystals29 for each spin-wave waveguide. These measurements can be extended in the time domain with modulated pulse excitation as in the literature14. Last, we used two antennas in our experiment (one for excitation of the spin wave in both waveguides and another for detection of the spin wave from both waveguides after propagation). However, one can also use one antenna (or any other instrument for magnon injection with a controllable k vector) per spin-wave waveguide with controlled phase (as in references 22 and 23) for excitation and one global antenna for detection. This would lead to spin-wave-based logics. If we have two antennas for the injection and still one for the reception, the two inputs would need to be out of phase to receive a signal at the receptor in the case of destructive interference. This would correspond to a kind of XNOR gate. With interferometers that are more complex (e.g., interferometers with more spin-wave waveguides), other logic functions can be designed, especially if the spin-wave-generated signal is stronger than the baseline12 and the spin-wave propagation direction is imposed17.
Methods
Sample preparation
The samples were prepared in four steps. First, a Co20Fe60B20 (20 or 10 nm)/Ta(5 nm)/Ru(10 nm)/Ta(5 nm) layer was deposited on a SiO2/Si wafer by sputtering. Second, the spin-wave waveguides were defined by optical lithography and etching with an argon ion beam. Third, the 100 nm thick insulator Al2O3 was deposited by sputtering everywhere except at the extremities of the spin-wave waveguides. Finally, the gold antennas Ti(4 nm)/Au(100 nm) and direct-current contacts were deposited using a combination of optical lithography, electron beam evaporation and lift-off processes.
Measurement
The measurements were made with a fixed in-plane bias magnetic field applied perpendicular to the length of the spin-wave waveguide with a magnetic field excitation generated by rf current, while sweeping the direct current applied through FM2. In spite of the good signal/baseline ratio obtained in a previous study12, we preferred to make measurements with a VNA. Thus, to remove the signal corresponding to inductive coupling between the two antennas from the transmitted spin-wave signals, measurements were performed under two magnetic fields, the one of interest and a reference magnetic field of 170 mT, where no spin waves were detected in the region of the measurement frequency. We then numerically removed the signals measured under the reference field from the signals measured under the field of interest to extract the signals corresponding only to the spin-wave propagation. The VNA basically measured two components of the transmitted signal: the real component (Re S21) that is in phase with the excitation signal and the imaginary component (Im S21) that is out of phase with the excitation signal. The signal corresponding to spin-wave propagation was thus clearly determined along with its phase.
Additional Information
How to cite this article: Rousseau, O. et al. Realization of a micrometre-scale spin-wave interferometer. Sci. Rep.5, 9873; doi: 10.1038/srep09873 (2015).
References
Bao, M. et al. Coplanar waveguide radio frequency ferromagnetic parametric amplifier. Appl. Phys. Lett. 93, 072509 (2008).
Demidov, V. E. et al. Generation of the second harmonic by spin waves propagating in microscopic stripes. Phys. Rev. B 83, 054408 (2011).
Demidov, V. E. et al. Excitation of microwaveguide modes by a stripe antenna. Appl. Phys. Lett. 95, 112509 (2009).
Demidov, V. E. et al. Resonant frequency multiplication in microscopic magnetic dots. Appl. Phys. Lett. 99, 012505 (2011).
Huber, R. et al. Reciprocal Damon-Eshbach-type spin wave excitation in a magnonic crystal due to tunable magnetic symmetry. Appl. Phys. Lett. 102, 012403 (2013).
Khitun, A., Bao, M. & Wang, K. L. Magnonic logic circuits. J. Phys. D: Appl. Phys. 43, 264005 (2010).
Khitun, A. & Wang, K. L. Non-volatile magnonic logic circuits engineering. J. App. Phys. 110, 034306 (2011).
Neusser, S. & Grundler, D. Magnonics: spin waves on the nanoscale. Adv. Mater. 21, 2927–2932 (2009).
Slavin, A. Spin-torque oscillators get in phase. Nat. Nanotech. 4, 479 (2009).
Yu, H. et al. High propagating velocity of spin waves and temperature dependent damping in a CoFeB thin film. Appl. Phys. Lett. 100, 262412 (2012).
Bailleul, M., Olligs, D. & Fermon, C. Propagating spin wave spectroscopy in a permalloy film: A quantitative analysis. Appl. Phys. Lett. 83, 972–974 (2003).
Rousseau, O., Yamada, M., Miura, K., Ogawa, S. & Otani, Y. Propagation of nonlinearly generated harmonic spin waves in microscopic stripes. J. Appl. Phys. 115, 053914 (2014).
Vlaminck, V. & Bailleul, M. Spin-wave transduction at the submicrometer scale: Experiment and modeling. Phys. Rev. B 81, 014425 (2010).
Schneider, T. et al. Realization of spin-wave logic gates. Appl. Phys. Lett. 92, 022505 (2008).
Ulrichs, H., Demidov, V. E., Demokritov, S. O. & Urazhdin, S. Spin-torque nano-emitters for magnonic applications. Appl. Phys. Lett. 100, 162406 (2012).
Khivintsev, Y. et al. Nonlinear amplification and mixing of spin waves in a microstrip geometry with metallic ferromagnets. Appl. Phys. Lett. 98, 042505 (2011).
Vogt, K. et al. Realization of a spin-wave multiplexer. Nat. Commun. 5, 3727 (2014).
Vogt, K. et al. Spin waves turning a corner. Appl. Phys. Lett. 101, 042410 (2012).
Lee, K. S. & Kim, S. K. Conceptual design of spin wave logic gates based on a mach-zehnder-type spin wave interferometer for universal logic functions. J. Appl. Phys. 104, 053909 (2008).
Kwon, J. H., Mukherjee, S. S., Jamali, M., Hayashi, M. & Yang, H. Spin waves interference from rising and falling edges of electrical pulses. Appl. Phys. Lett. 99, 132505 (2011).
Mukherjee, S. S., Kwon, J. H., Jamali, M., Hayashi, M. & Yang, H. Interference-mediated modulation of spin waves. Phys. Rev. B 85, 224408 (2012).
Sato, N., Sekiguchi, K. & Nozaki. Y. Electrical demonstration of spin-wave logic operation. Appl. Phys. Express 6, 063001 (2013).
Kostylev, M. P., Serga, A. A., Schneider, T., Leven, B. & Hillebrands, B. Spin-wave logical gates. Appl. Phys. Lett. 87, 153501 (2005).
Bauer, M. et al. Observation of spatiotemporal self-focusing of spin waves in magnetic films. Phys. Rev. Lett. 91, 3968 (1998).
Tamaru, S. et al. Imaging of quantized magnetostatic modes using spatially resolved ferromagnetic resonance. J. Appl. Phys. 91, 8034 (2002).
Damon, R. W. & Eshbach, J. R. Magnetostatic modes of a ferromagnet slab. J. Phys. Chem. Solids 19, 308–320 (1961).
Stancil. D. D. Theory of Magnetostatic Waves. Springer, Berlin(1993)).
Vlaminck, V. & Bailleul. M. Current-induced spin-wave doppler shift. Science 322, 410–413 (2008).
Chumak, A. V., Serga, A. A. & Hillebrands, B. Magnon transistor for all-magnon data processing. Nat. Commun. 5, 4700 (2014).
Acknowledgements
The authors thank R. Lassalle-Balier for fruitful discussions.
Author information
Authors and Affiliations
Contributions
O.R. conceived the project. O.R., B.R., K.M., M.Y. and R.A. prepared the samples. O.R., B.R. and R.A. performed the measurements. O.R., B.R., R.A., S.O. and Y.O. discussed the results. O.R. wrote the manuscript with input from B.R., S.O., and Y.O. Y.O. supervised the project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Rousseau, O., Rana, B., Anami, R. et al. Realization of a micrometre-scale spin-wave interferometer. Sci Rep 5, 9873 (2015). https://doi.org/10.1038/srep09873
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep09873
This article is cited by
-
Lumped circuit model for inductive antenna spin-wave transducers
Scientific Reports (2022)
-
Towards magnonic devices based on voltage-controlled magnetic anisotropy
Communications Physics (2019)
-
The role of Snell’s law for a magnonic majority gate
Scientific Reports (2017)
-
Spin-wave propagation steered by electric field modulated exchange interaction
Scientific Reports (2016)
-
Demonstration of a robust magnonic spin wave interferometer
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.