Abstract
Biphotons with narrow bandwidth and long coherence time can enhance light-atominteraction, which leads to strong coupling between photonic and atomic qubits.Such strong coupling is desirable in quantum information processing, quantumstorage and communication. In particular, paired photons with a long coherencetime over submicroseconds facilitate the direct manipulation of biphoton wavefunction.In this paper, we report the narrow-band biphotons with a coherence time of2.34 μs generated from spontaneous four-wave mixing (SFWM)in a dense cold atom cloud, in which the anti-Stokes photons go through anarrow electromagnetically-induced transparency (EIT) window. In our knowledge,this is the best record of coherence time for paired photons achieved so far.A number of factors limiting the coherence time are analyzed in detail. Wefind the EIT coherence plays an essential role in determining the coherencetime for paired photons. The EIT dephasing rate is the ultimate limit to thecoherence time and an ultra-long coherence time above ten microseconds ispossible by further improvement of the dephasing rate below 100 kHz.
Similar content being viewed by others
Introduction
Nonclassical paired photons play an important role in quantum informationprocessing, quantum storage and telecommunication. They are highly correlatedin pairs and their second-order cross correlation function violates the Cauchy-Schwartzinequality. These paired photons constitute heralded single photon source,i.e., when one of them is detected, its counterpart can be considered as asingle photon in Fock state. Traditional schemes, spontaneous parametric downconversion (SPDC) in nonlinear crystal, generate broadband paired photonswith linewidth up to the order of THz1,2,3,4,5. The pairedphotons produced in the SPDC scheme are usually considered to be simultaneous,with their coherent time separation, i.e., coherence time, of the order ofpicosecond. However, efficient quantum state transfer at light-atom interfacerequires narrow-band paired photon source or narrow-band single photons. SPDCwith high finesse cavity6,7,8,9 efficiently generates pairedphotons with linewidths around 10 MHz and further suppression belowatomic natural linewidth (e.g., 6 MHz for rubidium atoms) demands delicatecavity fabrication10. Write-read sequenced four-wave mixingprocess provide an access to the generation of narrow-band paired photonsin atomic gas11,12 and the paired photons produced throughatomic spin states storing and retrieving are shown to be highly correlated13. Instead of time-separate writing and reading processes, spontaneousfour-wave mixing (SFWM) with both controlling beams present simultaneouslyin a generation cycle is utilized to produce time-frequency entangled pairedphotons, i.e., biphotons, in cold atomic ensembles14,15,16.Therefore in time-frequency domain, the two-photon state can be expressedby a temporal correlation function, or a probability wavefunction17,18.
The coherence time of the biphotons is defined as the temporal length ofthe biphoton correlation function and it represents the largest time distanceof the biphotons emitted from a source. SPDC scheme produce wide-band biphotonswith the temporal wavefunction too short to be detected directly by the fastestsingle photon counter, or to be modulated directly in time domain. Moreover,the ultra-short coherence time complicates the future quantum networking basedon the entangled paired photons emitted from independent sources, which requireaccurate synchronization of the excitation laser pulses19,20.To largely increase the biphoton coherence time, in this report, we demonstratethe generation of biphotons from a cloud of laser cooled 85Rbatoms prepared in a two-dimensional magneto-optical trap (MOT), with the coherencetime exceeding far above nanoseconds. When electromagnetically induced transparency(EIT) is introduced into the SFWM process, the linewidth and correspondingtemporal length of the biphoton correlation function can be manipulated bycontrolling the slow light effect of the produced photons. More interestingly,if one could produce a single photon with temporal waveform up to tens of μs,demanding 10 kHz modulation bandwidth, the single photon source couldthen be easily manipulated as it is an optical pulse. These ultranarrow-bandpaired photons have shown great advantage in heralded single photon waveformmanipulation17,21,22,23, single photon quantum storage24 and imaging25.
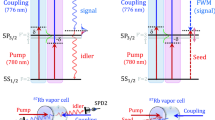
We would like to start with the four-level double-Λ atomic system forbiphoton generation, as shown in Figure 1(b). For theexcited states |3〉 and |4〉 of 85Rb atoms, the populationdecay rates are Γ3(4) = 2π × 6 MHz.The dephasing rates of the excited states are γ13(14)= (1/2)Γ3(4) for cold atomic ensemble. The states |1〉,|2〉 and 3〉 with a resonant strong coupling beam ωcconstitute a EIT configuration. Though the transition between the state |1〉and |2〉 is prohibited, the non-zero ground states dephasing rate γ12is caused by atomic collisions, atomic thermal motions and Lamer precessionof atoms in non-zero B field. In the MOT system we build, the Lamer precessionof atoms are expected to be the main reason. Further we estimate the dephasingrate of the EIT coherence by measuring the probe beam transmission spectrumwith the resonant coupling beam and thus obtain γ12= 2π × 0.03 MHz between 5S1/2F= 2 and 5S1/2F = 3. Figure 1(a)shows the backward geometry of four-wave mixing process, in which the opposite-arrangedpump ωp and coupling beams ωcgenerate paired Stokes (ωs) and anti-Stokes (ωas)emitted in opposite directions. The biphotons, Stokes and anti-Stokes photons,are simultaneously generated from the SFWM nonlinear process in the atomicensemble. The Stokes photons are usually far-detuned from atomic transitions,and therefore they propagate always with the speed of light in vacuum c.On the other hand, the anti-Stokes photons are produced with a resonant couplinglaser beam, which creates a coherent EIT window for the photons to propagatethrough with a slow group velocity Vg. In this regime, theEIT coherence determines the coherence of the paired photons. There are threeimportant parameters to determine the slow light feature. The first one isthe optical depth (OD) of the medium, defined as OD = Nα0L,where N denotes the atom density, α0 is the resonantabsorption coefficient and L is the effective length of the atom cloud.The second parameter is the coupling field Rabi frequency Ωc,representing the coupling field strength. The last but not the least factoris the dephasing rate γ12 of the EIT coherence. Whenignoring the dephasing rate, we could increase coherence time Tcof the biphoton simply by prolonging the EIT delay time τg= L/Vg, which is proportional to the ratio OD/|Ωc|2.For example, Du et al.26 reported time-frequency entangledpaired photons with 0.9 μs coherence time, generated froma laser-cooled atomic cloud with optical depth (OD) of 53. From a dark-linetwo-dimensional MOT29 with OD as high as 130, Zhao et al.27 reported that the coherence time of these narrow-band entangledpaired photons reaches 1.7 μs. By phase locking two spatialsymmetrical paths of the SFWM process, Liao et al.28show polarization entangled narrow-band paired photon with the coherence timeof 300 ns, which can be prolonged to 900 ns when they graduallyreduce the coupling laser power. However, with a very low laser field coupling,the dephasing rate between two hyperfine states becomes important. Reducingthe coupling laser power does not always prolong the coherence time Tc,but instead results in a maximum Tc at optimum Ωc.In the following sections, we demonstrate that the limit of Tcis corporately determined by OD and the dephasing rate of the EIT ground-statecoherence. In the case of extremely large OD, the coherence time of the biphotonfinally approaches the ultimate limit determined by the dephasing rate. Withan optimized dephasing rate and OD = 100 currently available in thesystem, we can realize a coherence time Tc up to 2.34 μs,which is the longest temporal length for biphoton reported to the best ofour knowledge.
System schematics.
(a), Backward SFWM experimental setup. The 85Rbatomic ensemble is prepared in a two-dimensional magneto-optical trap. (b),Energy level scheme for SFWM. The four energy levels activated are: |1〉= 5S1/2F = 2 (initial atomic state), |2〉 = 5S1/2F= 3, |3〉 = 5P1/2F = 3 and |4〉 = 5P3/2F= 3.
The two-photon state generated in the SFWM described in Figure1 can be described by a temporal biphoton wavefunction18,

in which, ψ is the wavefunctionamplitude and τ = tas − tsdenotes the delay time.  is the nonlinearparametric coupling coefficient and χ(3) is thethird-order nonlinear susceptibility. The longitudinal function
is the nonlinearparametric coupling coefficient and χ(3) is thethird-order nonlinear susceptibility. The longitudinal function  , where Δk = kas − ks −(kc − kp) cos θ is thephase mismatching for the backward geometry shown in Figure1. Also, we include the intensity distribution f(z) ofthe pump or coupling beam along the z axis. According to experimentsetup, we define a Gaussian beam distribution with a e−2full width of d = 1.2 cm for both pump and coupling laser beams,and thus
, where Δk = kas − ks −(kc − kp) cos θ is thephase mismatching for the backward geometry shown in Figure1. Also, we include the intensity distribution f(z) ofthe pump or coupling beam along the z axis. According to experimentsetup, we define a Gaussian beam distribution with a e−2full width of d = 1.2 cm for both pump and coupling laser beams,and thus  .
.
From equation(1), we obtain the numerical results forthe joint-detection probability. Furthermore, equation(1)indicates that the spectrum of two-photon wavefunction is determined by theproduct of the κ(ω) and Φ(ω). Nextwe take some approximations to obtain an analytic solution for the wavefunctionamplitude. Firstly, we assume that the EIT slow light effect play a dominantrole to decide the two-photon wavefunction. Therefore we consider the casewhere Δωg < Ωe, in which  denotes the full width half maximumbandwidth of the function Φ(ω) and
denotes the full width half maximumbandwidth of the function Φ(ω) and  is the spectral separation of the two symmetric peak value of κ(ω)26. Now, Φ(ω) decides the two-photon wavefunctionenvelope, while
is the spectral separation of the two symmetric peak value of κ(ω)26. Now, Φ(ω) decides the two-photon wavefunctionenvelope, while  is approximatedas a constant κ0. With this assumption, the coherencetime of the paired photons is solely ascribed to the fact that, the anti-Stokesphotons propagate through the atomic cloud with a slow velocity compared tothe paired Stokes photons. Secondly, we assume θ → 0 or
is approximatedas a constant κ0. With this assumption, the coherencetime of the paired photons is solely ascribed to the fact that, the anti-Stokesphotons propagate through the atomic cloud with a slow velocity compared tothe paired Stokes photons. Secondly, we assume θ → 0 or  and thus f(z) ≈ 1 andthe z integration term becomes a sinc function
and thus f(z) ≈ 1 andthe z integration term becomes a sinc function  .With the above assumption, we can simplify the wavefunction amplitude as,
.With the above assumption, we can simplify the wavefunction amplitude as,

where, the EIT loss term  is included. The EIT loss term αL is normallya small value close to 0. Through Taylor expansion at this small value, equation(2) gives an analytical solution after integral:
is included. The EIT loss term αL is normallya small value close to 0. Through Taylor expansion at this small value, equation(2) gives an analytical solution after integral:

In other regions τ < 0and τ > L/Vg, Ψ(τ)= 0. If we ignore EIT loss term αL completely, equation(3)becomes a rectangular function Π(τ: 0, τg= L/Vg) as Refs. 18,and thus the 1/e coherence time is directly equals to EIT delay time τg.Otherwise, the two-photon waveform amplitude exhibits a linear decay endingat τ = τg(1/αL + 1/2). When αLtends to be infinity, the coherence time is bounded by τg/2.
Results
We prepare the cold atom cloud with optical depth OD = 100, andfor SFWM process we set the coupling Rabi frequency as Ωc= 4.2γ13, 1.7γ13 and 1.2γ13,calculated from  . To guarantee thelow gain limit condition for SFWM process, we use a low pump power correspondingto Ωp = 0.36γ13. Figure2 shows the coincidence measurement results over these three cases,along with the numerical results of the two photon wavefunction amplitude equation(1). Figure 2(a) shows the caseof Ωc = 4.2γ13. Apart from thebiphoton optical precursor emerging immediately after τ = 0 ns,the two-photon joint detection waveform exhibits a Gaussian shape impressedfrom the controlling beams transverse beam profile f(z). At τ= 300 ns, the normalized cross-correlation function
. To guarantee thelow gain limit condition for SFWM process, we use a low pump power correspondingto Ωp = 0.36γ13. Figure2 shows the coincidence measurement results over these three cases,along with the numerical results of the two photon wavefunction amplitude equation(1). Figure 2(a) shows the caseof Ωc = 4.2γ13. Apart from thebiphoton optical precursor emerging immediately after τ = 0 ns,the two-photon joint detection waveform exhibits a Gaussian shape impressedfrom the controlling beams transverse beam profile f(z). At τ= 300 ns, the normalized cross-correlation function  . In contrast, we have
. In contrast, we have  and
and  . Thus the Cauchy-Schwartz inequality
. Thus the Cauchy-Schwartz inequality  is violated by a factor of 506. Therefore,the generated photon pair source is proved to be nonclassical. Further, withthe Stokes photon as reference, its paired anti-Stokes photon constitutesa heralded single photon. We measure the conditional second-order correlationfunction
is violated by a factor of 506. Therefore,the generated photon pair source is proved to be nonclassical. Further, withthe Stokes photon as reference, its paired anti-Stokes photon constitutesa heralded single photon. We measure the conditional second-order correlationfunction  for window lengths of 500 ns,and hence we verify the Fock-state single photon nature of the heralded anti-Stokesphotons. The 1/e coherence time of the two-photon waveform is 553 ns,and correspondingly the spectral bandwidth of the heralded single photon (alsofor the photon pair) is estimated as Δωg = 2π ×1.5 MHz, which is smaller than the atomic natural linewidth 2π ×6 MHz of 85Rb 5P state. Taking into account all thedetection efficiencies and 10% of duty cycle, the photon pairs generated rateis 6436 pairs/s. Figure 2(b) shows the case of Ωc= 1.7γ13 with the same OD. The 1/e coherencetime 2340 ns and corresponding bandwidth 2π × 0.38 MHz.The photon pair generation rate is 2043 pairs/s, with the maximum ofthe normalized cross-correlation function
for window lengths of 500 ns,and hence we verify the Fock-state single photon nature of the heralded anti-Stokesphotons. The 1/e coherence time of the two-photon waveform is 553 ns,and correspondingly the spectral bandwidth of the heralded single photon (alsofor the photon pair) is estimated as Δωg = 2π ×1.5 MHz, which is smaller than the atomic natural linewidth 2π ×6 MHz of 85Rb 5P state. Taking into account all thedetection efficiencies and 10% of duty cycle, the photon pairs generated rateis 6436 pairs/s. Figure 2(b) shows the case of Ωc= 1.7γ13 with the same OD. The 1/e coherencetime 2340 ns and corresponding bandwidth 2π × 0.38 MHz.The photon pair generation rate is 2043 pairs/s, with the maximum ofthe normalized cross-correlation function  .Therefore, the Cauchy-Schwartz inequality is still violated by a factor of12. With a lower pump beam power Ωp = 0.21γ13,we obtain
.Therefore, the Cauchy-Schwartz inequality is still violated by a factor of12. With a lower pump beam power Ωp = 0.21γ13,we obtain  for a 2400 ns coincidencewindow. Further decreasing the coupling power diminishes the visibility as Figure 2(c), Ωc = 1.2γ13,and distorts the two-photon waveform as a linear decay tail. The dash linein Figure 2(c) denotes the analytical solution of equation(3) and it matches the experimental data and numericalcalculation well. The EIT loss term αL largely reduces the wavefunctionvisibility and maximum
for a 2400 ns coincidencewindow. Further decreasing the coupling power diminishes the visibility as Figure 2(c), Ωc = 1.2γ13,and distorts the two-photon waveform as a linear decay tail. The dash linein Figure 2(c) denotes the analytical solution of equation(3) and it matches the experimental data and numericalcalculation well. The EIT loss term αL largely reduces the wavefunctionvisibility and maximum  is around3, with photon pair generation rate about 826 pair/s only. Consideringthe visibility, the near-rectangular waveform envelope in Figure2(b) is the best we obtain with our present experimental setup.
is around3, with photon pair generation rate about 826 pair/s only. Consideringthe visibility, the near-rectangular waveform envelope in Figure2(b) is the best we obtain with our present experimental setup.
Accumulated coincidence counts measurements.
(a), Ωc = 4.2γ13(over 600 s); (b), Ωc = 1.7γ13(over 600 s); (c) Ωc = 1.2γ13(over 1200 s). black circles denote the experimental data and thered solid curve denotes the numerical results calculated from Eq.1. The green dash line denotes the equation (3). Ωp= 0.36γ13, α0L = 100.
The second important result is concerning the lower bound for couplinglaser power. Figure 3 plots the measured 1/ecoherence time (denoted as Tc below) and  as a function of Ωc in four cases: OD= 22, 35, 50, 100. All of them satisfy the condition Δωg < Δωtr,in which
as a function of Ωc in four cases: OD= 22, 35, 50, 100. All of them satisfy the condition Δωg < Δωtr,in which  denotes the spectral widthof the EIT window. Accordingly, in Figure 3(a) we plotthe numerical results simulated from equation(1), andfor comparison, we also calculate the numerical curves for OD = 300,1000. If we take the atomic ground states dephasing rate as γ12= 2π × 45 kHz, the experimental data perfectly matchthe numerical curves, except that the data point at OD = 100, Ωc= 1γ13 is measured as 1900 ns, much lower thanthe calculated value. This is because the biphoton waveform visibility dropsand some part of the coincidence counts are buried into the accidental counts.As is discussed above, at a low level of coupling field, the EIT loss termseriously damages the waveform shape, which instead exhibits a linear decaytail as equation(3). Therefore, Figure3 shows that the numerical lines for various ODs all indicatea drop of Tc at small Ωc and theoptimum Ωc value increase with OD. On the other hand, Figure 3(b) shows the measured maximum of
denotes the spectral widthof the EIT window. Accordingly, in Figure 3(a) we plotthe numerical results simulated from equation(1), andfor comparison, we also calculate the numerical curves for OD = 300,1000. If we take the atomic ground states dephasing rate as γ12= 2π × 45 kHz, the experimental data perfectly matchthe numerical curves, except that the data point at OD = 100, Ωc= 1γ13 is measured as 1900 ns, much lower thanthe calculated value. This is because the biphoton waveform visibility dropsand some part of the coincidence counts are buried into the accidental counts.As is discussed above, at a low level of coupling field, the EIT loss termseriously damages the waveform shape, which instead exhibits a linear decaytail as equation(3). Therefore, Figure3 shows that the numerical lines for various ODs all indicatea drop of Tc at small Ωc and theoptimum Ωc value increase with OD. On the other hand, Figure 3(b) shows the measured maximum of  at these four OD cases. When Ωc < γ13,
at these four OD cases. When Ωc < γ13,  is below 2 and does not violate Cauchy-Schwartzinequality. The limit of the coherence time is corporately determined by ODand the atomic ground state dephasing rate γ12. Therefore,in Figure 4(a) we simulate the maximum Tcas a function of OD when keeping γ12 and in Figure4(b) vary γ12 when maintaining OD. Firstly, Figure 4(a) indicates extreme ODs bring the maximum Tcto approach 3.5 μs, which is determined by 1/γ12. Tcglows very slow after OD > 200. On the other hand, Figure4(b) shows a sensitive improvement of Tc when reducing γ12.Hence, γ12 is the ultimate limiting factor. To furtherimprove the biphoton coherence time, we need to minimize the dephasing rate γ12.
is below 2 and does not violate Cauchy-Schwartzinequality. The limit of the coherence time is corporately determined by ODand the atomic ground state dephasing rate γ12. Therefore,in Figure 4(a) we simulate the maximum Tcas a function of OD when keeping γ12 and in Figure4(b) vary γ12 when maintaining OD. Firstly, Figure 4(a) indicates extreme ODs bring the maximum Tcto approach 3.5 μs, which is determined by 1/γ12. Tcglows very slow after OD > 200. On the other hand, Figure4(b) shows a sensitive improvement of Tc when reducing γ12.Hence, γ12 is the ultimate limiting factor. To furtherimprove the biphoton coherence time, we need to minimize the dephasing rate γ12.
Experimental and theoretical results when varying Ωc.
(a), Paired photons coherence time as a function of coupling Rabifrequency Ωc. The cold atom cloud is prepared withvarious OD conditions and the curves represent the numerical results. Theblack filled circles, red squares, blue empty circles and purple trianglesdenote experimental data for OD = 22, 35, 50 and 100, respectively.(b), The experimental data of the maximum  .
.
In conclusion, we have demonstrated that optical depth OD, the couplingfield and the EIT dephasing rate corporately determine the biphoton coherencetime. In a dense cold atom cloud, the biphoton coherence time is efficientlymanipulated by the EIT slow light effect and therefore can be increased withhigher OD and lower coupling field amplitude. However, when the EIT couplingstrength is reduced further, the dephasing rate γ12becomes important and the EIT loss diminishes the two-photon waveform visibility,and thus ruin the nonclassical nature. The dephasing rate γ12is the ultimate limiting factor. In a two-dimensional MOT system, γ12is mainly caused by the quadruple field produced by the trapping coil. Asin our experiment, through balancing the cooling beams power to position theatomic cloud along the field center, we can reduce γ12to 283 kHz and thus produce paired photons with temporal coherencetime 2.34 μs with a reasonable OD of 100. The measured violationfactor of the Cauchy-Schwartz inequality is 12. The conditional second-orderauto-correlation function of anti-Stokes photons with reference to Stokesphotons is measured as  , which verifiesthe quantum Fock state nature. To push the limit even further, it is provedthat shutting down the trapping magnetic field in the measurement window andmaintaining a zero magnetic field at the atomic cloud is an efficient methodto reduce γ12 to below 100 kHz30.According to our calculation shown in Figure 4(b), onecould obtain Tc = 10 μs if γ12= 0.004γ13 ≈ 75 kHz.
, which verifiesthe quantum Fock state nature. To push the limit even further, it is provedthat shutting down the trapping magnetic field in the measurement window andmaintaining a zero magnetic field at the atomic cloud is an efficient methodto reduce γ12 to below 100 kHz30.According to our calculation shown in Figure 4(b), onecould obtain Tc = 10 μs if γ12= 0.004γ13 ≈ 75 kHz.
Methods
The cold atomic ensemble is prepared in a two-dimensional 85Rbmagneto-optical trap (MOT) with length L = 1.5 cm. The coolinglaser beam is red-detuned from the atomic transition 5S1/2F= 3 → 5P3/2F = 4 by 20 MHz. The totalpower of the six cooling beams is 130 mW and each beam has an intensityof 6.42 mW/cm2. The repump beam is on-resonanceto the atomic transition 5S1/2F = 2 → 5P3/2F= 2, which collects the atoms back to the cooling circulation. The total powerof the repump beam is 30 mW and it is applied onto the MOT along ±xaxis shown in Figure 1. The system is run periodicallywith a MOT preparation time of 4.5 ms followed with a measurement windowof 0.5 ms. The repump beam switches off 300 μs beforethe cooling beam is off and therefore over 99% of trapped atoms are pumpedto the ground state 5S1/2F = 2. The center gradientof the 2D MOT quadrature magnetic field is 10 G/cm and remains alwayson. To minimize the Zeeman shift for atomic energy state, we carefully balancethe six cooling beams to align the laser cooled atoms along the positionsof zero transverse B field.
After the atoms are cooled and trapped, we apply continuous pump (ωp)and coupling (ωc) lasers within the measurement window.Within the measurement window, the pump and coupling beam are present simultaneouslyon the cold atom cloud, with polarization σ+ and σ−respectively. The paired Stokes (ωs) with polarization σ+and anti-Stokes (ωas) photons σ−are emitted in opposite directions, to satisfy the angular momentum conservationin the FWM process. We collect the paired photons along the longitudinal axis(z axis as denoted), along which we obtain the largest OD for the cloud.To minimize the scattered optical noise from the strong laser beams, the pump-couplingaxis is deviated from the z axis by θ = 3°. The pumpbeam is blue-detuned to the transition |1〉 → |4〉 by Δp= 146 MHz, to avoid strong excitation and maintain low gain limit.The coupling beam is on-resonance to the transition |2〉 → |3〉,and therefore constitute a three-level Λ EIT scheme for anti-Stokes photons.
Either of the collection end is composed of a quarter wave plate followedby a polarization beam-splitter, a single mode fiber (SMF, fiber-fiber couplingefficiency 70%) and a Fabry-Perot filter (each with 70% transmission), andfinally a single photon counting module (SPCM-AQRH-14-FC from Excelitas, eachwith 50% detection efficiency). The coincidence measurements are carried outwith Time to Digital Converter (DPC-230 from Becker & Hickl GmbH).
References
Burnham, D. C. & Weinberg, D. L. Observation of simultaneity in parametric production of optical photon pairs. Phys. Rev. Lett. 25, 84–87 (1970).
Harris, S. E., Oshman, M. K. & Byer, R. L. Observation of tunable optical parametric flurescence. Phys. Rev. Lett. 18, 732–734 (1967).
Shih, Y. H. & Alley, C. O. New type of Einstein-Podolsky-Rosen-Bohm experiment using pairs of light quanta produced by optical parametric down conversion. Phys. Rev. Lett. 61, 2921–2924 (1988).
Kwiat, P. G., Mattle, K., Weinfurter, H. & Zeilinger, A. New high-intensity source of polarization-entangled photon pairs. Phys. Rev. Lett. 75, 4337–4341 (1995).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Ou, Z. Y. & Lu, Y. J. Cavity enhanced spontaneous parametric down conversion for the prolongation of correlation time between conjugate photons. Phys. Rev. Lett. 83, 2556–2559 (1999).
Kuklewicz, C. E., Wong, F. N. C. & Shapiro, J. H. Time-Bin-Modulated Biphotons from Cavity-Enhanced Down-Conversion. Phys. Rev. Lett. 97, 223601 (2006).
Neergaard-Nielsen, J. S., Melholt Nielsen, B., Takahashi, H., Vistnes, A. I. & Polzik, E. S. High purity bright single photon source. Opt. Express 15, 7940–7949 (2007).
Bao, X. H. et al. Generation of Narrow-Band Polarization-Entangled Photon Pairs for Atomic Quantum Memories, Phys. Rev. Lett. 101, 190501 (2008).
Fekete, J., Rieländer, D., Cristiani, M. & Riedmatten, H. Ultranarrow-Band Photon-Pair Source Compatible with Solid State Quantum Memories and Telecommunication Networks. Phys. Rev. Lett. 110, 220502 (2013).
van der Wal, C. H. et al. Atomic Memory for correlated photon states. Science 301, 196–200 (2003).
Kuzmich, A. et al. Generation of nonclassical photon pairs for scalable quantum communication with atomic ensembles. Nature 423, 731–734 (2003).
Thompson, J. K., Simon, J., Loh, H. & Vuletić, V. A high-brightness source of narrowband, identical-photon pairs. Science 313, 74–77 (2006).
Balić, V., Braje, D. A., Kolchin, P., Yin, G. Y. & Harris, S. E. Generation of paired photons with controllable waveforms. Phys. Rev. Lett. 94, 183601 (2005).
Kolchin, P., Du, S., Belthangady, C., Yin, G. Y. & Harris, S. E. Generation of narrow-bandwidth paired photons: use of a single driving laser. Phys. Rev. Lett. 97, 113602 (2006).
Du, S., Wen, J., Rubin, M. H. & Yin, G. Y. Four-wave mixing and biphoton generation in a two-level system. . Phys. Rev. Lett. 98, 053601 (2007).
Belthangady, C., Du, S., Chuu, C. S., Yin, G. Y. & Harris, S. E. Modulation and measurement of time-energy entangled photons. Phys. Rev. A 80, 031803(R) (2009).
Du, S., Wen, J. & Rubin, M. H. Narrowband biphoton generation near atomic resonance. J. Opt. Soc. Am. B 25, C98–C108 (2008).
Yang, T. et al. Experimental synchronization of independent entangled photon sources. Phys. Rev. Lett. 96, 110501 (2006).
Kaltenbaek, R., Blauensteiner, B., Żukowski, M., Aspelmeyer, M. & Zeilinger, A. Experimental interference of independent photons. Phys. Rev. Lett. 96, 240502 (2006).
Kolchin, P., Belthangady, C., Du, S., Yin, G. Y. & Harris, S. E. Electro-optic modulation of single photons. Phys. Rev. Lett. 101, 103601 (2008).
Chen, J. F. et al. Shaping Biphoton Temporal Waveform with Modulated Classical Fields. Phys. Rev. Lett. 104, 183604 (2010).
Zhang, S. et al. Optical precursor of a single photon. Phys. Rev. Lett. 106, 243602 (2011).
Zhou, S. et al. Optimal storage and retrival of single-photon waveforms. . Opt. Express 20, 24124–24131 (2012).
Ding, D. S., Zhou, Z. Y. Shi, B. S. & Guo, G. C. Single-photon-level quantum image memory based on cold atomic ensembles. Nat. Commun. 4, 2527 (2013).
Du, S., Kolchin, P., Belthangady, C., Yin, G. Y. & Harris, S. E. Subnatural linewidth biphotons with controllable temporal length. Phys. Rev. Lett. 100, 183603 (2008).
Zhao, L. et al. Photon pairs with coherence time exceeding one microsecond. Optica 1, 84 (2014).
Liao, K. et al. Subnatural-linewidth polarization-entangled photon pairs with controllable temporal length. Phys. Rev. Lett. 112, 243602 (2014).
Zhang, S. et al. A dark-line two-dimensional magneto-optical trap of 85Rb atoms with high optical depth. Rev. Sci. Instrum. 83, 073102 (2012).
Matsukevin, D. N. et al. Entanglement of a photon and collective atomic excitation. Phys. Rev. Lett. 95, 040405 (2005).
Acknowledgements
This work is supported by the National Natural Science Foundation of China(NSFC) through the major research plan (Precision Measurement Physics GrantNo. 91436211). Also, the work is supported by NSFC research programs, includingGrant No. 11204086, No. 11374003, No. 11234003, No. 11129402, National BasicResearch Program of China (973 Program Grants No. 2011CB921604) and ShanghaiScience and Technology Committee (Grant No.13PJ1402100).
Author information
Authors and Affiliations
Contributions
J.F.C. designed the experiment. Z.H. and P.Q. built up the system. Z.H.performed the experiment and analyzed the data. L.Z. worked out the analyticalsolution. J.F.C. wrote the manuscript and all authors contributed to the finalmanuscript. The whole program is under the supervision of W.P.Z.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensedunder a Creative Commons Attribution 4.0 International License. The imagesor other third party material in this article are included in the article'sCreative Commons license, unless indicated otherwise in the credit line; ifthe material is not included under the Creative Commons license, users willneed to obtain permission from the license holder in order to reproduce thematerial. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Han, Z., Qian, P., Zhou, L. et al. Coherence time limit of the biphotons generated in a dense cold atomcloud. Sci Rep 5, 9126 (2015). https://doi.org/10.1038/srep09126
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep09126
This article is cited by
-
Generation of correlated biphoton via four-wave mixing coexisting with multi-order fluorescence processes
Scientific Reports (2019)
-
Ultranarrow-bandwidth filter based on a thermal EIT medium
Scientific Reports (2018)
-
Subnatural-linewidth biphotons from a Doppler-broadened hot atomic vapour cell
Nature Communications (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.