Abstract
Similar to graphene, zero band gap limits the application of silicene in nanoelectronics despite of its high carrier mobility. By using first-principles calculations, we reveal that a band gap is opened in silicene nanomesh (SNM) when the width W of the wall between the neighboring holes is even. The size of the band gap increases with the reduced W and has a simple relation with the ratio of the removed Si atom and the total Si atom numbers of silicene. Quantum transport simulation reveals that the sub-10 nm single-gated SNM field effect transistors show excellent performance at zero temperature but such a performance is greatly degraded at room temperature.
Similar content being viewed by others
Introduction
Silicene, silicon analog of graphene, is predicted to possess a Dirac-cone-shaped energy band1 and ultra-high carrier mobility2 and thus has a potential application in high-performance nanoelectronics. Recently silicene has been successfully grown on Ag3,4,5,6,7, ZrB28, Ir9 and MoS210 substrates. However, zero band gap of pristine silicene limits its application as a logic element in electronic devices directly. It is critical to open the band gap of silicene without degrading its carrier mobility. Several methods have been proposed to open the band gap of silicene from first-principles calculations, such as vertical electric field2,11,12, surface adsorption13,14, or semihydrogenation15. Nonetheless, an experimentally approachable vertical electric field can only open a gap below 0.1 eV in silicene, evidently smaller than the minimum band gap requirement (0.4 eV) for traditional field effect transistors (FETs)2. Metal atom adsorption is able to induce a larger band gap up to 0.66 eV in silicene13,14,16, but a large supply voltage (Vdd) of about 1.7 ~ 30 V is required13,14. It is highly desirable to design a new silicene FET with a high on/off ratio under a low supply voltage.
Computing technology requires a channel length of FET smaller than 10 nm in next decades. However, bulk-Si FET will not perform at sub-10 nm channel length because of its short-channel effects17. In order to enable continued FET scaling, one can modify Si device structure or use an alternative channel geometry/material. Up to now, 8 ~ 10 nm advanced Si FETs (including Si nanowire with gate-all-round-configuration18, double-gated FinFET19 and extremely thin Si on insulator (ETSOI)20) and 9 nm carbon nanotube (CNT) FETs21 have been fabricated. It is interesting to examine whether silicene FETs are competitive with these existing advanced Si FETs and CNTFETs.
In this Article, we propose a novel method to open the band gap of silicene, namely, fabrication of silicene nanomesh (SNM). Theoretical calculations22,23,24,25,26,27,28,29,30,31,32 have shown that the band gap of graphene can be opened by making a periodic array of holes (namely nanomesh) and the size of the gap depends on the structural parameters of graphene nanomesh (GNM). Experimentally, a transport gap has been observed in GNM FETs with a triangular array of hexagonal holes33,34,35,36,37 and the on/off current ratio can reach 100 38, which is one order of magnitude larger than that of pristine graphene FETs. Based on density functional theory (DFT) calculations, a band gap is opened up in SNM, whose size strongly depends on the width W of the wall between the neighboring holes and has a maximum value of 0.68 eV. Subsequently, we simulate the transport properties of the sub-10 nm SNM FETs based on the non-equilibrium Green's function (NEGF). The simulated SNM FETs show excellent device performance with an on/off ratio up to 104 at a supply voltage of 0.5 V. When phonon scattering is considered, the performance is greatly degraded with an on/off ratio down to 100.
Results and Discussion
Geometry and electronic structure
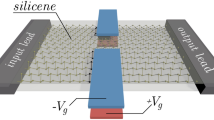
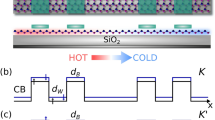
The SNM model is built by digging a simple triangular array of hexagonal holes in a silicene sheet, as shown in Fig. 1(a). The edge of the holes has zigzag shape and the edge Si atoms of the holes are passivated by hydrogen atoms. Each type of SNM is designated by the notation [R, W], where the R index reflects the radius of the hole calculated by Nremoved = 6R2 (Nremoved is the number of the removed Si atoms from one lattice cell) and the W index is the width of the wall between the nearest-neighboring holes. Fig. 1(a) shows an example of [R, W] = [1, 4] SNM.
(a) Geometric configuration of SNMs with R = 1 and W = 4. The yellow and white balls stand for Si and H atoms, respectively. Energy band structures of SNMs with odd (b) and even (c) W. (d) The band gap of SNM as a function of W with R = 1 and 2. (e) Band gap is plotted versus the quantity  (Nremoved is the number of removed Si atoms and Ntotal is equal to the number of atoms before the holes is made in the unit cell). The black line represents a linear fit to the data.
(Nremoved is the number of removed Si atoms and Ntotal is equal to the number of atoms before the holes is made in the unit cell). The black line represents a linear fit to the data.
After relaxation, the unit cell size of the SNM structures is nearly unchangeable compared with the corresponding silicene supercell. However, constructing periodic holes will slightly affect the buckling distance (Δ) of the edge silicon atoms, which is larger than that of pristine silicene (0.46 Å) and increases with the increase of W given the same R = 1 (Fig. S1(a)). For the silicon atoms far away from the holes, the Δ tends to be the value of pristine silicene, as shown in Fig. S1(b).
To investigate the stability of SNMs, the cohesive energy Ecoh and Gibbs free energy δG, are calculated. The per-atom cohesive energy Ecoh is calculated according to the follow equation:

where E(Si) and E(H) are the energies of the free silicon and hydrogen atoms, respectively, E(SNM) the total energy of a SNM in one supercell, NSi and NH the numbers of silicon and hydrogen atoms in a SNM supercell, respectively. The calculated Ecoh for [R = 1, W] SNM is positive (3.64 ~ 4.71 eV) and increases with the increasing W as shown in Fig. 2a. We define the per-atom Gibbs free energy (δG) of formation for SNMs as

where nSi and nH are the mole fraction of Si and H atoms, respectively, for a given structure and μSi and μH are the per-atom chemical potentials of Si and H, respectively, at a given state. We chose μSi and μH as the binding energies per atom of bulk Si and H2 molecule, respectively. As given in Fig. 2b, the calculated δG values for W = 1 ~ 3 are 0.012 ~ 0.075 eV and therefore a small amount of additional energy is required to make these reaction processes happen. However, SNMs have a negative δG when W > 3, indicating a higher thermodynamical stability relative to their elemental reservoirs. Based on the width dependence of Ecoh and δG, the stability of SNMs monotonically increases with the increasing W given the same R = 1. To further study its stability, a molecule dynamic simulation of the [R = 1, W = 2] SNM is performed at temperature of 1000 K. As shown in the Supplementary Movie S1 we added, the structure is well kept, suggesting SNMs are stable enough against the high temperature.
The calculations done by Liu et al.26 show that the band gap of graphene hexagonal nanomeshes is only opened when W is even. While W is odd, the GNMs behave semimetallically like pristine graphene. Our calculations show that SNMs have similar properties. The band structures of [1, W] SNMs with W = 1 ~ 10 are provided in Fig. 1(b) and 1(c). Similar to pristine silicene, the SNMs with odd W show semimetallic behavior, with a pair of linear bands crossing at the K point (Fig. 1(b)). By contrast, a direct band gap (Eg) is opened at the Г point when W is even (Fig. 1(c)). The band structures of [2, W] SNMs with even W are provided in Fig. S2 and the band gaps are also opened in them. The opened band gap when W is even monotonically decreases with the increasing W given the same R. A maximum band gap of about 0.68 eV is observed in both R = 1 and 2 cases (Fig. 1(d)).
Pedersen et al.25 found that the band gap Eg in GNM is determined by the relation

where Ntotal and Nremoved are the numbers of the total Si atoms before digging the holes and the removed hole atoms in a unit cell, respectively and g is a fitting factor. For GNM, one has g = 25 eV. Fig. 1(e) shows the band gap of SNM against N1/2removed/Ntotal. The linear relation remains with g = 7.246 eV, which is much smaller than that for GNM. Therefore, given the same Ntotal and Nremoved, i.e. with the same notation [R, W], the band gap in SNM is much smaller than that in GNM. The band gap opening in GNM is proved not directly caused by quantum confinement as in graphene nanoribbions (GNRs); instead, it has a geometric symmetry origin32,37. When the two reciprocal lattice vectors of a GNM overlap with Dirac points of the pristine graphene, degeneracy at the Dirac points is lifted and a sizable band gap appears; otherwise, it's semimetal like graphene. SNM shares similar mechanism of band gap opening with GNM. In [R, W] SNMs, when W is even its two reciprocal lattice vectors overlap with Dirac points of the pristine silicene, i.e. the K and K' points of pristine silicene are folded into the Г points of SNM. Due to the intervalley scattering, a band gap is opened in SNMs when W is even.
 can be explained if we approximately treat SNM as a periodic potential perturbation U(r) to pristine silicene. If K − K′ = G, where G is one reciprocal lattice vector of the SNM supercell, there is interaction between the two degenerate Dirac points. As a result, a band gap is opened and is expressed in terms of degeneracy perturbation theory as,
can be explained if we approximately treat SNM as a periodic potential perturbation U(r) to pristine silicene. If K − K′ = G, where G is one reciprocal lattice vector of the SNM supercell, there is interaction between the two degenerate Dirac points. As a result, a band gap is opened and is expressed in terms of degeneracy perturbation theory as,

where S is the square of the supercell of SNM,  and
and  are the Bloch function of A sublattice at the K and K′ points, with periodic part of
are the Bloch function of A sublattice at the K and K′ points, with periodic part of  and
and  , respectively. The external periodical potential U(r) induced by the hole is assumed to be rather localized. Given the same hole of different SNMs,
, respectively. The external periodical potential U(r) induced by the hole is assumed to be rather localized. Given the same hole of different SNMs,  is approximately independent of the size of the supercell and we therefore have
is approximately independent of the size of the supercell and we therefore have  due to Ntotal ∝ S.
due to Ntotal ∝ S.
Fig. 3 presents the effective mass (m*) of the conduction band bottom of SNMs along the Γ → K (meΓK) and Γ → M (meΓM) directions as a function of W. The effective mass is calculated by using the formula:

The effective mass m* monotonically decreases from 0.093 to 0.022 m0 for R = 1 and from 0.151 to 0.034 m0 for R = 2 with the increasing W because of the reduced band gap, where m0 is the free electron mass. meΓK is approximately equal to meΓM except for W = 2 case. At the same W, the m* values with R = 2 are slightly larger than their respective m* values with R = 1.
Transport properties of SNM FETs
The schematic model of a single-gated FET based on the [1, 2] SNM is presented in Fig. 4(a). The electrodes are composed of semi-infinite silicene. To avoid the interaction between SNM and SiO2 dielectric, a hBN buffer layer is inserted between the SNM and SiO2 substrate2 and the thickness of SiO2 dielectric plus hBN buffer region is di = 11 Å. To start with, we calculated the transmission spectrum of a 6.5 nm-gate-length SNM FET by using the DFT method with single-ζ (SZ) basis set to benchmark our SE extended Hückel result (Fig. S3). The transmission spectra calculated between the two methods are similar, except that the size of the transmission gap generated by the SE method (0.9 eV) is a litter larger than that by the DFT method (0.7 eV) and the transmission coefficients generated by the SE method near the Fermi level are unsmooth and generally larger than those by the DFT method. The larger transmission gap generated by the SE method can cause the decrease of on/off ratio compared with that by the DFT method given the same gate voltage window. The on/off ratio may be further slightly decreased when using the SE method due to the relative larger conductance in the off-state contributed by the larger transmission coefficient near Ef. However these won't affect much the results. Then we focus on the transport properties of the SNM FET with a larger gate length Lgate = 9.1 nm. The conductance in SNMs can be modulated by applying a gate voltage to the channel and an on/off switch is expected.
(a) Schematic of a graphdiyne device structure. The yellow and white balls stand for Si and H atoms, respectively. (b) Transmission spectra of the SNM transistor with Lgate = 9.1 nm at Vg = 0 and 0.5 V. The bias voltage is fixed at Vbias = 0.2 V. The vertical red dashed-lines denote the bias voltage window. The Fermi level is set to zero. (c) Transfer characteristic of the device at Vbias = 0.2 V. (d) Transmission eigenstates of the off-state (Vg = 0 V) and on-state (Vg = 0.5 V) at E = 0.05 eV and k = (0, 0). The isovalue is 0.2 a.u.
The transmission spectra of the 9.1 nm-gate-length SNM FET at Vg = 0 and 0.5 V with Vbias = 0.2 V are presented in Fig. 4(b). When Vg = 0 V, there is a transport gap of 0.9 eV centered at the Fermi level (Ef). The transmission coefficient nearly vanishes within the bias window, indicating an off state. By applying a positive gate voltage, the transport gap can be shifted towards low energy direction. At Vg = 0.5 V, relatively large transmission coefficients are moved inside the bias window. According to Eq. (6) in the Method section, the drain current is calculated and then normalized by the channel width to obtain the current density Ids (Fig. 4(c)). Clear on/off current modulation is achieved. If we set Vdd = Von−Voff = 0.5 V and Vg = 0.5 V is chosen as the on-state, the on/off ratio can reach 5.1 × 104, which is about three orders of magnitude larger than the maximum on/off ratios obtained in dual-gated silicene FET2 and already meets the requirement of 104 ~ 107 for the high-speed logic applications. The subthreshold swing (SS, here is defined as dVgate/d(logI)) is 68 mV/dec, which approaches the 60 mV/dec switching limit of the classical transistors. To provide an insight into the switch capability, we investigate the transmission eigenchannels of the off-state (Vg = 0 V) and on-state (Vg = 0.5 V) at E = 0.05 eV and k = (0, 0), as shown in Fig. 4(d). The transmission eigenvalue of the off-state is merely 6.71 × 10−7 and the corresponding incoming wave function is obviously scattered and unable to reach to the other lead. On the contrary, the transmission eigenvalue of the on-state is 0.78; as a result, the scattering is weak and the most of the incoming wave is able to reach to the other lead.
To determine the scaling effect of the gate length Lgate on the device performance, we calculate the transfer characteristics of the SNM FET with different gate lengths (3.8 ~ 9.1 nm) at a fixed bias voltage of Vbias = 0.2 V as shown in Fig. 5. The maximum current Imax is insensitive to Lgate. By contrast, the minimum current Imin increases with the decreasing Lgate. Such a scaling behavior is attributed to the increasing off-state leakage current with the decreased Lgate. Therefore, the maximum and minimum current ratio Imax/Imin decreases significantly from 5.8 × 105 at Lgate = 9.1 nm to 1.9 × 102 at Lgate = 3.8 nm (Fig. 6(a)). The on/off current ratio Ion/Ioff (the gate voltage window is limited to a supply voltage) is a more important parameter than Imax/Imin to characterize switching effect of an electronic device. We limit the gate voltage window to 0.5 V and show the Lgate dependent Ion/Ioff in Fig. 6(b). It also monotonously decreases from 5.1 × 104 at Lgate = 9.1 nm to 17 at Lgate = 3.8 nm.
Critical device performance parameters of the SNM field effect transistors as a function of the gate length at Vbias = 0.2 V: (a) Imax/Imin current ratio, (b) on/off current ratio at a gate voltage window of 0.5 V, (c) subthreshold swing, (d) transconductance, (e) intrinsic gate capacitance, (f) charge carrier transit time, (g) intrinsic cut-off frequency and (h) carrier drift velocity.
The subthreshold swing SS = dVgate/d(logI) is another important parameter of FET and determines how effectively the transistor can be turned off by changing the gate voltage. The SS of the SNM FETs monotonously increases from to 68 to 336 mV/dec when Lgate scales down from 9.1 to 3.8 nm. Transconductance gm is another important parameter to characterize switching effect of an electronic device, which is computed from gm = ∂Ids/∂Vg. The gm value decreases from 555 μS/μm at Lgate = 3.8 nm to 351 μS/μm at Lgate = 9.1 nm (Fig. 6(d)). Another key parameter the intrinsic gate capacitance Cg is calculated in Fig. 6(e). Cg is defined as Cg = ∂Qch/∂Vg, where Qch is the total charge of the channel. The relationship between the Cg and Lgate is the following equation39: Cg = ε0εrWgateLgate/tox, where ε0 and εr are the dielectric constant of vacuum and the relative dielectric constant of the gate dielectric, Wgate is the width of the gate and tox is the thickness of the gate dielectric. As shown in Fig. 6(e), Cg indeed increases almost linearly with Lgate from 159 aF/μm at Lgate = 3.8 nm to 258 aF/μm at Lgate = 9.1 nm. According to the charge control model at low bias,  , since Cg ∝ Lgate, if we assume the mobility is a constant, the transconductance gm tends to vary inversely with Lgate and our results is consistent with this tendency.
, since Cg ∝ Lgate, if we assume the mobility is a constant, the transconductance gm tends to vary inversely with Lgate and our results is consistent with this tendency.
Fig. 6(f) shows Lgate dependence of charge carrier transit time τ based on the calculated Cg and gm, i.e. τ = Cg/gm. τ increases from 0.29 to 0.73 ps when Lgate increases from 3.8 to 9.1 nm. The intrinsic cut-off frequency fT indicates how fast the channel current is modulated by the gate and is described as fT = 1/(2πτ)40,41,42. fT decreases monotonically with Lgate from 557 GHz at Lgate = 3.8 nm to 217 GHz at Lgate = 9.1 nm (Fig. 6(g)), which is much smaller compare with that in the sub-10 nm graphene FETs (4 ~ 22 THZ)43. The drift velocity of a transistor can be derived by vdrift = Lgate/τ. As shown in Fig. 6(h), vdrift is insensitive to the gate length and is 12.4 × 105 ~ 13.3 × 105 cm/s when Lgate = 3.8 ~ 9.1 nm.
Future FET technologies will require operation at voltages at or below 0.5 V to reduce power consumption. To compare the SNM FETs with the Si based and CNT transistors at a supply voltage Vdd = 0.5 V, we summarize the critical performance parameters of the sub-10 nm SNM (9.1 and 7.8 nm), advance Si and CNT FETs at Vbias = 0.5 V in Table 1. The 9.1 nm SNM FET carries an on-state current of 464 μA/μm, which is larger than those (41 ~ 300 μA/μm) of the 8 ~ 10 nm advanced Si devices but slightly smaller than that (630 μA/μm) of the 9 nm CNT device. The on/off current ratio of the 9.1 nm SNM FET is 7.4 × 103, which is a little smaller than those (1 × 104) of the 10 nm Si nanowire, 8 nm ETSOI and 9 nm CNT devices but larger than that (1 × 103) of 10 nm Si Fin device. The SS value (82 mV/dec) of the 9.1 nm SNM FET is slightly smaller than those (83 ~ 125 mV/dec) of the 10 nm Si nanowire and Si Fin, 8 nm ETSOI and 9 nm CNT devices. Taking the three criterions together, the 9.1 nm SNM FET is competitive with the sub-10 nm advanced Si devices but is inferior to the 9 nm CNT device.
Adding the total area of the gates is an effective way to strengthen the gates' control over the channel, the gate control ability of a FET is expected to be improved by using a dual gate configuration. The transfer characteristic of the 9.1 nm dual-gated SNM FET at Vbias = 0.5 V is provided in Fig. 7(a) to compare with that of the single-gated one with the same Lgate and improved gate control is apparent. The performance parameters of the 9.1 nm dual-gated SNM FET are generally better than those of the single-gated counterpart as listed in Table 1. The SS is reduce by 8 meV/dec, the large on/off current ratio is increased by a factor of 2.7 and the on-state current is increased by a factor of 1.6. The 9.1 nm dual-gated SNM FET delivers an on-state current of 870 μA/μm, which is larger than those (41 ~ 630 μA/μm) of the 8 ~ 10 nm advanced Si devices and 9 nm CNT device. The on/off current ratio of the 9.1 nm dual-gated SNM FET is 1.2 × 104, which is comparable with those of the 10 nm Si nanowire, 8 nm ETSOI and 9 nm CNT devices and one order of magnitude larger than that of the 10 nm Si Fin device. The SS (74 mV/dec) of the 9.1 nm dual-gated SNM is smaller than those (83 ~ 125 mV/dec) of the 8 ~ 10 nm advanced Si devices and 9 nm CNT device. Taking the three criterions together, the 9.1 nm dual-gated SNM has a better performance than the sub-10 nm advanced Si devices and 9 nm CNT device. The excellent performance of the SNM FET is attributed to the depressed short channel effects due to their extremely small thickness and fewer traps on semiconductor-dielectric interface due to the smooth interface (Fig. 8).
(a) Transfer characteristics of the 9.1 nm dual-gated SNM FET at Vbias = 0.5 and 0.71 V compared with that of the single-gated SNM FETs with the same Lgate at Vbias = 0.5 V. The inset is the side view of the dual-gated SNM transistor device. (b) Output characteristics for the 9.1 nm single- and dual-gated SNM FETs at different gate voltages.
Schematic of FET channel made of traditional 3D material (Si) and 2D material (SNM) and their corresponding vertical potential diagrams.
2D materials have clean surface with fewer traps in semiconductor-dielectric interface and are extremely thin compared to traditional 3D materials, leading to a better gate control. V(x) and |Ψ(x)|2 represent the potential and the probability density of the electronic charges, respectively.
The output characteristics for the 9.1 nm SNM FET at different gate voltages are shown in Fig. 7(b). The source-drain ballistic current increases with the applied bias voltage and no current saturation is observed until Vbias = 0.7 V. The current of the dual-gated SNM FET is much larger than that of the single-gated SNM FET at the same Vbias under Vg = 0.5 V, indicating an improved gate controlling.
The transfer and output characteristics of the 7.8 nm SNM FET are provided in Fig. S4. Although the performance of the 7.8 nm single-gated SNM FET is inferior to the sub-10 nm advanced Si devices and the 9 nm CNT device, the 7.8 nm dual-gated SNM FET is sufficiently improved: The SS is reduce by 4 meV/dec to 68 mV/dec, the large on/off current ratio is increased by a factor of 2.7 to 8.9 × 103 and the on-state current is increased by a factor of 3 to 607 μA/μm at a supply voltage of 0.5 V (Table 1). Consequently, the 7.8 nm dual-gated SNM FET has a better performance than the sub-10 nm advanced Si devices and is competitive with the 9 nm CNT device.
It is interesting to examine whether the SNM FETs can meet the requirements for the high-performance FETs from the 2013 edition of the International Technology Roadmap for Semiconductors (ITRS)44. The required gate lengths of HP logic of 2022 and 2023 are 8.9 nm and 8.0 nm and supply voltages are 0.72 and 0.71 V, respectively. The transfer characteristic of the 9.1 nm dual-gated SNM FET at Vbias = 0.72 V is provided in Fig. 6(a). The 9.1 nm dual-gated SNM FET, whose gate length is approximately meet the requirement of HP logic of 2022 (8.9 nm), carries an on-state current of 3122 μA/μm at a supply voltage of Vdd = 0.72 V and greatly satisfies the requirement of Ion = 1350 μA/μm for the HP logic of ITRS of 2022. As shown in Fig. S4(a), the calculated on-state current (1963 μA/μm) of the 7.8 nm dual-gated SNM FET at a supply voltage of Vdd = 0.71 V also meets the requirement (Ion = 1330 μA/μm) of the HP logic of ITRS of 2023. Unfortunately, the on/off current ratios of the 9.1 and 7.8 nm dual-gated SNM FETs are only 1.8 × 103 and 1.2 × 103, respectively. Both of them cannot meet the requirement of HP logic of ITRS (1.33 × 104 in 2022 and 1.35 × 104 in 2022).
We perform a molecular dynamics (MD) simulation of the channel region in a 9.1 nm single-gated SNM FET at room temperature to check how the transport properties change as phonon effect is partially included (only elastic scattering is considered) in the device. Compared with the transmission spectra of 9.1 nm single-gated SNM FET at Vbias = 0.2 V without considering the phonon scattering, the transport gap is increased from 0.9 eV to 1.5 eV and the transmission coefficients of both the conduction and valence bands are greatly depressed at 300 K after phonon scattering effect is included, as shown in Fig. 9. The off-state current at Vg = 0 V isn't affected much. Whereas the on-state current is decreased significantly to 3.9 × 10-2 μA/μm and the on/off current ratio is decreased to 39 at Vbias = 0.2 V when the gate bias window is fixed at 0.5 V. When Vbias = 0.5 V, the on-state current is decreased to 4.0 μA/μm and the on/off current ratio is decreased to 100. Therefore, SNM FETs still works at room temperature, but its performance is greatly degraded. Phonon scattering plays an import role on accurate assessment of SNM FETs even at a short-gate length below 10 nm.
In summary, a band gap is opened in SNM when the width W of the wall between the neighboring holes is even from the first-principles calculations. The size of the band gap increases with the reduced W and is proportional to the ratio of the removed Si atom and the total Si atom numbers of silicene. We simulate the transport of the FETs with a sub-10 nm SNM channel based on quantum transport theory and find that the sub-10 nm SNM FETs have an excellent performance at zero temperature, characterized by a large on-state current up to 870 μA/μm, a large on/off current ratio up to 1.2 × 104 and a small subthreshold swing low to 68 mV/dec at a supply voltage of 0.5 V. However the performance is greatly degraded when phonon scattering effect is included.
Methods
The geometry optimizations and the band structure calculations are performed using the double numerical basis set plus polarization (DNP), implemented in the DMol3 package45. We chose the generalized gradient approximation (GGA)46 of the Perdew-Burke-Ernzerhof (PBE) form to the exchange-correlation functional47. Both the atomic positions and lattice constant are relaxed without any symmetry constraints until the maximum force is smaller than 0.01 eV/Å. A 16 × 16 × 1 Monkhorst-Pack k-points grid48 is used in the first Brillouin zone sampling. A vacuum space of 20 Å normal to silicene plane is used to avoid spurious interaction between periodic images. To examine the thermal stability of SNMs, ab initio MD simulation within the NVT ensemble is carried out using the DMol3 package at 1000 K and the process lasts for more than 1.0 ps with a time step of 1.0 fs.
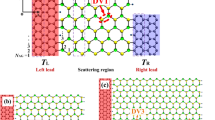
A single-gated two-probe model is built to simulate the transport of SNM and the pristine silicene is used as source and drain electrodes for simplicity. Transport properties are calculated by the semi-empirical (SE) extended Hückel method coupled with NEGF formalism implemented in the Atomistix Tool Kit (ATK) 11.2 package49,50,51. The Hoffman basis is used and the temperature is set at 300 K. The k-point meshes of the electrodes and central region are set to 1 × 50 × 50 and 1 × 50 × 1, respectively. The current is calculated with the Landauer-Bűttiker formula52:

where T(E, Vg, Vbias) is the transmission probability at a given gate voltage Vg and bias voltage Vbias, fL/R the Fermi-Dirac distribution function for the left(L)/right(R) electrode and μL/μR the electrochemical potential of the L/R electrode.
To include the phonon effect in the calculation of transport properties, ab initio MD simulation of the central region of the device within the NVT ensemble is performed by using the Dmol3 package at 300 K and the process lasts for 3.0 ps with the electrode extension parts constrained. The time step is 1.5 fs. Then different configurations of the central region are built into two-probe models after every 400 MD steps and their transport properties are evaluated and finally averaged over 5 configurations using a NEGF approach implemented in the ATK package.
During the production of this paper we would like to add that we are aware that silicene FET operating at room temperature has been fabricated recently53, corroborating theoretical expectations regarding its ambipolar Dirac charge transport.
References
Cahangirov, S., Topsakal, M., Aktük, E., Sahin, H. & Ciraci, S. Two- and one-dimensional honeycomb structures of silicon and germanium. Phys. Rev. Lett. 102, 236804 (2009).
Ni, Z. et al. Tunable bandgap in silicene and germanene. Nano Lett. 12, 113 (2012).
Feng, B. et al. Evidence of silicene in honeycomb structures of silicon on Ag(111). Nano Lett. 12, 3507 (2012).
Chen, L. et al. Evidence for Dirac fermions in a honeycomb lattice based on silicon. Phys. Rev. Lett. 109, 056804 (2012).
Chen, L. et al. Spontaneous symmetry breaking and dynamic phase transition in monolayer silicene. Phys. Rev. Lett. 110, 085504 (2013).
Vogt, P. et al. Silicene: Compelling experimental evidence for graphenelike two-dimensional silicon. Phys. Rev. Lett. 108, 155501 (2012).
Chiappe, D., Grazianetti, C., Tallarida, G., Fanciulli, M. & Molle, A. Local electronic properties of corrugated silicene phases. Adv. Mater. 24, 5088–5093 (2012).
Fleurence, A. et al. Experimental evidence for epitaxial silicene on diboride thin films. Phys. Rev. Lett. 108, 245501 (2012).
Meng, L. et al. Buckled silicene formation on Ir(111). Nano Lett. 13, 685 (2013).
Chiappe, D. et al. Two-dimensional Si nanosheets with local hexagonal structure on a MoS2 surface. Adv. Mater. 26, 2096–2101 (2013).
Drummond, N. D., Zólyomi, V. & Fal'ko, V. I. Electrically tunable band gap in silicene. Phys. Rev. B 85, 075423 (2012).
Motohiko, E. A topological insulator and helical zero mode in silicene under an inhomogeneous electric field. New J. Phys. 14, 033003 (2012).
Quhe, R. et al. Tunable and sizable band gap in silicene by surface adsorption. Sci. Rep. 2, 10.1038/srep00853 (2012).
Ni, Z. et al. Tunable band gap and doping type in silicene by surface adsorption: towards tunneling transistors. Nanoscale 6, 7609–7618 (2014).
Pan, F. et al. Gate-induced half-metallicity in semihydrogenated silicene. Phys. E 56, 43 (2014).
Gao, J., Zhang, J., Liu, H., Zhang, Q. & Zhao, J. Structures, mobilities, electronic and magnetic properties of point defects in silicene. Nanoscale 5, 9785 (2013).
Ieong, M., Doris, B., Kedzierski, J., Rim, K. & Yang, M. Silicon device scaling to the sub-10-nm regime. Science 306, 2057 (2004).
Li, M. et al. Sub-10 nm gate-all-around CMOS nanowire transistors on bulk Si substrate. Paper presented at VLSI Technol., Honolulu, HI. VLSI Technology, 2009 Symposium on: IEEE. (2009, June 16–18).
Yu, B. et al. FinFET scaling to 10 nm gate length. Paper presented at IEEE Int. Electron Devices Meeting. San Francisco CA USA. IEDM '02. International: IEEE. ( 10.1109/IEDM.2002.1175825)(2002 Dec. 8–11).
Doris, B. et al. Device design considerations for ultra-thin SOI MOSFETs. Paper presented at IEEE Int. Electron Devices Meeting. Washington DC USA. IEDM '03 Technical Digest: IEEE. ( 10.1109/IEDM.2003.1269360)(2003 Dec. 8–10).
Franklin, A. D. et al. Sub-10 nm carbon nanotube transistor. Nano Lett. 12, 758 (2012).
Oswald, W. & Wu, Z. Energy gaps in graphene nanomeshes. Phys. Rev. B 85, 115431 (2012).
Vanević, M., Stojanović, V. M. & Kindermann, M. Character of electronic states in graphene antidot lattices: Flat bands and spatial localization. Phys. Rev. B 80, 045410 (2009).
Petersen, R. & Pedersen, T. G. Quasiparticle properties of graphene antidot lattices. Phys. Rev. B 80, 113404 (2009).
Pedersen, T. G. et al. Graphene antidot lattices: Designed defects and spin qubits. Phys. Rev. Lett. 100, 136804 (2008).
Ouyang, F., Peng, S., Liu, Z. & Liu, Z. Bandgap opening in graphene antidot lattices: The missing half. ACS Nano 5, 4023 (2011).
Liu, X., Zhang, Z. & Guo, W. Universal rule on chirality-dependent bandgaps in graphene antidot lattices. Small 9, 1405 (2013).
Jippo, H., Ohfuchi, M. & Kaneta, C. Theoretical study on electron transport properties of graphene sheets with two- and one-dimensional periodic nanoholes. Phys. Rev. B 84, 075467 (2011).
Petersen, R., Pedersen, T. G. & Jauho, A.-P. Clar sextet analysis of triangular, rectangular and honeycomb graphene antidot lattices. ACS Nano 5, 523 (2011).
Liu, W., Wang, Z. F., Shi, Q. W., Yang, J. & Liu, F. Band-gap scaling of graphene nanohole superlattices. Phys. Rev. B 80, 233405 (2009).
Lopata, K., Thorpe, R., Pistinner, S., Duan, X. & Neuhauser, D. Graphene nanomeshes: Onset of conduction band gaps. Chem. Phys. Lett. 498, 334 (2010).
Dvorak, M., Oswald, W. & Wu, Z. Bandgap opening by patterning graphene. Sci. Rep. 3, 2289, 2210.1038/srep02289 (2013).
Liu, L. et al. Nanosphere lithography for the fabrication of ultranarrow graphene nanoribbons and on-chip bandgap tuning of graphene. Adv. Mater. 23, 1246 (2011).
Kim, M., Safron, N. S., Han, E., Arnold, M. S. & Gopalan, P. Fabrication and characterization of large-area, semiconducting nanoperforated graphene materials. Nano Lett. 10, 1125 (2010).
Eroms, J. & Weiss, D. Weak localization and transport gap in graphene antidot lattices. New J. Phys. 11, 095001 (2009).
Peters, E. C., Giesbers, A. J. M. & Burghard, M. Variable range hopping in graphene antidot lattices. Phys. Status Solidi B 249, 2522 (2012).
Dvorak, M. & Wu, Z. Geometrically induced transitions between semimetal and semiconductor in graphene. Phys. Rev. B 90, 115415 (2014).
Bai, J., Zhong, X., Jiang, S., Huang, Y. & Duan, X. Graphene nanomesh. Nature nanotech. 5, 190 (2010).
Wu, Y. et al. High-frequency, scaled graphene transistors on diamond-like carbon. Nature 472, 74–78 (2011).
Burke, P. J. AC performance of nanoelectronics: towards a ballistic THz nanotube transistor. Solid-State Electron. 48, 1981 (2004).
Schwierz, F. & Liou, J. J. RF transistors: Recent developments and roadmap toward terahertz applications. Solid-State Electron. 51, 1079 (2007).
Liao, L. et al. Sub-100 nm channel length graphene transistors. Nano Lett. 10, 3925 (2010).
Zheng, J. et al. Sub-10 nm gate length graphene transistors: Operating at terahertz frequencies with current saturation. Sci. Rep. 3, 1314, 1310.1038/srep01314 (2013).
ITRS-The International Technology Roadmap for Semiconductors. [Oline], (2014) Available at: http://www.itrs.net. (Accessed: 8th April 2014).
Delley, B. An all-electron numerical-method for solving the local density functional for polyatomic-molecules. J. Chem. Phys. 92, 508 (1990).
Perdew, J. P. & Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 45, 13244 (1992).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).
Lin, X. & Ni, J. Much stronger binding of metal adatoms to silicene than to graphene: A first-principles study. Phys. Rev. B 86, 075440 (2012).
Taylor, J., Guo, H. & Wang, J. Ab initio modeling of open systems: Charge transfer, electron conduction and molecular switching of a C60 device. Phys. Rev. B 63, 121104 (2001).
Brandbyge, M., Mozos, J.-L., Ordejón, P., Taylor, J. & Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 65, 165401 (2002).
Datta, S. Electronic transport in mesoscopic systems. (Cambridge University Press, 1995).
Tao, L. et al. Silicene field-effect transistors operating at room temperature. Nature Nanotech. advance online publication, 10.1038/nnano.2014.325 (1995).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Nos. 11274016, 51072007 and 61471301), the National Basic Research Program of China (Nos. 2013CB932604 and 2012CB619304), National Foundation for Fostering Talents of Basic Science (Nos. J1030310/J1103205), Program for New Century Excellent Talents in University of MOE of China and the Special Fund of Education Department of Shaanxi Province, China (Grant No. 2013JK0635).
Author information
Authors and Affiliations
Contributions
J.L. conceived the idea. F.P. and Y.W. did the transport simulations. K.J. performed the electronic calculations. The data analyses were performed by F.P., Y.W., K.J., Z.N. and J.M. J.Z., R.Q., J.S., J.Y. and C.C. helped discussing. This manuscript was written by F.P., Y.W. and J.L. All authors reviewed this manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Supplementary Information
movie S1
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Pan, F., Wang, Y., Jiang, K. et al. Silicene nanomesh. Sci Rep 5, 9075 (2015). https://doi.org/10.1038/srep09075
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep09075
This article is cited by
-
Understanding porosity and temperature induced variabilities in interface, mechanical characteristics and thermal conductivity of borophene membranes
Scientific Reports (2021)
-
The stability, structural, electronic, and optical properties of hydrogenated silicene under hydrostatic pressures: a first-principle study
Journal of Molecular Modeling (2021)
-
Rise of silicene and its applications in gas sensing
Journal of Molecular Modeling (2021)
-
Effects of temperature and intrinsic structural defects on mechanical properties and thermal conductivities of InSe monolayers
Scientific Reports (2020)
-
Strain-induced energetic and electronic properties of stanene nanomeshes
Journal of Computational Electronics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.