Abstract
We derive an easily computable quantum speed limit (QSL) time bound for open systems whose initial states can be chosen as either pure or mixed states. Moreover, this QSL time is applicable to either Markovian or non-Markovian dynamics. By using of a hierarchy equation method, we numerically study the QSL time bound in a qubit system interacting with a single broadened cavity mode without rotating-wave, Born and Markovian approximation. By comparing with rotating-wave approximation (RWA) results, we show that the counter-rotating terms are helpful to increase evolution speed. The problem of non-Markovianity is also considered. We find that for non-RWA cases, increasing system-bath coupling can not always enhance the non-Markovianity, which is qualitatively different from the results with RWA. When considering the relation between QSL and non-Markovianity, we find that for small broadening widths of the cavity mode, non-Markovianity can increase the evolution speed in either RWA or non-RWA cases, while, for larger broadening widths, it is not true for non-RWA cases.
Similar content being viewed by others
Introduction
The problem of how fast can a quantum system evolve is of particular interest and has attracted much attention. Quantum mechanics, as a fundamental law of nature, provides ultimate constraints known as quantum speed limits (QSLs) which are virtually at the center of all areas of quantum physics and thus they are of manifold applications, including exploring the physical limits of computation1, providing fundamental limit of precision under quantum metrology2,3, restricting efficiency of quantum optimal control algorithms4,5 and providing a minimal time bound to perform the optimal process6. The maximal rate υ of evolution can be described by the QSL time defined as the minimal time τQSL needed to evolve the initial state (pure or mixed) ρ0 to a target state ρt through a unitary evolution acted by a time-independent Hamiltonian H, i.e., the shorter time τQSL means the higher rate υ. The evolution time is lower-bounded by Refs. 7,8,9:

where  is the Bures fidelity which can be used to characterize the distance between the two states and
is the Bures fidelity which can be used to characterize the distance between the two states and  is the standard deviation of the initial-state energy. On the other hand, some researchers found that in several cases, the evolution time can be bounded more tightly by the average energy above the ground state, E − E010,11, namely,
is the standard deviation of the initial-state energy. On the other hand, some researchers found that in several cases, the evolution time can be bounded more tightly by the average energy above the ground state, E − E010,11, namely,

where the initial state ρ0 and target state ρt can be pure or mixed and the energies of the initial state is E = Tr(Hρ0) and the ground state energy is E0 = Tr(Hρground). Therefore, based on the two results above, people usually define the QSL time as  .
.
Most previous studies focus on unitary dynamics of isolated quantum systems7,8,9,10,11,12,13,14,15, while, all systems are unavoidably coupled to their environments. Therefore, it is necessary to determine a QSL time for open systems16,17,18,19. Recently, Taddei et al.16 developed a method to investigate the QSL problem in open systems described by positive non-unitary maps by using of quantum Fisher information for time estimation. While, for the case of the initial mixed states, a Hermitian operator is required to minimize the Fisher information in the enlarged system-environment space, which is generally a challenging task. Soon later, del Campo et al.17 employed the concept of relative purity to derive an analytical and computable QSL time for open systems undergoing a completely positive and trace preserving evolution. Actually, their bound also easily accounts for the non-Markovian dynamics. It should be noted that relative entropy can perfectly make a distinction between an initial pure state and its target state, however it may fail to distinguish an initial mixed state to its target state. Because in the latter case, relative purity can reach the value of 1, even though the two states are not completely consistent (see examples in the following section). Recently, Deffner and Lutz18 formulated a tight bound on the minimal evolution time of an arbitrarily driven open system and showed that non-Markovian effects can speed up quantum evolution. However, their time bound is derived from pure initial states and can not be directly applied into the mixed initial states.
Therefore, motivated by the recent studies above, we employ an alternative fidelity definition different from relative entropy in order to derive a new computable QSL time bound, which can easily account for the situations where the initial states are mixed. From this point of view, we emphasize that the new QSL time bound is superior to all the previous bounds in the cases of initial mixed states. On the other hand, the system-environment interaction will introduce quantum decoherence, which is one of the most important problem in quantum information processing20. How does the decoherence process affect the QSL time, consequently, affect the evolution speed of the system? In order to give a constructive answer, we study the QSL time problem in a qubit system interacting with a bosonic bath. Moreover, by using of a hierarchy equation method, we try to find the effects of counter-rotating terms and non-Markovianity on the QSL time bound, which are short of study in the previous literatures.
Usually, the description of the dynamics of open systems involves various approximations, such as the Born and Markovian approximation. An effective method that avoids the above two approximations was developed by Tanimura et al.21,22,23,24,25, who established a set of hierarchical equations that includes all orders of system-bath interactions. The derivation of the hierarchy equations requires that the time-correlation function of the bath can be decomposed into a set of exponential functions25. At finite temperature, this requirement is fulfilled if the system-bath coupling can be described by a Drude spectrum. The hierarchy equation method has been successfully used in describing quantum dynamics of chemical and biophysical systems23,24,25,26,27,28. On the other hand, the hierarchy equation method is also powerful to study the dynamics of qubit devices at low operating temperature29, when the environment is usually modeled by a Lorentz-broadened cavity mode.
The set of hierarchy equations derived here provides an exact treatment of decoherence and employs neither the rotating-wave, Born, nor Markovian approximations. The hierarchy equation method enables us to deeply explore the effects of the environment on the QSL time bound, which is presented as follows: (i) system-bath correlations are here fully accounted during the entire time evolution, which is different from that the correlations are truncated to second order. High-order correlations are shown30 to be very important, even producing a totally different physics; (ii) without weak coupling approximation, the hierarchy equation method is a promising method for studying strong- and ultrastrong- coupling physics31,32. (iii) Refs. 33 and 34 found that the RWA may lead to faulty results. Especially, recent developments in physical implementation lead to strong coupling between qubit and cavity modes31,32, which requires a careful consideration of the effect of counter-rotating terms. Fortunately, the RWA can be avoided in hierarchy equation method; (iv) Markovian approximation is naturally avoided in hierarchy equation method, thus we can consider the effects of non-Markovianity. Recently more and more attention and interest have been devoted to the study of non-Markovian processes35,36,37,38,39,40,41,42.
In the following sections, we will first give the QSL time bound derived from a fidelity which is different from the relative purity and Bures fidelity. Secondly, we synoptically introduce hierarchy equation method, then we will consider the QSL time in a qubit system interacting with a broadened cavity mode. The qubit-cavity coupling spectrum is described as Lorentz type. The results obtained by hierarchy equations will be compared with those obtained within RWA. The relation between QSL and non-Markovianity will also be explored.
Results
Derivation of quantum speed limit time
Firstly, we should employ the concept of fidelity as the distance measure of two quantum states. It is well known that the Bures fidelity may be a perfect definition of fidelity43. However, due to the difficulty in the calculation, people try to find alternative definitions of fidelity44,45,46. Among them, we find the definition studied by Wang et al. from the point of Hilbert–Schmidt product for two operators46, has some desirable properties and could be a good distance measure for two states density. The definition reads

where the ρ1, ρ2 denote two arbitrary density matrices This fidelity F satisfies Jozsa's four axioms43 up to a normalization factor that:
-
1
F is normalized. The maximum 1 is attained if and only if ρ1 = ρ2;
-
2
F is invariant under swapping the two states, i.e., F (ρ1, ρ2) = F (ρ2, ρ1);
-
3
The fidelity is invariant under unitary transformation U on the state space, i.e., F (Uρ1U, Uρ2U) = F (ρ1, ρ2);
-
4
When one of the state is pure, say, ρ2 = |ψ〉 〈ψ|, the fidelity reduces to
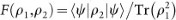 .
.
In addition to these advantages, the fidelity (3) is relatively easy to calculate since it only contains the Hilbert–Schmidt inner product and purity. Therefore, it has been well applied in experiment studies such as in NMR system47. Here, it should be compared with the definition of relative purity used in Ref. 17, i.e.,  . One can easily find that the relative purity ξ fails to satisfy axioms (1) and (2) for general mixed states, e.g., for two different states
. One can easily find that the relative purity ξ fails to satisfy axioms (1) and (2) for general mixed states, e.g., for two different states  (
( is 2-dimensional identity matrix) and ρ2 an arbitrary 2-dimensional density matrix, one can still obtain ξ (ρ1, ρ2) = 1. From this point of view, relative purity is not suitable to act as a distance measure when the initial state of ρ1 is a mixed state and thus it may induce some defects into the derivation of QSL time for this case.
is 2-dimensional identity matrix) and ρ2 an arbitrary 2-dimensional density matrix, one can still obtain ξ (ρ1, ρ2) = 1. From this point of view, relative purity is not suitable to act as a distance measure when the initial state of ρ1 is a mixed state and thus it may induce some defects into the derivation of QSL time for this case.
Let us now calculate the changing rate of the fidelity (3). By denoting the initial state as ρ0 and the state at time t as ρt, the derivative of fidelity F (ρ0, ρt) becomes

The rate above can be further bounded by using Cauchy-Schwarz inequality for operators, i.e., |Tr (AB)|2 ≤ Tr(AA)Tr(BB), then we have

Integrating Eq. (5) over a time period τ leads to the following inequality

where Fτ = F (ρ0, ρτ) denotes the target value of the fidelity in Eq. (3) at time τ and the kernel parameter is defined as

where we retain the time derivative  in order that the time limit τQSL in Eq. (6) can be used to consider either Markovian or non-Markovian dynamics.
in order that the time limit τQSL in Eq. (6) can be used to consider either Markovian or non-Markovian dynamics.
We should note that for the case of a initial pure state |ψ (0)〉 under a unitary evolution  , then we have
, then we have  , consequently,
, consequently,  . Thus the second term in the first line in Eq. (4) equals zero and the coefficient 2 in Xτ should be omitted. Furthermore, the minimum time required for the time evolving state |ψ (t)〉 to become orthogonal to its initial state |ψ (0)〉, i.e., the so-called passage time12,
. Thus the second term in the first line in Eq. (4) equals zero and the coefficient 2 in Xτ should be omitted. Furthermore, the minimum time required for the time evolving state |ψ (t)〉 to become orthogonal to its initial state |ψ (0)〉, i.e., the so-called passage time12,  , with (ΔE)2 = 〈ψ (0)| H2 |ψ (0)〉 − 〈ψ (0)| H |ψ (0)〉2, which is consistent with that of Ref. 17. However, for mixed initial states and non-unitary evolutions, our result will be inevitably different from that of Ref. 17.
, with (ΔE)2 = 〈ψ (0)| H2 |ψ (0)〉 − 〈ψ (0)| H |ψ (0)〉2, which is consistent with that of Ref. 17. However, for mixed initial states and non-unitary evolutions, our result will be inevitably different from that of Ref. 17.
Moreover, when we take into account a fact that  (with d the dimension of ρt), then we will obtain a looser time bound by substituting
(with d the dimension of ρt), then we will obtain a looser time bound by substituting  into Eq. (6). Consequently, when considering a Lindblad-form evolution, we will provide a QSL time bound depending on the initial state and the generators of the dynamical channel similar to the result in Ref. 17.
into Eq. (6). Consequently, when considering a Lindblad-form evolution, we will provide a QSL time bound depending on the initial state and the generators of the dynamical channel similar to the result in Ref. 17.
The system-environment model and the hierarchy equation method
Here we consider qubits interacting with a bosonic bath, also known as the spin-boson model:

where HS is the free Hamiltonian of the qubit (with  ) and here we choose
) and here we choose

where σz(x,y) is the Pauli operator, and

where V is the operator of the qubit and here we choose V = σx.  and bk are the creation and annihilation operators of the bath, while gk is the coupling strength between the qubit and the kth mode of the bath.
and bk are the creation and annihilation operators of the bath, while gk is the coupling strength between the qubit and the kth mode of the bath.
The exact dynamics of the system in the interaction picture can be derived as Ref. 25

if the qubit and bath are initially in a separable state, i.e.  , where ρB is the initial state of the bath. In Eq. (11),
, where ρB is the initial state of the bath. In Eq. (11),  is the chronological time-ordering operator, which orders the operators inside the integral such that the time arguments increase from right to left. Two superoperators are introduced, A × B ≡ [A, B] = AB − BA and A°B ≡ {A, B} = AB + BA. Also, CR (t2 − t1) and CI (t2 − t1) are the real and imaginary parts of the bath time-correlation function
is the chronological time-ordering operator, which orders the operators inside the integral such that the time arguments increase from right to left. Two superoperators are introduced, A × B ≡ [A, B] = AB − BA and A°B ≡ {A, B} = AB + BA. Also, CR (t2 − t1) and CI (t2 − t1) are the real and imaginary parts of the bath time-correlation function

respectively, and

Equation (11) is difficult to solve directly, due to the time-ordered integral. An effective method for this problem was developed21,22,23,24,25,26,27 by solving a set of hierarchy equations, such as the form of Eq. (17). A key condition in deriving the hierarchy equation is that the correlation function (13) should be decomposed into a sum of exponential functions of time as  , with parameters fk and γk depend on the system-bath coupling spectrum and the temperature. Then, the hierarchy equations are obtained by repeatedly taking the derivative of the right-hand side.
, with parameters fk and γk depend on the system-bath coupling spectrum and the temperature. Then, the hierarchy equations are obtained by repeatedly taking the derivative of the right-hand side.
At finite temperatures, the system-bath coupling can be described by the Drude spectrum, however, when we consider qubit devices, which are generally prepared in nearly zero-temperature environments. Then the coupling spectrum between the qubits and cavity modes is usually Lorentz type and the hierarchy method can also be applied29.
Now we consider one qubit interacting with a single mode of the cavity, with transition frequency ω0. Due to the imperfection of the cavity, the single mode is broadened and the qubit-cavity coupling spectrum becomes Lorentz-type

where λ is the broadening width of the cavity mode which is connected to the bath correlation time  . The relaxation time scale on which the state of the system changes is related to γ by τs = γ−1 and γ partly reflects the system-bath coupling strength, because when integrating the spectrum J (ω) over the entire region of ω, one will give the effective coupling strength as
. The relaxation time scale on which the state of the system changes is related to γ by τs = γ−1 and γ partly reflects the system-bath coupling strength, because when integrating the spectrum J (ω) over the entire region of ω, one will give the effective coupling strength as  .
.
At zero temperature, if the cavity is initially in a vacuum state  , the time-correlation function (13) becomes
, the time-correlation function (13) becomes

which is an exponential form that we need to use for the hierarchy equations. For a limit case,  , i.e.,
, i.e.,  , then we have a flat spectrum of Eq. (14) and the correlation tends to δ function that C (t2 − t1) → γδ (t2 − t1), this is the so-called Markovian limit and the Markovian decay rate γM = γ.
, then we have a flat spectrum of Eq. (14) and the correlation tends to δ function that C (t2 − t1) → γδ (t2 − t1), this is the so-called Markovian limit and the Markovian decay rate γM = γ.
To derive the hierarchy equation in a convenient form, we further write the real and imaginary parts of the time-correlation function (15) as

where νk = λ + (−1)kiω0. Then, following procedures shown in Refs. 21, 25, the hierarchy equations of the qubits are obtained as

where the subscript  is a two-dimensional index, with integer numbers n1(2) ≥ 0 and
is a two-dimensional index, with integer numbers n1(2) ≥ 0 and  . The vectors,
. The vectors,  ,
,  and
and  . We emphasize that
. We emphasize that  with
with  are auxiliary operators introduced only for the sake of computing, they are not density matrices and are all set to be zero at t = 0. The hierarchy equations are a set of linear differential equations and can be solved by using the Runge-Kutta method. The contributions of the bath to the dynamics of the system, including both dissipation and Lamb shift, are fully contained in the hierarchy equation (17). The Lamb shift term, which is related to the imaginary part of the bath correlation function, can be written explicitly in the common non-Markovian equations. Since the real and imaginary parts of the bath correlation function are taken into considered here, the effects of the Lamb shift exist in the hierarchy equations, although not in an explicit form.
are auxiliary operators introduced only for the sake of computing, they are not density matrices and are all set to be zero at t = 0. The hierarchy equations are a set of linear differential equations and can be solved by using the Runge-Kutta method. The contributions of the bath to the dynamics of the system, including both dissipation and Lamb shift, are fully contained in the hierarchy equation (17). The Lamb shift term, which is related to the imaginary part of the bath correlation function, can be written explicitly in the common non-Markovian equations. Since the real and imaginary parts of the bath correlation function are taken into considered here, the effects of the Lamb shift exist in the hierarchy equations, although not in an explicit form.
For numerical computations, the hierarchy equation (17) must be truncated for large enough  . We can increase the hierarchy order
. We can increase the hierarchy order  until the results of ρS(t) converge. The terminator of the hierarchy equation is
until the results of ρS(t) converge. The terminator of the hierarchy equation is

where we dropped the deeper auxiliary operators  . The numerical results in this paper were all tested and converged and the density matrix ρS(t) is positive. The detailed derivation of Eq. (17) can be found in Refs. 21, 29.
. The numerical results in this paper were all tested and converged and the density matrix ρS(t) is positive. The detailed derivation of Eq. (17) can be found in Refs. 21, 29.
Numerical results
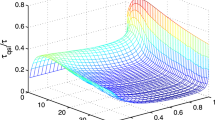
In Fig. 1, for a pure initial state, i.e.,  , where |1〉, |0〉 denote the eigenstates of the Pauli operator σz, we plot τQSL of Eq. (6) versus parameter γ by using hierarchy equation method (γ and λ are in units of ω0, which is omitted in the following for simplicity). The system-bath interaction Hamiltonian is
, where |1〉, |0〉 denote the eigenstates of the Pauli operator σz, we plot τQSL of Eq. (6) versus parameter γ by using hierarchy equation method (γ and λ are in units of ω0, which is omitted in the following for simplicity). The system-bath interaction Hamiltonian is  , so non-RWA case is considered here. The broadening-width parameter λ = 0.2 and the actual evolution time is t = 30. For comparison, we also plot
, so non-RWA case is considered here. The broadening-width parameter λ = 0.2 and the actual evolution time is t = 30. For comparison, we also plot  which are derived from operator norm, trace norm and Hilbert-Schmidt norm respectively in Ref. 18. For a Hermitian operator A, if its singular values are μi, the operator norm is given by the largest singular value
which are derived from operator norm, trace norm and Hilbert-Schmidt norm respectively in Ref. 18. For a Hermitian operator A, if its singular values are μi, the operator norm is given by the largest singular value  , the trace norm is equal to the sum
, the trace norm is equal to the sum  and the Hilbert-Schmidt norm is defined as
and the Hilbert-Schmidt norm is defined as  . Subsequently, the QSL time
. Subsequently, the QSL time  can be obtained by substituting
can be obtained by substituting  into Eq. (6). From numerical results, one can find that
into Eq. (6). From numerical results, one can find that  corresponding to the highest curve is the tightest bound. And our QSL time τQSL presents the lowest values in most region of γ, except for small values of γ it gives tighter bound than
corresponding to the highest curve is the tightest bound. And our QSL time τQSL presents the lowest values in most region of γ, except for small values of γ it gives tighter bound than  . Despite the fact that our bound is not tight, it presents similar behavior with the tighter bounds. In the sense of the application in mixed state cases, it allows us to explore the effects of the parameters of the driven Hamiltonian and the purity of the initial states on the QSL time in later parts.
. Despite the fact that our bound is not tight, it presents similar behavior with the tighter bounds. In the sense of the application in mixed state cases, it allows us to explore the effects of the parameters of the driven Hamiltonian and the purity of the initial states on the QSL time in later parts.
Quantum speed limit time versus different parameter γ (in units of ω0).
The initial state is pure state. Different QSL time definitions are shown.  are derived from the operator norm, trace norm and Hilbert-Schmidt norm in Ref. 18. The actual driving time τ = 30.
are derived from the operator norm, trace norm and Hilbert-Schmidt norm in Ref. 18. The actual driving time τ = 30.
In the following figures, we choose a mixed initial state of Werner-type:

where  , the parameter 0 ≤ p ≤ 1 and
, the parameter 0 ≤ p ≤ 1 and  denotes a 2 × 2 identity matrix.
denotes a 2 × 2 identity matrix.
In Fig. 2, Fig. 3 and Fig. 4, we numerically investigate QSL time bound τQSL versus parameter γ. A reasonable comparison between the solutions within and without RWA will enable us to understand the contribution of the counter-rotating terms. The analytical results of the density matrix at arbitrary time t for RWA case is shown in the method section. Moreover, in order to find the relation between QSL time and non-Markovianity, we also numerically plot the measure of non-Markovianity M for RWA and non-RWA cases. Physically speaking, non-Markovian dynamics implies that the distinguishability of the pair of states increases at certain times. This can be interpreted as a flow of information from the environment back to the system, which prevents the coherence information loss of the system and thus helps to distinguish the two states. Therefore, it is nature to consider that whether non-Markovianity can accelerate the evolution of the system. The definition of the measure M is shown in the method section.
(a) Quantum speed limit time versus different parameter γ (in units of ω0). The broadening-width parameter λ = 0.03 (in units of ω0). The initial state is chosen as a mixed state in Eq. (19) with mixed parameter p = 0.8. (b) Measure of non-Markovianity M versus different parameter γ. The cases of non-RWA (black solid line with dots) and RWA (blue solid line with circles) are plotted. The actual driving time τ = 30.
(a) Quantum speed limit time versus different parameter γ (in units of ω0). The broadening-width parameter λ = 0.1 (in units of ω0). (b) Measure of non-Markovianity versus different parameter γ. The cases of non-RWA (black solid line with dots) and RWA (blue solid line with circles) are plotted. The initial state and other parameters are chosen as Fig. 2.
(a) Quantum speed limit time versus different parameter γ (in units of ω0). The broadening-width parameter λ = 0.6 (in units of ω0). (b) Measure of non-Markovianity versus different parameter γ. The cases of non-RWA (black solid line with dots) and RWA (blue solid line with circles) are plotted. The initial state and other parameters are chosen as Fig. 2.
In Fig. 2a, a small broadening width of the cavity mode λ = 0.03 is chosen, then increasing parameter γ means increasing the qubit-cavity coupling strength. We find that for a long region of γ from 0 to about 26.46, τQSL of non-RWA case (dotted black line) is not longer than that of RWA case (blue line with circles), which means the counter-rotating-wave term retained in the non-RWA case can reduce the τQSL, i.e., increase the evolving speed. While, when γ is too large, τQSL of non-RWA increases quickly and becomes larger than that of RWA case.
Fig. 2b shows the non-Markovianity measure M versus parameter γ. In RWA case (blue line with circles), M increases with increasing γ, while in non-RWA case (dotted black line), it is obviously different. Due to the counter-rotating terms, it is no longer the case that larger γ can induce greater non-Markovianity. When γ is larger than a certain value, M begins to decline.
If contrasting the two subfigures Fig. 2a and Fig. 2b, we find that increasing non-Markovianity will decrease the τQSL in both RWA and non-RWA cases. While, in non-RWA case, the remarkable reducing process of M for larger γ corresponds to the increase of τQSL. Therefore, in this small λ case, non-Markovianity directly affects the QSL time bound, i.e., larger non-Markovianity decreases τQSL, while, smaller non-Markovianity will increase τQSL.
When we choose a larger parameter λ = 0.1 in Fig. 3, one can see some similar behaviors of τQSL and non-Markovianity with Fig. 2, e.g., there is also a crossing of τQSL for RWA and non-RWA cases, while the crossing point occurs at a smaller value of γ where the non-Markovianity of non-RWA case begins to decrease.
Different phenomena are shown in Fig. 4, when we continue to enlarge the width to λ = 0.6, there no longer exists the crossing of τQSL in the two cases of RWA and non-RWA. Instead, τQSL of non-RWA is always lower than that of RWA case in the presented region of γ. Different dependence behaviors of τQSL on M are also found for the non-RWA case. When the non-Markovianity decreases (dotted black line in Fig. 4b), τQSL (dotted black line in Fig. 4a) also decreases, which is quite different from the former results in Fig. 2 and Fig. 3 where λ is smaller.
Therefore, if someone draws the conclusions that non-Markovianity can decrease QSL time τQSL18, our results will provide important additions and amendments that with using RWA, non-Markovianity can indeed decrease QSL time τQSL. However, without using RWA, only in the condition of small broadening-width parameter λ, increasing non-Markovianity can depress τQSL. On the contrary, decreasing non-Markovianity will increase τQSL. However, if the width λ is large enough, the dependence of τQSL on non-Markovianity will change. Instead, non-Markovianity reaches the maximum followed by that τQSL also gets its maximum.
On the other hand, from Fig. 2, Fig. 3 and Fig. 4, one can see the effects of the broadening-width parameter λ. If averaging τQSL over the presented region of γ, one can see that the QSL time in Fig. 4a is larger than that in Fig. 2a and Fig. 3a. Correspondingly, the averaged value of non-Markovianity M in Fig. 4b is obviously smaller than those of Fig. 2b and Fig. 3b, which implies that increasing the cavity mode width, i.e., enhancing the damping rate of the mode, will reduce the non-Markovianity and enlarge the τQSL and thus decelerate the evolution. We should note that the difference between RWA and non-RWA cases demonstrated by τQSL and M becomes more and more evident when the two parameters γ and λ increase. It is to say, when the time scales of the system and the bath become small, the counter-rotating terms will play an important role. Then, the double excitations followed by the virtual exchanges of energy, which are introduced by the counter-rotating terms, may prevent the information backow from the environment and thus weaken the non-Markovianity.
In Fig. 5, we plot τQSL versus γ for different initial states of Eq. (19) with different mixed coefficients p. Since the purity is defined as  . Thus, larger value of p corresponds to higher purity, namely closer to a pure state. Surprisingly, the non-RWA case in Fig. 5a shows some crossings of τQSL, namely, it is not always a truth that pure state may induce lower QSL time bound than mixed states. Obviously, for larger values of γ, mixed state such as p = 0.1 which is far from pure state, can bring much lower QSL time. But for RWA case, there will not be the strange phenomena any more.
. Thus, larger value of p corresponds to higher purity, namely closer to a pure state. Surprisingly, the non-RWA case in Fig. 5a shows some crossings of τQSL, namely, it is not always a truth that pure state may induce lower QSL time bound than mixed states. Obviously, for larger values of γ, mixed state such as p = 0.1 which is far from pure state, can bring much lower QSL time. But for RWA case, there will not be the strange phenomena any more.
Discussion
We have derived a computable QSL time bound which can be easily applied in the open systems of mixed initial states undergoing non-Markovian dynamics. By making use of the hierarchy equation method, we considered a qubit system coupled to a broadened cavity mode. We have found that the counter-rotating terms (in non-RWA case) can be helpful to decrease QSL times, i.e., accelerate quantum evolution. In non-RWA case, for narrow broadening-width λ of the cavity mode, properly enlarging the qubit-cavity coupling can decrease QSL time, however, too strong coupling will cause a quickly increasing process of QSL time. While, for wider λs, there exists a maximal QSL time, after that, QSL time decreases monotonically with increasing qubit-cavity coupling strength.
On the other hand, in non-RWA case, non-Markovianity exhibits quite different behavior from RWA case. Too strong qubit-cavity coupling may weaken non-Markovianity. Our results have also demonstrated the close relationship between QSL time and non-Markovianity. Especially for narrow broadening-widths of the cavity mode, increasing non-Markovianity helps to shorten QSL time (for both RWA and non-RWA), while weaker non-Markovianity may increase QSL time (for non-RWA). While, enlarging broadening-width λ will weaken non-Markovianity and increase QSL time. We also considered initial states with different purity and found that in non-RWA case, the mixed state with lower purity can also lead to shorter QSL time when the qubit-cavity coupling is strong enough.
Several tighter bounds depend on exact time-evolution of the density matrix. However, if so, people prefer to consider the exact dynamics behaviour of the density rather than the bound. Therefore, the purpose of deriving a bound is to describe the evolution speed even though we have not grasped enough information of the dynamics. Moreover, the simpler the computation of the bound is, the better it will be applied. From this point of view, we found the only practical QSL bound derived for open systems is that of Ref. 17, which only depends on the initial state and the generators in the Lindblad-form evolution. Beyond that, our bound is more available in the case of initial mixed states. Certainly, it is still attractive to explore tight and practical QSL bound in open systems and which leaves lots of interesting problems.
Method
Density matrix within RWA
If we make use RWA, the interaction Hamiltonian in the total Hamiltonian (8) becomes

then with the Lorentz-type coupling spectrum and the vacuum initial state of the cavity mode, the density matrix for arbitrary time t can be obtained analytically20 as

where the time-dependent parameter

with  .
.
Measure of non-Markovianity: Let us give a brief introduction of the measure of non-Markovianity defined by Breuer et al.35. For a quantum process, the measure is defined as:

where η [t, ρ1,2 (0)] denotes the changing rate of the trace distance that

where  is the trace distance of the quantum states ρ1 and ρ2 with the trace norm definition for a operator
is the trace distance of the quantum states ρ1 and ρ2 with the trace norm definition for a operator  . The distance D above characterizes the distinguishability between two quantum states and satisfies 0 ≤ D ≤ 1. It has been pointed that all completely positive and trace-preserving (CPT) maps cannot increase the distance D. For example, η ≤ 0 for all dynamical semigroups and all time-dependent Markovian processes, while, if there exists a pair of initial states and a certain time interval such that η > 0, then we can say that the non-Markovianity appears.
. The distance D above characterizes the distinguishability between two quantum states and satisfies 0 ≤ D ≤ 1. It has been pointed that all completely positive and trace-preserving (CPT) maps cannot increase the distance D. For example, η ≤ 0 for all dynamical semigroups and all time-dependent Markovian processes, while, if there exists a pair of initial states and a certain time interval such that η > 0, then we can say that the non-Markovianity appears.
It should be noted that the time integration in Eq. (23) is extended over all time intervals (ai, bi) in which η is positive and the maximum is taken over all pairs of initial states. The measure can be rewritten as:

References
Lloyd, S. Ultimate physical limits to computation. Nature 406, 1047; 10.1038/35023282 (2000).
Lloyd, S. & Maccone, L. Advances in quantum metrology. Nature Photonics 5, 222; 10.1038/nphoton.2011.35 (2011).
Alipour, S., Mehboudi, M. & Rezakhani, A. T. Quantum Metrology in Open Systems. Phys. Rev. Lett. 112, 120405; DOI:http://dx.doi.org/10.1103/PhysRevLett.112.120405 (2014).
Caneva, T. et al. Optimal Control at the Quantum Speed Limit. Phys. Rev. Lett. 103, 240501; DOI:http://dx.doi.org/10.1103/PhysRevLett.103.240501 (2009).
Hegerfeldt, G. C. Driving at the Quantum Speed Limit: Optimal Control of a Two-Level System. Phys. Rev. Lett. 111, 260501; DOI:http://dx.doi.org/10.1103/PhysRevLett.111.260501 (2013).
Lloyd, S. & Montanger, S. Information Theoretical Analysis of Quantum Optimal Control. Phys. Rev. Lett. 113, 010502; DOI:http://dx.doi.org/10.1103/PhysRevLett.113.010502 (2014).
Uhlmann, A. An energy dispersion estimate. Phys. Lett. A 161, 329; 10.1016/0375-9601(92)90555-Z (1992).
Pfeifer, P. How fast can a quantum state change with time? Phys. Rev. Lett. 70, 3365–3368; DOI:http://dx.doi.org/10.1103/PhysRevLett.70.3365 (1993).
Chau, H. F. Tight upper bound of the maximum speed of evolution of a quantum state. Phys. Rev. A 81, 062133; DOI:http://dx.doi.org/10.1103/PhysRevA.81.062133 (2010).
Margolus, N. & Levitin, L. B. The maximum speed of dynamical evolution. Physica D 120, 188–195; 10.1016/S0167-2789(98)00054-2 (1998).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum limits to dynamical evolution. Phys. Rev. A 67, 052109; DOI:http://dx.doi.org/10.1103/PhysRevA.67.052109 (2003).
Anandan, J. & Aharonov, Y. Geometry of quantum evolution. Phys. Rev. Lett. 65, 1697–1700; DOI:http://dx.doi.org/10.1103/PhysRevLett.65.1697 (1990).
Levitin, L. B. & Toffoli, T. Fundamental limit on the rate of quantum dynamics: the unified bound is tight. Phys. Rev. Lett. 103, 160502; DOI:http://dx.doi.org/10.1103/PhysRevLett.103.160502 (2009).
Jones, P. & Kok, P. Geometric derivation of the quantum speed limit. Phys. Rev. A 82, 022107; DOI:http://dx.doi.org/10.1103/PhysRevA.82.022107 (2010).
Deffner, S. & Lutz, E. Energy-time uncertainty relation for driven quantum systems. J. Phys. A: Math. Theor. 46, 335302; 10.1088/1751-8113/46/33/335302 (2013).
Taddei, M. M., Escher, B. M., Davidovich, L. & de Matos Filho, R. L. Quantum speed limit for physical processes. Phys. Rev. Lett. 110, 050402; DOI:http://dx.doi.org/10.1103/PhysRevLett.110.050402 (2013).
del Campo, A., Egusquiza, I. L., Plenio, M. B. & Huelga, S. F. Quantum speed limits in open system dynamics. Phys. Rev. Lett. 110, 050403; DOI:http://dx.doi.org/10.1103/PhysRevLett.110.050403 (2013).
Deffner, S. & Lutz, E. Quantum speed limit for non-Markovian dynamics. Phys. Rev. Lett. 111, 010402; DOI:http://dx.doi.org/10.1103/PhysRevLett.111.010402 (2013).
Zhang, Y. J. et al. Quantum speed limit for arbitrary initial states. Sci. Rep. 4, 4890; 10.1038/srep04890 (2014).
Breuer, H.-P. & Petruccione, F. The Theory of Open Quantum Systems (Oxford Univ. Press, New York, 2002).
Tanimura, Y. & Wolynes, P. G. Quantum and classical Fokker-Planck equations for a Gaussian-Markovian noise bath. Phys. Rev. A 43, 4131; DOI:http://dx.doi.org/10.1103/PhysRevA.43.4131 (1991).
Tanaka, M. & Tanimura, Y. Multistate electron transfer dynamics in the condensed phase: Exact calculations from the reduced hierarchy equations of motion approach. J. Chem. Phys. 132, 214502; DOI:http://dx.doi.org/10.1063/1.3428674 (2010).
Ishizaki, A. & Tanimura, Y. Modeling vibrational dephasing and energy relaxation of intramolecular anharmonic modes for multidimensional infrared spectroscopies. J. Chem. Phys. 125, 084501; DOI:http://dx.doi.org/10.1063/1.2244558 (2006).
Ishizaki, A. & Tanimura, Y. Dynamics of a Multimode System Coupled to Multiple Heat Baths Probed by Two-Dimensional Infrared Spectroscopy. J. Phys. Chem. A 111, 9269; 10.1021/jp072880a (2007).
Tanimura, Y. Stochastic Liouville, Langevin, Fokker–Planck and Master Equation Approaches to Quantum Dissipative Systems. J. Phys. Soc. Jpn. 75, 082001; DOI:http://dx.doi.org/10.1143/JPSJ.75.082001 (2006).
Xu, R.-X. et al. Exact quantum master equation via the calculus on path integrals. J. Chem. Phys. 122, 041103; 10.1063/1.1850899 (2004).
Xu, J., Xu, R.-X. & Yan, Y. J. Exact quantum dissipative dynamics under external time-dependent driving fields. New J. Phys. 11, 105037; 10.1088/1367-2630/11/10/105037 (2009).
Ishizaki, A. & Fleming, G. R. Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature. PNAS 106, 17255; 10.1073/pnas.0908989106 (2009).
Ma, J., Sun, Z., Wang, X. & Nori, F. Entanglement dynamics of two qubits in a common bath. Phys. Rev. A 85, 062323; DOI:http://dx.doi.org/10.1103/PhysRevA.85.062323 (2012).
Dijkstra, A. G. & Tanimura, Y. Non-Markovian Entanglement Dynamics in the Presence of System-Bath Coherence. Phys. Rev. Lett. 104, 250401; DOI:http://dx.doi.org/10.1103/PhysRevLett.104.250401 (2010).
You, J. Q. & Nori, F. Atomic physics and quantum optics using superconducting circuits. Nature 474, 589; 10.1038/nature10122 (2011).
Niemczyk, T. et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nature Phys. 6, 772; 10.1038/nphys1730 (2010).
Larson, J. Absence of Vacuum Induced Berry Phases without the Rotating Wave Approximation in Cavity QED. Phys. Rev. Lett. 108, 033601; DOI:http://dx.doi.org/10.1103/PhysRevLett.108.033601 (2012).
Sun, Z., Ma, J., Wang, X. & Nori, F. Photon-assisted Landau-Zener transition: Role of coherent superposition states. Phys. Rev. A 86, 012107; DOI:http://dx.doi.org/10.1103/PhysRevA.86.012107 (2012).
Breuer, H.-P., Laine, E.-M. & Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 103, 210401; DOI:http://dx.doi.org/10.1103/PhysRevLett.103.210401 (2009).
Lu, X.-M., Wang, X. & Sun, C. P. Quantum Fisher information ow and non-Markovian processes of open systems. Phys. Rev. A 82, 042103. DOI:http://dx.doi.org/10.1103/PhysRevA.82.042103 (2010).
Rivas, A., Huelga, S. F. & Plenio, M. B. Entanglement and Non-Markovianity of Quantum Evolutions. Phys. Rev. Lett. 105, 050403; DOI:http://dx.doi.org/10.1103/PhysRevLett.105.050403 (2010).
Bellomo, B., Lo Franco, R. & Compagno, G. Non-Markovian Effects on the Dynamics of Entanglement. Phys. Rev. Lett. 99, 160502; DOI:http://dx.doi.org/10.1103/PhysRevLett.99.160502 (2007).
Liu, J., Lu, X.-M. & Wang, X. Nonunital non-Markovianity of quantum dynamics. Phys. Rev. A 87, 042103; DOI:http://dx.doi.org/10.1103/PhysRevA.87.042103 (2013).
Wißmann, S. et al. Optimal state pairs for non-Markovian quantum dynamics. Phys. Rev. A 86, 062108; DOI:http://dx.doi.org/10.1103/PhysRevA.86.062108 (2012).
Chruściński, D. & Maniscalco, S. Degree of Non-Markovianity of Quantum Evolution. Phys. Rev. Lett. 112, 120404; DOI:http://dx.doi.org/10.1103/PhysRevLett.112.120404 (2014).
Xu, Z. Y., Yang, W. L. & Feng, M. Proposed method for direct measurement of the non-Markovian character of the qubits coupled to bosonic reservoirs. Phys. Rev. A 81, 044105; DOI:http://dx.doi.org/10.1103/PhysRevA.81.044105 (2010).
Jozsa, R. Fidelity for mixed quantum states. J. Mod. Opt. 41, 2315; 10.1080/09500349414552171 (1994).
Mendonca, P. et al. Alternative fidelity measure for quantum states. Phys. Rev A 78, 052330; DOI:http://dx.doi.org/10.1103/PhysRevA.78.052330 (2008).
Chen, J. L., Fu, L. B., Ungar, A. A. & Zhao, X. G. Alternative fidelity measure between two states of an N-state quantum system. Phys. Rev. A 65, 054304; DOI:http://dx.doi.org/10.1103/PhysRevA.65.054304 (2002).
Wang, X., Yu, C.-S. & Yi, X. X. An alternative quantum fidelity for mixed states of qudits. Phys. Lett. A 373, 58–60; 10.1016/j.physleta.2008.10.083 (2008).
Lu, D. et al. Simulation of Chemical Isomerization Reaction Dynamics on a NMR Quantum Simulator. Phys. Rev. Lett. 107, 020501; DOI:http://dx.doi.org/10.1103/PhysRevLett.107.020501 (2011).
Acknowledgements
The authors thank Prof. C. P. Sun, X. X. Yi, Yong Li, Jiangbin Gong, Dario Poletti and Dr. Xiao-Ming Lu and Shengwen Li for valuable discussions. Z.S. acknowledges support from the National Natural Science Foundation of China under Grant No. 11375003, the Zhejiang Natural Science Foundation with Grant No. LZ13A040002, SUTD Start-Up Grant 2012-045 the, Program for HNUEYT under Grant No. 2011-01-011 and the funds from Hangzhou City for the Hangzhou-City Quantum Information and Quantum Optics Innovation Research Team. X.W. acknowledges support from NFRPC through Grant No. 2012CB921602 and the NSFC through Grants No. 11475146 and Synergetic Innovation Center of Quantum Information and Quantum Physics, University of Science and Technology of China, Hefei, Anhui 230026, China.
Author information
Authors and Affiliations
Contributions
Z.S., J.L. and X.G.W. calculated and analyzed the results. Z.S. and J.M. finished the numerical calculation. Z.S., J.L. and X.G.W. co-wrote the paper. All authors reviewed the manuscript and agreed with the submission.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sun, Z., Liu, J., Ma, J. et al. Quantum speed limits in open systems: Non-Markovian dynamics without rotating-wave approximation. Sci Rep 5, 8444 (2015). https://doi.org/10.1038/srep08444
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep08444
This article is cited by
-
Experimental investigation of geometric quantum speed limits in an open quantum system
Communications Physics (2024)
-
Quantum Speed Limit Time of Topological Qubits Influenced by the Fermionic and Bosonic Environments
Brazilian Journal of Physics (2022)
-
Non-Markovian Speedup Dynamics in Markovian and Non-Markovian Channels
International Journal of Theoretical Physics (2021)
-
Quantum acceleration by an ancillary system in non-Markovian environments
Quantum Information Processing (2021)
-
Quantum speed limit based on the bound of Bures angle
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

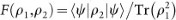 .
.



