Abstract
Arctic glaciers and ice caps are major contributors to past, present and future sea-level fluctuations. Continued global warming may eventually lead to the equilibrium line altitudes of these ice masses rising above their highest points, triggering unstoppable downwasting. This may feed future sea-level rise considerably. We here present projections for the timing of equilibrium-line loss at the major Arctic ice cap Vestfonna, Svalbard. The projections are based on spatially distributed climatic mass balance modelling driven by the outputs of multiple climate models from the Coupled Model Intercomparison Project Phase 5 (CMIP5) forced by the Representative Concentration Pathways (RCPs) 2.6, 4.5, 6.0 and 8.5. Results indicate strongly decreasing climatic mass balances over the 21st century for all RCPs considered. Glacier-wide mass-balance rates will drop down to −4 m a−1 w.e. (water equivalent) at a maximum. The date at which the equilibrium line rises above the summit of Vestfonna (630 m above sea level) is calculated to range between 2040 and 2150, depending on scenario.
Similar content being viewed by others
Introduction
Climate change is one of the major challenges humanity has to face during the 21st century1. Its observed effects are numerous, with increased mass loss from glaciers and ice caps and their substantial contribution to 20th century sea-level rise being among the most prominent2,3. In this context, Arctic glaciers and ice caps are especially important due to their large ice volumes and extensive surfaces4 that provide a direct interface with respect to climatic and oceanic forcing and thus to climate change itself. As the Arctic is, moreover, the region of highest predicted future air-temperature increases5 the importance of Arctic ice masses for sea-level rise is expected to persist or even increase in the future6.
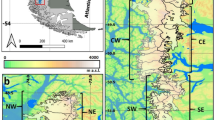
The major Arctic ice bodies surround the Arctic Ocean at similar latitudes. However, they show inhomogeneous behaviour in recent times. The glaciers and ice caps of the Canadian Arctic archipelagos experienced a mass loss of 61 ± 7 Gt a−1 that is equivalent to a negative mass balance of −0.41 m w.e. a−1 (ref. 7). In contrast, over the Eurasian Arctic archipelagos distinctly smaller mass loss occurred. The Russian Arctic ice caps lost 9.1 ± 2.0 Gt a−1 or −0.17 m w.e. a−1 (ref. 8), while the glaciers and ice caps of Svalbard only lost 4.3 ± 1.4 Gt a−1 or −0.12 m w.e. a−1 (ref. 9). The second largest single ice body of Svalbard, the ice cap Vestfonna, that covers ~2340 km2 of the island Nordaustlandet with surface elevations of up to 630 m a.s.l. (above sea level)10 at around 80°N (Fig. 1), even showed a slightly positive mass balance of +0.05 m w.e. a−1 (ref. 11) over the period 1990–2005 and a slightly positive climatic mass balance (CMB) over the last three decades12,13. Firn core data further reveal slightly increased accumulation rates since the early 1990s14.
The behaviour of Svalbard's ice masses is underlain by a significant increase of precipitation over the 20th century15. Furthermore, Svalbard experiences the highest winter and spring warming across all the Arctic since approximately 198016. All together, the response of the glaciers and ice caps on the archipelago appears to be rather moderate when compared to the other Arctic regions7,8,9. However, in the near future the response might be considerably amplified, as air temperature and precipitation increases predicted for the Arctic over the 21st century are highest in the Svalbard region5 and especially over Nordaustlandet17. This suggests that, in addition to the Canadian Arctic glaciers, also the ice masses of Svalbard will experience considerably negative mass balances or will even approach a state of fatal downwasting.
The most widely used and most intuitive parameter for glacier health is the accumulation area ratio (AAR)18. It is defined as the ratio of the extent of the accumulation area to the extent of the entire glacier and thus represents the fraction of the area over which the glacier gains mass. The AAR is related to the mass balance via the equilibrium line altitude (ELA)19,20. More negative mass balance implies both a rising ELA and a diminishing AAR. This implies that as soon as the long-term average ELA rises above the maximum glacier elevation, i.e. the AAR reduces to zero, the glacier is condemned to final meltdown. A turning point is reached and thenceforth mass loss continues until the glacier disappears.
Responsible for the timing of this event is the evolution of the relation between the future increases of air temperature and precipitation. To a limited extent, an increase of precipitation is able to buffer the negative effects of an increase in air temperature21. However, as most glaciers show distinctly higher sensitivity to air temperature than to precipitation22 a continued increase of ablation soon dominates any possible increase of accumulation and drives the glacier mass balance into more and more negative states. For Svalbard, the future evolution of glacier mass balance has so far only been obtained for the tidewater glacier Hansbreen (southern Spitsbergen)23,24 or as part of global-scale studies for the entire archipelago6,25,26,27. We here present a refinement of these studies for a specific glacier on Svalbard that benefits from more detailed and thus accurate model-parameter calibrations and a spatially distributed model setup which, per se, suggests results of higher accuracy28. Forcing such a spatially distributed mass-balance model with downscaled global circulation model (GCM) output is known to provide a reliable way to project future mass-balance evolutions29,30,31.
We present projections of the reference-surface CMB of the ice cap Vestfonna until the end of the 21st century. The CMB of a glacier is formed by the sum of surface accumulation, surface ablation, meltwater that refreezes within the glacier and internal ablation32. In our calculations internal ablation is neglected and the CMB is calculated as a reference-surface balance. This means that both glacier extent and glacier surface elevations are kept constant over the entire modelling period32. No feedback between mass balance and the ice body occurs. The influence of possibly changing glacier topography on climate data is not included. We calculate only reference-surface CMB instead of the conventional mass balance because in addition to considerations of computational cost we wish to focus on glacier–climate relationships unobscured by the slower dynamical response of the glacier.
The spatially distributed mass balance model employed for this purpose was especially designed to reproduce local conditions on the ice cap12 on the basis of ERA-Interim data and has already been successfully used for a calculation of three decades of past CMB13. The model combines an accumulation scheme that is fitted to extensive field observations with a calibrated temperature-net radiation index approach for ablation modelling. The calculation of net shortwave radiation uses standard solar geometry algorithms and additionally accounts for modifications by cloud coverage and for temporally and spatially distributed surface albedo variations on the ice cap that are incorporated using a specially tailored minimal, statistical model33. Statistically downscaled daily air temperature and precipitation data as well as cloud cover data of the four climate-change scenarios Representative Concentration Pathways (RCP) 2.6, 4.5, 6.0 and 8.5 (ref. 34) are used as model input (Fig. 2). Each of these scenarios is represented by an ensemble of ten different GCM runs (Table S26) that were part of the Coupled Model Intercomparison Project Phase 5 (CMIP5). The ten GCMs are BCC-CSM1.1, CSIRO-Mk3.6.0, GFDL-ESM2G, HadGEM2-ES, IPSL-CM5A-LR, MIROC5, MIROC-ESM, MIROC-ESM-CHEM, MRI-CGCM3 and NorESM1-M.
Climate data used as input to the climatic mass balance model.
Downscaled air temperatures are shown in the first column, downscaled precipitation in the second column and cloud cover in the third column. Each line graph shows the outputs of ten different GCMs (colour code) and their means (black line). Ensembles belonging to the same RCP (2.6, 4.5, 6.0 and 8.5) are shown in the same row. The lower row shows a compilation of the respective means of the four RCPs.
Special emphasis is placed in this study on the implications of future mass-balance variability for ELA and AAR evolution. With this study we present the first detailed modelling of future mass-balance evolution of any ice body on Svalbard. We also present estimated date ranges for the rise in ELA above the summit of Vestfonna under the influence of projected future climate forcing.
Results
Results are presented for the modelled CMB quantities and for the derived quantities CMB gradient, ELA and AAR. A separate subsection is dedicated to a description of model uncertainties.
Climatic mass balance
The projected 21st century evolution of the CMB of Vestfonna differs substantially according to the considered scenario. However, the overall picture shows continuously decreasing CMB for all four RCPs (Fig. 3). Starting at balanced or even slightly positive conditions at the beginning of the modelling period, the CMB become increasingly negative towards the end of the century. During the first decade (2006/2007–2015/2016) the mean annual CMB of all four scenarios are comparable at an overall mean of +0.03 m w.e. a−1 with the four scenario means ranging between −0.03 and +0.07 m w.e. a−1. The last decade (2089/2090–2098/2099), in contrast, shows considerably different CMB for the different scenarios (Fig. 3). Following the RCP 2.6, the CMB reaches −0.68 ± 0.02 m w.e. a−1. This value decreases to −1.58 ± 0.10 m w.e. a−1 and to −2.32 ± 0.11 m w.e. a−1 in the RCPs 4.5 and 6.0, respectively. For the RCP 8.5, the CMB over the last decade of the 21st century even shows a mean of −3.79 ± 0.19 m w.e. a−1. All but one out of forty runs indicate a continuously decreasing CMB over the modelling period. Only the GFDL-ESM2G run of the RCP 2.6 ensemble projects slightly increasing CMB values.
Modelled annual glacier-wide surface accumulation(a), rainfall (b), surface ablation (c), refreezing (d) and climatic mass balance (d) at Vestfonna.
The line graphs represent the ensemble means of the given RCPs with the error bars to the right of the line graphs indicating the 1σ intra-ensemble uncertainty ranges at the end of the modelling period. The grey-scale colour code of the error bars refers to the colour code of the line graphs. The colour shading behind the line graphs indicates periods with increases or decreases of the temporal trend of the respective quantity segmented according to RCP (indicated by the labels at the right).
The evolution of the CMB of Vestfonna is largely controlled by the annual ablation rates, which increase continuously and substantially over the 21st century (Fig. 3). Annual accumulation, in contrast, only increases over the first decades of the modelling period. All ensemble means start continuous decreases by no later than 2031 that persist over the entire century. When following the RCP 8.5 annual accumulation is even ~19% lower at the end of the century than at the beginning. Correspondingly, liquid precipitation (rainfall) increases strongly and continuously over the entire modelling period (Fig. 3). As a deduced value that is dependent on the three mass balance-relevant quantities ablation, accumulation and rainfall, refreezing shows the most complex evolution over the 21st century (Fig. 3). Within all scenarios strongly increasing annual refreezing sums are predicted for the first two decades. In the RCP 8.5 projections the refreezing sums even increase by almost 20% within the first decade and the increase continues at reduced rates until the early 2040s. For the other three scenarios the increase of refreezing continues until the early 2090s. After reaching a maximum the annual refreezing decreases in all scenarios until the end of the century. The annual refreezing in RCP 8.5 even drops back to values similar to those at the beginning of the modelling period. However, even if the absolute amounts of refreezing tend to decrease over the 21st century, the relative importance of refreezing for CMB does not (Fig. 4). Whereas refreezing contributes around 40% to the absolute annual mass gain of Vestfonna at the beginning of the modelling period, the projections indicate that this share increases slightly and continuously to between 43 and 47% at the end of the century.
Variability of the relevance of refreezing processes for the climatic mass balance of Vestfonna over the 21st century.
The line graphs show annual values of the fraction of refreezing sums in the overall mass gain of Vestfonna (a) and of the fraction of meltwater that refreezes (b). Data represent the ensemble means of the RCPs.
Derived quantities
The CMB gradient experiences a continuous steepening that starts to level off towards the end of the modelling period (Fig. 5). The ELA of the ice cap shows a continuous increase over the 21st century starting from 350 ± 32 m a.s.l. (mean ± one standard deviation of all 40 ensemble members) during the first decade (Fig. 5). The projected ELA evolutions, however, differ considerably between the four scenarios. The ensemble-mean ELA increases at decadal rates of 19.0 m (RCP 2.6), 35.8 (RCP 4.5), 53.4 m (RCP 6.0) and 75.5 m (RCP 8.5). This means that for the RCP 2.6 the ensemble-mean ELA stays within the altitude range of Vestfonna over the entire modelling period. Only one GCM out of ten (MIROC-ESM) predicts an ELA exceeding the summit altitude before the end of the century (Fig. 5).
Modelled annual climatic mass balance gradients (first column), equilibrium line altitudes (second column) and accumulation area ratios (third column).
Each graph shows outputs of ten different GCMs (colour code) and their mean. Given means are either calculated on an annual basis from values of all ten GCMs of the respective ensemble (black line) or estimated by also using extrapolated annual values for some GCMs (dashed black line, cf. also subsection Analysis of results). Ensembles belonging to the same RCP (2.6, 4.5, 6.0 and 8.5) are shown in the same row.
The dates of equilibrium-line loss, i.e. of the dates when the projected ELAs exceed the summit altitude of Vestfonna and the extent of the accumulation area reduces to zero, range between 2043/2044 (RCP 8.5) and 2151/2152 (RCP 2.6) (Fig. 6, Table 1). While the initial AAR of Vestfonna, 0.59 ± 0.06 (mean ± one standard deviation of all 40 ensemble members) during the first decade of modelling, indicates a quasi steady-state glacier, this situation rapidly changes over the modelling period. Halving of the initial AAR already occurs between the 2020s (RCP 8.5) and the 2080s (RCP 2.6) (Table 1).
Timing of equilibrium-line loss for the four RCPs.
Timings for the individual GCMs of the respective ensemble members are indicated by colour code. For GCMs where no permanent equilibrium-line loss is observed during the modelling period, the timings are derived from extrapolations of the linear temporal trends. In this case also the 95% confidence intervals of the linear fits are shown. The period before equilibrium-line loss is calculated from the mean ELA time series shown in Figure 5.
Uncertainties
Ref. 35 presents a detailed discussion of the main sources of uncertainty that influence the accuracy of future projections in the context of climate change. The two main sources are the scenario uncertainty and the model uncertainty. The former describes the spread between the different scenarios, i.e. the RCPs and the latter the spread between the different GCM runs of each scenario. The third source considered by ref. 35 is the natural uncertainty which represents the variance of the future climate projections and thus short-term departures from the long-term trend. An integrated consideration of these three sources is not feasible. The individual uncertainties need to be considered separately.
We here use given future climate projections to drive a glacier mass-balance model, which is another source of uncertainty. We call this last source 'method uncertainty'. It also needs to be considered separately from the other three sources of uncertainty.
The four sources of uncertainty show substantially different behaviour with respect to time. For the beginning of the study period, scenario uncertainty and model uncertainty are assumed to be negligible because all climate data from the different GCMs and RCPs were downscaled to fit present local conditions and the uncertainties are thus subtracted out. Afterwards, both uncertainties show an increase over time. The natural uncertainty, in contrast, is characterized by an indistinct behaviour with time. The evolution of method uncertainty is not quantifiable at all when statistical methods are applied. Statistical methods assume stationarity of the present conditions under which their calibration was carried out. With respect to mass-balance modelling, future changes of snowpack characteristics or ice rheology might thus increase method uncertainty in the future. However, neither these potential changes nor their impacts can be quantified with present knowledge. For the uncertainty discussion we thus only refer to the present magnitude of method uncertainty without considering its potential increase over time.
The overall picture of model results is very consistent and individual values are sufficiently accurate to serve as reliable indicators for future ice-cap behaviour. This can be seen from a comparison of the CMB values modelled in this study and the CMB values modelled by ref. 13. Both studies show an overlap in the period 2006–2011 and used the same CMB model. During the original calibration the model was forced with ERA-Interim data13. As the CMB values of the earlier study13 result from a forcing by statistically downscaled ERA-Interim data, a comparison to these earlier results forms an indirect but straightforward indication of the method uncertainty in the modelled CMB. A comparison with 20 in situ measured point balances from the period 2008–2012 gives additional insights.
Root mean square (RMS) errors of the differences between annual, glacier-wide CMB in this study and in the earlier study13 lie in the range 0.11 ± 0.02 m w.e. a−1 to 0.16 ± 0.04 m w.e. a−1 (mean ± one standard deviation of the individual ensemble RMS errors) for the four scenario ensembles (Table 2, Table S27, Fig. S1). Taking into account the original RMS error (0.18 m w.e.) of the CMB values in the earlier study13 the overall method uncertainty for this study can be expected to lie between 0.21 and 0.24 m w.e. when applying error propagation (Table 2). This estimation matches the RMS errors derived from the comparison of the CMB in this study to the 20 stake-based point balance measurements that range between 0.20 ± 0.03 m w.e. and 0.23 ± 0.06 m w.e. depending on scenario (Table 2, Table S28, Fig. S2).
The model uncertainty, i.e. the one sigma intra-ensemble spread, of the CMB time series of RCP 4.5 (6.0, 8.5) exceeds the method uncertainty of 0.22 m w.e. (0.23 m w.e., 0.24 m w.e.) from the first half of the 2030s onwards (Fig. S3). In case of RCP 2.6 the model uncertainty exceeds the method uncertainty of 0.21 m w.e. from the first half of the 2040s onwards. All dates for equilibrium line-loss lie beyond these dates. Therefore, model uncertainties are exclusively given in the presentation of results. Scenario uncertainty is additionally accounted for by presenting the results separately for each RCP.
Regarding the timings of equilibrium-line loss it has to be borne in mind that the given dates represent the instant when the loss occurs at the latest. The CMB modelling in this study is based on a fixed reference surface. However, in reality the increasingly negative CMB will induce a lowering of the surface across the entire ice cap. This, in turn, causes a feedback chain, resulting in even more negative CMB and thus faster and stronger surface lowering. Therefore, it is likely that the real date of equilibrium-line loss will be earlier than derived from the calculated CMB gradients with a fixed surface geometry. It can be expected that the time delay in modelling lies in the order of years in RCP 8.5 and increases towards the order of decades in RCP 2.6. The dates of equilibrium-line loss presented here are thus very conservative estimates.
Additionally, unquantifiable uncertainty is introduced by the fact that our model does not account for any glacier dynamics, including calving losses at the marine-terminating outlet glaciers. Calving losses do not alter the CMB profile that is used to determine the dates of equilibrium-line loss but they influence glacier dynamics in a way that might change the rates of ice-cap lowering. Any quantification of the calving losses and their potential influences on the results is, however, far beyond the possibilities and the scope of this study.
Also the assumption of stationarity of present conditions that has to be made in any statistical approach calibrated under present conditions induces unquantifiable uncertainty into the results. This includes the fixed parameters of air temperature and precipitation downscaling that might be inaccurate under different conditions of regional atmospheric circulation. The fixed refreezing parameterization and the parameters of the statistical albedo model might also become inaccurate under changed future snow-cover conditions.
Taken together, we acknowledge that the calculation approach used in this study shows a variety of unquantifiable uncertainties that weakens the accuracy of the results. However, it is expected that the model uncertainty combined with the scenario uncertainty is far larger than any of the unquantified influences. This gives our results the potential to act as a reliable 'crystal ball' into the future of Vestfonna ice cap. However, the findings should still be consolidated with more advanced models using increasing computational capacities in the future.
Discussion
For the mass-balance years 1979/1980 to 2010/2011 a mean CMB rate of +0.09 ± 0.15 m w.e. a−1 was modelled for Vestfonna, showing a slight but insignificant negative trend13. The positive mean of CMB was associated with a mean ELA of 326 ± 55 m a.s.l. that increased with time, corresponding to the negative CMB trend13. Recent geodetic mass balance estimates covering all of Svalbard9,11 indicate that Vestfonna shows a distinctly above average mass balance. This qualitative relation is also backed by the fact that the AAR of Vestfonna at the beginning of the 21st century (~0.59; Fig. 5) lies almost at the upper one sigma error bound of the archipelago wide mean of 0.49 ± 0.15 presented by ref. 36. As expected, our projections are similar to these findings at the beginning of our modelling period. Furthermore, they indicate an unabated continuation of the observed trends into the future at distinctly higher rates. While no clear ELA trend was observed over the decades preceding our study period, the ELA evolution over the 21st century shows clearly positive trends that range between +19 m per decade according to the RCP 2.6 ensemble mean and +76 m per decade when following the RCP 8.5 (Fig. 5).
The ELA distribution over Svalbard shows higher altitudes towards the inner parts of the archipelago and lower ones towards the coasts when compared to the ELA at Vestfonna37. The surface elevations over the archipelago show, in general, a similar pattern and Vestfonna is the most extensive ice mass situated at rather low elevations. Taken together, these facts imply that on Vestfonna the ELA shows the highest relative position compared to the local vertical range of surface elevations. As the northeastern part of Svalbard is projected to show the most intensive warming in the future17, Vestfonna will become an archipelago-wide pioneer when it comes to equilibrium-line loss under the continued influence of climate change on Svalbard. However, even under present conditions several much smaller ice bodies on the archipelago have already lost their accumulation areas due to their low surface elevations (e.g. ref. 38).
Refreezing processes are known to form an important component of the mass balance of cold or polythermal glaciers and therefore of Vestfonna12,13,39. However, refreezing shows considerable future variability. For the last decades of the 20th century refrozen meltwater contributed about one third to the overall mass gain of Vestfonna as more than 40% of annual ablation was retained by refreezing13. The relative importance of refreezing for the CMB of the ice cap increased with time concurrent with the positive trend of annual exchange, i.e. of annual accumulation minus annual ablation, a quantity that increases with higher air temperature and higher precipitation. The substantial increases of air temperature and precipitation over the 21st century (Fig. 2) suggest a continuation of this trend. However, the consistent increase of air temperature leads to a rapid tailing off of the increase in annual accumulation. This occurs to the benefit of rainfall, which shows a disproportionate increase in the course of the 21st century (Fig. 3). Thus, the share of liquid precipitation, i.e. rainfall, in total precipitation increases linearly and reaches 16% (27%, 35%, 46%) in RCP 2.6 (4.5, 6.0, 8.5) by the end of the century. The specific combination of increasing air temperature and accumulation leads to an unabated increase of refreezing sums over the first decades of the modelling period. However, the rate of increase decreases (Fig. 3) and the share of refreezing becomes capped at about 47% (Fig. 4). Concurrent with that, a progressively smaller share of ablation is retained by refreezing processes. More and more meltwater turns into runoff and leaves Vestfonna into the ocean.
Projections by ref. 25 of glacier change over all of Svalbard based on the four RCPs yielded cumulative, archipelago-wide volume losses until the end of the 21st century of ~70–90%, depending on scenario. Ref. 26, in contrast, only modelled ensemble mean volume losses of ~65% for the RCP 4.5 and of ~70% for the RCP 8.5. A comparable modelling with forcing of the earlier mid-range A1B emission scenario40 showed an intra-ensemble spread between 30% and 80% of volume loss over the same period7. Transferring these results to region-wide mass balance, ref. 26 states a cumulative CMB of −115 ± 55 m w.e. between the first two and last two decades of the 21st century for the RCP 4.5. The RCP 4.5 projections for Vestfonna in our study yield a distinctly less negative cumulative CMB of −69 ± 41 m w.e. over the modelling period. Much of the difference might be attributable to the fact that our study projects reference-surface CMB evolutions that are based on unchanged glacier topographies, i.e. on a fixed surface extent combined with fixed surface elevations. Ref. 26, in contrast, accounted for continuous changes of the surface topography.
Taken together, these findings indicate that also in the future Vestfonna might retain its present qualitative relation to the archipelago-wide mass balance, i.e. a distinctly more positive state than Svalbard as a whole, even if our projections show that it will probably become a regional pioneer regarding equilibrium-line loss.
Methods
CMB projections are performed in a modelling framework consisting of an elevation dependent accumulation model, a fully spatially distributed ablation model and an elevation dependent surface-albedo model. The model is forced by daily air temperature, precipitation and cloud cover data. The implemented surface-albedo calculations, furthermore, require monthly values of positive degree-day (PDD) sums, snowfall and rain/snow ratio. The following sections describe data preparation and mass-balance modelling and finally an outline of the methods applied during the analysis of results.
Data preparation
The reference-surface CMB projections are based on a fixed surface extent of Vestfonna that was derived by manually digitizing the glacier outlines from a satellite image dating from August 17 2000. The image (EOS Data Gateway Granule ID: SC:ASTL1B 00-08-12:36:0010269001) was acquired by the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) onboard the Terra satellite. It is combined with a void-filled, 250 m-resolution version of the ASTER global digital elevation model (GDEM)12 for final representation of the static glacier surface.
All GCM data used to force the CMB projections originate from grid points in the vicinity of the study area (Fig. 1). From each GCM the four grid points situated closest to the centre of Vestfonna are considered. Each of the final air temperature and precipitation input time series (Fig. 2) is generated from data of the four grid points by using a statistical downscaling procedure in order to make those data fit local conditions at the ice cap. By using statistical instead of dynamical downscaling we exploit the advantage of smaller computational costs. We implicitly assume that present-day transfer functions will hold true also in the future. This assumption of stationarity is a well-recognized drawback that has to be accepted when using any statistical method for future projections. Regarding accuracies, the statistical downscaling used in this study yields ranges of uncertainty comparable to those of costly, high-resolution dynamical downscaling studies that were conducted for different locations on Svalbard41,42.
We use adjusted ERA-Interim data as in-situ reference during the downscaling. These adjusted ERA-Interim data had earlier also been used during the calibration of all parameters of the CMB model12,13,33. The reference period ranges from September 2006 to August 2011. Each of the cloud-cover input time series (Fig. 2) is formed by data from the closest grid point, without downscaling. The time series of monthly PDD sums, snowfall and rain/snow ratio are calculated from the downscaled air temperature and precipitation input time series.
Air temperature was downscaled by combining linear regression and variance inflation techniques13,43,44 following a two-step procedure45. By using this method it was possible to adjust the variance of the daily data as well as their annual cycle46. However, it had to be assumed that the synoptic situation is the only driver for local air-temperature variability45. The original daily GCM air temperatures are downscaled separately for each month i (i = 1, 2, 3, …, 12) in order to account for the intra-annual variability of air-temperature variance in the study area13. In the first step, the synoptic-scale air temperatures of the four grid points j (j = 1, 2, 3, 4) considered (Tsyn,j,i) are adjusted to the reference ERA-Interim air temperatures:

The parameters ai and bj,i are determined separately for each combination of GCM and RCP by using linear regression (cf. Tables S1 to S10). In the second step, the variances of the various  are inflated to match the variances of the local-scale reference (Tloc,i), i.e. the ERA-Interim data:
are inflated to match the variances of the local-scale reference (Tloc,i), i.e. the ERA-Interim data:

The monthly mean air temperature of the local-scale reference ( ) is subtracted out before the variance is inflated in order to avoid the introduction of artificial biases into the final, downscaled air temperatures Ti13. After the inflation the monthly mean is re-added. Table S11 gives an overview of the accuracy of the various Ti. For CMB modelling, the downscaled air temperatures are distributed over the ice cap by applying a constant linear lapse rate of −7.0 K km−1 that was calibrated from in situ measurements earlier12.
) is subtracted out before the variance is inflated in order to avoid the introduction of artificial biases into the final, downscaled air temperatures Ti13. After the inflation the monthly mean is re-added. Table S11 gives an overview of the accuracy of the various Ti. For CMB modelling, the downscaled air temperatures are distributed over the ice cap by applying a constant linear lapse rate of −7.0 K km−1 that was calibrated from in situ measurements earlier12.
Precipitation was downscaled by combining linear regression and local scaling techniques30,47. This method facilitates an adjustment of the monthly sums derived from daily data and therewith a simultaneous adjustment of the overall annual cycle. However, day-to-day precipitation variability is not affected and thus remains unchanged when compared to the original GCM time series. At first, the synoptic-scale precipitation time series of each grid point j (j = 1, 2, 3, 4) are adjusted to the ERA-Interim precipitation data according to the relative differences between the mean local-scale ( ) and synoptic-scale (
) and synoptic-scale ( ) annual cycles represented by characteristic means of each month i (i = 1, 2, 3, …, 12) during the reference period:
) annual cycles represented by characteristic means of each month i (i = 1, 2, 3, …, 12) during the reference period:

Afterwards, the various  are combined linearly to yield the final, downscaled precipitation sums Pi:
are combined linearly to yield the final, downscaled precipitation sums Pi:

The parameters ci and dj,i are determined separately for each combination of GCM and RCP by using linear regression analysis between the  and the corresponding ERA-Interim precipitation. Tables S12 to S21 document the various parameters ci and dj,i and Table S22 gives an overview of the accuracies of the final Pi. For CMB modelling, the downscaled precipitation is distributed over all elevations z of Vestfonna according to a quadratic scaling function derived from extensive snow-cover studies on the ice cap12,48.
and the corresponding ERA-Interim precipitation. Tables S12 to S21 document the various parameters ci and dj,i and Table S22 gives an overview of the accuracies of the final Pi. For CMB modelling, the downscaled precipitation is distributed over all elevations z of Vestfonna according to a quadratic scaling function derived from extensive snow-cover studies on the ice cap12,48.

From the downscaled daily air temperature and precipitation data monthly PDD sums, snowfall sums and rain/snow ratios are derived. For calculation of the quantities cumulative snowfall and cumulative PDD, that are needed during albedo modelling, the respective monthly sums at each elevation of the ice cap are summed up over the course of a mass-balance year, each beginning in September. The monthly rain/snow ratios at each elevation are then calculated as the quotient of the respective rainfall and snowfall sums. The threshold value for discrimination between rain and snow is set to 0°C within the albedo model32.
Mass-balance modelling
The CMB model consists of separate modules for calculation of accumulation, ablation and refreezing with the individual results being summed up to yield the CMB on a daily basis. Daily values of the period September 1 to August 31 are summed up to annual values representing one mass-balance year.
The daily surface accumulation c(z) at elevation z is calculated from the share of snowfall in the scaled GCM precipitation data (P(z)). Below 0°C all precipitation is assumed to fall as snow. Above 2°C all precipitation is assumed to fall as rain. The transition between pure snowfall and pure rainfall is realized on the basis of a hyperbolic function49 that describes the varying shares of both types of precipitation according to air temperature (T(z)):

The daily surface ablation a(z) at elevation z is calculated using a temperature-net shortwave radiation-index model formulation13,50:

The temperature (fT = 1.736 mm w.e. K−1 d−1) and radiation (fR = 0.141 mm w.e. W−1 m2 d−1) factors have been calibrated on the basis of mass balance stake measurements for an earlier study13. Spatially distributed global radiation (R) is calculated from modelled clear sky direct solar radiation by considering decreases caused by cloud coverage and increases caused by multiple scattering and reflection between clouds and glacier surface12. The cloud cover is provided by GCM-derived time series (Fig. 2), while the elevation-varying albedo fields (α) are calculated on a monthly updated basis from the downscaled GCM data by applying a minimal, statistical model that was especially designed for application at the ice cap Vestfonna33. Details of radiation and albedo modelling are described in the supplement.
Refreezing is calculated on the basis of the Pmax approach51. Both meltwater produced by surface ablation and rainfall are assumed to percolate down into the snow and firn of the ice cap and refreeze in situ until a predefined maximum amount is reached. For Vestfonna, this amount is assumed to reach 90% of the accumulation sum of the preceding winter season13, i.e. we set Pmax = 0.9. Any further meltwater or rainfall input is assumed to leave the glacier system as runoff. With the value of 0.9 we depart from the original value of 0.6 used by ref. 51. This is done in response to recent findings at neighbouring Austfonna ice cap, where refreezing fractions of up to 100% were assessed52.
Analysis of results
The annual values of the mean ELA time series (Fig. 5) of each RCP are calculated from the annual values of the individual ELA time series that belong to the respective ensemble members. Therefore, some ELA time series needed to be extrapolated beyond the date of equilibrium-line loss in order to obtain complete data availability for ELA averaging. Each extrapolation is done according to the linear temporal trend of the ELA over the modelling period. The trends of the individual ELA time series are derived by linear regression. An overview of all regression equations and their coefficients of determination is provided in Table S23.
The dates of equilibrium-line loss for each RCP are calculated by extrapolating the linear temporal trends of the mean ELA time series. Table S23 also gives an overview of the linear regressions for these trends. Departing from this procedure, the annual values of the mean AAR time series (Fig. 5) of each RCP are directly calculated from the mean ELA time series and not from the individual AAR time series within each ensemble.
References
Rockström, J. et al. A safe operating space for humanity. Nature 461, 472–475 (2009).
Dyurgerov, M. B. & Meier, M. F. Twentieth century climate change: Evidence from small glaciers. Proc. Natl. Acad. Sci. 97, 1406–1411 (2000).
Nicholls, R. J. & Cazenave, A. Sea-level rise and its impact on coastal zones. Science 328, 1517–1520 (2010).
Kaser, G., Cogley, J. G., Dyurgerov, M. B., Meier, M. F. & Ohmura, A. Mass balance of glaciers and ice caps: Consensus estimates for 1961–2004. Geophys. Res. Lett. 33, L19501; 10.1029/2006GL027511 (2006).
Rinke, A. & Dethloff, K. Simulated circum-Arctic climate changes by the end of the 21st century. Global Planet. Change 62, 173–186 (2008).
Radić, V. & Hock, R. Regionally differentiated contribution of mountain glaciers and ice caps to future sea-level rise. Nature Geosc. 4, 91–94 (2011).
Gardner, A. S. et al. Sharply increased mass loss from glaciers and ice caps in the Canadian Arctic Archipelago. Nature 473, 357–360 (2011).
Moholdt, G., Wouters, B. & Gardner, A. S. Recent mass changes of glaciers in the Russian High Arctic. Geophys. Res. Lett. 39, L10502; 10.1029/2012GL051466 (2012).
Moholdt, G., Nuth, C., Hagen, J. O. & Kohler, J. Recent elevation changes of Svalbard glaciers derived from ICESat laser altimetry. Remote Sens. Environ. 114, 2756–2767 (2010).
Braun, M. et al. Changes of glacier frontal positions of Vestfonna (Nordaustlandet, Svalbard). Geogr. Ann. A 93, 301–310 (2011).
Nuth, C., Moholdt, G., Kohler, J., Hagen, J. O. & Kääb, A. Svalbard glacier elevation changes and contribution to sea level rise. J. Geophys. Res. 115, F01008; 10.1029/2008JF001223 (2010).
Möller, M. et al. Climatic mass balance of Vestfonna ice cap, Svalbard: A spatially distributed assessment using ERA-Interim and MODIS data. J. Geophys. Res. 116, F03009; 10.1029/2010JF001905 (2011).
Möller, M., Finkelnburg, R., Braun, M., Scherer, D. & Schneider, C. Variability of the climatic mass balance of Vestfonna ice cap (northeastern Svalbard), 1979–2011. Ann. Glaciol. 54, 254–264 (2013).
Beaudon, E. et al. Spatial and temporal variability of net accumulation from shallow cores from Vestfonna ice cap (Nordaustlandet, Svalbard). Geogr. Ann. A 93, 287–299 (2011).
Kattsov, V. M. & Walsh, J. E. Twentieth-century trends of Arctic precipitation from observational data and a climate model simulation. J. Clim. 13, 1362–1369 (2000).
Richter-Menge, J. et al. State of the Arctic Report NOAA OAR Special Report (NOAA/OAR/PMEL, SeattleWA, 2006).
Førland, E. J., Benestad, R., Hanssen-Bauer, I., Haugen, J. E. & Skaugen, T. E. Temperature and precipitation development at Svalbard 1900-2100. Adv. Meteorol. 893790; 10.1155/2011/893790. (2011).
Pelto, M. S. Forecasting temperate alpine glacier survival from accumulation zone observations. Cryosphere 4, 67–75 (2010).
Hock, R., Kootstra, D.-S. & Reijmer, C. Deriving glacier mass balance from accumulation area ratio on Storglaciären, Sweden. Paper presented at IAHS Assembly in Foz do Iguaçu: Glacier Mass Balance Changes and Meltwater Discharge, Brazil. IAHS Publ. 318, 163–170 (2007).
Mernild, S. H. et al. Identification of snow ablation rate, ELA, AAR and net mass balance using transient snowline variations on two Arctic glaciers. J. Glaciol. 59, 649–659 (2013).
Oerlemans, J. et al. Estimating the contribution of Arctic glaciers to sea-level change in the next 100 years. Ann. Glaciol. 42, 230–236 (2005).
Oerlemans, J. & Reichert, B. K. Relating glacier mass balance to meteorological data by using a seasonal sensitivity characteristic. J. Glaciol. 46, 1–6 (2000).
Oerlemans, J., Jania, J. & Kolondra, L. Application of a minimal glacier model to Hansbreen, Svalbard. Cryosphere 5, 1–11 (2011).
Vieli, A., Jania, J. & Kolondra, L. The retreat of a tidewater glacier: observations and model calculations on Hansbreen, Svalbard. J. Glaciol. 48, 592–600 (2002).
Marzeion, B., Jarosch, A. H. & Hofer, M. Past and future sea-level change from the surface mass balance of glaciers. Cryosphere 6, 1295–1322 (2012).
Radić, V. et al. Regional and global projections of twenty-first century glacier mass changes in response to climate scenarios from global climate models. Clim. Dyn. 10.1007/s00382-013-1719-7.
Raper, S. C. B. & Braithwaite, R. J. Low sea level rise projections from mountain glaciers and icecaps under global warming. Nature 439, 311–313 (2006).
Hock, R. A distributed temperature-index ice- and snowmelt model including potential direct solar radiation. J. Glaciol. 45, 101–112 (1999).
Möller, M. & Schneider, C. Calibration of glacier volume-area relations from surface extent fluctuations and its application to future glacier change. J. Glaciol. 56, 33–40 (2010).
Möller, M. & Schneider, C. Climate sensitivity and mass balance evolution of Gran Campo Nevado Ice Cap, southwest Patagonia. Ann. Glaciol. 48, 32–42 (2008).
Radić, V. & Hock, R. Modeling future glacier mass balance and volume changes using ERA-40 reanalysis and climate models: sensitivity study at Storglaciären, Sweden. J. Geophys. Res. 111, F03003; 10.1029/2005JF000440 (2006).
Cogley, J. G. et al. Glossary of Glacier Mass Balance and Related Terms IHP-VII Technical Documents in Hydrology No. 86 (IACS Contribution No. 2, UNESCO-IHPParis, 2011).
Möller, M. A minimal, statistical model for the surface albedo of Vestfonna ice cap, Svalbard. Cryosphere 6, 1049–1061 (2012).
Moss, R. H. et al. The next generation of scenarios for climate change research and assessment. Nature 463, 747–756 (2010).
Hawkins, E. & Sutton, R. The potential to narrow uncertainty in regional climate predictions. B. Am. Meteorol. Soc. 90, 1095–1107 (2009).
Mernild, S. H., Lipscomb, W. H., Bahr, D. B., Radić, V. & Zemp, M. Global glacier changes: a revised assessment of committed mass losses and sampling uncertainties. Cryosphere 7, 1565–1577 (2013).
Hagen, J. O., Melvold, K., Pinglot, F. & Dowdeswell, J. A. On the net mass balance of the glaciers and ice caps in Svalbard, Norwegian Arctic. Arct. Antarct. Alp. Res. 35, 264–270 (2003).
Jonsson, S. On the present glaciation of Storøya, Svalbard. Geogr. Ann. A 64, 53–79 (1982).
Palosuo, E. Ice layers and superimposition of ice on the summit and slope of Vestfonna, Svalbard. Geogr. Ann. A 69, 289–296 (1987).
Nakicenovic, N. et al. Special Report on Emissions Scenarios: A Special Report of Working Group III of the Intergovernmental Panel on Climate Change (Cambridge University Press, Cambridge, U.K., 2000).
Claremar, B. et al. Applying a Mesoscale Atmospheric Model to Svalbard Glaciers. Adv. Meteorol. 2012, Article ID 321649; 10.1155/2012/321649 (2012).
van Pelt, W. J. J. et al. Simulating melt, runoff and refreezing on Nordenskiöldbreen, Svalbard, using a coupled snow and energy balance model. Cryosphere 6, 641–659 (2012).
Huth, R. Statistical downscaling in central Europe: evaluation of methods and potential predictors. Climate Res. 13, 91–101 (1999).
Karl, T. R., Wang, W.-C., Schlesinger, M. E., Knight, R. W. & Portman, D. A method relating general circulation model simulated climate to the observed local climate. Part I: seasonal statistics. J. Climate 3, 1053–1079 (1990).
Von Storch, H. On the use of ‘inflation’ in statistical downscaling. J. Climate 12, 3505–3506 (1999).
Huth, R., Kyselý, J. & Dubrovský, M. Time structures of observed, GCM-simulated, downscaled and stochastically generated daily temperature series. J. Climate 14, 4047–4061 (2001).
Widmann, M., Bretherton, C. S. & Salathé Jr, E. P. Statistical precipitation downscaling over the Northwestern United States using numerically simulated precipitation as a predictor. J. Climate 16, 799–816 (2003).
Möller, M. et al. Snowpack characteristics of Vestfonna and De Geerfonna (Nordaustlandet, Svalbard) – a spatiotemporal analysis based on multiyear snow-pit data. Geogr. Ann. A 93, 273–285 (2011).
Möller, M., Schneider, C. & Kilian, R. Glacier change and climate forcing in recent decades at Gran Campo Nevado, southernmost Patagonia. Ann. Glaciol. 46, 136–144 (2007).
Pellicciotti, F. et al. An enhanced temperature-index glacier melt model including the shortwave radiation balance: development and testing for Haut Glacier d'Arolla, Switzerland. J. Glaciol. 51, 573–587 (2005).
Reeh, N. Parameterization of melt rate and surface temperature on the Greenland ice sheet. Polarforschung 59, 113–128 (1991).
Østby, T., Schuler, T. V., Hagen, J. O., Reijmer, C. H. & Hock, R. Parameter uncertainty, refreezing and surface energy balance modelling at Austfonna ice cap, Svalbard, over 2004–2008. Ann. Glaciol. 54, 229–240 (2013).
Acknowledgements
This study was financed through grant no. 03F0623B of the German Federal Ministry of Education and Research (BMBF). Additional funding was provided by grant no. MO2653/1-1 of the German Research Foundation (DFG) and by project EUI2009-04096 from the Spanish Euro-Research Programme. The study forms a legacy of the International Polar Year core project “IPY Kinnvika”. In this context funding through grant no. SCHN680/2-1 and 2-2 of the DFG is also acknowledged. The authors thank all people involved in the fieldwork activities that have been carried out for this study.
Author information
Authors and Affiliations
Contributions
C.S. initiated the overall study. M.M. designed the explicit outline of the study as well as the analysis and modelling methods. M.M. also carried out all calculations, wrote the manuscript and prepared all figures. C.S. contributed to the discussion of the results at all stages. Both authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Möller, M., Schneider, C. Temporal constraints on future accumulation-area loss of a major Arctic ice cap due to climate change (Vestfonna, Svalbard). Sci Rep 5, 8079 (2015). https://doi.org/10.1038/srep08079
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep08079
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.