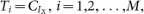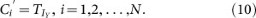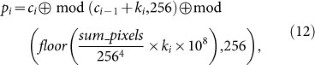Abstract
Quantum computation has achieved a tremendous success during the last decades. In this paper, we investigate the potential application of a famous quantum computation model, i.e., quantum walks (QW) in image encryption. It is found that QW can serve as an excellent key generator thanks to its inherent nonlinear chaotic dynamic behavior. Furthermore, we construct a novel QW-based image encryption algorithm. Simulations and performance comparisons show that the proposal is secure enough for image encryption and outperforms prior works. It also opens the door towards introducing quantum computation into image encryption and promotes the convergence between quantum computation and image processing.
Similar content being viewed by others
Introduction
With the advancements of Internet and multimedia communication, the exchange of multimedia data over the Internet plays an important role in modern society in which images are widely used as a good information carrier. Image content security receives more and more attention. Generally encryption can effectively ensure the secure transmission of images through public channels. Many image encryption algorithms have been proposed in recent years1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27.
There are mainly two branches of image encryption: image encryption on a quantum computer and image encryption on a classical computer. As for the former, some works have been proposed4,27. Although there are some advanced proposals for quantum networks28, the practical and useful quantum network, even quantum computer cannot be realized in the near future. So in this paper, we focus on image encryption on a classical computer.
Due to the attractive features such as high sensitivity to initial conditions, unpredictability, pseudo-randomness and ergodicity, chaotic maps are employed for image encryption. In 1989, Matthews first proposed a chaos-based encryption algorithm5. Since then, a variety of chaos-based image encryption algorithms have been proposed2,6,7,8,9,10,11,12,13. Unfortunately, most chaotic systems are unstable due to the periodicity of the chaotic mapping29. Image encryption systems based on such maps are prone to attacks6,7.
Another important system, optical systems have been developed extensively for image encryption due to the distinct properties of processing 2D complex data with parallelism and high speed. Optics-based image encryption started from the double random-phase encoding (DRPE) algorithm14. Unfortunately, the DRPE method was broken by various attack strategies15,16,17. Nowadays, most optical image encryption systems are far satisfactory due to some defects like the huge size, poor flexibility and stability for optical elements used in the free space and the difficulty of implementation. So, it should be used cautiously in practice.
As we know, the security of an image encryption algorithm depends on the design of the details of the algorithm, in particular the design of the key generation rule. A good key generator is of vital importance to a desirable image encryption algorithm. Obviously, the security of chaos-based image encryption algorithms lies heavily in the chaotic systems' features. However, existing chaotic systems are not perfect, i.e., the instability and periodicity cause most chaos-based image encryption algorithms to be prone to various attacks6,7.
It is natural to ask whether there exist other chaotic systems with more excellent cryptographic performances. Inspired by the above reasons, we are motivated to seek novel chaotic functions and further construct image encryption algorithms based on such chaotic functions.
Quantum computation is a rapidly growing field and lots of breakthroughs have been achieved during the past decades. As a universal quantum computation model, quantum walks (QW) has been developed as a useful tool for solving various problems, including element distinctness30, triangle finding31 and data clustering32 and so on. Furthermore, the importance of classical random walks in many fields like physics, biology, computer science, finance, etc., implies the possibility that its quantum analog, namely, QW, could be a useful tool for many future applications.
In this paper, we investigate the potential application of QW in image encryption and find that QW can serve as an excellent key generator thanks to its inherent unpredictably 'chaotic' nonlinear dynamic behavior. Further, we construct a novel QW-based image encryption algorithm. Compared with the previous chaos-based image encryption works, our QW-based proposal has not only the same merits as chaos' systems like high sensitivity to initial values and system parameters, unpredictability, pseudo-randomness, but also the advantages like stability and non-periodicity. The infinite possibilities of the coin states make QW own an ability of producing a theoretically infinite key space to resist brute-force attacks. Numerical simulations show that the proposal is secure enough for image encryption. It also opens the door towards introducing quantum computation into image encryption and promotes the convergence between quantum computation and image processing.
Results
The chaotic behavior of Quantum walks
There are two types of QWs, continuous33 and discrete ones and several studies have highlighted how the properties and dynamics of QWs differ from their classical counterparts34,35,36. The basic discrete QW includes two quantum systems: walker and coin. The state of the walker-coin system is denoted by a vector in the Hilbert space  , where the subscripts p and c stand for walker and coin, respectively. The motion of the walk is conditioned by the coin state via a conditional shift operator
, where the subscripts p and c stand for walker and coin, respectively. The motion of the walk is conditioned by the coin state via a conditional shift operator

where the summation symbol denotes the sum over all possible positions. The evolution of the total quantum system can be implemented by repeating the sequence of the coin flipping operator and the conditional shift operator in equation (1) step by step (so-called discrete time), expressed by

where  is the identity operator of the walker and
is the identity operator of the walker and  is the flipping operator applied to the coin state. Hence the final state |ψ〉rafter r steps is expressed by
is the flipping operator applied to the coin state. Hence the final state |ψ〉rafter r steps is expressed by

and the probability of locating the walker at position x after r steps is

where |ψ〉initial is the initial state of the total quantum system.
For multi-walker, multi-coin discrete QW, the final state  after r steps is expressed by
after r steps is expressed by

and the probability of locating the n walkers at position x1,x2,…,xn after r steps is

where |ψ〉0 is the initial state of the total n-walker, n-coin quantum system.
It can be seen that the resulting probability distribution in equation (6) is the sum of squares of the norms of amplitudes so that there exists a non-linearity map between the initial state and the resulting probability distribution. The resulting probability distribution is not only of high sensitivity to initial states, unpredictability, pseudo-randomness, but also of stability and non-periodicity. And different coin states will produce different probability distributions. The infinite possibilities of the coin states make QW own an ability of producing a theoretically infinite key space to resist brute-force attacks, which underlies the image encryption.
Image encryption algorithm based on quantum walks
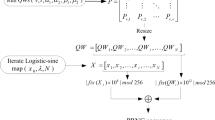
To demonstrate QW's utility as an excellent key generator, we further construct a novel image encryption algorithm based on the one-dimensional two-particle discrete-time QW on a circle. The algorithm includes three phases: (i) the generation of the key sequences using the one-dimensional two-particle discrete-time QW on a circle, (ii) the image encryption phase and (iii) the image decryption phase.
Generation of the key sequences using the one-dimensional two-particle discrete-time QW on a circle.
-
i
Choose the parameters (n, (α, β, χ, δ)), r, θ) and run the one-dimensional two-particle discrete QW on a circle of n nodes to generate the corresponding probability matrix with size n × n. Here α, β, χ, δ are the amplitudes of the initial coin state |υ,τ〉 = (α|00〉 + β|01〉 + χ|10〉 + δ|11〉). r is the step number and θ is a parameter of the quantum coin operator

-
ii
Resize the resulting probability matrix in terms of the size of the original image and multiply all values in the resulting probability matrix by 108 modulo 256 to form a random key sequence K = {k1,k2,…,kM × N}, where M × N is the size of the original image I.
Image encryption procedure.
-
i
Convert the original image I into a vector P = {p1,p2,…,pM × N} and then calculate the sum of the original image pixels according to equation (8):

-
ii
Calculate ci (i = 1,2,…,M × N) by equation (9):

where c0 = 127. And the cipher image is denoted as C = {c1,c2,…,cM× N}.
-
iii
Select M and N values from the beginning and the end of the key sequence K, respectively and get two sequences X = {X1,X2,…,XM} and Y = {Y1,Y2,…,YN}, respectively.
-
iv
Order X and Y in an ascending order, respectively and get two new sequences
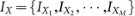 and
and  .
. -
v
Permute the cipher image C in terms of IXand IY, respectively and get the final encrypted image
 , i.e.,
, i.e., 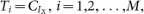
Image decryption procedure
The decryption process is the reverse of the encryption one.
-
i
Use the same way above to generate IXand IY and decrypt the cipher image C′ into the cipher image C by using IXand IY.
-
ii
Generate the random key sequence K = {k1,k2,…,kM× N} with the same parameters (n, (α, β, χ, δ), r, θ).
-
iii
Recover the image pixels P = {p1,p2,…pM× N}from C = {c1,c2,…,cM× N} by equations (11) and (12):

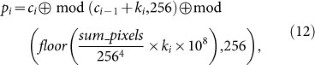
where i is from M × N to 1 and the initial value of sum_pixels is 0.
-
iv
Reshape P = {p1,p2,…,pM× N} into an image with size M × N and get the recovered image.
Experimental simulations and performance analyses
Simulations
Experiments are performed on a laptop with Intel(R) Core(TM) i3-2370M CPU 2.40 GHz 4 GB RAM running on Windows 7 professional equipped with the MATLAB R2012a environment. Here, we selected ten 256 × 256 gray-scale images taken by Q.-X. Pan as the original images (see Supplementary Figs. S1–S10 online). And we chose the initial key parameters (n = 5, (α = 1/2, β = 1/2, χ = 1/2, δ = 1/2), r = 30, θ = π/3). Using QW as the key generator and the proposed image encryption algorithm, we obtained the cipher images of the ten test images.
From Supplementary Figs. S1–S10 online, we showed that the encrypted image is smoother and more uniform than the original image. Hence, it does not provide any hint for attackers by applying statistical attacks on the proposed image encryption scheme.
Security analyses of the QW-based image encryption algorithm
To analyze the security of the proposed image encryption algorithm, we did from two aspects. On the one hand, we analyzed the statistical properties of the QW-based key generator as a pseudorandom number generator (PRNG). On the other hand, we analyzed the statistical properties of cipher images. To analyze the QW-based PRNG, two main quantifiers are adopted, i.e., (i) quantifiers based on information theory37,38,39, (ii) quantifiers based on recurrence plots40,41.
Statistical complexity measure
Complexity is a measure of off-equilibrium ‘order'. Statistical complexity measures (SCM) were proposed as quantifiers of the degree of physical structure in a signal37,42,43. They are null for total random processes. The intensive SCM (CJ[P]) quantifies not only randomness but also the presence of correlational structures43,44 of the dynamical system and can be used to study the intricate structures hidden in the dynamics. The SCM CJ[P] is defined as44:

where the normalized entropic measure HS[P] = S[P]/Smax is associated with the probability distribution P,with Smax = S[Pe] (0 ≤ HS ≤ 1) for the equilibrium distribution Pe and S[·] is the Shannon entropy. The disequilibrium QJ is defined in terms of the Jensen-Shannon divergence38,44 by

with Q0 being the normalization constant (0 ≤ QJ ≤ 1). Thus, the disequilibrium QJ is an intensive quantity. Following the methodology proposed by Bandt and Pompe45, the normalized entropy HS and the intensive SCM CJ as functions of the number of 8 bits and 16 bits-words are shown in Figs. 1(a) and 1(b) respectively. From Fig. 1, when the number of words of the analyzed sequence increases, the statistical complexity and the normalized Shannon entropy tend to 0 and 1 respectively. It can be concluded that, the randomness of the proposed QW-based PRNG is successfully verified.
(a) Normalized Shannon entropy. (b) Intensive statistical complexity measure. The normalized entropy HS and the intensive statistical complexity measure CJ as functions of the number of 8 bits and 16 bits-words are shown in (a) and (b) respectively. When the number of words of the analyzed sequence increases, the statistical complexity and the normalized Shannon entropy tend to 0 and 1 respectively. (see text in the section entitled Results).
Recurrence plots
Recurrence is a fundamental property of dynamical systems, which can be exploited to characterize the system's behavior in phase space. In 1987, Eckmann et al. introduced a powerful tool for visualization and analysis of recurrences called recurrence plot (RP)40. To visualize the recurrences of states of a dynamical system, the RP of a trajectory  can be formally expressed by the matrix
can be formally expressed by the matrix

where N is the number of measured points  , ε is a threshold distance, Θ (·) is the Heaviside function (i.e. Θ (x) = 0, if x < 0 and Θ (x) = 1 otherwise) and
, ε is a threshold distance, Θ (·) is the Heaviside function (i.e. Θ (x) = 0, if x < 0 and Θ (x) = 1 otherwise) and  is a norm.
is a norm.
RPs with different r exhibit visually the recurrences of the QW-based PRNG with an embedding dimension m = 4 and the delay τ = 1 (see Supplementary Fig. S11 online). It is shown that the QW-based PRNG causes a rather homogeneous RP with numerous single points and some short, diagonal or vertical lines.
Because the visual impact produced by the RP is insufficient to demonstrate the quality of the QW-based PRNG because of the 'small-scale' structures41, several measures of complexity which quantify the small scale structures in RPs, have been proposed46,47,48 and are known as recurrence quantification analysis (RQA). In this paper, these measures based on the recurrence point density and the diagonal and vertical line structures are considered.
Measures based on the recurrence density
The simplest measure of the RQA is the recurrence rate (RR)

which is a measure of the density of recurrence points in the RP. In the limit N → ∞, RR is the probability that a state recurs to its ε-neighbourhood in phase space. For PRNGs, the ideal value would be RR = 0. It is indicated that the values of the RR range from 0.004 to 0.007 for different r, which exhibits the good randomness of the QW-based PRNG (see Supplementary Fig. S12 online).
Measures based on diagonal lines
The measures are related to the histogram P(ε,l) of the diagonal line lengths l, given by

Supplementary Fig. S13 online demonstrates the histogram of the diagonal line lengths of the RP in Supplementary Fig. S11 online with r = 50. It is shown that the diagonal line lengths are mainly very short exhibiting the good randomness.
Processes with uncorrelated or weakly correlated and stochastic or chaotic behaviors cause none or very short diagonals, whereas deterministic processes cause longer diagonals and less single, isolated recurrence points. Therefore, the ratio of recurrence points that form diagonal structures (of at least length lmin) to all recurrence points

is introduced as a measure for determinism (or predictability) of the system. The threshold lmin excludes the diagonal lines which are formed by the tangential motion of the phase space trajectory.
A diagonal line of length l means that a segment of the trajectory is rather close during l time steps to another segment of the trajectory at a different time; thus these lines are related to the divergence of the trajectory segments. The average diagonal line length

is the average time that two segments of the trajectory are close to each other and can be interpreted as the mean prediction time.
Another RQA measure considers the length Lmax of the longest diagonal line found in the RP,

where  is the total number of diagonal lines. These measures are related to the exponential divergence of the phase space trajectory. The faster the trajectory segments diverge, the shorter are the diagonal lines.
is the total number of diagonal lines. These measures are related to the exponential divergence of the phase space trajectory. The faster the trajectory segments diverge, the shorter are the diagonal lines.
The measure entropy refers to the Shannon entropy of the probability p(l) = P(ε,l)/Nl to find a diagonal line of exactly length l in the RP, where  is the total number of diagonal lines.
is the total number of diagonal lines.

ENTR reflects the complexity of the RP in respect of the diagonal lines, e.g. for uncorrelated noise the value of ENTR is rather small, indicating its low complexity, as shown in Supplementary Fig. S14 online.
Measures based on vertical lines
The total number of the vertical lines of the length v in the RP is then given by the histogram

Supplementary Fig. S15 online shows the histogram of vertical line lengths of the RP in Supplementary Fig. S11 online with the parameter r = 50. It is shown that the vertical line lengths are mainly very short exhibiting the good randomness.
Analogous to the definition of the determinism in equation (22), the ratio between the recurrence points forming the vertical structures and the entire set of recurrence points can be computed,

The computation of LAM is realized for those v that exceed a minimal length vmin in order to decrease the influence of the tangential motion. LAM will decrease if the RP consists of more single recurrence points than vertical structures.
The average length of vertical structures is given by

and is called trapping time. TT estimates the mean time that the system will abide at a specific state or how long the state will be trapped.
Finally, the maximal length of the vertical lines in the RP

can be defined, analogously to the standard measure Lmax (Nv is the absolute number of vertical lines).
Figs. 2,3 indicate the RQA measures, i.e., DET, Lmax, L, LAM, Vmax and TT for different r and demonstrate the good statistical properties of the QW-based PRNG.
Degree of non-periodicity
In order to detect and study non-periodicity in the QW-based PRNG, the scale index analysis (SIA) is carried out which is introduced by Benìtez et al.49. The SIA method is often used as a framework to enhance the general performance of cryptosystems in designing new chaos-based cryptosystems and PRNGs. For example, recently Akhshani et al. proposed a new scheme for generating good PRNGs based on quantum logistic map50. They used the SIA technique to assess the degree of non-periodicity of the chaotic sequences of the quantum map.
The SIA technique is based on the continuous wavelet transform (CWT) and the wavelet multi-resolution analysis51. To study non-periodicity of the QW-based PRNG52, we assumed that the key sequence f is compactly supported and is defined over a finite time interval I = [a, b]. The CWT of f at time u and scale s is defined as51:

and it provides the frequency components (or details) of f corresponding to scale s and time t.
The scalogram of f is defined as follows:

where ζ(s) is the energy of the CWT of f at scale s. The scalogram is a useful tool for studying a signal, since it allows the detection of its most representative scales or frequencies49,52. Also, the inner scalogram of f at a scale s can be defined by:

where  is the maximal subinterval in I for which the support of ψu,s is included in I for all
is the maximal subinterval in I for which the support of ψu,s is included in I for all  . As the length of J(s) depends on the scale s, the values of the inner scalogram at different scales cannot be compared. Therefore, the inner scalogram should be normalized as follows49:
. As the length of J(s) depends on the scale s, the values of the inner scalogram at different scales cannot be compared. Therefore, the inner scalogram should be normalized as follows49:

It is shown that the normalized inner scalogram can be a valuable tool for detecting the non-periodicity of the signal, where a signal with details at every scale is non-periodic (see Supplementary Fig. S16 online).
The scale index of f in the scale interval [s0,s1] can be defined by:

where smax is the smallest scale such that ζ(s) ≤ ζ(smax) for all  and smin the smallest scale such that ζ(smin) ≤ ζ(s) for all
and smin the smallest scale such that ζ(smin) ≤ ζ(s) for all  . Note that for compactly supported signals only the normalized inner scalogram will be considered49. From its definition, the scale index iscale meets 0 ≤ iscale ≤ 1 and it can be interpreted as a measure of the degree of non-periodicity of the signal: the scale index will be zero or close to zero for periodic sequences and close to one for highly non-periodic sequences49. Fig. 4 shows the SIA of the QW-based key sequence. It can be concluded that the best value of the scale index is iscale ≈ 0.9 and remains at this value for all θ. Thus, the key sequence in this state is highly non-periodic and it can be used for any PRNG purposes.
. Note that for compactly supported signals only the normalized inner scalogram will be considered49. From its definition, the scale index iscale meets 0 ≤ iscale ≤ 1 and it can be interpreted as a measure of the degree of non-periodicity of the signal: the scale index will be zero or close to zero for periodic sequences and close to one for highly non-periodic sequences49. Fig. 4 shows the SIA of the QW-based key sequence. It can be concluded that the best value of the scale index is iscale ≈ 0.9 and remains at this value for all θ. Thus, the key sequence in this state is highly non-periodic and it can be used for any PRNG purposes.
The scale index of the QW-based key sequence for different r.
The scale index of the QW-based key sequence change with different step number r and θ, the parameter of the quantum coin operator. Generally, the more the scale index is close to one, the more non-periodic the key sequence is. It can be found that the best value of the scale index is iscale ≈ 0.9 and remains at this value for all θ. (see text in the section entitled Results).
Random tests for the key sequences
We used NIST SP800-22 to test the randomness of the QW-based key sequences (see Supplementary Table S1 online). Each test produces a P-value in [0, 1]. If the P-value is higher than a preset thresholdα, it means that the cipher image passes the test. In our tests, we set α = 0.01. The results of different QW-based key sequences are all 'success' in terms of the average of P-value shown in the second column. Hence, our key generator passes the NIST SP800-22 tests.
Information entropy analysis
The information entropy is often used to measure the randomness of the cipher images. The entropy H(x) of a message source m is given by

where p(xi) represents the probability of the occurrence of symbol xi. We compared the information entropy using our proposal and the algorithms using hyper-chaotic system53,54 (see Supplementary Table S2 online). In terms of the results, the proposed scheme is stable and secure against entropy attack.
Randomness test for the cipher images
We used ten different cipher images with size 1024 × 1024 because of the software NIST requirements for the magnitude 1000000 (see Supplementary Table S3 online). The results of ten different images are all 'success' and we get the average of P-value show in the second column. Hence, we can judge that our proposed algorithm passes the NIST SP800-22 tests.
Further, we applied the most stringent test by TestU0155. As for tests by TestU01, there are three different types of crush batteries: SmallCrush, Crush and BigCrush. To test the randomness of the cipher images, one should apply SmallCrush, Crush and BigCrush test batteries. For each test, a P-value is calculated. If the P-value is within the range [0.0001, −0.9999], it implies a success. Or it is considered as a failure. According to Supplementary Table S4 online, the proposed encryption system passes the TestU01 tests.
Speed performance analysis
Speed is an important factor for evaluating the performance of an image encryption algorithm. For the proposed encryption algorithm, we measured the time cost in the running environment: Windows 7, Matlab R2012a, Intel(R) Core(TM) i3-2370M CPU 2.40 GHz 4 GB RAM and the average time cost for cipher images of size 256 × 256 is 0.1371721s or so. Compared with prior image encryption works, our algorithm is not so fast, which should be improved in our future work.
Key space analysis
A desirable image encryption scheme should have a sufficiently large key space to resist brute-force attacks. The encryption key of our algorithm can be represented by (n, (α, β, χ, δ), r, θ). Although there is an infinite key space theoretically, because of finite precision of digital computers, the key space actually turns out to be finite. Considering that the calculation precision is 10−14, the size of key space for initial conditions and control parameters would be roughly 2325, which is large enough for any encryption purposes and is also large enough to resist all kinds of brute-force attacks.
Comparison with other image encryption techniques
Experimental results of the proposed image encryption scheme will be compared with three classes of image encryption techniques, i.e., the quantum image encryption algorithm4, the DRPE optical image algorithm14, the chaos-based image encryption algorithm56.
Correlation analysis
A desirable image encryption algorithm should produce the cipher image with extremely low correlation between adjacent pixels. We tested the correlation between 10000 pairs of adjacent pixels (in horizontal, vertical and diagonal directions respectively) and drew the correlation distribution of adjacent pixels in the Arch image and its cipher image (see Supplementary Fig. S17 online). It is shown that the cipher image is quite random.
The correlation coefficients rxy of adjacent pixels can be defined by

where E(x) and D(x) are the expectation and variance of variable x, respectively.
The average of the correlation coefficients rxy of adjacent pixels in horizontal, vertical and diagonal directions respectively can be defined as

where H, V and D are the correlation coefficients of adjacent pixels in horizontal, vertical and diagonal directions respectively.
The comparisons between our algorithm and these three classes of image encryption algorithms are shown in Supplementary Tables S5, S6 and S7 online respectively. It is shown that our algorithm outperforms these three classes of image encryption algorithms in terms of the correlation coefficients, the average and the value of Average (H,V,D) and is secure against statistical attack.
Sensitivity analysis
The difference caused by a little change in the plain image and the key can reflect the relationship between the original image and the cipher image to some extent. In general, two common performance measures are used to test the influence of a little change in the key on the cipher image, i.e., the number of pixels change rate (NPCR) and the unified average changing intensity (UACI). NPCR is expressed by

where

and c1 and c2 are two cipher images with size m × n.
UACI is defined by

In our tests, we considered the influence of slightly different keys and one pixel change on a 256-gray image with size 256 × 256, respectively. Generally two kinds of sensitivity analyses should be made. One is key sensitivity analysis and the other is plaintext sensitivity analysis respectively. Next, we first made a key sensitivity analysis.
We first encrypted Arch image with the key (n = 5, (α, β, χ, δ) = (1/2, 1/2, 1/2, 1/2), r = 100, θ = π/3) to obtain the cipher image in Fig. 5(a) and then we encrypted Arch image by making a little change with θ = π/2.99999999 again and got the cipher image in Fig. 5(b). We drew the differential image between Fig. 5(a) and Fig. 5(b), i.e., Fig. 5(c). By calculation, we got the difference between Figs. 5(a) and 5(b) is 99.6124267578125%, which implies the encryption process is quite sensitive to the encryption key. Moreover, the NPCR and UACI between cipher images with slightly different keys are calculated in the second and third columns of Supplementary Table S8 online. It can be seen that the average of NPCR and UACI is 0.9965778100586 and 0.3357151989507, respectively, higher than the one in Ref. 56. It implies that the encryption process is highly sensitive to the encryption key.
Key sensitivity tests.
(a) Arch image is encrypted with the key (n = 5, (α, β, χ, δ) = (1/2, 1/2, 1/2, 1/2), r = 100, θ = π/3) to obtain the cipher image in (a); (b) Arch image is encrypted by making a little change with θ = π/2.99999999 again to get the cipher image in (b); (c) The differential image between (a) and (b) is drawn in (c); (d) The cipher image of (a) is decrypted with the correct decryption key to obtain the correct original image in (d); (e) The cipher image of (a) is decrypted again with the decryption key with a little change of θ = π/2.99999999to obtain the image in (e). (see text in the section entitled Results). We acknowledge Qing-Xiang Pan who took the Arch image in Supplementary Fig. S1(a) online and all figures in Fig. 5 were obtained by simulations using Matlab software by Qing-Xiang Pan.
To verify the high sensitivity to the decryption key, we first decrypted the cipher image of Fig. 5(a) with the correct decryption key to obtain the correct original image (see Fig. 5(d)) and then we decrypted the cipher image of Fig. 5(a) again with the decryption key with a little change of θ = π/2.99999999 to obtain the image in Fig. 5(e). We calculated out the difference between Fig. 5(d) and Fig. 5(e) is 99.5590209960938%. Therefore, the decryption process is also highly sensitive to the decryption key. To sum up, our algorithm can provide a high key sensitivity.
Plaintext sensitivity means that a little change in the plaintext image can cause a large change in the cipher image. Firstly, we encrypted a plaintext image to generate a cipher image. Secondly, we randomly selected a pixel in the same plaintext image to let its pixel value plus one. Thirdly, we encrypted the modified plaintext image by using the same encryption key to generate another encrypted image. Finally, the NPCR and UACI between the two resulting cipher images with only one pixel difference in their respective original images were calculated in Supplementary Table S8 online respectively. As shown in the fourth and fifth columns, we can see that the average of NPCR is over 99.65% and that of UACI is over 33.52%, which are higher than the ones in Ref. 56. This also implies that our proposed scheme have a good ability to resist differential attack.
Discussion
In this paper, we investigated the potential application of QW in image encryption. It is found that QW can serve as an excellent key generator thanks to its inherent nonlinear chaotic dynamic behavior. Compared with previous works, our QW-based proposal has the following features:
-
It has not only the same merits as chaos' systems like high sensitivity to initial values and system parameters, unpredictability, pseudo-randomness, but also the different advantages like stability and non-periodicity.
-
The infinite possibilities of the coin states make the QW own an ability of producing a theoretically infinite key space to resist brute-force attacks.
-
It also opens the door towards introducing quantum computation into image encryption and promotes the convergence between quantum computation and image processing.
Although our QW-based algorithm has some advantages over other algorithms, our proposal also has some shortcomings in terms of the encryption speed. That is, the encryption speed of the proposed algorithm is not fast compared to other competitive algorithms. So our future work will focus on the improvement of the proposed algorithm.
Methods
One-dimensional two-particle discrete QW algorithm on a circle of n nodes
There is a one-dimensional two-particle discrete QW on a circle of n nodes defined as follows. We choose the quantum coin operators  ,
,  and an initial state of the total quantum system
and an initial state of the total quantum system

Here

where |α|2 + |β|2 + |χ|2 + |δ|2 = 1. We define  and
and  . The difference between a line and a circle is that the circle has only n nodes and is cyclical. The difference of walks on the line and on circles is that the operators
. The difference between a line and a circle is that the circle has only n nodes and is cyclical. The difference of walks on the line and on circles is that the operators  and
and  of two-particle QW on circles becomes
of two-particle QW on circles becomes

Here  is similar to
is similar to  .
.
Here we let

The initial value of the QW, i.e., (n, (α, β, χ, δ), r, θ) are tunable parameters. By running the one-dimensional two-particle discrete QW on a circle of n nodes, QW is capable of producing chaotic behavior as the value of (n, (α, β, χ, δ), r, θ) changes.
References
Akhshani, A., Akhavan, A., Lim, S.-C. & Hassan, Z. An image encryption scheme based on quantum logistic map. Commun. Nonlinear Sci. Numer. Simulat. 17, 4653–4661 (2012).
Huang, X. L. & Ye, G. D. An efficient self-adaptive model for chaotic image encryption algorithm. Commun. Nonlinear Sci. Numer. Simulat. 19, 4094–4104 (2014).
Abd El-Latif Ahmed, A., Li, L., Wang, N., Han, Q. & Niu, X. M. A new approach to chaotic image encryption based on quantum chaotic system, exploiting color spaces. Signal Process. 93, 2986–3000 (2013).
Yang, Y.-G., Xia, J., Jia, X. & Zhang, H. Novel image encryption/decryption based on quantum Fourier transform and double phase encoding. Quantum Inf. Process. 12, 3477–3493 (2013).
Matthews, R. On the derivation of a ‘chaotic’ encryption algorithm. Crypt. 13, 29–42 (1989).
Li, C., Li, S. & Lo, K. T. Breaking a modified substitution–diffusion image cipher based on chaotic standard and logistic maps. Commun. Nonlinear Sci. Numer. Simulat. 16, 837–843 (2011).
Rhouma, R. & Belghith, S. Cryptanalysis of a new image encryption algorithm based on hyper chaos. Phys. Lett. A 372, 5973–5978 (2008).
Wong, K. W., Kwok, B. S. H. & Law, W. S. A fast image encryption scheme based on chaotic standard map. Phys. Lett. A 372, 2645–2652 (2008).
Patidar, V., Pareek, N. K. & Sud, K. K. A new substitution–diffusion based image cipher using chaotic standard and logistic maps. Commun. Nonlinear Sci. Numer. Simulat. 14, 3056–3075 (2009).
Gao, T. & Chen, Z. A new image encryption algorithm based on hyper-chaos. Phys. Lett. A 372, 394–400 (2008).
Schack, R. & Caves, C. M. Hypersensitivity to perturbations in the quantum baker's map. Phys. Rev. Lett. 71, 525–528 (1993).
Schack, R., D'Ariano, G. M. & Caves, C. M. Hypersensitivity to perturbation in the quantum kicked top. Phys. Rev. E 50,972–987 (1994).
Schack, R. & Caves, C. M. Chaos for Liouville probability densities. Phys. Rev. E 53, 3387–3401 (1996).
Refregier, P. & Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 20,767–769 (1995).
Qin, W. & Peng, X. Vulnerability to known-plaintext attack of optical encryption schemes based on two fractional Fourier transform order keys and double random phase keys. J. Opt. A 11, 075402 (2009).
Carnicer, A., Montes-Usategui, M., Arcos, S. & Juvells, I. Vulnerability to chosen-ciphertext attacks of optical encryption schemes based on double random phase keys. Opt. Lett. 30,1644–1646 (2005).
Peng, X., Wei, H. & Zhang, P. Chosen-plaintext attack on lensless double-random phase encoding in the Fresnel domain. Opt. Lett. 31, 3261–3263 (2006).
Guo, Q., Liu, Z. J. & Liu, S. T. Color image encryption by using Arnold and discrete fractional random transforms in IHS space. Opt. Las. Engineering 48, 1174–1181 (2010).
Chen, W., Quan, C. & Tay, C. J. Optical color image encryption based on Arnold transform and interference method. Opt. Commun. 282, 3680–3685 (2009).
Bourbakis, N. & Alexopoulos, C. Picture data encryption using SCAN pattern. Pattern Recogn. 25, 567–581 (1992).
Liu, Z. J., Guo, Q., Xu, L., Ahmad, M. A. & Liu, S. T. Double image encryption by using iterative random binary encoding in gyrator domains. Opt. Exp. 18, 12033–12043 (2010).
Chang, C. C., Hwang, M. S. & Chen, T. S. A new encryption algorithm for image cryptosystems. J. Syst. Soft. 58, 83–91 (2001).
Chang, H. K. L. & Liu, J. L. A linear quad tree compression scheme for image encryption. Signal Process. 10, 279–290 (1997).
Cheng, H. & Li, X. B. Partial encryption of compressed image and videos. IEEE Trans. Signal Process. 48, 2439–2451 (2000).
Scharinger, J. Fast encryption of image data using chaotic Kolmogorov flow. J. Elect. Engineering 7, 318–325 (1998).
Shen, J. B., Jin, X. G. & Zhou, C. A color image encryption algorithm based on magic cube transformation and modular arithmetic operation. Adv. Multimedia Inf. Process. 3768, 270–280 (2005).
Yang, Y.-G., Jia, X., Sun, S. J. & Pan, Q. X. Quantum cryptographic algorithm for color images using quantum Fourier transform and double random-phase encoding. Inf. Sci. 277, 445–457 (2014).
Kimble, H. J. The quantum internet. Nature (London), 453, 1023–1030 (2008).
Lou, D. C. & Sung, C. H. A steganographic scheme for secure communications based on the chaos and euler Theorem. IEEE Trans. Multimedia 6, 501–509 (2004).
Ambainis, A. Quantum walk algorithm for element distinctness. SIAM J. Comput. 37, 210–239 (2007).
Magniez, F., Santhaand, M. & Szegedy, M. Quantum algorithm for the triangle problem. SIAM J. Comput. 37, 413–424 (2007).
Li, Q., He, Y. & Jiang, J.-P. A hybrid classical-quantum clustering algorithm based on quantum walks. Quantum Inf. Process. 10,13–26 (2011).
Elías V.-Andraca, S. Quantum walks: a comprehensive review. Quantum Inf. Process. 11, 1015–1106 (2012).
Kempe, J. Quantum random walks—an introductory overview. Contemp. Phys. 44, 307–327 (2003).
Shapira, D., Biham, O., Bracken, A. J. & Hackett, M. One-dimensional quantum walk with unitary noise. Phys. Rev. A 68, 062315 (2003).
Blanchard, P. & Hongler, M.-O. Quantum random walks and piecewise deterministic evolutions. Phys. Rev. Lett. 92, 120601 (2004).
López-Ruiz, R., Mancini, H. L. & Calbet, X. A statistical measure of complexity. Phys. Lett. A 209, 321–326 (1995).
Lamberti, P. W., Martin, M. T., Piastino, A. & Rosso, O. A. Intensive entropy non-triviality measure. Physica A 334, 119–131 (2004).
Rosso, O. A., Larrondo, H. A., Martin, M. T., Plastino, A. & Fuentes, M. A. Distinguishing noise from chaos. Phys. Rev. Lett. 99, 154102 (2007).
Eckmann, J. P., Oliffson Kamphorst, S. & Ruelle, D. Recurrence plots of dynamical systems. Europhys. Lett. 4, 973–977 (1987).
Marwan, N., Romano, M. C., Thiel, M. & Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 438, 237–329 (2007).
Shiner, J. S., Davison, M. & Landsberg, P. T. Simple measure for complexity. Phys. Rev. E 59,1459–1464 (1999).
Martin, M. T., Plastino, A. & Rosso, O. A. Statistical complexity and disequilibrium. Phys. Lett. A 311,126–132 (2003).
Larrondo, H. A., González, C. M., Martin, M. T., Plastino, A. & Rosso, O. A. Intensive statistical complexity measure of pseudorandom number generators. Physica A 356, 133–138 (2005).
Bandt, C. & Pompe, B. Permutation Entropy: A natural complexity measure for time series. Phys. Rev. Lett. 88, 174102 (2002).
Marwan, N., Wessel, N., Meyerfeldt, U., Schirdewan, A. & Kurths, J. Recurrence plot based measures of complexity and its application to heart rate variability data. Phys. Rev. E 66, 026702 (2002).
Zbilut, J. P. & Webber, C. L. Embeddings and delays as derived from quantification of recurrence plots. Phys. Lett. A 171, 199–203 (1992).
Webber, C. L. & Zbilut, J. P. Dynamical assessment of physiological systems and states using recurrence plot strategies. J. Appl. Physiol. 76, 965–973 (1994).
Benítez, R., Bolós, V. J. & Ramírez, M. E. A wavelet-based tool for studying non-periodicity. Comput. Math. Appl. 60, 634–641 (2010).
Akhshani, A., Akhavan, A., Mobaraki, A., Lim, S.-C. & Hassan, Z. Pseudo random number generator based on quantum chaotic map. Commun. Nonlinear Sci. Numer. Simulat. 19, 101–111 (2014).
Mallat, S. A wavelet tour of signal processing. Academic Press London (1999).
Chandre, C., Wiggins, S. & Uzer, T. Time-frequency analysis of chaotic systems. Physica D 181,171–196 (2003).
Zhu, C. X. A novel image encryption scheme based on improved hyper chaotic sequences. Opt. Commun. 285, 29–37 (2012).
Ye, G. D. & Zhou, J. W. A block chaotic image encryption scheme based on self-adaptive modelling. Appl. Soft Comput. 22, 351–357 (2014).
L'Ecuyer, P. & Simard, R. J. TestU01: A C library for empirical testing of random number generators. ACM Trans. Math. Soft. 33, 22 (2007).
Borujeni, S. E. & Eshghi, M. Chaotic image encryption system using phase-magnitude transformation and pixel substitution. Telecommun. Sys. 52, 525–537 (2013).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 61003290); Beijing Natural Science Foundation (Grant No. 4122008); The Importation and Development of High-Caliber Talents Project of Beijing Municipal Institutions (No.CIT&TCD201304039); National Cipher Development Fund during the 12th Five-Year Plan Period (No.MMJJ201401006); Postgraduate Science and Technology Innovation Foundation of Beijing University of Technology (No.ykj-2014-11167).
Author information
Authors and Affiliations
Contributions
Y.Y.G. proposed the theoretical method and wrote the main manuscript text. P.Q.X., S.S.J. and X.P. made the numerical simulations. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplemental materials
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Yang, YG., Pan, QX., Sun, SJ. et al. Novel Image Encryption based on Quantum Walks. Sci Rep 5, 7784 (2015). https://doi.org/10.1038/srep07784
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07784
This article is cited by
-
Entanglement entropy distinguishes PT-symmetry and topological phases in a class of non-unitary quantum walks
Quantum Information Processing (2023)
-
Contemporary Quantum Computing Use Cases: Taxonomy, Review and Challenges
Archives of Computational Methods in Engineering (2023)
-
Circuit implementation of discrete-time quantum walks via the shunt decomposition method
Quantum Information Processing (2023)
-
Toward implementing efficient image processing algorithms on quantum computers
Soft Computing (2023)
-
An image encryption scheme based on particle swarm optimization algorithm and hyperchaotic system
Soft Computing (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

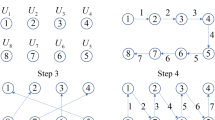
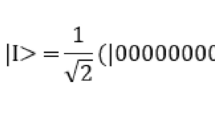



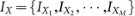 and
and  .
. , i.e.,
, i.e.,