Abstract
Quasi two-dimensional metasurfaces composed of subwavelength nanoresonator arrays can dramatically alter the properties of light in an ultra-thin planar geometry, enabling new optical functions such as anomalous reflection and refraction, polarization filtering and wavefront modulation. However, previous metasurface-based nanostructures suffer from low efficiency, narrow bandwidth and/or limited field-of-view due to their operation near the plasmonic resonance. Here we demonstrate plasmonic metasurface-based nanostructures for high-efficiency, angle-insensitive polarization transformation over a broad octave-spanning bandwidth. The structures are realized by optimizing the anisotropic response of an array of strongly coupled nanorod resonators to tailor the interference of light at the subwavelength scale. Nanofabricated reflective half-wave and quarter-wave plates designed using this approach have measured polarization conversion ratios and reflection magnitudes greater than 92% over a broad wavelength range from 640 to 1290 nm and a wide field-of-view up to ±40°. This work outlines a versatile strategy to create metasurface-based photonics with diverse optical functionalities.
Similar content being viewed by others
Introduction
Optical metasurfaces are a new class of quasi two-dimensional metamaterials composed of a single layer of metallic nanostructures that provide exceptional capabilities for manipulating light in an ultrathin, planar platform1,2,3. In comparison to their three-dimensional counterparts, metasurfaces also exhibit reduced loss and fabrication complexity, making them attractive for integration in practical optical systems4. By engineering the geometry of the nanostructured metasurfaces, the spectral and spatial dispersion of their optical response can be tailored to generate a specific abrupt interfacial phase change and cross-polarized response on a subwavelength scale. Such unique optical properties have been exploited to demonstrate a variety of new physical phenomena and associated optical devices over the past few years, including anomalous reflection and refraction5,6,7,8, optical wavefront manipulation9,10,11, frequency-selective near-perfect absorption12,13,14, spin-hall effect of light15,16, spin-controlled photonics17, polarization-dependent unidirectional surface plasmon polariton excitation18,19 and metasurface holograms20,21.
Optical waveplates that achieve broadband polarization conversion with a wide field-of-view (FOV) are highly desirable for systems that perform optical characterization, sensing and communications functions22. However, simultaneously achieving broadband and wide-angle properties is difficult using conventional multilayer stacks of birefringent materials because these structures rely on the dispersive properties of the birefringence. In contrast, metasurfaces provide a promising pathway towards broadband and wide-angle polarization conversion in a submicron-thick layer. A variety of optically thin, metasurface-based polarization-control components have been theoretically proposed and demonstrated, including various polarizers23,24, near-field polarization shapers25 and ultrathin waveplates26,27,28,29,30,31,32,33,34.
Most metasurface-based waveplates have employed homogenous arrays of weakly coupled anisotropic resonant building blocks, including crossed nanodipoles24,26 and nanoslits27,28,29, L-shaped30 or V-shaped31 nanoantennas and elliptical nanoholes32. These structures typically suffer from a narrow FOV, limited bandwidth, and/or low efficiency because their anisotropic optical response relies on the resonance of each isolated building block, where strong dispersion and impedance mismatch may exist. More recently, a near-infrared (IR) quarter-wave plate achieved broadband circular-to-linear polarized light conversion by tailoring the dispersive properties of an array of orthogonally coupled nanodipole elements. However, the waveplate had an average power efficiency of less than 50%33. In addition, to obtain broadband circularly polarized transmitted light from this design, incident linearly polarized light with a wavelength-dependent electric field polarization direction was required. An alternative inhomogeneous metasurface design strategy has also been used to produce an ultrathin broadband quarter-wave plate34. The demonstrated design achieves a power efficiency of only 10% over a narrow FOV and has a wavelength-dependent directivity of the outgoing polarization.
In this paper, we demonstrate wide-angle reflective plasmonic metasurface-based half-wave and quarter-wave plates that have a high polarization conversion efficiency and reflection magnitude over a broad bandwidth in the visible-to-near IR wavelength range. This is achieved by optimizing the anisotropic optical response of the metasuface, which is composed of an array of strongly coupled nanorod resonator building blocks with controlled aspect ratio, to tailor the spectral dispersion of light interference between the metasurface and a metallic reflector. In contrast to previously reported metasurface waveplates, the anisotropic optical response and light interference are controlled across the broad wavelength range and wide-FOV rather than merely near the resonant wavelength of the metasurface building blocks. Both the nanofabricated half-wave and quarter-wave plates achieved measured polarization conversion ratios (PCRs) higher than 92% over more than an octave bandwidth from 640 nm to 1290 nm with a wide field-of-view of ±40°. This work represents a new state-of-the-art for optical metasurface-based devices and will enable other types of ultrathin optical components with broad operational bandwidth, wide FOV and high efficiency.
Results
Structure and operation of reflective plasmonic metasurface-based waveplate
Figure 1a shows a simplified schematic of our metasurface-based waveplate that is used for simulation. The multilayer structure comprises a top homogeneous anisotropic metasurface, an intermediate silicon dioxide (SiO2) layer separated from the metasurface by a subwavelength air spacer and a bottom continuous gold (Au) layer. The metasurface is characterized by uniaxial surface polarizability tensors  and
and  35. Because the metasurface has no magnetic component and is modelled as an infinitely thin sheet, the surface polarizability tensors can be simplified to
35. Because the metasurface has no magnetic component and is modelled as an infinitely thin sheet, the surface polarizability tensors can be simplified to  and
and  . The air layers above and below the metasurface are included in the design to account for the small phase retardation present in the fabricated nanostructure that has a finite thickness of tm ≈ λ0/30. The value of the phase retardation can thus be approximated by
. The air layers above and below the metasurface are included in the design to account for the small phase retardation present in the fabricated nanostructure that has a finite thickness of tm ≈ λ0/30. The value of the phase retardation can thus be approximated by  .
.
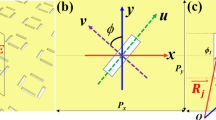
Schematics of the proposed plasmonic metasurface-based waveplates.
(a) 3D view of the multilayer structure model including an anisotropic homogenous metasurface located at a distance of tm/2 above the SiO2 layer. The metasurface is characterized by electric and magnetic surface polarizability tensors  and
and  . Optically thin strongly-coupled nanorod array is used to realize the metasurface. (b) Interference model for evaluating the optical response of the multilayer structure based on the surface polarizability tensor parameters of the metasurface.
. Optically thin strongly-coupled nanorod array is used to realize the metasurface. (b) Interference model for evaluating the optical response of the multilayer structure based on the surface polarizability tensor parameters of the metasurface.
The operating principle of the metasurface-based waveplate is illustrated in Figure 1b and resembles that of a modified Gires-Tournois (G-T) etalon36. Here, a plane wave with prescribed polarization illuminates the multilayer structure from an incident direction (θi, ϕi), where θi denotes the angle between the z-axis and  , while ϕi is the angle formed by the x-axis and the projection of
, while ϕi is the angle formed by the x-axis and the projection of  on the x-y plane. When the incident wave interacts with the multilayer structure, both s- and p-polarized reflected and transmitted waves are generated by the metasurface. The transmitted waves undergo multiple reflections between the metasurface and the bottom Au layer, where they interfere with one another to create the final reflected wave. Due to the anisotropy of the metasurface, both co-polarized and cross-polarized reflected waves are collected at the direction (θi, ϕi–180°). The dielectric spacer and the Au ground plane increase the design degrees of freedom for controlling the amplitudes and phases of the waves produced by the multiple reflections and thus can be optimized to increase the bandwidth of the anisotropic reflection from the three-layer nanostructure. The complex reflection coefficients that describe the polarization-dependent optical response of this structure (rss, rsp = rps and rpp) can be calculated analytically using an interference model37 (details available in Supplementary Information, Eq. S1a to S1d). By tailoring the dispersive anisotropy of the metasurface as well as the interference of the s- and p-polarized wave components, the polarization state of the final reflected wave is controlled over a broad spectral and wide angular range.
on the x-y plane. When the incident wave interacts with the multilayer structure, both s- and p-polarized reflected and transmitted waves are generated by the metasurface. The transmitted waves undergo multiple reflections between the metasurface and the bottom Au layer, where they interfere with one another to create the final reflected wave. Due to the anisotropy of the metasurface, both co-polarized and cross-polarized reflected waves are collected at the direction (θi, ϕi–180°). The dielectric spacer and the Au ground plane increase the design degrees of freedom for controlling the amplitudes and phases of the waves produced by the multiple reflections and thus can be optimized to increase the bandwidth of the anisotropic reflection from the three-layer nanostructure. The complex reflection coefficients that describe the polarization-dependent optical response of this structure (rss, rsp = rps and rpp) can be calculated analytically using an interference model37 (details available in Supplementary Information, Eq. S1a to S1d). By tailoring the dispersive anisotropy of the metasurface as well as the interference of the s- and p-polarized wave components, the polarization state of the final reflected wave is controlled over a broad spectral and wide angular range.
Anisotropic optical response of the metasurface nanorod building blocks
The desired anisotropic homogenous metasurface can be realized using a single-layer metallic nanoresonator array provided that its periodicity is much smaller than the wavelength of interest3. As shown in Figure 1a, we employed a 2D array of Au nanorod building blocks with strong inter-element coupling because the dimensions and inter-element spacing of this simple geometry can be: (1) optimized to provide a widely varying anisotropic response and (2) scaled to fabricate devices that operate at visible wavelengths. Before designing nanorod-based metasurfaces with the uniaxial surface polarizability properties required for our quarter-wave and half-wave plate devices, the optical properties of both isolated and strongly coupled pairs of Au nanorods were determined for a normally incident linearly polarized wave with its electric field either parallel or perpendicular to the long axis of the rod (Fig. 2a).
Anisotropic scattering of single and coupled nanorod pair.
(a) Schematics of an incident x- and y-polarized wave at normal incidence illuminating a single nanorod or a pair of coupled nanorods. The dimensions are ax = 250, ay = 75, tm = 30, g = 20 (all in nm). (b) Electric field distribution on the single nanorod at 930 and 550 nm and electric field distribution on the coupled nanorod at 1125 and 550 nm. (c) Scattering field magnitudes (normalized) and phases of the single (top) and twin (bottom) nanorod. (d) Dispersion of Δφ showing the impact of nanorod length (ax), nanorod aspect ratio (ay/ax) and gap size (g).
Figure 2c plots the calculated amplitude (normalized) and phase of the scattered light from a single nanorod with a length ax = 250 nm, a width-to-length aspect ratio ay/ax = 0.3 and a thickness tm = 30 nm as well as a strongly coupled pair of nanorods with an inter-element gap g = 20 nm. The electric fields are concentrated at the ends of the isolated nanorod (Fig. 2b), resulting in an x-directed dipolar resonance at 930 nm with a scattering phase of around 90°. The localized surface plasmon polariton (LSPP) mode causes the nanorod to resonate at a wavelength much larger than twice its length. In contrast, for a pair of strongly coupled nanorods, the enhanced electric fields are effectively confined within the air gap between the two rods (Fig. 2b). The capacitance formed in the air gap between the nanorods is much larger than the capacitance at the two ends of each individual nanorod38, resulting in an x-directed LSPP dipolar resonance occurring at 1125 nm, which is only 21% larger than the resonating wavelength of the single nanorod. This resonance also has a lower quality factor as demonstrated by the flatter phase response. For the mode corresponding to y-polarized incident light, the single and paired nanorod elements exhibit a similar response. Specifically, both have a dipolar resonance at 550 nm with a weaker strength and a phase slightly larger than 90° due to the inertia of the electrons at high frequencies and the finite cross section of the nanorods39.
For the nanorod structure in Fig. 2a, the anisotropic scattering behavior causes a large phase difference over the broad wavelength region between the two orthogonally polarized resonating modes even at oblique angles of incidence (see Supplementary Information, Fig. S2 and Fig. S3), which provides a percentage bandwidth of 62% for phase difference Δφ > 90° and 39% for Δφ > 135°. This is central to achieving broadband metasurface-enabled polarization transformations. To understand the effect of the nanorod structure on the phase of the scattered light, we first evaluated the phase difference as the length (ax) and aspect ratio (ay/ax) of a single isolated rod was varied with all other parameters remaining unchanged. As shown in Fig. 2d, increasing the length and decreasing the aspect ratio both broaden the bandwidth of the large Δφ region, which is indicative of the degree of scattering anisotropy. For the strongly coupled nanorod pair, the data in Fig. 2d also demonstrates that the bandwidth of Δφ increases exponentially as the air gap size drops due to the large increase in air gap capacitance of the structure. It should be noted that even though the nanorod building block has a wavelength-dependent scattering magnitude, all of the incident waves will be reflected by the bottom solid Au layer. By designing the nanostructure such that it is operating away from its absorption band, the reflection magnitude for both polarizations will possess a flat response.
Most previously demonstrated plasmonic metasurfaces1,2,3 have been designed by optimizing the geometry of the single isolated resonant building block. This investigation reveals that strong inter-element coupling plays a critical role in controlling the scattering phase difference for achieving the tailored anisotropic optical dispersion required for broadband, low-loss performance. As discussed in the following sections, the bandwidth broadening due to inter-element coupling can be further enhanced when the strongly coupled nanorods are arranged in a 2D array.
Optimized broadband and wide-angle metasurface-based half-wave plate
Broadband and wide-angle plasmonic metasurface-based waveplates can be efficiently designed by using the interference model of the multilayer structure and the optical properties of the strongly coupled nanorod array. As a proof-of-concept, here we consider a half-wave plate covering a wide-FOV up to ±40° in the wavelength range from 640 to 1290 nm using the three-layer Au-SiO2-Au nanostructure shown in Fig. 3a, which transforms an s-polarized incident wave from a propagation direction of (θi, ϕi = 135°) into a p-polarized reflected wave at a propagation direction of (θi, ϕi = −45°). During the design process, the effective polarizability tensors  and
and  of the anisotropic nanorod array metasurface were retrieved using the complex transmission and reflection coefficients for both polarizations at two angles of incidence (see Supplementary Information). The extracted effective surface polarizabilities were then used in the interference model to calculate the complex reflection coefficients (rps, rss) of the entire nanostructure over a wide angular range. In contrast to most of the previous observations and explanations of multilayer metallodielectric nanostructures in which magnetic resonances are identified40,41, here it is found that the near-field interaction between the nanorod array and the continuous Au ground layer is weak enough to be neglected. Consequently, the interference model, which is more efficient in terms of the computation time, can be applied even though the dielectric layer thickness is on a subwavelength scale42.
of the anisotropic nanorod array metasurface were retrieved using the complex transmission and reflection coefficients for both polarizations at two angles of incidence (see Supplementary Information). The extracted effective surface polarizabilities were then used in the interference model to calculate the complex reflection coefficients (rps, rss) of the entire nanostructure over a wide angular range. In contrast to most of the previous observations and explanations of multilayer metallodielectric nanostructures in which magnetic resonances are identified40,41, here it is found that the near-field interaction between the nanorod array and the continuous Au ground layer is weak enough to be neglected. Consequently, the interference model, which is more efficient in terms of the computation time, can be applied even though the dielectric layer thickness is on a subwavelength scale42.
Broadband and wide-angle plasmonic metasurface-based half-wave plate.
(a) Tilted 3D view of the metasurface-based half-wave plate. An s-polarized wave incident from an angle of (θi, ϕi = 135°) is converted into a p-polarized wave upon reflection. Inset shows the side view of the nanostructure and light path. (b) Unit cell configuration of the optimized half-wave plate. The dimensions are ax = 210, ay = 70, px = 252, py = 252, tm = 42, td = 114, tm2 = 100 (all in nm). (c) Top-view FESEM image of a portion of the fabricated nanostructure showing the nanorod array. Scale bar: 400 nm. The inset shows the magnified top view of two by three unit cells. Scale bar: 100 nm. (d) Theoretically predicted and experimentally measured polarization conversion ratio (PCR) and reflection magnitude (Refl. Mag.) as a function of wavelength at different angles of incidence (4°, 20°, 40°). (e) Theoretically predicted and experimentally measured polarization state in the plane perpendicular to the wave vector at 700, 900 and 1150 nm for different angles of incidence (4°, 20°, 40°).
A powerful covariance matrix adaptation evolutionary strategy (CMA-ES) optimization technique43 was employed to identify the nanostructure dimensions that meet the challenging multi-objective half-wave plate design criteria, i.e. highly-efficient polarization conversion spanning a wide spectral and angular range44. Predefined constraints on the allowable unit cell size, nanorod length and width, as well as the thickness of metal and dielectric layers were incorporated into the optimization algorithm to avoid generating structures that are impractical to fabricate. Additionally, experimentally measured dispersive optical properties for the constituent metal and dielectric materials were used to minimize discrepancies between the theoretically predicted and experimentally fabricated nanostructure response45.
For each design candidate, the calculated reflection coefficients for both polarizations (rps, rss) in the targeted wavelength and angular range are compared with the user-input-defined target values to determine the Cost, which is expressed as:

where λ and θi denote the wavelength and incident angles included in the optimization. For this work, we selected wavelengths from 640 to 1290 nm in steps of 50 nm and angles from 0° to 40° in steps of 10°. The CMA-ES evolved solutions until it converged on a three-layer metal-dielectric nanostructure with a sufficiently low overall Cost value that achieved the desired half-wave plate optical properties. The optimized geometry of the structure that meets these design criteria is shown in Figs. 3a and 3b. The Au nanorods have a length of 210 nm and a width of 70 nm, which corresponds to an aspect ratio of 0.33. The periodicity in both the x- and y-directions is 252 nm, giving an inter-element gap of 42 nm in the x-direction, which provides strong electromagnetic coupling to the neighboring nanorods. The thickness values for the top Au nanorod array layer, the SiO2 layer and the bottom Au layer are 42 nm, 114 nm and 100 nm, respectively, resulting in a structure that is only 256 nm thick.
The polarization conversion ratio (PCR) of the metasurface-based half-wave plate was calculated using the semi-analytical interference model, defined as:

As shown by the theoretical curves plotted in Fig. 3d, the calculated PCRhwp is greater than 94% across the targeted broad wavelength and wide angular range and remains above 90% over a wider band from 640 to 1400 nm. Throughout this spectral and angular range, the reflection magnitude is greater than 95%, thereby achieving a much higher power efficiency than previous plasmonic metamaterial and metasurface-based designs3,4,23,33,34,46. Even for angles of incidence as large as 50°, the reflection magnitude of the nanostructure is maintained above 94% with a PCRhwp of greater than 83% (see Fig. S6). Notably, this example demonstrates that the bandwidth of the 2D array of strongly coupled nanorods is significantly wider than that of the freestanding pairs of nanorods (Fig. 2c–d).
For the optimized 2D nanorod array structure, at large incident angles, the in-band PCRhwp is limited by: (1) the higher quality factors of two resonant peaks that correspond to the x- and y-directed LSPP dipolar modes of the coupled Au nanorods; and (2) the increase in phase retardation in the dielectric spacer. As a result, in the spectral range bracketed by the two modes, the reflection phase difference between the x- and y-directed electric field components exceeds 180° for incident angles greater than 40°. This causes the observed decrease in the PCRhwp near the middle of the band between the resonant peaks, which restricts the FOV for >90% PCRhwp to approximately ±40°.
The state of polarization (SOP) traces of the incident and reflected light are presented in Fig. 3e at several angles of incidence and wavelengths within the band. Clearly defined cosine-shaped patterns can be identified, indicating that the reflected wave possesses a high degree of linear polarization (DoLP). The SOP patterns of the incident light have their maxima along the −90°/90° directions, while the SOP patterns of the reflected light have their maxima along the 0°/180° directions. The 90° rotation over the broad spectral and wide angular range confirms that the optimized plasmonic metasurface-based half-wave plate indeed transforms a linearly polarized incident wave into a reflected wave with a cross polarization.
Experimental realization and characterization
The optimized plasmonic metasurface-based half-wave plate was fabricated using conventional top-down lithography. Briefly, the process began by depositing the bottom continuous Au layer and the SiO2 layer on a Si handle wafer. The structure was completed by defining the topmost periodic nanorod array using electron-beam lithography followed by a Au lift-off process (see Methods for details). Field emission scanning electron microscope (FESEM) images of the fabricated nanostructure are shown in Fig. 3c. The measured dimensions of Au nanorod length, width and minimum inter-element gap spacing are 210 ± 5 nm, 70 ± 3 nm and 42 ± 4 nm. The lithographic process produces nanorods that have rounded corners, which results in effective electromagnetic gap spacing of 50 ± 2 nm. The PCRhwp and reflection magnitude of the fabricated structure was characterized using a custom-built optical setup (see Fig. S8) that utilizes a supercontinuum source to illuminate the structure at incident angles of 4°, 20° and 40° (see Methods). The strong peak in the power spectrum of the source at 1064 nm (the pump wavelength used to generate the supercontinuum) introduces significant measurement error; thus, data collected in the wavelength range between 1040 and 1080 nm are excluded from the plots.
The optical properties of the fabricated metasurface-based half-wave plate shown in Fig. 3d–e are in strong agreement with theoretical predictions. The measured PCRhwp and reflection magnitude both remain above 92% over the targeted broad wavelength range from 640 to 1290 nm and wide-FOV from 0° to 40°. Even at a larger 50° angle of incidence, the PCRhwp and reflection magnitude are still 86% and 87%, respectively (see Fig. S6). In comparison to the design, the long-wavelength cut-off for the 90% PCRhwp bandwidth at a 4° incident angle is blue-shifted from 1400 to 1330 nm without a change in the short-wavelength cutoff. This small discrepancy is attributed to the wider inter-rod gap spacing in the fabricated structure compared to the optimized design dimensions. This is consistent with the trend found in the freestanding nanorod pair scattering analysis in Fig. 2c–d, which shows a blue shift in the x-directed LSPP dipolar resonance without affecting the y-directed dipolar resonance as the gap increases.
Polarization conversion is experimentally verified by the measured SOP patterns shown in Fig. 3e. The cosine-shaped patterns confirm the high DoLP of the reflected light. In addition, the angle between the maxima of the reflected and incident light patterns is 90° throughout the entire wavelength band and 40° FOV, indicating that the maximum light is reflected from the sample when the polarizers for the incident and reflected light are oriented orthogonally to each other. Compared to the current experimentally demonstrated plasmonic metasurface-based polarization-control devices, the nanorod array half-wave plate presented here achieves a high power efficiency over a wide spectral and angular range.
Demonstration of a metasurface-based quarter-wave plate
To show the versatility of the proposed platform and design approach, a metasurface-based quarter-wave plate was also optimized for the same spectral range of 640 to 1290 nm and wide-FOV from 0 to 40°. The three-layer structure shown in Fig. 4a transforms a circularly polarized incident wave from a direction (θi, ϕi = 180°) into a linearly polarized reflected wave at a direction (θi, ϕi = 0°), which provides an in-phase superposition of both the s- and p-polarizations. One unit cell of the optimized doubly periodic array is composed of 180 nm long and 70 nm wide Au nanorods that are centered within the 240 nm × 282 nm cell. This array structure possesses a weaker degree of anisotropy compared to the half-wave plate because of the larger nanorod aspect ratio of 0.5 and wider inter-element gap of 60 nm. As plotted in Fig. 4d, the simulated PCRqwp is greater than 90% over a wider than targeted wavelength range from 620 to 1500 nm for incident angles up to 50° (see Fig. S7). The reflection magnitude is greater than 93% across the targeted spectral and angular range except for a narrow dip near 680 nm. The SOP traces presented in Fig. 4e show that the nanostructure transforms the incident wave with a circular SOP pattern into a reflected wave with a cosine pattern that has a maximum along the 45°/225° direction.
Broadband and wide-angle plasmonic metasurface-based quarter-wave plate.
(a) Tilted 3D view of the metasurface-based quarter-wave plate. A circularly-polarized wave incident from an angle of (θi, ϕi = 0°) is converted into a linearly-polarized wave upon reflection. Inset shows the polarization of the reflected and incident waves in the plane perpendicular to the wave vector. The angle between the electric field and the plane of incidence of the reflected light is 45°. (b) Unit cell configuration of the optimized quarter-wave plate. The dimensions are ax = 180, ay = 90, px = 240, py = 282, tm = 40, td = 150, tm2 = 100 (all in nm). (c) Top-view FESEM image of a portion of the fabricated nanostructure showing the nanorod array. Scale bar: 400 nm. The inset shows the magnified top view of two by three unit cells. Scale bar: 100 nm. (d) Theoretically predicted and experimentally measured polarization conversion ratio (PCR) and reflection magnitue (Refl. Mag.) as a function of wavelength at different angles of incidence (4°, 20°, 40°). (e) Theoretically predicted and experimentally measured polarization state in the plane perpendicular to the wave vector at 700, 900 and 1150 nm for different angles of incidence (4°, 20°, 40°).
Figure 4c displays FESEM images of the nanofabricated quarter-wave plate. The measured dimensions of the Au nanorod length, width and minimum inter-element gap spacing are 180 ± 6 nm, 90 ± 4 nm and 60 ± 5 nm, which agree well with the design target. Similar to the quarter-wave plate, the rounded nanorod edges result in an effective gap of 68 ± 3 nm that is wider than the design target. During the characterization process, a commercial quarter-wave plate was used to generate circularly polarized incident light (see Fig. S8). As shown in Fig. 4d, the measured PCRqwp is greater than 91% within the targeted wavelength band and angular range, with the reflection magnitude higher than 92%. The reduced PCRqwp value in the long wavelength range can be attributed to the imperfect circular polarization of the incident wave above 1300 nm, which is outside of the operational band of the commercial quarter-wave plate. The measured SOP patterns are in strong agreement with the simulated predictions, indicating that the circularly polarized incident wave is effectively converted to a linearly polarized reflected wave.
Discussion
In conclusion, we have demonstrated a versatile approach to create highly efficient, wide-FOV plasmonic metasurface-based waveplates that control the polarization response of light over more than an octave bandwidth from the visible to the near-IR. The ultrathin reflective waveplates are realized by tailoring the spectral phase properties of a strongly coupled anisotropic nanorod array in conjunction with the interference of light between the array and the ground plane. A half-wave plate and a quarter-wave plate were designed and fabricated, achieving a PCR and reflection magnitude higher than 92% over more than an octave bandwidth from 640 to 1290 nm within a wide field-of-view of ±40° for both devices. Beyond the two proof-of-concept waveplates, the general design approach presented in this work can be extended to nanostructured optical components that exhibit arbitrary polarization conversion properties, as well as other optical functionalities endowed by metasurfaces with engineered dispersion, over a broad wavelength and wide angular range.
Methods
Numerical full-wave simulations
The high frequency structure simulator (HFSS) (http://ansys.com/Products/Simulation+Technology/Electronics/Signal+Integrity/ANSYS+HFSS) finite element solver was used to perform all the full-wave simulations. For the scattering simulations of the single and coupled nanorod pair elements, the structures were placed in the center of an airbox whose outer edges were assigned a radiation boundary to prevent undesired reflections. The nanorod was oriented such that its long side coincides with the x-direction and its short side with the y-direction. Two linearly polarized plane waves, one x-polarized and the other y-polarized, were normally incident from the top surface of the nanorod elements. The scattered fields were evaluated at a distance of 3 μm below the bottom surface of the nanorod. The phase of the scattered fields was defined relative to that of the excitation when no nanorod elements are present. For the unit cell simulations of the three-layer metallodielectric waveplate and the metasurface on a SiO2 half space, periodic boundary conditions were assigned to the lateral walls of the simulation domain to approximate an infinite array. Floquet ports were then added on the top and bottom faces of the simulation domain to obtain the reflection and transmission coefficients of a plane wave illuminating the nanostructure at an arbitrary angle of incidence.
Device fabrication
The three-layer metallodielectric structures were fabricated by first depositing a 10 nm Ti adhesion layer and the bottom 100 nm Au ground plane on a Si handle wafer by electron-beam evaporation (Kurt J Lesker Lab18) at a rate of 1.4Å/s. A second 1 nm Ti adhesion layer was deposited immediately before electron-beam evaporating the SiO2 dielectric spacer layer (114 nm for the half-wave plate and 150 nm for the quarter-wave plate) at a rate of 1.4Å/s. The nanorod array pattern was defined by electron-beam lithography (Vistec EBPG 5200A). Specifically, a layer of ZEP520A positive electron-beam resist (ZEP520A, diluted with anisole 1 to 1) was spin coated on the SiO2 dielectric layer at 3000 rpm for 50 sec, baked at 180°C for 3 min and exposed with a 100 keV electron beam at a dose of 170 μC/cm2. After exposure, the nanorod features were developed in n-amyl-acetate for 3 min and MIBK:IPA = 8:1 for 1 min. A 1 nm Ti adhesion layer and the top Au layer (42 nm for the half-wave plate and 40 nm for the quarter-wave plate) were deposited at a rate of 1Å/s. The metal on top of the unexposed resist was lifted-off by dissolving the resist in Microposit 1165 Remover (Rohm & Haas). The thicknesses of the Au and SiO2 layers were verified with Atomic Force Microscopy (AFM, Bruker Icon). The optical properties of all of the constituent materials were characterized by spectroscopic ellipsometry (RC2® Ellipsometer, J.A. Woollam Co.) over the wavelength range of 240 to 1690 nm and used in the electromagnetic simulations.
Optical characterization
The broadband supercontinuum source was generated by coupling a sub-nanosecond Q-switched pulsed laser into a 20 m long highly-nonlinear photonics crystal fiber (PCF). A smooth intensity spectrum was maintained throughout the wavelength range of interest except for a very narrow band around 1064 nm where a strong peak from the pump wavelength exists. This narrow band was removed using a notch filter during post processing. To characterize the plasmonic metasurface-based half-wave plate, an s-polarized beam was produced by a polarizing beam splitter and used as the incident light source. The polarization state of the reflected light was characterized by rotating a broadband analyzer in steps of 10° (Glan-Thompson Calcite Polarizer, Newport 10GT04) in the plane perpendicular to the wave vector of the reflected light and detecting the transmitted power with an Optical Spectrum Analyzer (Ando, OSA AQ-6315A). The metasurface based quarter-wave plate was characterized by confining the long axis of the nanorod within the plane of incidence, i.e. the x-z plane in Fig. 4a. The circularly polarized incident light was provided by inserting a conventional broadband quarter-wave plate immediately after the polarization beam splitter and in front of the sample.
References
Kildishev, A. V., Boltasseva, A. & Shalaev, V. M. Planar photonics with metasurfaces. Science 339, 1232009 (2013).
Yu, N. & Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 13, 139–150 (2014).
Holloway, C. L. An overview of the theory and applications of metasurfaces: the two-dimensional equivalents of metamaterials. IEEE Antennas Propagat. Magazine 54, 10–35 (2012).
Soukoulis, C. M. & Wegener, M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photon. 5, 523–530 (2011).
Yu, N. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 334–337 (2011).
Ni, X., Emani, N. K., Kildishev, A. V., Boltasseva, A. & Shalaev, V. M. Broadband light bending with plasmonic nanoantennas. Science 335, 427 (2012).
Huang, L. et al. Dispersionless phase discontinuities for controlling light propagation. Nano Lett. 12, 5750–5755 (2012).
Sun, S. et al. High-efficiency broadband anomalous reflection by gradient meta-surfaces. Nano Lett. 12, 6223–6229 (2012).
Aieta, F. et al. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces. Nano Lett. 12, 4932–4936 (2012).
Ni, X., Ishii, S., Kildishev, A. V. & Shalaev, V. M. Ultra-thin, planar, Babinet-inverted plasmonic metalenses. Light Sci. Appl. 2, e27 (2013).
Pors, A., Nielsen, M. G., Eriksen, R. L. & Bozhevolnyi, S. I. Broadband focusing flat mirrors based on plasmonic gradient metasurfaces. Nano Lett. 13, 829–834 (2013).
Liu, N., Mesch, M., Weiss, T., Hentschel, M. & Giessen, H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 10, 2342–2348 (2010).
Jiang, Z. H., Yun, S., Toor, F., Werner, D. H. & Mayer, T. S. Conformal dual-band near-perfectly absorbing mid-infrared metamaterial coating. ACS Nano 5, 4641–4647 (2011).
Bossard, J. A., Lin, L., Yun, S., Liu, L., Werner, D. H. & Mayer, T. S. Near-ideal optical metamaterial absorbers with super-octave bandwidth. ACS Nano 8, 1517–1524 (2014).
Yin, X., Ye, Z., Rho, J., Wang, Y. & Zhang, X. Photonic spin-Hall effect at metasurfaces. Science 339, 1405–1407 (2013).
Shitrit, N., Bretner, I., Gorodetski, Y., Kleiner, V. & Hasman, E. Optical spin Hall effects in plasmonic chains. Nano Lett. 11, 2038–2042 (2011).
Shitrit, N. et al. Spin-optical metamaterial route to spin-controlled photonics. Science 340, 724–726 (2013).
Huang, L. et al. Helicity dependent directional surface plasmon polariton excitation using a metasurface with interfacial phase discontinuity. Light Sci. Appl. 2, e70 (2013).
Lin, J. et al. Polarization-controlled tunable directional coupling of surface plasmon polaritons. Science 340, 331–334 (2013).
Ni, X., Kildishev, A. V. & Shalaev, V. M. Metasurface holograms for visible light. Nat. Commun. 4, 2807 (2013).
Huang, L. et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 4, 2808 (2013).
Born, M. & Wolf, E. Principles of Optics, 6th edn (Cambridge University Press, 2002).
Zhao, Y., Belkin, M. A. & Alù, A. Twisted optical metamaterials for planarized ultrathin broadband circular polarizers. Nat. Commun. 3, 870 (2012).
Ellenbogen, T., Seo, K. & Crozier, K. B. Chromatic plasmonic polarizers for active visible color filtering and polarimetry. Nano Lett. 12, 1026–1031 (2012).
Biagioni, P. et al. Near-field polarization shaping by a near-resonant plasmonic cross antenna. Phys. Rev. B 80, 153409 (2009).
Pors, A. et al. Plasmonic metamaterial wave retarders in reflection by orthogonally oriented detuned electrical dipoles. Opt. Lett. 36, 1626–1628 (2011).
Roberts, A. & Lin, L. Plasmonic quarter-wave plate. Opt. Lett. 37, 1820–1822 (2012).
Khoo, E. H., Li, E. P. & Crozier, K. B. Plasmonic wave plate based on subwavelength nanoslits. Opt. Lett. 36, 2498–2500 (2011).
Baida, F. I., Boutria, M., Oussaid, R. & van Labeke, D. Enhanced-transmission metamaterials as anisotropic plates. Phys. Rev. B 84, 035107 (2011).
Sung, J. et al. Nanoparticle spectroscopy: birefringence in two-dimensional arrays of L-shaped silver nanoparticles. J. Phys. Chem. C 112, 3252–3260 (2008).
Kats, M. A. et al. Giant birefringence in optical antenna arrays with widely tailorable optical anisotropy. Proc. Natl. Acad. Sci. U.S.A. 109, 11364–12368 (2012).
Gordon, R. et al. Strong polarization in the optical transmission through elliptical nanohole arrays. Phys. Rev. Lett. 92, 037401 (2004).
Zhao, Y. & Alù, A. Tailoring the dispersion of plasmonic nanorods to realize broadband optical meta-waveplates. Nano Lett. 13, 1086–1091 (2013).
Yu, N. et al. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett. 12, 6328–6333 (2012).
Kuester, E. F., Mohamad, M. A., Piket-May, M. & Holloway, C. L. Averaged transition conditions for electromagnetic fields at a metafilm. IEEE Trans. Antenn. Propag. 51, 2641–2651 (2003).
Gires, F. & Tournois, P. Interferometre utilisable pour la compression d'impulsions lumineuses modulees en frequence. C. R. Acad. Sci. Paris 258, 6112 (1964).
Chew, W. C. Waves and Fields in Inhomogeneous Media, 2nd edn (IEEE Press, 1995).
Ghenuche, P., Cherukulappurath, S., Taminiau, T. H., van Hulst, N. F. & Quidant, R. Spectroscopic mode mapping of resonant plasmon nanoantennas. Phys. Rev. Lett. 101, 116805 (2008).
Huang, C.-P., Yin, X.-G., Huang, H. & Zhu, Y.-Y. Study of plasmon resonance in a gold nanorod with an LC circuit model. Opt. Express 17, 6407–6413 (2009).
Yun, S. et al. Low-loss impedance-matched optical metamaterials with zero-phase delay. ACS Nano 6, 4475–4482 (2012).
Liu, N., Fu, L., Kaiser, S., Schweizer, H. & Giessen, H. Plasmonic building blocks for magnetic molecules in three-dimensional optical metamaterials. Adv. Mater. 20, 3859–3865 (2008).
Kats, M. A., Blanchard, R., Genevet, P. & Capasso, F. Nanometre optical coatings based on strong interference effects in highly absorbing media. Nat. Mater. 12, 20–24 (2013).
Hansen, N. & Ostermeier, A. Completely derandomized self-adaptation in evolutionary strategies. Evol. Comput. 9, 159–195 (2001).
Gregory, M. D., Bayraktar, Z. & Werner, D. H. Fast optimization of electromagnetic design problems using the covariance matrix adaptation evolutionary strategy. IEEE Trans. Antennas Propag. 59, 1275–1285 (2011).
Jiang, Z. H. et al. Tailoring dispersion for broadband low-loss optical metamaterials using deep-subwavelength inclusions. Sci. Rep. 3, 1571 (2013).
Gansel, J. K. et al. Gold helix photonic metamaterial as broadband circular polarizer. Science 325, 1513–1515 (2009).
Acknowledgements
This work was supported by the NSF MRSEC Grant No. DMR-0820404. The metasurface-based waveplates were fabricated at the Penn State NSF NNIN Site. We thank Jeremy P. Turpin for assistance and discussion during the preparation of the manuscript.
Author information
Authors and Affiliations
Contributions
Z.H.J. designed the metasurface-waveplate and developed the interference model. L.L. and S. Yun fabricated the samples and took FESEM images. Measurements were performed by D.M. together with L.L. and Z.H.J., D.H.W., Z.L. and T.S.M. supervised the project. All authors discussed the results and wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Jiang, Z., Lin, L., Ma, D. et al. Broadband and Wide Field-of-view Plasmonic Metasurface-enabled Waveplates. Sci Rep 4, 7511 (2014). https://doi.org/10.1038/srep07511
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07511
This article is cited by
-
Highly efficient transmissive metasurface for polarization control
Optical and Quantum Electronics (2021)
-
Structured graphene metamaterial selective absorbers for high efficiency and omnidirectional solar thermal energy conversion
Nature Communications (2020)
-
Ultrawide-angle and high-efficiency metalens in hexagonal arrangement
Scientific Reports (2020)
-
Broadband wave plates made by plasmonic metamaterials
Scientific Reports (2018)
-
A broadband reflective-type half-wave plate employing optical feedbacks
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.