Abstract
The linear function is possibly the simplest and the most used relation appearing in various areas of our world. A linear relation can be generally determined by the least square linear fitting (LSLF) method using several measured quantities depending on variables. This happens for such as detecting the gradient of a magnetic field. Here, we propose a quantum fitting scheme to estimate the magnetic field gradient with N-atom spins preparing in W state. Our scheme combines the quantum multi-parameter estimation and the least square linear fitting method to achieve the quantum Cramér-Rao bound (QCRB). We show that the estimated quantity achieves the Heisenberg-scaling accuracy. Our scheme of quantum metrology combined with data fitting provides a new method in fast high precision measurements.
Similar content being viewed by others
Introduction
Magnetometry is important for mineral exploration and probing moving magnetic objects. High precision magnetometry1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 also has wide applications in modern sciences and technologies, such as in nuclear magnetic resonance (NMR)17, magnetic resonance imaging (MRI)18,19, biomedical science20 and quantum control21. In some cases, the quantity interested is not the absolute strength of magnetic field but its difference and gradient. A standard measuring instrument for determining the gradient is differential atom interferometry, which utilizes two completely polarized atomic ensembles. Recently, quantum-enhanced measurements of magnetic field gradient have been proposed22,23,24,25.
It is by now well established that quantum metrology has advantages in enhancing precision of estimation26 which is beyond the classical method. In quantum metrology, the general framework for precision bound of estimation has been proposed and developed in Refs. 27–34, which is based on Fisher information (FI) and Cramér-Rao inequality. The precision of estimation depends on the amount of resources employed in the scheme, which might be for instance the number N of identical probes (photons, atoms) or the energy of probing field. The standard quantum limit, a consequence of the central limit theorem for statistics, shows that the precision is proportional to  . With quantum strategies such as entanglement and squeezing applied, one may attain better accuracy scaling as 1/N, which is the ultimate limit of precision named as Heisenberg limit. The NOON and GHZ states have been demonstrated to be able to provide a Heisenberg-limit sensitivity in some schemes35,36,37,38,39,40,41. Also some experiments have implemented the quantum enhanced metrology42,43,44,45,46,47.
. With quantum strategies such as entanglement and squeezing applied, one may attain better accuracy scaling as 1/N, which is the ultimate limit of precision named as Heisenberg limit. The NOON and GHZ states have been demonstrated to be able to provide a Heisenberg-limit sensitivity in some schemes35,36,37,38,39,40,41. Also some experiments have implemented the quantum enhanced metrology42,43,44,45,46,47.
In this work, we propose a quantum scheme of multi-parameter estimation to detect the gradient of magnetic field by employing N-atom spins. These atoms are initially prepared in W state, a genuine multipartite entangled state that can be generated in spin chain48 and has been experimentally produced by trapped ions49. These technologies can be utilized to implement our scheme in experiment. By applying the least square linear fitting method to the quantum enhanced multi-parameter estimation, we show that our scheme saturates the QCRB with Heisenberg-scaling accuracy. Let us highlight some advantages of this scheme: (i) Our scheme does not depend on the prior assumed linear assumption for the magnetic field, we essentially apply the reliable LSLF method. We also discuss that even if the linearity of the magnetic field is prior assumed, the bound of precision is exactly the same one. (ii) This simultaneous estimation scheme is in principle faster than repeated individual estimations. (iii) This is a general quantum fitting method and can be applied to measure other physical quantities with various fitting functions.
Results
Multi-parameter estimation combined with the least square linear fitting method
We consider the problem of measuring the gradient of a magnetic field. Our scheme is to simultaneously estimate the strength of magnetic field at different locations through quantum measurements and then to apply the LSLF method. We employ a N-atom spin chain as the probes, as shown in FIG. 1, to estimate the magnetic field gradient, where the j-th atom is located at xj = x1 + (j − 1)a, ( ) and the uncertainty of the location xj can be neglected. The Hamiltonian describes that each atom with two hyperfine spin states is coupled to the local magnetic field and it takes the form,
) and the uncertainty of the location xj can be neglected. The Hamiltonian describes that each atom with two hyperfine spin states is coupled to the local magnetic field and it takes the form,

where Bj and  are the magnetic field and Pauli operator of atom j and each atom has the same gyromagnetic ratio γ. The task of our scheme is to obtain optimal uncertainty bound of estimating the magnetic field gradient G that quantum mechanics permitted.
are the magnetic field and Pauli operator of atom j and each atom has the same gyromagnetic ratio γ. The task of our scheme is to obtain optimal uncertainty bound of estimating the magnetic field gradient G that quantum mechanics permitted.
Initially, the atomic spins are prepared in a W state  , where
, where  . Considering that there are multiple independent parameters being estimated, they should be investigated in common ground. Then by symmetry consideration, W state is a good choice in multi-parameter estimation, which is largely different from single-parameter tasks. Further researches are needed to determine the best choice. For this closed quantum system, then the quantum state evolves under the action of magnetic field as
. Considering that there are multiple independent parameters being estimated, they should be investigated in common ground. Then by symmetry consideration, W state is a good choice in multi-parameter estimation, which is largely different from single-parameter tasks. Further researches are needed to determine the best choice. For this closed quantum system, then the quantum state evolves under the action of magnetic field as  , where
, where  due to Schrödinger equaiton. The initial pure state acquired multiple phases through the unitary transformation is given by
due to Schrödinger equaiton. The initial pure state acquired multiple phases through the unitary transformation is given by

Because of an overall unobservable phase, it is proper to think that B1 = 0 always holds. Thus the covariance matrix Cov(B) and Fisher information matrix  are size (N − 1) × (N − 1). Generalizing the expression of estimation for unitary dynamical processes33, the quantum Fisher information (QFI) matrix is given by
are size (N − 1) × (N − 1). Generalizing the expression of estimation for unitary dynamical processes33, the quantum Fisher information (QFI) matrix is given by  52, where
52, where  ,
,  . By straightforward calculations, one gets
. By straightforward calculations, one gets  ,
,  and
and  , where δm,n is Kronecker's delta. Then the (N − 1) × (N − 1) sized QFI matrix and its inverse associated with the estimation of the magnetic field in our scheme is
, where δm,n is Kronecker's delta. Then the (N − 1) × (N − 1) sized QFI matrix and its inverse associated with the estimation of the magnetic field in our scheme is


where m,  .
.
Applying the LSLF method, we have the fitting gradient of the magnetic field as,

where  ,
,  . Because each atom is separated with a distance a in the x-direction, then we get
. Because each atom is separated with a distance a in the x-direction, then we get  and
and  . Thus the gradient of magnetic field is
. Thus the gradient of magnetic field is  , where the coefficients are
, where the coefficients are  . Since the uncertainties of xj are neglected, the quantum Cramér-Rao inequality gives a lower bound on the variance of the magnetic field gradient
. Since the uncertainties of xj are neglected, the quantum Cramér-Rao inequality gives a lower bound on the variance of the magnetic field gradient

This bound is clearly a Heisengberg-scaling accuracy for large N. And the commutability of corresponding symmetric logarithmic derivatives (SLD) guarantees this bound can be saturated.
Now, we turn to the problem of constructing measurement strategy that can achieve quantum advantages in multi-parameter estimation. In this scheme, we construct two von Neumann measurement strategies, labeled by a, b respectively,  , to be performed on the atomic spin chain as the following forms,
, to be performed on the atomic spin chain as the following forms,



where  . Both of these two sets of quantum states are orthonormal eigenstates of the coherence operator expressed as
. Both of these two sets of quantum states are orthonormal eigenstates of the coherence operator expressed as  , see Ref. 25. To implement these two von Neumann measurements in experiment, it requires performing global operators on N atoms instead of local operators on each atom. On the other hand, based on quantum theory, we can also first make a corresponding unitary transformation on those N atoms, then perform the local measurements in computational basis. These theoretical measurement strategies set a new goal for experimental physicists. By performing these operations
, see Ref. 25. To implement these two von Neumann measurements in experiment, it requires performing global operators on N atoms instead of local operators on each atom. On the other hand, based on quantum theory, we can also first make a corresponding unitary transformation on those N atoms, then perform the local measurements in computational basis. These theoretical measurement strategies set a new goal for experimental physicists. By performing these operations  , one obtains the ratio of each outcome
, one obtains the ratio of each outcome  , then determines the parameters Bj through comparing these observed ratios with the probability distributions p(ξ|B). Based on the knowledge in the Methods section, one obtains the Fisher information matrices of these two measurement strategies, respectively,
, then determines the parameters Bj through comparing these observed ratios with the probability distributions p(ξ|B). Based on the knowledge in the Methods section, one obtains the Fisher information matrices of these two measurement strategies, respectively,


see supplementary material for detailed calculations. For strategy b, the limiting process B → 0 is equivalent to the small phases requirement  of local estimation theory in Method Section. For strategy a, we firstly choose the path Bj = (j − 1)Ga to approach the limit B → 0. It's interesting that the Fisher information matrix has the same expression if one supposes that Bj = (j − 1)Ga. So Eq. (10) takes the limit of Bj → (j − 1)Ga.
of local estimation theory in Method Section. For strategy a, we firstly choose the path Bj = (j − 1)Ga to approach the limit B → 0. It's interesting that the Fisher information matrix has the same expression if one supposes that Bj = (j − 1)Ga. So Eq. (10) takes the limit of Bj → (j − 1)Ga.
For measurement strategy a, the Fisher information matrix is positive semi-definite and irreversible, which confirms that it is not an effective deterministic estimation. Applying Fourier transformation, we have  and
and  . This shows that the prerequisite for determining the magnetic field Bj is knowing the module and argument of all λξ. Because the probability distributions associated with experimental outcomes are p(ξ|B) = |λξ|2/N, it is impossible to determine the argument of λξ. Thus this strategy is invalid for estimating magnetic field Bj.
. This shows that the prerequisite for determining the magnetic field Bj is knowing the module and argument of all λξ. Because the probability distributions associated with experimental outcomes are p(ξ|B) = |λξ|2/N, it is impossible to determine the argument of λξ. Thus this strategy is invalid for estimating magnetic field Bj.
For measurement strategy b, which yields the QFI matrix, the probability of each outcome is transparently related to the magnetic field B, with p(1|B) involving only B2, p(2|B) involving only B2, B3 and so on34. Through comparing the ratio of observed measurement outcomes with the probability distributions, the estimator could sequentially determine the magnetic field  . Then the gradient can be obtained by applying the LSLF method. Based on the results of asymptotically large ν independent experiments, this measurement strategy is optimal which can locally achieve quantum Cramér-Rao bound with Heisenberg-scaling accuracy. It is intriguing to explore how bad will be the degradation of this Heisenberg-scaling accuracy as some realistic imperfections kick in. Further researches are needed to conduct when one considers relevant imperfections like decoherence and particle losses.
. Then the gradient can be obtained by applying the LSLF method. Based on the results of asymptotically large ν independent experiments, this measurement strategy is optimal which can locally achieve quantum Cramér-Rao bound with Heisenberg-scaling accuracy. It is intriguing to explore how bad will be the degradation of this Heisenberg-scaling accuracy as some realistic imperfections kick in. Further researches are needed to conduct when one considers relevant imperfections like decoherence and particle losses.
Single parameter estimation with linear assumption
If we assume that the magnetic field satisfies the linear condition Bj = B1 + G(j − 1)a, the single parameter representing gradient G of magnetic field needs be estimated. In this case, the unitary transformation for the atomic spin chain is  and the QFI can be expressed as33
and the QFI can be expressed as33

where  . Applying this equation, we obtain
. Applying this equation, we obtain  . It is straightforward to determine that the quantum Cramér-Rao bound
. It is straightforward to determine that the quantum Cramér-Rao bound  which is exactly the same as the Heisenberg-scaling accuracy for scheme of the multi-parameter estimation. Immediately, we'll show that the previously proposed measurement strategies are optimal because they both yield the QFI and QCRB.
which is exactly the same as the Heisenberg-scaling accuracy for scheme of the multi-parameter estimation. Immediately, we'll show that the previously proposed measurement strategies are optimal because they both yield the QFI and QCRB.
For measurement strategy a, its probability distributions and Fisher Information are


where the detailed calculations are showed in the supplementary material. The probability distribution pa(ξ|G) is clearly peaked around (−ξ/N + j)π/(γta) with approximate width π/(Nγta), where j is an arbitrary integer. If the condition 0 < G < π/(γta) is satisfied, one can successfully estimate G with Heisenberg-scaling accuracy. This measurement strategy is essentially a quantum Fourier algorithm for phase estimation53,54.
For measurement strategy b, we consider the estimation is local, i.e., the unknown parameter satisfies  . We show in the supplementary material that its Fisher information is
. We show in the supplementary material that its Fisher information is

This implies that the Heisenberg-scaling QCRB can be reached locally via performing measurement strategy b.
Discussion
Determining the gradient of magnetic field is inherently a multi-parameter estimation problem. We employ quantum enhanced multi-parameter estimation and the least square linear fitting method to achieve the Heisenberg-scaling quantum Cramér-Rao bound. Our scheme provides attainable high precision in magnetometry. This proposal is the first data fitting scheme possessing Heisenberg-scaling accuracy. This opens a new avenue for the investigations of general data fitting problems.
Methods
Here, let us introduce the method used in this work. We next will present a brief review of local estimation theory, the Fisher information and Cramér-Rao inequality27,28,29,30,31,32,33.
Considering a curve  characterizing dynamical process on the space of density matrix, the problem of determining the value of the parameter vector
characterizing dynamical process on the space of density matrix, the problem of determining the value of the parameter vector  is a fundamental problem of statistical inference based on the experimental results. Before the measurements, we know that an observable random variable ξ carries information about the unknown parameter vector y, which is described by the smooth probability distribution p(ξ|y). The normalization is
is a fundamental problem of statistical inference based on the experimental results. Before the measurements, we know that an observable random variable ξ carries information about the unknown parameter vector y, which is described by the smooth probability distribution p(ξ|y). The normalization is  and ξ could be discrete or multivariate although it is written here as a single continuous real variable.
and ξ could be discrete or multivariate although it is written here as a single continuous real variable.
Then we take a random sample of size ν to estimate the parameter vector y via comparing the ratio of observed measurement outcomes with the probability distribution. An essential premise of effective deterministic estimation is requiring that the smooth map p(ξ|y) ↔ y is bijective. In order to avoid the periodical problems of determining the parameters yi, it is generally assumed that all components yi are small, which is called local estimation. For an effective deterministic observable random variable ξ, one estimates the parameter vector y via funtions  based on experimental results. The general framework of quantum parameter estimation is shown in FIG. 2. Then the expectation and covariance matrix of estimation are
based on experimental results. The general framework of quantum parameter estimation is shown in FIG. 2. Then the expectation and covariance matrix of estimation are


Taking the partial derivative of Eq.(16) with respect to yj and combining them into a bilinear quadratic form via two arbitrary real vectors  ,
,  , we obtain
, we obtain

Applying the Cauchy-Schwarz inequality to Eq.(18) yields Cramér-Rao bound27,28,29,30,31,32

where the Fisher information (FI) matrix is defined by

Based on Eq.(19), for all α, there exits β s.t.  and because βTCov(yest)β ≥ 0, then we find that the Fisher information matrix
and because βTCov(yest)β ≥ 0, then we find that the Fisher information matrix  is positive. Noticing that Eq.(19) only holds for effective deterministic estimation, the Fisher information matrix defined by Eq.(20) is merely positive semi-definite for arbitrary observable random variables.
is positive. Noticing that Eq.(19) only holds for effective deterministic estimation, the Fisher information matrix defined by Eq.(20) is merely positive semi-definite for arbitrary observable random variables.
The asymptotic theory of maximum-likelihood estimation states that27,31,32, in the approximate sense for large ν, the estimation achieves the Cramér-Rao bound and is unbiased locally, i.e.  , where Cov(yest) is the matrix describing the deviation between the estimated values and real values. Thus for unbiased effective deterministic estimation, the Cramér-Rao inequality can be written as refs. 29, 32
, where Cov(yest) is the matrix describing the deviation between the estimated values and real values. Thus for unbiased effective deterministic estimation, the Cramér-Rao inequality can be written as refs. 29, 32

which means that it is a positive semi-definite matrix.
For quantum mechanics, the generalized measurement performed on the density matrix  is described by a set of of non-negative Hermitian operators
is described by a set of of non-negative Hermitian operators  53, which are complete in the sense that
53, which are complete in the sense that  . And the probability distribution for measurement outcomes ξ is given by
. And the probability distribution for measurement outcomes ξ is given by  . As proven in ref. 31, we have
. As proven in ref. 31, we have

where  is the so-called quantum Fisher information (QFI) matrix defined as refs. 29, 30, 32
is the so-called quantum Fisher information (QFI) matrix defined as refs. 29, 30, 32

where these Hermitian operators are the so-called symmetric logarithmic derivatives (SLD), defined by the following equation

The sufficient and necessary conditions for equality holding in Eq.(22) are

where  is real. For single parameter estimation, the equality in Eq.(22) can always be satisfied by choosing the Hermitian operators to be one-dimensional projectors onto a complete set of orthonormal eigenstates of
is real. For single parameter estimation, the equality in Eq.(22) can always be satisfied by choosing the Hermitian operators to be one-dimensional projectors onto a complete set of orthonormal eigenstates of  31. Thus quantum Fisher information is the maximum of Fisher information over all possible measurement strategies31,33, i.e.
31. Thus quantum Fisher information is the maximum of Fisher information over all possible measurement strategies31,33, i.e.  . For multi-parameter estimation, the equality in Eq.(22) generally is not achievable, which means that the quantum Cramér-Rao inequality
. For multi-parameter estimation, the equality in Eq.(22) generally is not achievable, which means that the quantum Cramér-Rao inequality  cannot always be saturated29,30,32,34,50,51,52. One obvious sufficient condition for the attainability of QCRB is the commutators of SLDs are zero.
cannot always be saturated29,30,32,34,50,51,52. One obvious sufficient condition for the attainability of QCRB is the commutators of SLDs are zero.
References
Budker, D. & Romalis, M. Optical magnetometry. Nat. Phys. 3, 227 (2007).
Vengalattore, M. et al. High-resolution magnetometry with a spinor Bose-Einstein condensate. Phys. Rev. Lett. 98, 200801 (2007).
Shah, V., Vasilakis, G. & Romalis, M. V. High bandwidth atomic magnetometery with continuous quantum nondemolition measurements. Phys. Rev. Lett. 104, 013601 (2010).
Wasilewski, W. et al. Quantum noise limited and entanglement-assisted magnetometry. Phys. Rev. Lett. 104, 133601 (2010).
Wolfgramm, F. et al. Squeezed-light optical magnetometry. Phys. Rev. Lett. 105, 053601 (2010).
Horrom, T., Singh, R., Dowling, J. P. & Mikhailov, E. E. Quantum-enhanced magnetometer with low-frequency squeezing. Phys. Rev. A 86, 023803 (2012).
Sewell, R. J. et al. Magnetic sensitivity beyond the projection noise limit by spin squeezing. Phys. Rev. Lett. 109, 253605 (2012).
Taylor, J. M. et al. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys 4, 810 (2008).
Maze, J. R. et al. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 455, 644 (2008).
Balasubramanian, G. et al. Nanoscale imaging magnetometry with diamond spins under ambient conditions. Nature 455, 648 (2008).
de Lange, G. et al. Single-spin magnetometry with multipulse sensing sequences. Phys. Rev. Lett. 106, 080802 (2011).
Magesan, E. et al. Reconstructing the profile of time-varying magnetic fields with quantum sensors. Phys. Rev. A 88, 032107 (2013).
Cooper, A. et al. Time-resolved magnetic sensing with electronic spins in diamond. Nat. Commun. 5, 3141 (2014).
Chaudhry, A. Z. Utilizing mitrogen-vacancy centers to measure oscillating magnetic fields. Phys. Rev. A 90, 042104 (2014).
Chaudhry, A. Z. & Gong, J. B. Protecting and enchancing spin squeezing via continuous dynamical decoupling. Phys. Rev. A 86, 012311 (2012).
Kolkowitz, S. et al. Coherent sensing of a mechanical resonator with a single-spin qubit. Science 335, 1603 (2012).
Greenberg, Y. S. Application of superconducting quantum interference devices to nuclear magnetic resonance. Rev. Mod. Phys. 70, 175 (1998).
Lauterbur, P. C. Image formation by induced local interaction: examples employing nuclear magnetic resonance. Nature 242, 190 (1973).
Mansfield, P. Snapshot magnetic resonance imaging (Nobel lecture). Angew. Chem. Int. Ed. Engl. 43, 5456–5464 (2004).
Hämäläinen, M. et al. Magnetoencephalographyłtheory, instrumentation and applications to noninvasive studies of the working human brain. Rev. Mod. Phys. 65, 413 (1993).
Grinolds, M. S. et al. Quantum control of proximal spins using nanoscale magnetic resonance imaging. Nat. Phys. 7, 687 (2011).
Eckert, K. et al. Differential atom interferometry beyond the standard quantum limit. Phys. Rev. A 73, 013804 (2006).
Ng, H. T. Quantum-limited measurement of magnetic-field gradient with entangled atoms. Phys. Rev. A 87, 043602 (2013).
Urizar-Lanz, I. et al. Macroscopic singlet states for gradient magnetometry. Phys. Rev. A 88, 013626 (2013).
Ng, H. T. & Kim, K. Heisenberg-limited measurement of magnetic-field gradient with multipartite entangled states. Opt. Commun. 331, 353 (2014).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photon. 5, 222 (2011).
Fisher, R. A. Theory of statistical estimation. Proc. Camb. Soc. 22, 700 (1925).
Cramér, H. Mathematical Methods of Statistics (Princeton University, Princeton, NJ, 1946).
Helstrom, C. W. Quantum Dectection and Estimation Theory (Academic Press, Massachusetts, 1976).
Holevo, A. S. Probabilistic and Statistical Aspects of Quantum Theory (North-Holland, Amsterdam, 1982).
Braunstein, S. L. & Caves, C. M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439 (1994).
Gill, R. D. & Massar, S. State estimation for large ensembles. Phys. Rev. A 61, 042312 (2000).
Escher, B. M., de Matos Filho, R. L. & Davidovich, L. General framework for estimating the ultimate precision limit in noisy quantum-enhanced metrology. Nat. Phys. 7, 406 (2011).
Humphreys, P. C., Barbieri, M., Datta, A. & Walmsley, I. A. Quantum enhanced multiple phase estimation. Phys. Rev. Lett. 111, 070403 (2013).
Bollinger, J. J., Itano, W. M., Wineland, D. J. & Heinzen, D. J. Optimal frequency measurements with maximally correlated states. Phys. Rev. A 54, R4649 (1996).
Huelga, S. F. et al. Improvement of frequency standards with quantum entanglement. Phys. Rev. Lett. 79, 3865 (1997).
Lee, H., Kok, P. & Dowling, J. P. A quantum Rosetta stone for interferometry. J. Mod. Opt. 49, 2325 (2002).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum-enhanced measurements: beating the standard quantum limit. Science 306, 1330 (2004).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum metrology. Phys. Rev. Lett. 96, 010401 (2006).
Kessler, E. M. et al. Heisenberg-limited atom clocks based on entangled qubits. Phys. Rev. Lett. 112, 190403 (2014).
Kómár, P. et al. A quantum network of clocks. Nat. Phys. 10, 582 (2014).
Nagata, T., Okamoto, R., O'Brien, J. L., Sasaki, K. & Takeuchi, S. Beating the standard quantum limit with four-entangled photons. Science 316, 726 (2007).
Higgins, B. L. et al. Entanglement-free Heisenberg-limited phase estimation. Nature 450, 393 (2007).
Kacprowicz, M. et al. Experimental quantum-enhanced estimation of a lossy phase shift. Nat. Photon. 4, 357 (2010).
Afek, I., Ambar, O. & Silberberg, Y. High-NOON states by mixing quantum and classical light. Science 328, 879 (2010).
Xiang, G. Y. et al. Entanglement-enhanced measurement of a completely unknown phase. Nat. Photon. 5, 43 (2011).
Yonezawa, H. et al. Quantum-enhanced optical-phase tracking. Science 337, 1514 (2012).
Bruß, D. et al. Multipartite entanglement in quantum spin chains. Phys. Rev. A 72, 014301 (2005).
Häffner, H. et al. Scalable multiparticle entanglement of trapped ions. Nature 438, 643 (2005).
Vaneph, C., Tufarelli, T. & Genoni, M. G. Quantum estimation of a two-phases spin rotation. Quantum Measurements and Quantum Metrology 1, 12 (2013).
Genoni, M. G. et al. Optimal estimation of joint parameters in phase space. Phys. Rev. A. 87, 012107 (2013).
Yue, J. D., Zhang, Y. R. & Fan, H. Quantum-enhanced metrology for multiple phase estimation with noise. Sci. Rep. 4, 5933 (2014).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, 2000).
Chuang, I. L. Quantum algorithm for distributed clock synchronization. Phys. Rev. Lett. 85, 2006 (2000).
Acknowledgements
This work was supported by the 973 Program (2010CB922904), NFFTBS (J1103205, J1030310), NSFC (11175248), grants from the Chinese Academy of Sciences and the Chun-Tsung scholar fund of Peking University.
Author information
Authors and Affiliations
Contributions
Y.L.Z. and H.F. proposed this project, Y.L.Z. made the main calculations. H.W. and L.J. involved in analyzing the results and discussions. Y.L.Z. and H.F. wrote the paper with comments from all other authors. H.F. and L.Z.M. supervised the project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhang, YL., Wang, H., Jing, L. et al. Fitting magnetic field gradient with Heisenberg-scaling accuracy. Sci Rep 4, 7390 (2014). https://doi.org/10.1038/srep07390
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07390
This article is cited by
-
Quantum Fisher information matrix of quantum metrology in a Heisenberg XXZ model
Quantum Studies: Mathematics and Foundations (2024)
-
Protecting Quantum Coherence and Quantum Fisher Information in Ohmic Reservoir
International Journal of Theoretical Physics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

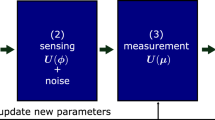




 , evolved from a known initial state allowed by quantum mechanics, carries about the parameter vector characterizing dynamical process and yest is obtained from the measurement results performed on the final state.
, evolved from a known initial state allowed by quantum mechanics, carries about the parameter vector characterizing dynamical process and yest is obtained from the measurement results performed on the final state.