Abstract
By merging bottom-up and top-down strategies we tailor graphene's electronic properties within nanometer accuracy, which opens up the possibility to design optical and plasmonic circuitries at will. In a first step, graphene electronic properties are macroscopically modified exploiting the periodic potential generated by the self assembly of metal cluster superlattices on a graphene/Ir(111) surface. We then demonstrate that individual metal clusters can be selectively removed by a STM tip with perfect reproducibility and that the structures so created are stable even at room temperature. This enables one to nanopattern circuits down to the 2.5 nm only limited by the periodicity of the Moiré-pattern, i.e., by the distance between neighbouring clusters and different electronic and optical properties should prevail in the covered and uncovered regions. The method can be carried out on micro-meter-sized regions with clusters of different materials permitting to tune the strength of the periodic potential.
Similar content being viewed by others
Introduction
Two main routes are usually followed to modify graphene's electronic and optical properties. On the one hand, bottom up approaches have proven to be efficient to change the overall electronic structure of graphene, enabling for example, the gap opening at the Fermi energy1,2,3, renormalization of the Fermi velocity4,5,6 or controllable n- and p-type electronic doping7,8,9,10. On the other hand, with top down approaches it is possible to induce these alterations on a local scale enabling one to pattern graphene to quantum confine electrons11,12,13,14, to induce local magnetic and superconducting properties15,16, or to use a scanning probe to selectively tune its electronic properties13,17,18. Still, a remaining challenge is the realization of controlled nanopatterning below 10 nm sizes19,20, key for the comprehensive integration of graphene in real devices. Here, we show that combining both approaches, i.e., bottom-up and top-down, one can reach a 2.5 nm patterning, enriching graphene's capabilities even more.
Let us first outline the bottom-up approach1,2,4,5,21,22 for graphene monolayers on several metallic substrates which can be epitaxially grown with unrivaled quality23. An interesting common feature of most of these graphene-metal interfaces is the presence of superperiodicities, known as Moiré patterns, resulting from the lattice mismatch and rotation angle between graphene and metal lattices24. This creates a periodic potential superimposed to graphene whose strength can be tuned by the preferential adsorption of different adsorbates on specific positions of the Moiré superlattice1,2,3,25. A graphene metal interface particularly interesting for our purposes is the graphene monolayer epitaxially grown on Ir(111) substrates. It allows for growing single Moiré domains extending over micrometers25,26 while at the same time, the interaction with the substrate remains weak leaving almost unaltered the electronic properties of the graphene layer, i.e., the π-bands with the characteristic linear dispersion and Fermi velocity of free standing graphene are only modified by the appearance of a small gap less than 100 meV2,27,28, see Fig. 1b.
Tailoring graphene with 2.5 nm accuracy.
(a) Upper panel illustrates the patterning process, with a schematic STM tip drawn on top of a real experimental image, removing selected W clusters from the G/Ir(111) surface to write the word “graphene”. Lower panel shows a 95 × 35 nm2 STM image with the final result. (b), (c) Graphene π bands, in the vicinity of EF, for pristine G/Ir(111) and G/Ir(111) covered with an Ir cluster superlattice respectively, as measured by photoemission in ref (2). (d) Example of a graphene-based nanostructure formed by two different “graphene” with the electronic properties depicted in (b) and (c). (e) – (g) 30 × 30 nm2 STM images showing the validity of our method for clusters of different materials, in particular Ir (e,f) and W (g). Tunneling parameters: IT = 20 pA, Vs = +2.2 V (a); IT = 150 pA, Vs = +1.5 V (d); IT = 150 pA, Vs = +1.5 V(e); IT = 160 pA, Vs = +2.0 V (f); IT = 40 pA, Vs = +1.5 V (g). We have used the following color code in all our images: reddish corresponds to pristine G/Ir(111), bluish to Ir clusters and grayish to W ones. All STM data were acquired and analyzed using the WSXM software46.
Additionally, this Moiré pattern formed by the graphene monolayer and the Ir(111) substrate can be used as a template for networks of monodisperse clusters of transition metals25,29. As recently reported, the adsorption of these cluster superlattices strengthens the periodic potential created by the Moiré pattern, modifying the electronic properties of the graphene layer2. In particular, an increase of the band gap up to 400 meV and large anisotropies of the electron group velocity close to the Dirac point have been measured for Ir cluster superlattices2, see Fig 1c.
Results
The experimental bottom-up procedure is the following. We first grow a graphene monolayer on an Ir(111) substrate by chemical vapor deposition (CVD) of ethylene in UHV environments with the Ir(111) substrate held at 1050°C. Then, by evaporationg W or Ir from high purity filaments, we subsequently cover it with a hexagonal array of metal clusters with 2.5 nm periodicity (see methods for details on the sample preparation).
We will now turn to the above mentioned top-down approach where STM appears as an ideal technique to tackle local manipulation on such samples due to its ability to modify and pattern 2D samples with ultimate resolution30,31,32. In Fig 1a, we write “graphene” on the G/Ir(111) surface using the STM tip to completely remove the selected clusters which demonstrates the patterning on top of graphene with 2.5 nm accuracy and a very high degree of complexity, see also examples of Figs 1 e–g. In this way, by deliberately removing metallic clusters from the graphene layer, we can recover the electronic properties corresponding to the pristine G/Ir(111) interface in specific regions of the sample and can architecture nanostructures formed by two different kinds of ‘graphene’ regions, i.e., ones covered with clusters and uncovered ones, with supposedly different electronic properties. It is noteworthy that our method can be used with clusters of different metallic elements, see Figs 1e–g where Ir (e–f) and W (g) clusters formed by approx. 50 atoms have been removed. This might allow tuning the strength of the periodic potential superimposed to the graphene layer and, consequently, the electronic and optical properties for the covered regions.
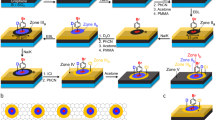
The procedure we have developed to engineer graphene nanostuctures consists in selectively removing single metallic clusters on top of graphene by gently approaching the STM tip towards them, as schematized in Fig 2a. We first image a large graphene sample area completely covered with metallic clusters, see Fig 2b. Next, we choose a metal cluster to be removed and stop the STM tip above it. With the tip above the chosen cluster, we open the feedback loop and bring the tip towards the sample at a constant rate for a distance of typically 0.6 nm. Then, we retract the tip back and close the feedback loop returning to the initial tunneling conditions. This completely removes the selected cluster as shown in Fig 2c. Finally, we systematically repeat this procedure to remove all selected clusters and thus form the designed nanostructure. As an example, the complete sequence for writing a “C” by consecutively removing 9 Ir clusters is shown in Figs 2b–k.
Cluster extraction procedure.
(a) Illustration of our cluster extraction method by the vertical displacement of a STM tip. (b–k) Sequence of 23 × 23 nm2 STM images, showing the writing of the carbon chemical symbol by consecutively removing one by one Ir clusters. All the images were acquired at RT with IT = 160 pA and Vs = +2.0 V. To remove each cluster, the STM tip was approached 0.6 nm to the surface at 100 mV. (l) Curves of the probability of removing a cluster as a function of approaching distance for several applied voltages. In all cases, stabilization current was set to 70 pA before opening the feedback loop. (m) Conductance histogram constructed from I(z) measurements on 1200 single cluster extraction events. Each curve was obtained at RT, with 0.1 V sample voltage. Inset shows an example of the conductance curve recorded during one of such cluster extraction events.
During the patterning process, the tip resolution is very robust and we usually observe almost no changes in our resolution after each cluster removal (see supplementary material). It further appears that the extracted clusters wet the STM tip and indeed, we remove the metal cluster as a whole since no traces of metal atoms are observed on the graphene surface after each single extraction event. This is likely due to the large cohesive energy of both W and Ir compared to the binding energies of C-Ir and C-W, respectively25,33. Such high cohesive energies together with the strong W-Ir binding should thus be responsible of the observed tip stability; once the cluster material wets the STM tip, it remains there in an extremely stable manner such that we have not been able to place the metal cluster back on the graphene surface.
The possibility of picking up or manipulating individual clusters formed on the Moiré-pattern was previously mentioned25,34. But on these works the cluster manipulation was a rather rare and statistical event. In fact, it was even considered a disturbing effect since it happened more or less statistically during the scanning process that could only be avoided under suitable tunneling conditions. Our work thus goes far beyond these earlier observations as we are now able to demonstrate that these cluster manipulations can be controlled to form arbitrary patterns stable even at room temperature. An essential issue regarding the validity of the procedure just described thus stems from its actual efficiency to extract the selected clusters.
To this end, we have performed a careful study of the probability of removing a cluster as a function of both the tip-sample approaching distance and the bias voltage applied to the sample during the whole process, see Fig. 2l and the supplementary material for details. The most important finding is that, for all voltages investigated during this study, we can reach a 100% probability for extracting a cluster by approaching the tip towards the sample a distance exceeding a certain value, between 0.5–0.7 nm, slightly different for each voltage. This allows to nanopattern the graphene surface with almost any degree of complexity and perfection. We also observed that, while the probability of extracting a cluster strongly depends on the approaching distance, the dependence on the applied voltage is much more moderate and basically independent of the voltage polarity, i.e., the direction of the electric field between tip and sample. For all voltages investigated here, the shape of the probability curves is essentially the same with only a rigid shift between them. This shift originates from the initial tip-sample distance dependence on the bias voltage set prior to open the feedback loop. Thus, our results point to a cluster removal procedure mainly driven by the actual distance between the STM tip and metal cluster.
To get more insight into the physical processes involved in the cluster extraction, we recorded the current during the vertical displacement of the STM tip (I-Z curves), see for example inset of Fig 2m. As usual when investigating the approach between two metallic electrodes, individual conductance curves were inherently irreproducible (see supplementary material), which is generally attributed to variations in the actual atomic-scale configuration of the metallic electrodes during the transition from tunneling to direct contact35,36,37,38. Thus, to perform an objective analysis of our experimental data, we constructed a conductance histogram from the evolution of the conductance traces of more than a thousand single cluster extraction events, see Fig 2m. Peaks in such conductance histograms are related to statistically more probable configurations in the contact formation36,37,38. The histogram shows a clear peak for a quantum of conductance (G0 = 2e2/h, e: electron charge; h: Planck's constant), indicating that the extraction of a metal cluster involves the formation of an atomic size contact. Similar G ≈ G0 values have been reported for contacts between an atomically sharp Au tip and graphene regions strongly bonded with a metal substrate39. In such regions, carbon atoms bind strongly to the metal surface and the hybridization of the graphene orbitals is transformed from sp2 to sp3, in a similar way as reported for graphene regions underneath metal clusters on the graphene/Ir(111) system33.
Let us now address several key points to infer the actual potential of our method to architecture functional graphene nanostructures, in particular, size limits, stability and quality. The range of applicability is obviously limited by the size of the nanostructures that can be created. We can build nanostructures from the 2.5 nm limit given by the Moiré pattern distance to the few micrometers one which is given by the typical STM scanning range; the possibility of growing single Moiré patterns domains extends over several micrometers26. As an example, a 0.25 × 0.25 μm2 STM image of a graphene region uniformly covered by metallic clusters is shown in Fig 3a. Since the graphene layer grows as a carpet on top of the Ir substrate40, monoatomic steps, as the one existing in the middle of the image, have very little influence on the cluster superlattice. Another important question deals with the stability of the created nanostructures since any practical application would require them to be stable at room temperature. Previous studies found that the cluster superlattices as a whole are stable up to temperatures of 400 K29. Here, we investigated the room temperature stability of several nanostructures with very different shapes and found them to be perfectly stable within our time scale (days). As an example, we show in Figs 3b–c two STM images acquired with 24 hours difference on the same sample area where an “A” nanostructure constructed by removing 10 W clusters and presenting a single isolated cluster in its center can be appreciated. The comparison of both images clearly reveals that even complex nanostructures keep exactly the same appearance one day after their construction.
Nanostructures' size, stability and quality.
(a) STM image of a 0.25 × 0.25 μm2 region fully covered by W clusters. Upper left inset shows a zoom of the region outlined by the green square. (b,c) 16 × 16 nm2 STM images of an artificially created nanostructure measured at room temperature with 24 hours difference. (d) 40 × 40 nm2 STM image of a W cluster superlattice on G/Ir(111). (e) STM image showing the same region as in d) after deliberately removing a large number of clusters from it. f) 7.2 × 7.2 nm2 STM image showing, with atomic resolution, the region outlined by a blue square in (e). Tunneling parameters: IT = 50 pA, Vs = 1.5 V (a); IT = 270 pA, Vs = 2.3 (b, c); IT = 50 pA, Vs = 2.2 V(d, e); IT = 5 nA, Vs = 35 mV (f).
Finally, we want to comment on the state of the graphene layer after the removal of the clusters. We aim to use pristine graphene on Ir(111) domains as one of our building blocks, thus, we need our cluster extraction method to produce perfectly clean graphene regions. To this end, we show in Figs 3d–f a sequence of STM images illustrating the evolution of a region where we have removed a large number of clusters. First, we show a STM image with the pristine W cluster superlattice, see Fig. 3d. Then, in Fig 3e, we show exactly the same sample region after using the STM tip to remove all the metal clusters from its central part. Last, in Fig 3f, we show an atomically resolved STM image of the cleaned region, acquired in the central area outlined by a blue square in Fig 3e. As can be observed, no single trace of the metal clusters is found on the cleaned region which is indistinguishable from the ones obtained on pristine graphene on Ir(111) prior to the W cluster.
Discusion
The full potential and applicability of our nanostructures is realized if the covered and uncovered regions display different electronic properties which has only been demonstrated for the homogeneous systems2, see Fig 1c. Scanning Tunneling Spectroscopy (STS) would seem to be the ideal tool to show if different gaps are also present in our nanostructures. Nevertheless, we were not able to obtain unambiguous data in order to detect noticeable changes in the evolution of the LDOS as the clusters were subsequently removed. In fact, for graphene on Ir(111) surfaces, dI/dV spectra seem to be mostly sensitive to a holelike surface resonance of the Ir(111) substrate rather than to any states of the graphene layer which was attributed to the selectivity of the tunneling current for states with small parallel momentum41. But even though transport and STS measurements are difficult due to the metallic substrate, optics and plasmonics seem within reach and in the following we discuss two new features that have the potential for sensors, metamaterials or data processing.
First, in the graphene/Ir(111) system, plasmonic excitations have been measured by electron energy loss spectroscopy42. We propose that they could be used to reach high field intensities since they are related to π→π* transitions between the valence and conduction band, so-called interband plasmons43. Assuming local band-gap variations between covered and uncovered graphene regions2, interband processes with transition energies 0.1 eV ≤ E ≤ 0.4 eV should be forbidden in the covered, but allowed in the uncovered regions and can thus be localized to small graphene areas by removing the upper Ir-clusters, see Fig. 4a. In this way, quantum dots/wires can be designed at will with 2.5 nm precision by selectively removing metallic clusters. Quantum dots/wires with diameter/width L posses normal modes corresponding to the wave number q = nπ/L of the interband plasmon ( ), we thus expect large field enhancement due to resonant feedback effects which might be used, for instance, for spectroscopy on macro-molecules. For charge resonances at in-plane momentum q ≈ 0.03(0.05)Å−1 and energy E ≈ 0.25(0.375) eV42, the predicted field enhancement would occur for characteristic dot/wire dimensions of L ≈ 10.5(6.2) nm for n = 1 or L ≈ 21(12.5) nm for n = 2. These length scales are well within the reach of our technique (see supplementary information for details). In the same way, similar ideas can be applied to periodic structures where the excitation can be achieved also via propagating light.
), we thus expect large field enhancement due to resonant feedback effects which might be used, for instance, for spectroscopy on macro-molecules. For charge resonances at in-plane momentum q ≈ 0.03(0.05)Å−1 and energy E ≈ 0.25(0.375) eV42, the predicted field enhancement would occur for characteristic dot/wire dimensions of L ≈ 10.5(6.2) nm for n = 1 or L ≈ 21(12.5) nm for n = 2. These length scales are well within the reach of our technique (see supplementary information for details). In the same way, similar ideas can be applied to periodic structures where the excitation can be achieved also via propagating light.
Field enhancement and mass confined quantum dots for Dirac electrons.
(a) Energy dispersion near the Dirac points of the uncovered and covered areas displaying different mass gaps Δ1 < Δ2. Interband transitions with energies Δ1 <  ω<Δ2 are assumed to be allowed in the uncovered dot, but forbidden in the surrounding region covered with Iridium clusters. (b) Schematic view of the set up leading to field enhancement by resonantly exciting interband acoustic plasmons by an electron beam or near-field techniques. (c) Energy spectrum of a circular quantum dot with radius R and discontinuous mass profile m = Δ1θ(R – r)+Δ2θ(r – R) where the mass parameters are Δ1 = 0.1 eV and Δ2 = 0.4 eV. The unshaded region left from the red vertical line indicates the qubit regime of only one excitonic state. (d) Schematic energy diagram of two mass confined quantum dots in the qubit regime. Electron-hole excitations (excitons) can efficiently change sites via Förster energy transfer rate which is several orders of magnitude larger than the intrinsic decay rate.
ω<Δ2 are assumed to be allowed in the uncovered dot, but forbidden in the surrounding region covered with Iridium clusters. (b) Schematic view of the set up leading to field enhancement by resonantly exciting interband acoustic plasmons by an electron beam or near-field techniques. (c) Energy spectrum of a circular quantum dot with radius R and discontinuous mass profile m = Δ1θ(R – r)+Δ2θ(r – R) where the mass parameters are Δ1 = 0.1 eV and Δ2 = 0.4 eV. The unshaded region left from the red vertical line indicates the qubit regime of only one excitonic state. (d) Schematic energy diagram of two mass confined quantum dots in the qubit regime. Electron-hole excitations (excitons) can efficiently change sites via Förster energy transfer rate which is several orders of magnitude larger than the intrinsic decay rate.
A second and exciting new feature is given by the possibility to confine charged carriers, i.e., electrons as well as holes, within arbitrary geometrical regions due to locally modifying the electronic gap. One could hence design graphene quantum dots or nanowires of arbitrary size and form limited only by the cluster size of 2.5 nm which has to be contrasted with graphene nanostructures obtained by electron beam lithography and subsequent etching which have typical dimensions L = 20–100 nm. Using the effective-mass-approximation and thus the standard Dirac Hamiltonian with a variable mass profile, the discrete spectrum of a circular quantum dot as function of the radius R can be obtained, see Fig 4c and the supplementary information. As indicated by the unshaded region, it displays only one localized state for R ≤ 7 nm. In this regime, the uncovered area could resemble a quantum bit with qubit states “zero exciton” or “one exciton”. The excitonic states can further arbitrarily be connected by conventional wave function overlap or via Förster energy transfer which is mediated by the Coulomb interaction between the excitonic states, see Fig 4d. This would lead to the emergence of excitonic bands with high lifetimes as estimated via Fermi's Golden Rule (see supplementary information).
The feasibility of the above proposals crucially depends on the impact that the Iridium substrate and the clusters on top have on the electronic properties of the graphene layer. Even though from ARPES experiments the band structure hardly seems to be affected beyond the gap of Δ ≈ 0.1 eV and ≈ 0.4 eV, respectively, the graphene Dirac cone has been reported to hybridize near the Fermi level with the S1 surface state of Ir(111)28 and also graphene's lattice structure changes from sp2- to sp3-bonding on the covered regions33. Additionally, graphene optics on a metallic substrate is challenging since the induced electric dipoles in the graphene layer are usually strongly quenched by the metallic substrate. Screening effects of the underlying Iridium acting as a metallic gate will further limit the lifetime of the electron-hole pairs47. The implications of the Ir-substrate involving optical (q = 0) transitions and consequently the feasibility of the proposed emergence of excitonic bands, thus need to be tested experimentally. Nevertheless, as revealed by our analysis (see SI) on the experimentally measured plasmonic dispersion on graphene on Ir(111)42, the screening influence of the metal on the charge excitations with finite q is surprisingly small suggesting that plasmonic excitations involving finite q-transitions should be almost unaffected by the Ir-substrate.
To conclude, we have presented a perfectly reproducible nanopatterning technique for graphene that combines bottom-up with top-down approaches. The precision is related to the periodicity of the Moiré-pattern that is formed by the graphene layer with the underlying substrate. Presupposing locally distinct electronic gaps in the covered and uncovered regions, new devices could be tailored with nano precision and we propose a novel platform for plasmonics relying on inter- rather than on intraband transitions. Also single graphene quantum dots/wires could be designed at will and arranged to arbitrary circuitries. Determining the optical gap and relaxation properties of mass-confined Dirac electrons via optical near-field scanning spectroscopy, emission spectroscopy or even transmission spectroscopy by chemically reduce the thickness of the sample would provide new insight on the role of the Ir(111) substrate on the excitonic decay rate. Finally, we note that the electronic spectrum drastically changes in the presence of a magnetic field due to the appearance of the zeroth Landau level not present in conventional semiconductor quantum dots which could be observable via Terahertz magneto-Raman spectroscopy.
Methods
The STM experiments were performed with a home-built variable temperature instrument44,45. Tips were made of W and prepared by electrochemically etching and subsequently annealing in UHV conditions. STM data were acquired with a fully automated workstation that incorporates digital feedback control based on DSP (digital signal processor) technology. All the surface manipulation experiments, data acquisition and image processing were performed using the WSxM software46. STM images were all acquired in the constant current mode.
Sample preparation
Ir(111) surfaces were cleaned by 1 keV Ar+ sputtering at 850°C. The growth of graphene on the clean Ir(111) surface was performed by chemical vapor deposition (CVD) of ethylene (3 × 10−7 Torr during 1 min) in UHV environments with the Ir(111) substrate held at 1050°C. Under such conditions, small areas of the Ir(111) substrate remained intentionally uncovered by graphene, which allowed us to estimate the coverage of W or Ir used for the cluster formation. W and Ir were evaporated from high purity filaments composed of each corresponding material. An accurate calibration of the deposition rate as a function of the filament temperature, measured by an infrared pyrometer, was performed by means of STM images acquired on areas of bare -uncovered by graphene- Ir(111).
Theory and Modeling
The experimental data (plasmonic excitations in graphene on Ir(111) and Pt(111)) was obtained from the original publications and fitted to the theoretical predictions using the least-square method. The electronic properties of graphene were modeled using the standard effective-mass-approximation. Exciton lifetimes and hopping amplitudes were estimated via Fermi's Golden Rule.
References
Balog, R. et al. Bandgap opening in graphene induced by patterned hydrogen adsorption. Nature Mater. 9, 315–319 (2010).
Rusponi, S. et al. Highly Anisotropic Dirac Cones in Epitaxial Graphene Modulated by an Island Superlattice. Phys. Rev. Lett. 105, 246803 (2010).
Papagno, M. et al. Large Band Gap Opening between Graphene Dirac Cones Induced by Na Adsorption onto an Ir Superlattice. Acs Nano 6, 199–204 (2012).
Luican, A. et al. Single-Layer Behavior and Its Breakdown in Twisted Graphene Layers. Phys. Rev. Lett. 106, 126802 (2011).
Brihuega, I. et al. Unraveling the Intrinsic and Robust Nature of van Hove Singularities in Twisted Bilayer Graphene by Scanning Tunneling Microscopy and Theoretical Analysis. Phys. Rev. Lett. 109, 196802 (2012).
Hwang, C. et al. Fermi velocity engineering in graphene by substrate modification. Sci. Rep. 2, 590; 10.1038/srep00590 (2012).
Ohta, T., Bostwick, A., Seyller, T., Horn, K. & Rotenberg, E. Controlling the electronic structure of bilayer graphene. Science 313, 951–954 (2006).
Wehling, T. O. et al. Molecular doping of graphene. Nano Lett. 8, 173–177 (2008).
Chen, W., Chen, S., Qi, D. C., Gao, X. Y. & Wee, A. T. S. Surface transfer p-type doping of epitaxial graphene. J. Am. Chem. Soc. 129, 10418–10422 (2007).
Wei, D. C. et al. Synthesis of N-Doped Graphene by Chemical Vapor Deposition and Its Electrical Properties. Nano Lett. 9, 1752–1758 (2009).
Berger, C. et al. Electronic confinement and coherence in patterned epitaxial graphene. Science 312, 1191–1196 (2006).
Ponomarenko, L. A. et al. Chaotic dirac billiard in graphene quantum dots. Science 320, 356–358 (2008).
Tapaszto, L., Dobrik, G., Lambin, P. & Biro, L. P. Tailoring the atomic structure of graphene nanoribbons by scanning tunnelling microscope lithography. Nature Nanotechnol. 3, 397–401 (2008).
Stampfer, C. et al. Energy Gaps in Etched Graphene Nanoribbons. Phys. Rev. Lett. 102, 056403 (2009).
Heersche, H. B., Jarillo-Herrero, P., Oostinga, J. B., Vandersypen, L. M. K. & Morpurgo, A. F. Bipolar supercurrent in graphene. Nature 446, 56–59 (2007).
Ugeda, M. M., Brihuega, I., Guinea, F. & Gómez-Rodríguez, J. M. Missing Atom as a Source of Carbon Magnetism. Phys. Rev. Lett. 104, 096804 (2010).
Wei, Z. Q. et al. Nanoscale Tunable Reduction of Graphene Oxide for Graphene Electronics. Science 328, 1373–1376 (2010).
Sessi, P., Guest, J. R., Bode, M. & Guisinger, N. P. Patterning Graphene at the Nanometer Scale via Hydrogen Desorption. Nano Lett. 9, 4343–4347 (2009).
Wang, X. R. & Dai, H. J. Etching and narrowing of graphene from the edges. Nature Chem. 2, 661–665 (2010).
Biro, L. P., Nemes-Incze, P. & Lambin, P. Graphene: nanoscale processing and recent applications. Nanoscale 4, 1824–1839 (2012).
Li, G. H. et al. Observation of Van Hove singularities in twisted graphene layers. Nature Phys. 6, 44–48 (2010).
Hunt, B. et al. Massive Dirac Fermions and Hofstadter Butterfly in a van der Waals Heterostructure. Science 340, 1427–1430.
Wintterlin, J. & Bocquet, M. L. Graphene on metal surfaces. Sur. Sci. 603, 1841–1852 (2009).
Land, T. A., Michely, T., Behm, R. J., Hemminger, J. C. & Comsa, G. STM Investigation of Single Layer Graphite Structures Produced on Pt(111) by Hydrocarbon Decomposition. Surf. Sci. 264, 261–270 (1992).
N'Diaye, A. T., Bleikamp, S., Feibelman, P. J. & Michely, T. Two-dimensional Ir cluster lattice on a graphene moire on Ir(111). Phys. Rev. Lett. 97, 215501 (2006).
N'Diaye, A. T., Coraux, J., Plasa, T. N., Busse, C. & Michely, T. Structure of epitaxial graphene on Ir(111). New J. Phys. 10, 043033 (2008).
Pletikosic, I. et al. Dirac Cones and Minigaps for Graphene on Ir(111). Phys. Rev. Lett. 102, 056808 (2009).
Starodub, E. et al. In-plane orientation effects on the electronic structure, stability and Raman scattering of monolayer graphene on Ir(111). Phys. Rev. B 83, 125428 (2011).
N'Diaye, A. T. et al. A versatile fabrication method for cluster superlattices. New J. Phys. 11, 103045 (2009).
Eigler, D. M. & Schweizer, E. K. Positioning Single Atoms with a Scanning Tunneling Microscope. Nature 344, 524–526 (1990).
Lyding, J. W., Shen, T. C., Hubacek, J. S., Tucker, J. R. & Abeln, G. C. Nanoscale patterning and oxidation of H-passivated Si(100)-2x1 surfaces with an ultrahigh-vacuum scanning tunneling microscope. Appl. Phys. Lett. 64, 2010–2012 (1994).
Brihuega, I., Custance, O. & Gómez-Rodríguez, J. M. Surface diffusion of single vacancies on Ge(111)-c(2x8) studied by variable temperature scanning tunneling microscopy. Phys. Rev. B 70, 165410 (2004).
Feibelman, P. J. Pinning of graphene to Ir(111) by flat Ir dots. Phys. Rev. B 77, 165419 (2008).
Donner, K. & Jakob, P. Structural properties and site specific interactions of Pt with the graphene/Ru(0001) moire overlayer. J. Chem. Phys. 131, 164701 (2009).
Pascual, J. I. et al. Quantum Contact in Gold Nanostructures by Scanning-Tunneling-Microscopy. Phys. Rev. Lett. 71, 1852–1855 (1993).
Krans, J. M., Vanruitenbeek, J. M., Fisun, V. V., Yanson, I. K. & Dejongh, L. J. The signature of conductance quantization in metallic point contacts. Nature 375, 767–769 (1995).
Halbritter, A. et al. Transition from tunneling to direct contact in tungsten nanojunctions. Phys. Rev. B 68, 035417 (2003).
Agrait, N., Yeyati, A. L. & van Ruitenbeek, J. M. Quantum properties of atomic-sized conductors. Phys. Rep. 377, 81–279 (2003).
Altenburg, S. J. et al. Graphene on Ru(0001): Contact Formation and Chemical Reactivity on the Atomic Scale. Phys. Rev. Lett. 105, 236101 (2010).
Coraux, J., N'Diaye, A. T., Busse, C. & Michely, T. Structural coherency of graphene on Ir(111). Nano Lett. 8, 565–570 (2008).
Altenburg, S. J. et al. Local Gating of an Ir(111) Surface Resonance by Graphene Islands. Phys. Rev. Lett. 108, 206805 (2012).
Langer, T. et al. Sheet plasmons in modulated graphene on Ir(111). New J. Phys. 13, 053006 (2011).
Stauber, T. Plasmonics in Dirac systems: from graphene to topological insulators. J. Phys.: Condens. Matter 26, 123201 (2014).
Custance, O. et al. Single adatom adsorption and diffusion on Si(111)-(7x7) surfaces: Scanning tunneling microscopy and first-principles calculations. Phys. Rev. B 67, 235410 (2003).
Martinez-Galera, A. J. & Gomez-Rodriguez, J. M. Nucleation and Growth of the Prototype Azabenzene 1,3,5-Triazine on Graphite Surfaces at Low Temperatures. J. Chem. Phys. C 115, 11089–11094 (2011).
Horcas, I. et al. WSXM: A software for scanning probe microscopy and a tool for nanotechnology. Rev. Sci. Instrum. 78, 013705 (2007).
Guinea, F., Jalabert, R. A. & Sols, F. Electronic lifetimes in ballistic quantum dots electrostatically coupled to metallic environments. Phys. Rev. B 70, 085310 (2004).
Acknowledgements
We thank F. Guinea, G. Gómez-Santos, B. Amorim and T. Michely for helpful discussions. This work was supported by Spain's MINECO under Grants No. MAT2013-41636-P, No. FIS2013-44098-P, No. CSD2010-00024; AJMG was supported by a Marie Curie action under the Seventh Framework Programme.
Author information
Authors and Affiliations
Contributions
A.J.M.G. carried out the experiments supported by I.B. and J.M.G.R. A.J.M.G. and J.M.G.R. designed the research helped by I.B. A.J.M.G., I.B and J.M.G.R. analyzed the data. T.S. performed the main calculations with the collaboration of A.G.R. I.B. wrote the manuscript with the help of T.S. All authors contributed to the scientific discussion and revised the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Material for the article Towards scalable nano-engineering of graphene
Supplementary Information
Nano-lithographing Graphene with 2.5nm precision
Supplementary Information
Nano-lithographing Ir on graphene with 2.5nm precision
Supplementary Information
Nano-lithographing W on graphene with 2.5nm precision
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Martínez-Galera, A., Brihuega, I., Gutiérrez-Rubio, A. et al. Towards scalable nano-engineering of graphene. Sci Rep 4, 7314 (2014). https://doi.org/10.1038/srep07314
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07314
This article is cited by
-
There is life after coking for Ir nanocatalyst superlattices
Nano Research (2022)
-
Influence of metal support in-plane symmetry on the corrugation of hexagonal boron nitride and graphene monolayers
Nano Research (2018)
-
CAD/CAM for scalable nanomanufacturing: A network-based system for hybrid 3D printing
Microsystems & Nanoengineering (2017)
-
Dual response of graphene-based ultra-small molecular junctions to defect engineering
Nano Research (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.