Abstract
Wet chemical reduction of metal ions, a common strategy for synthesizing metal nanoparticles, strongly depends on the electric potential of the metal and its applications to late transition metal clusters have been limited to special cases. Here, we describe copper nanoclusters grown by synchrotron radiolysis in concert with wet chemistry. The local structure of copper aggregates grown by reducing Cu(II) pentanedionate using synchrotron x-ray beam was studied in situ by x-ray absorption spectroscopy. A detailed analysis of the XANES and EXAFS spectra, compared with DFT calculations and full-potential non-muffin-tin multiple scattering calculations, identified the nanocluster as Cu13 with icosahedral symmetry. The novel “charged” nanoclusters tightly bound to electron-donating amido molecules, which formed as a result of photo-induced deprotonation of ligand amines, were stabilized by irradiation. Monodispersive deposition of nanoclusters was enabled by controlling the type and density of “monomers”, in remarkable contrast to the conventional growth of metallic nanoparticles.
Similar content being viewed by others
Introduction
Metal nanoclusters (NCs) have attracted great interest in fundamental science and industrial applications over the past decade, because of size-dependent properties such as tailoring of optical gap1, unusual magnetism2, or enhanced catalytic activity3. Ligated (wet) NCs are of particular interest to researchers anticipating novel catalytic functions through strong perturbations of the electron states of the cluster core by ligand molecules.
Late transition metal NCs are obtained by stabilizing against aggregation into larger nanoparticles (NPs). In contrast to noble metal clusters, such as gold NCs synthesized by agglomeration from colloidal solution4,5, late transition metal clusters are typically difficult to stabilize because of an intrinsic stability as ions arising from an atom-specific electron configuration6. Despite advances in wet synthesis methods, e.g., two-phase synthesis5 and real-time monitoring of reactions by in situ local probes7,8, stabilizing smaller NCs has long been a challenge to researchers9,10.
The principle of wet chemistry synthesis of late transition metal NCs involves a simple reduction of multivalent ions, which is strongly dependent on the standard electrode potential (SEP). Taking copper as an example, which contrasts with a more positive SEP metal such as gold, most previous studies focused on special cases with a stabilization mechanism such as weakly interacting environments (e.g., solid argon)11,12 or strongly interacting ligation. In fact, in our previous work on Cu13 NCs prepared by wet chemistry in a microfluidic cell13, rapid reduction, particularly at elevated temperature, led to an immediate nucleation of monomers and subsequent growth. According to classical nucleation theory (CNT)14, nucleation is the localized appearance of a new phase (monomers) from a supersaturated phase and the density of monomers must be minimized to decrease the probability of forming multimers (nucleus). Thus, we anticipated that if the precursor stabilizes multivalent ions against reduction, the reduction kinetics would slow down and decrease the density of monomers.
On the other hand, it has been recognized that radiation-induced reduction (radiolysis) of aqueous solutions form monodispersed metallic NPs15,16 or NCs17. The advantage of radiolysis18 using synchrotron radiation is its atomic tunability and controllability of doses (irradiation parameters such as photon energy, band path, flux, polarization and elapsed time, etc.). By tuning the photon energy to the core level of atoms of interest, one can selectively create core holes, ionize atoms, excite electrons to unoccupied anti-bonding states, thus causing bond breaking and generating secondary electrons. Although bond energies (e.g., for the N-H bond, D0 = ΔH ≈ 385 kJ/mol) lie in the VUV to soft x-ray regime (<600 eV), secondary electrons are a common feature of the radiation effect with higher energy (hard x-ray) excitation. Interestingly, the effect of secondary electrons ejected to the vicinity of excited atoms may provide a novel means of selective (local) reduction. In this paper, we describe how synchrotron radiolysis combined with wet chemistry can stabilize late transition metal NCs, choosing copper as a model system. The results point to a novel category of nanomaterial-charged NCs.
Results
Nanoclusters formed by synchrotron radiolysis
In our previous study on Cu NCs, the reaction process consisted of the two sequential procedures illustrated in Fig. 1(a): ligation to form a divalent planar amino-complex (R1) and a subsequent reduction procedure (R2)13. The reduction of Cu2+ to Cu0 is, in general, a two-step reaction: the first reduction to Cu+ ions and the second “disproportionation” into Cu2+ ions and Cu0 monomers (R3: 2Cu+ → Cu2+ + Cu0), which reflects the stability of Cu2+ (3d9) states over Cu+ (3d10) states, because of the strong metal-ligand interaction. As the stability of ions depends on ionization potential as well as solvation energy, we conducted extensive screening experiments to find the optimum reaction conditions (combinations with various chemical substances and concentrations), trying to shift R2eq toward Cu2+ ions (or suppressing Cu+ ions) to slow down R3 kinetics. Suppression of the bottleneck reaction (R3) was anticipated to lower the density of metal monomers, which is proportional to the nucleation rate and therefore the nucleus density.
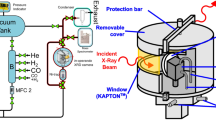
The equilibrium precursor solution (R2eq) was prepared from four-fold planar Cu(II) complexes, as described in TABLE I, in an inert (N2) atmosphere at room temperature. The precursor solution (total volume of 1.5 ml) was prepared for C1 and S, with a constant concentration of Cu2+ ions (2.4 mM/l). Extreme care was taken to avoid air exposure so that oxidation would not occur by performing all reactions in a vacuum-tight glovebox. The equilibrium solution filled into a TEFLON cell with a KAPTON window was irradiated for 4 h with a focused undulator x-ray beam (1 × 1012 photons/s) at 9.0 keV using the NW2A of the 6.5 GeV PF-AR at High Energy Accelerator Research Organization, Tsukuba. During the in situ XAS experiments, we found that synchrotron radiolysis of R2eq, tuned to the Cu K-shell excitation, changed the copper valence of the precursor solution and copper aggregates were simultaneously formed on the x-ray window. The nature (growth mode and particle size) of aggregates strictly depended on the R2eq which was measured by K (K = [Cu2+]/[Cu+]). See Fig. S1 in Supporting Materials for the experimental determination of K-values. We focused on the two extreme cases: the Cu+-dominant R2eq (K = 0), which led to a control denoted as C1 and Cu2+-dominant R2eq (K = 3.2), which deposited a cluster sample S. The photo-induced reduction of the precursor solution and aggregation were monitored by in situ XAS (Fig. S5, Supporting Materials) and a telescopic TV camera (Fig. 1(a)). The in situ XAS measurement of the aggregates (C1 and S) separated from the precursor solution showed that a very thin and flat layer of small clusters is deposited when K ≫ 1 by synchrotron radiolysis on a nitrogen-terminated organic film (KAPTON), as shown in Fig. 2(c).
Evolution of Cu K-XANES spectra for R2eq during irradiation, together with those for the references Cu(II)[HFPD]2, Cu2O and Cu metal.
The inset plots the intensity variation of the fluorescence signal at 9.05 keV during irradiation for C1 (a). Cu K-XANES spectra for C1 and R2eq before irradiation and the references, viz., an fcc metal, Cu2O and Cu(II)[HFPD]2. The inset is a blowup of the 1s-4p transition (b). Cu-K XANES spectra for S compared with those of R2eq before irradiation and of the references, viz., an fcc metal and Cu(II)[TMHD]2 (c).
It is well known that irradiation of organic solutions causes electronic excitation and bond-breaking, generating radicals, e.g., negatively charged alkyl ions and H+. Although the effect of irradiation can in general be complicated, the effect of monochromatic x-ray irradiation here can safely be described as a donation of secondary electrons or a photo-reduction in the vicinity of absorbed atoms. Thus, in the K = 0 case (C1), the Cu+ intermediates were reduced to Cu0 monomers and likewise the Cu2+ planar complexes were reduced mostly to Cu+ monomers in the K ≫ 1 case (S). As seen in Figs. 1(c) and (d), the 2D mapping optical and x-ray images for S reveal that copper aggregates were formed on the focused x-ray beam spot (600 μm(H) × 300 μm(V)), which was horizontally expanded for geometrical reasons (an incidence angle of 45°). The AFM data for S in Fig. 1(e) indicate a smooth surface (surface roughness ≈ 80 nm) resulting from a very slow deposition rate (~10 nm/h).
XAS experiments and analysis
In Fig. 2(a), the Cu K-XANES spectra for R2eq (C1), measured as an average of the reactant solution and aggregates, show the evolution of the near-edge features upon irradiation, indicating a gradual change from the Cu2+ to Cu0 states, linear with respect to elapsed time. Such photo-reduction of copper ions was also found at other synchrotron radiation beamlines that provide high-flux photon beams, typically 1012 photons/s19. Characteristic features A–D in the XANES data for R2eq after irradiation match with well-known signatures of fcc metals. By contrast, for separated aggregates recovered by in situ washing of the solution cell (Fig. 1(b)), the irradiation effect gave remarkably different XANES spectra. Strikingly, the results indicated that the radiolysis product depends on R2eq (the K-value); Figs. 2(b) and (c) show that the irradiation-induced aggregates C1 and S are fcc-like NPs and NCs, respectively. In contrast to the control, S exhibited featureless near-edge structures indicative of a small cluster (n < 19)13.
The Cu+ state is often associated with a sharp 1s-4p transition due to a “shakedown” process simultaneously with a ligand-to-metal charge transfer20, which is strongly polarized in the axial ligand direction. The inset blowup of the 1s-4p transition shows that the peak shifts slightly to higher energies in the case of S relative to the completely metallic energy level for C1, pointing to a possible incomplete photo-reduction that left some copper atoms positively charged after clustering. The intermediate energy position of the 1s-4p transition, which is absent for NPs12, could be common to small clusters with a large optical (HOMO-LUMO) gap unlike fcc metals or NPs11,12,13. The 1s-4p transition for S lies close to that of the Cu+ state, indicative of an intermediate valence state, although the true electron configuration of copper atoms in NCs (S) remains an open question.
In Fig. 3(a), normalized EXAFS oscillations multiplied by k2 are plotted as a function of photoelectron wavenumber, k, for C1, S and an fcc metal (reference). It can be seen that although the EXAFS oscillations for C1 resemble those of an fcc lattice, those for S are significantly different both in magnitude and profile. The low-k region indicated by an arrow at k = 3 Å−1 (inset) shows a systematic increase in magnitude, evidence for the emergence of a low-z element (nitrogen) in the nearest neighbor (N.N.) shell with decreasing size.
EXAFS oscillations as a function of wavenumber, k, for C1 and S, compared with those of an fcc metal (a).
The inset shows a blowup of the low-k region (k = 2.5–6 Å−1). The Fourier transform magnitude functions for C1 (b) and S (c). Open circles denote the curve-fitted results compared to the reference (an fcc metal). Model structure for the Cu13 ligated with various amines, derived by DFT geometrical optimization. Inhomogeneous electron distribution (NBO net charge) is displayed in a graded color scale. Local structures for Cu13 clusters with Ih and c-Oh symmetry and RDFs shown in separate columns (d).
In the Fourier transform of the k2-weighted χ(k) functions (Figs. 3(b) and (c)), a prominent N.N. peak at R = 2.2 Å decreases sharply in magnitude for C1 and, more significantly, for S. The magnitude drop in the N.N. peak is caused by a size variation21, as well as increased defects and disorder. The FT magnitude for S shows a strikingly different double peak consisting of (short) Cu-N bonds and (long) Cu-Cu bonds, which is evidence for a small cluster, consistent with the emergence of a low-z element scatterer (Fig. 3(a)). The emergence of Cu-N bonds is indicative of a ligated small cluster, which contains information on the cluster size and ligand coordination.
The open circles in the FT magnitude in Figs. 3(b) and (c) show the results of curve fitting in k-space (Table II). The size-dependent magnitude variation in the N.N. peak is consistent with previous studies21, while a similar short M-L bond was reported in the case of noble metal clusters8. The average coordination numbers of the Cu-N and Cu-Cu bonds, 0.7 ± 0.3 and 3.5 ± 0.6, respectively, were consistent with our DFT optimization of model clusters consisting of thirteen atoms. Montano et al.11 and Tamura et al. reported much shorter Cu-Cu distances in solid Cu NCs22 prepared onto solid argon and a p-type GaAs (100) surface, respectively. In our experiment, the observed Cu-Cu distance, 2.56 Å (S), was close to the fully relaxed bond23. The disorder parameter, σ2, fell in the range of 7.6–9.8 (10−3 Å2), in good agreement with Jayanetti et al.19. Compared to the Cu-N distance in Cu2+ complexes such as 2.05 Å [Cu(H2O)2(NH3)4] or 2.08 Å in the pyridine complex, the short Cu-N distance (1.90 Å) remains puzzling. Such a short distance implies a strong interaction between the surface atoms and ligand molecules which may provide a clue to interpreting the 1s-4p peak shift.
Discussion
NCs prepared by radiolysis consist of a small number of atoms (n = 13–19). Taking into account the coordination number evaluated by EXAFS analysis, we chose a model cluster of thirteen atoms12,13. Let us first focus on the possible model clusters with different symmetries, viz., icosahedron (Ih), cubo-octahedron (c-Oh), hexagonal close-packed (hcp), bicapped double-decker sandwich, etc.24. First-principle calculations on bare clusters (n ≤ 10)25,26 have established the structural evolution of electron affinity and ionization potential, reflecting the electronic shell and subshell closing. One of the most striking results was the inhomogeneous electron distribution illustrated in the map of NBO charge (net charge) in Fig. 3(d). Using the optimized atomic coordinates of the ligated model cluster, XANES spectra were calculated by the full potential multiple scattering (FPMS) approach beyond the muffin-tin approximation27. For localized systems such as NCs, the muffin-tin approximation often fails and FPMS is required27. The XANES spectra were calculated on the basis of geometrically optimized atomic coordinates for ligated model clusters using the FPMS approach.
Our DFT calculation of all possible symmetry cases narrowed down the candidates to the two symmetry models Ih and c-Oh. A comparison of the experimental XANES for S with the FPMS calculation (Fig. 4(a)) indicates that the symmetry is likely to be icosahedral, consistent with recent work on Cu clusters in Ar shells12. Our analysis of the radial distribution functions (RDFs) revealed that the structural difference between the Ih and c-Oh models is essentially the broader distribution of the second shell in the Ih symmetry. This rearrangement of the second shell could minimize the Cu-Cu distance variation and lower the Coulombic repulsion between surface atoms. Also, the absence of the experimental double-peak XANES feature around 9,000 eV observed for n > 43 (an fcc lattice) in Fig. 2(c)12,13 is consistent with the symmetry of the model cluster. Highly distorted nature of the Ih cluster was reported by computational studies for bare Cu13 and Au1329 while for M@Au12 series of clusters (M = W, Mo), the Ih symmetry is lower in energy than the Oh30. As the symmetry dependence of stability for the two cases is marginal, it is likely that the metal-ligand interaction becomes crucial.
Theoretical Cu K-XANES spectra for Cu13 clusters with Ih and c-Oh symmetry, obtained by the FPMS calculation, compared with the experiment (a). The RDFs calculated for the Ih and c-Oh model clusters coordinated with ligand amine RNH2 (neutral model cluster, NMC) and deprotonated amido RNH− (charged model cluster, CMC) (b). Orbital energy diagram (α-spin orbitals only, for simplicity) with the HOMO-LUMO gap also illustrated (c).
The RDFs in Fig. 4(b) calculated for optimized model structures were compared with the EXAFS-RDF constructed from the experimental structural parameters of EXAFS analysis (Table II). The N.N. region was well reproduced by the optimized “neutral” model cluster (NMC) consisting of 13 Cu0 atoms. However, the metal-ligand interaction in this model cluster appears to be underestimated, as the experimental Cu-N distance (1.90 Å) is 0.2 Å shorter than that in the model.
Thus, we examined a “charged” model cluster (“CMC”) in Fig. 4(b), in contrast to NMC (“Ih-NMC” and “c-Oh-NMC” in the same panel). The CMC is highlighted by twelve positively charged surface atoms ligated with highly electron-donating molecules canceling the local charge imbalance. Amido (RNH−), which is formed by radiation-induced deprotonation, is more likely to serve as an electron donor than amine (RNH2). N−H bond-forming and -breaking processes often relate to catalytic activities such as ammonia synthesis31 and occur by photon irradiation. Recent work by Jonson et al.32 suggested that decay processes, rather than photo-excitation, generate a large number of secondary electrons, which would populate the antibonding orbitals and thus initiate bond-breaking. As a result, an amido complex with low-valence metal ions would strengthen the M-L bond and be detectable as a bond length shortening. Indeed, the RDF calculated for CMC gave a Cu-N distance (1.90 Å) in good agreement with the experimental value.
The calculated HOMO-LUMO gaps ligated by methyl amine were 0.79 and 0.73 eV for Ih-NMC and c-Oh-NMC, respectively, in remarkable contrast to the 1.2 eV for Ih-CMC (Fig. 4(c)). The large HOMO-LUMO gap of CMC is consistent with the observed short Cu-N distance. The MO levels and their shapes around the gap in Fig. 4(c) and Fig. S5, where only α-spin orbitals are shown for simplicity, suggest that the electronic states of the two models are quite different. Compared with congested MOs in NMC, discrete MOs with different shapes are found around the gap in CMC. The frontier MOs from HOMO-4 to LUMO+3 in NMC consist of σ-type orbitals over the space extending to the ligands or surface Cu atoms. In contrast, the HOMO and LUMO in CMC are due to π-type orbitals localized to the Cu-N-C bonds. The difference on the frontier MOs may lead to a different redox reactivity.
How does the precursor equilibrium R2eq between Cu2+ ions and Cu+ ions control the product of synchrotron radiolysis? In the case of C1, with its strong reducing power (see Table I), wet chemistry (R2) completely transforms Cu2+ ions into Cu+ ions (See Fig. 2(c)). The disproportionation reaction (R3) converts half of the Cu+ ions into Cu0 monomers ligated by amine molecules. In contrast, the R2eq for S is dominated by the Cu2+ states, owing to an extremely slow kinetics or a strong reverse reaction, which would lead to monomer starvation.
In our schematic model (Fig. 5), what determines the nature of radiolysis is the type and density of “monomers”. The pathway to CMC is governed by its monomer ligated to amido whose σ orbital strongly interacts with the Cu+ 4s and 3d orbitals, which would be further strengthened by π orbital overlapping as a result of hybridization change from sp3 nitrogen atom (tetrahedral) to sp2 one (trigonal planar) upon the formation of CMC, in sharp contrast to a linear complex with two ligand amines with sp2 nitrogen atom in the case of NMC. For K = 0, photo-reduction eventually creates Cu0 monomers (amine complexes) that assemble into nuclei, which later grow into NPs. In contrast, for K ≫ 1, the monomer is a singly ligated amido whose nitrogen atoms are strongly bound to surface copper atoms (Fig. 5). Such Cu+ amido complexes may also exist in the case of C1, but they would be overwhelmed in density by the Cu0 monomers.
In this work, wet chemistry and radiolysis controlled the type and density of “monomers” in a concerted fashion, so that nucleation is suppressed while charged clusters are stabilized. We show that combining the advantages of these two complementary reducing techniques could provide a novel means of stabilizing late transition metal clusters with unique electronic states.
Methods
X-ray absorption spectroscopy
XAS spectra were measured in the fluorescence mode with an energy resolution of ~1.5 eV (9 keV). The EXAFS oscillation functions were extracted using ATHENA33 and least-squares parameter fitting was performed using ARTEMIS33, both of which were implemented in the IFEFFIT package34. The k2-weighted χ(k) functions were Fourier transformed into R-space using a Hanning window over a typical k-range of 2.5–10.5 Å−1. The ab initio multiple-scattering code FEFF8.20 with the muffin-tin approximation and FPMS27 and MXAN35 codes for the full potential multiple scattering calculation were used for the calculation of XANES for model clusters.
DFT calculations
The DFT calculations were performed to obtain the optimized geometries and electronic structures of model clusters. These NCs were treated as open-shell systems and calculated by the unrestricted scheme of Becke's three-parameter hybrid functional with the correlation functional of Lee, Yang and Parr, i.e., uB3LYP36. The LanL2DZ basis set was adopted for all DFT calculations. In the LanL2DZ, the double-zeta functions and Los Alamos effective core potential (ECP) were adopted for valence and core electrons of the Cu atom, respectively37. On the other hand, the Dunning/Huzinaga valence double-zeta functions (D95V)38 were adopted for the other atoms (H, C and N) in the basis set. For the DFT calculations, out of possible model symmetries, four models with different symmetries were taken into account, i.e., icosahedron (Ih), cubo-octahedron (c-Oh) or face-centered cubic (fcc), hexagonal close-packed (hcp) or truncated hexagonal bipyramid and bicapped double-decker sandwich of five-fold geometry (bicapped)24. Although those models optimized as a bare cluster in vacuum at T = 0 K do not always give the lowest energy structure under the realistic condition39, those models can be candidates for liganded clusters in solution at a finite temperature.
Four different model structures were prepared by GaussView 5.0 and the geometrical parameters were fully optimized without symmetry constraints by the Gaussian09 program package. The lowest energy spin multiplicities were studied for a neutral bare cluster over seven different spin multiplicities 2, 4, 6, 8, 10, 12 and 14. Out of starting four different symmetries, most stable spin multiplicity was found for the two models Ih and c-Oh, with spin multiplicity S = 6 and 2, respectively while other two models (hcp and bicapped) failed to keep the symmetry during the optimization. The energy minima were confirmed for the Ih and c-Oh models by performing a frequency analysis.
On the other hand, for amine liganded clusters, there are numerous possibilities on the conformation of 12 amine molecules. It is very hard to determine the lowest energy spin multiplicities for the liganded cluster because a lot of local minimum structures are expected. Therefore, for simplicity, the ground-state spin multiplicities S = 6 and 2 determined for the bare Cu13 nanoclusters were adopted for the amine liganded Cu13 models with Ih and c-Oh symmetries, respectively. Natural bond orbital (NBO) population analyses (Gaussian NBO Version 3.1) were applied to find out the charge distribution on the optimized structures, which were illustrated by GaussView 5.0.
References
Aiken, J. D., III & Finke, R. G. A review of modern transition-metal nanoclusters: their synthesis, characterization and applications in catalysis. J. of Mol. Catal. A: Chemical 145, 1–44 (1999).
Crespo, P. et al. Permanent Magnetism, Magnetic Anisotropy and Hysterisis of Triol-Capped Gold Nanoparticles. Phys. Rev. Lett. 93, 087204–087208 (2004).
Haruta, M. et al. Gold Catalysts Prepared by Coprecipitation for Low-Temperature Oxidation of Hydrogen and of Carbon Monoxide. J. Catal. 115, 301–309 (1989).
Faraday, M. The Bakerian Lecture: Experimental Relations of Gold (and Other Metals) to Light. Philos. Trans. R. Soc. London, 147, 145–181 (1857).
Brust, M. et al. Synthesis of Thiol-derivatised Gold Nanoparticles in a Two-phase Liquid-Liquid System. J. Chem. Soc. Chem. Commun., Issue 7 801–802 (1994).
Watzky, M. A. et al. A New Mechanism When Hydrogen Is the Reductant: Slow, Continuous Nucleation and Fast Autocatalytic Surface Growth. J. Am. Chem. Soc. 119, 10382–10400 (1997).
Smolentsev, G. & Soldatov, A. V. Quantum local structure refinement from XANES: multi-dimensional interpretation approach. J. Synch. Rad. 13, 19–29 (2006).
Yao, T. et al. Probing Nucleation Pathways for Morphological Manipulation of Platinum Nanocrystals. J. Am. Chem. Soc., 134, 9410–9416 (2012).
Ostwald, W. Stüdien uber die Bildung und Umwandlung fester Körper. Zeitschrift für physikalische Chemie, 22, 289–330 (1897).
Nishijima, S. et al. In Situ Time-Resolved XAFS Study on the Formation Mechanism of Cu Nanoparticles Using Poly (N-vinyl-2-pyrrolidone) as a Capping Agent. Langmuir 26, 4473–4479 (2010).
Montano, P. A. et al. Structure of Copper Monoclusters Isolated in Solid Argon. Phys. Rev. Lett. 56, 2076–2079 (1986).
Mazalova, V. L. et al. Small Copper Clusters in Ar Shells: A Study of Local Structure. J. Phys. Chem. C 113, 9086–9091 (2009).
Oyanagi, H. et al. Small copper clusters studied by x-ray absorption near-edge structure. J. Appl. Phys. 111, 084315–084319 (2012).
LaMe, V. & Dinegar, R. H. Theory, Production and Mechanism of Formation of Monodispersive Hydrosols. J. Am. Chem. Soc. 72, 4847–4854 (1950).
Buxton, G. V. & Green, J. C. Reactions of some simple α- and β-hydroxyalkyl radicals with Cu2+ and Cu+ ions in aqueous solution. A radiation chemical study. J. Chem. Soc. Faraday Trans. I 74, 697–714 (1978).
Freiberg, M. & Meyerstein, D. Reactions of aliphatic free radicals with copper cations in aqueous solution Part 2.-Reactions with cupric ions: a pulse radiolysis study. ibid 76, 1825–1837 (1980).
Khatouri, J. et al. Radiation-induced copper aggregates and oligomers. Chem. Phys. Lett. 191, 351–356 (1992).
Jonah, C. D. A short history of the radiation chemistry of water. Radiat. Res. 144, 141–147 (1995).
Jayanetti, S. et al. Analysis of radiation-induced small Cu particle cluster formation in aqueous CuCl2 . J. Chem. Phys. 115, 954–962 (2001).
Bair, R. A. & Goddard, W. A. Ab initio studies of the x-ray absorption edge in copper complexes I. Atomic Cu2+ and Cu(II)Cl2 . Phys. Rev. B 22, 2767–2776 (1980).
Roscioni, O. M. et al. Computational prediction of L3 EXAFS spectra of gold nanoparticles from classical molecular dynamics simulations. Phys. Rev. B 83, 115409–115417 (2011).
Tamura, K. et al. Structural Study of Electrochemically Deposited Cu on p-GaAs(100) in H2SO4 Solution by In Situ Surface-Sensitive X-ray Absorption Fine Structure Measurements. J. Phys. Chem. B 104, 9017–9024 (2000).
Mesu, J. G. et al. Probing the Influence of X-rays on Aqueous Copper Solutions Using Time-Resolved in Situ Combined Video/X-ray Absorption Near-Edge/Ultraviolet-Visible Spectroscopy. J. Phys. Chem. B 110, 17671–17677 (2006).
Demuynck, J. et al. Bulk properties or not: The electronic structure of small metal clusters. ibid., 75, 3443–3453 (1981).
Massobrio, C. et al. Structural and electronic properties of small Cun clusters using generalized-gradient approximation within density functional theory. J. Chem. Phys. 109, 6626–6630 (1998).
Ito, M. et al. Behaviours and Electronic Structures of Na and Cu Nanoclusters: The Role of sp-d Hybridization. Int. J. Modern Physics B 19, 2421–2426 (2005).
Hatada, K. et al. Full-potential multiple scattering for x-ray spectroscopies. Phys. Rev. B 76, 060102–060106(R) (2007).
Hatada, K. et al. Full-potential multiple scattering theory with space-filling cells for bound and continuum states. J. Phys.: Cond. Matt., 22, 185501–185524 (2010).
Li, X. et al. Experimental Observation and Computation of Icosahedral W@Au12 and Mo@Au12 Molecules. Angew Chem. Int. Ed. 41, 4786–4789 (2002).
Chou, J. P. et al. Ab initio random structure search for 13-atom clusters of fcc elements. J. Phys.: Condens. Matter 25, 125305–7 (2013).
Ertl, G. Catalytic Ammonia Synthesis Jennings, J. R. (ed.) 109–131 (Plenum Press, New York, 1991).
Johnson, P. S. et al. Universal mechanism for breaking amide bonds by ionizing radiation. J. Chem. Phys. 135, 044702–044709 (2011).
Ravel, B. et al. Data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Rad. 12, 537–541 (2005).
Newville, M. IFEFFIT: interactive XAFS analysis and FEFF Fitting. ibid, 8, 322–324 (2001).
Hayakawa, K. et al. Progresses in the MXAN Fitting Procedure. AIP Conf. Proc. 882, 111–113 (2007).
Lee, C. et al. Development of the Colle-Salvetti correlation-energy formula into a function of the electron density. Phys. Rev. B, 37, 785–789 (1988).
Hay, P. J. & Wadt, W. R. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 82, 270–285 (1985).
Dunning Jr, T. H. & Hay, P. J. Modern Theoretical Chemistry Vol. 3 Schaefer, H. F. (ed.) 1–28 (Plenum, New York, 1976).
Yan, M. et al. Structure and shape variation in intermediate-size copper clusters. J. Chem. Phys. 124, 024308–6 (2006).
Acknowledgements
The authors would like to thank Y. Niwa for technical assistance during the synchrotron experiments performed under Proposal 2010G097 supported by CREST. The DFT calculations were performed using the computational facilities at the Research Institute for Information Technology, Kyushu University. A part of this work was supported by European FP7 MSNano network under Grant No. PIRSES-GA-2012-317554.
Author information
Authors and Affiliations
Contributions
All authors contributed substantially to this work. H.O. and Y.O. wrote the main manuscript text and figures 1–5. The experiments were performed by H.O., Y.O., L.Z., K.Y., H.N., M.U., A.F. and Y.O. while Y.O. carried out the DFT calculation. K. Hay. and K. Hat. performed the FPMS calculations of XANES while Z.S. analyzed the EXAFS experimental data. H.M. coordinated the research team. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supporting Online Materials
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Oyanagi, H., Orimoto, Y., Hayakawa, K. et al. Nanoclusters Synthesized by Synchrotron Radiolysis in Concert with Wet Chemistry. Sci Rep 4, 7199 (2014). https://doi.org/10.1038/srep07199
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07199
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.