Abstract
The thermoelectric properties of multiple core-shell nanowires are investigated by using nonequilibrium Green's function method and molecular dynamics simulations. The results show that the thermoelectric performance of multiple core-shell NWs can be improved observably with the increase of shell number compared with the single component NWs due to the significant reduction of phonon thermal conductance. The ZT value of multiple core-shell NWs can reach three times greater than that of the single component GaSb NWs at room temperature. Moreover, the ZT values of both the core-shell NWs and single component NWs are increased with the increasing temperature, but the ZT value of core-shell NWs increases more slowly than that of single component NWs. These results show that the single component NWs is suitable as thermoelectric material at much high temperature, but the multiple core-shell NWs is more suitable as thermoelectric material at room temperature.
Similar content being viewed by others
Introduction
The thermoelectric energy conversion technology, which can directly convert heat into electricity and vice versa without moving parts, have received considerable attention in recent years due to their great potential in both cooling system and power generation1,2. The most important factor that determines the conversion efficiency is captured by a dimensionless figure of merit of the materials, defined as ZT = σS2T/(λe + λph), where σ is the electrical conductivity, S is the Seebeck coefficient, T is the absolute temperature, λe is the electrical thermal conductivity and λph is the phonon thermal conductivity. A good thermoelectric material has a large ZT value which requires a large power factor (σS2) along with a low thermal conductivity (λe + λph). However, it is very difficult to significantly improve the thermoelectric performance of conventional materials because the σ, S and λe are coupled unfavorably3,4. For instance, a high electrical conductivity usually leads to a low Seebeck coefficient and a high electrical thermal conductivity, both of which are undesirable for thermoelectric applications. A major breakthrough came in the 1993, Hicks et al. theoretically predicated that low-dimensional structures may increase the ZT value by reducing lattice thermal conductivity with phonon-boundary scattering5. Since then, a strong research activity has been focused on the low-dimensional structures, such as superlattices6,7, nanowires (NWs)8,9,10,11,12, nanoribbons13,14,15, nanocomposites16,17, etc, for thermoelectric applications.
Recent years, semiconductor NWs have received considerable attention due to their great potential for thermoelectric application18. Primary interest in nanowires is motivated by the significantly suppressed phonon thermal conductivity due to the phonon-boundary scattering and possible phononics engineering19,20,21. Another advantage of nanowires is a high power factor due to enhanced electrical density of states near the Fermi level, which is caused by quantum confinement5. Indeed, recent experimental and theoretical efforts have demonstrated that silicon NWs can be regarded as efficient thermoelectric materials although bulk silicon is not22. In addition, compared to the single component semiconductor NWs, the physical properties of core-shell NWs can be further manipulated by changing the configurations and compositions. For example, intrinsic core-shell NWs exhibit high carrier mobility due to the suppression of ionized impurity scattering and surface charges23. At the same time, the core-shell NWs have a very low phonon thermal conductance due to the enhancement of surface scattering20. So the high mobility and low phonon thermal conductance may give us an opportunity to improve the thermoelectric properties of the NWs.
However, there are only a few theoretical studies on the thermoelectric properties of Si/Ge core-shell NWs24,25,26 and the thermoelectric properties in multiple core-shell NWs are still in its infancy. Recently, GaSb/InAs and InAs/GaSb core-shell NWs have been fabricated experimentally and exhibit excellent electrical performances27. Therefore, in the present work, we investigate systematically the thermoelectric properties of GaSb/InAs and InAs/GaSb core-shell NWs. To further improve the thermoelectric performance, we also research the thermoelectric properties of multiple GaSb/InAs core-shell NWs. The results show that the thermoelectric performance of both the GaSb/InAs core-shell NWs and InAs/GaSb core-shell NWs are improved observably compared with the single component NWs. We also find that the thermoelectric performance of multiple core-shell NWs can be further improved significantly with the increase of shell number. The ZT value can reach three times greater than that of the single component GaSb NWs at room temperature. Moreover, we also investigate the influence of temperature on the thermoelectric properties in core-shell NWs. The results show that the ZT values in core-shell NWs and single component NWs are both increased with the increasing temperature. However, the ZT value in core-shell NWs increases more slowly than that of single component NWs, which means the multiple core-shell NWs is more suitable as thermoelectric material at room temperature.
Results
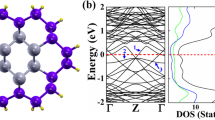
To research the influence of core-shell structure on the electron transport properties, we plot the energy band structure and the electrical transmission function for GaSb NWs, GaSb/InAs core-shell NWs, InAs NWs and GaSb/InAs multiple core-shell NWs, as shown in Fig. 1(a)–(d), the inset is the corresponding geometry. Here, we adopt the notation mA/nB to designate the GaSb/InAs core-shell NWs. A and B indicate the GaSb and InAs, m and n indicate the radius of core and the thickness of shell respectively. For instance, the 4A/2B indicates that the radius of GaSb core is of four layers atoms; the thickness of InAs shell is of two layers atoms. From Fig. 1, it is clearly shown that the transmission functions display clear stepwise structures, which shows the number of electron channels. The quantized transmission can also be obtained by counting the numbers of energy bands at any given energy. Based on the electron transmission function, we calculate the electrical conductance G, the Seebeck coefficient S and the power factor S2G of GaSb NWs, GaSb/InAs core-shell NWs and InAs NWs at toom temperature, as shown in Fig. 2(a). It is worth saying explicitly that we use the electrical conductance to define the power factor instead of electrical conductivity, because the electrical conductivity in a nanoscale system cannot be well defined since the cross-sectional area is not well defined and the ZT will not be affected because we use the thermal conductance in the definition of ZT, not thermal conductivity at the same time. Here, the G, S and S2G correspond to the optimal values to achieve the maximum value of ZT. It is shown that the core-shell NW has a lower electrical conductance compared with the single component NW, but the Seebeck coefficient of core-shell NW is higher than that of single component NW. In sum, the power factor is little changed in different core-shell NW.
To evaluate the ZT value explicitly, we calculated the phonon thermal conductance and electron thermal conductance of GaSb/InAs core-shell NW with different proportions as shown in Fig. 2(b). The electron thermal conductance corresponds to the optimal value to achieve the maximum value of ZT. It is shown that the phonon thermal conductance is one order of magnitude higher than electron thermal conductance, which shows phonon thermal conductance being dominant in semiconductor NW. This figure also shows that the phonon thermal conductance decreases at first and reaches a minimum value at 5A/1B and then increases with the further increase of the thickness of shell. The similar trend also appears in InAs/GaAs core-shell NWs and Si/Ge core-shell NWs20,28. The reduction in the thermal conductance of core-shell NWs stems from the depression and localization of long-wavelength phonon modes at the core-shell interface and high frequency nonpropagating diffusive modes20 and the increase in thermal conductance with the increase of shell thickness is because the dominant heat transfer channel changes from core to shell28. In addition, it is worth noting that the electrical conductance has a similar trend with electron thermal conductance, since the charge carriers are also heat carriers. Actually, the correlation between electrical conductance and electrical thermal conductance is one of the main reasons that most of the experiments by regulating the carrier concentration failed to achieve high ZT.
Based on the calculated power factor S2G, the electrical thermal conductance κe and the phonon thermal conductance κph, we calculate the maximum ZT value of core-shell NWs with different proportions at room temperature as shown in Fig. 2(c). The ZTmax curve first increases and reaches the maximum value at 5A/1B and then decreases with the further increases of the shell thickness. The optimal ZT value can reach 0.79, which is about 65% higher than that of single component GaSb NW. It is because the 5A/1B has the lowest thermal conductance, at the same time, the power factor is not deteriorated. In other words, the lower thermal conductance combining with the unaffected power factor produces the peak ZT.
To prove the conclusion that the thermoelectric performance of core-shell NW is much better than that of single component NW is universal, we also calculated the thermoelectric properties of InAs/GaSb core-shell NW at room temperature as shown in Figs. 3(a)–(c). Fig. 3(a) shows the optimal power factor in different proportions InAs/GaSb core-shell NW. It is clearly shown that the power factor in core-shell NW is lower than that in single component InAs NW. The similar trend also appears in the electrical thermal conductance due to the Wiedemann-Franz law as shown in Fig. 3(b). Besides, the phonon thermal conductance in InAs/GaSb core-shell NW rapidly goes down compared with the single component NW. This result is consistent with above calculation in GaSb/InAs core-shell NW. Based on the calculated power factor S2G and thermal conductance, we calculate the optimal ZT value in InAs/GaSb core-shell NW with different proportions at roon temperature as shown in Fig. 3(c). It is clearly shown that the 3A/3B has the maximum ZT value, since the 3A/3B has the lowest thermal conductance. Although the power factor of 3A/3B is lower than that of 6A/0B, the maximum ZT value originates from the competition between power factor and thermal conductance.
It is important to note that the shape of the ZT curve of InAs/GaSb NW is different from that of GaSb/InAs NW. This is due to the difference of phonon thermal conductance, which originates from the difference of thermal conductance between core and shell28. If the thermal conductance of core is larger than that of shell, the core is dominant thermal transport channel, however, in case the thermal conductance of core is less than that of shell, the dominant thermal transport channel will change from core to shell with the increasing shell thickness. This result also agrees with previous studies28,30. As shown in Fig. 2 and Fig. 3, the 5A/1B has the largest ZT due to the 5A/1B being of the lowest phonon thermal conductance and so does 3B/3A. In short, the difference of ZT curve shape between GaSb/InAs core-shell NW and InAs/GaSb core-shell NW originates from the difference of thermal conductance in core and shell. However, this does not violate the conclusion that the thermoelectric performance of core-shell NW is much better than the single component NW at room temperature.
In order to further improve the thermoelectric performance of core-shell NWs exploratory, we design a novel multiple GaSb/InAs core-shell structure and calculate the thermoelectric properties as shown in Figs. 4(a)–(c). As a comparison, the thermoelectric properties of GaSb NW are also given. Fig. 4(a) shows the power factor of the four different structures at room temperature. It is clearly shown that the core-shell NWs have lower power factor than the single component GaSb NWs and the power factor is almost constant with the increasing shell number. This is due to the fact that the Seebeck coefficient and electrical conductance depend on the electrical band structure and the electrical band structure of multiple core-shell structure is of little change with the increase of shell number, as shown in Fig. 1(b) and Fig. 1(d). The electron thermal conductance has a same trend as power factor due to the Wiedemann-Franz law, as shown in Fig. 4(b). In addition, the phonon thermal conductance rapidly goes down as the increasing shell number due to the enhancement of phonon-boundary scattering, which is very important in the quasi-one-dimensional nanowire due to the size effect and high surface to volume ratio29. In short, the decreasing phonon thermal conductance combining with the almost constant power factor leads to the increase of ZT in multiple core-shell NWs, as shown in Fig. 4(c). The ZT value of 2A/1B/1A/1B/1A can reach about three times greater than that of the single component GaSb NW at 300 K. In other words, the ZT in multiple core-shell NW can be enhanced significantly compared with the single component NW at room temperature due to the decreasing phonon thermal conductance and unaffected power factor.
So far, we have seen that the thermoelectric performance of multiple core-shell NW is much better than that of single component NW at room temperature. In order to verify whether this advantage still exists at other temperatures, we plot the temperature dependence of ZT of different core-shell NWs, as shown in Fig. 5(a). From the panel (a), two facts are apparent: (i) The ZT values of the four structures are all increased as the temperature increases. (ii) The GaSb NW has a lower ZT value than that of other core-shell NWs at 300 K, but it goes up much faster than that of other core-shell NWs with increasing temperature, thus the ZT values of GaSb NWs exceed those of core-shell NWs in the temperature region above 400 K. In order to explain the two facts, we plot the power factor, phonon thermal conductance and electron thermal conductance of the four different structures as a function of temperature in Figs. 5(b)–(d), respectively. Obviously, the power factors of the four structures are all increased with the increasing temperature. It is because that a growing number of electrons can be excited into the conductance band and contribute to the electrical conductance with the increasing temperature. For the same reason, the electron thermal conductance has also a similar trend with the power factor due to the charge carriers are also heat carriers. Besides, the phonon thermal conductance of the GaSb NWs rapidly goes down as the temperature increases due to the significant enhancement of Umklapp phonon-phonon scattering. On the contrary, the phonon thermal conductance of core-shell NWs shows little change with the increasing temperature. Therefore, the increasing power factor and electron thermal conductance combining with the decreasing phonon thermal conductance lead to the increase of ZT values as the temperature is increased. In addition, the rapid increase of ZT value in GaSb NW is because the phonon thermal conductance goes down rapidly due to the enhancement of Umklapp phonon-phonon scattering with the increasing temperature and the slow increase of ZT value in core-shell NWs is due to the phonon thermal conductance shows little change with the increasing temperature as shown in Fig. 5(c). In short, the multiple core-shell NWs is more suitable as thermoelectric material at room temperature, but the single component NWs is more suitable as thermoelectric material at high temperature.
The temperature dependence of thermal conductance in core-shell NWs is shown in Fig. 5(c). The phonon thermal conductance of the GaSb NWs rapidly goes down as the temperature increases, but that of core-shell NWs is of little change. The similar phenomenon also appears in the Si/Ge core-shell NW30. This phenomenon can be understood from the phonon scattering mechanism. The increase of the temperature has two effects on phonon thermal conductance. On the one hand, the Umklapp phonon-phonon scattering is enhanced with an increase in temperature. On the other hand, with the increase of temperature, the heat capacities of phonons increase significantly, especially for the high-frequency phonons29. So the temperature dependence of thermal conductance is determined by the competition between the two effects.
Discussion
In summary, the thermoelectric properties of InAs and GaSb multiple core-shell NWs are investigated by using nonequilibrium Green's function method and molecular dynamics simulations. A slight decrease of power factor is observed when the core-shell structure is introduced, associated with remarkable reduction of phonon thermal conductance. These two forces make the ZT of core-shell NWs increase obviously. We also find that the thermoelectric performance of multiple core-shell NWs is significantly improved due to the remarkable reduction of phonon thermal conductance. The ZT value can reach three times greater than that of the single component GaSb NW at room temperature. Moreover, we investigate the influence of temperature on the thermoelectric properties in core-shell NWs. The result shows that the multiple core-shell NW is more suitable as thermoelectric material at room temperature, but the single component NW is more suitable as thermoelectric material at high temperature.
Methods
We adopt the nonequilibrium Green's function method in combination with density functional theory, which is implemented in the Atomistix ToolKit (ATK) software package31,32, to optimize structure and calculate the electrical transmission. Here, a ballistic transport is assumed and this will not affect the relative variation of the electrical conductance in different structures. The single-zeta plus polarization basis set are employed and the exchange-correlation potential is described by the local-density approximation. The cutoff energy is set to 150 Ry. The Brillouin zone is sampled with 1 × 1 × 100 Monkhorst-Pack k-mesh. All atomic positions are relaxed until the maximum atomic force becomes smaller than 0.02 eV/A. According to the Caroli formula, the electron transmission is calculated as

where Gr = (Ga)† is the advanced Green function of the central scattering region and ΓL(R) represents the coupling interaction with the left (right) semi-infinite lead. Thus, the electrical physical quantities involved in the ZT formula can be calculated by, respectively,



With

where f(E,μ,T) is the Fermi-Dirac distribution function at the chemical potential μ and temperature T.
We calculate the lattice thermal conductance by using the nonequilibrium molecular dynamics (NEMD) simulations implemented in the LAMMPS software package. In our simulations, the Tersoff potential, which is widely used in the atomistic simulations of the group III–V semiconductors, is employed to model the atomic interactions33,34,35,36,37. The parameterization of the Tersoff potential we used, which is obtained by fitting the 12 parameters in the functional form to experimental and density functional theory calculated values of the cohesive energy, the lattice parameter, the three elastic constants, comes from the reference 34. The initial structure is relaxed in Nosé-Hoover thermostats at temperature T, T is the average temperature. The velocity Verlet algorithm is used to integrate the differential equations of motions with an integration time step of 1.0 fs. After structure relaxation for 1 × 106 steps, the Nosé-Hoover heat baths with different temperaetures, TL = T + ΔT and TR = T − ΔT, are applied to the two ends of nanowires to establish a temperature gradient along the longitudinal direction. The simulations are performed long enough (2 × 107 time steps) such that the system reaches a nonequilibrium stationary state where the heat current going through the system is time independent, the thermal conductivity is calculated from the Fourier law, λph = J/∇T, where J is the heat flux along the longitudinal direction and ∇T is the temperature gradient, which is calculated from linear fitting to the temperature profile and it can be written as ∇T = (TL − TR)/L, with L is the length of NWs. Having obtained the λph, the thermal conductance can be calculated by κph = λph·S/L, where S is the cross-sectional area. In addition, the length of all the nanowires in our simulation is about 20 nanometres. It is worth noting that the NEMD results heavily depend on the system size. However, the focus of the work is the effect of core-shell structure for thermoelectric properties in the same system size, so the finite-size effects will not affect the conclusions.
References
Majumdar, A. Thermoelectricity in semiconductor nanostructures. Science 303, 777 (2004).
Zebarjadi, M., Esfarjani, K., Dresselhaus, M. S., Ren, Z. F. & Chen, G. Perspectives on thermoelectrics: from fundamentals to device applications. Energy Environ. Sci. 5, 5147 (2012).
Mahan, G. D., Sales, B. & Sharp, J. Thermoelectric materials: New approaches to an old problem. Phys. Today 50, 42 (1997).
Chung, D. Y. et al. CsBi4Te6: A High-Performance Thermoelectric Material for Low-Temperature Applications. Science 287, 1024–1027 (2000).
Hicks, L. D. & Dresselhaus, M. S. Thermoelectric figure of merit of a one-dimensional conductor. Phys. Rev. B 47, 16631–16634 (1993).
Zhou, W. W. et al. Multi-Phased Nanoparticles for Enhanced Thermoelectric Properties. Adv. Mater. 21, 3196–3200 (2009).
Balandin, A. A. & Lazarenkova, O. L. Mechanism for thermoelectric figure-of-merit enhancement in regimented quantum dot superlattices. Appl. Phys. Lett. 82, 3 (2003).
Zhang, G., Zhang, Q., Bui, C. T., Lo, G. Q. & Li, B. Thermoelectric performance of silicon nanowires. Appl. Phys. Lett. 94, 213108 (2009).
Yan, Q. Y. et al. A Simple Chemical Approach for PbTe Nanowires with Enhanced Thermoelectric Properties. Chem. Mater. 20, 6298–6300 (2008).
Bejenari, I., Kantser, V. & Balandin, A. A. Thermoelectric properties of electrically gated bismuth telluride nanowires. Phys. Rev. B 81, 075316 (2010).
Nika, D. L. et al. Suppression of phonon heat conduction in cross-section-modulated nanowires. Phys. Rev. B 85, 205439 (2012).
Takahashi, K. et al. Bifunctional thermoelectric tube made of tilted multilayer material as an alternative to standard heat exchangers. Sci. Rep. 3, 1501 (2013).
Xie, Z. X. et al. Enhancement of thermoelectric properties in graphene nanoribbons modulated with stub structures. Appl. Phys. Lett. 100, 183110 (2012).
Sevincli, H., Sevik, C., Cagin, T. & Cuniberti, G. A bottom-up route to enhance thermoelectric figures of merit in graphene nanoribbons. Sci. Rep. 3, 1228 (2013).
Jiang, J. W., Wang, J. S. & Li, B. A nonequilibrium Green's function study of thermoelectric properties in single-walled carbon nanotubes. J. Appl. Phys. 109, 014326 (2011).
Liu, W. S. et al. Thermoelectric property studies of Cu-doped n-type CuxBi2Te2.7Se0.3 nanocomposites. Adv. Energy Mater. 1, 577 (2011).
Joshi, G. et al. Enhancement in thermoelectric figure-of-merit of an n-type half-Heusler compound by the nanocomposite approach. Adv. Energy Mater. 1, 643–647 (2011).
Hochbaum, A. I. & Yang, P. Semiconductor Nanowires for Energy Conversion. Chem. Rev. 110, 527–546 (2010).
Chen, J., Zhang, G. & Li, B. W. Impacts of Atomistic Coating on Thermal Conductivity of Germanium. Nano Lett. 12, 2826–2832 (2012).
Hu, M., Giapis, K. P., Goicochea, J. V., Zhang, X. L. & Poulikakos, D. Significant Reduction of Thermal Conductivity in Si/Ge Core-Shell Nanowires. Nano Lett. 11, 618–623 (2011).
Yang, R. G., Chen, G. & Dresselhaus, M. S. Thermal Conductivity Modeling of Core-Shell and Tubular Nanowires. Nano Lett. 5, 1111–1115 (2005).
Hochbaum, A. et al. Enhanced thermoelectric efficiency of rough silicon nanowires. Nature 451, 163 (2008).
Xiang, J. et al. Ge/Si nanowire heterostructures as high-performance field-effect transistors. Nature 441, 489–493 (2006).
Chen, X., Wang, Y. & Ma, Y. High Thermoelectric Performance of Ge/Si Core−Shell Nanowires: First-Principles Prediction. J. Phys. Chem. C 114, 9096–9100 (2010).
Markussen, T. Surface Disordered Ge–Si Core–Shell Nanowires as Efficient Thermoelectric Materials. Nano Lett. 12, 4698–4704 (2012).
Moon, J., Kim, J. H., Chen, Z. C. Y., Xiang, J. & Chen, R. Gate-Modulated Thermoelectric Power Factor of Hole Gas in Ge–Si Core–Shell Nanowires. Nano Lett. 13, 1196–1202 (2013).
Ganjipour, B. et al. Carrier control and transport modulation in GaSb/InAsSb core/shell nanowires. Appl. Phys. Lett. 101, 103501 (2012).
Liu, Y. Y., Zhou, W. X., Tang, L. M. & Chen, K. Q. Core-shell nanowire serves as heat cable. Appl. Phys. Lett. 103, 263118 (2013).
Zhang, G. & Li, B. Thermal conductivity of nanotubes revisited: Effects of chirality, isotope impurity, tube length and temperature. J. Chem. Phys. 123, 114714 (2005).
Hu, M., Zhang, X., Giapis, K. P. & Poulikakos, D. Thermal Conductivity Reduction in Core-Shell Nanowires. Phys. Rev. B 84, 085442 (2011).
Taylor, J., Guo, H. & Wang, J. Ab initio modeling of quantum transport properties of molecular electrical devices. Phys. Rev. B 63, 245407 (2001).
Brandbyge, M., Mozos, J. L., Ordejon, P., Taylor, J. & Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 65, 165401 (2002).
Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B 39, 5566 (1989).
Powell, D., Migliorato, M. A. & Cullis, A. G. Optimized Tersoff potential parameters for tetrahedrally bonded III–V semiconductors. Phys. Rev. B 75, 115202 (2007).
Monteverde, U., Migliorato, M. A., Pal, J. & Powell, D. Elastic and vibrational properties of group IV semiconductors in empirical potential modeling. J. Phys.: Condens. Matter 25, 425801 (2013).
Hammerschmidt, T., Kratzer, P. & Scheffler, M. Analytic many-body potential for InAs/GaAs surfaces and nanostructures: Formation energy of InAs quantum dots. Phys. Rev. B 77, 235303 (2008).
Jeong, C. & Lundstrom, M. Analysis of thermal conductance of ballistic point contacts. Appl. Phys. Lett. 100, 233109 (2012).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Nos. 11274105 and 91227125), by the National Basic Research Program of China (Nos. 2012CB932703 and 2011CB606405), by Hunan Provincial Natural Science Foundation of China (No. 12JJ2002), by the Specialized Research Fund for the Doctoral Program of Higher Education of China (No. 20130161130004) and by Open Research Fund Program of the State Key Laboratory of Low-Dimensional Quantum Physics. The work was carried out at National Supercomputer Center in Tianjin and the calculations were performed on TianHe-1(A).
Author information
Authors and Affiliations
Contributions
K.Q.C. and W.X.Z. conceived the research. W.X.Z. did the numerical simulations. K.Q.C. and W.X.Z. oversaw all research phases. Everyone contributed to the writing of the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhou, WX., Chen, KQ. Enhancement of Thermoelectric Performance by Reducing Phonon Thermal Conductance in Multiple Core-shell Nanowires. Sci Rep 4, 7150 (2014). https://doi.org/10.1038/srep07150
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07150
This article is cited by
-
Thermoelectric properties of SnSe nanowires with different diameters
Scientific Reports (2018)
-
Excellent thermoelectric properties induced by different contact geometries in phenalenyl-based single-molecule devices
Scientific Reports (2017)
-
Excellent Thermoelectric Properties in monolayer WSe2 Nanoribbons due to Ultralow Phonon Thermal Conductivity
Scientific Reports (2017)
-
Remote p-type Doping in GaSb/InAs Core-shell Nanowires
Scientific Reports (2015)
-
First-Principles Determination of Ultralow Thermal Conductivity of monolayer WSe2
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.