Abstract
It has been recently reported that in presence of low Reynolds number (Re ≪ 1) transport, preformed bacterial biofilms, several hours after their formation, may degenerate in form of filamentous structures, known as streamers. In this work, we explain that such streamers form as the highly viscous liquid states of the intrinsically viscoelastic biofilms. Such “viscous liquid” state can be hypothesized by noting that the time of appearance of the streamers is substantially larger than the viscoelastic relaxation time scale of the biofilms and this appearance is explained by the inability of a viscous liquid to withstand external shear. Further, by identifying the post formation dynamics of the streamers as that of a viscous liquid jet in a surrounding flow field, we can interpret several unexplained issues associated with the post-formation dynamics of streamers, such as the clogging of the flow passage or the exponential time growth of streamer dimensions. Overall our manuscript provides a biophysical basis for understanding the evolution of biofilm streamers in creeping flows.
Similar content being viewed by others
Introduction
The normal form of bacterial growth in most environments is now recognized to occur as a biofilm, which is a social form of growth associated with solid phase surfaces1,2,3,4. Biofilms include differentiated populations of cells embedded in a matrix of self-produced extracellular polymeric substances (EPS)5,6, displaying physiological properties that vary significantly from that of a dispersed cell population. Biofilms have attracted significant interdisciplinary attention as they can lead to persistent infections7,8, fouling of surfaces9,10 and at the same time help in waste-water treatment11.
Biofilms are excellent examples of viscoelastic materials12,13, exhibiting a complex range of behaviors to external force including deformation, fracture and strain-hardening6. Recently, multiple researchers have demonstrated that even in low Reynolds number (Re ≪ 1) flows, appearance of surface-hugging biofilms was followed, after a time lag of several hours, by the appearance of filamentous structures (extruding from the pre-formed biofilms) known as streamers14,15,16,17,18,19. These streamers that we study here are in creeping (Re ≪ 1) background flow (e.g., Re ~ 0.1 in Rusconi et al.15 and Drescher et al.20 and Re ~ 0.01 in Valiei et al.17) and hence are distinctly different from the streamers formed in turbulent background flow in a multitude of scenarios21,22,23,24,25,26,27. Streamer formation in low Re has wide repercussions as they can act as precursors to the formation of mature biofilms in complex microstructures17,20, lead to more rapid and catastrophic clogging of devices20, cause substantial flow-structure interactions28, etc. Despite the recent interests in biofilm streamer dynamics, there remain several open questions, e.g., What is the effect of biofilm rheology in streamer formation? What is the reason for the substantial time lag between the formation of biofilms and the appearance of streamers? How can one explain different effects associated with the post-formation dynamics of streamers, such as the rapid clogging of the flow device20, or the very fast growth of the streamer dimensions with time15?
In this work, we provide answers to all of the above questions. We start by explaining that the streamers form as the “viscous liquid” state of the intrinsically viscoelastic biofilms, with shear modulus G, viscosity μb and the viscoelastic relaxation time τve = μb/G (see Fig. 1 and Supplementary Information section 1). Such a hypothesis allows us to explain the large time lag (henceforth denoted as ts) between the formation of the biofilms and the appearance of the streamers and at the same time quantify the role of biofilm rheology in streamer formation. This hypothesis is also corroborated by the experimental signature of streamer formation, which suggests the involvement of extrusion process (Fig. 2). Being in the “viscous liquid” state, the biofilms fail to resist the flow-driven shear forces (often too weak to cause any substantial elastic extrusion) resulting in degeneration as streamers. Secondly, we explain the post-formation dynamics of the streamers as that of a highly viscous liquid jet in a background flow. In case the background flow can be approximated to be co-axial to the streamer jet transport, we demonstrate that the typical conditions pertaining to streamer formation15,16,17,18,20 will lead to “absolute instability”29,30 of the streamer liquid jet, enforcing the jet to break down into smaller drops. We derive scaling relationships to quantify the breakup length characterizing such breakup and demonstrate that these lengths are often too large to cause any drop formation in microfluidic systems studying streamer formation17. On the contrary, dictated by the geometry, if the streamer jet is in “crossflow” to the background flow20, the streamers break down into drops almost instantly after their formation. This can explain the unbroken filamentous morphology of streamers in the experiment of Valiei et al.17 and at the same time account for the “porous-matrix-like” structure inside the flow domain witnessed in the experiment of Drescher et al.20. Finally, we establish that only by considering the streamers to evolve as viscous drops, we can quantify effects such as exponential increase in streamer dimensions15,20 and catastrophic clogging of flow devices.
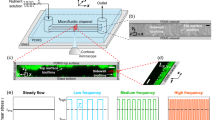
(a) Pictorial representation of the proposed hypothesis that streamers form as viscous liquid jets. (b) We show green fluorescent bacteria forming a streamer (demarcated by dashed ellipses). Flow is from top to bottom as shown by arrow. Scale bar is 20 μm (experimental set up identical to that of Valiei et al.17). Streamers form several hours after the start of formation of the biofilms and directional growth is not observed. Also the biofilms employed here are formed from Pseudomonas fluorescence bacterium – these biofilms are considered to have viscoelastic relaxation time of a few minutes.
Results
Post-formation streamer dynamics - streamers as highly viscous liquid jets
Our primary hypothesis is that streamers are formed when the biofilm attains a “viscous” state. Basis of this hypothesis is that the biofilms are viscoelastic liquids (with relaxation time τve) and the time scale of streamer formation is substantially larger than τve (see Table I, Discussions section, Supplementary Information sections I, II, Tables I and II in Supplementary Information). Streamers being formed from the “viscous liquid” biofilms, their post-formation dynamics can be interpreted as that of highly viscous liquid jets moving through a background flow. This dynamics depends on the direction of the background flow with respect to the direction of the streamer jet. In case the background flow is in the same direction as that of the streamers, we can invoke the study of Guillot et al.29,30 to describe the streamer dynamics: we perform stability analysis of the streamers, represented by a thin cylindrical viscous jet of viscosity μb and radius Rs, moving coaxially with a flow (of viscosity μf) inside a capillary of radius ξ (see section III and Fig.1 in Supplementary Information). The instability equation, characterized by the parameters Ka = (−∂p/∂z)ξ2/γ = μfuc/γ (∂p/∂z is the pressure gradient, uc is the characteristic speed of the surrounding liquid, γ is the surface tension between the streamer liquid and the bulk liquid and Ka is an effective capillary number at the scale of the capillary) and ratios Rs/ξ and μb/μf, can be expressed as (see Refs. 29, 30 and section III and Fig. 1 in Supplementary Information):

where  and E and F are functions, expressed as:
and E and F are functions, expressed as:


The resulting instability phase diagram is shown in Fig. 3. Above the lines the viscous streamer jet will be convectively unstable, whereas below the lines the jet is absolutely unstable29,30. The “absolute instability” regime is characterized by spontaneous breakdown of the jet into drops with the perturbations propagating both upstream and downstream. This is in contrast to the classical convective instability, where the perturbations propagate only downstream. In Fig. 3, we plot the experimental conditions (characterized by Ka and Rs/ξ values; see Table II for determination of these parameters) corresponding to the streamer formation, as reported in the literature15,17,20. For these experiments, we typically encounter μb/μf ~ 107 and accordingly these data points are located below the instability phase line, indicating that the streamer formation conditions are such that the streamer liquid jet will spontaneously break down into smaller drops, with the breakdown being characterized by the break up length lbs.
Phase diagram for the instability (for a circular jet in a circular capillary) in the Ka = (−∂p/∂z)ξ2/γ = μfuc/γ and Rs/ξ planes for different μb/μf values (blue dashdot line for μb/μf = 0.01, green dashed line for μb/μf = 1 and magenta solid line for μb/μf ≥ 100).
We have convective instability above the curves and absolute instability below the curves. Absolute instability leads to spontaneous breakdown of the jet into drops. We plot the experimental results [i.e., the corresponding Ka (see Table II in Supplementary Information) and Rs/ξ or Rs/(h/2) values; here h is the characteristic dimension of a possible rectangular geometry, see Supplementary Information] for different experiments (circle for Valiei et al.17, triangles for Rusconi et al.15 and squares for Drescher et al.20). Also for all the experiments μb/μf = 107 (since we take μf = 10−3 Pa-s and μb = 104 Pa-s13) and we take Rs/ξ [orRs/(h/2)] = 0.01. Therefore the experimental Ka and Rs/ξ values signify an absolute instability regime, which will suggest a spontaneous breakdown of the jet into droplets for all the streamer-forming experiments15,17,20.
Following Javadi et al.31, we can develop a scaling argument to quantify this break up length lbs for streamers in coaxial flow (see section IV in the Supplementary Information for detailed derivation) as:

Consequently, for the experiment of Valiei et al.17, we get lbs ~ 100 μm (using Rs ~ 1 μm, μb ~ 104 Pa-s, γ ~ 0.01 N/m, uc ~ 10−4 m/s) – we indeed find that the streamers continue as long unbroken jets/filaments between two microposts having separation distance much smaller than lbs (see Fig. 2 in Supplementary Information). Using the same scaling, we would get lbs ~ 1–10 mm (employing Rs ~ 1 μm, μb ~ 104 Pa-s, γ ~ 0.01 N/m, uc ~ 10−3–10−2 m/s) for the experiment of Rusconi et al.15 and Drescher et al.20. However in these experiments15,20, as per our hypothesis, the streamer viscous jet will rapidly break down into smaller drops. This can be explained by noting that in these experiments15,20, because of the flow passage geometry the streamer jet is not aligned to the background flow; rather, the jet can be assumed to be partly in a crossflow scenario (with respect to the background flow) (see Fig. 3 in Supplementary Information). In case the streamer jet is assumed to be completely in crossflow with the background flow, the breakup length can be expressed as (see section V and in Supplementary Information for detailed derivation):

The principle behind the derivation is to quantify the breakup length as the length where the momenta of the background crossflow and the streamer jet balance each other. The factor k in eq.(5) depends on the choice of the velocity scale used to quantify the flow of the streamer jet – it is equal to 2 if the velocity scale of the streamer jet is equal to the average velocity (of the background flow) and is equal to 8 if the velocity scale is the maximum velocity (of the background flow). lbs computed from eq.(5) can become even smaller than Rs (see section V and Fig. 4 in Supplementary Information) - therefore the drop formation (from streamers) is caused by the presence of geometry-induced crossflow elements15,20. Presence of such drops and its corresponding growth owing to the mass addition (see below) ensures the “porous-matrix-like” structure inside the flow domain20.
Time variation of streamer dimensions
The key physics behind the temporal variation of the streamer dimensions, as explained by Drescher et al.20, is the addition of mass to the streamers by the incoming cells. In their experiments, Rusconi et al.15 reported a close to exponential (for small times) increase in the streamer dimensions with time. They also reported a smaller streamer dimension at a given time for a weaker flow rate. Drescher et al.20 demonstrated that the time scale for this exponential streamer growth varies as 1/(flow rate). Analysis of Drescher et al.20, considering streamers as a “solid” body, cannot recover this exponential behavior - on the contrary, their analysis will exhibit a growth dynamics expressed as (see section VI in the Supplementary Information):

We rectify Drescher et al.'s analysis; we demonstrate that such exponential increase in the streamer thickness can be accounted by considering that the streamers evolve as drops. The corresponding growth dynamics can be expressed as (see section VI in the Supplementary Information):

In the above equations, C is the bacterial cell concentration, Aac is the area added by an advected cell to the streamer, β is the fraction of cells that get caught in the streamer, Δp is the pressure drop across the streamer (assuming it to be a “solid" cylinder) and Rs,0 is the thickness of the streamer at the time when streamer starts to form. In Fig. 4, we show the comparison of the experimental results15 and our theoretical prediction of the temporal variation of the streamer thickness for different flow rates. For smaller flow rates (~0.5 μL/min), we get excellent agreement with the experimental results, whereas for higher flow rates (~1 μL/min) the agreement is primarily at smaller times. At larger flow rates and at substantially large times, the flow clogging mechanism induced by the streamers will cause a weaker than exponential increase of the streamer dimensions. In the inset of the Fig. 4, we compare our theoretical prediction (τtheory,2) with the experimental result20 of the streamer formation time scale τ as a function of the flow rate and recover the 1/(flow rate) dependence of the time scale. Such dependence is also recovered for the time scale (τtheory,1) corresponding to the “solid state” streamer, although the magnitude of τtheory,1 is substantially larger, which will fail to recover the τ values observed in experiments (see inset of Fig. 4). In this context, it is worthwhile to mention that had we considered streamers as long cylindrical liquid entities with constant length with the addition of cells increasing the surface area, we would have also got dRs/dt ~ Rs, yielding an exponential growth rate of the streamers (with a time constant different from τtheory,2). The main limitation for such a hypothesis (i.e., considering streamers as long, cylindrical liquid entities) is that we assume that the streamers persist as stable jets, which is a notion not supported by the experimental systems (e.g., the systems of Drescher et al. [20] and Rusconi et al. [15]), where the streamer jets are in partial cross flow and this growth dynamics becomes evident and important. Contrary to the studies of Rusconi et al.15 and Drescher et al.20, in experimental set up of Valiei et al.17 the streamers being coaxial to the background flow, the flow direction is tangential to the direction of axis of the cylindrical jet (which does not break into droplets, see above) and hence the transfer of cells to the streamer can only occur diffusively (with diffusivity D), yielding (see section VI in the Supplementary Information):

Temporal variation of the streamer diameter ds = 2Rs.
Experimental results correspond to the streamer formation in a microchannel with 330° bend reported in the experiment of Rusconi et al.13 for different flow rates (circles for 1 μL/min and triangles for 0.5 μL/min). The continuous lines (solid line for flow rate for 1 μL/min and dashed line for 0.5 μL/min) are the theoretical predictions using an exponential variation expressed as Rs/Rs,0 = ds/ds,0 = exp[(t−t0)/τtheory,2] [this is a modification of eq.(2), considering ds(t = t0) = ds,0; here ds,0 and t0 are the values obtained from the experiment]. To compute τtheory,2, we use eq.(7), with parameters uc = 10−3 m/s (for flow rate 1 μL/min) and uc = 0.5×10−3 m/s (for flow rate 0.5 μL/min), C = 5 × 10−4 cells/μm315, Aac = 2 μm2 and β = 0.67 × 10−3. In the inset we show the variation of time scale (τ) of streamer dynamics with the flow rate. Experimental results20 are shown by markers, whereas our prediction (τtheory,2) is shown by a solid line. For this prediction, we consider the same dependence of ucon flow rate and keep all other parameters same, except for C, which is now C = 2 × 10−4 cells/μm320.
Clogging effect of streamers
As discussed by Drescher et al.20, one of the key signatures of the streamer dynamics is the manner in which it clogs the flow by causing a substantial reduction in the flow rate. Drescher et al.20 argued that such a behavior could be attributed to the “solid” state of the streamers and the fact that the streamers are positioned in the bulk and not at the walls. We find, on the contrary, that on being located in the bulk, the “liquid” state of the streamers may actually lead to a greater reduction in the flow rate (this flow rate is denoted as Qst,l) for certain ranges of streamer thickness values (see section VII and Fig. 6 in the Supplementary Information). This reduction can be explained by noting (see section VII in the Supplementary Information for detailed derivation):

where Q0 is the volume flow rate for a steady pressure-driven fully-developed flow inside a cylindrical capillary of radius ξ. This reduction gets severely more enhanced (see Fig. 6) and is manifested over the complete spectrum of the streamer thickness values, when the “viscous liquid” streamer jet, on account of geometry-induced crossflow, breaks down into smaller dimensions, which would now occupy a much larger cross sectional area of the channel. This reduction (see Fig. 5 in the Supplementary Information) can be explained from the corresponding expression of the volume flow rate. Considering that the streamer jet has broken down into 3 equal identical segments that are symmetrically placed across the capillary height, we can express the corresponding flow rate (Qst,3l) as (see section VII in the Supplementary Information):

Discussion
Why Streamers form as “viscous liquid” state of biofilms
Biofilms are viscoelastic liquids12,13,25,32 – therefore, at times t ≪ tve they exhibit a behavior analogous to elastic solids, whereas at times t ≫ tve they exhibit a behavior identical to that of highly viscous liquids (see section I in the Supplementary Information for a more elaborate discussion). Rheological measurements exhibit wide ranges of values of the shear modulus G and viscosity μb of the biofilms12,13,25,27,33,34,35,36,37, although there is a remarkable commonality in the viscoelastic relaxation time τve = μb/G13 (see section I and Table I in the Supplementary Information). In order to understand the rheological state of the biofilms that lead to streamer formation, we must compare ts with τve. In Table I, we summarize the ts values corresponding to different experiments reporting the formation of streamers, as well as the corresponding τvevalues (for the biofilms forming the streamers) obtained from separate rheological measurements. From this table it is clear that we always encounter t ≫ tve, establishing the validity of our hypothesis of considering streamers as “viscous liquid” state of the biofilms (see Fig. 1 and section I in the Supplementary Information for more details). Please note that in an earlier study, Rusconi et al.16 used this idea of t ≫ tve to hypothesize streamers as viscous liquid; however, they did not provide any further analysis to establish their claims. Also we shall like to distinguish between the streamers that we describe from that of the aggregation-driven streamers witnessed by Yazdi and Ardekani19. Our analysis negates the idea that the streamers form from the “elastic” degeneration of the biofilms15,20,38, since the imposed elastic strain (e) from the flow shear is invariably very weak, i.e., e ~ 10−2–10−415,16,17,18,20 (see Table II and section II in Supplementary Information for details). On the contrary, when the biofilms attain the “viscous liquid” state, it will fail to resist any imposed shear, thereby degenerating into streamers. Note that the quantitative relationship between the strain e (or applied stress σ) and ts, obtained from different experiments, are not well explained. In this context, it is worthwhile to point out the impact of biological growth in the streamer formation process. We shall like to emphasize here that we are not discounting biological growth based on time-scales. In fact, since streamer formation time-scales (few to several hours) are much longer than cell division time-scale (~30 min) it is not possible to rule out the role of growth based on time-scale alone. The physical basis for neglecting growth, on the contrary, is illustrated in Fig. 2. If preferential accumulation and/or growth contributed to streamer formation, then the experimental signature of streamer formation would be similar to Fig. 2a. However, in reality17, the experimental signature is similar to the illustration in Fig. 2b. This experimental signature suggests that in the initial phase, streamer formation is dominated by mechanical response of viscoelastic biofilms to externally imposed shear.
Streamers as jets and their breakup
We have based our analysis and results under the assumption that the biofilm streamers are formed as jets of highly viscous liquids. These jets are formed by the shearing action of the background flow on the viscoelastic biofilm. In this light, streamer formation is indeed “shear-driven”. Once formed, they are either in co-flow or cross-flow (partly) with the background pressure-driven transport. For the former case, in order to ensure stable base state of the jet, the axial pressure-gradient needs to be identical in both the streamer jet and the background flow and the streamer jet will be driven by an imparted shear from the background flow [see eqs.(2,3) in the Supplementary Information]. It is also important to distinguish here between the streamer jets in co-flow and cross-flow. Although like the streamers jets in co-flow, streamer jets in cross-flow also form due to the shearing action of the background transport, it need not conform to the background pressure-driven transport as is done by the jets in co-flows. This difference, as has been established here, dictate the break-up dynamics of the jet. In context of the jet break-up, we shall like to emphasize here that the jet breakup is strictly a liquid instability phenomenon. In other words, elasticity has no role to play here as evident from the fact that the corresponding elastic or elastocapillary bending length39 (considering G ~ 10 Pa for Pseudomonas aeruginosa, Rs ~ 1 μm, γ = 0.01 N/m), i.e., much smaller than the break up length for jets in both co-flow and cross-flow. Had elasticity effects been important, the break up length of the jets would have been of the same order as lEB. Finally, we shall like to mention here that we start with an assumption that the streamers, once formed, start with a radius Rs,0. Our theory of jet break up and growth dynamics of streamers remain valid as long as Rs,0 is finite. Exact prediction of the value of Rs,0 would require a full-scale numerical simulation, which is beyond the scope of the present study.
(considering G ~ 10 Pa for Pseudomonas aeruginosa, Rs ~ 1 μm, γ = 0.01 N/m), i.e., much smaller than the break up length for jets in both co-flow and cross-flow. Had elasticity effects been important, the break up length of the jets would have been of the same order as lEB. Finally, we shall like to mention here that we start with an assumption that the streamers, once formed, start with a radius Rs,0. Our theory of jet break up and growth dynamics of streamers remain valid as long as Rs,0 is finite. Exact prediction of the value of Rs,0 would require a full-scale numerical simulation, which is beyond the scope of the present study.
To summarize, we have provided a theory to establish that the biofilm streamers, witnessed at very low Reynolds number (Re ≪ 1) microfluidic transport, form as viscous liquid jets. Our theory allows us to explain the very large time scales (~several hours) associated with the streamer formation, that occurs in presence of extremely weak flow-driven shear stresses (direct experimental validation of the presented theory remains a challenging task at present). Further, our theory reproduces the experimental results15,20 of growth dynamics of the streamers quantitatively, hitherto missing from the existing studies. Finally, it is important to note that the streamer jets, which will invariably form as viscous jets, may attain viscoelastic rheology on account of entrapment of bacterial cells that produce EPS. The time scale of this change of rheology will be similar to that of the growth of process (~hours). Hence it will not affect the initial streamer viscous jet dynamics with much smaller characteristic time - we probe this initial dynamics to explain the unbroken streamers in Valiei et al.17 and jet-to-drop transition in Rusconi et al.15 and Drescher et al.20. But at larger times, this change of rheology can help explain issues such as the C0.6 dependence of timescale dictating the streamer growth20, or the physical origin of the fitting factor β. Such explanation, along with those forwarded in this study will lead to a more comprehensive understanding of the biofilms in low Reynolds number hydrodynamics.
Methods
In this study, we employ different theoretical methods, which are discussed below:
-
Stability Analysis: We have employed the Stability Analysis proposed by Guillot et al.30. The method, described in details in section III in the Supplementary Information, performs a perturbation analysis on the co-axial flow field base state (i.e., flow field that describes the transport of the highly viscous liquid streamer jet in a co-axial background microfluidic transport), provides the stability curve as a function of system parameters describing, whether or not the streamer jet will break down into drops.
-
Fluid Flow Analysis for estimating the jet breakup length: When the viscous streamer jets are co-axial to the background flow, we employ a fluid flow analysis method similar to that proposed by Javadi et al.31 to compute the breakup length of the streamer. The method is based on balancing the viscous stress term (highly magnified since the streamers are extremely viscous) with the background flow induced shear stresses (see section IV in the Supplementary Information for more details). In case the streamers are in cross-flow, we employ a fluid flow analysis method similar to that proposed by Muppidi and Mahesh40 to obtain the breakup length. The method is based on computing the distance at which the momentum of the cross-flow becomes equal to the momentum of the jet – it is at this distance the jet breaks (see section V in the Supplementary Information for more details).
-
Mass balance analysis for estimating growth rate of streamer dimensions: The streamers, assumed to evolve as liquid jets, grow in mass due to addition of advected cells. This analysis is similar to that employed by Drescher et al.20, with two exceptions. First, it consider the streamer as a liquid jet (and not a “solid” cylinder as considered by Drescher et al.20) and second the mass addition is assumed to increase the surface area of the streamers and not the cross sectional area. These exceptions ensure that we do recover the experimentally observed exponential increase in the streamer growth rate (see section VI in the Supplementary Information for more details).
-
Flow rate analysis for estimating clogging action of the streamers: The method employed here is the calculation of the net flow rate within the micro-conduit neglecting the flow inside the streamers. Calculations are done for the following cases: a) the biofilm is adhered to the conduit wall (Drescher et al. have also done this calculation20), b) the biofilm has extruded into a single “solid” streamer of cylindrical configuration (Drescher et al. have also done this calculation20), c) the biofilm has extruded into a single “liquid” streamer of cylindrical configuration and d) the biofilm has extruded into multiple “liquid” streamers (see section VII in the Supplementary Information for more details).
References
Costerton, J. W., Lewandowski, Z., Caldwell, D. E., Korber, D. R. & Lappin-Scott, H. M. Microbial biofilms. Annu. Rev. Microbiol. 49, 711–745 (1995).
Häussler, S. & Parsek, M. R. Biofilms 2009: new perspectives at the heart of surface-associated microbial communities. J. Bacteriol. 192, 2941–2949 (2010).
Neethirajan, S. et al. in Encyclopedia of Nanotechnology 213–219 (Springer, 2012).
Wong, G. C. & O'Toole, G. A. All together now: integrating biofilm research across disciplines. MRS Bull. 36, 339–345 (2011).
Flemming, H.-C. & Wingender, J. The biofilm matrix. Nat. Rev. Microbiol. 8, 623–633 (2010).
Wilking, J. N., Angelini, T. E., Seminara, A., Brenner, M. P. & Weitz, D. A. Biofilms as complex fluids. MRS Bull. 36, 385–391 (2011).
Costerton, J., Stewart, P. S. & Greenberg, E. Bacterial biofilms: a common cause of persistent infections. Science 284, 1318–1322 (1999).
Fux, C., Costerton, J., Stewart, P. & Stoodley, P. Survival strategies of infectious biofilms. Trends Microbiol. 13, 34–40 (2005).
Callow, J. A. & Callow, M. E. Trends in the development of environmentally friendly fouling-resistant marine coatings. Nat. Commun. 2, 244 (2011).
Lappin-Scott, H. M. & Costerton, J. W. Bacterial biofilms and surface fouling. Biofouling 1, 323–342 (1989).
Van Loosdrecht, M. & Heijnen, S. J. Biofilm bioreactors for waste-water treatment. Trends Biotechnol. 11, 117–121 (1993).
Klapper, I., Rupp, C., Cargo, R., Purvedorj, B. & Stoodley, P. Viscoelastic fluid description of bacterial biofilm material properties. Biotechnol. Bioeng. 80, 289–296 (2002).
Shaw, T., Winston, M., Rupp, C., Klapper, I. & Stoodley, P. Commonality of elastic relaxation times in biofilms. Phys. Rev. Lett. 93, 098102 (2004).
Marty, A., Roques, C., Causserand, C. & Bacchin, P. Formation of bacterial streamers during filtration in microfluidic systems. Biofouling 28, 551–562 (2012).
Rusconi, R., Lecuyer, S., Autrusson, N., Guglielmini, L. & Stone, H. A. Secondary flow as a mechanism for the formation of biofilm streamers. Biophys. J. 100, 1392–1399 (2011).
Rusconi, R., Lecuyer, S., Guglielmini, L. & Stone, H. A. Laminar flow around corners triggers the formation of biofilm streamers. J. R. Soc. Interface 7, 1293–1299 (2010).
Valiei, A., Kumar, A., Mukherjee, P. P., Liu, Y. & Thundat, T. A web of streamers: biofilm formation in a porous microfluidic device. Lab Chip 12, 5133–5137 (2012).
Weaver, W. M., Milisavljevic, V., Miller, J. F. & Di Carlo, D. Fluid flow induces biofilm formation in Staphylococcus epidermidis polysaccharide intracellular adhesin-positive clinical isolates. Appl. Environ. Microbiol. 78, 5890–5896 (2012).
Yazdi, S. & Ardekani, A. M. Bacterial aggregation and biofilm formation in a vortical flow. Biomicrofluidics 6, 044114 (2012).
Drescher, K., Shen, Y., Bassler, B. L. & Stone, H. A. Biofilm streamers cause catastrophic disruption of flow with consequences for environmental and medical systems. Proc. Natl. Acad. Sci. U. S. A. 110, 4345–4350 (2013).
Hallberg, K. B., Coupland, K., Kimura, S. & Johnson, D. B. Macroscopic streamer growths in acidic, metal-rich mine waters in north wales consist of novel and remarkably simple bacterial communities. Appl. Environ. Microbiol. 72, 2022–2030 (2006).
Hall-Stoodley, L., Costerton, J. W. & Stoodley, P. Bacterial biofilms: From the natural environment to infectious diseases. Nat. Rev. Microbiol. 2, 95–108 (2004).
Lewandowski, Z. & Stoodley, P. Flow induced vibrations, drag force and pressure drop in conduits covered with biofilm. Water Sci. Technol. 32, 19–26 (1995).
Meyer-Dombard, D. R. et al. Hydrothermal ecotones and streamer biofilm communities in the Lower Geyser Basin, Yellowstone National Park. Environ. Microbiol. 13, 2216–2231 (2011).
Stoodley, P., Cargo, R., Rupp, C. J., Wilson, S. & Klapper, I. Biofilm material properties as related to shear-induced deformation and detachment phenomena. J. Ind. Microbiol. Biot. 29, 361–367 (2002).
Stoodley, P., Dodds, I., Boyle, J. D. & Lappin-Scott, H. M. Influence of hydrodynamics and nutrients on biofilm structure. J. Appl. Microbiol. 85, 19s–28s (1999).
Stoodley, P., Lewandowski, Z., Boyle, J. D. & Lappin-Scott, H. M. Structural deformation of bacterial biofilms caused by short-term fluctuations in fluid shear: An in situ investigation of biofilm rheology. Biotechnol. Bioeng. 65, 83–92 (1999).
Taherzadeh, D., Picioreanu, C. & Horn, H. Mass Transfer Enhancement in Moving Biofilm Structures. Biophys. J. 102, 1483–1492 (2012).
Guillot, P., Colin, A. & Ajdari, A. Stability of a jet in confined pressure-driven biphasic flows at low Reynolds number in various geometries. Phys. Rev. E 78, 016307 (2008).
Guillot, P., Colin, A., Utada, A. S. & Ajdari, A. Stability of a jet in confined pressure-driven biphasic flows at low Reynolds numbers. Phys. Rev. Lett. 99, 104502 (2007).
Javadi, A., Eggers, J., Bonn, D., Habibi, M. & Ribe, N. Focus: Dripping Honey Explained. Phys. Rev. Lett. 110, 144501 (2013).
Winstanley, H., Chapwanya, M., McGuinness, M. & Fowler, A. C. A polymer–solvent model of biofilm growth. Proc. R. Soc. A. 467, 1449–1467 (2011).
Di Stefano, A. et al. Viscoelastic properties of Staphylococcus aureus and Staphylococcus epidermidis mono-microbial biofilms. Microbiol. Biotechnol. 2, 634–641 (2009).
Hohne, D. N., Younger, J. G. & Solomon, M. J. Flexible microfluidic device for mechanical property characterization of soft viscoelastic solids such as bacterial biofilms. Langmuir 25, 7743–7751 (2009).
Houari, A. et al. Rheology of biofilms formed at the surface of NF membranes in a drinking water production unit. Biofouling 24, 235–240 (2008).
Lau, P. C., Dutcher, J. R., Beveridge, T. J. & Lam, J. S. Absolute quantitation of bacterial biofilm adhesion and viscoelasticity by microbead force spectroscopy. Biophys. J. 96, 2935–2948 (2009).
Towler, B. W., Rupp, C. J., Cunningham, A. B. & Stoodley, P. Viscoelastic properties of a mixed culture biofilm from rheometer creep analysis. Biofouling 19, 279–285 (2003).
Autrusson, N., Guglielmini, L., Lecuyer, S., Rusconi, R. & Stone, H. A. The shape of an elastic filament in a two-dimensional corner flow. Phys. Fluids 23, 063602 (2011).
Roman, B. & Bico, J. Elasto-capillarity: deforming an elastic structure with a liquid droplet. J. Phys-Condens. Mat. 22 (2010).
Muppidi, S. & Mahesh, K. Study of trajectories of jets in crossflow using direct numerical simulations. J. Fluid. Mech. 530, 81–100 (2005).
Iannitelli, A. et al. Potential antibacterial activity of carvacrol-loaded poly (DL-lactide-co-glycolide)(PLGA) nanoparticles against microbial biofilm. Int. J. Mol. Sci. 12, 5039–5051 (2011).
Acknowledgements
AK acknowledges support from the NSERC Discovery Program. The authors would like to thank Mr. Amin Valiei for providing images used in Fig. 1(b).
Author information
Authors and Affiliations
Contributions
S.D. and A.K. conceived the problem. S.D. developed the theory. S.D. and A.K. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Das, S., Kumar, A. Formation and post-formation dynamics of bacterial biofilm streamers as highly viscous liquid jets. Sci Rep 4, 7126 (2014). https://doi.org/10.1038/srep07126
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07126
This article is cited by
-
Investigating fouling at the pore-scale using a microfluidic membrane mimic filtration system
Scientific Reports (2019)
-
Stenosis triggers spread of helical Pseudomonas biofilms in cylindrical flow systems
Scientific Reports (2016)
-
Nonlinear deformation and localized failure of bacterial streamers in creeping flows
Scientific Reports (2016)
-
Bacterial floc mediated rapid streamer formation in creeping flows
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.