Abstract
The coalescence process of oppositely charged drops for different electrical conductivities of liquids is presented. When the electrical conductivity was relatively low, oppositely charged drops failed to coalesce under sufficiently high electrical fields and capillary ripples were formed on the surfaces of droplets after rebound. For a high electrically conductive liquid, it was found that a crown profile of drop fission always appeared on the top surface of negatively charged drops after the two charged drops contacted and bounced off. Furthermore, we report here, for the first time, the newly found phenomenon and argue that the break up might be caused by Rayleigh instability, a form of Coulomb fission. The different mobility of positive and negative ions is the underlying mechanism that explains why the break up always happened on the negative side of charged drops.
Similar content being viewed by others
Charged droplets and their dynamics are of interest not only in fundamental research but also in industrial applications such as electrostatic spraying, phase-separation in ion-containing mixtures, ink printing, mass spectrometry etc. Although some technology regarding charged droplets such as those used in electrostatic sprays has been used widely in industry, the problem still has many unsolved mechanisms together with interesting new phenomena which, until now, have not been found1,2,3.
Ristenpart et al.4 demonstrated a finding that two oppositely charged droplets bounced off each other and would not coalesce if their charge exceeded a threshold value. Among the suggested three possible mechanisms5, the capillary pinch-off mechanism offered a reasonable explanation for the observation, which is in good agreement with the experiments. The coalescence behavior of oppositely charged droplets depends on the cone angle, which was controlled by varying the drop size and the applied voltage across the droplets. The cone angle formed under the balance of charge induced pressure from the applied electric field and capillary pressure resisting interfacial deformation, is commonly referred to as Taylor cones6. We recently conducted a series of experiments to verify this phenomenon, during which, a significant and interesting phenomena occurred with the pinch-off droplets. We experimentally studied coalescence dynamics of liquid droplets with different conductivities. The coalescence dynamics of droplets having low conductivity was demonstrated clearly in the present research and the non-coalescence also appeared. However for droplets having higher conductivity under the electric field, the droplets burst after recoil, which always happened on the negative electrode side. This unique droplet breakup phenomenon has not been reported before.
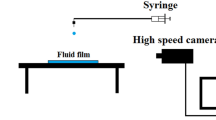
The schematics of the experimental setup are illustrated in Fig. 1. The experimental setup consisted of one stainless steel needle (Iwashita Engineering, Inc. OD 0.36 mm, ID 0.18 mm) and a substrate used to hold the lower droplet. A small droplet was first generated by the micro syringe and placed on the bottom substrate. Then the upper droplet was carefully produced using the micro syringe and suspended on the needle. The position of the upper droplet and lower droplet were aligned by a precise xyz-translation stage. The dynamics of droplet coalescence were visualized by a high speed camera (Redlake, HK-100G) mounted with a long-distance zoom lens (Navitar ZOOM 6000) at 10 K frames per second. The pre-trigger function within the camera was used to ensure that the entire dynamics of droplet coalescence with lower conductivity and droplet bursting with higher conductivity was fully captured. A halogen light (Kodak, EKTAPRO 5000 projector) was installed opposite the camera to provide backlighting. It should be pointed out that all the experiments were conducted at room temperature 23 ± 0.5°C and under atmospheric pressure conditions. The analytical sodium chloride was added into deionized water to vary the liquid conductivity.
In view of the range of conductivity, the research content discussed in this paper will be divided into two parts. One part considers the lower conductivity range from 0.5 μScm−1 (DI water) to 261 μScm−1, the other considers the higher conductivity range that varied from 5 mScm−1 to 30 mScm−1. The phenomenology of these two cases is markedly different. Previous research always used the relatively low conductive liquid as the working fluid. However, our experiment results show that droplet coalescence with different conductivity induced by an electrostatic field behaves differently. Before the experiment was conducted, the copper wire was cleaned using abrasive paper. The SEM picture in Fig. 2 (b) indicates the microstructure generated using abrasive paper. The lower droplet can stand on the copper wire in a stable manner due to the wetting dynamics of Wenzel state7. A fixed voltage 1000 V was applied across the needle and copper wire. The measurement results are shown in Fig. 3. We herein propose that the entire dynamics of droplet coalescence can be divided into the following stages. First, two droplets generally approached each other and deformed into a double cone when the electric field was activated. On contact with each other, a liquid bridge formed and the two droplets were quickly repelled. This phenomenon has been observed by Bird et al5 where two oppositely charged droplets recoiled rather than attracted5. After the stage of repelling, the two droplets eventually coalesced because of the attractive Coulomb force between the opposite charges on the surface of the droplets. In this case, as shown in Fig. 4, liquid widths varied with time under different conductivities. It is clear to see that the width of the liquid bridge, along with time, can satisfy the power scaling law rb ∝ tα with the exponent 0.35, when the conductivity is in the moderate range (34.3 μScm−1 and 93.5 μScm−1). It should be pointed out that the scaling law in our case is not close to the theory suggested by Egger et al.9. However, in the cases of very low conductivity (0.5 μScm−1) or very high conductivity 261 μScm−1), the exponent is changed to 0.44 and 0.57, respectively. The behavior reported here is similar to previous work where two mercury droplets coalesced on a planar surface8. Nevertheless it is reasonable to get a different exponent due to very weak or very strong capillary wave interface. Furthermore, such kind of capillary waves propagating on the surface of the droplet are of significant interest. To quantitatively obtain the fluctuation amplitude of the capillary waves, a coordinate stage was built and illustrated in Fig. 5(a) where the x axis denotes the capillary wave fluctuation amplitude and the y axis the arc length along the original droplet shape. A Matlab code was written to locate the center point of the original droplet. A radial line originating at the center point rotates along the droplet periphery with a small angle θ. This radial line will generate two nodal points (P1 and P2) with a droplet shape if the two images are added together. The geometric length of the two nodal points was used to characterize the amplitude of the capillary waves. It should be noted that the measured geometric distance is a little different from the tangent direction distance adopted in Reference10. Fig. 5(b) and (c) demonstrate the capillary waves at several stages of recoil. It is indicated in Fig. 5 that the fluctuation of the capillary waves versus arc length grows in a self-similar manner. Comparing the results in Fig. 5(b) and Fig. 5(c), we found that the fluctuation of the capillary waves was nearly the same under various levels of conductivity. However it seems that the waves in Fig. 5(c) propagate slightly faster than those in Fig. 5(b), which may be explained by more charges on the droplets due to larger conductivity.
(a) A DC voltage Δϕ = 1000 V is applied across the two droplets. The bottom droplet is carefully placed on the treated copper wire with diameter about 0.17 mm by the needle and the upper droplet is generated by the needle driven by the syringe. (b) The SEM picture demonstrates the treated copper wire surface microstructure which can hold the bottom droplet stably due to wetting dynamics at the Wenzel state.
Liquid bridge widths as a function of time.
Symbols are the experimental data under different conductivity and coalescence models and the lines are power laws fittings. The exponent of the scaling power law is 0.44, 0.35, 0.35 and 0.57 for the droplet liquid conductivity of 0.54 μScm−1, 34.3 μScm−1, 93.5 μScm−1 and 261 μScm−1, respectively.
However, when we conducted the experiment of droplet coalescence in the case of higher conductivity, a new phenomenon with respect to uni-polarization droplet bursting was observed. When two highly conductive droplets approach closely under the electric field, one of the droplets will burst. Specifically, the bursting always happened with the droplet connected to the negative electrode. Several experiments were carried out to establish the underlying mechanism and the experiment setup is shown in Fig. 1. First, the lower droplet was carefully placed on a copper wire and then the upper droplet was generated by the micro syringe. Fig. 6 shows the high-speed camera images of the droplet bursting always on the negative electrode side. The typical size of droplets in the experiment was about 1~2 mm. In case A, the upper droplet was used as the anode and the lower droplet served as the cathode, while in case B the inverse applied. The conductivity of the liquid droplet was 20.48 mS/cm and the analytical sodium sulfate was added into deionized water to change the conductivity. It is clear to see that, from Fig. 6, bursting happened at the droplet surface crest after the initial contact between these two droplets and a crown profile appeared on the droplet's surface connected with the negative electrode. The radial outward liquid surface motion from the bursting point was clearly observed in the images. It is noteworthy that, as shown in Fig. 6, both in case A and case B, the droplet bursting point always happened at the cathodic droplet crest. Fig. 7 illustrates the details of two cases of droplet bursting process. It is evident that even with a large discrepancy in droplet size, the bursting still happened at the negative side. Fig. 8 shows the droplet bursting dynamics of diluted hydrochloric, which shows that droplet bursting also happened at the cathodic droplet crest. Actually, in order to verify the effect of different ions and droplet size to droplet bursting dynamics, we tried to use different ions including sodium chloride, sodium sulfate, potassium chloride as well as diluted hydrochloric, all of the experimental results show the same phenomena that droplet bursting always happened at the cathodic droplet crest. In particular, we considered whether droplet size had any effect to such uni-polarization bursting.
What makes the droplets burst after the two charged droplets contact and why does the burst always happen on the negative electrode? We propose the possibility that the bursting is a consequence of the Rayleigh instability and Coulomb fission of charged droplets. The Rayleigh limit11 model explains the mechanism that the charge on a droplet surface would cause instability to fission before reaching a limiting value. For a certain droplet size, a maximum charge quantity on the surface was given by the Rayleigh limit11,12 . When the surface charge density is sufficiently high, the Coulombic repulsion force overcomes surface tension and the droplet disrupts, which is termed Coulomb fission11. During the approach of the two spherical droplets, the charges on the droplets' surface increases. When they contact, a liquid bridge generates between the two droplets due to coalescence and the ions in the liquid will flow from one side to the other under the electrical potential through the liquid bridge. According to Fig. 5, it demonstrated that the higher conductivity, the shorter capillary wavelength. Therefore, the higher conductivity liquid is easier to reach the bursting condition of Coulomb fission.
. When the surface charge density is sufficiently high, the Coulombic repulsion force overcomes surface tension and the droplet disrupts, which is termed Coulomb fission11. During the approach of the two spherical droplets, the charges on the droplets' surface increases. When they contact, a liquid bridge generates between the two droplets due to coalescence and the ions in the liquid will flow from one side to the other under the electrical potential through the liquid bridge. According to Fig. 5, it demonstrated that the higher conductivity, the shorter capillary wavelength. Therefore, the higher conductivity liquid is easier to reach the bursting condition of Coulomb fission.
We also suggest a mechanism that could lead to this break up for the negatively charged droplets after coalescence. The research on chemical physics shows a reasonable excuse for this phenomenon. When the liquid bridge is formed, the negative ions run from the negative electrode to the positive electrode and at the same time positive ions in the liquid move to the negative side. The distribution of ions on the charged droplets indicates the negative ion concentration at the surface exceeds the positive ion concentration in larger quantities due to the difference of the ion's running mobility13. Hunter and Ray14 analyzed this mobility quantitatively and concluded that the higher mobility of negative ions would make the charge on the droplet's surface of the negative electrode much higher than the positive side. In this case the charge to mass ratio or charge to surface ratio around the area of the liquid bridge connected with the droplet would reach the Rayleigh limit earlier than the positive one. This is also the reason why the droplet break up happened on the negative electrode. The bursting happens on the surface crest of the droplet and shows a crown profile around the position where the liquid bridge was located. Due to the movement of negative ions and their high running mobility, the charge concentration at the connection of the negative charged droplet surface to the liquid bridge approached the Rayleigh limit earlier than the positive side. So the bursting would always appear on the negatively charged drops. Actually we also found that every peak of the crown similar to a Taylor jet of charged droplets. The bursting pattern caused by Coulomb fission in this paper is quite different to the existing findings of charged droplet break up. For lower conductive liquid, we found that increasing the charging voltage could only make the oppositely charged droplet fail to coalesce when the two drops directly contact but no break up appeared on the negative side droplets (Fig. 3). It could also be explained by the suggested mechanism of ion mobility that the ions concentration is lower in the low conductive liquid which is difficult to reach the Rayleigh limit and cause Coulomb fission.
In summary, we reported experiments on the interaction of oppositely charged droplets for different conductive liquids. The coalescence dynamics of the droplets are affected mainly by the Taylor cone angle which was caused by the coupled field of surface tension and electric force. For highly conductive liquids, special bursting phenomena due to Coulomb fission occurred after the droplets' coalescence, which was discovered for the first time. Deeper research on the mechanism of bursting phenomena and instability of the charged droplet's surface will be conducted in the future.
References
Duft, D., Achtzehn, T., Müller, R., Huber, B. A. & Leisner, T. Rayleigh jets from levitated microdroplets. Nat. 421, 128–128 (2003).
Collins, R. T., Jones, J. J., Harris, M. T. & Basaran, O. A. Electrohydrodynamic tip streaming and emission of charged drops from liquid cones. Nat.Phy. 4,149–154 (2008).
Gomez, A. & Tang, K. Charge and fission of droplets in electrostatic sprays. Phys. Fluids 6, 404–414 (1994).
Ristenpart, W. D., Bird, J. C., Belmonte, A., Dollar, F. & Stone, H. A. Non-coalescence of oppositely charged drops. Nat. 461, 377–380 (2009).
Bird, J. C., Ristenpart, W. D., Belmonte, A. & Stone, H. A. Critical angle for electrically driven coalescence of two conical droplets. Phys. Rev. Lett. 103, 164502 (2009).
Fernández de la Mora, J. The fluid dynamics of Taylor cones. Annu. Rev. Fluid Mech. 39, 217–243 (2007).
Wenzel, R. N. Surface roughness and contact angle. J. Phys. Colloid Chem. 53, 1466–1467 (1949).
Menchaca-Rocha, A., Martinez-Davalos, A., Nunez, R., Popinet, S. & Zaleski, S. Coalescence of liquid drops by surface tension. Phys. Rev. E. 63, 046309 (2001).
Eggers, J., Lister, J. R. & Stone, H. A. Coalescence of Liquid Drops. J. Fluid Mech. 401, 293–310 (1999).
Thoroddsen, S. T., Qian, B., Etoh, T. G. & Takehara, K. The initial coalescence of miscible drops. Phys. Fluids 19, 072110 (2005).
Rayleigh, L. On the Equilibrium of liquid conducting masses charged with electricity. Phil. 14, 184–186 (1882).
Hendricks, C. D. & Schneider, J. M. Stability of a conducting droplet under influence of surface tension and electric charge. Am. J. Phys. 31, 450–453 (1963).
Tang, K. Q. & Gomez, A. On the structure of an electrostatic spray of monodisperse droplets. Phys. Fluids 6, 2317–2331 (1994).
Hunter, H. C. & Ray, A. K. On progeny droplets emitted during Coulombic fission of charged microdrops. Phys. Chem. Chem. Phys. 11, 6156–6165 (2009).
Acknowledgements
This work was supported by the Research Grants Council (RGC Project No. 618210) of Hong Kong government and the National Natural Science Foundation of China (NSFC project No. 51006047 and 51376084).
Author information
Authors and Affiliations
Contributions
B.W. and H.Q. designed research; B.W. performed experiments; B.W., H.Q. and J.W. analyzed data; B.W., J.W. and H.Q. wrote the paper. All authors participated in discussion.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Wang, J., Wang, B. & Qiu, H. Coalescence and Breakup of Oppositely Charged Droplets. Sci Rep 4, 7123 (2014). https://doi.org/10.1038/srep07123
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07123
This article is cited by
-
Effect of gas ionization on interphase interaction of adjacent oppositely charged droplets
Experiments in Fluids (2020)
-
Sessile multidroplets and salt droplets under high tangential electric fields
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.