Abstract
While a two-dimensional (2D) metallic surface state in bismuth has been proposed, experimental 2D evidence of quantum transport, e.g., angular dependent Shubnikov-de Haas (SdH) oscillations is still lacking. Here, we report the angular-dependent magnetoresistance measurements in single-crystal Bi nanoribbons and found that both the low-field weak antilocalization behavior and the high-field angle-dependent SdH oscillations follow exactly the 2D character, indicative of the 2D metallic surface states which dominate the transport properties of thin Bi nanoribbons. Moreover, by controllable exposing the ribbons to ambient environment (1 atm and room temperature), the metallic surface states were found to be robust to the oxidation although the carrier density in the surface states are modified after the exposures. These results suggest that the metallic surface states in Bi nanoribbons should be topologically protected which can provide key information in understanding the surface properties of Bi in nanometer scale.
Similar content being viewed by others
Introduction
Bismuth is a semimetal with unusual electronic properties, such as highly anisotropic Fermi surface, low carrier density, small effective mass and long mean free path. Many interesting physical phenomena have been observed due to these properties1,2,3,4. In recent years, investigations of metallic surface states of Bi have attracted an increased interest, both from the experimental and the theoretical side5 due to its strong spin-orbital interaction and in relation to the Bi-based topological insulators (Bi1-xSbx, Bi2Se3, Bi2Te3)6,7. Angle-resolved photoemission spectroscopy (ARPES) studies of Bi films have proved that the surfaces of Bi films are characterized by quasi-two-dimensional (quasi-2D) metallic surface states with unique spin properties that are quite distinct from the bulk semimetal due to the existence of electronic surface states crossing the Fermi level8,9,10,11. However, at present, direct quantum transport evidence of such 2D metallic surface states is still lacking, especially in a Bi with confined geometries although some previous transport measurements were reported in Bi ultrathin films12,13,14 or quasi-1D nanowires15,16,17,18. Recently, we have successfully fabricated single-crystal Bi nanoribbons with high quality by solvothermal method19. The nanoribbon is an ideal system to distinguish the 2D surface character from transport properties due to large surface-to-volume ratio and perfect planar surface. Through the detailed transport measurements of nanoribbons under high magnetic field (~31 T) and low temperature (~ 400 mK), we have presented clear transport evidence of the 2D surface state of nanoribbon. Furthermore, our studies clearly suggested that the surface state of Bi nanoribbon might be topological nontrivial.
To further verify the topological properties, we report the investigation of 2D surface states of single-crystal Bi nanoribbons through the antilocalization (WAL) effect and Shubnikov-de Haas (SdH) effect in titled magnetic fields. Our data show clearly that 2D WAL effect can be observed in nanoribbons with different thickness, i.e., thinner ribbon (~40 nm) with insulating state and thicker ribbon (~80 nm) with metallic behavior. Meanwhile, a well-defined 2D 1/2-shifted SdH oscillation can be identified in thin ribbons. As comparison, the SdH oscillations reveal a 3D Fermi surface in the thick ribbons. These results suggest that the surface states dominate the transport properties in thin ribbons while the bulk carriers contribute the most transport properties in thick ribbons. Moreover, we have measured the aging effect of surface states in thin nanoribbons by exposing the ribbons to air environment with different times, i.e., one day, two days and seven days. We found that the 2D WAL effect and 1/2-shifted SdH oscillations still survive after the exposure which indicates that the surface states are robust to oxidation although the surfaces are modified due to the exposure. Our results provide further evidence that the metallic surface should be topological protected.
Results
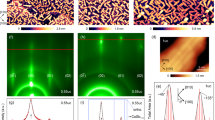
Single crystal Bi nanoribbons were synthesized by solvothermal method, as described in Ref. 20 and 21. Fig. 1(a) shows the image of the nanoribbons by transmission electron microscopy (TEM). The majority of nanoribbons display a typical width of 100 ~ 350 nm, a thickness of 30 ~ 150 nm and a length of several micrometers. Selected area electron diffraction pattern on a randomly selected nanoribbon confirm its single-crystal morphology with a rhombohedral bulk crystal structure and a preferential [110] growth direction. The four-probe devices on an individual Bi nanoribbon were fabricated by a FEI NanoLab 600i SEM/FIB dual beam system. The SEM image of a four-probe device is shown in the inset of Fig. 1b.
TEM image and temperature-dependent resistance of Bi nanoribbons.
(a) transmission electron microscopy image of nanoribbons. (b) The resistance as a function of temperature of two individual nanoribbons, S1 (curve b) and S2 (curve a) with thickness about 40 nm and 80 nm, respectively, where a metallic behavior can be observed in S2 and a non-metallic can be observed in S1. The curves for S1 after exposed to air condition with 2 day (curve c) and 7 days (curve d) are also shown. The inset is a SEM image of a nanoribbon device for four-probe transport measurements.
In Figure 1b, curves a and b, respectively, show the temperature-dependent resistance of two nanoribbons with different thickness. As temperature decreases from room temperature, a metallic behavior can be observed for the thicker ribbon S2 (d ~80 nm) which is similar to bulk crystal. Whereas, the thin nanoribbon S1 (d ~ 40 nm) exhibits a non-metallic behavior with plateau feature at low temperature regime. The non-metallic behavior has been observed in thin Bi films12 and small diameter nanowires15,16,18,22. Such a semimetal to semiconductor transition was ever considered to be due to the quantum size confinement effect12,23,24 when the thickness of films or diameters of nanowires are comparable to the Fermi wavelength (~30 nm) in low-dimensional Bi nanostructures1. Since the low-temperature plateau behavior has also been widely observed in the 3D topological insulators with an enhanced insulating bulk state, where the surface conductivity plays a crucial role in low temperatures25,26,27,28, the evolution of resistance with temperature in thinner ribbon S1 might be attributed to the competition between the reduction of bulk conductivity and the increase of surface conductivity as decreasing temperature. In Fig. 1(b), curve c and d are the R-T curves for S1obtained after exposing the ribbon to air for 2 and 7 days.
Two-dimensional weak antilocalization (WAL) effect in Bi nanoribbons
Fig. 2a shows the low-field angle-dependent magnetoresistance (MR) of S1 in tilted field B measured at T = 2 K. The schematic of the measurement are shown in the inset of Fig. 2a where θ is the angle between B and the unit vector normal to the surface of the nanoribbon. At θ = 0°, the MR is positive and displays a sharp dip feature. As the field B rotated in binary-bisectrix plane, the shape of the MR curves change gradually from convex to concave. When θ = 90°, i.e., parallel to the ribbon plane, the MR shows a semiclassical B2-dependence behavior, indicating the typical scattering mechanism of the Lorentz deflection of carriers. Similar behavior has been observed in topological insulator Bi2Se3 ultrathin films (~5 nm)29, the convex shape of the MR curves at perpendicular field B can be interpreted by the weak antilocalization (WAL) of charge carriers in the two-dimensional surface states and it varies only with the component of magnetic field normal to the surface, i.e., B⊥ = Bcosθ. The concave feature in the parallel field indicates the disappearance of WAL in the surface state, but the classical nature of the charge carriers under magnetic field. The similarity of both MR data in topological insulator Bi2Se3 films and Bi nanoribbons allows us to assume that the MR behavior in Bi nanoribbon perhaps have the same origin. To verify such an assumption, the parabolic MR at θ = 90° was considered to be independent with the 2D WAL in the surface state and thus the WAL induced quantum corrections can be obtained by subtracting the parabolic MR, i.e., ΔG(θ, B) = G(θ, B)− G(90°, B), with G(θ, B) = 1/R(θ, B) and G(90°, B) = 1/R(90°, B). Fig. 2 (b) shows the obtained ΔG(θ, B)as a function of B⊥ for various tilted angles θ. It is seen that all of the traces collapse to a single curve, clearly indicating a 2D nature of the WAL effect. Since the thickness (d ~ 40 nm) of the ribbon is on the order of the Fermi wave length25, we cannot exclude such a possibility that the bulk Bi is actually a quasi-2D system so that the 2D WAL is not a consequence of the 2D surface states. To further clarify the origin of this WAL effect, we investigated the low-field MR properties of the thicker nanoribbon S2 (d ~ 80 nm) which can be considered as a true 3D system.
The 2D WAL effect in Bi nanoribbons.
(a) and (c) respectively show the angle- dependent MR of nanoribbons S1 (d = 40 nm) and S2 (d = 80 nm) measured at 2 K. The solid curve in (a) is a parabolic fit to the MR data measured at θ = 90°; Inset: schematic of the measurement setup where θ denotes the angle between the direction of the magnetic field and the current flow in the nanoribbons. (b) and (d) respectively show the magnetoconductance as a function of the perpendicular component B⊥ = Bcosθ by subtracting the magnetoconductance at θ = 90° for S1 and S2. The solid lines (red) are fits of 2D localization theory. All the traces were normalized to a single curve in low field range, indicating the 2D surface nature of the magnetoconductance.
The angle-dependent MR data for sample S2 (d ~ 80 nm) are shown in Fig. 2c. The most interesting feature is that the MR curve at θ = 90° displays a convex shape, which is in sharp contrast to the concave behavior in thinner sample S1. The convex feature of MR curve is usually considered to be a result of the WAL effect, the occurrence of WAL observed at θ = 90° should be ascribed to a 3D WAL effect that has a bulk origin and does not depend on the titled angle30. Therefore, to extract out the pure surface state contribution, we subtract the 3D WAL contribution at θ = 90° from the total magnetoconductance at various angles, i.e., ΔG(θ, B) = 1/R(θ, B) − 1/R(90°, B). The obtained ΔG plotted as function of the normal component B⊥ = Bcosθ was shown in Fig. 2d. Surprisingly, all the ΔG curves at various angles also coincide with each other in low field range and deviate from each other in the high field regime. Thus, by subtracting out the 3D bulk WAL effects, we obtain the WAL effect from the 2D surface states of the nanoribbon S2, which also indicates the existence of 2D surface states in the thick nanoribbons with metallic bulk. By comparing the results in sample S1 and S2, we can confirm the existence of 2D surface states in Bi nanoribbons with different thickness and bulk states.
According to the 2D localization theory, the quantum correction to the 2D magnetoconduction can be described by the Hikami-Larkin-Nagaoka (HLN) model31. In a strong spin-orbit interaction system, the conduction correction is given by

where α is a WAL coefficient, ψ is the digamma function, e is the electronic charge, ħ is the reduced Planck's constant,  is a magnetic field characterized by coherence length lφ. The fitting results of magnetoconductance change ΔG with equation (1) for sample S1 and S2, are shown in Fig. 2(b) and 2(d) respectively. The fitting yields α = − 0.52 and lφ = 310 nm for sample S1 and α = −0.37 and lφ = 58 nm for sample S2. The values of extracted coefficient α are close to 1/2 for two samples. Same value has also been obtained in the 3D topological insulators with a single Dirac cone. Experimentally, α equals 1/2 for single coherence channel while equals 1 for two independent conducting channels32,33,34. Thus the fitting results of α closing to 1/2 indicate that there is only one conducting channel. It means that, for thinner sample S1 with insulating bulk, the metallic surface states (top, bottom and side surfaces together) forms a continuous 2D spin-orbit metal as expected for the surface states of topological insulator, while for sample S2 with metallic bulk, top and bottom surfaces are connected though bulk electrons35.
is a magnetic field characterized by coherence length lφ. The fitting results of magnetoconductance change ΔG with equation (1) for sample S1 and S2, are shown in Fig. 2(b) and 2(d) respectively. The fitting yields α = − 0.52 and lφ = 310 nm for sample S1 and α = −0.37 and lφ = 58 nm for sample S2. The values of extracted coefficient α are close to 1/2 for two samples. Same value has also been obtained in the 3D topological insulators with a single Dirac cone. Experimentally, α equals 1/2 for single coherence channel while equals 1 for two independent conducting channels32,33,34. Thus the fitting results of α closing to 1/2 indicate that there is only one conducting channel. It means that, for thinner sample S1 with insulating bulk, the metallic surface states (top, bottom and side surfaces together) forms a continuous 2D spin-orbit metal as expected for the surface states of topological insulator, while for sample S2 with metallic bulk, top and bottom surfaces are connected though bulk electrons35.
Two-dimensional Shubnikov-de Haas (SdH) oscillations
In Fig. 3, we illustrate the MR behaviors at higher field range (~16 T) for sample S1. Besides the strong positive behavior in low field region due to the 2D WAL effect, negative behavior in high magnetic field can also observed. These complex MR properties are also seen in Bi nanowires17,36. As shown in Fig. 3a, pronounced quantum oscillations can be identified which evolve with the tilt angle θ. After subtracting the smooth background, the detailed oscillations can be obtained, as shown in Fig. 3b (The details of the background subtraction can be found in Figure S1 in the supporting information). It is seen that the oscillatory part ΔR displays periodic peaks (maximum) and valleys (minimum) with 1/B, illustrating that these oscillations are due to the Shubnikov-de Haas (SdH) effect. Meanwhile, the positions of the maxima and minima depend only on the perpendicular component of the magnetic field B⊥, providing clear evidence of a 2D character of the SdH oscillations, i.e., the SdH oscillations originate from the 2D metallic state. As mentioned above, the bulk of the ribbon is also a quasi-2D system. To exclude the 2D bulk origin of the oscillations, we have performed the low-field anisotropic magnetoresistance (AMR) measurements on nanoribbon S1, where the R-θ spectra always display a twofold rotational symmetry (not shown), which significantly deviates from the three- or sixfold rotational symmetry for the bulk crystal37 and indicates that the carriers from bulk electronic bands have no contribution on the MR. By contrast, the oscillations in sample S2 survive up to θ = 90° (Supporting information Fig.S3 and S4). Meanwhile, no clear 2D SdH characteristic can be identified which indicates that the bulk carriers dominate the transports.
2D SdH oscillations of Bi nanoribbon S1 (~40 nm).
(a) The resistance of sample S1 as a function of magnetic field at different tilted angle θ at 2 K. The inset is the schematic of B orientation in different planes of nanoribbon. The arrows mark the involution of the peak at B = 8.65 T. Inset: schematic of the measurement setup where θ denotes the angle between the direction of the magnetic field and the current flow in the nanoribbons. (b) Amplitude of the resistance oscillations ΔR versus 1/B⊥. Two sets of oscillation can be identified which were marked by solid and hollow arrows respectively. The oscillation spectra show periodic behavior with 1/Bcosθ, indicating a typical 2D character of electronic structure. (c) SdH oscillations for sample S1 (~40 nm) under a perpendicular B at different temperature; (d) Temperature dependence of the scaled oscillation amplitudes at B = 8.65 T, yielding a effective mass of 0.21 me. The curves were offset for clarity.
Furthermore, as shown in Fig. 3b, two sets of oscillations, as marked by the solid and hollow arrows, can be identified which can be further confirmed by the fast Fourier transform (FFT) spectra result where two oscillation frequencies (F) can be extracted, i.e. F = 14.8 T and 29.6 T for the low-field regime and high-field regime oscillations, respectively (Supplementary Fig. S5). For a 2D system, the SdH oscillation frequency is directly related to the cross sectional area SF of the Fermi surface with  , where
, where  , kF is the Fermi vector, e is the electron charge and ħ is Planck's constant divided by 2π. Thus the Fermi vector kF can be determined to be ~ 0.023 Å−1 and 0.047 Å−1, respectively. As the 2D surface carrier density n2D is related to kF by
, kF is the Fermi vector, e is the electron charge and ħ is Planck's constant divided by 2π. Thus the Fermi vector kF can be determined to be ~ 0.023 Å−1 and 0.047 Å−1, respectively. As the 2D surface carrier density n2D is related to kF by  , we obtain n2D = 3.5 × 1012 cm−2 and 6.9 × 1012 cm−2. The observed two sets oscillations might be origin from the two (top and bottom) surface states where the bottom surface contacts with the substrate and has different carrier density with the top surface34. Similar behavior has also been observed in our earlier studies with magnetic field up to 31 T.
, we obtain n2D = 3.5 × 1012 cm−2 and 6.9 × 1012 cm−2. The observed two sets oscillations might be origin from the two (top and bottom) surface states where the bottom surface contacts with the substrate and has different carrier density with the top surface34. Similar behavior has also been observed in our earlier studies with magnetic field up to 31 T.
To get more information of the surface states, we have investigated the temperature dependence of the oscillations in the low field regime as an example. The ΔR vs.1/B curves with field aligned perpendicular to nanoribbon at different temperatures were shown in Fig. 3c. It can be found that the oscillation amplitudes decrease rapidly as T increases from 2 K to 10 K. According to theory, the temperature-dependent amplitude ΔR of the SdH oscillations can be described as ΔR(T)/ΔR(0) = λ(T)/sinh(λ(T)) [ref. 38] with the thermal factor of λ(T) = 2π2kBTm*/(ħeB), where m* is the effective mass of surface state carriers and kB is Boltzmann's constant. For the peak at B = 8.65 T (as marked in Fig. 3a), the theoretical fit of the oscillation amplitude with above equation leads to an effective mass of surface m*~ 0.21 m0(m0 is the static electron mass), as shown in Figure 3d. This value is consistent with our previous observation under high magnetic field (~31 T) and low temperature (400 mK) and also close to the value of surface-state carriers in topological insulator, Bi2Se3 or Bi2Te325,26,37,39,40.
Robustness of the 2D surface states in air exposure
It is interesting to note that all the data discussed above were obtained after the ribbon devices have been exposed to the air for several days (i.e., 2 days for sample S1) and the ribbons were naturally oxidized. Thus, the observation of 2D WAL effect and SdH oscillations after air exposure indicates that such surface states are rather robust to the environment. To further confirm the robustness of the surface states, we have investigated the evolution of surface states with oxidation. Fig. 1b and Fig. 4 show the data of S1 with different exposing time, e.g. 1 day, 2 days, 7 days where the data of 2 days have been partly discussed above. As shown in Fig. 1b, the resistance of sample S1 increases significantly after exposing the sample to air. We note that the increase of resistance with oxidation might be due to the n-type doping with environment which has been observed in Bi2Se3 single crystals. However, the Hall effect measurements of our Bi nanoribbon suggest that the dominant carriers are n-type (Supporting information S6) and thus the n-type doping effect can be excluded here. Furthermore, we found that the main characteristic of the R-T curves still remain, e.g. the insulating behavior and the plateau at low temperatures, which are different to Bi2Se3 single crystals and indicate the persistence of metallic surface states. The MR behaviors of three exposing process under perpendicular field B (θ = 0°) were shown in Fig. 4a. The main feature of MR for three measurements is very similar, including the strong positive behavior in low field region due to the WAL effect and negative behavior in high magnetic field. More importantly, it can be found that the 2D SdH oscillations from the surface states can also be observed after 7 days exposure although the amplitude of the oscillations is weakened, as shown in Fig. 4b. Recently, similar 2D WAL and the robustness to the oxidation have also been observed in Bi thin films41.
(a) Normalized magnetoresistance in perpendicular magnetic field of three measurements for sample S1 (~40 nm). The MR oscillations superimposed on the background curves were observed. (b) Amplitude of the resistance oscillations ΔR versus 1/B⊥ for three measurements. (c) 1/B versus the Landau index number, n, for sample S1 with three measurements. The dips of oscillations correspond to n. The solid lines correspond to the best fits to the experimental data.
In Fig. 4c, we show Landau level (LL) index number n versus 1/B for S1 at three exposing times. In a 2D metal, the LL index n of a SdH oscillation is inversely proportional to the magnetic field, 2π(n + γ) = SF(ħ/eB), where the LL index n is related to the extremal cross-section, SF25. For a regular electron gas, γ is equal to 0. While for an ideal topological Dirac fermions, γ is equal to 1/2. As shown in Fig. 4c, the linear extrapolation yields a finite intercept of γ = 0.50, 0.37 and 0.36 for the data obtained after three exposing processes, respectively. They are very close to the ideal value of 0.5 for Dirac electrons, resulting in a 1/2-shifted SdH oscillation, which suggest the topological nature of the surface states. In addition, the slopes of the linear fitting decrease gradually after further air exposure, indicating the frequency of the oscillations, as well as the surface carrier densities of the surface states are reduced after further oxidation.
Discussion
While the oscillation amplitudes and values of intercept γ were reduced after air exposure, the most remarkable features of the transport properties still survive, including the SdH, the low-temperature plateau and 2D WAL effect from the surface states after 7 days exposure. Similar behaviors have been observed in Bi2Se3 single crystals where the SdH oscillations were smeared after 1 h air exposure26. The smearing of oscillations in Bi2Se3 were attributed to the degradation of surface transport properties after exposure in the ambient environment26,42. Interestingly, we found that the surface state degradation in Bi nanoribbons is relative slow since all the characteristic 2D SdH spectra can be recognized after even one week air exposure. Furthermore, although the value of γ decreases from 0.5 to 0.37 after 2 days exposure, it almost remains unchanged with further exposure (7 days) within the experimental uncertainty, indicating the surface states in Bi nanoribbons are much more robust to the exposure than the Bi2Se3 single crystals. A possible origin might be from the large surface-to-volume ratio in nanoribbons compared with bulk system, as well as the high quality of single-crystal nature. The evolution of oscillations perhaps related to the modification of surfaces of nanoribbons during the oxidation process by chemical reactions under ambient conditions, e.g. the decreasing of surface carrier densities. In the recent study of Bi thin films, the surface transport properties were also found to be robust to the oxidation. Thus the observation of robust surface states in Bi nanoribbons might not be surprising as they might be stabilized or formed by the size confinement effect. However, to full understand these evolutions of surface states with oxidation and get a more reasonable conclusion, further experimental investigations are needed.
In summary, we have investigated the metallic surface states of Bi single-crystal nanoribbons fabricated by solvothermal method. Through both studies on the weak antilocalization (WAL) effect and Shubnikov-de Haas (SdH) oscillations, we presented the clear evidence of 2D surface states in ribbons with different thickness. It was found that the surface states dominate the transport properties in thinner sample (~40 nm) with insulating bulk, while the bulk carriers contribute most of the MR behavior in thicker ribbons (~80 nm) with a metallic bulk. Furthermore, through the investigation of the SDH oscillations after controllable exposing to air, we confirm that the surface states are robust to the environment although the properties of the surface states, i.e. carrier density, have been modified. All these results suggest that the surface states might be topological protected.
Methods
Growth of Bi nanoribbons and Characterizations
The Bi nanoribbons were synthesized by solvothermal method. In a typical process, 0.15 g analytical grade sodium bismuthate (NaBiO3.2H2O) dissolved in 30 ml glycerol, stirred vigorously for 30 min and then the solution was transferred to Teflon-lined stainless steel autoclave with a capacity of 50 ml. The solution was bubbled with a flow of pure nitrogen gas for 10 min, before the autoclave was sealed and maintained at 200°C for 24 h. After reaction, the resulting black solid product was collected by filtration, washed with ethanol to remove all of impurities. The morphology of the synthesized nanoribbons are obtained using a scanning electron microscope (FEI NanoLab 600i SEM/FIB). The structural characteristics of Bi nanoribbons were investigated using an JEOL—2011 TEM.
Device fabrication and transport measurements
To make standard four-probe devices on an individual Bi nanoribbon for transport measurement, the solution contain nanostructure with different morphology were firstly dispersed on a silicon substrate with a 1 μm thick Si3N4 insulating layer and then transferred into FEI NanoLab 600i SEM/FIB dual beam system for deposition of electrodes. The nanoribbons with different width were choose and then several platinum (Pt) strips were deposited onto the ribbons along the [110] direction as the contact electrodes. The magnetotransport measurements were performed using physical property measurement system (PPMS, Quantum Design Inc.) equipped with a 16 T superconducting magnet.
References
Ashcroft, N. W. & Mermin, D. N. Solid state physics (Thomson Learning, Toronto, 1976), 1st ed.
Yang, F. Y. et al. Large magnetoresistance of electrodeposited single-crystal bismuth thin films. Science 284, 1335–1337 (1999).
Behnia, K., Balicas, L. & Kopeleivch, Y. Signatures of electron fractionalization in ultraquantum bismuth. Science 317, 1729–1731 (2007).
Li, L. et al. Phase transitions of Dirac electrons in bismuth. Science 321, 547–550 (2008).
Seradjeh, B., Wu, J. & Phillips, P. Signatures of surface states in bismuth at high magnetic fields. Phys. Rev. Lett. 103, 136803 (2009).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulator and superconductor. Rev. Mod. Phys. 83, 1057–1110 (2011).
Hofmann, P. The surfaces of bismuth: structural and electronic properties. Prog. Surf. Sci. 81, 191–245 (2006).
Ast, C. R. & Höchst, H. Electronic structure of a bismuth bilayer. Phys. Rev. B 67, 113102 (2003).
Hirahara, T. et al. Role of spin-orbit coupling and hybridization effects in the electronic structure of ultrathin Bi films. Phys. Rev. Lett. 97, 146803 (2006).
Kim, T. K. et al. Evidence against a charge density wave on Bi(111). Phys. Rev. B 72, 085440 (2005).
Xiao, S., Wei, D. & Jin, X. Bi(111) Thin film with insulating interior but metallic surfaces. Phys. Rev. Lett. 109, 166805 (2012).
Hirahara, T., Matsuda, I., Yamazaki, S., Miyata, N. & Hasegawa, S. Large surface-state conductivity in ultrathin Bi films. Appl. Phys. Lett. 91, 202106 (2007).
Yin, S.-L., Liang, X.-J. & Zhao, H. W. Effect of a highly metallic surface state on the magneto-transport properties of single crystal Bi films. Chin. Phys. Lett. 30, 087305 (2013).
Huber, T. E. et al. Confinement effects and surface-induced charge carriers in Bi quantum wires. Appl. Phys. Lett. 84, 1326–1328 (2004).
Huber, T. E., Nikolaeva, A., Konopko, L. & Graf, M. J. Observation of three-dimensional behavior in surface states of bismuth nanowires and the evidence for bulk-Bi surface quasiparticles. Phys. Rev. B 79, 201304 (2009).
Huber, T. E. et al. Surface state band mobility and thermopower in semiconducting bismuth nanowires. Phys. Rev. B 83, 235414 (2011).
Kim, J. et al. Weak antilocalization and conductance fluctuation in a single crystalline Bi nanowire. Appl. Phys. Lett. 104, 043105 (2014).
Ning, W. et al. Evidence of topological two-dimensional metallic surface states in thin bismuth nanoribbons. ACS Nano 8, 7506–7512 (2014).
Wang, Y., Chen, J. Chen, L., Chen, Y.-B. & Wu, L.-M. Shape-controlled solventless syntheses of nano Bi disks and spheres. Cryst. Growth Des. 10, 1578–1584 (2010).
Wang, F. D., Tang, R., Yu, H., Gibbons, P. C. & Buhro, W. E. Size- and shape-controlled synthesis of bismuth nanoparticles. Chem. Mater. 20, 3656–3662 (2008).
Heremans, J. et al. Bismuth nanowire arrays: synthesis and galvanomagnetic properties. Phys. Rev. B 61, 2921–2930 (2000).
Sandomirskii, V. B. Quantum size effect in a semimetal film. Sov. Phys. JETP 25, 101 (1967).
Hoffman, C. A. et al. Semimetal-to-semiconductor transition in bismuth thin films. Phys. Rev. B 48, 11431 (1993).
Qu, D. X., Hor, Y. S., Xiong, J., Cava, R. J. & Ong, N. P. Quantum oscillations and Hall anomaly of surface states in the topological insulator Bi2Te3 . Science 329, 821–824 (2010).
Analytis, J. G. et al. Two-dimensional surface state in the quantum limit of a topological insulator. Nat. Phys. 6, 960–964 (2010).
Ren, Z., Taskin, A. A., Sasaki, S., Segawa, K. & Ando, Y. Large bulk resistivity and surface quantum oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B 82, 241306(R) (2010).
Hong, S. S. et al. Ultra-low carrier concentration and surface-dominant transport in antimony-doped Bi2Se3 topological insulator nanoribbons. Nat. Commun. 3, 757 (2012).
He, H. et al. Impurity effect on weak antilocalization in the topological insulator Bi2Te3 . Phys. Rev. Lett. 106, 166805 (2011).
Rammer, J. Quantum Transport Theory (Perseus Books, Massachusetts, 1998).
Hikami, S., Larkin, A. I. & Nagaoka, Y. Spin-orbit interaction and magnetoresistance in the two dimensional random system. Prog. Theor. Phys. 63, 707 (1980).
Chen, J. et al. Gate-voltage control of chemical potential and weak antilocalization in Bi2Se3 . Phys. Rev. Lett. 105, 176602 (2010).
Bao, L. et al. Weak anti-localization and quantum oscillations of surface states in topological insulator Bi2Se2Te. Sci. Rep. 2, 726 (2012).
He, L. et al. Evidence of the two surface states of (Bi0.53Sb0.47)2Te3 films grown by van der Waals epitaxy. Sci. Rep. 3, 3406 (2013).
Taskin, A. A. et al. Manifestation of topological protection in transport properties of epitaxial Bi2Se3 thin films. Phys. Rev. Lett. 109, 066803 (2012).
Shim, W., Ham, J., Kim, J. & Lee, W. Shubnikov-de Haas oscillations in an individual single-crystalline bismuth nanowire grown by on-film formation of nanowires. Appl. Phys. Lett. 95, 232107 (2009).
Zhu, Z. W., Collaudin, A., Fauqué, B., Kang, W. & Behnia, K. Field-induced polarization of dirac valleys in bismuth. Nat. Phys. 8, 89–94 (2011).
Xiu, F. X. et al. Manipulating surface states in topological insulator nanoribbons. Nat. Nanotechnol. 6, 216–221 (2011).
Peng, H. et al. Aharonov-Bohm interference in topological insulator nanoribbons. Nat. Mater. 9, 225–229 (2010).
Tian, M. L. et al. Dual evidence of surface Dirac states in thin cylindrical topological insulator Bi2Te3 nanowires. Sci. Rep. 3, 1212 (2013).
Zhu, K. et al. The emergence of topologically protected surface states in epitaxial Bi(111) thin films. arXiv, 1403.0066 (2014).
Kong, D. S. et al. Rapid surface oxidation as a source of surface degradation factor for Bi2Se3 . ACS Nano 5, 4698–4703 (2011).
Acknowledgements
This work was supported by the National Key Basic Research of China (Grant No. 2011CBA00111); the National Nature Science Foundation of China (Grant No. U1332139, U1332209, U1432251, 11374302, 11104280 and 11174294).
Author information
Authors and Affiliations
Contributions
M.T. and Y.Z. supervised the research and contributed to the analysis. F.K. and W.N. synthesized the Bi nanoribbons. W.N., Y.H., J.Y. and H.D. fabricated the devices. W.N., Y.H. and H.D. carried out the transport measurement in high magnetic field and performed structural analysis. M.T. and W.N wrote the paper, together with help of all other co-authors.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Ning, W., Kong, F., Han, Y. et al. Robust surface state transport in thin bismuth nanoribbons. Sci Rep 4, 7086 (2014). https://doi.org/10.1038/srep07086
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07086
This article is cited by
-
Shubnikov-de Haas (SdH) Oscillation in Self-Flux Grown Rhombohedral Single-Crystalline Bismuth
Journal of Superconductivity and Novel Magnetism (2023)
-
Imaging current distribution in a topological insulator Bi2Se3 in the presence of competing surface and bulk contributions to conductivity
Scientific Reports (2021)
-
Enhancement of carrier transport characteristic in the Sb2Se2Te topological insulators by N2 adsorption
Scientific Reports (2017)
-
Spatial potential ripples of azimuthal surface modes in topological insulator Bi2Te3 nanowires
Scientific Reports (2016)
-
Topologically nontrivial bismuth(111) thin films
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.