Abstract
Thermodynamics plays an increasingly important role in modeling and engineering metabolism. We present the first nonempirical computational method for estimating standard Gibbs reaction energies of metabolic reactions based on quantum chemistry, which can help fill in the gaps in the existing thermodynamic data. When applied to a test set of reactions from core metabolism, the quantum chemical approach is comparable in accuracy to group contribution methods for isomerization and group transfer reactions and for reactions not including multiply charged anions. The errors in standard Gibbs reaction energy estimates are correlated with the charges of the participating molecules. The quantum chemical approach is amenable to systematic improvements and holds potential for providing thermodynamic data for all of metabolism.
Similar content being viewed by others
Introduction
Thermodynamics is fundamental for understanding the design principles of natural metabolic processes and for engineering efficient new metabolic pathways. Accurate standard Gibbs reaction energies of biochemical reactions  are crucial inputs for thermodynamics-based flux balance analysis, in which they are used to impose constraints on metabolite concentrations1 and to determine the ratios of forward and backward fluxes2. However, experimental
are crucial inputs for thermodynamics-based flux balance analysis, in which they are used to impose constraints on metabolite concentrations1 and to determine the ratios of forward and backward fluxes2. However, experimental  values are available only for a small fraction of all known metabolic reactions3. The group contribution methods (GCMs) are empirical computational approaches that are currently used for estimating
values are available only for a small fraction of all known metabolic reactions3. The group contribution methods (GCMs) are empirical computational approaches that are currently used for estimating  values from standard Gibbs formation energies of reactants and products4,5,6,7. GCMs employ additive schemes with increments for functional groups obtained from fitting to experimental data. Modern GCMs account for pH and combine group contribution estimates with more accurate reactant contributions7,8.
values from standard Gibbs formation energies of reactants and products4,5,6,7. GCMs employ additive schemes with increments for functional groups obtained from fitting to experimental data. Modern GCMs account for pH and combine group contribution estimates with more accurate reactant contributions7,8.
Here, we present the first nonempirical high-throughput computational method for estimating  values of metabolic reactions from quantum chemistry. Our objective is to develop a quantum-chemistry based computational framework for thermodynamics of metabolism that is competitive with GCMs. Using first-principles methods for predicting thermodynamic parameters offers several crucial advantages: Nonempirical methods are not limited by the available experimental data, thus reducing the risk of overfitting and providing a consistent approach throughout all of metabolism. Additionally, they can take advantage of an established hierarchy of increasingly accurate (and increasingly costly) quantum chemical methods. In this work, we analyze the different contributions to the errors in predicting Gibbs reaction energies using quantum chemistry. Finally, we outline future research directions that can deliver chemical accuracy to metabolic reaction thermochemistry by using quantum chemical approaches.
values of metabolic reactions from quantum chemistry. Our objective is to develop a quantum-chemistry based computational framework for thermodynamics of metabolism that is competitive with GCMs. Using first-principles methods for predicting thermodynamic parameters offers several crucial advantages: Nonempirical methods are not limited by the available experimental data, thus reducing the risk of overfitting and providing a consistent approach throughout all of metabolism. Additionally, they can take advantage of an established hierarchy of increasingly accurate (and increasingly costly) quantum chemical methods. In this work, we analyze the different contributions to the errors in predicting Gibbs reaction energies using quantum chemistry. Finally, we outline future research directions that can deliver chemical accuracy to metabolic reaction thermochemistry by using quantum chemical approaches.
Quantum chemistry has been successful at predicting the thermodynamics of gas phase chemical reactions with chemical accuracy9,10,11. However, predicting standard Gibbs reaction energies of metabolic reactions is significantly more challenging since biochemical reactions occur in solution. Solution phase thermochemistry faces two major challenges. First, it has to accurately account for the different minimal energy geometric conformations that coexist in the solution phase. The Gibbs energy of a particular species comprises contributions from many geometric conformers and can thus be obtained by averaging over their respective Gibbs energies.
Second, a useful first-principles quantum chemistry methodology should accurately reflect the protonation equlibria in aqueous solution at neutral pH12. Metabolites usually contain multiple ionizable groups such as amine, phosphate, or carboxylate and at a given pH, each compound consists of an ensemble of different protonation states. The apparent Gibbs formation energy of a metabolite can then be found by applying the Legendre transform of Alberty12 to the standard Gibbs formation energies of the individual protonation states. Ignoring the change in the relative abundance of the different protonation states with pH can result in errors in the estimated standard Gibbs reaction energy. Importantly, some metabolic compounds carry large negative charges in aqueous solutions and solution phase thermochemistry needs to accurately model these highly charged species. For example, phosphate groups, ubiquitous throughout biochemistry, are largely deprotonated at pH = 7. Therefore, metabolites with phosphate groups, such as fructose-1,6-biphosphate, have a highly negative charge. Accurate description of negatively charged molecules presents challenges to approximate density functional methods13,14,15,16.
Finally, hydrogen bonding between the metabolite and solvent molecules requires that one or more solvation shells be included in the quantum chemical model17. Since the computational cost of quantum chemical methods scales with the size of the molecular system, accurate solution thermochemistry studies are expectedly computationally more demanding than the corresponding gas-phase thermochemistry calculations18.
In contrast to empirical methods such as GCMs, the quantum chemical approach presented here aggregates the detailed information about the structures and energies of metabolites in solution into a transformed absolute Gibbs energy, G′, at the given pH and temperature. This “bottom up” strategy makes necessary a heuristic exhaustive sampling of conformers and protonation states of metabolites in solution. We represent each metabolite by an ensemble of protonation states (microspecies)–molecular structures that differ in their degree of protonation–which are present in the equilibrium mixture at a given pH and temperature. We represent each protonation state by an ensemble of conformers–distinct stable three-dimensional structures associated with it. The short-range solvation effects, in particular hydrogen bonding, are taken into account by explicit inclusion of a fixed number of water molecules. The long-range electrostatic interactions are described by means of a continuum solvation model19.
We investigate the effect of the explicit and implicit solvation modeling on the accuracy of the quantum chemical predictions. To this end, we consider a test set of 9 reactions from core metabolism, for which accurate standard Gibbs free reaction energies in solution are available from experiment. We investigate the influence of the size of the explicit water cluster, the water molecule balancing procedure and the inclusion of the conductor-like screening model (COSMO)20 to account for long-range electrostatic effects. Furthermore, we assess the accuracy of our computational procedure using a broader test set of 113 metabolic reactions from the NIST-TECR database3. We find that the quantum chemical approach is comparable in accuracy to GCMs for isomerization and group transfer reactions and for reactions not including multiply charged anions. The errors in the standard Gibbs reaction energy estimates are correlated with the charges of the participating molecules.
Results
Assessments of density functional methodologies
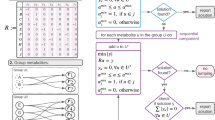
We performed the molecular structure optimizations on complexes of common metabolites with explicit water molecules using density functional theory (DFT) with the B3LYP functional21 and 6–31G* basis sets22. All calculations were carried out using the ORCA package23. The immediate output of each quantum chemical calculation is the absolute Gibbs energy, G, of each metabolite–water complex, which was computed in the rigid rotor–harmonic oscillator approximation. The transformed standard Gibbs reaction energies of metabolic reactions was then computed using the following three-step strategy: (i) The averaged absolute Gibbs energy,  , of each protonation state in solution was computed as the Boltzmann average of the standard Gibbs formation energies of the metabolite–water complexes; (ii) The averaged absolute Gibbs energy,
, of each protonation state in solution was computed as the Boltzmann average of the standard Gibbs formation energies of the metabolite–water complexes; (ii) The averaged absolute Gibbs energy,  , values of all protonation states present in the equilibrium mixture at a given pH were combined using the pH-dependent Legendre transform shown by Alberty12 to yield the transformed absolute Gibbs energy of the metabolite in water, G′; (iii) the transformed standard Gibbs energy of reaction,
, values of all protonation states present in the equilibrium mixture at a given pH were combined using the pH-dependent Legendre transform shown by Alberty12 to yield the transformed absolute Gibbs energy of the metabolite in water, G′; (iii) the transformed standard Gibbs energy of reaction,  , was obtained from the difference of the G′ values of products and reactants while balancing the numbers of explicit water molecules.
, was obtained from the difference of the G′ values of products and reactants while balancing the numbers of explicit water molecules.
In order to determine a cost-efficient and accurate treatment of solvation for high-throughput computation of  , we investigated 4 different solvation schemes across a test set of 9 biochemical reactions (Table 1). The water molecules were initially placed randomly around the metabolite molecule and subjected to unconstrained structure optimization. The test set contained three reactions from each of the following common reaction types: isomerizations, (de)hydrations and carbon–carbon bond cleavage/formation reactions. The solvation scheme has to balance the requirement of accurately representing the short-range environment of the solute with a tractable size for an explicit quantum chemical treatment. The solvation schemes investigated in this work included 5 or 10 explicit water molecules, which should on average provide sufficient donor and acceptor sites for hydrogen bonding in most metabolites. In addition, the importance of the long-range electrostatic interactions was probed by including the COSMO implicit solvation model20. For (de)hydrations and carbon–carbon bond cleavage/formation reactions, two strategies were employed to balance the number of water molecules on both sides of the reaction equation. We refer to them as large cluster (LC) and additional cluster (AC). The AC strategy added an extra cluster of water molecules to the side with fewer metabolites. The LC strategy increased the size of the water cluster surrounding the metabolite on the side with fewer molecules. Both strategies are illustrated in more detail in the Supporting Information.
, we investigated 4 different solvation schemes across a test set of 9 biochemical reactions (Table 1). The water molecules were initially placed randomly around the metabolite molecule and subjected to unconstrained structure optimization. The test set contained three reactions from each of the following common reaction types: isomerizations, (de)hydrations and carbon–carbon bond cleavage/formation reactions. The solvation scheme has to balance the requirement of accurately representing the short-range environment of the solute with a tractable size for an explicit quantum chemical treatment. The solvation schemes investigated in this work included 5 or 10 explicit water molecules, which should on average provide sufficient donor and acceptor sites for hydrogen bonding in most metabolites. In addition, the importance of the long-range electrostatic interactions was probed by including the COSMO implicit solvation model20. For (de)hydrations and carbon–carbon bond cleavage/formation reactions, two strategies were employed to balance the number of water molecules on both sides of the reaction equation. We refer to them as large cluster (LC) and additional cluster (AC). The AC strategy added an extra cluster of water molecules to the side with fewer metabolites. The LC strategy increased the size of the water cluster surrounding the metabolite on the side with fewer molecules. Both strategies are illustrated in more detail in the Supporting Information.
 values and deviations of computed
values and deviations of computed  values from experiment in kcal/mol for nine test reactions using different solvation schemes. Solvation schemes: 5(10), explicit solvation with 5(10) water molecules; I, implicit solvation model. Balancing strategies: LC, large cluster; AC, additional cluster. MAD: Mean Absolute Deviation. Metabolites: Glc-6-P, glucose-6-phosphate; Fru-6-P, fructose-6-phosphate; G3P, glyceraldehyde-3-phosphate; DHAP, dihydroxyacetone phosphate; 2PG, 2-phosphoglycerate; 3PG, 3-phosphoglycerate; PEP, phosphoenolpyruvate; F-1,6-BP, fructose-1,6-biphosphate; 2MMA, 2-methylmalate; Ac, acetate; Pyr, pyruvate
values from experiment in kcal/mol for nine test reactions using different solvation schemes. Solvation schemes: 5(10), explicit solvation with 5(10) water molecules; I, implicit solvation model. Balancing strategies: LC, large cluster; AC, additional cluster. MAD: Mean Absolute Deviation. Metabolites: Glc-6-P, glucose-6-phosphate; Fru-6-P, fructose-6-phosphate; G3P, glyceraldehyde-3-phosphate; DHAP, dihydroxyacetone phosphate; 2PG, 2-phosphoglycerate; 3PG, 3-phosphoglycerate; PEP, phosphoenolpyruvate; F-1,6-BP, fructose-1,6-biphosphate; 2MMA, 2-methylmalate; Ac, acetate; Pyr, pyruvateThe models including only explicit water molecules (denoted in Table as 1 5/LC and 10/AC, respectively) varied in their accuracy across different reaction types. Isomerizations gave the smallest deviations from experiment and we found that the 10/AC model was more accurate than the 5/LC model. The  values for isomerizations of three-carbon species (D-glyceraldehyde 3-phosphate (G3P) → dihydroxyacetone phosphate (DHAP) and 2-phospho-D-glycerate (2PG) → 3-phospho-D-glycerate (3PG)) were predicted with an accuracy of ~1 kcal/mol. For hydrations, predicted
values for isomerizations of three-carbon species (D-glyceraldehyde 3-phosphate (G3P) → dihydroxyacetone phosphate (DHAP) and 2-phospho-D-glycerate (2PG) → 3-phospho-D-glycerate (3PG)) were predicted with an accuracy of ~1 kcal/mol. For hydrations, predicted  values were within 2 kcal/mol of the experiment for two out of three reactions with the 10/AC scheme. These results compared favorably with the average accuracy of 1.6 kcal/mol found for the latest-generation GCMs7. However, carbon-bond cleavage/formation reactions showed large deviations from experiments for explicit-only solvation schemes irrespective of the number of explicit water molecules.
values were within 2 kcal/mol of the experiment for two out of three reactions with the 10/AC scheme. These results compared favorably with the average accuracy of 1.6 kcal/mol found for the latest-generation GCMs7. However, carbon-bond cleavage/formation reactions showed large deviations from experiments for explicit-only solvation schemes irrespective of the number of explicit water molecules.  of the retroaldol reaction of D-fructose-1,6-bisphosphate (F-1,6-BP, aldolase reaction) was underestimated by more than 40 kcal/mol with both 5/LC and 10/AC models.
of the retroaldol reaction of D-fructose-1,6-bisphosphate (F-1,6-BP, aldolase reaction) was underestimated by more than 40 kcal/mol with both 5/LC and 10/AC models.
Combining explicit solvation shells with the COSMO implicit solvation model (denoted as 5/I/LC and 10/I/AC in Table 1, respectively) reduced the deviation from experimental  values across all reaction types. The improvements were rather small for isomerizations and some hydrations but quite substantial for carbon-bond cleavage/formation reactions, with the aldolase reaction showing the largest improvement. We attribute these results to the considerable change in the molecular charge of the most abundant microspecies at pH = 7 from −4 for F-1,6-BP to −2 for G3P and DHAP. Inclusion of an implicit solvation model is important for the description of long-range electrostatic effects, improving accuracy. However, the experimental
values across all reaction types. The improvements were rather small for isomerizations and some hydrations but quite substantial for carbon-bond cleavage/formation reactions, with the aldolase reaction showing the largest improvement. We attribute these results to the considerable change in the molecular charge of the most abundant microspecies at pH = 7 from −4 for F-1,6-BP to −2 for G3P and DHAP. Inclusion of an implicit solvation model is important for the description of long-range electrostatic effects, improving accuracy. However, the experimental  value of this reaction is still underestimated by more than 10 kcal/mol with the 5/I/LC and 10/I/AC models. Tentative studies on larger metabolite–water complexes containing 10 or 20 explicit water molecules showed that further improvements in accuracy are possible by increasing the size the explicit solvent shell, however at the expense of higher computational cost. See Supporting Information for further details. This finding indicates that the deviations of the 5/I/LC and 10/I/AC models from the experiment (Table 1) are at least partly due to medium-range solvation effects associated with second and further solvent shells.
value of this reaction is still underestimated by more than 10 kcal/mol with the 5/I/LC and 10/I/AC models. Tentative studies on larger metabolite–water complexes containing 10 or 20 explicit water molecules showed that further improvements in accuracy are possible by increasing the size the explicit solvent shell, however at the expense of higher computational cost. See Supporting Information for further details. This finding indicates that the deviations of the 5/I/LC and 10/I/AC models from the experiment (Table 1) are at least partly due to medium-range solvation effects associated with second and further solvent shells.
Furthermore, the anionic metabolites at pH = 7 are challenging systems for approximate DFT methods, in particular multiply charged anions. As is well known from previous theoretical and computational works, the errors in the asymptotic shape of the approximate exchange–correlation potential lead to an incomplete cancellation of the interelectronic Coulomb repulsion at larger distances. As a result, electron affinities of molecules are typically overestimated in approximate DFT13,14,15,16. The use of hybrid functionals such as B3LYP13,14 or converged orbitals from Hartree–Fock calculations have been shown to improve the accuracy16. However, the extent of the error cancellation in reactions involving metabolites of different negative charges is not entirely known. We investigate this issue later in this work.
The choice of the initial placement of explicit water molecules can affect which conformation of the metabolite–water complex is reached by structure optimizations, the final minimal energy obtained after energy optimization and therefore the final  estimate. In order to explore the effect of the initial water placement, we generated multiple initial solvent conformations of the reactants and products of the aldolase reaction from snapshots of an equilibrated classical molecular dynamics (MD) trajectory at room temperature. The median absolute deviation (MAD) from the experimental
estimate. In order to explore the effect of the initial water placement, we generated multiple initial solvent conformations of the reactants and products of the aldolase reaction from snapshots of an equilibrated classical molecular dynamics (MD) trajectory at room temperature. The median absolute deviation (MAD) from the experimental  value of the aldolase reaction using this alternative methodology was 14.7 kcal/mol for the 20/LC solvation, which offered no improvement compared with 11.9 kcal/mol MAD obtained by random initial placement of explicit water molecules24. We refer to the Supplementary Information for additional details.
value of the aldolase reaction using this alternative methodology was 14.7 kcal/mol for the 20/LC solvation, which offered no improvement compared with 11.9 kcal/mol MAD obtained by random initial placement of explicit water molecules24. We refer to the Supplementary Information for additional details.
Large-scale density functional benchmark study
In order to balance the computational cost and accuracy, we selected the 5/I/LC solvation scheme to investigate the accuracy of the predicted Gibbs free reaction energies with respect to experimental values of 113 reactions from the NIST–TECR database3 (Figure 1). We used the Enzyme Commission (EC) codes of the corresponding enzymatic reactions as proxies for different reaction classes25. The test set was restricted to reactions that did not involve large cofactors and covered reactions from classes EC 2 (isomerases), EC 4 (lyases) and EC 5 (transferases). (See the Supplementary Information for the full list of test reactions and selection procedure.) The full test set consists of 5976 quantum chemical calculations and the median run time for geometry optimization and harmonic analysis of one conformer was 3.4 h when parallelized over 16 CPUs. The isomerase and transferase reactions showed MAD from experiment of 2.6 kcal/mol and 3.1 kcal/mol, respectively, which were comparable to those of GCMs4,5,6,7. The predicted  values of lyase reactions were less accurate with MAD of 4.7 kcal/mol.
values of lyase reactions were less accurate with MAD of 4.7 kcal/mol.
Within each reaction class, some reactions showed significantly larger deviations from experiment. Four outlier isomerase reactions had deviations from experimental  values > 10 kcal/mol. The ring-opening reaction converting dihydro-oxofuran-acetate to cis-cis-muconate (EC 5.5.1.1) exhibited the largest error in the test set of 18.7 kcal/mol. Within the set of transferase reactions, the phosphorolysis of guanosine monophosphate (EC 2.4.2.8) yielded the largest deviation from experiment of 13.6 kcal/mol. Whether these large deviations are due to differences in solvation patterns between reactants and products, to complex tautomeric equlibria, or to errors of the underlying quantum chemical methodology, are still open questions.
values > 10 kcal/mol. The ring-opening reaction converting dihydro-oxofuran-acetate to cis-cis-muconate (EC 5.5.1.1) exhibited the largest error in the test set of 18.7 kcal/mol. Within the set of transferase reactions, the phosphorolysis of guanosine monophosphate (EC 2.4.2.8) yielded the largest deviation from experiment of 13.6 kcal/mol. Whether these large deviations are due to differences in solvation patterns between reactants and products, to complex tautomeric equlibria, or to errors of the underlying quantum chemical methodology, are still open questions.
Effect of metabolite charges
We explored the effects of the metabolite charges on the accuracy of the predicted  values. For each metabolite in a reaction, we found the protonation state with the lowest transformed absolute Gibbs energy G′ (i.e. most abundant) and classified reactions according to the most negative charge among the most abundant microspecies (Figure 2). The groups of reactions not including multiply charged anions showed MAD of 3.0 kcal/mol or smaller, comparable to GCMs. The median and the width of the error distribution increased as the charge of the dominant microspecies became more negative. Since errors of approximate DFT could be responsible for the larger deviations for reaction involving multiply charged anions, we computed the Gibbs free reaction energies of two test reactions using electronic energies from Møller–Plesset perturbation theory with resolution of the identity (RI-MP2)26,27,28 instead of DFT. For the DHAP → G3P isomerization, we observed moderate improvement in accuracy, while for the aldolase reaction the improvement was quite substantial. See Supplementary Information for details. As discussed above, the tentative results for the aldolase reaction using larger explicit solvation shells also showed an improvement in the predicted Gibbs free reaction energies. These findings are consistent with the interpretation that multiply charged anions might require both a larger solvent shell to adequately represent the electrostatic screening in solution and quantum chemical methods that possess the correct asymptotic behavior of the potential. The increased accuracy for reactions with a lowest charge of +1 is probably due to a small sample size.
values. For each metabolite in a reaction, we found the protonation state with the lowest transformed absolute Gibbs energy G′ (i.e. most abundant) and classified reactions according to the most negative charge among the most abundant microspecies (Figure 2). The groups of reactions not including multiply charged anions showed MAD of 3.0 kcal/mol or smaller, comparable to GCMs. The median and the width of the error distribution increased as the charge of the dominant microspecies became more negative. Since errors of approximate DFT could be responsible for the larger deviations for reaction involving multiply charged anions, we computed the Gibbs free reaction energies of two test reactions using electronic energies from Møller–Plesset perturbation theory with resolution of the identity (RI-MP2)26,27,28 instead of DFT. For the DHAP → G3P isomerization, we observed moderate improvement in accuracy, while for the aldolase reaction the improvement was quite substantial. See Supplementary Information for details. As discussed above, the tentative results for the aldolase reaction using larger explicit solvation shells also showed an improvement in the predicted Gibbs free reaction energies. These findings are consistent with the interpretation that multiply charged anions might require both a larger solvent shell to adequately represent the electrostatic screening in solution and quantum chemical methods that possess the correct asymptotic behavior of the potential. The increased accuracy for reactions with a lowest charge of +1 is probably due to a small sample size.
Absolute deviations of computed  values from experiment in kcal/mol for reaction test set of Fig. 1 by charge of dominant microspecies.
values from experiment in kcal/mol for reaction test set of Fig. 1 by charge of dominant microspecies.
Discussion
The quantum chemical approach is a promising avenue to fill the gaps in thermodynamic data. It has broad coverage and is a first-principles approach independent of experimental input. We have demonstrated that a quantum chemical approach to estimate the thermodynamics of metabolic reactions can achieve accuracies comparable to empirical methods currently used by the metabolic engineering community. Although our results are highly encouraging, several challenges remain to be overcome for ab initio metabolic thermochemical estimates. The harmonic approximation approach taken here has limitations. In particular, the inclusion of explicit water molecules results in low-frequency, highly anharmonic intermolecular translational and rotational modes, which can make significant contributions to the vibrational entropy component of the free energy. However, it can be expected that the effect of these vibrations on reaction energies are smaller due to considerable error cancellation between reactants and products. A promising alternative that avoids the harmonic approximation completely is to use autocorrelation functions from ab initio MD simulations to compute thermodynamic properties of the reactants and products29,30. Based on our tentative studies, another direction for obtaining more accurate predictions is to increase the number of explicit water molecules surrounding each metabolite. The considerable computational cost associated with increasing the number of explicit water for hundreds of metabolites is a challenge that could be addressed in the near future with the use of GPU clusters.
Additionally, improvements in accuracy can be expected from using range-separated exchange–correlation functionals31 from performing single-point energies of optimized structures with wave-function methods26,27,28,32 (e.g. MP2 or coupled-cluster methods), from improved description of solvation using Quantum Mechanics/Molecular Mechanics (QM/MM) methods33 and from MD-based approaches to thermochemistry29,30.
One approach towards high-throughput quantum chemical methods for predicting metabolic thermodynamics with chemical accuracy is to improve on the density functional utilized. In this work we have used the B3LYP density functional, however other functionals can potentially yield higher accuracies for organic molecules in solution phase34. For example, the long-range corrected ωB97X-D functional31, when tested against a molecular test set, yields improvements on the accuracy of the predicted thermodynamic properties.
The use of wave function methods instead of DFT to perform single-point energy estimates on DFT-optimized geometries can also lead to potential improvements in accuracy. Wave-function methods, such as MP2 and coupled-cluster, although resulting in a higher computational cost, can yield higher accuracies when used to perform single point energy estimates of DFT-optimized geometries to obtain the electronic contribution to the standard Gibbs formation energy32. Recent advances in linear-scaling coupled-cluster methods, such as DLPNO-CCSD(T)35, are a promising avenue to develop accurate metabolic thermochemical methods that are useful for high-throughput applications. Also, recent highly parallelized GPU implementations of MP2 perturbation theory can significantly accelerate calculations28.
One approach to increase the size of the water cluster surrounding the solute is to include a larger number of waters, which are modeled with molecular mechanics, around the quantum mechanical systems. Such Quantum Mechanics/Molecular Mechanics (QM/MM) approaches have been used to predict transition states and equilibrium structures of organic reactions in solution and in enzymes33,36. This water modeling strategy can be coupled to an alternative approach to exploring the potential energy landscape of each metabolic species, which is performing molecular dynamics simulations of the system. Ab initio MD can be used to obtain thermodynamic properties of molecular systems. In this approach, the vibrational contribution to the Gibbs formation energy can be obtained from autocorrelation function techniques29,30.
Finally, another challenge is the treatment of larger metabolites such ATP/ADP and NAD+/NADH. The larger number of minimal energy conformations and complex formation with cations such as Mg2+ make an accurate treatment of these compounds computationally expensive. Possible solutions for reactions involving cofactors include using highly parallelized computational frameworks37 and combining ab initio Gibbs energies of small metabolites with experimental formation energy values for the cofactors. This latter approach has been used in the context of GCM with encouraging results7. We are conducting further work along all of these lines.
Methods
Computational details
We compute reaction Gibbs free energies from differences of absolute Gibbs free energies of individual metabolites in solution. Each metabolite is represented by an ensemble of protonation states (microspecies), which exist at equilibrium concentrations at a given pH12. Each protonation state has a different number of protons and therefore electric charge. An ensemble of conformers, distinct geometrical configurations of the atoms composing the protonation state, represents each microspecies. The geometry of each conformer is a local minimum in the potential energy surface (PES) of the molecular system.
We begin with a SMILES string representation of each metabolite involved in a metabolic reaction38 (see Supplementary Information for the complete list of SMILES representation strings). From the SMILES representation of each metabolite, we sample microspecies and conformers using empirical rules as implemented in the ChemAxon conformation tool, version 5.2.2.). We first generate a set of protonation states that are predicted to be above a 0.5% relative equilibrium abundance cutoff at pH = 7. For each microspecies we then generate a set of 10 geometric conformers that approximate the minimal energy conformations of each metabolite. Each conformer is described as a set of atoms accompanied by its Cartesian coordinates.
Once we have obtained an ensemble of microspecies and conformers for each metabolite involved in the reaction, we account for solvation effects by surrounding each conformer with several explicit water molecules. This method is coined the “explicit water model” since it involves the placement of individual waters in the system, in contrast to the implicit water model described below. We use the software PACKMOL to randomly place water molecules in a 5 Å radius around the metabolite24.
In order to account for long-range electrostatic interactions in solution, we also use the conductor-like screening model (COSMO)20. This implicit water model helps to account for long-range electrostatic interactions by approximating the bulk solvent as a uniform conducting continuum with a cavity where the metabolite and explicit waters reside. By solving for the charge density on the surface of the cavity and scaling the charge density according to the dielectric constant of water, we can imitate the effects of bulk solvent when we run quantum chemistry calculations on these systems. We use the static dielectric constant of water ε = 80.4 and the refractive index n = 1.33, respectively.
The initially generated conformers approximate the minima of the potential energy surface using heuristics. To find minimal energy conformers we optimize the geometry of the solvated conformers using B3LYP18 functional and the 6-31G* basis19 within the ORCA quantum chemical program (version 2.9)23. Normal mode frequencies are obtained by calculating the Hessian matrix in the basis of displacements along all 3N − 6 internal coordinates. The Hessian matrix is then diagonalized to find the normal mode frequencies.
With the information we have calculated using quantum chemistry, we can find the translational, rotational and vibrational enthalpies and entropies in the rigid rotor–harmonic oscillator approximation39. We assume the solvated conformer behaves as an ideal gas since it is in a dilute solution.
Using these formulas and the final electronic energy after the structure optimization, we can then calculate the standard state enthalpy and entropy for each solvated conformer and therefore the absolute Gibbs free energy of each conformer.
The absolute Gibbs energy of a protonation state is obtained as the Boltzmann average of the absolute Gibbs energies of the sampled conformers,

Where the index k refers to conformers and the index j refers to protonation states. An alternative approach is to treat the system as an equilibrated mixture consisting of all the minimal energy structures found to obtain a Gibbs free energy,

Importantly, our results are not sensitive to using either approach to combining conformer Gibbs energies. We combine the Gibbs energies of the different protonation states by applying the Legendre transform12. This transform yields the appropriate thermodynamic potential of each microspecies at the pH and ionic strength specified in the experimental database,

where the formation energy of a proton is taken to be −268.61 kcal/mol. This value was obtained by computing the solvation Gibbs energy of a hydronium ion using 4 explicit water molecules and the COSMO implicit model.
These transformed G′(j) values are then combined into a single transformed Gibbs energy for each reactant at a given pH, temperature and ionic strength according to

where the index i refers to a reactant. Finally, The G′(i) values of the substrates are subtracted from those of the products

where νi is the stoichiometric coefficient of each metabolite and is negative for substrates and positive for products. This yields the prediction for the standard Gibbs reaction free energy  .
.
For many reactions, the NIST-TECR database contains multiple experimental equilibrium constant values3. These are generally specified at different values of temperature and pH. For each reaction, we account for all different experimental values in NIST-TECRDB when estimating the deviation from experiment. For each reported value in NIST, we estimate a  at the specified temperature and pH and compute the deviation from experiment for that particular value. We repeat this for all experimental values for the particular reaction in NIST and average the deviation from experiment over all of these estimates.
at the specified temperature and pH and compute the deviation from experiment for that particular value. We repeat this for all experimental values for the particular reaction in NIST and average the deviation from experiment over all of these estimates.
Random subsampling of geometric conformers
Our  estimates depend on the exact geometry of the ensemble of conformers used to represent each protonation state of each metabolite. In order to minimize the sensitivity of our estimates on the exact set of conformers used, we average out the variability of
estimates depend on the exact geometry of the ensemble of conformers used to represent each protonation state of each metabolite. In order to minimize the sensitivity of our estimates on the exact set of conformers used, we average out the variability of  estimates due to the conformers distinct geometries and absolute Gibbs energies. To do this, we perform the following conformer subsampling procedure.
estimates due to the conformers distinct geometries and absolute Gibbs energies. To do this, we perform the following conformer subsampling procedure.
We first perform a filtering step to discard conformers with outlier absolute Gibbs energies. After obtaining the absolute Gibbs energy of every conformer associated to a given protonation state, we filter out conformers according to an interquartile range (IQR) procedure. Specifically, we discard conformers with absolute Gibbs energies that are more than one standard deviation - obtained after multiplication the intermediate quartile by an IQR factor of 1.349 - away from the median absolute Gibbs energy of all conformers.
After filtering, we are then left, for each protonation state (j) involved in a reaction, with a set of conformers of size Nj. We then randomly sample, without replacement, a subset of size njof these filtered conformers. We compute the Boltzmann average of their absolute Gibbs energies, equation (1). As mentioned above, an alternative approach is to treat the system as an equilibrated mixture consisting of all the minimal energy structures found to obtain a Gibbs free energy, equation (4). This yields an individual estimate for the absolute Gibbs energy of each individual protonation state (microspecies).
For a fixed value of nj - the number of conformers subsampled after filtering - we perform this random subsampling procedure for every protonation state of every metabolite in a reaction. This yields, for every protonation state involved in the reaction, an absolute Gibbs energy estimate. These can then be combined, as detailed in the hierarchical procedure described above, to obtain a single  estimate for the reaction.
estimate for the reaction.
We then iterate, for a fixed subsample size nj, this conformer subsampling procedure I = 30 times. This effectively averages out the variability of the  estimate due to distinct geometries of conformers. Averaging the individual
estimate due to distinct geometries of conformers. Averaging the individual  estimates obtained in each of these 30 iterations yields the final value for the estimated standard Gibbs reaction energy.
estimates obtained in each of these 30 iterations yields the final value for the estimated standard Gibbs reaction energy.
We tested the effect of subsampling different numbers of geometric conformers, on the summary statistics of the reaction test set. We vary the value of nj– the number of subsampled conformers for each microspecies involved in the reaction - from 1 to njMax. njMax is the number of conformers associated to the protonation state with the smallest value of Nj - the total number of conformers belonging to that protonation state, 1 ≤ nj ≤ minj{Nj}.
Although the  estimate of a particular reaction may vary by a few kcal/mol with conformer subsample size, the summary statistics (i.e. median absolute deviation from experimental value) of the reaction test set are insensitive to the number of conformers subsampled. Additionally, the correlation between the charge of protonation states and the accuracy of predicted
estimate of a particular reaction may vary by a few kcal/mol with conformer subsample size, the summary statistics (i.e. median absolute deviation from experimental value) of the reaction test set are insensitive to the number of conformers subsampled. Additionally, the correlation between the charge of protonation states and the accuracy of predicted  values is observed for all subsample sizes considered here We refer to the Supporting Information for further details on the subsampling procedure.
values is observed for all subsample sizes considered here We refer to the Supporting Information for further details on the subsampling procedure.
Reaction test set
The reaction test set was chosen from the NIST – TECRDB3 database according to the following criteria. Since computational cost of quantum chemical calculations increases with molecular size, we ordered the available reaction data set according to the sum of the number of atoms in all molecules involved in the reaction. We approximated the number of atoms of each metabolite by the length of its SMILES string representation. We defined the reaction size as the sum of the numbers of atoms for all metabolites involved in the reaction. We divided reactions in NIST-TECRDB according to the Enzyme Commission (EC) number scheme24. Within each EC class, reactions were sorted according to the reaction size measure, from smallest to largest. We excluded EC classes with reactions involving large cofactor molecules such as ATP/ADP and NADH/NAD+ and focused on EC classes 2, 4 and 5 for further analysis. Given our available computational resources, we performed DFT calculations for a total of 113 metabolic reactions.
We refer to the Supplementary Information for the full list of reactions used in the test set, the deviations from experimental values obtained, as well as the set of SMILES35 strings used to represent each metabolite.
References
Henry, C. S., Broadbelt, L. J. & Hatzimanikatis, V. Thermodynamics-Based Metabolic Flux Analysis. Biophys. J. 92, 1792–1805 (2007).
Beard, D. A. & Qian, H. Relationship between Thermodynamic Driving Force and One-Way Fluxes in Reversible Processes. PLoS ONE 2, e144 (2007).
Goldberg, R. N., Tewari, Y. B. & Bhat, T. N. Thermodynamics of enzyme-catalyzed reactions–a database for quantitative biochemistry. Bioinformatics 20, 2874–2877 (2004).
Mavrovouniotis, M. L. Group Contributions for Estimating Standard Gibbs Energies of Formation of Biochemical Compounds in Aqueous Solution. Biotechnol. Bioeng. 36, 1070–1082 (1990).
Mavrovouniotis, M. L. Estimation of Standard Gibbs Energy Changes of Biotransformations. J. Biol. Chem. 266, 14440–14445 (1991).
Jankowski, M. D., Henry, C. S. & Broadbelt, L. J. Group Contribution Method for Thermodynamic Analysis of Complex Metabolic Networks. Biophys. J. 95, 1487–1499 (2008).
Noor, E., Haraldsdóttir, H. S., Milo, R. & Fleming, R. M. T. Consistent Estimation of Gibbs Energy Using Component Contributions. PLoS Comput Biol 9, e1003098 (2013).
Noor, E. et al. An integrated open framework for thermodynamics of reactions that combines accuracy and coverage. Bioinformatics 28, 2037–2044 (2012).
Curtiss, L. A., Redfern, P. C. & Frurip, D. J. Theoretical Methods for Computing Enthalpies of Formation of Gaseous Compounds. Rev. Comput. Chem. 15, 147–211 (2000).
Quantum-Mechanical Prediction of Thermochemical Data (ed Cioslowski, J.) (Kluwer, New York, 2002).
Boese, A. D. et al. W3 theory: Robust Computational Thermochemistry in the kJ/mol Accuracy Range. J. Chem. Phys. 120, 4129–4141 (2004).
Alberty, R. A. Thermodynamics of Biochemical Reactions (Wiley, Hoboken NJ, 2005).
Tschumper, G. S. & Schaefer, H. F., III Predicting Electron Affinities with Density Functional Theory: Some Positive Results for Negative Ions. J. Chem. Phys. 107, 2529–2541.
Rienstra-Kiracofe, J. C., Tschumper, G. S., Schaefer, H. F., III, Nandi, S. & Ellison, G. B. Atomic and Molecular Electron Affinities: Photoelectron Experiments and Theoretical Computations. Chem. Rev. 102, 231–282 (2002).
Simons, J. Molecular Anions. J. Phys. Chem. A 112, 6401–6511 (2008).
Lee, D., Furche, F. & Burke, K. Accuracy of Electron Affinities of Atoms in Approximate Density Functional Theory. J. Chem. Phys. Lett. 1, 2124–2129 (2010).
Jensen, J. H. & Gordon, M. S. On the Number of Water Molecules Necessary To Stabilize the Glycine Zwitterion. J. Am. Chem. Soc. 117, 8159–8170 (1995).
Marenich, A. V., Ding, W., Cramer, C. J. & Truhlar, D. G. Resolution of a Challenge for Solvation Modeling: Calculation of Dicarboxylic Acid Dissociation Constants Using Mixed Discrete–Continuum Solvation Models. J. Phys. Chem. Lett. 3, 1437–1442 (2012).
Cramer, C. J. & Truhlar, D. G. Continuum Solvation Models. Solvent Effects and Chemical Reactivity. (eds Tapia, O. & Bertán, J.) 1–80 (Kluwer, New York, 2002).
Klamt, A. & Schüürmann, G. COSMO: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and its Gradient. J. Chem. Soc. Perkin Trans. 2, 799–805 (1993).
Becke, A. D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 98, 5648–5652 (1993).
Hehre, W. J., Ditchfield, R. & Pople, J. A. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 56, 2257–2261 (2003).
Neese, F. The ORCA program system. Wiley Interdisciplinary Reviews: Computational Molecular Science 2, 73–78 (2012).
Martinez, L., Andrade, R., Birgin, E. G. & Martinez, J. M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 30, 2157–2164 (2009).
Webb, E. C. Enzyme Nomenclature 1992. Recommendations of the Nomenclature Committee of the International Union of Biochemistry and Molecular Biology on the Nomenclature and Classification of Enzymes (Academic Press, San Diego CA, 1992).
Møller, C. & Plesset, M. S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 46, 618–622 (1934).
Weigend, F., Häser, M., Patzelt, H. & Ahlrichs, R. RI-MP2: Optimized Auxiliary Basis Sets and Demonstration of Efficiency. Chem. Phys. Lett. 294, 143–152 (1998).
Watson, M., Olivares-Amaya, R., Edgar, R. G. & Aspuru-Guzik, A. Accelerating Correlated Quantum Chemistry Calculations Using Graphical Processing Units. Comput. Sci. Eng. 12, 40–51 (2010).
Lin, S.-T., Maiti, P. K. & Goddard, W. A. Two-Phase Thermodynamic Model for Efficient and Accurate Absolute Entropy of Water from Molecular Dynamics Simulations. J. Phys. Chem. B 114, 8191–8198 (2010).
Berens, P. H., White, S. R. & Wilson, K. R. Molecular dynamics and spectra. II. Diatomic molecules. J. Chem. Phys. 75, 515–529 (1981).
Chai, J. D. & Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 10, 6615–6620 (2008).
Baboul, A. G., Curtiss, L. A. & Redfern, P. C. Gaussian-3 theory using density functional geometries and zero-point energies. J. Chem. Phys. 110, 7650–7657 (1999).
Senn, H. M. & Thiel, W. QM/MM Methods for Biomolecular Systems. Angew. Chem. Int. Ed. 48, 1198–1229 (2009).
Steinmetz, M., Hansen, A., Ehrlich, S., Risthaus, T. & Grimme, S. Accurate Thermochemistry for Large Molecules with Modern Density Functionals. Top. Curr. Chem 1–23; 10.1007/128_2014_543 (2014).
Riplinger, C. & Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 138, 034106 (2013).
Acevedo, O. & Jorgensen, W. L. Advances in Quantum and Molecular Mechanical (QM/MM) Simulations for Organic and Enzymatic Reactions. Acc. Chem. Res. 43, 142–151 (2009).
Ufimtsev, I. S. & Martínez, T. J. Graphical Processing Units for Quantum Chemistry. Comput. Sci. Eng. 10, 26–34 (2008).
Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Model. 28, 31–36 (1988).
McQuarrie, D. A. Statistical Mechanics (University Science Books, Sausalito CA, 2000).
Acknowledgements
A.J. acknowledges support by the Fundación Mexico en Harvard, A.C. and the Consejo Nacional de Ciencia y Tecnología (CONACYT, Mexico). A.A.-G. and D.R. were supported by the Cyberdiscovery Initiative Type II (CDI2) grant of the National Science Foundation (NSF), grant number OIA-1125087. The authors thank Ron Milo for insightful advice.
Author information
Authors and Affiliations
Contributions
A.J., D.R., E.N., A.B.E. and A.A.G. designed the research. A.J., I.D., B.S.L. and R.O.A. carried out the research. A.J. and D.R. analyzed the data and wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Supplementary Information
Supplementary Dataset
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Jinich, A., Rappoport, D., Dunn, I. et al. Quantum Chemical Approach to Estimating the Thermodynamics of Metabolic Reactions. Sci Rep 4, 7022 (2014). https://doi.org/10.1038/srep07022
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07022
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

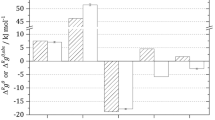

 values from experiment in kcal/mol for test set of 113 reactions as classified by the Enzyme Commission (EC) codes.
values from experiment in kcal/mol for test set of 113 reactions as classified by the Enzyme Commission (EC) codes.