Abstract
Quantum discord is the minimal bipartite resource which is needed for a secure quantum key distribution, being a cryptographic primitive equivalent to non-orthogonality. Its role becomes crucial in device-dependent quantum cryptography, where the presence of preparation and detection noise (inaccessible to all parties) may be so strong to prevent the distribution and distillation of entanglement. The necessity of entanglement is re-affirmed in the stronger scenario of device-independent quantum cryptography, where all sources of noise are ascribed to the eavesdropper.
Similar content being viewed by others
Introduction
One of the hot topics in the quantum information theory is the quest for the most appropriate measure and quantification of quantum correlations. For pure quantum states, this quantification is provided by quantum entanglement1 which is the physical resource at the basis of the most powerful protocols of quantum communication and computation2,3,4. However, we have recently understood that the characterization of quantum correlations is much more subtle in the general case of mixed quantum states5,6.
There are in fact mixed states which, despite being separable, have correlations so strong to be irreproducible by any classical probability distribution. These residual quantum correlations are today quantified by quantum discord7, a new quantity which has been studied in several contexts with various operational interpretations and applications, including work extraction8, quantum state merging9,10, remote state preparation11, entanglement distribution12, discrimination of unitaries13 and quantum channel discrimination14. Discord-type quantum correlations also play a crucial role in tasks such as quantum state broadcasting15 and quantum metrology16,17.
In this paper, we identify the basic role of quantum discord in one of the most practical tasks of quantum information, i.e., quantum key distribution (QKD)18. The claim that quantum discord must be non-zero to implement QKD is intuitive. In fact, quantum discord and its geometric formulation are connected with the concept of non-orthogonality, which is the essential ingredient for quantum cryptography. That said, it is still very important to characterize the general framework where discord remains the only available resource for QKD. Necessarily, this must be a scenario where key distribution is possible despite entanglement being absent.
Here we show that this general scenario corresponds to device-dependent (or trusted-device) QKD, which encompasses all realistic protocols where the noise affecting the devices and apparata of the honest parties is assumed to be trusted, i.e., not coming from an eavesdropper but from the action of a genuine environment. This can be preparation noise (e.g., due to imperfections in the optical switches/modulators or coming from the natural thermal background at lower frequencies19,20,21,22,23) as well as measurement noise and inefficiencies affecting the detectors (which could be genuine or even added by the honest parties24,25). Such trusted noise may be high enough to prevent the distribution and distillation of entanglement, but still a secure key can be extracted due to the presence of non-zero discord.
By contrast, if the extra noise in the apparata cannot be trusted and is considered to be the effect of side-channel attacks26, then we have to enforce device-independent QKD2,27,28. In this more demanding scenario, quantum discord is still necessary for security but plays a secondary role with respect to the coherent information, which directly provides the optimal secret-key rates, so that key distribution is a consequence of entanglement distillation. A similar situation occurs in ideal QKD protocols, where state preparation and quantum detections are assumed to be perfect, with no other noise present except that channel noise.
Results
We start with a brief review on quantum discord, specifying its relation with the coherent information. We then introduce the device-dependent QKD protocols, characterized by extra trusted noise and we explain why non-zero discord is a necessary cryptographic resource. Next we analyze the optimal secret-key rates which are achievable in device-dependent QKD, showing that key distribution can be secure in the absence of entanglement. We then consider device-independent QKD, where the extra noise is assumed to be untrusted and also ideal QKD, where no extra noise is present. In these cases we reaffirm the crucial role of entanglement, with quantum discord providing an upper bound to the optimal rates.
Quantum discord
Discord comes from different quantum extensions of the classical mutual information. The first is quantum mutual information1, measuring the total correlations between two systems, A and B and defined as I(A, B) : = S(A) − S(A|B), where S(A) is the entropy of system A and S(A|B) : = S(AB) − S(B) its conditional entropy. The second extension is C(A|B) : = S(A)−Smin(A|B), where Smin(A|B) is the entropy of system A minimized over an arbitrary measurement on B. This local measurement is generally described by a positive operator valued measure (POVM) {My}, defining a random outcome variable Y = {y, py} and collapsing system A into conditional states ρA|y. Thus, we have

where the minimization can be restricted to rank-1 POVMs7. (In our formulas, variables can be discrete or continuous; in the latter case, sums become integrals and probability distributions become densities).
The quantity C(A|B) quantifies the classical correlations between the two systems, corresponding to the maximal common randomness achievable by local measurements and one-way classical communication (CC)29. Thus, quantum discord is defined as the difference between total and classical correlations5,6,7

An equivalent formula can be written by noticing that Ic(A〉B) : = −S(A|B) is the coherent information30,31. Then, introducing an ancillary system E which purifies ρAB, we can apply the Koashi-Winter relation32,33 and write Smin(A|B) = Ef (A, E), where the latter is the entanglement of formation between A and E. Therefore

It is important to note that D(A|B) is different from D(B|A), where system A is measured. For instance, in classical-quantum states  , where A embeds a classical variable via the orthonormal set {|x〉} and B is prepared in non-orthogonal states {ρB(x)}, we have D(B|A) = 0 while D(A|B) > 0. By contrast, for quantum-classical states (B embedding a classical variable), we have the opposite situation, i.e., D(A|B) = 0 and D(B|A) > 0.
, where A embeds a classical variable via the orthonormal set {|x〉} and B is prepared in non-orthogonal states {ρB(x)}, we have D(B|A) = 0 while D(A|B) > 0. By contrast, for quantum-classical states (B embedding a classical variable), we have the opposite situation, i.e., D(A|B) = 0 and D(B|A) > 0.
Device-dependent QKD protocols
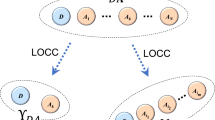
Any QKD protocol can be recast into a measurement-based scheme, where Alice sends Bob part of a bipartite state, then subject to local detections. Adopting this representation, we consider a device-dependent protocol where extra noise affects Alice's state preparation, as in Fig. 1 (this is generalized later). In her private space, Alice prepares two systems, A and a, in a generally mixed state ρAa. This state is purified into a 3-partite state ΦPAa with the ancillary system P being inaccessible to Alice, Bob or Eve.
Device-dependent protocol with preparation noise.
Alice prepares a generally-mixed input state ρAa, which is purified into a state ΦPAa by adding an extra system P inaccessible to all parties. System a is sent through an insecure line, so that Alice and Bob share an output state ρAB. By applying rank-1 POVMs on their local systems, A and B, they derive two correlated random variables, X and Y, which are processed into a secret key. In the middle, Eve attacks the line using a unitary U which couples system a with a pure-state ancilla e. The output ancilla E is then stored in a quantum memory, which is coherently detected at the end of the protocol.
System a is then sent to Bob, who gets the output system B. From the shared state ρAB, Alice and Bob extract two correlated variables: System A is detected by a rank-1 POVM {Mx}, providing Alice with variable X = {x, px}, while B is detected by another rank-1 POVM {My}, providing Bob with variable Y = {y, py}, whose correlations with X are quantified by the classical mutual information I(X, Y).
After the previous process has been repeated many times, Alice and Bob publicly compare a subset of their data. If the error rate is below a certain threshold, they apply classical procedures of error correction and privacy amplification with the help of one-way CC, which can be either forward from Alice to Bob (direct reconciliation), or backward from Bob to Alice (reverse reconciliation). Thus, they finally extract a secret key at a rate K ≤ I(X, Y), which is denoted by K(Y|X) in direct reconciliation and K(X|Y) in reverse reconciliation.
To quantify these rates, we need to model Eve's attack. The most general attack is greatly reduced if Alice and Bob perform random permutations on their classical data34,35. As a result, Eve's attack collapses into a collective attack, where each traveling system is probed by an independent ancilla. This means that Eve's interaction can be represented by a two-system unitary Uae coupling system a with an ancillary system e prepared in a pure state (up to isometries which do not increase Eve's information). The output ancilla E is then stored in a quantum memory which is coherently measured at the end of the protocol (see Fig. 1). In this attack, the maximum information which is stolen on X or Y cannot exceed the Holevo bound.
Non-zero discord is necessary
Before analyzing the secret-key rates, we briefly clarify why discord is a necessary resource for QKD. Suppose that Alice prepares a quantum-classical state  with {|k〉} orthogonal, so that D(A|a) = 0. Classical system a is perfectly clonable by Eve. This implies that the three parties will share the state
with {|k〉} orthogonal, so that D(A|a) = 0. Classical system a is perfectly clonable by Eve. This implies that the three parties will share the state

with Eve fully invisible, since her action is equivalent to an identity channel for Alice and Bob, i.e., ρAB = ρAa.
Direct reconciliation fails since ρABE is symmetric under B–E permutation, which means that Eve decodes Alice's variable with the same accuracy of Bob. Reverse reconciliation also fails. Bob encodes Y in the joint state  , where pk|y : = 〈k|My|k〉. Then, Eve retrieves K = {k, pk|y} by a projective POVM, while Alice decodes a variable X with distribution
, where pk|y : = 〈k|My|k〉. Then, Eve retrieves K = {k, pk|y} by a projective POVM, while Alice decodes a variable X with distribution

This equation defines a Markov chain Y → K → X, so that I(Y, K) ≥ I(Y, X) by data processing inequality, i.e., Eve gets more information than Alice. (This reasoning can easily be extended to considering coherent detections for Eve and Alice.)
As expected, system a sent through the channel must be quantum D(A|a) > 0 in order to have a secure QKD. Indeed, this is equivalent to sending an ensemble of non-orthogonal states. By contrast, the classicality of the private system A is still acceptable, i.e., we can have D(a|A) = 0. In fact, we may build QKD protocols with preparation noise using classical-quantum states

whose local detection (on system A) prepares any desired ensemble of non-orthogonal signal states {ρa(x),px}. For instance, the classical-quantum state of two qubits ρAa = (|0, 0〉Aa〈0, 0| + |1, φ〉Aa〈1, φ|)/2, with {|0〉, |1〉} orthonormal and 〈0|φ〉 ≠ 0, realizes the B92 protocol36.
Secret-key rates
Once we have clarified that non-zero input discord D(A|a) > 0 is a necessary condition for QKD, we now study the secret-key rates which can be achieved by device-dependent protocols. Our next derivation refers to the protocol of Fig. 1 and, more generally, to the scheme of Fig. 2, where Alice and Bob share an output state ρAB, where only part of the purification is accessible to Eve (system E), while the inaccessible part P accounts for all possible forms of extra noise in Alice's and Bob's apparata, including preparation noise and detection noise (quantum inefficiencies, etc…) Note that the scheme of Fig. 2 can also derive from QKD protocols with an untrusted relay, where Alice's and Bob's apparata are trusted while Eve controls a relay whose measurement creates remote correlations37.
In direct reconciliation, Alice's variable X is the encoding to guess. The key rate is then given by K(Y|X) = I(X,Y) − I(E,X), where I(E,X) = S(E) − S(E|X) is the Holevo bound quantifying the maximal information that Eve can steal on Alice's variable. We can write an achievable upper bound if we allow Bob to use a quantum memory and a coherent detector. In this case, I(X, Y) must be replaced by the Holevo quantity I(B,X) = S(B) − S(B|X) and we get the forward Devetak-Winter (DW) rate38,39

The optimal forward-rate is defined by optimizing on Alice's individual detections  .
.
We can write similar quantities in reverse reconciliation, where Bob's variable Y is the encoding to infer. The secret key rate is given by K(X|Y) = I(X, Y) − I(E, Y), where I(E, Y) = S(E) − S(E|Y) is Eve's Holevo information on Y. Assuming a coherent detector for Alice, this rate is bounded by the backward DW rate

which gives the optimal backward-rate  by maximizing on Bob's individual detections {My}.
by maximizing on Bob's individual detections {My}.
Playing with system P, we can easily derive upper and lower bounds for the two optimal rates. Clearly, we get lower bounds K* ≤ K if we assume P to be accessible to Eve, which means to extend E to the joint system E = EP in previous equations (7) and (8). By exploiting the purity of the global state ΨABE and the fact that the encoding detections are rank-1 POVMs (therefore collapsing pure states into pure states), we can write the entropic equalities S(AB) = S(E), S(B|X) = S(E|X) and S(A|Y) = S(E|Y). Then we easily derive

where the coherent information Ic(A〉B) and its reverse counterpart40,41Ic(B〉A) quantify the maximal entanglement which is distillable by local operations and one-way CC, forward and backward, respectively.
It is also clear that we get upperbounds K* ≥ K by assuming P to be accessible to the decoding party, Alice or Bob, depending on the reconciliation. In direct reconciliation, we assume P to be accessible to Bob, which means extending his system B to B = BP in equation (7). Using the equalities S(AB) = S(E) and S(B|X) = S(E|X), we get

where I(A, P|B) ≥ 0 is the conditional quantum mutual information. Then, in reverse reconciliation, we assume P to be accessible to Alice, so that A becomes A = AP in equation (8). Using S(AB) = S(E) and S(A|Y) = S(E|Y), we get  .
.
Thus, the optimal key rates satisfy the inequalities


where the right hand sides can be bounded using

According to equations (11) and (12), key distribution can occur (K ≥ 0) even in the absence of distillable entanglement (Ic = 0). This means that device-dependent QKD is the crucial scenario for quantum discord. In device-dependent QKD, we can indeed build protocols which are secure (K > 0) despite entanglement being completely absent (in any form, distillable or bound) as long as the minimal discord condition D(A|a) > 0 is satisfied. A secure protocol based on separable Gaussian states41 is explicitly shown in the Supplementary Information.
In general, there is an easy way to design device-dependent protocols which are secure and free of entanglement. Any prepare and measure protocol whose security is based on the transmission of non-orthogonal states {ρa(x), px} can be recast into a device-dependent protocol, which is based on a classical-quantum state ρAa as in equation (6), whose classical part A is detected while the quantum part a is sent through the channel. This is as secure as the original one as long as the purification of the classical-quantum state is inaccessible to Eve. Thus, in such assumption of trusted noise, any prepare and measure protocol has an equivalent discord-based representation, where non-zero discord guarantees security in the place of non-orthogonality.
Side-channels and device-independent QKD
Let us consider the more demanding scenario where all sources of noise are untrusted. This means that the extra noise in Alice's and Bob's apparata comes from side-channel attacks, i.e., system P in Fig. 2 is controlled by Eve. In this case, the secret-key rates are given by

so that QKD is equivalent to entanglement distillation.
It is easy to check that quantum discord upperbounds these key rates. Applying equation (3) to equation (14), we obtain the cryptographic relations


The optimal forward rate  , where Alice's variable must be inferred, equals the difference between the output discord D(A|B), based on Bob's detections and the entanglement of formation Ef(A, E) between Alice and Eve. Situation is reversed for the other rate
, where Alice's variable must be inferred, equals the difference between the output discord D(A|B), based on Bob's detections and the entanglement of formation Ef(A, E) between Alice and Eve. Situation is reversed for the other rate  . Note that quantum discord not only provides an upper bound to the key rates, but its asymmetric definition, D(A|B) or D(B|A), is closely connected with the reconciliation direction (direct
. Note that quantum discord not only provides an upper bound to the key rates, but its asymmetric definition, D(A|B) or D(B|A), is closely connected with the reconciliation direction (direct  or reverse
or reverse  ).
).
Ideal QKD protocols
In practical quantum cryptography, extra noise is always present and we distinguish between device-dependent and device-independent QKD on the basis of Eve's accessibility of the extra system P. In theoretical studies of quantum cryptography, it is however common to design and assess new protocols by assuming no-extra noise in Alice's and Bob's apparata (perfect state preparation and perfect detections).
This is an ideal scenario where system P of Fig. 2 is simply absent. For such ideal QKD protocols, the secret-key rates satisfy again equations (14), (15) and (16), computed on the corresponding output states. Remarkably, the discord bound can be found to be tight in reverse reconciliation. In fact, as we show in the Supplementary Information, we can have  in an ideal protocol of continuous-variable QKD, where Alice transmits part of an Einstein-Podolsky-Rosen (EPR) state over a pure-loss channel, such as an optical fiber.
in an ideal protocol of continuous-variable QKD, where Alice transmits part of an Einstein-Podolsky-Rosen (EPR) state over a pure-loss channel, such as an optical fiber.
Discussion
Quantum discord can be regarded as a bipartite formulation of non-orthogonality, therefore capturing the minimal requisite for QKD. In this paper we have identified the general framework, device-dependent QKD, where discord remains the ultimate cryptographic primitive able to guarantee security in the place of quantum entanglement. In this regard, our work is radically different from previous studies where security was based on the presence of entanglement, distillable or bound42.
We have considered a general form of device-dependent protocol, where Alice and Bob share a bipartite state which can be purified by two systems: One system (E) is accessible to Eve, while the other (P) is inaccessible and accounts from the presence of trusted noise, e.g., coming from imperfections in the state preparation and/or the quantum detections. This is a scenario where the optimal key rate may outperform the coherent information and key distribution may occur in the complete absence of entanglement (in any form, distillable or bound) as long as discord is non-zero. As a matter of fact, any prepare and measure QKD protocol whose security is based on non-orthogonal quantum states can be recast into an entanglement-free device-dependent form which is based on a classical-quantum state, with non-zero discord transmitted through the channel.
This discord-based representation is secure as long as the extra system P is truly inaccessible to Eve, i.e., Alice's and Bob's private spaces cannot be accessed. Such a condition fails assuming side-channel attacks, where no noise can be trusted and P becomes part of Eve's systems. In this case, the secret-key rates are again dominated by the coherent information, which means that quantum entanglement remains the crucial resource for device-independent QKD. For both device-independent QKD and ideal QKD (where system P is absent), discord still represents an upper bound to the optimal secret-key rates achievable in direct or reverse reconciliation, with non trivial cases where this bound becomes tight.
Note that, in our analysis, we have assumed a simplified scenario for device-independent QKD, which captures minimal requirements such as security and robustness against detector inefficiencies and imperfect preparations. This minimal or partial device-independent scheme is already sufficient to prove the necessity of quantum entanglement, which continues to be needed in more advanced formulations43. In our simplified scenario, Alice and Bob are able to reconstruct their shared state by comparing a subset of their outcomes. More generally, such state tomography could be not possible and the quantum measurements could be totally uncharacterised43.
In conclusion, quantum discord is a necessary resource for secure QKD. This is particularly evident in device-dependent QKD where entanglement is a sufficient but not a necessary resource. Entanglement becomes necessary in device-independent and ideal QKD, where discord still provides an upper bound to the secret-key rates. Future work may involve the derivation of a direct mathematical relation between the amount of quantum discord in Alice and Bob's output state and the optimal secret-key rates which are achievable in device-dependent QKD.
References
Wilde, M. M. Quantum Information Theory (Cambridge University Press, Cambridge, 2013).
Ekert, A. K. Quantum cryptography based on Bell's theorem. Phys. Rev. Lett. 67, 661 (1991).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895 (1993).
Shor, P. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 26, 1484–1509 (1997).
Ollivier, H. & Zurek, W. H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 88, 017901 (2001).
Henderson, L. & Vedral, V. Classical, quantum and total correlations. J. Phys. A 34, 6899 (2001).
Modi, K., Brodutch, A., Cable, H., Paterek, T. & Vedral, V. The classical-quantum boundary for correlations: discord and related measures. Rev. Mod. Phys. 84, 1655–1707 (2012).
Zurek, W. H. Quantum Discord and Maxwell's Demons. Phys. Rev. A 67, 012320 (2003).
Cavalcanti, D. et al. Operational interpretations of quantum discord. Phys. Rev. A 83, 032324 (2011).
Madhok, V. & Datta, A. Interpreting quantum discord through quantum state merging. Phys. Rev. A 83, 032323 (2011).
Dakic, B. et al. Quantum discord as resource for remote state preparation. Nature Phys. 8, 666–670 (2012).
Chuan, T. K. et al. Quantum discord bounds the amount of distributed entanglement. Phys. Rev. Lett. 109, 070501 (2012).
Gu, M. et al. Observing the operational significance of discord consumption. Nature Phys. 8, 671–675 (2012).
Weedbrook, C., Pirandola, S., Thompson, J., Vedral, V. & Gu, M. Discord Empowered Quantum Illumination. Preprint arXiv,1312.3332 (2013).
Piani, M., Horodecki, P. & Horodecki, R. No-Local-Broadcasting Theorem for Multipartite Quantum Correlations. Phys. Rev. Lett. 100, 090502 (2008).
Girolami, D., Tufarelli, T. & Adesso, G. Characterizing Nonclassical Correlations via Local Quantum Uncertainty. Phys. Rev. Lett. 110, 240402 (2013).
Adesso, A. Gaussian interferometric power. Phys. Rev. A 90, 022321 (2014).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum Cryptography. Rev. Mod. Phys. 74, 145 (2002).
Filip, R. Continuous-variable quantum key distribution with noisy coherent states. Phys. Rev. A 77, 022310 (2008).
Usenko, V. C. & Filip, R. Feasibility of continuous-variable quantum key distribution with noisy coherent states. Phys. Rev. A 81, 022318 (2010).
Weedbrook, C., Pirandola, S., Lloyd, S. & Ralph, T. C. Quantum Cryptography Approaching the Classical Limit. Phys. Rev. Lett. 105, 110501 (2010).
Weedbrook, C., Pirandola, S. & Ralph, T. C. Continuous-variable quantum key distribution using thermal states. Phys. Rev. A 86, 022318 (2012).
Weedbrook, C., Ottaviani, C. & Pirandola, S. Two-way quantum cryptography at different wavelengths. Phys. Rev. A 89, 012309 (2014).
Renner, R., Gisin, N. & Kraus, B. Information-theoretic security proof for quantum-key-distribution protocols. Phys. Rev. A 72, 012332 (2005).
Pirandola, S., García-Patrón, R., Braunstein, S. L. & Lloyd, S. Direct and Reverse Secret-Key Capacities of a Quantum Channel. Phys. Rev. Lett. 102, 050503 (2009).
Braunstein, S. L. & Pirandola, S. Side-Channel-Free Quantum Key Distribution. Phys. Rev. Lett. 108, 130502 (2012).
Acín, A. et al. Device-Independent Security of Quantum Cryptography against Collective Attacks. Phys. Rev. Lett. 98, 230501 (2007).
Pironio, S. et al. Device-independent quantum key distribution secure against collective attacks. New J. of Phys. 11, 045021 (2009).
Devetak, I. & Winter, A. Distilling Common Randomness From Bipartite Quantum States. IEEE Trans. Inform. Theory. 50, 3183 (2004).
Schumacher, B. & Nielsen, M. A. Quantum data processing and error correction. Phys. Rev. A 54, 2629 (1996).
Lloyd, S. Capacity of the noisy quantum channel. Phys. Rev. A 55, 1613 (1997).
Koashi, M. & Winter, A. Monogamy of quantum entanglement and other correlations. Phys. Rev. A 69, 022309 (2004).
Fanchini, F. F., Cornelio, M. F., de Oliveira, M. C. & Caldeira, A. O. Conservation law for distributed entanglement of formation and quantum discord. Phys. Rev. A 84, 012313 (2011).
Renner, R. Symmetry of large physical systems implies independence of subsystems. Nature Phys. 3, 645 (2007).
Renner, R. & Cirac, J. I. de Finetti Representation Theorem for Infinite-Dimensional Quantum Systems and Applications to Quantum Cryptography. Phys. Rev. Lett. 102, 110504 (2009).
Bennett, C. H. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 68, 3121–3124 (1992).
Pirandola, S. et al. High-rate quantum cryptography in untrusted networks. Preprint arXiv,1312.4104 (2013).
Devetak, I. & Winter, A. Relating Quantum Privacy and Quantum Coherence: An Operational Approach. Phys. Rev. Lett. 93, 080501 (2004).
Devetak, I. & Winter, A. Distillation of secret key and entanglement from quantum states. Proc. R. Soc. Lond. A 461, 207–235 (2005).
García-Patrón, R., Pirandola, S., Lloyd, S. & Shapiro, J. H. Reverse Coherent Information. Phys. Rev. Lett. 102, 210501 (2009).
Weedbrook, C. et al. Gaussian Quantum Information. Rev. Mod. Phys. 84, 621 (2012).
Horodecki, K., Horodecki, M., Horodecki, P. & Oppenheim, J. Secure Key from Bound Entanglement. Phys. Rev. Lett. 94, 160502 (2005).
Brunner, N., Cavalcanti, D., Pironio, S., Scarani, V. & Wehner, S. Bell Non-Locality. Rev. Mod. Phys. 86, 419 (2014).
Acknowledgements
S.P. was supported by a Leverhulme Trust research fellowship and EPSRC (grant no. EP/J00796X/1 and grant no. EP/L011298/1).
Author information
Authors and Affiliations
Ethics declarations
Competing interests
The author declares no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Pirandola, S. Quantum discord as a resource for quantum cryptography. Sci Rep 4, 6956 (2014). https://doi.org/10.1038/srep06956
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06956
This article is cited by
-
Visualizing sudden transition of decoherence via quantum steering ellipsoid
Applied Physics B (2024)
-
Global Quantum Discord and Entanglement in two Coupled Double Quantum Dots AlGaAs/GaAs
International Journal of Theoretical Physics (2023)
-
Quantum correlation dynamics of a three-qubit XXZ spin chain with spin–orbit coupling in the presence of intrinsic decoherence
Quantum Information Processing (2023)
-
Environment-assisted quantum discord in the chromophores network of light-harvesting complexes
Quantum Information Processing (2022)
-
The advantages of quantum dissonance under the environment effect
Quantum Information Processing (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.