Abstract
MoS2 is a layered two-dimensional material with strong spin-orbit coupling and long spin lifetime, which is promising for electronic and spintronic applications. However, because of its large band gap and small electron affinity, a considerable Schottky barrier exists between MoS2 and contact metal, hindering the further study of spin transport and spin injection in MoS2. Although substantial progress has been made in improving device performance, the existence of metal-semiconductor Schottky barrier has not yet been fully understood. Here, we investigate permalloy (Py) contacts to both multilayer and monolayer MoS2. Ohmic contact is developed between multilayer MoS2 and Py electrodes with a negative Schottky barrier, which yields a high field-effect mobility exceeding 55 cm2V−1s−1 at low temperature. Further, by applying back gate voltage and inserting different thickness of Al2O3 layer between the metal and monolayer MoS2, we have achieved a good tunability of the Schottky barrier height (down to zero). These results are important in improving the performance of MoS2 transistor devices; and it may pave the way to realize spin transport and spin injection in MoS2.
Similar content being viewed by others
Introduction
Molybdenum disulphide (MoS2) is a layered two-dimensional (2D) material, which draws intensive attention because of its unique electrical, optical and mechanical properties. It has been considered as a promising candidate for various future nanoelectronic and spintronic applications. It is a semiconductor with an indirect bandgap (1.2 eV) for its bulk material and a direct bandgap (1.8 eV) for monolayer MoS21,2,3,4,5,6. The presence of the direct bandgap in monolayer MoS2 allows room-temperature FETs with an on/off current ratio exceeding 1087. Studies also point out that MoS2 could be used in sensors8 or for photoluminescence9 applications. The spin transport properties were theoretically predicted with a spin diffusion length of 400 nm at room temperature and it becomes longer than 800 nm at low temperature (T < 77 K)10. Because of the semiconducting nature, the contacts between MoS2 and metal electrodes naturally forms Schottky barriers, which plays a crucial role in spin transport. To cope with this problem, theorists proposed that titanium is a suitable electrode material because of favorable geometry and large electronic density of state at the interface11. And experimentalists found that devices with scandium electrodes have very good performance because of low metal work function12. However, until now there is not much research on the ferromagnetic contact with MoS213,14, which may lead to the reduced conductance mismatch and the enhanced spin polarization.
In this letter, we study the contact between MoS2 and ferromagnetic permalloy (Py) electrodes. The Schottky barrier height (SBH) is extracted by 2D thermionic emission theory13,15. For multilayer MoS2, we observed a barrier height of −5.7 mV. This negative Schottky barrier leads to a perfect Ohmic contact between MoS2 and Py electrodes which dramatically enhances the field effect transistor (FET) performance of MoS2: the mobility of multilayer MoS2 with a single back gate reaches 55 cm2 V−1s−1 at low temperature. For monolayer MoS2, the SBH has a positive value, which can be readily tuned by both back gate voltage and by the insertion of an Al2O3 tunneling layer. When inserting 2.5 nm Al2O3, the SBH is reduced from 80.2 to 2.7 mV; by applying a back gate voltage of 30 V on the samples without Al2O3, the SBH is reduced to −8.3 mV. These two approaches of tuning the barrier height are important for realizing spin injection into monolayer MoS2.
Results
Structure of the FET devices and method for extracting SBH
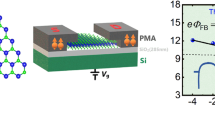
A schematic diagram of our devices is shown in Figure 1a. Electrode on Si substrate is used as a back gate to tune Fermi level and carrier density. Figure 1b shows a scanning electron microscopy (SEM) picture of the device. The channel length of the device is 2 μm and the width of exfoliated MoS2 is about 4 μm. The channel material is verified to be tri-layer MoS2 by a Raman spectrum16 as shown in Figure 1c. The devices were characterized by two-probe I-V measurement for Schottky barrier height and by ID-VG measurement for mobility.
(a) A schematic diagram of the device. Py electrodes are covered by Au to prevent oxidation. (b) A SEM image of the multilayer MoS2 device. All the data are measured from electrode 1 and 2. (c) A Raman spectrum of the multilayer MoS2. It is estimated to be a tri-layer MoS2 through the distance of ~22.5 cm−1 between two vibrating modes (in-plane mode E12g and out-of-plane mode A1g)16. (d) A band diagram of Py and MoS2. EF of Py is close to EC of the tri-layer MoS2.
The forward I-V characteristics of an ideal Schottky diode can be described as follows17:

where

Is is the diode saturation current, A is the Richardson constant, S is the contact area of junction, q is the electron charge, ΦB is the Schottky barrier height and kB is the Boltzmann constant. As the device is thin enough to be treated as a 2D material, the drain-source current IDS can be defined by 2D thermionic emission equation18, which employs the reduced power law T3/2 for a 2D transport channel:

where A*2D is the 2D equivalent Richardson constant, n is the ideality factor and VDS is the drain-source bias voltage. To determine the Schottky barrier height ΦB, temperature dependent I-V measurements were carried out. Figure 2a shows the I-V curves at several temperatures on a logarithmic scale. To investigate the barrier, it is common to use Arrhenius plot, i.e., ln(IDS/T3/2) against 1000/T for various VDS in Figure 2b. By fitting the data to each VDS, we obtained the slopes with  . Then by plotting the slopes as a function of VDS, the SBH could be extracted from the y-intercept
. Then by plotting the slopes as a function of VDS, the SBH could be extracted from the y-intercept  (Figure 2c).
(Figure 2c).
(a) I-V curves of the tri-layer MoS2 FET device with Py directly contacting to MoS2 from T = 100 to 200 K. (b) Arrhenius plot ln(IDS/T3/2) vs 1000/T at different drain-source voltages (VDS). (c) Extraction of ΦB via the y-intercept value. Each data point here represents the slope obtained from the Arrhenius plot in (b) under a specific VDS. (d) A band diagram showing a negative Schottky barrier.
Schottky barrier height between Py and tri-layer MoS2
For our tri-layer MoS2 transistor device, ΦB is found to be −5.7 mV in the temperature regime of 100 ~ 200 K. Such a negative Schottky barrier produces a good Ohmic contact with a perfect linear I-V curve between MoS2 and Py electrodes (Figure S1). Similar results were also reported in p-type MoS2 transistors with MoOx electrodes19. According to the Schottky-Mott model20, we could roughly estimate the SBH based on the work function of the metal Φmetal relative to the electron affinity (or vacuum ionization energy) of the semiconductor χsemi:

The negative Schottky barrier suggests that the work function of Py is slightly smaller than the affinity of MoS2, as shown in Figure 1d.
To investigate the FET performance, we have performed temperature-dependent ID-VG measurements. Figure 3a shows typical gate-dependent conductance curves at different temperatures and Figure 3b displays the temperature-dependent conductance under different gate voltage. It is noted that when applying a small back gate voltage (VG < 35 V), the channel tri-layer MoS2 shows an insulating behavior that the conductance decreases as temperature decreases. While VG > 35 V the conductance increases as temperature decreases. This is a hallmark of metallic behavior which suggests that the tri-layer MoS2 has entered a metallic state.
(a) Conductance G as a function of VG at different temperatures for the tri-layer MoS2 device. (b) Temperature dependence of G at different VG. When VG < 35 V the G-T curve shows an insulating behavior while VG > 35 V it becomes metallic. (c) Mobility as function of temperature under different VDS. μFET is independent of T when T < 10 K, while above ~30 K μFET decreases following a T−γ dependence with γ = 0.56 ~ 0.66.
The field effect mobility can be calculated from the linear regime (40 ~ 50 V) of conductance curves using the following expression21:

where dG/dVG is the slope of the conductance curve in the linear regime, L = 2 μm is the channel length, W = 4 μm is channel width and Cox = 1.3 × 10−4 F m−2 is the capacitance between the channel and the back gate per unit area (Cox = ε0εr/d; εr = 3.9; d = 270 nm). Figure 3c shows the extracted mobility as a function of temperature under different drain-source voltage. The mobility is nearly independent of temperature when T < 20 K, indicating that the scattering of charged impurities is reduced by drain-source voltage22,23. At higher temperatures (T > 100 K), the mobility of the tri-layer MoS2 is mainly influenced by the phonon scattering23,24. Fitting to the expression μ ~ T−r, the range of exponent part γ can be obtained between 0.47 and 0.66. This value is much smaller than the theoretical prediction, i.e., γ = 1.69 for single-layer MoS225 or γ = 2.6 for bulk crystals26, indicative of a weak electron-phonon interaction20. The mobility of our tri-layer MoS2 exceeds 55 cm2V−1s−1, which is a comparatively high value for single back gate MoS2 transistor devices. As the Schottky barrier can significantly impact the electron mobility12, the high mobility of our device also provides a strong evidence of a low SBH between Py and tri-layer MoS2.
Schottky barrier height between Py and monolayer MoS2
Different from the tri-layer, the SBH between Py and the monolayer MoS2 turns out to be 80.2 mV (Figure 4d). This can be understood by the fact that the monolayer MoS2 has a large bandgap of 1.8 eV and consequently it has a smaller electron affinity4. Thus, the increase of Schottky barrier height in the monolayer system is consistent with the Schottky-Mott model (Equation 4), i.e., for the same metal work function, when the vacuum affinity decreases, the Schottky barrier height increases.
(a–c) Arrhenius plot of monolayer MoS2 with Py electrodes in a large temperature range. A back gate voltage of VG = 0 V, 10 and 20 V was applied to the device as shown in (a), (b) and (c), respectively. (d) Schottky barrier height ΦB as a function of VG. The insets show the band diagram of Schottky barrier between Py and monolayer MoS2.
However, great caution must be exercised when the Arrhenius plot is used to extract SBH. The data in Figure 4Figure 4a are not completely linear for the entire temperature range. In the high temperature regime (T > 130 K), the data show negative slopes, corresponding to the positive SBH. At low temperatures, however, ln(IDS/T3/2) versus 1000/T has positive correlations, suggesting negative SBH. These fitted results are contradictory to the observation of “S” shape I-V curves at low temperatures (Figure S2), which are strong evidence of positive Schottky barriers. To explain this contradiction, one needs to take the semiconducting nature of MoS2 into consideration. As the temperature decreases, the resistivity of monolayer MoS2 increases and the device reaches an “off” state. It is well known that at the off state the channel resistance is too large that the current does not change much with temperature20. Thus, the thermionic emission equation is no longer suitable to describe the current. With this limitation, the SBH could only be extracted in the high temperature regime (above the turning points) using 2D thermionic emission equation, while the “V” shaped turning point in the Arrhenius plot represents the entrance of device “off” state.
To investigate the tunability of the Schottky barrier, we have performed the gate-dependent I-V measurements (Figure 4a–c). When VG = 0 V, the turning point is about 130 K. As the voltage is increased to 10 and 20 V, the turning point shifts to 20 and 8 K, respectively. Further increasing the gate voltage (up to 30 V) makes the turning point completely vanished (Figure S3). For traditional field effect transistors, the channel conductance can be tuned by gate voltage. When VG > 0 V, the conduction channel is broadened such that it needs a much lower temperature to turn the device off, which explains the systematic shift of the turning point. Figure 4d summarizes the SBH as a function of VG: the SBH is reduced to 20.4, 1.1 and −8.3 mV when VG changes from 10, 20 to 30 V, respectively. This is attributed to the upwards shift of Py Fermi level by positive gate voltage (Figure 4d inset)27.
For the spin injection into monolayer MoS2, the contact between ferromagnetic metal and semiconductor is crucial28. The spin polarization of injected carriers through Ohmic contact is extremely small due to the conductance mismatch13. In order to alleviate this issue, the resistance-area (RA) product should be designed properly to obtain a significant spin polarization and magnetoresistance29. In conventional 3D semiconductors, the Schottky barrier can provide the required resistance30, but the surface doping is needed to facilitate single step tunneling31. Another approach to obtain the proper RA product is to achieve a pinning-free FM/Oxide/SC interface by inserting a tunneling oxide layer, which could lower the SBH and the resistance could be tuned by the thickness of the oxide layer. Here we choose Al2O3 as the tunneling oxide layer, which is well known for high spin injection efficiency and large tunneling magnetoresistance in magnetic tunnel junctions32,33,34,35,36,37.
Similar to the back gate voltage, the insertion of Al2O3 layer also causes the “V” shaped turning point in the Arrhenius plot to shift towards lower temperatures (Figure 5a–c). When the thickness of Al is 0.8, 1.7 and 2.5 nm, the turning point shifts to 40, 25 and 10 K respectively. This can be explained by the reduction of conductance mismatch38 (or reduced SBH) between the electrodes and monolayer MoS2 as Al2O3 thickness increases. For that reason, the shift of the turning point could be regarded as an evidence of the alleviation of conductance mismatch with the inserted Al2O3 layer. The corresponding SBH is extracted to be 32.1, 15.9 and 2.7 mV (Figure 5d), respectively. Such a dramatic decrease shows an effective control of the SBH via changing the thickness of oxide layer. By the combination of applying a gate voltage and inserting an Al2O3 layer, we could minimize the conductance mismatch and tune the Schottky barrier height down to zero, which may help to achieve the proper RA product.
(a–c) Arrhenius plot of monolayer MoS2 with different thickness of Al2O3 inserted. Al2O3 thickness is 0.8, 1.7 and 2.5 nm in (a), (b) and (c), respectively. (d) Schottky barrier height ΦB as a function of the Al2O3 thickness. The inset shows the band diagram of Schottky barrier when inserting the Al2O3 tunneling layer.
Discussion
In conclusion, we have investigated the properties of MoS2 FET with ferromagnetic Py electrodes; the Schottky barrier height is extracted using 2D thermionic emission analysis of I-V curves. For the tri-layer MoS2, there is a negative Schottky barrier between Py and MoS2 and this Ohmic contact yields a high mobility due to low contact resistance. For the monolayer MoS2, there is a positive Schottky barrier, which is dramatically reduced either by applying a gate voltage or inserting a tunneling Al2O3 layer. To some extent, the insertion of Al2O3 layer also alleviates the conductance mismatch. Such control of Schottky barrier paves the way of proper design of the RA product, which sheds light on the future research of spin transport and spin injections in MoS2.
Experimental Section
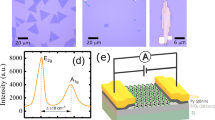
Multilayer MoS2 is obtained through mechanical exfoliation from bulk MoS2 crystals onto pre-patterned SiO2/Si substrate (the thickness of SiO2 is 270 nm). FET devices were fabricated by e-beam lithography (EBL) using PMMA/MMA bilayer polymer. Subsequently, Py electrodes are deposited by magnetron sputtering, followed by a deposition of gold layer to protect Py from oxidation. All the data are measured from electrode 1 and 2 in Figure 1b. For the monolayer transistors, MoS2 is obtained via chemical vapor deposition (CVD) using high purity molybdenum and sulphur as the source materials, similar to the previous report39. After growth, they were transferred onto clean SiO2/Si substrate for the following EBL process using PMMA stamping method40. The tunneling Al2O3 layer was produced as follows: first a thin layer of Al was deposited by e-beam evaporation (the SEM picture in Figure S4 shows a high-quality Al layer without visible pinholes). Then the samples were placed in the air overnight for natural oxidation to develop Al2O3. The thickness of Al2O3 can be estimated by  41. Before measurement, the devices were annealed at 360 K for two hours in vacuum to remove polymer residues between the interface of Py and MoS242,43.
41. Before measurement, the devices were annealed at 360 K for two hours in vacuum to remove polymer residues between the interface of Py and MoS242,43.
References
Han, S. W. et al. Band-gap transition induced by interlayer van der Waals interaction in MoS_{2}. Phys. Rev. B 84 (2011).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically Thin MoS_{2}: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 105 (2010).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010).
Lee, H. S. et al. MoS(2) nanosheet phototransistors with thickness-modulated optical energy gap. Nano Lett. 12, 3695–3700 (2012).
Lebègue, S. & Eriksson, O. Electronic structure of two-dimensional crystals from ab initio theory. Phys. Rev. B 79 (2009).
Kuc, A., Zibouche, N. & Heine, T. Influence of quantum confinement on the electronic structure of the transition metal sulfide TS_{2}. Phys. Rev. B 83 (2011).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 6, 147–150 (2011).
Yin, Z. et al. Single-layer MoS2 phototransistors. ACS nano 6, 74–80 (2011).
Eda, G. et al. Photoluminescence from chemically exfoliated MoS2. Nano Lett. 11, 5111–5116 (2011).
Bishnoi, B. & Ghosh, B. Spin transport in monolayer molybdenum disulfide (MoS2). J. Comput. Electron. (2013).
Popov, I., Seifert, G. & Tománek, D. Designing Electrical Contacts to MoS_{2} Monolayers: A Computational Study. Phys. Rev. Lett. 108, 156802 (2012).
Das, S., Chen, H. Y., Penumatcha, A. V. & Appenzeller, J. High performance multilayer MoS2 transistors with scandium contacts. Nano Lett. 13, 100–105 (2013).
Chen, J. R. et al. Control of Schottky Barriers in Single Layer MoS Transistors with Ferromagnetic Contacts. Nano Lett. (2013).
Dankert, A., Langouche, L., Kamalakar, M. V. & Dash, S. P. High-Performance Molybdenum Disulfide Field-Effect Transistors with Spin Tunnel Contacts. ACS nano 8, 476–482 (2014).
Tao, M., Udeshi, D., Agarwal, S., Maldonado, E. & Kirk, W. P. Negative Schottky barrier between titanium and n-type Si() for low-resistance ohmic contacts. Solid·State Electron. 48, 335–338 (2004).
Lee, Y. H. et al. Synthesis of large-area MoS2 atomic layers with chemical vapor deposition. Adv. Mater. 24, 2320–2325 (2012).
Bhuiyan, A., Martinez, A. & Esteve, D. A new Richardson plot for non-ideal schottky diodes. Thin Solid Films 161, 93–100 (1988).
Anwar, A., Nabet, B., Culp, J. & Castro, F. Effects of electron confinement on thermionic emission current in a modulation doped heterostructure. J. Appl. Phys. 85, 2663 (1999).
Chuang, S. et al. MoS2 P-type Transistors and Diodes Enabled by High Workfunction MoOx Contacts. Nano Lett. (2014).
Sze, S. M. & Ng, K. K. Physics of semiconductor devices. (John Wiley & Sons, 2006).
Fang, F. & Triebwasser, S. Effect of surface scattering on electron mobility in an inversion layer on p-type silicon. Appl. Phys. Lett. 4, 145 (1964).
Fang, F. & Fowler, A. Transport Properties of Electrons in Inverted Silicon Surfaces. Phys. Rev. 169, 619–631 (1968).
Radisavljevic, B. & Kis, A. Mobility engineering and a metal-insulator transition in monolayer MoS(2). Nat. Mater. 12, 815–820 (2013).
Ando, T. Electronic properties of two-dimensional systems. Rev. Mod. Phys. 54, 437–672 (1982).
Kaasbjerg, K., Thygesen, K. S. & Jacobsen, K. W. Phonon-limited mobility in n-type single-layer MoS_{2} from first principles. Phys. Rev. B 85 (2012).
Fivaz, R. & Mooser, E. Mobility of Charge Carriers in Semiconducting Layer Structures. Phys. Rev. 163, 743–755 (1967).
Xiu, F. et al. Manipulating surface states in topological insulator nanoribbons. Nat. Nanotechnol. 6, 216–221 (2011).
Fert, A. & Jaffrès, H. Conditions for efficient spin injection from a ferromagnetic metal into a semiconductor. Phys. Rev. B 64 (2001).
Min, B. C., Motohashi, K., Lodder, C. & Jansen, R. Tunable spin-tunnel contacts to silicon using low-work-function ferromagnets. Nat. Mater. 5, 817–822 (2006).
Hanbicki, A. T., Jonker, B. T., Itskos, G., Kioseoglou, G. & Petrou, A. Efficient electrical spin injection from a magnetic metal/tunnel barrier contact into a semiconductor. Appl. Phys. Lett. 80, 1240 (2002).
Zhou, Y. et al. Engineering of tunnel junctions for prospective spin injection in germanium. Appl. Phys. Lett. 94, 242104 (2009).
Meservey, R. & Tedrow, P. Spin-polarized electron tunneling. Phys. Rep. 238, 173–243 (1994).
van't Erve, O. M. J. et al. Comparison of Fe/Schottky and Fe/Al[sub 2]O[sub 3] tunnel barrier contacts for electrical spin injection into GaAs. Appl. Phys. Lett. 84, 4334 (2004).
Jain, A. et al. Electrical spin injection and detection at Al2O3/n-type germanium interface using three terminal geometry. Appl. Phys. Lett. 99, 162102 (2011).
Tran, M. et al. Enhancement of the Spin Accumulation at the Interface between a Spin-Polarized Tunnel Junction and a Semiconductor. Phys. Rev. Lett. 102 (2009).
Jonker, B. T., Kioseoglou, G., Hanbicki, A. T., Li, C. H. & Thompson, P. E. Electrical spin-injection into silicon from a ferromagnetic metal/tunnel barrier contact. Nat. Phys. 3, 542–546 (2007).
Dlubak, B. et al. Are Al[sub 2]O[sub 3] and MgO tunnel barriers suitable for spin injection in graphene? Appl. Phys. Lett. 97, 092502 (2010).
Datta, S. Electronic transport in mesoscopic systems. (Cambridge university press, 1997).
Zhan, Y., Liu, Z., Najmaei, S., Ajayan, P. M. & Lou, J. Large-area vapor-phase growth and characterization of MoS(2) atomic layers on a SiO(2) substrate. Small 8, 966–971 (2012).
Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 5, 722–726 (2010).
Dlubak, B. et al. Highly efficient spin transport in epitaxial graphene on SiC. Nat. Phys. 8, 557–561 (2012).
Tongay, S. et al. Tuning Interlayer Coupling in Large-Area Heterostructures with CVD-Grown MoS and WS Monolayers. Nano Lett. (2014).
Chen, J. J. et al. Layer-by-layer assembly of vertically conducting graphene devices. Nat. Commun. 4, 1921 (2013).
Acknowledgements
This work was supported by the National Young 1000 Talent Plan, Pujiang Talent Plan in Shanghai, National Natural Science Foundation of China (61322407) and the Chinese National Science Fund for Talent Training in Basic Science (J1103204). Part of the sample fabrication was performed at Fudan Nano-fabrication Laboratory.
Author information
Authors and Affiliations
Contributions
F.X. conceived the ideas and supervised the overall research. W.W. fabricated the devices and carried out the entire characterizations. Y.L. and T.Z. contributed to the sample preparation and measurement. L.T. and Y.J. provided the monolayer MoS2 and took the Raman spectrum. W.W. and F.X. wrote the paper. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Wang, W., Liu, Y., Tang, L. et al. Controllable Schottky Barriers between MoS2 and Permalloy. Sci Rep 4, 6928 (2014). https://doi.org/10.1038/srep06928
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06928
This article is cited by
-
Quantification of Schottky barrier height and contact resistance of a Au electrode on multilayer WSe2
Journal of the Korean Physical Society (2022)
-
Monolayer MoS2 field effect transistor with low Schottky barrier height with ferromagnetic metal contacts
Scientific Reports (2019)
-
Patterning metal contacts on monolayer MoS2 with vanishing Schottky barriers using thermal nanolithography
Nature Electronics (2019)
-
Ultra-high Photoresponsivity in Suspended Metal-Semiconductor-Metal Mesoscopic Multilayer MoS2 Broadband Detector from UV-to-IR with Low Schottky Barrier Contacts
Scientific Reports (2018)
-
Comparative study on interfacial properties of Mo, Nb, and W contacts with monolayer \(\hbox {MoS}_{2}\) MoS 2
Journal of Computational Electronics (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.