Introduction

DNA at elevated osmotic pressures, accessible in highly concentrated DNA solutions in vitro, exhibits a sequence of ordered liquid-crystalline mesophases1,2,3 whose properties determine the nature of high density DNA compaction also in the biological milieu characterized by similar DNA densities, bathing solution conditions and osmotic pressures. These biologically relevant examples of high density DNA compaction include most importantly DNA packing within virus capsids at osmotic pressures exceeding 60 atm and at densities within the regime of highly concentrated DNA solutions4,5,6,7,8. Moreover, in eukaryotic sperm cells, DNA is packaged by a variety of simple basic proteins with positively charged polypeptide chains9,10,11,12 that condense DNA as condensing agents do in solution conditions13,14. While the general outlines of the long-fragment (few microns long) DNA phase diagram seem to be properly characterized, with a well established progressive ordering sequence, isotropic → cholesteric → line hexatic → orthorhombic phases, many details including the fragment length dependence15 remain to be systematically investigated.

In this paper, we concentrate on the question of the organization and packing of genomic length DNA chains and parameterization of the forces governing their interactions at biologically relevant DNA densities and osmotic pressures. The two most important DNA liquid-crystalline phases at these densities are the line hexatic1 (LH) and the cholesteric16. The more ordered LH phase is observed at higher DNA densities, i.e., from approximately 300 mg/ml to 700 mg/ml, while the cholesteric phase then extends all the way to the isotropic phase, in which DNA is not ordered. In both the cholesteric and LH phases, DNA is locally oriented and positionally organized in a lattice with hexagonal bond orientational order17. However, while the bond orientational order in the cholesteric phase is short-range, it becomes macroscopic in the LH phase18, leading to the appearance of a sixfold azimuthally modulated x-ray diffraction intensity of the first-order diffraction peak when the chains are aligned parallel to the x-ray beam1. Previous work could not definitively address the question whether this change in the nature of order is continuous or not.

While for long-fragment DNA the positional order in both phases remains liquid-like, the range of ordering changes quantitatively as the system is pushed through the transition between these two phases. In what follows, we present evidence that the range of the bond orientational order and the nature of the local positional ordering change abruptly at the transition between these two phases, leading to a discontinuous jump in the DNA density and thus exhibiting the characteristics of a first-order transition. Furthermore, we note that the abrupt change in the radial widths of the first-order diffraction peaks, indicating the range of the positional order, occurs concurrently with the appearance of the sixfold azimuthal modulation of the first-order diffraction peak. A sharper well-defined peak seen in the LH phase indicates strong suppression of conformational fluctuations and the interaxial separation between the neighboring DNA chains changes discontinuously at the cholesteric → LH transition, signaling a discontinuous change also in DNA density, controlled and varied by the osmotic stress of the bathing solution19. In order to observe this discontinuous change induced by the solution osmotic pressure, separating a first-order from a second-order transition between these two mesophases, a very precise means of controlling the DNA density is needed, implying also an accurate tuning of the osmotic pressure of the DNA solution. The latter is accomplished by fine temperature tuning of the bathing solution and its osmotic pressure, as described below.

We address two important unresolved issues pertaining to the phase diagram of long-fragment DNA: (i) the nature and the ionic strength dependence of the cholesteric → LH phase transition and (ii) the connection between this DNA ordering transition in monovalent salts and the DNA condensation transition in polyvalent salts20. By using a new method of finely temperature-tuning the osmotic pressure, we thus find that the cholesteric → LH transition in monovalent salts is first order, just like the cholesteric → columnar hexagonal transition in short-fragment (≈50 nm long) DNA15, with a small but finite volume change. We also find a continuity of states, as opposed to the qualitatively different behavior usually invoked when comparing monovalent and polyvalent salt DNA solutions20, between this ordering transition in monovalent salts and the condensation transition induced by osmotic pressure at subcritical (i.e., CoHex) concentration. The elucidation of these features of the DNA phase diagram in various solution conditions is particularly important for the description of DNA packing in bacteriophage capsids4,5,6,7,8, occurring within the same range of DNA densities and osmotic pressures, as well as for understanding the long-range interactions that drive the DNA condensation in polyvalent salts. They have both been the subject of focused theoretical efforts21,22,23.

Ever since its discovery1,24, the nature of the cholesteric → LH transition has remained unresolved and was presumed to be either continuous (second order) or weak first-order with a small volume discontinuity. The implied caveat has always been that the available accuracy of osmotic pressure resolution does not allow for a definitive resolution of the order of the transition and that the absence of detectable density discontinuity in the equation of state should not be interpreted as a definitive evidence that the transition is second order. A distinct possibility would thus exist that there is an extremely narrow phase-coexistence window that can not be resolved by the osmotic stress method2. However, this phase-coexistence window, on the order of ~1–2Å interaxial spacing wide, has now been detected in monovalent salt DNA solutions through high resolution control of the osmotic pressure, based on its known temperature variation25. While not completely unexpected, the existence of this phase-coexistence window in monovalent salt solutions is nevertheless surprising. In fact, phase coexistence at finite osmotic pressures has been heretofore observed only in the case of DNA solutions with polyvalent counterions, e.g., with CoHex, or other condensing agents, when the polyvalent counterion concentration is below a critical value that would induce an immediate precipitation of DNA. In fact, at these subcritical polyvalent salt concentrations DNA condensation does not occur spontaneously but has to be induced by an additional solution osmotic pressure26 that then pushes DNA through a clearly detectable first-order expanded → condensed transition. If the concentration of the polyvalent salt is then increased above a critical value that depends on other solution parameters, DNA condenses spontaneously without any need for an additional osmotic pressure push from the solution. The ensuing DNA condensation transition then becomes second order.

We now connect the existence of the finite density jump for subcritical polyvalent salt solutions with a similar first-order cholesteric → LH transition in the case of monovalent (NaCl) salts. This effectively unifies the phase diagrams of DNA for mono- and polyvalent salts and allows us to describe quantitatively the whole regime of DNA equation of state, i.e., the osmotic pressures vs. density dependence, including the volume discontinuity at the cholesteric → LH for monovalent salts or expanded → condensed DNA transitions for polyvalent salts, with a simple empirical equation of state. It identifies a universal attractive interaction between DNA molecules, even in a monovalent (NaCl) salt, that probably stems from a structural adaptation of DNA helices to the strong interaxial hydration and/or electrostatic interactions at high densities. A picture showing more intimate connection between the nature of the positional, orientational and bond orientational order17,18,27 and the ensuing interaxial interactions between DNA double helices is thus clearly emerging. This change in perspective should be relevant also for understanding the high-density DNA packing in viruses4,5,6,7,8,28,29,30, where DNA is under high osmotic pressure/high density conditions identical to those studied in our experiments and on ejection driven by these osmotic stored forces undergoes a series of phase transitions7,8 directly related to those addressed in this work. Indeed, the osmotic pressures (≈60 atm)28,29 and the corresponding DNA interaxial spacings (≈26–27Å)31 are right in the regime studied in this manuscript.

The details of the organization of DNA and genome regulation processes in eukaryotic cells are beyond the scope of this study. Briefly, in eukaryotic cells, DNA is packaged in repeating units, a length of DNA (≈50 nm) wound around nucleosomal core particles which consist of positively charged histone proteins32. In this diffuse packaging, the DNA molecule and its genome is organized in a way that specific genes are still available for transcription. However, in the compaction of DNA in eukaryotic sperm cells, the histones are replaced with much simpler arginine-rich protamines that pack DNA into a highly condensed hexagonal lattice34, identical to DNA-protamine condensation in vitro14,33. The repeating unit of the hexagonal lattice consists of a length of DNA chain and an associated protamine polypeptide chain, as observed in x-ray diffraction of sperm chromatin34, with the polypeptide chain locked in the major groove of the DNA double helix so that the DNA charge is almost completely neutralized11,34,35,36. The volume occupied by DNA in the sperm cell is small compared with the volume of chromatin in somatic cells. The highly condensed, inactive state of the DNA in sperm nuclei confers additional protection against damage from the effects of mutagens and genotoxic factors37,38,39.

The study of highly concentrated DNA solutions is thus not only relevant from the fundamental biophysics point of view, but it also sheds light on the molecular mechanisms of DNA packing in bacteriophages and eukaryotic sperm cells. It also constrains possible mechanisms of gene delivery40 and illuminates fundamental physical principles that extend to other areas of condensed matter physics17,18.

Results

Our first significant observation is the abrupt change in the DNA density and order at the cholesteric → LH transition in NaCl solutions. The abrupt transition, from less-ordered cholesteric phase into the more-ordered LH phase, is evident in the x-ray diffraction behavior of unoriented26 and oriented41 long-fragment DNA samples. Higher-order peaks in the diffraction intensity profiles confirm hexagonal packing in the LH phase; hexagonal packing is assumed in the cholesteric phase. With our new experimental methodology of finely tuning the osmotic pressure (Π) of PEG solutions via temperature (T) variations25, the transitions are measured with high accuracy (see Fig. 1). From DNA samples in NaCl solutions at different [PEG] and T (but approximately the same Π), the same interaxial distance (dint) and full width at half-maximum (FWHM) are obtained. The impact of T (i.e., for 15°C ≤ T ≤ 45°C) on dint and FWHM is thus only through its effect on Π; changing T in the cases considered does not translate into a direct effect on the interactions between the DNA chains as is the case for, e.g., Mn2+ condensation42. This is evident in the data shown for [NaCl] = 0.1 M (see Fig. 1) and a large number of similar measurements under 0.05 M ≤ [NaCl] ≤ 0.4 M. We undertake further measurements of the cholesteric → LH transitions based on this fact (see Fig. 2).

Figure 1
figure 1

First-order peaks in the 1D x-ray diffraction intensity profiles of the DNA samples, when [NaCl] = 0.1 M, after a linear background is subtracted.

The 1D intensity profiles (i.e., I(q) vs. q) are obtained by radial integration of the intensity distributions in the 2D raw x-ray images of the samples. Intensity distributions are fitted (black lines) to either one Lorentzian in the cholesteric (blue) and LH (red) phases or the sum of two Lorentzians in the coexistence region (green). The procedure used for processing x-ray diffraction data and peak fits is described in detail elsewhere25. I(q) is the scattering intensity, with q being the scattering wave vector, i.e., q = (4π/λ)sin(θ/2), where θ is the scattering angle and λ is the x-ray wavelength. The interaxial distances between the neighboring DNA chains (dint) are determined from the peak positions (qmax) as , where dBragg = 2π/qmax. (a): First-order diffraction peaks when [PEG] = 20 wt%, 22 wt%, 25 wt%, 30 wt% and 40 wt% with temperature fixed at T = 40°C (with corresponding pressures Π = 5.3 atm, 6.7 atm, 9.5 atm, 15.6 atm and 38.3 atm)19,43 from left to right, respectively. At low pressures (Π = 5.3 atm and 6.7 atm), the DNA precipitate is in the cholesteric phase, where the full width at half-maximum (FWHM) of the first-order peak is (increases with increasing dint). Instrumental resolution and experimental error in the determination of FWHM of the first-order diffraction peaks are ≈0.001Å−1 FWHM and vary slightly with q. At high pressures (Π = 15.6 atm and 38.3 atm), DNA bundles are in the LH phase, which is characterized by a narrow first-order peak, i.e., (increases with decreasing dint). When Π = 9.5 atm, the narrow LH peak is superimposed with the broad cholesteric peak in the diffraction profile. The two distinct types of peaks coexist over a small range of Π, i.e., coexistence region. (b): Phase coexistence observed when [PEG] = 22 wt% and T = 30°C (with corresponding pressure Π = 7.7 atm). (c): Phase coexistence observed when [PEG] = 20 wt% and T = 15°C (with corresponding pressure Π = 7.4 atm).

Full size image
Figure 2
figure 2

Examples of the use of temperature variations for fine tuning the osmotic pressure to induce and measure the cholesteric → LH transitions.

(a), (b) and (c): [NaCl] = 0.1 M, 0.2 M and 0.3 M, respectively. In (b) and (c), the left and right axes show temperature variations and the corresponding osmotic pressures Π, respectively, when [PEG] = 20 wt%. It is clearly observed in the [NaCl] = 0.1 M data shown in (b) and (c) in Fig. 1 and a large number of similar measurements at various [NaCl] (i.e., for 0.05 M ≤ [NaCl] ≤ 0.4 M) that the only impact of T (i.e., for 15°C ≤ T ≤ 45°C) on the DNA-DNA interactions is through its effect on Π. Temperature does not have a detectable effect on the DNA-DNA interactions in the absence of CoHex over the range of osmotic pressures considered in this study. Under certain concentrations of CoHex, the effect of temperature on the DNA-DNA interactions is also negligible and we can use the same methodology for the fine-measuring of the cholesteric → LH transitions (see caption to Fig. 7). DNA samples are equilibrated at each temperature at least one hour before the measurements. Temperature is controlled before and during the measurements using a Peltier device. The biggest interaxial spacings in LH phase () are determined from x-ray diffraction profiles at the lowest pressures in the coexistence region. Cholesteric phase data points given here are from the diffraction profiles characterized by only the broad peak (without the narrow LH peak), i.e., cholesteric phase data are not shown in the coexistence region. In (a), temperature variations (right axes) and the corresponding pressures (left axis) are shown for two different [PEG], i.e., [PEG] = 20 wt% (blue solid circles) and [PEG] = 22 wt% (purple right-facing triangles). The two right axes in (a) showing the temperature variations are for [PEG] = 20 wt% and [PEG] = 22 wt% from left to right, respectively. As explained in the text (see also the caption to Fig. 1), the variations of dint and FWHM with pressure are independent of temperature for all [NaCl]. Note that (a) is adapted from ref. 25.

Full size image

In the cholesteric phase, there is a broad first-order x-ray diffraction peak (see Fig. 1). Upon increasing Π, at the cholesteric → LH transition, the diffraction intensity profile changes abruptly and a sharp peak (with FWHM approximately 5 times bigger than the instrumental resolution) is superimposed on the broad cholesteric peak. In addition, oriented DNA samples, with the helical axis parallel to the x-ray beam, give sixfold symmetric first-order diffraction peaks in the LH phase, indicating macroscopic bond orientational order1 perpendicular to the local axis of the molecules. Disorder in the packing increases with increasing DNA density in the LH phase (see Fig. 1), which points to the possibility of frustrated ordering at high densities27. After progressive disordering at high densities in LH phase, DNA eventually crystallizes through a LH → orthorhombic transition (discussed below) into an orthorhombic crystal. Conversely, in the cholesteric phase, we observed further broadening of the diffraction peak with decreasing DNA density. It is also worth emphasizing that in the cholesteric phase the diffraction peak width is sensitive to [NaCl] and increases with increasing [NaCl] at fixed DNA density (see Fig. 2).

We measured the osmotic pressure of DNA arrays via the osmotic stress method19,43,44. The osmotic pressure data Π vs. dint, for different [NaCl] are shown in Fig. 3. In order to parameterize in a simple way the experimentally determined dependence of the osmotic pressure on dint and ionic strength, we invoke a cylindrical cell model formulation of the linearized Poisson-Boltzmann theory45. This does not imply that this approximate theory can describe all the details of the DNA-DNA interaction appropriately. Nevertheless it serves the purpose of parsimoniously parameterizing a vast amount of data by intuitive effective parameters. In this simplified model, a molecule of radius a (≈10Å for B-DNA) is considered to be surrounded by a cylindrical cell of radius R = dint/2, yielding the electrostatic part of the osmotic pressure as

to the leading order. Here K0(x) and K1(x) are the cylindrical Bessel functions of the second kind. λD is the Debye length and , where σ is the effective surface charge density of DNA and is the dielectric permittivity of the medium ( is vacuum permittivity and for water). The effect of T on , over the range of temperatures used in the measurements, is small and can be ignored. For fully charged B-DNA, σ = e0/(2πab), where e0 is the elementary charge and b ≈ 1.7Å is the linear density of phosphates on the DNA. In LH phase, where conformational fluctuation effects are negligible, the net repulsion is equal to the bare interaction osmotic pressure, i.e., Π0(R) = Πh(R) + Πe(R). The hydration repulsion46, Πh(R), being the universal short-range component of the interactions, can be described phenomenologically by the same formalism as the electrostatic repulsion, with

LH phase data sets for each [NaCl] are fitted simultaneously to Π0. The common hydration repulsion parameters (Ah and λh) are enforced to be the same for all [NaCl]. The dependencies of Ae and Ah on dint were neglected, an approximation we discuss later. We simultaneously fitted different combinations of two out of four data sets. Ah and λh were linked for all [NaCl], while Ae was allowed to be different for different [NaCl]. In addition, for each [NaCl], the Debye decay length was allowed to vary within ±3% from its calculated value using , where I(M) is the molar ionic concentration. We found λh ≈ 2.2Å with an error ≈ 10% and then performed a global fitting with four data sets. In this step, λh was fixed at 2.2Å, while Ah and Ae were free parameters. Ah was linked for all [NaCl] and Ae was allowed to be different for different [NaCl]. In this way Ah = 1019 atm and Ae ≈ 155 atm, about the same for all [NaCl], with an uncertainty ≈ 10%. The results of the simultaneous fits of the LH phase data to Π0 are shown in Fig. 3 (see also SI for details). The treatment of the cholesteric and the LH phase data separately was missing in the available fits in the literature. In addition, the forms for the repulsions and the functions used in those fits are not identical to the forms used in this study. Nevertheless, it was already noted in the literature47 that the osmotic pressure data (i.e., Π vs. dint) at small interaxial separations vary exponentially with the decay length reported as 2 to 3Å. We stress again that the above forms of the electrostatic and the hydration part of the total interaction osmotic pressure should be seen as parsimonious empirical fits rather than attempts at a comprehensive theoretical description of the complicated DNA-DNA interactions that have been reviewed extensively in the literature21,22.

Figure 3
figure 3

Osmotic pressure data for different [NaCl], shown for .

Cholesteric phase data are shown with filled symbols while unfilled symbols represent LH phase data. At low pressures, DNA bundles are in the cholesteric phase. Cholesteric → LH transitions take place at transition pressures Πtr ≈ 7.4, 6.3, 6.0, 5.8 atm for [NaCl] = 0.1 (blue circles), 0.2 (red squares), 0.3 (green triangles), 0.4 M (brown inverted triangles), respectively with abrupt changes in dint (from to ) at the transition. Πtr, and do not vary significantly for [NaCl] ≥ 0.4 M. The interaxial separations and are given in the top axes for [NaCl] = 0.1, 0.2, 0.3, 0.4 M from bottom to top, respectively. Horizontal lines show the transitions. The overall error in the determination of the interaxial separations in the LH phase is about 0.1Å. The overall error in the cholesteric phase is bigger (as big as ≈0.2Å) due to the positional disorder and broadening of diffraction peaks. Upon increasing osmotic pressure in the LH phase, dint decreases monotonically and osmotic pressure curves for all [NaCl] converge. Here data are shown up to the pressure (Π ≈ 72 atm) where the differences between the measured dint for the given ionic conditions are ≈0.1Å, i.e., close to the uncertainty in the determination of dint. Therefore, in the fits of LH phase data to Π0, data from to dint ≈ 26Å are used. The dashed lines represent the fits for [NaCl] = 0.1, 0.2, 0.3, 0.4 M from top to bottom, respectively.

Full size image

The cholesteric phase of long DNA fragments, being less ordered, gives a broad x-ray diffraction peak with DNA chains fluctuating in their cylindrical cells, leading to positional disorder of the Bragg planes. The fluctuational free energy of DNA molecules is modulated by bare interactions with their neighbors and depends on their bending stiffness. It can be calculated from Frank's elastic free energy for polymer nematics48 by integrating out the Gaussian fluctuations around a straight configuration2. The fluctuational free energy per DNA chain (Ffl), at densities where fluctuations are prominent, is then obtained as

where the wavelength cutoff (i.e., qmax) takes into account the molecular size. Bb is the bare bulk compressibility modulus of the DNA cholesteric phase (relative change in the bare interaction pressure with changing cell area), i.e.,

K is the bending elastic constant defined as K = ρKc, where ρ is the 2D number density of DNA chains perpendicular to their helical axes and Kc = (kBT)Lp is the bending rigidity of a single DNA chain. We can ignore the effect of [NaCl] on the persistence length, Lp (≈500Å for B-DNA), as it is less than 5% for 0.1 M ≤ [NaCl] ≤ 0.4 M49,50. VDNA is the volume per DNA chain in the cylindrical cell model, i.e., VDNA = L(πR2), where L is the length of DNA chains. We replace qmax with a scaling prefactor (c) times the Brillouin zone (per DNA chain) radius, i.e., qmax → c × (π/dint), which is equivalent to replacing dint with an effective separation, deff = dint/c. Using the thermodynamic relation Π = −∂F/∂V, the osmotic pressure due to fluctuations is

with

when R and Bb are in units of Å and atm, respectively. The total repulsion in the cholesteric phase is described as Πcho(R) = Π0(R) + Πfl(R). The fits of the cholesteric phase osmotic pressure data to Πcho(R) (shown in Fig. 4) yield c ≈ 3. Calculations, fits and variations of Bb, Ffl, and Πfl with R for each [NaCl] are explained in detail in SI .

Figure 4
figure 4

Cholesteric phase data fits.

Colors, symbols and [NaCl] are the same as in Fig. 3. Dashed lines are the bare interaction pressures, Π0(dint), calculated using the parameters extracted from LH phase data fittings (see Fig. 3). Solid lines show the fits of the cholesteric phase data to Πcho(dint). Each data set for each [NaCl] is fitted individually and the prefactor c is extracted from the fits as given on top right for each [NaCl]. It is independent of the ionic strength, i.e., c ≈ 3. Horizontal lines show the transitions from cholesteric phase to LH phase.

Full size image

A discontinuous change in dint, i.e., from to , at the transition osmotic pressure Πtr for cholesteric → LH transition then results from the balance between the osmotic pressure in the cholesteric phase, Πcho, containing a strong fluctuation contribution and the osmotic pressure in the LH phase, composed of the bare repulsive interaction pressure Π0 plus an effective attractive component (Πea) viz. diminished repulsion, analogous to the interaction decomposition in the case of the van der Waals gas transition. The contribution of the conformational fluctuations to the osmotic pressure in the much stiffer LH phase is assumed to be nil. Πea increases with increasing [NaCl]. In addition, there is a common decay length at small interaxial distances, as can be discerned clearly in Fig. 5. We propose that the effective attraction follows the same form as the bare interaction repulsion, i.e., the sum of two terms accounting for the two interactions of different origin, with different characteristic decay lengths,

where and are proportional to λh and λD in Π0, respectively, i.e., and . The parameters , as well as fh, fe were determined from the fits of Πea vs. dint data to by further assuming f = fh = fe (see Fig. 5 and SI for details). The effective attractive component in the total osmotic pressure, , then yields a discontinuous first-order transition by the application of the standard Maxwell equal-area construction. We obtain a common for all [NaCl], with an uncertainty ≈ 10%. The parameter attributed to the electrostatic interactions for [NaCl] = 0.1, 0.2, 0.3, 0.4 M, respectively. The common short-range component suggests the structural adaptation of the DNA chains to hydration interactions at high densities. Furthermore, the variations of the magnitude and decay length of the effective attraction, as well as the variation of Πtr, with salt (as evidenced on Fig. 5) imply the contribution due to electrostatic effects.

Figure 5
figure 5

The application of the standard Maxwell equal-area construction in order to extract the effective attractive component Πea in the total osmotic pressure.

Colors, symbols and [NaCl] are the same as in Fig. 3. Top panel: Solid lines show the net repulsion with the fluctuation part, i.e., fits of the cholesteric phase data to Πcho(dint). They converge at high pressures. In the LH phase, there are no fluctuation effects and the net repulsion is equal to Π0(dint). Brown dashed line shows Π0(dint) for [NaCl] = 0.4 M in LH phase. Bottom panel: Thick colored lines show Πea(dint). Each line ends at due to the transition to the cholesteric phase, where Πatt = 0. From the simultaneous fits of Πea vs. dint data to (thin black dashed lines), we extract the decay length ratios, f = fh = fe ≈ 2.4 (see SI for the details).

Full size image

We proceed to thermodynamic analysis of the data. The change in the free energy per DNA chain (per unit length) upon changing the DNA density from cell radius R1 to R2 is

At the cholesteric → LH transitions, where the radius changes abruptly from to , the free energy change is

where is the change in the cell area across the transition. The change in the number of Na+ ions (per length) with the change in DNA cell radius, (ΔN/L), can be calculated using Maxwell cross relation, −(∂Π/∂μ) = (∂N/∂V), which with V = L(πR2) reduces to

where μ is the chemical potential of the salt, i.e., NaCl. The above relation implies that as the concentration of DNA varies due to the imposed osmotic pressure, the salt is taken up from the bulk reservoir and is redistributed within the DNA subphase, all the while keeping the full electroneutrality of the system. While the detailed nature of this redistribution cannot be derived without a microscopic model of the ionic atmosphere around the DNA molecule, the change in the number of salt ions in the DNA subphase would indicate that it is indeed taking place. In addition, we will show that most of the changes in the distribution of ions around DNA takes place within the cholesteric phase.

In what follows we assume that the chemical potential of the salt has the ideal form, i.e., μ = kBT log[NaCl]. While in the concentration range 0.1 M to 0.4 M the activity coefficient of NaCl is clearly not equal to 1 and its behavior is not ideal, the chemical potential of the salt appears only in derivative and thus only its changes are important. The change in the activity coefficient of NaCl over the range of concentrations used in our experiments is about 10%51 and the final effect of the assumption of ideality is less than other sources of error in the determination and analysis of the data.

We consider three regions separately in the analysis: (1) cholesteric phase (from R → ∞ to ); (2) cholesteric → LH transition region (from to ); (3) LH phase (from to R = R0). We calculate the change in the number of Na+ ions per DNA base pair, (ΔN/bp)C, (ΔN/bp)tr and (ΔN/bp)H, in regions (1), (2) and (3), respectively. Here R0 is the smallest cell radius in LH phase, with clearly discernible hexagonal symmetry in the x-ray diffraction pattern. For larger DNA densities the hexagonal symmetry is lost and the LH → orthorhombic transition ensues. Using the quadratic and line fits in Fig. 6 (see also SI for the details of the calculations), we find (ΔN/bp)H = 0.59, (ΔN/bp)tr = 0.01 and (ΔN/bp)C = 1.76 − 0.65 log[NaCl] with [NaCl] in mM.

Figure 6
figure 6

Calculated free energy per length, (W/L), vs. log[NaCl] in different regions of the phase diagram.

[NaCl] is in mM concentration units. (a): Cholesteric phase. (b): LH phase. (c): Cholesteric → LH transition. (d): From R → ∞ to R = R0. Black dashed curves are quadratic (a and d) and line (b and c) fits.

Full size image

These results suggest that the change in the number of Na+ ions in the DNA subphase is independent of [NaCl] at the transition and in the LH phase (discussed later). However, (ΔN/bp)C varies with [NaCl] and upon changing the DNA density from infinite dilution up to the cholesteric → LH transition, about 23%, 13%, 7% and 3% of the bare DNA charge is neutralized at [NaCl] = 0.1, 0.2, 0.3, 0.4 M, respectively, if we assume that of the salt ions taken up by the DNA subphase, Na+ ends up being located in close proximity to the DNA charges. There is thus a detectable difference in the number of Na+ ions near DNA phosphates under different [NaCl] at the infinite dilution limit and at a finite concentration in the cholesteric phase.

For short-fragment (≈50 nm long) DNA, in NaCl solutions, the hexagonal → orthorhombic transition occurs near DNA density corresponding to dint = 23.7Å15. Lindsay et al.52 showed that long Na-DNA fibers also go through a similar transition at around 90% relative humidity that, in addition, coincides with a B to A conformational transition of DNA with a helical pitch length change from ≈34Å for B-form to ≈29Å for A-form. In the orthorhombic phase the DNA density does not change anymore upon further drying52. Our osmotic stress experiments, in which the water content of DNA is accurately controlled and the corresponding osmotic pressures are known, indicate that on increase of the osmotic pressure in LH phase the first-order x-ray diffraction peak first broadens, followed by the LH → orthorhombic transition at Π ≈ 170 atm, characterized by the complete disappearance of the hexagonal symmetry of the scattering intensity (see Fig. 7).

Figure 7
figure 7

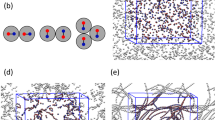
Osmotic pressure-induced transitions for different [CoHex] at [NaCl] = 0.3 M.

Horizontal dashed lines show the cholesteric → LH transitions. Horizontal solid lines show the LH → orthorhombic transitions. For [CoHex] = 3 mM (blue left-facing triangles) and [CoHex] = 12 mM (brown right-facing triangles), data are shown up to the pressure where dint is approximately 0.1Å bigger than the interaxial distance measured when [CoHex] = [CoHex]* = 28 mM (purple inverted triangles); above that they superimpose with [CoHex]* data. Black dashed curve (with jump at the transition) is the fit of [CoHex] = 0 (green trirangles) data to the total osmotic pressure. At less than [CoHex]*, the dependence of osmotic pressure on dint is slightly sensitive to temperature at low pressures () and [CoHex] = [CoHex]* data is shown only for T = 20°C. No detectable temperature dependence for other [CoHex] (see SI and ref. 25 for details) and the transitions can be measured with high accuracy using temperature variations. Insets: Typical x-ray images of oriented DNA bundles in LH phase with DNA helical axis parallel and perpendicular to the x-ray beam in (a) and (b), respectively. The sixfold symmetry in (a) shows the long-range bond orientational order in the LH phase. This symmetry does not exist in the x-ray images of DNA samples in the cholesteric phase. The twofold symmetry in (b) shows the parallel alignment of DNA chains. In the oriented sample preparations41, we align the bundles of DNA chains in the same direction in order to make macroscopically oriented samples so that 2D ordering of DNA chains can be seen in the x-ray images. The angular widths of the arcs are due to the mosaic spread in our samples.

Full size image

The order of the cholesteric → LH transition in NaCl solutions, together with its equation of state and the pertinent Maxwell equal-area construction, are relevant also for DNA condensation transition induced by osmotic pressure at subcritical CoHex concentrations (see Fig. 7). Obviously the subcritical condensation transition (i.e., abrupt change in the volume per base pair (vbp) and the ensuing collapse of DNA into a highly ordered structure, induced by osmotic pressure, in the presence of low concentrations of polyvalent salts) bears a striking similarity to the cholesteric → LH transition in NaCl solutions even in terms of the identical diffraction fingerprint. The cholesteric → LH transition thus exists also at subcritical [CoHex] in osmotic pressure-induced condensation of long DNA, i.e., for any [CoHex] ≤ [CoHex]*, where [CoHex]* is the minimum critical [CoHex] necessary for condensation at zero osmotic pressure. We find that [CoHex]* = 28 mM in [NaCl] = 0.3 M solutions. The osmotic pressure-induced transitions for [CoHex] = 0, [CoHex] = 3 mM and [CoHex] = 12 mM at [NaCl] = 0.3 M are shown in Fig. 7. With increasing [CoHex], Δvbp increases and Πtr decreases. The effective attraction leading to the first-order condensation transition, that can be deduced in the same way as in the monovalent salt case, increases with the addition of CoHex in the solution.

These results point to a continuity of thermodynamic states between the cholesteric → LH transition in monovalent salts and DNA polyvalent salt-induced condensation, frequently viewed as completely distinct phenomena. In fact, addition of CoHex (at subcritical concentrations) simply increases Δvbp at the cholesteric → LH transition already present in NaCl solutions. As the polyvalent salt concentration increases, the cholesteric branch density first moves to higher values, following the LH branch, but then eventually starts moving toward lower densities. At the critical concentration of the polyvalent salt, it moves out to infinity, i.e., the DNA condenses at zero external osmotic pressure. This last part of the polyvalent salt dependence is experimentally difficult to quantify53, but the existence of the condensation at zero imposed osmotic pressure indicates that indeed the cholesteric branch must recede to infinite dilution at the critical concentration.

Discussion

With increasing osmotic pressure, delicately controlled with small temperature variations25, DNA undergoes a transition from a less ordered fluctuating (cholesteric) state to a more ordered LH state with negligible conformational fluctuations. Changes in DNA density and packing at the cholesteric → LH transition are discontinuous, as observed in the x-ray scattering of long DNA fragments. We measured this transition with high accuracy and investigated its sensitivity to solution conditions. The sixfold symmetric azimuthal intensity profile of the first-order diffraction peak in the x-ray images of oriented DNA suggests that long-fragment DNA packs in a straight parallel untwisted arrangement in the LH phase, with long-range bond orientational order perpendicular to the axis of the molecules1,24. At the transition from the more ordered LH phase to the cholesteric phase, the sixfold azymuthal symmetry in the diffraction peak disappears; the vanishing of long-range bond orientational order and the abrupt change in DNA density occur simultaneously.

The osmotic pressure and inverse ionic strength dependence of the cholesteric → LH transition is similar to the pressure and temperature dependence of the gas-liquid transition, i.e., cholesteric → LH transition is shifted to higher osmotic pressures upon decreasing ionic strength of the solution. Furthermore, Δvbp at the cholesteric → LH transition decreases and DNA osmotic pressure curves become progressively more flat around the transition region with decreasing ionic strength. When [NaCl] = 50 mM (the smallest [NaCl] for which we measured the cholesteric → LH transition) and for the first-order x-ray diffraction peak is lost because of strong electrostatic repulsion. For this reason, [NaCl] = 50 mM data (available only for and shown in SI ) were not used in the simultaneous Πcho(dint) fits. For [NaCl] = 50 mM, the transition in fact occurs at Πtr = 9.7 atm and the abrupt change in the interaxial distance (Δdint) is 1.2Å ( and ). With increasing [NaCl], Πtr decreases and Δdint increases. For [NaCl] = 0.4 M, Πtr = 5.8 atm and Δdint = 2Å, they do not vary any more upon further increase in [NaCl].

The estimated value for the effective charge (see Eq. 1) from the simultaneous fits of LH phase data is ≈155 atm (approximately the same for all [NaCl], with an uncertainty ≈ 10%). For fully charged DNA chains, Ae would be approximately twice as large as what we extracted from the fits. If the parameter Ae is a measure of the net charge, then about half the bare DNA charge is neutralized in the LH phase. Conversely, if the net charge decreases with increasing (N/bp)H, then one would also expect Ae to decrease with increasing DNA density. The change in the number of Na+ ions from cholesteric → LH transition up to the LH → orthorhombic transition, is (ΔN/bp)H = 0.59 and is independent of [NaCl].

The fact that (ΔN/bp)H is independent of [NaCl] is instructive. Combined with the observation that the osmotic pressure curves converge at high pressures, it suggests that the number of salt ions per base pair is already the same for all [NaCl] at the cholesteric → LH transition and that the transition occurs when the net charge drops to a certain value. is zero in the cholesteric phase, i.e., when the net DNA charge is above a certain limit. Lee et.al.54 predict similar transitions of DNA in NaCl solutions and underline the role of structural adaptation of DNA helices to the interactions which is a function of ionic conditions and dint. Their theory predicts a ratio of ≈2 between the decay lengths for attractive and repulsive interactions21. In our experiments, the measured effective attraction Πea is approximately an order of magnitude smaller then the net repulsion in LH phase Π0. The magnitude of Πea is also sensitive to the ionic strength and decreases with decreasing [NaCl] (see Fig. 5). The ratio of the decay length of Πea to the decay length of Π0 is extracted by fitting the osmotic pressure data. The obtained factor f = fh = fe ≈ 2.4 is reasonable, although our analysis was based on several simplifying assumptions.

The emerging connection between the cholesteric → LH transition in univalent NaCl solution and the DNA condensation transition in the presence of polyvalent salts26, such as CoHex, at subcritical concentrations indicates a major change in DNA behavior in various solution conditions. We observe that osmotic pressure-induced DNA condensation at subcritical [CoHex] occurs in the same way as the cholesteric → LH transition in NaCl solutions. Our experiments now reveal that the osmotic pressure-induced condensation of long DNA indeed occurs at all polyvalent salt concentrations, for example at any [CoHex] ≤ [CoHex]*, where [CoHex]* is the minimum [CoHex] necessary for condensation at zero osmotic pressure. It depends also on the concentration of monovalent salt so that when [NaCl] = 0.3 M, [CoHex]* = 28 mM. With increasing [CoHex], Δvbp increases slightly and the transition pressure Πtr decreases. With the addition of CoHex to the bathing solution, the effective attraction therefore increases.

The general similarity between these two transitions therefore points to a continuity of thermodynamic states between the cholesteric → LH transition and the osmotic pressure-induced DNA condensation transition at subcritical [CoHex], thus bridging the gap between superficially distinctly different behaviors of DNA in monovalent and polyvalent salt bathing solutions.

Methods

Sample preparation and data collection

Oriented41 and unoriented25,26 DNA samples are prepared using calf thymus or salmon sperm DNA (molecular weight ≈ 107 Daltons). Oriented fibers are prepared by wet-spinning using the apparatus (designed by A. Rupprecht) in ILL (Grenoble, France). X-ray diffraction measurements are made using our in-house setup25 at UMass Amherst. Diffraction peak fits are done using IGOR Pro multi-peak fitting package. Brief explanations of x-ray diffraction data collection and analysis are given in the caption to Fig. 1. See also ref. 25 and SI for more details on sample preparations and data collection.

Osmotic pressure data

Temperature-dependent osmotic pressure data of PEG (molecular weight of 8000 Daltons) solutions are from ref. 19. Osmotic pressure decreases almost linearly with increasing T at constant [PEG] for 20°C ≤ T ≤ 40°C. The osmotic pressure of PEG, as well as the temperature dependence of the osmotic pressure of PEG, are not new. They have been described, analyzed and used for decades, being also extensively documented in various publications and reproduced by a variety of experimental methods (e.g., vapor pressure osmometer, membrane osmometer). In addition, the effect of salt on PEG activity (measured at room temperature by Wescor vapor pressure osmometer 5600) is insignificant at salt concentrations used in the experiments.

Cholesteric → LH transition measurements

The novel methodology used in this study takes advantage of the dependence of PEG (molecular weight of 8000 Daltons) osmotic pressure on temperature in order to achieve a heretofore unattained accuracy in fixing the value of this pressure. This enables also a much-improved accuracy in the determination of the equation of state of DNA (i.e., Π vs. dint), which reveals additional fine features of this equation of state that have been previously missed, enabling a deeper insight into the behavior of DNA at high concentrations. Note that using temperature to vary the osmotic pressure of the PEG solution in equilibrium with a DNA subphase is possible because under certain conditions, DNA-DNA interactions are almost independent of temperature over the range 15°C to 45°C. We therefore take advantage of the fact that temperature has no detectable effect on the DNA-DNA interactions to use it to accurately set the osmotic pressure of the DNA solution. The use of temperature variation methodology to measure the cholesteric → LH transitions is described briefly in the captions to Fig. 1 and Fig. 2. See also ref. 25 and SI for more details.