Abstract
We design a novel long-range hybrid wedge plasmonic (LRHWP) waveguide composed of two identical dielectric nanowires symmetrically placed on two opposed wedges of a diamond shaped metal wire. With strong coupling between the dielectric nanowire mode and long-range surface plasmon polariton (SPP) mode, both deep subwavelength mode confinement and low propagation loss are achieved. On one hand, when compared to the previous long-range hybrid SPP waveguide, LRHWP waveguide can achieve smaller mode size with similar propagation length; on the other hand, when compared to the previous hybrid wedge SPP waveguide, LRHWP waveguide can provide an order of magnitude longer propagation length with similar level of mode confinement. The designed LRHWP waveguide also features an overall advantage of one-order improvement of Figure of Merit. We further evaluate in detail the impacts of possible practical fabrication imperfections on the mode properties. The obtained results of mode properties show that the proposed LRHWP waveguide with an optimized wedge tip angle of 140 degree is fairly tolerant to practical fabrication errors in geometry parameters such as misalignment in the horizontal direction, asymmetry in the vertical direction, variation of wedge tip angle, tilt or rotation of metal wire and variation of wedge tip curvature radius.
Similar content being viewed by others
Introduction
Downscaling optical components and achieving high-integration density of optical devices remain major challenges in micro and nanotechnology. Surface plasmon polariton (SPP) waveguide can offer tight light confinement in deep subwavelength scale, which is regarded as one of the most promising candidates for future large-scale integrated optical circuits1,2. Compared to other types of well-known nanophotonic waveguides, e.g., silicon-on-isulator (SOI)3,4 and photonic crystals (PC)5, SPP waveguides can break the diffraction limit1,2,6 and lead to truly nanoscale light confinement. Many structures have been theoretically or experimentally studied, including metal slot SPP waveguides7,8,9,10, channel SPP waveguides11,12 and wedge SPP waveguides13,14,15,16. However, these waveguides also suffer huge propagation loss due to the ohmic loss17 introduced by the metal.
In general, mode confinement and attenuation are intrinsically correlated. In order to improve the trade-off between mode confinement and propagation loss, a hybrid plasmonic waveguide18 consisting of a cylindrical dielectric nanowire on a metal surface is proposed, which is able to provide tight mode confinement with moderate loss. After that, hybrid plasmonic waveguides have been hotly studied and several structures have been proposed19,20,21,22,23,24. The interaction between dielectric waveguide mode and pure SPP mode leads to longer propagation length while maintaining relatively-small mode size.
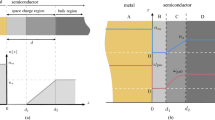
Recently, in order to further improve either the propagation length or the mode confinement, two attractive structures have been presented. On one hand, in order to extend the propagation length, as shown in Fig. 1(b), long-range hybrid SPP, i.e. a structure with two symmetrically placed nanowires on two sides of a flat metal film is proposed25,26. The coupling of traditional long-range SPP mode27 and dielectric cylinder mode can achieve similar level mode confinement to a hybrid SPP but offer one-order of magnitude longer propagation length25,26. On the other hand, in order to further shrink the mode size, as shown in Fig. 1(c), a hybrid wedge SPP waveguide is proposed by employing a triangular metal wedge instead of a flat metal surface28. The use of metal wedge enables a stronger mode confinement with the same level of propagation length. Remarkably, long-range hybrid SPP waveguide25,26 (Fig. 1(b)) and the hybrid wedge SPP waveguide28 (Fig. 1(c)) separately improve the propagation length and mode confinement compared to the hybrid SPP waveguide (Fig. 1(a)). One further laudable goal would be to simultaneously reduce the mode size and increase the propagation length.
In this paper, we combine the advantages of hybrid SPP, long-range SPP and wedge SPP and bring forward a long-range hybrid wedge SPP waveguide, which is also called long-range hybrid wedge plasmonic (LRHWP) waveguide. Compared with the previous long-range hybrid SPP waveguide and hybrid wedge SPP waveguide, the LRHWP waveguide can provide either reduced mode area or increased propagation length. Moreover, one-order improvement of figure of merit is achieved. Practical fabrication issues (i.e. fabrication error tolerance) of the designed LRHWP waveguide are also analyzed in detail.
Results
Waveguide structures and mode properties
Figure 1 illustrates the structures of the waveguides mentioned above (hybrid SPP waveguide, long-range hybrid SPP waveguide and hybrid wedge SPP waveguide) and the designed LRHWP waveguide, showing how we come up with the idea. In the proposed LRHWP waveguide (shown in Fig. 1(d)), two identical cylindrical Si nanowires with a diameter of d are placed on two opposed wedges of a diamond shaped metal wire with a small gap distance of h and the wedge tip angle is θ (0 < θ < 180 deg). The surrounding low-index dielectric layer is SiO2 and the metal wire is silver with a fixed cross section area of 1200 nm2. In the simulations, we choose the working wavelength at 1550 nm. The permittivities of Si, SiO2 and silver are εd = 12.25, εc = 2.25 and εm = −129 + 3.3i at 1550 nm29, respectively. The mesh size in the Si nanowire, metal wire, gap region and SiO2 cladding are set to be 50 nm, 10 nm, 1 nm and 500 nm, respectively. The mode distribution and normalized power density along x = 0 for previous three kinds of waveguides are also illustrated in Fig. 1(a), (b) and (c).
The mode distribution and normalized power density for different wedge tip angles (140 deg, 100 deg, 60 deg and 20 deg) of the designed LRHWP waveguide are shown in Fig. 2. The cylinder diameter and gap thickness are set at 240 and 2 nm, respectively. One can see the tight mode confinement in the low-index gap together with expected long propagation length owing to the long-range SPP. Remarkably, as the gap thickness decreases further (i.e. h → 0), one can expect the reduction in the mode area to continue with the propagation distance, tending to that of a dielectric–metal interface, subject to constraints of non-local effects18.
We first compare the mode properties of the designed LRHWP waveguide with the previous long-range hybrid SPP waveguide. Figure 3(a) and (b) show the propagation length and normalized effective mode area (Aeff/A0) as gap thickness h varies from 2 to 18 nm. When θ = 140 deg, one can clearly see that the normalized effective mode area of the LRHWP waveguide is smaller while the propagation length is longer than the long-range hybrid SPP waveguide. Here the cylinder diameter d is set at 240 nm for both LRHWP waveguide and long-range hybrid SPP waveguide.
We then compare the mode properties of the proposed LRHWP waveguide with the previous hybrid wedge SPP waveguide. Figure 4(a) and (b) show the dependence of propagation length and normalized effective mode area (Aeff/A0) on the cylinder diameter d for the proposed LRHWP waveguide and previous hybrid wedge SPP waveguide. The wedge tip angle and gap thickness are set at 140 deg and 2 nm. One can clearly see that the proposed LRHWP waveguide can achieve more than one-order of magnitude longer propagation length than the previous hybrid wedge SPP waveguide, while the normalized effective mode area can keep on the same level.
Figure of Merit
We apply a unit-less figure of merit (FoM)30 to quantitatively compare the proposed LRHWP waveguide with previous long-range hybrid SPP waveguide and hybrid wedge SPP waveguide. The FoM can be an appropriate measurement for the trade-off between the propagation length and mode confinement.
We consider the case of small gap thickness with tight mode confinement. Figure 5(a) and (b) show the dependence of FoM for all three waveguides on the nanowire cylinder diameter d. The wedge tip angle is 140 deg for both hybrid wedge SPP waveguide and the proposed LRHWP waveguide. The gap thickness is set at 2 and 8 nm in Fig. 4(a) and (b), respectively. One can clearly see that, the proposed LRHWP waveguide is superior to the previous two kinds of SPP waveguides for its nearly one-order improvement of FoM compared to the previous long-range hybrid SPP waveguide and more than one-order improvement of FoM compared to the previous hybrid wedge SPP waveguide.
Fabrication method
The designed LRHWP waveguide can be regarded as the combination of two hybrid wedge SPP waveguides with the two metal wedges forming a diamond shaped metal wire. So it is straightforward that the proposed LRHWP waveguide could be fabricated following the fabrication methods used for hybrid wedge SPP waveguide28. To fabricate a hybrid wedge SPP waveguide, the focused-ion beam (FIB) technique could be used to form the metal wedge with high accuracy. After depositing a thin SiO2 layer on the wedge metal as the low-index gap, a Si nanowire which could be prepared by vapor-liquid-solid method31 is placed on the SiO2 layer above the metal wedge to form the hybrid wedge SPP waveguide. The Si nanowire is then covered by SiO2 cladding. After that, the hybrid wedge SPP waveguide is flipped. Similar procedures of FIB forming metal wedge, depositing SiO2 layer, placing Si nanowire and covering SiO2 cladding are followed to obtain a second hybrid wedge SPP waveguide, which is combined with the first hybrid wedge SPP waveguide to form the expected LRHWP waveguide.
Alternatively, a reverse step could also be considered to fabricate the hybrid wedge SPP waveguide. The Si nanowire is positioned on a SiO2 substrate and covered with SiO2 cladding first. The metal wedge will later be deposited after milling a V-shape groove in the upper SiO2 layer, which is similar to the fabrication process for the wedge plasmon polariton waveguides15. After that, FIB forming metal wedge, depositing SiO2 layer, placing Si nanowire and covering SiO2 cladding are followed to form the designed LRHWP waveguide.
Fabrication error tolerance
Considering the increased complexity of the designed LRHWP waveguide, we also analyze possible practical fabrication issues, i.e. fabrication error tolerance. While the size of the dielectric nanowire, the gap thickness and the metal wire could be controlled with high precision32, accurate alignment between the metal wire and the Si nanowire is not easy, asymmetric positioning of two Si nanowires with respect to the metal wire is possible, the wedge tip angle may slight change, the metal wire may tilt and deviate from the center point with a rotation angle and the curvature radius of the metal wedge tip may vary. Therefore, we further investigate in detail the impacts of these possible practical fabrication imperfections on the mode properties.
1) Misalignment in the horizontal direction
The deviation of Si nanowires from the metal wire might influence the mode properties. Figure 6(a) and (b) show that the proposed LRHWP waveguide suffers <6% fluctuation of propagation length and <4% variation of effective mode area Aeff under ±10 nm misalignment on one of the nanowires in the horizontal direction. Figure 7(a) and (b) show the case when both of the two nanowires deviate from the metal wire in the horizontal direction up to ±10 nm. When the wedge tip angle is 140 deg, the propagation length and effective mode area Aeff show less than 10% fluctuation.
2) Asymmetry in the vertical direction
The asymmetric positioning of two Si nanowires with respect to the metal wire, i.e. different thickness of upper and lower gap, might influence the mode properties. Figure 8(a) and (b) show the mode properties with one gap setting at 2 nm and the other gap varying from 2 nm to 12 nm. Slight fluctuation of propagation length is shown in Fig. 8(a). The effective mode area Aeff increases with the gap thickness as shown in Fig. 8(b). For a small variation of gap thickness from 2 nm to 4 nm, slight change is found for the effective mode area Aeff.
3) Variation of wedge tip angle
The variation of wedge tip angle might influence the mode properties. Figure 9(a) and (b) show the mode properties when varying the wedge tip angle from 135 deg to 145 deg, i.e. ±5 deg offset from 140 deg. The fluctuations of propagation length and effective mode area Aeff are less than 5% and 10%, respectively.
4) Tilt or rotation of metal wire
The metal wire may deviate from its center point with a rotation angle δθ, which might affect the mode properties. Figure 10(a) and (b) show the mode properties when tilting or rotating metal wire up to ±10 deg. The propagation length changes slightly as shown in Fig. 10(a). For the effective mode area Aeff, smaller wedge tip angle suffers severer fluctuation of Aeff. When the wedge tip angle is 140 deg, one can see slight variation under moderate tilt or rotation of metal wire.
5) Variation of wedge tip curvature radius
In practical fabrications, the wedge tip may not be sharp but round and the variation of tip curvature radius might also influence the mode properties. Figure 11(a) and (b) show the impacts of tip curvature radius on the mode properties. One can clearly see that LRHWP waveguide with small wedge tip angles (e.g. 20 deg, 60 deg) is sensitive to the tip curvature radius. Both propagation length and effective mode area Aeff increase with the tip curvature radius. In contrast, LRHWP waveguide with relatively large wedge tip angles (e.g. 100 deg, 140 deg) is tolerable to the tip curvature radius and slight variations of propagation length and effective mode area Aeff are found as changing the tip curvature radius.
The obtained results indicate that some of the fabrication errors in geometry parameters like misalignment in the horizontal direction, slight asymmetry in the vertical direction and variation of wedge tip angle around 140 deg have slight impacts on the mode properties (propagation length, effective mode area Aeff). Other fabrication errors like tilt or rotation of metal wire and variation of wedge tip curvature radius might cause variation of mode properties, especially for small wedge tip angles. Such impacts are greatly alleviated for relatively large wedge tip angles. Remarkably, the designed LRHWP waveguide with a wedge tip angle of 140 deg is fairly tolerant to all the above practical fabrication errors in geometry parameters.
Discussion
In summary, we have designed a novel LRHWP waveguide based on two identical cylindrical nanowires symmetrically placed on two opposed wedges of a diamond shaped metal wire. The combination of hybrid SPP, long-range SPP and wedge SPP provides the benefit of longer propagation length and similar mode size when compared with previous long-range hybrid SPP waveguide and hybrid wedge SPP waveguide. The optimized wedge tip angle of the proposed LRHWP waveguide is 140 deg. For such optimized LRHWP waveguide, on one hand, its propagation length is longer while its effective mode area is smaller than the long-range hybrid SPP waveguide; on the other hand, its propagation length is more than one-order longer than the hybrid wedge SPP waveguide while its effective mode area is in a similar level. These lead to one order of improvement for the figure of merit.
The proposed LRHWP waveguide combines the advantages of hybrid SPP, long-range SPP and wedge SPP. So there are similarities in the working principle between the designed LRHWP waveguide and existing hybrid SPP, long-range SPP and wedge SPP waveguides. A comprehensive interpretation on the operation mechanism of the LRHWP waveguide is as follows.
SPP is essentially light wave trapped on the interface between dielectric and metal as a result of the interaction between the light wave and free electrons of the metal. The electromagnetic fields of light wave cause in-resonance surface collective oscillations of free electrons. Such resonant interaction between light wave and surface charge oscillations forms SPP with its electric field component perpendicular to the surface peaking at the interface and decaying exponentially away into dielectric and metal. The electric field in the perpendicular direction is evanescent with non-radiative nature which prevents power from propagating away from the surface. In the dielectric, typically air or glass, the field decay length is on the order of half the light wavelength. In the metal, the field decay length into the metal is dependent on the skin depth. Hence, SPP waveguides can break the diffraction limit while pay the price of metal-induced huge propagation loss. Also, SPP waveguide with single metal-dielectric interface has no extra mode confinement in the dielectric side with more electric field penetration compared to the metal side.
SPP is one kind of surface science at the interface between a dielectric and a metal. Another kind of surface science is known as the discontinuity of electric field at the interface between high-contract-index dielectrics (one low-index dielectric and one high-index dielectric). Slot waveguide confining and guiding light in the low-index slot region is a typical example using surface science, i.e. two high-contrast-index dielectric-dielectric interfaces with a small spacing (low-index slot) form a slot waveguide with its electric field greatly enhanced in the low-index slot region4.
Hybrid SPP is another example using surface science, i.e. one high-contrast-index dielectric-dielectric interface and one metal-dielectric interface with a small spacing (nanoscale low-index dielectric) form a hybrid SPP or hybrid plasmonic waveguide. The discontinuity of electric field at the high-contrast-index dielectric-dielectric interface and the SPP at the metal-dielectric interface contribute together to the supermode which is greatly enhanced in the nanoscale low-index region. Such supermode, also called hybrid mode, features tight mode confinement with moderate propagation loss.
Long-range SPP is also an example using surface science, i.e. two metal-dielectric interfaces with a small spacing (thin metal film) form a long-range SPP waveguide. Typical long-range SPP waveguide structure with a thin metal film bounded by two symmetric dielectric claddings is also called a dielectric-metal-dielectric (DMD) structure. A DMD structure can support two kinds of supermodes with a thin metal film27, i.e. symmetric bound mode and asymmetric bound mode. The main transverse electric field component of the symmetric bound mode has a symmetric profile across the structure and therefore, the corresponding charge density distribution in the thin metal film is asymmetric over the metal thickness. Thus, the mode field is expelled from the metal film, i.e. less mode penetration into the metal while more mode penetration into the dielectric cladding. Consequently, the absorption loss of the symmetric bound mode is low with long propagation length, which is called long-range SPP mode. The property of the asymmetric bound mode is opposite to the symmetric bound mode. It suffers a high absorption loss with short propagation length, which is called short-range SPP mode.
Wedge SPP is one more example using surface science but the surface is shaped into a wedge, i.e. wedge-shaped metal-dielectric interface forms a wedge SPP waveguide. By exploiting the extraordinary confinement property of the wedge plasmon polariton at the corner of the wedge, even tighter mode confinement is achievable by using a wedge SPP waveguide.
Long-range hybrid SPP combines the ideas of hybrid SPP and long-range SPP and provides similar propagation length to long-range SPP together with similar mode confinement to hybrid SPP. Hybrid wedge SPP combines the ideas of hybrid SPP and wedge SPP and offers similar propagation length to hybrid SPP and similar mode confinement to wedge SPP. The proposed LRHWP waveguide can be regarded as the long-range hybrid SPP waveguide with its thin metal film replaced by a diamond shaped metal wire or two hybrid wedge SPP waveguides placed in reverse. It further combines the advantages of long-range hybrid SPP and hybrid wedge SPP and features similar propagation length to long-range hybrid SPP and similar mode confinement to hybrid wedge SPP. As a consequence, even longer propagation length and much tighter mode confinement are both achieved in the designed LRHWP waveguide. From SPP to hybrid SPP, long-range SPP, wedge SPP, long-range hybrid SPP, hybrid wedge SPP and finally LRHWP waveguide, the basic working mechanisms all rely on various surface sciences (SPP at dielectric-metal interface, electric field discontinuity at dielectric-dielectric interface, wedge dielectric-metal interface). The distinct supermode properties of LRHWP waveguide take all the advantages from SPP, hybrid SPP, long-range SPP, wedge SPP, long-range hybrid SPP and hybrid wedge SPP.
The designed LRHWP waveguide could be fabricated with existing mature nano-fabrication techniques as aforementioned. Although the size of the dielectric nanowire, the gap thickness and the metal wire could be fabricated with high precision, other practical fabrication issues are still challengeable such as the misalignment in the horizontal direction, asymmetry in the vertical direction, variation of wedge tip angle, tilt or rotation of metal wire and variation of wedge tip curvature radius. Fortunately, the detailed analyses of these geometry parameters indicate that proposed LRHWP waveguide features favorable fabrication error tolerance, especially at an optimized wedge tip angle of 140 deg.
Methods
The mode properties are investigated by means of the finite-element method (FEM) using COMSOL™ with the scattering bound condition and the simulation domain is surrounded by rectangular perfectly matched layer (PML).
Propagation length
The propagation length is given by

where Aeff is the effective refractive index.
Normalized effective mode area
The normalized effective mode area is defined by (Aeff/A0), where A0 is the diffraction-limited mode area and defined as λ2/4 and the effective mode area Aeff is caculated by17

where Wm and W(r) are the electromagnetic energy and energy density, respectively (per unit length along the direction of propagation).
Figure of merit
The figure of merit (FoM) is defined as the ratio of the propagation length to the diameter of effective mode area Aeff27

References
Barnes, W. L. et al. Surface plasmon subwavelength optics. Nature 424, 824–830 (2003).
Wang, J. A review of recent progress in plasmon-assisted nanophotonic devices. Front. Optoelectron. 7, 320–337 (2014).
Tsuchizawa, T. et al. Microphotonics devices based on silicon microfabrication technology. J. Sel. Top. Quantum. Electron. 11, 232–240 (2005).
Almeida, V. R. et al. Guiding and confining light in void nanostructure. Opt. Lett. 29, 1209–1211 (2004).
Thylén, L. et al. Photonic crystals–a step towards integrated circuits for photonics. ChemPhysChem. 5, 1268–1283 (2004).
Gramotnev, D. K. & Bozhelvonyi, S. I. Plasmonics beyond the diffraction limit. Nat. Photonics. 4, 83–91 (2010).
Veronis, G. & Fan, S. H. Guided subwavelength plasmonic mode supported by a slot in a thin metal film. Opt. Lett. 30, 3359–3361 (2005).
Pile, D. F. P. et al. Two-dimensionally localized modes of a nanoscale gap plasmon waveguide. Appl. Phys. Lett. 87, 261114 (2005).
Liu, L. et al. Novel surface plasmon waveguide for high integration. Opt. Express. 13, 6645–6650 (2005).
Dionne, J. A. et al. Plasmon slot waveguides: towards chip-scale propagation with subwavelength-scale localization. Phys.l Rev. B. 73, 035407 (2006).
Bozhevolnyi, S. I. et al. Channel plasmon subwavelength waveguide components including interferometers and ring resonators. Nature 440, 508–511 (2006).
Moreno, E. et al. Channel plasmon-polaritons: modal shape, dispersion and losses. Opt. Lett. 31, 3447–3449 (2006).
Pile, D. F. P. et al. Theoretical and experimental investigation of strongly localized plasmons on triangular metal wedges for subwavelength waveguiding. Appl. Phys. Lett. 87, 061106 (2005).
Moreno, E. et al. Guiding and focusing of electromagnetic fields with wedge plasmon polaritons. Phys. Rev. Lett. 100, 023901 (2008).
Boltasseva, A. et al. Triangular metal wedges for subwavelength plasmon-polariton guiding at telecom wavelengths. Opt. Express. 16, 5252–5260 (2008).
Ogawa, T. et al. Numerical and experimental investigation of wedge tip radius effect on wedge plasmons. J. Appl. Phys. 104, 033102 (2008).
Zia, R. et al. Geometries and materials for subwavelength surface plasmon modes. J. Opt. Soc. Am. A. 21, 2442–2446 (2004).
Oulton, R. F. et al. A hybrid plasmonic waveguide for subwavelength confinement and long-range propagation. Nat. Photonics. 2, 496–500 (2008).
Dai, D. X. & He, S. L. A silicon-based hybrid plasmonic waveguide with a metal cap for a nano-scale light confinement. Opt. Express. 17, 16646–16653 (2009).
Bian, Y. S. et al. Symmetric hybrid surface plasmon polariton waveguides for 3D photonic integration. Opt. Express. 17, 21320–21325 (2009).
Avrutsky, I. et al. Sub-wavelength plasmonic modes in a conductor-gap-dielectric system with a nanoscale gap. Opt. Express. 18, 348–363 (2010).
Bian, Y. S. et al. Dielectric-loaded surface plasmon polariton waveguide with a holey ridge for propagation-loss reduction and subwavelength mode confinement. Opt. Express. 18, 23756–23762 (2010).
Zhao, Y. S. & Zhu, L. Coaxial hybrid plasmonic nanowire waveguides. J. Opt. Soc. Am. B. 27, 1260–1265 (2010).
Xiang, C. et al. Proposal and numerical study of ultra-compact active hybrid plasmonic resonator for sub-wavelength lasing applications. Sci. Rep. 4, 3720 (2014).
Chen, L. et al. Novel hybrid plasmonic waveguide consisting of two identical dielectric nanowires symmetrically placed on each side of a thin metal film. Opt. Express. 20, 20535–20544 (2012).
Xiang, C. & Wang, J. Long-range hybrid plasmonic slot waveguide. IEEE Photon. J. 5, 4800311 (2013).
Berini, P. Long-range surface plasmon-polaritons. Adv. Opt. Photonics. 1, 484–588 (2009).
Bian, Y. et al. Hybrid wedge plasmon polariton waveguide with good fabrication-error-tolerance for ultra-deep-subwavelength mode confinement. Opt. Express. 19, 22417–22422 (2011).
Johnson, P. B. & Christy, R. W. Optical constants of the noble metals. Phys.l Rev. B. 6, 4370–4379 (1972).
Buckley, R. & Berini, P. Figures of merit for 2D surface plasmon waveguides and application to metal stripes. Opt. Express. 15, 12174–12182 (2007).
Kuykendall, T. et al. Crystallographic alignment of high-density gallium nitride nanowire arrays. Nat. Material. 3, 524–528 (2004).
Oulton, R. F. et al. Plasmon lasers at deep subwavelength scale. Nature 461, 629–632 (2009).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC) under grants 61222502, 11274131 and L1222026, the National Basic Research Program of China (973 Program) under grant 2014CB340004, the Program for New Century Excellent Talents in University (NCET-11-0182), the Wuhan Science and Technology Plan Project under grant 2014070404010201, the Fundamental Research Funds for the Central Universities (HUST) under grants 2012YQ008 and 2013ZZGH003 and the seed project of Wuhan National Laboratory for Optoelectronics (WNLO). The authors thank Chengcheng Gui and Chao Xiang for their helpful discussions.
Author information
Authors and Affiliations
Contributions
J.W. developed the concept and conceived the design. Z.Z. performed the numerical simulations. Z.Z. and J.W. analyzed the data. Z.Z. and J.W. contributed to writing and finalizing the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Zhang, Z., Wang, J. Long-range hybrid wedge plasmonic waveguide. Sci Rep 4, 6870 (2014). https://doi.org/10.1038/srep06870
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep06870
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.